PMSM电机Ld Lq参数测量方法
永磁同步电机极对数,内阻,Ld,Lq,背板电动势常数的测量(权威版)
1IntroductionThe vector control, also known as the field-oriented control (FOC), of a permanent magnet synchronous motor (PMSM) is the algorithm often used in today’s advanced motor control drives. Such advanced motor control algorithms require the setting of motor electrical parameters for its proper functionality. This application note deals with themeasurement of electrical parameters needed for vectorcontrol of PMSM. The electrical parameters are needed to set the current PI controller gains to get the desired closed-loop performance and for BEMF observer constants. The proposed measurement techniques determine a number of pole pairs, a stator resistance, synchronous inductances, and an electrical constant with common measurement equipment. A summary of PMSM sensorless control and explanation of motor control terms can be found in [1 ].2Motor parameters needed for PMSM FOCOne of the possible methods to set the PI controller gains, is to calculate them from motor parameters. The current PIcontroller gains in time domain are calculated from the motor electrical parameters [1]; see the following equations.Application NoteRev. 0, 02/2013PMSM Electrical Parameters Measurementby:Viktor Bobek© 2013 Freescale Semiconductor, Inc.Contents1Introduction................................................................12Motor parameters needed for PMSM FOC (13)Motor pole pairs........................................................33.1Background.....................................................33.2Guide.............................................................34Stator resistance.........................................................54.1Background.....................................................54.2Guide.............................................................55Synchronous inductances..........................................75.1Background.....................................................75.2Guide...........................................................116Back-EMF constant................................................126.1Background...................................................126.2Guide (13)7Conclusion...............................................................148References (149)Acronyms and Abbreviated Terms (15)Equation 1Equation 2Where ω0 is the natural frequency of the current closed-loop system (loop bandwidth) and ξ is the current loop attenuation.Therefore, the PMSM vector control algorithm typically requires the following parameters.The speed PI controller gains in time domain are calculated from the motor/load mechanical parameters; see Equation 1 on page 1 and Equation 2 on page 2Equation 3Equation 4Where ω0ω is the natural frequency of the speed closed-loop system (loop bandwidth) and ξ is the speed loop attenuation.Therefore, the PMSM vector control algorithm typically requires the following parameters.The measurement of individual electrical parameters is described in the following chapters of this application note.Motor pole pairs3.1BackgroundThe motor pole pairs parameter defines a ratio between mechanical and electrical quantities (mechanical vs electrical rotor position/speed). The motor pole pairs represent the number of north and south segments the rotor contains.3.2GuideThe equipment required to measure motor pole pairs depend on the method used for measurement.•DC power supply•Three-phase inverter, oscilloscope, hand velocity meter, and a current probe •Driving motor, oscilloscope and a voltage probeUsually, the number of the motor pole pairs is written on the label of the motor. If there is no information regarding the number of pole pairs, it can be determined. See the following subsections.3.2.1Method to determine low number of the pole pairsGuide : The following steps describe the method to determine the low number of motor pole pairs. See Figure 1.1.Connect the phase A wire to the positive potential (+) and phase B and C to negative potential (-) of the voltage source.2.Set a current limit of the power supply to such a level so that the user is able to rotate the shaft manually, and the rotor is aligned in the stable position. Common current limit is about 10% of the rated motor current. For more powerful motor, the current limit is lower.3.Draw a line/sign for every stable position in which the rotor is aligned.4.Number of stable positions is equal to the motor pole pairs.3Figure 1. Method for the determination of low number of pole pairs3.2.2Method to determine high number of the pole pairIt is possible to use two methods for determination high number of pole pairs. Selection of the method depends on available measuring equipment. An oscilloscope is required for measurement in both the methods•Method A : a current probe and an inverter using Volt/Herz method to spin the motor with unknown parameters •Method B : a voltage probe and driving motor, which spins the motorGuide for Method A : The following steps describe the method to determine the high number of motor pole pairs.1.Spin the motor by an inverter using Volt/Herz method and set the frequency in such a way that the motor will spin at a constant, and preferably higher speed.2.Measure the phase current frequency using oscilloscope current probe. The frequency of the phase current must be the same as that generated by Volt/Herz method.3.Measure the speed of the motor by some hand velocity meter. The speed reading must be constant.4.Calculate the number of pole pairs using the equation given below. The result should be very close to an integernumber.Equation 5Figure 2. Current waveform for the determination of high number of the pole pairGuide for Method B : The following steps describe the method to determine the high number of motor pole pairs.1.Spin the motor by an external driving motor at a constant speed.2.Measure the generated voltage frequency.3.Measure the speed of the motor by some hand velocity meter.4.Calculate the motor pole pairs using Equation 5 on page 4.Stator resistance4.1BackgroundA resistance of the stator winding Rs is defined as a resistance between a phase terminal and the center of the winding. The winding resistance is temperature dependent. Usually the resistance value at 25 °C or specified temperature is listed in the motor’s datasheet.Calculate resistance R at operational temperature t (°C) of stator winding (if the temperature is known), using the resistance value measured at temperature t 0 (°C).Equation 6where α is the constant determined by the material (for copper, α = 0.004 K -1)Equation 7For 50 °C temperature difference, R can be calculated as given below.Equation 84.2GuideThe equipment required to measure stator resistance depend on the method used for measurement:•Digital multimeter •RLC meter4Higher values of stator resistance ( > 10 Ω) can be measured by a digital multimeter. The usual stator winding configurationis the wye, so the final stator resistance is half of the measured resistance. The following figure shows the stator resistor measurement using a digital multimeter.Figure 3. Stator resistance measurement by a digital multimeter4.2.2RLC meterLower values of stator resistance can be measured by an RLC meter, for example MOTECH MT 4080A. The four-terminalmeasurement reduces the effect of the test lead resistance. See Figure 4. Usual measurement range is between (10 mΩ–10kΩ). Before the measurement, calibrate the RLC meter (open-circuit, and short circuit). The usual stator windingconfiguration is the wye, so the final stator resistance is half of measured resistance.Figure 4. Four-terminal measurement schematicSynchronous inductances5.1BackgroundThe synchronous inductances of Interior Permanent Magnet Synchronous Motor (IPMSM) winding are different (L d <L q ),because of lower reluctance in q -axis. The synchronous inductances of Surface Mounted Permanent Magnet Synchronous Motor (SMPM) motor are almost equal, because the permanent magnets are surface mounted and reluctance is the same in every position, that is:μPM ≈ μair → L d ≈ L q ,where μPM is the relative permeability of the permanent magnet , and μair is the relative permeability of the air.See the following figure depicting the reluctance paths of d - and q-axis in IPMSM.Figure 5. Reluctance paths in d - and q -axis of IPMSM5In practice, magnetic circuits are subject to saturation as the current increases. Especially, when current I q is increased, the value of L q is decreased. Since I d is maintained to zero or negative value (demagnetizing) in most operating conditions,saturation of L d rarely occurs. The flux linkage λm and L dare subject to armature reaction. See the following figure.Figure 6. Typical inductance characteristic of PMSMNOTEMajority of the applications use single value; however the determination of inductances depends on selected working conditions.In order to measure synchronous inductance, the users must maintain balanced three-phase current condition. When the rotor is aligned with the center of phase A winding, L d (L q ) can be derived from the measured equivalent inductance L of thecircuit, as shown in the following figure.Figure 7. Inductance measurement circuitDepending on the rotor angle θel , it is possible to measure inductance in d -axis or q -axis, where L is the total inductance forserial-parallel connection of the stator winding:Equation 9Equation 10When the rotor is aligned with phase A (θel= 0°) and locked, then the current response is first order RL circuit.Where τ is a time constant of the circuitAfter measuring τ, the inductance LdEquation 13Figure 8. Equivalent phase model of PMSM in d/q axis for a locked rotor shaftSince V d = (2/3)V, V q = 0, and I is the same as I d and the total resistance of the circuit is (3/2)R s , the equivalent inductance seen from the supply source is (3/2)L d . Similar explanation can also be applied to L q when the rotor is locked at 90°electrical.5.1.1Q-axis alignmentTo measure the inductance in q -axis without an inverter, an alignment has to be done into the q -axis. The alignment into d -axis is done by phase A connected to the positive potential (+) and phase B and C are grounded (-). It can be seen from the following figure that 90° electrical shifted position is when phase B terminal is connected to the positive potential (+) of thevoltage source, phase C is grounded (-), and phase A is floating (NC).Figure 9. Explanation of q-axis alignment5.2GuideThe equipment required to measure inductances in q -axis and d -axis are as follows.•DC power supply, oscilloscope, current and voltage probeFigure 10. Set up to measure inductance in q-axisGuide to measure d -axis inductance (non-saturated inductance measurement): Follow the steps given below to measure the d -axis inductance L d .1.Align the rotor to phase A. Phase A is connected to the positive potential (+) and phase B and C are grounded (-).2.Lock the rotor shaft.3.Apply negative step voltage. Phase A is grounded (-) and phases B and C are connected to the positive potential (+).Usual level of the current is about 10% of the rated phase current.4.Measure the step response of the current by a current probe. See Figure 11.5.Calculate inductance L d.Figure 11. Current step response waveformGuide to measure q -axis inductance : Follow the steps given below to measure the q -axis inductance L q .1.Align the rotor to the q -axis. Connect the phase B terminal to the positive potential (+) of the voltage source and phaseC is grounded (-). Phase A terminal is floating.2.Lock the rotor shaft firmly because current step response in q -axis creates torque .3.Generate a current step response in this configuration: phase A is connected to the positive potential (+) of the voltage source and phases B and C are grounded.4.Calculate inductance L q in the same way as L d .Back-EMF constant6.1BackgroundThe back-EMF (BEMF) constant (flux linkage of the PM denoted by λm ) can be obtained by measuring the no-load line voltage V pk of the motor while it is driven through the shaft at a constant speed of ωm . The constant gives a ratio between BEMF voltage and the angular electrical frequency/speed.6Figure 12. Three-phase measurement of the BEMF constant6.2GuideThe equipment required to measure the BEMF constant are listed below.•Oscilloscope and at least one voltage probe•Driving motor or hand drill machineThe steps given below must be followed to determine the BEMF constant.1.Spin the motor by an external driving motor or a hand drill machine at a constant speed. Higher speed is preferred,because the voltage measurement error is lower.2.One-phase measurement : Measure the generated phase voltage (between one phase terminal and neutral point of the motor). Usually the neutral point is not accessible; then measure the line-to-line voltage.Three-phase measurement : If the neutral point is not accessible, it’s possible to create the artificial neutral point from all three voltage probe clips connected together. See Figure 13.3.Calculate the Back-EMF constant according to Equation 14 on page 13.Single phase measurement (line-to-line voltage measurement):Equation 14Three-phase measurement (phase voltage measurement):Equation 15Figure 13. Three-phase oscilloscope measurement of the electrical constant7ConclusionThe application note summarizes methods for determining electrical parameters of PMSM. The precise parametersdetermination is needed for sensorless control applications and desired closed-loop performance. The proposed measurement techniques determine the number of pole pairs, the stator windings resistance, the synchronous inductances, and the electrical constant with common measurement equipment. The parameters are determined using measured applied voltages and responding currents. A single-phase DC voltage power supply can be used to determine the synchronous inductances of three-phase PMSM with sufficient accuracy.8References 1.DRM110: Sensorless PMSM Control for an H-axis Washing Machine Drive, available on .2.MOTECH 4080A Operation Manual, available at9Acronyms and Abbreviated TermsThe following table contains acronyms and abbreviated terms used in this document.How to Reach Us:Home Page:Web Support:/supportUSA/Europe or Locations Not Listed:Freescale SemiconductorTechnical Information Center, EL5162100 East Elliot RoadTempe, Arizona 85284+1-800-521-6274 or +/supportEurope, Middle East, and Africa:Freescale Halbleiter Deutschland GmbH Technical Information CenterSchatzbogen 781829 Muenchen, Germany+44 1296 380 456 (English)+46 8 52200080 (English)+49 89 92103 559 (German)+33 1 69 35 48 48 (French)/supportJapan:Freescale Semiconductor Japan Ltd.HeadquartersARCO Tower 15F1-8-1, Shimo-Meguro, Meguro-ku,Tokyo 153-0064Japan0120 191014 or +81 3 5437 9125support.japan@Asia/Pacific:Freescale Semiconductor China Ltd.Exchange Building 23FNo. 118 Jianguo RoadChaoyang DistrictBeijing 100022China+86 10 5879 8000@Document Number: AN4680Rev. 0, 02/2013Information in this document is provided solely to enable system and software implementers to use Freescale Semiconductors products. There are no express or implied copyright licenses granted hereunder to design or fabricate any integrated circuits or integrated circuits based on the information in this document.Freescale Semiconductor reserves the right to make changes without further notice to any products herein. Freescale Semiconductor makes no warranty, representation, or guarantee regarding the suitability of its products for any particular purpose, nor does Freescale Semiconductor assume any liability arising out of the application or use of any product or circuit, and specifically disclaims any liability, including without limitation consequential or incidental damages. "Typical" parameters that may be provided in Freescale Semiconductor data sheets and/or specifications can and do vary in different applications and actual performance may vary over time. All operating parameters,including "Typicals", must be validated for each customer application by customer's technical experts. Freescale Semiconductor does not convey any license under its patent rights nor the rights of others. Freescale Semiconductor products are not designed,intended, or authorized for use as components in systems intended for surgical implant into the body, or other applications intended to support or sustain life, or for any other application in which failure of the Freescale Semiconductor product could create a situation where personal injury or death may occur. Should Buyer purchase or use Freescale Semiconductor products for any such unintended or unauthorized application,Buyer shall indemnify Freescale Semiconductor and its officers, employees, subsidiaries,affiliates, and distributors harmless against all claims, costs, damages, and expenses, and reasonable attorney fees arising out of, directly or indirectly, any claim of personal injury or death associated with such unintended or unauthorized use, even if such claims alleges that Freescale Semiconductor was negligent regarding the design or manufacture of the part.RoHS-compliant and/or Pb-free versions of Freescale products have the functionality and electrical characteristics as their non-RoHS-complaint and/or non-Pb-free counterparts.For further information, see or contact your Freescale sales representative.For information on Freescale's Environmental Products program, go to /epp.Freescale™ and the Freescale logo are trademarks of Freescale Semiconductor, Inc.All other product or service names are the property of their respective owners.© 2013 Freescale Semiconductor, Inc.。
PMSM参数测量
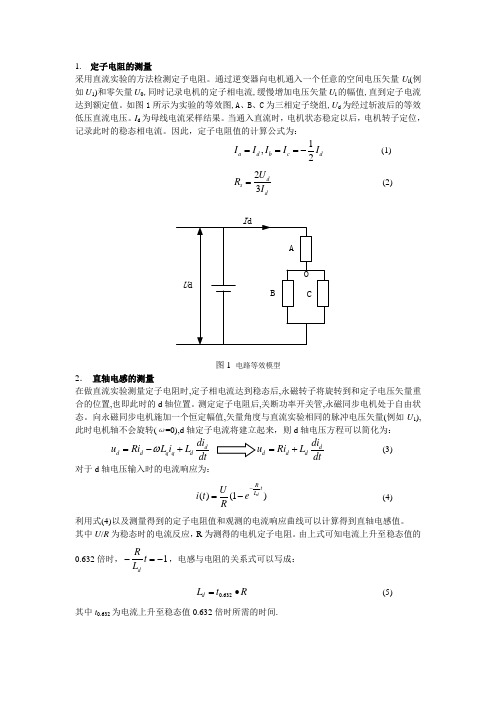
采用直流实验的方法检测定子电阻。
通过逆变器向电机通入一个任意的空间电压矢量U i (例如U 1)和零矢量U 0,同时记录电机的定子相电流,缓慢增加电压矢量U i 的幅值,直到定子电流达到额定值。
如图1所示为实验的等效图,A 、B 、C 为三相定子绕组,U d 为经过斩波后的等效低压直流电压。
I d 为母线电流采样结果。
当通入直流时，电机状态稳定以后，电机转子定位，记录此时的稳态相电流。
因此，定子电阻值的计算公式为： 1,2a dbcd I I I I I ===-(1)23ds dU R I =(2)图1 电路等效模型2． 直轴电感的测量在做直流实验测量定子电阻时,定子相电流达到稳态后,永磁转子将旋转到和定子电压矢量重合的位置,也即此时的d 轴位置。
测定定子电阻后,关断功率开关管,永磁同步电机处于自由状态。
向永磁同步电机施加一个恒定幅值,矢量角度与直流实验相同的脉冲电压矢量(例如U 1),此时电机轴不会旋转(ω=0),d 轴定子电流将建立起来，则d 轴电压方程可以简化为：d d d q q ddi u Ri L i L dtω=-+dd d ddi u Ri L dt=+ (3)对于d 轴电压输入时的电流响应为：()(1)d Rt L Ui t e R-=-(4)利用式(4)以及测量得到的定子电阻值和观测的电流响应曲线可以计算得到直轴电感值。
其中U /R 为稳态时的电流反应，R 为测得的电机定子电阻。
由上式可知电流上升至稳态值的0.632倍时，1dRt L -=-，电感与电阻的关系式可以写成：0.632d L t R =∙(5)其中t 0.632为电流上升至稳态值0.632倍时所需的时间.测出L d 之后,在q 轴方向(d 轴加90°)施加一脉冲电压矢量。
电压矢量的作用时间一般选取的很短,小于电机的机械时间常数,保证电机轴在电压矢量作用期间不会转动。
则q 轴电压方程可以简化为：q q q d d qdi u Ri L i L dtωωψ=+++q q q qdi u Ri L dt=+ (6)q 轴电流将按如下的指数形式建立:()(1)qR t L Ui t e R-=-(7)利用测量直轴电感的方法同样可以测量交轴电感。
永磁同步电机的转子磁极位置辨识方法综述
L2 sin 2 s ˆd s i Rs L1 L2 cos 2 s
（2.17）
ˆd s i Rs L1 L2 cos 2 s 2 us s Rs 2 Rs L1 s L1 L2 L1 L2 s 2
华南理工大学 自动化学院 游林儒教授实验室文档
PMSM 转子磁极位置静止型学习方法研究
华南理工大学 黄招彬 2013-3-15 Email: abinhill@ 永磁同步电机（PMSM）的起动与矢量控制需要知道转子磁极的当前位置（相对于 A 相/ 轴） 。本文针对永磁同步电机的转子磁极初始位置辨识，研究了利用 PMSM 凸极效应或饱和凸 极效应的几种磁极位置辨识方法，包括相等脉冲宽度电压注入法、高频正弦电压注入法和高频 旋转电压注入法。 1. 前言 永磁同步电机中编码器（增量式或绝对式）的安装一般如图 1.1 所示，电机的定子（含线 圈）与编码器的定子固定在一起，电机的转子（含永磁体）与编码器的转子固定在一起（含零 位信号 Z 或者 R） 。设电机定子的静止坐标系参考为 A 相绕组，定为 轴，同时设编码器定子 的静止参考为 A ，可记 1） 2） 3） 4） （变化） ； NA 为矢量控制的解耦角度（转子磁极 N 极位置到 轴之间的电气角）
NZ 为转子磁极 N 极位置到编码器转子零位信号 Z 之间的机械角（固定） ；
； ZA 为编码器转子零位信号 Z 到编码器定子静止参考 A 之间的机械角（变化） 。 AA 为编码器定子静止参考 A 到电机定子 A 相/ 轴之间的机械角（固定）
设电机的极数为 P ，即极对数为
P ，则有 2
的时间，最后时刻的 d 轴电流峰值在转子磁极方向与其反向时达到最大值。由式（2.10） （2.11） 可知，当施加相同伏秒数（电压乘以时间）时，时间越短（对应电压越高） ，定子电阻影响越小。
电压矢量定向的PMSM转子初始位置测量方法及应用
中图分类号 ： Ｍ３ １ Ｔ ５ 文献标识码 ： Ａ 文章编号 ：０ ４ ７ １ （０ ２ ０ — ０ ５ ｏ １０ － ０ ８ ２ １ ）７ ０ １ 一 ４
Ａｎ Ｉ ｉ ａ ｎ ｔ ｌ ｉ ＰＭ Ｓ ｔ ｒ Ｐ ｓｔ ｎ Ｍ ｅ ｓ ｒ ｍ ｅ ｔＭ ｅ ｈ ｄ Ｂａ ｅ ｌａ ｅ Ｖｅ ｔ ｒ Ｏｒ ｅ ｔ ｔ ｎ Ｍ Ｒｏ ｏ ｏ ｉ ｏ ａ ｕ ｅ ｎ ｔ ｏ ｓ ｄ Ｏｎ Ｖｏｔ ｇ ｃ ｏ ｉｎ ｉ ｉ ａ ｏ
动， 系统 软件 实现 编程容 易等 优点 。
１Ｐ Ｍ 矢量控 制基本原理 ＭＳ
采用矢量控制算法时 ，Ｍ Ｍ 的控制 系统需要 ＰＳ
精确 的转 子位 置信 号 以实 现磁 场 定 向控制 ， 当转子
假设不考虑温度等变化对 电机参数的影响 ， 并 电压矢量定向 忽 略磁饱 和及铁 心 损 耗 以及 高次 谐 波 分 量 的影 响 ， 在转子 同步旋转 ｄ ｇ 、 轴坐标 系下 ，Ｍ Ｍ 的数学模 ＰＳ
步 电动机 的数学模型 出发 ， 提出了一种新 型的基 于电压矢量定 向的转 子位置测 量方法 ， 以实现安装 绝对值编码 可
器 的永磁 同步 电动机 的转子初始位置补偿角 的计算 。在永 磁 同步 电动机驱 动控制 系统 中对 该方法进行 了实验验
证 和应用 。实验结果表 明， 使用该方法 的永磁 同步 电动 机转 子初始位 置测量算 法简便 ， 无需 电流传感 器工作 ， 始 初 定位不存在抖动 ， 系统 编程 容易实现 。 关键词 ： 永磁 同步电动机 ； 转子初始位置 ； 矢量控制
基于Ansoft maxwell 的PMSM 的Ld,Lq 线性解耦仿真
基于Ansoft maxwell 的PMSM 的Ld,Lq 线性解耦仿真作者：陆海斌，等来源：《中小企业管理与科技·上中下旬刊》 2016年第3期陆海斌1 辜贇21.长安轻型车研发中心河北定州073000；2.长城汽车股份有限公司技术中心，河北省汽车工程技术研究中心河北保定071000摘要基于车用永磁同步电机的特点，以一台三相内埋式永磁同步电机为例，借助Ansoft Maxwell 软件采用有限元方法分析磁路饱和对交、直轴电感的影响，确定电机的交、直轴电感矩阵，为进一步控制电机做指导。
关键词 PMSM；有限元；交直轴电感；电磁饱和基于AnsoftMaxwell 软件，以一台车用三相永磁同步电机为例进行有限元仿真。
求解出内置式永磁同步电机的交、直轴电感矩阵。
并总结磁路饱和对交、直轴电感的影响趋势。
为进一步实现电机控制提供输入和参考。
1 电机模型的建立及基本参数模型建立：2 使用Ansoft 软件进行参数扫描2.1 添加电流激励模型建立完成后，定子三相绕组添加电流激励，在AnsoftMaxwell 里点击Excitations->PhaseA->将Id×1.414×cos(2×pi×p×n/60×time)+Iq×1.414×sin(2×pi×p×n/60×time)。
B、C 相相同。
2.2 添加扫描参数由于计算量较大，为节省时间，在利用Ansoft MaxwellTM 进行计算时，可以使用参数扫描。
目前的做法是固定Iq，扫描同一Iq 下不同Id 的情况。
将每次计算的结果进行傅里叶分解出电压基波幅值及相位。
2.3 仿真结果根据永磁电机矢量控制原理，定子电流Is 分解到d-q 轴系上的Id、Iq,依据激励条件对Id 进行参数扫描，扫描范围是覆盖电机所有工况的电流范围。
基于级联MRAS的PMSM参数在线辨识算法
基于级联MRAS的PMSM参数在线辨识算法朱雅;贺昱曜;许宇豪;成月【摘要】针对PMSM多参数在线辨识存在的欠秩问题,提出一种级联辨识模型,该模型通过2个模型参考自适应(MRAS)结构级联,分步实现对PMSM转速的估计和定子电阻、磁链的在线辨识;结合零极点配置方法对MRAS自适应机理中的PI参数进行设计,克服了试凑方法调节PI参数所带来的不足.仿真结果表明,文中提出的级联辨识模型能在宽速度范围内实现对PMSM转速的准确估计和参数的有效辨识,提高了系统的动静态性能和鲁棒性.%Aiming at the owe rank problem of on-line identification of PMSM multi-parameters, a cascade identification model is proposed.The model consists of two model reference adaptive (MRAS) constructions to realize the estimation of the PMSM speed and the identification of stator resistance、flux linkage.And the PI parameters of the MRAS adaptive mechanism are deduced by the method of zero pole assignment, which overcomes the shortcomings of traditional PI method.The simulation results show that the cascade identification model can estimate speed accurately, identify PMSM parameters effectively in the wide speed range, and maintain good dynamic and static performance.【期刊名称】《西北工业大学学报》【年(卷),期】2017(035)003【总页数】8页(P486-493)【关键词】永磁同步电机;级联MRAS模型;欠秩【作者】朱雅;贺昱曜;许宇豪;成月【作者单位】西北工业大学航海学院, 陕西西安 710072;西北工业大学航海学院, 陕西西安 710072;西北工业大学航海学院, 陕西西安 710072;西北工业大学航海学院, 陕西西安 710072【正文语种】中文【中图分类】TP273永磁同步电机(PMSM)在运动控制系统中通常采用机械式传感器来获取转子速度信号，但传统机械式传感器存在成本高、安装维护困难、抗干扰能力差、可靠性低等缺点，因此永磁同步电机无速度传感器控制成为电机控制中的热点问题。
STM32 PMSM SDK V4.2 使用指南中文版
60
基于shunt的相电流采样
• 必须合理配置运放电路的增益及偏置电压 • Workbench中专门设计了一个放大电路的设计工具
3-shunt
• 3-shunt：必须在下桥臂打开时才能采样到相电流
OpAmp + Offset Gate
STM32 PMSM FOC SDK V4.2概述
STM32 PMSM FOC SDK V4.2
• SDK V4.2软件包包含：PMSM FOC 固件库和ST MC Workbench(GUI)， 允许用户使用STM32进行单或双PMSM马达的FOC的驱动，其支持 STM32F0xx, STM32F1xx, STM32F2xx, STM32F3xx及STM32F4xx
• State Observer + PLL
• 基于马达的BEMF，使用相电流及相电压估计 马达转子的位置 • 适用于马达的转速范围：额定转速的5% - 100%
• State Observer + CORDIC
9
9
无传感观测器
29
22
X-NUCLEO-IHM07M1
• 供电电压：8V—48VDC • 2.8A峰值电流 • 最大工作频率100KHz • 兼容STM32 Nucleo/ ST Morpho接口 • 支持三电阻/单电阻电流采样 • 支持Hall/Encoder
X-NUCLEO-IHM08M1
• 供电电压：10V—48VDC • 最大30 A峰值电流 • 最大工作频率100KHz • 兼容STM32 Nucleo/ ST Morpho接口 • 支持三电阻/单电阻电流采样 • 支持Hall/Encoder
永磁同步电机参数测量试验方法(精编文档).doc
【最新整理，下载后即可编辑】永磁同步电机参数测量实验一、实验目的1. 测量永磁同步电机定子电阻、交轴电感、直轴电感、转子磁链以及转动惯量。
二、实验内容1. 掌握永磁同步电机dq 坐标系下的电气数学模型以及机械模型。
2. 了解三相永磁同步电机内部结构。
3. 确定永磁同步电机定子电阻、交轴电感、直轴电感、反电势系数以及转动惯量。
三、拟需实验器件1. 待测永磁同步电机1台；2. 示波器1台；3. 西门子变频器一台；4. 测功机一台及导线若干；5. 电压表、电流表各一件；四、实验原理1. 定子电阻的测量采用直流实验的方法检测定子电阻。
通过逆变器向电机通入一个任意的空间电压矢量U i (例如U 1)和零矢量U 0,同时记录电机的定子相电流,缓慢增加电压矢量U i 的幅值,直到定子电流达到额定值。
如图1所示为实验的等效图,A 、B 、C 为三相定子绕组,U d 为经过斩波后的等效低压直流电压。
I d 为母线电流采样结果。
当通入直流时，电机状态稳定以后，电机转子定位，记录此时的稳态相电流。
因此，定子电阻值的计算公式为：1,2a dbcd I I I I I ===- (1) 23d s d U R I = (2)图1 电路等效模型 2． 直轴电感的测量在做直流实验测量定子电阻时,定子相电流达到稳态后,永磁转子将旋转到和定子电压矢量重合的位置,也即此时的d 轴位置。
测定定子电阻后,关断功率开关管,永磁同步电机处于自由状态。
向永磁同步电机施加一个恒定幅值,矢量角度与直流实验相同的脉冲电压矢量(例如U 1),此时电机轴不会旋转(ω=0),d 轴定子电流将建立起来，则d 轴电压方程可以简化为：d d d q q d di u Ri L i L dt ω=-+d d d d di u Ri L dt =+ (3)对于d 轴电压输入时的电流响应为：()(1)d R t L U i t e R -=- (4)利用式(4)以及测量得到的定子电阻值和观测的电流响应曲线可以计算得到直轴电感值。
IPM马达的Ld-Lq电感计算
JAC122-文獻內容
線圈在0°相位角的不同位置的電感分佈 計算0°相位角的Ld, Lq電感值 JMAG模型設定要點
不同位置的電感分佈
由於運用到電感定義式(L=dΨ/di)：
需設定2不同電流值的分析檔，以或獲得各別的磁通分佈 除電流的差異(5.00 vs. 5.25 [A])外，其他條件、參數設定完 全相同 將各別電流值的線圈磁通分佈、電流數據輸出並儲存成 Excel檔
Coil Flux
0.25 0.2 0.15
Flux (Wb)
0.1 0.05 0
0 15 Coil Flux (5.25 [A]) Coil Flux (5.00 [A]) 30 45 60 75 90
-0.05 -0.1 -0.15
Angle (deg)
Coil Current
5.3 5.25 5.2
JAC122文獻計算
-1.06 -2.09 -3.06 -3.94 -4.69 -5.30 -5.75 -6.03 6.03 5.75 5.30 4.69 3.94 3.06 2.09 1.06
Phase vs. Inductance (Ld, Lq)
35 30
Inductance (mH)
25 20 15 10 5 0
模型設定 – [FEM Coil]
只設定一相線圈的[FEM Coil]
模型設定 – 驅動電路
只設定一相線圈的[FEM Coil]元件
JAC122 - 參考模型檔
電流值5.00 [A]： IPM_LdLq_5.00[A].jcf 電流值5.25 [A]： IPM_LdLq_5.25[A].jcf
IPM馬達的 Ld-Lq電感計算
電磁分析部門 / CAE 事業處 勢流科技股份有限公司
一种永磁同步电机参数测量方法
一种永磁同步电机参数测量方法
刘军;吴春华;黄建明;俞金寿
【期刊名称】《电力电子技术》
【年(卷),期】2010(044)001
【摘要】基于永磁同步电机(Permanent Magnet Synchronous Motor,简称PMSM)的数学模型,由数学推导得出PMSM在d,q坐标系下电感参数的理论公式,通过电桥测量电机的静态三相电感和三相电阻参数即可计算得到d,q轴电感和相电阻参数.该方法无需考虑电机永磁转子的当前位置,无需额外测量电路及进行驱动控制,具有理论清晰、测量简单、通用性强等特点.针对PMSM磁链参数,将电机加速到一定转速后通过测量开路电压及转子频率,即可计算获得磁链系数.实验验证了该测量方法的正确性和准确性.
【总页数】3页(P46-48)
【作者】刘军;吴春华;黄建明;俞金寿
【作者单位】华东理工大学,上海,200237;上海电机学院,上海,200240;上海大学,上海,200072;上海大学,上海,200072;华东理工大学,上海,200237
【正文语种】中文
【中图分类】TM301.2
【相关文献】
1.调速型永磁同步电机参数优化设计的一种图形化方法 [J], 高瑾;胡育文
2.一种自适应补偿死区的异步电机参数测量方法 [J], 徐飞;史黎明;李耀华
3.一种永磁同步电机转子位置传感器零位偏差高精度测量方法 [J], 张猛;郭超勇;梁骄雁;吕振华
4.一种无刷直流电机参数的测量方法 [J], 易慧斌;邓惠文;邓元实;李昊
5.基于克隆选择差分进化算法的永磁同步电机参数辨识 [J], 陈强;傅煜;蔡琦盼因版权原因，仅展示原文概要，查看原文内容请购买。
【精品】永磁同步电机(PMSM)角度测量
本文参照意法半导体文章：STM32F103xx PMSM FOC software library UM.pdf；内容：通过霍尔信号与相线反电动势相位信息获取准确转子相位信息；测试设备：R&S RTE系列示波器一台，无刷直流电机一台，500W FOC矢量控制器一台;具体实现：首先，使用三电阻确定中性点；然后使控制器与霍尔传感器相连接，上电，手动旋转电机；最后，令通道CH1的参考电压线连接电机中性点，而探针测量某一相线（蓝色），另一探针CH2先后测量三相霍尔传感器输出信号，具体电路参照附图，测量结果如下：<图1>黄色信号：蓝色相线反电动势电压信号；绿色信号：黄色霍尔传感器信号；霍尔信号的上升沿与第一个相反电动势波峰角度：(13.6ms*360度)/16.4ms=298.5度；<图2>黄色信号：蓝色相线反电动势电压信号；绿色信号：绿色霍尔传感器信号；霍尔信号的上升沿与第一个相反电动势波峰角度：(2.7ms*360度)/16.5ms=58.9度(此时，在软件中取－58.9o)；<图3>黄色信号：蓝色相线反电动势电压信号；绿色信号：蓝色霍尔传感器信号；霍尔信号的上升沿与第一个相反电动势波峰角度：(7.6ms*360度)/15.2ms=180度；<图4>蓝色波形：蓝色Hall信号；黄色波形：绿色相反电动势；绿色波形：蓝色相反电动势；橙色波形：黄色相反电动势；<图5>蓝色波形：蓝色相反电动势；黄色波形：黄色Hall信号；绿色波形：绿色Hall信号；橙色波形：蓝色Hall信号；<图6><图7>紫色波形：A相电机线对地反电动势；绿色波形：A相电机线对中性点反电动势；峰峰角差：由以上两图可知:(3.2ms/39.2ms)*360度≈29.4度结论：1、关于霍尔偏移角度，以及它的用处，只想通过一副简图及一段文字说明：如下图所示，dq 为旋转坐标系，转子磁链矢量轴Ψr （即转子磁场方向）与d 轴重合。
EPS系统中PMSM转子位置的测量方法
EPS系统中PMSM转子位置的测量方法蒋翔;汪剑鸣;袁臣虎【摘要】为获取EPS系统中永磁同步电机的转子位置，设计一种利用磁旋转编码器AS5045测量电机转子位置的方法，并通过对电机转子位置初始定位，实现了永磁同步电机转子位置的绝对角度测量。
经实验证明，此方法设计简单，安装方便，获取的转子位置定位准确，测得角度实时性好，满足EPS系统对转子位置信息的要求。
%A kind of method to measure the rotor position of permenent magnet synchronous motor in EPS system is designed by using magnetic rotary encoder AS5045. The system realize the measurement of rotor positon absolute angle after initial positon of rotor position. The experiment proves that the design is simple and easy to install , compared with other method, the output of this system is accurately and without delay, which is satisfied with the environment of entire EPS system.【期刊名称】《天津工业大学学报》【年(卷),期】2014(000)001【总页数】4页(P55-58)【关键词】EPS系统;永磁同步电机(PMSM);转子位置检测;AS5045【作者】蒋翔;汪剑鸣;袁臣虎【作者单位】天津工业大学电子与信息工程学院，天津 300387;天津工业大学电子与信息工程学院，天津 300387;天津工业大学电气工程与自动化学院，天津300387【正文语种】中文【中图分类】TM351;TN712继电子技术在发动机、变速器、悬挂架和制动器等系统得到广泛应用后，汽车电动助力（EPS）转向已逐步取代传统汽车助力转向系统，成为世界汽车技术发展的热点[1].电动机根据电控单元的指令输出相应的扭矩，是影响EPS系统性能的关键部件之一，所以对电机的选型十分重要.随着近年来用于实时处理的DSP芯片的出现和普及，交流伺服技术中大量复杂的坐标变换、函数计算、参数调节等运算可在极短时间内完成，满足交流伺服系统实时运算的要求，使得交流伺服传动逐渐走向前台，取代了传统的直流电机[2].而永磁同步三相电机（PMSM）以其体积小、功率大、模型简单等优点脱颖而出，成为目前EPS系统的主流电动机.在基于PMSM 的EPS系统中，获取实时的转子位置角度是系统工作的必要条件.只有获得精确、及时的转子角度位置信息，才能准确地将电机模型等效为dq坐标系的模型，也才能有效控制电机，从而实现EPS良好的工作性能.另外，人们对EPS系统性能要求越来越高，主动回正、线性助力等概念的相继提出，都需要获取准确的电机转子位置信息.因此，高效、及时、准确的转子位置测量方法研究势在必行.目前，测量转子位置的方法主要有：旋转变压器法、光电编码器法、磁旋转编码器法等.旋转变压器是电机转子位置测量的有效手段，曾应用在本文所涉及的EPS系统中，并获得了较好的转子位置信息.但在实验过程中仍有一些缺陷.首先，旋转变压器需要外部激励注入，这无疑繁复了系统硬件，不利于控制器小型化；其次，旋变输出信号需要复杂的滤波解调算法才能得到较为准确的转子位置信息，增加了系统软件的运算负担，并可能造成角度信息的延时；最后，旋变价格较高，增加了控制器成本.光电编码器主要分为绝对式和增量式.绝对式光电编码器通过光盘编码，得到转子位置的绝对角度，但是由于其装置较为复杂，同样不利于EPS的批量生产和小型化；增量式光电编码器结构简单，响应迅速，但缺点是掉电后容易造成数据损失，而且有误差累积现象[3].磁旋转编码器通过集成在芯片内部的霍尔传感器感应磁铁极性变化，并经芯片内部处理，得到转子转角的绝对角度信息.相比较于旋转变压器和光电编码器，其安装简便，价格低廉，适合工业生产；且通过串行方式向EPS电控单元输入数字化的转子角度信息，满足EPS系统对转子位置角度信息精确、实时的要求；另外得到的角度信息无需滤波解调，节省了CPU资源.本文选用AS5045作为磁旋转编码芯片.AS5045是一款无接触式的磁旋转编码器，可精确测量360°范围内轴转角度.芯片内部集成了霍尔器件、DSP、模拟前端和数字处理模块，其中霍尔器件感应外部磁场变化，通过数字处理输出12位精度的数字转角信息，并以SSI的方式传输给EPS的电控单元.在使用时，只需要将一块纽扣形磁铁固定在电机转子轴心上，并将芯片置于磁铁的上方或下方，即可方便地读出转子转过的角度.图1即为AS5045的典型安装方式.本文采用MC56F8367作为EPS系统的电控单元，该DSP具有串行外设接口（SPI），能够处理AS5045的绝对角度信号.对AS5045安装位置初始定位的主要目的是获得电机转子实际位置与编码器输出角度之差，据此才能使AS5045输出的绝对角度与电机转子实际角度对准标定[4]. 通过AS5045的安装方式可以看出，由于安装时磁铁、芯片和电机转子位置的随机性，导致编码器输出的角度与转子实际位置不一致，其关系如图2所示.图2中：θ为转子位置角度；Ax为编码器输出角度；α1为磁铁磁极轴线与转子的夹角；α2为芯片轴线与电机定子A轴的夹角.由此可得转子位置角度，如式1所示.由于AS5045轴线与定子保持相对静止，磁铁轴线与转子保持相对静止，故式（1）中α1-α2为一常数.为求得α1-α2，可令电机转子位置角度θ=0，此时得式（2）：即在电机转子位置角度θ=0时，磁旋转编码器AS5045的读数Ax=θ0=α1-α2，此时的θ0即为电机转子实际位置与编码器输出的差值.为得到θ0，文献[5]提出了一种基于获取反电动势过零点的方法对电机进行初始定位，但是在电机低速或零速状态下，反电动势较小，对采集模块的精度要求较高，不易实现；文献[6]与文献[7]均使用高频注入法对转子位置进行估算，可获得较为精确的电机转子位置，但是由于该方法的实验过程较为复杂，不适用于实际工业生产.文献[8]提出了一种磁定位法来确定转子的初始位置，通过给定电流矢量观察电机转动方向，同时统计增量编码器的输出脉冲，多次试验后转子位置与设定电流矢量方向基本吻合，此方法可以测量出转子的初始位置，但是需要多次试验才可得出较为精确的角度初始值.在此提出一种简便的方法对永磁同步三相电机转子位置进行初始定位.由于转子位置与三相定子的输入电流有关，故考虑一种强制给三相定子加电的方式，使转子在三相定子产生的磁场作用下，在预期的位置达到力矩平衡.具体原理如下分析.永磁同步三相电机dq轴下的电磁转矩方程如式（3）所示：式中：p为电机极对数；K为电磁转矩系数；Lq与Ld为dq轴上的电感量；id、iq分别为d、q轴上的电流.由式（2）可以看出，电磁转矩的方向与iq同向，于是在电机空载时，当转子处于平衡位置，电磁转矩即为0，如式（4）所示：易得此时iq=0.设此时id=C为一定值，如式（5）所示：旋转坐标系与三相坐标系关系可用式（6）表示：式中：θ1为转子N极与A相正方向的夹角；iA、iB、iC分别为电机的三相定子电流.欲得到转子在θ1=0达到平衡时三相定子加电方式，可令式（6）坐标变换矩阵中θ1=0，并将式（5）代入式（6），即可得到三相电流间的关系如式（7）所示：因此若按照式（7）所示的方式对三相定子施加电流，即式（8）所示的方式对三相定子强制注入电流，在电机转子达到平衡位置时，即可认为此时转子位置角度θ=0：在实验中，需要一台直流电源，将其正极与电机A相相连，负极与B、C相同时相接，如图3所示.需要注意的是，直接将普通直流电源连接电机会造成过流，从而对实验设备造成极大损害，此处使用MOTECH生产的LPS-305直流电源，此直流电源有限流功能，直接与电机连线其电流不会超过设定上限.实验中设置上限电流0.5 A，故而不会因电流过大而损害实验设备.另外在加电过程中，电机须无负载，这样才能对电机转子零位准确定位.图3中：A、B、C分别为电机的三相定子；A′、B′、C′分别为三相定子通电后产生的磁场，I则为限流电源的电流上限，通过将电源的正极与A相相连，B、C相与电源的负极相连接.由图3中各相产生的磁场A`、B`、C`经矢量合成易知，电机内部空间磁场的方向指向A相正方向，即可认为此时转子位置处于θ=0处.而此时，编码器AS5045的输出角度即为式（2）中的A0.为使编码器输出的绝对角度与实际转子位置角度一一对应，根据式（3），转子位置角度的表达式如式（9）所示. 由于编码器为12位输出，输出数字范围是0～ 4 095，减去α1-α2后会有溢出现象，故需在小于0的部分加上4 095.在整个初始定位过程中，无需手工调整编码器和磁铁的相对位置，操作方便可行. 磁旋转编码芯片AS5045每次发出18位数字信息，包括12位转子位置信息和6位校验码，与EPS的电控单元通过SSI通信，输出转子绝对位置.在硬件上，只需要将AS5045的Do、SCLK、CSn引脚分别与DSP的3个I/O相连即可；在软件方面，只需要将时钟信号、片选信号发送给编码器，即可从Do口读出编码器输出的转子角度信息.值得注意的是，通过磁旋编码器测量的转子位置信息为电机转子的机械角度，而EPS系统中电控单元需要的则是电角度，在此需将磁旋编码器输出转化为电角度；至于其关系可用式（10）表示.式中：p为电机极对数；θm为转子机械角度；θe为电机转子电角度.从上面的过程可以看到，只需在安装时确定编码器的初始位置，就可以方便读取出电机转子的绝对角度，并将其转化为EPS控制器所需要的电机转子电角度.实验采用7对极电机，DSP采用为Freescale生产的MC56F8367，在CodeWarrior环境下编译，并通过上位机来观察转子位置信号波形.注入电流法的实验波形如图4所示.实验中，先令转子位置处于任意位置，此时图4中的编码器的输出数值为135.在某一时刻（图中31 s至32 s之间），对电机的三相定子按式（8）所示方式施加电流，转子即转动至电机实际0位置，编码器的输出也随之变化.图4中可以看出初始定位后的编码器输出数值变为95，而该数值即为式（2）中的θ0.为验证初始定位的效果，本文进行了如下实验。
无刷电机参数的含义及测量方法
无刷电机参数的含义及测量方法4.0电机参数的含义及仪器仪表测量方法1.首先给出workbench中设置电机参数的两张图片：根据workbench 中对电机需要的参数来看，作如下的整理翻译及解释2.Magnetic structure 电机磁结构英文名中文翻译解释Surface Mounted PMSM 表面安装式永磁同步电动机 也叫作外转子电机，作为转子的永磁体在电机结构的外圈 Internal PMSM内部永磁同步电动机 也叫作内转子电机，作为转子的永磁体在电机结构的内部外转子电机的Ld:Lq 可以近似认为为1。
3. Electrical parameters 电气参数英文名 中文翻译 单位解释Pole Pairs 极对数三相交流电机每组线圈都会产生N 、S 磁极，每个电机每相含有的磁极个数就是极数Max.最大转rpm 转每分电机运转速度的常用单位，指一英文名 中文翻译 单位解释Application Speed速分钟电机转多少圈Nominal Current 额定电流 Apk电机工作的额定电流，实际电流过大，容易烧电机，过小的话电机就会不出力 Nominal DC Voltage 额定电压 V 伏电机额定的工作电压Rs 相电阻 Ohm 欧姆 电机的三根相线是Y 型连接的状态，相线端点到中星点的阻值 Ldd 轴电感 mH 毫亨Ld/Lq ratio Ld 与Lq 的比值B-Emf constant 反电动势 Vrms/krpm 每1千转产生的伏特 Inertia 转动惯量uN m s2Friction阻尼系数uN m s4. Sensors 传感器英文名 中文翻译 单位 解释 Hall Sensors霍尔传感器与电机的定子长在一起，感应转子磁体与定子的角度偏差，为定子的绕组电流换向提供重要依据；同时根据霍尔传感器的信号变化频率，可以计算出电机的运转速度SensorDisplacement 传感器安装角度 deg角度电机厂家在生产制造时，将三颗霍尔传感器按两种不同位置或正反极性放置，会在检测转子时产生120° 60° 两种位置信号 Placement electrical angle放置的电角度 deg角度霍尔传感器在与定子安装的时候，不一定能完整的对应到零角度偏差，所以在实际使用的时候还会有一个偏移电角度的参数。
电动机的运行参数测量与分析
电动机的运行参数测量与分析电动机是现代社会中广泛应用的一种电力驱动设备，其运行参数的测量与分析对于电机的性能评估、故障诊断以及系统优化具有重要意义。
本文将从测量方法、常见参数以及参数分析方面进行介绍与阐述。
一、测量方法电动机的运行参数测量通常包括电流、电压、功率、转速及转矩等多个方面的测量。
下面将分别介绍几种常用的测量方法。
1. 电流测量：电流可以通过电动机的电流表直接测量，也可以通过电流互感器、电流变送器等外部装置间接测量。
2. 电压测量：电压可以通过电动机的电压表直接测量，也可以通过电压互感器、电压变送器等外部装置间接测量。
3. 功率测量：功率可以通过电动机的功率表直接测量，也可以通过电压和电流的测量结果计算得出。
4. 转速测量：转速可以通过装置测量，如转速测量仪、霍尔传感器等。
5. 转矩测量：转矩通常可以通过电动机的输出轴上的力传感器或者通过测量电动机输出端的电流得出。
二、常见参数电动机的运行参数通常包括额定功率、额定电压、额定电流、额定频率、功率因数、效率等。
1. 额定功率：电动机在额定工作条件下能够连续输出的功率。
2. 额定电压：电动机在额定工作条件下运行所需的电压。
3. 额定电流：电动机在额定工作条件下运行所需的电流。
4. 额定频率：电动机在额定工作条件下运行所需的电源频率。
5. 功率因数：电动机在运行过程中，有助于将电力转换为机械功率的比例。
6. 效率：电动机输出的实际功率与输入的电力之间的比例。
三、参数分析通过对电动机运行参数的测量和分析，可以得到电动机的性能评估、故障诊断以及系统优化等 valuable 信息。
1. 性能评估：通过测量额定功率和效率等参数，可以评估电动机的性能指标，比如能源利用效率、运行稳定性等。
2. 故障诊断：通过测量电流、电压和转速等参数，可以对电动机的故障进行诊断，如过载、短路、绕组断路等。
3. 系统优化：通过对电动机运行参数的测量与分析，可以提供优化方案，如提高电动机的功率因数、改进系统效率等。
基于电动汽车用PMSM永磁同步电机MTPA_MTPV算法生成idiq表
基于产品级车用PMSM永磁同步电机MTPA/MTPV算法生成id/iq表内置式永磁电机驱动控制方案：PMSMPIPI2r /3sSVPWM2s /2rAD Samplei ui vi di q--+i *d θθ2 L e v e l+V dcV dcu dutyuu dutyv u dutywReso lver3s /2si *qTcmdAngle compensationAngle DetectSpeed DetectVdcvFwdvFwq++++T e3ABCODE FGHMTPAMTPVMTPA/MTPVLdLq LookUpTable_LdLookUpTable_LqZero Position offsetωC1C2How to generate id/iq map for MTPA/MTPV control?本方案主要针对新能源电动汽车用内置式永磁同步电机矢量控制，主要提供怎样得到核心算法MTPA/MTPV电流参考指令解决方案。
在工程实际应用中由于永磁同步电机的电感参数随电流变化明显，使用电流idref/iqref查表法是最行之有效的方法，而使用弱磁环的方案总会有个动态调节过程会出现电机输出电流过流现象，特别是在高速弱磁，直流侧的电压利用率不够时。
本方案使用纯MATLAB M脚本自动解算出高效(id,iq)工作点,并生成电流参考指令表满足MTPA/MTPV曲线控制。
注：本案已在实车上得到实验验证，电机的输出外特性均能满足客户需求，满足产品级开发。
另外：本案也可以灵活应用，只使用id map,iq指令通过电机扭矩方程计算出，但特别注意不同转速电压下，扭矩的输出能力内置式永磁电机原始数据输入：DC_voltage=350V电机极对数= 6相电流RMS_max= 450A Torque_max= 685N.MNem_max=5500rpm使用简单操作说明如下：1、运行Loaddata2、运行FitLdLq3、运行Mtpa1、Mtpa24、运行TorqueFluxSpeedCmd5、运行DebugMFpt6、运行GetMtpvIdIq7、运行GetIdIqMap相关M脚本截图：适应电感随电流变化-40-200204060800.030.0310.0320.0330.0340.0350.036转子温度（℃）空载磁链（V s ）磁链随温度变化关系磁链e p d q d 3[()]2f q T N L L i i ψ=+-转矩公式：1、磁链随温度变化2、dq 轴电感随电流变化适应参数变化得到高精度扭矩控制适应电感随电流变化-250-200-150-100-5050100150200250-250-200-150-100-50050100150200250电流极限圆和最大转矩电流比关系曲线最大电流=251A 最大扭矩=101NmMTPA 计算结果对比24681012141618200102030405060708090100转矩（n m ）电机转矩精度对比给定转矩定电感转矩变电感转矩MTPA 实测结果对比定电感MTPA 曲线实际变电感MTPA 曲线MTPA/Torque_Curve/Current_Circle/Voltage_Circle电流极限圆电压极限圆族扭矩曲线族核心是解算出电压极限圆族，电流极限圆，扭矩曲线族三者之间的交点解算生成MTPA/MTPV的id和iq Map生成的原始数据文件为idmap.csv和iqmap.csv.最终将数据表转换为idmap.c与iqmap.c文件，这两个.c map文件可基于插值查表算法应用于MCU软件程序开发，也可以将.csv文件直接导入到simulink中的lookup table模块中用于MTPA/MTPV模型仿真。
永磁同步电机 实际 id iq 电流
永磁同步电机实际 id iq 电流
永磁同步电机（PMSM）是一种高效且精密的电机，广泛应用于电动汽车、家电、机械制造等领域。
在 PMSM 控制中，通常采用 dq 坐标系进行控制和运算。
其中，i_d 和 i_q 为 dq 坐标系中的电机电流分量。
i_d 电流是直轴电流成分，其大小决定了电机在转子 d 轴方向上的力矩大小。
i_q 电流是交轴电流成分，其大小决定了电机在转子q 轴方向上的力矩大小。
通过调节 i_d 和 i_q 电流，可以控制永磁同步电机的转速、转矩和效率。
在永磁同步电机控制中，通常采用矢量控制的方法来实现精准的电机控制。
该方法将 i_d、i_q 电流转换为 d、q 轴磁链，进而控制电机的磁场和转速。
此外，为了保证电机的稳定性和精度，还需要对i_d、i_q 电流进行闭环控制和反馈，以实现电机控制的高精度和高效率。
总之，i_d、i_q 电流是永磁同步电机控制的重要参数，通过对其加以控制和调节，可以实现对电机的精准控制，从而满足不同应用场景下的需求。
PMSM电机Ld-Lq参数测量方法
1 I a I d , Ib I c I d 2
Rs 2U d 3
C
图 1 电路等效模型 2． 直轴电感的测量 在做直流实验测量定子电阻时,定子相电流达到稳态后,永磁转子将旋转到和定子电压矢量重 合的位置,也即此时的 d 轴位置。测定定子电阻后,关断功率开关管,永磁同步电机处于自由状 态。向永磁同步电机施加一个恒定幅值,矢量角度与直流实验相同的脉冲电压矢量(例如 U1), 此时电机轴不会旋转(ω =0),d 轴定子电流将建立起来，则 d 轴电压方程可以简化为：
Te TL J t
(9)
在电机恒转矩运行过程中，测量时间 t 内电机转速的变化 ，即可计算得转动惯量。 保持永磁电机定子端开路，首先用测功机以恒定转矩拖动电机加速运行，分别记录 t1 与 t2 时刻转速 ω1 与 ω2；然后让电机自由停机，并分别记录 t3 与 t4 时刻的转速 ω3 与 ω4。列写方 程组：
2 1 J t t Tm T0 2 1 3 J 4 0 T0 t4 t3
(10)
式中 Tm 为测功机施加给永磁电机转子的转矩，可由测功机的功率与转速求得，即 Tm=P/ （npω） ，T0 为空载转矩。解方程组即可得转动惯量 J。
R t 1 ，电感与电阻的关系式可以写成： Ld
Ld t0.632 R
其中 t0.632 为电流上升至稳态值 0.632 倍时所需的时间.
(5)
3． 交轴电感的测量 测出 Ld 之后,在 q 轴方向(d 轴加 90°)施加一脉冲电压矢量。电压矢量的作用时间一般选取 的很短,小于电机的机械时间常数,保证电机轴在电压矢量作用期间不会转动。则 q 轴电压方 程可以简化为：
ud Rid Lqiq Ld
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
哇哈哈
PMSM 参数测量实验
测量永磁同步电机定子电阻、交轴电感、直轴电感、转子磁链以及转动惯量。
1. 定子电阻的测量
采用直流实验的方法检测定子电阻。
通过逆变器向电机通入一个任意的空间电压矢量U i (例如U 1)和零矢量U 0,同时记录电机的定子相电流,缓慢增加电压矢量U i 的幅值,直到定子电流达到额定值。
如图1所示为实验的等效图,A 、B 、C 为三相定子绕组,U d 为经过斩波后的等效低压直流电压。
I d 为母线电流采样结果。
当通入直流时，电机状态稳定以后，电机转子定位，记录此时的稳态相电流。
因此，定子电阻值的计算公式为：
1,2a d b c d I I I I I ===- (1) 23d s d U R I = (2)
图1 电路等效模型
2． 直轴电感的测量
在做直流实验测量定子电阻时,定子相电流达到稳态后,永磁转子将旋转到和定子电压矢量重合的位置,也即此时的d 轴位置。
测定定子电阻后,关断功率开关管,永磁同步电机处于自由状态。
向永磁同步电机施加一个恒定幅值,矢量角度与直流实验相同的脉冲电压矢量(例如U 1),此时电机轴不会旋转(ω=0),d 轴定子电流将建立起来，则d 轴电压方程可以简化为：
d d d q q d di u Ri L i L dt ω=-+d d d d di u Ri L dt =+ (3)
对于d 轴电压输入时的电流响应为：
()(1)d R t L U i t e R -=- (4) 利用式(4)以及测量得到的定子电阻值和观测的电流响应曲线可以计算得到直轴电感值。
其中U /R 为稳态时的电流反应，R 为测得的电机定子电阻。
由上式可知电流上升至稳态值的0.632倍时，1d
R
t L -=-，电感与电阻的关系式可以写成：
0.632d L t R =∙ (5) 其中t 0.632为电流上升至稳态值0.632倍时所需的时间.
3． 交轴电感的测量
测出L d 之后,在q 轴方向(d 轴加90°)施加一脉冲电压矢量。
电压矢量的作用时间一般选取的很短,小于电机的机械时间常数,保证电机轴在电压矢量作用期间不会转动。
则q 轴电压方程可以简化为：
q q q d d q di u Ri L i L dt ωωψ=+++ q q q q di u Ri L dt =+ (6)
q 轴电流将按如下的指数形式建立: ()(1)q R t L U i t e R -=- (7) 利用测量直轴电感的方法同样可以测量交轴电感。
此外，由于没有正好超前d 轴90°的电压矢量，需要施加一个60°和120°合成矢量来完成等效q 轴电压矢量的施加过程。
并且在进行脉冲电压实验的过程中,电压幅值和作用时间 应选择适当。
电压幅值选择太小,影响检测精度,过大可能使电流超过系统限幅值影响系统安全。
作用时间过短,采样点少,获取的电流信息少,也会影响检测精度,作用时间过长,电流同样可能过大影响系统安全，并且电机容易发生转动。
4． 反电势系数的测量
采用空载实验法，即用测功机带动被测永磁同步电机以一定的转速旋转，同时保持被测电机负载开路，测试此时的电机空载相电压，即为反电势电压。
结合转速、反电势可以计算得出相应的反电势系数，计算公式如下： 1000e E K n =⨯ (8) 式中：E 为反电势，n 为转速。
电机的反电势系数，其定义为每1000PRM 时电机每相绕组上的反电势电压的有效值（请注意不是线线电压，是线到中性线的电压，单位为：V/KRPM/相）
这种方法需要将被测电机运行至发电状态，并且需要负载开路手动测试反电势。
5． 转动惯量的测量
根据简化的电机运动方程： e L T T J t ω∆-=∆ (9) 在电机恒转矩运行过程中，测量时间t ∆内电机转速的变化ω∆，即可计算得转动惯量。
保持永磁电机定子端开路，首先用测功机以恒定转矩拖动电机加速运行，分别记录t 1与t 2时刻转速ω1与ω2；然后让电机自由停机，并分别记录t 3与t 4时刻的转速ω3与ω4。
列写方程组： 21021430430m J T T t t J T t t ωωωω-⎧⋅=-⎪-⎪⎨-⎪⋅=-⎪-⎩
(10)
式中T m为测功机施加给永磁电机转子的转矩，可由测功机的功率与转速求得，即T m=P/（n pω），T0为空载转矩。
解方程组即可得转动惯量J。