平行四边形的证明题
平行四边形(含答案)

平行四边形参考答案典型例题例1.证明:∵DM⊥AC, BN⊥AC,DM=BN,AM=CN ∴△ADM≌△CBN ∴AD=CB,∠DAM=∠BCN ∴AD∥CB ∴平行四边形ABCD是平行四边形例2.解:∵BC∥AD,BC=AD, ∴ED=BF∴四边形BFDE是平行四边形,所以EB与DF平行且相等①成立,因为ED=BF,四边形BFDE仍是平行四边形,所以EB与DF仍平行且相等②成立,只要ED=BF,就成立③成立。
∵∠ABC=∠ADC, ∠BAD=∠BCD, ∠ABE=∠CDF∴∠EBF=∠EDF, ∠BED=∠BFD∴四边形BFDE是平行四边形,所以EB与DF平行且相等例3.解:PF∥AB,PE∥AC,则四边形AEPF是平行四边形,其周长为2(PE+PF)点P是BC的三等分点,则13PF CPAB CB==,23PE BPAC BC==, 又AB=AC,所以2(PE+PF)=2*12()33+AB=2AB例4.解:①连结AC,BD②将AD和BC四等分,连结对应分点③连结AC,取BC和AD的中点分别为E、F,连结AE、CF例5.解:CF=BE ∵DE∥BC EF∥AC ∴四边形EDCF是平行四边形∴CF=ED ∵BD平分∠ABC, ∠CBD=∠BDE ∴∠DBE=∠BDE ∴BE=ED ∴CF=BE例6.解:连结BD,则GF∥BD,HE∥BD, GF=HE=12BD,所以四边形EFGH是平行四边形例7.(1)证明:旋转90°时,EF⊥AC,又AB⊥AC 则AB∥EF,又AF∥BE,所以四边形ABEF是平行四边形(2)∵AO=CO,∠AOF=∠COE, ∠OAF=∠OCE∴△AOF≌△COE ∴AF=CE(3)可能。
此时EF⊥BD,旋转的角度为∠AOF=90°-∠AOB, AC=2,AO=1=AB,所以∠AOB=45°,所以旋转的角度为45°双基练习1.19,112.1203.1444.185. 50°6.C7.D8.D9.解:∵∠AEB=∠DAE, ∠DAE=∠BAE∴AB=BE=BC-CE=3∴周长为2(AD+AB)=18巩固练习1.AO=CO或BO=DO2.C3.D4.C5.156.187.15,108.解:∵AO=CO,EO为公共边,∠AOE=∠COE∴△AOE≌△COE,∴AE=CE∴周长为CD+DE+CE=CD+AD=89.10.DF和AE相互平分。
(完整版)平行四边形证明典型题
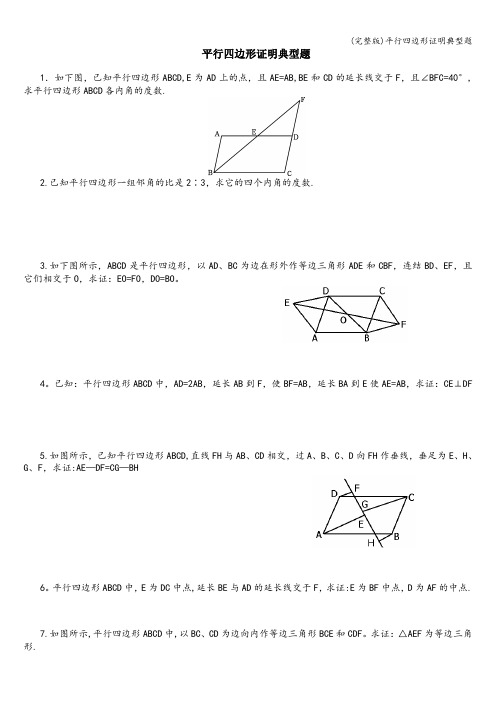
平行四边形证明典型题1.如下图,已知平行四边形ABCD,E为AD上的点,且AE=AB,BE和CD的延长线交于F,且∠BFC=40°,求平行四边形ABCD各内角的度数.2.已知平行四边形一组邻角的比是2∶3,求它的四个内角的度数.3.如下图所示,ABCD是平行四边形,以AD、BC为边在形外作等边三角形ADE和CBF,连结BD、EF,且它们相交于O,求证:EO=FO,DO=BO。
4。
已知:平行四边形ABCD中,AD=2AB,延长AB到F,使BF=AB,延长BA到E使AE=AB,求证:CE⊥DF5.如图所示,已知平行四边形ABCD,直线FH与AB、CD相交,过A、B、C、D向FH作垂线,垂足为E、H、G、F,求证:AE—DF=CG—BH6。
平行四边形ABCD中,E为DC中点,延长BE与AD的延长线交于F,求证:E为BF中点,D为AF的中点.7.如图所示,平行四边形ABCD中,以BC、CD为边向内作等边三角形BCE和CDF。
求证:△AEF为等边三角形.8。
如图所示,在△ABC中,BD平分∠B,DE∥BC交AB于E,EF∥AC交BC于F,求证:BE=FC9。
如图所示,平行四边形ABCD中,E是AB的中点,F是CD中点,分别延长BA和DC到G、H,使AG=CH,连结GF、EH,求证:GF∥EH10.如图所示,平行四边形ABCD中,E、F分别在AD、BC上,且AE=CF,AF与BE相交于G,CE与DF相交于H.求证:EF与GH互相平分11.在四边形ABCD中,AB∥DC,对角线AC、BD交于O,EF过O交AB于E,交DC于F,且OE=OF,求证:四边形ABCD是平行四边形.12。
如图所示,已知△ABC,分别以AB、BC、AC为边向BC同侧作等边三角形ABE、BCD、ACF。
求证:DEAF 为平行四边形.13。
已知:如下图,在四边形ABCD中,AB=DC,AE⊥BD,CF⊥BD,垂足分别是E、F,AE=CF,求证:四边形ABCD 是平行四边形.14.点O是平行四边形ABCD的对角线的交点,△AOB的面积为7cm2,求平行四边形ABCD的面积.15.有两个村庄A和B位于一条河的两岸,假定河岸是两条平行的直线,现在要在河上架一座与河岸垂直的桥PQ,问桥应架在何处,才能使从A到B总的路程最短。
平行四边形的证明题

平行四边形的证明题平行四边形的证明题一.解答题(共30小题)1.如图,已知四边形ABCD为平行四边形,AE⊥BD于E,CF⊥BD于F.(1)求证:BE=DF;(2)若M、N分别为边AD、BC上的点,且DM=BN,试判断四边形MENF 的形状.2.如图所示,▱AECF的对角线相交于点O,DB经过点O,分别与AE,CF交于B,D.求证:四边形ABCD是平行四边形.3.如图,在四边形ABCD中,AB=CD,BF=DE,AE⊥BD,CF⊥BD,垂足分别为E,F.(1)求证:△ABE≌△CDF;(2)若AC与BD交于点O,求证:AO=CO.4.已知:如图,在△ABC中,∠BAC=90°,DE、DF是△ABC的中位线,连接EF、AD.求证:EF=AD.5.如图,已知D是△ABC的边AB上一点,CE∥AB,DE交AC于点O,且OA=OC,猜想线段CD与线段AE的大小关系和位置关系,并加以证明.6.如图,已知,▱ABCD中,AE=CF,M、N分别是DE、BF的中点.求证:四边形MFNE是平行四边形.7.如图,平行四边形ABCD,E、F两点在对角线BD上,且BE=DF,连接AE,EC,CF,FA.求证:四边形AECF是平行四边形.8.在▱ABCD中,分别以AD、BC为边向内作等边△ADE和等边△BCF,连接BE、DF.求证:四边形BEDF是平行四边形.9.如图所示,DB∥AC,且DB=AC,E是AC的中点,求证:BC=DE.10.已知:如图,在梯形ABCD中,AD∥BC,AD=24cm,BC=30cm,点P自点A向D以1cm/s的速度运动,到D点即停止.点Q自点C向B以2cm/s的速度运动,到B点即停止,直线PQ截梯形为两个四边形.问当P,Q同时出发,几秒后其中一个四边形为平行四边形?12.已知:如图,在▱ABCD中,对角线AC交BD于点O,四边形AODE是平行四边形.求证:四边形ABOE、四边形DCOE都是平行四边形.13.如图,已知四边形ABCD中,点E,F,G,H分别是AB、CD、AC、BD 的中点,并且点E、F、G、H有在同一条直线上.求证:EF和GH互相平分.15.已知:如图所示,平行四边形ABCD的对角线AC,BD相交于点O,EF 经过点O并且分别和AB,CD相交于点E,F,点G,H分别为OA,OC的中点.求证:四边形EHFG是平行四边形.16.如图,已知在▱ABCD中,E、F是对角线BD上的两点,BE=DF,点G、H分别在BA和DC的延长线上,且AG=CH,连接GE、EH、HF、FG.(1)求证:四边形GEHF是平行四边形;(2)若点G、H分别在线段BA和DC上,其余条件不变,则(1)中的结论是否成立?(不用说明理由)(17题图)17.如图,在△ABC中,D是AC的中点,E是线段BC延长线一点,过点A 作BE的平行线与线段ED的延长线交于点F,连接AE、CF.(1)求证:AF=CE;(2)如果AC=EF,且∠ACB=135°,试判断四边形AFCE是什么样的四边形,并证明你的结论.18.如图平行四边形ABCD中,∠ABC=60°,点E、F分别在CD、BC的延长线上,AE∥BD,EF⊥BF,垂足为点F,DF=2(1)求证:D是EC中点;(2)求FC的长.18题图(19题图)19.如图,已知△ABC是等边三角形,点D、F分别在线段BC、AB上,∠EFB=60°,DC=EF.(1)求证:四边形EFCD是平行四边形;(2)若BF=EF,求证:AE=AD.26.如图,在直角梯形ABCD中,AB∥CD,∠BCD=Rt∠,AB=AD=10cm,BC=8cm.点P从点A出发,以每秒3cm的速度沿折线ABCD方向运动,点Q 从点D出发,以每秒2cm的速度沿线段DC方向向点C运动.已知动点P、Q 同时发,当点Q运动到点C时,P、Q运动停止,设运动时间为t.(1)求CD的长;(2)当四边形PBQD为平行四边形时,求四边形PBQD的周长;(3)在点P、点Q的运动过程中,是否存在某一时刻,使得△BPQ的面积为20cm2?若存在,请求出所有满足条件的t的值;若不存在,请说明理由.28.已知平行四边形ABCD的周长为36cm,过D作AB,BC边上的高DE、DF,且cm,,求平行四边形ABCD的面积.30.如图所示.▱ABCD中,AF平分∠BAD交BC于F,DE⊥AF交CB于E.求证:BE=CF.1、解答:(1)∵四边形ABCD是平行四边形,∴AB=CD,AB∥CD,∴∠ABD=∠CDB,∵AE⊥BD于E,CF⊥BD于F,∴∠AEB=∠CFD=90°,∴△ABE≌△CDF(A.A.S.),∴BE=DF;(2)四边形MENF是平行四边形.证明:有(1)可知:BE=DF,∵四边形ABCD为平行四边行,∴AD∥BC,∴∠MDB=MBD,∵DM=BN,∴△DNF≌△BNE,∴NE=MF,∠MFD=∠NEB,∴∠MFE=∠NEF,∴MF∥NE,∴四边形MENF是平行四边形.2、解答:证明:∵四边形AECF是平行四边形∴OE=OF,OA=OC,AE∥CF,∴∠DFO=∠BEO,∠FDO=∠EBO,∴△FDO≌△EBO,∴OD=OB,∵OA=OC,∴四边形ABCD是平行四边形.3、解答:证明:(1)∵BF=DE,∴BF﹣EF=DE ﹣EF,即BE=DE,∵AE⊥BD,CF⊥BD,∴∠AEB=∠CFD=90°,∵AB=CD,∴Rt△ABE≌Rt△CDF(HL);(2)∵△ABE≌△CDF,∴∠ABE=∠CDF,∴AB∥CD,∵AB=CD,∴四边形ABCD是平行四边形,∴AO=CO.4、解答:证明:∵DE,DF是△ABC的中位线,∴DE∥AB,DF∥AC,∴四边形AEDF是平行四边形,又∵∠BAC=90°,∴平行四边形AEDF是矩形,∴EF=AD.5、解答:解:猜想线段CD与线段AE的大小关系和位置关系是:平行且相等.证明:∵CE∥AB,∴∠DAO=∠ECO,∵OA=OC,∴△ADO≌△ECO,∴AD=CE,∴四边形ADCE是平行四边形,∴CD AE.6、解答:证明:由平行四边形可知,AD=CB,∠DAE=∠FCB,又∵AE=CF,∴△DAE≌△BCF,∴DE=BF,∠AED=∠CFB又∵M、N分别是DE、BF的中点,∴ME=NF 又由AB∥DC,得∠AED=∠EDC∴∠EDC=∠BFC,∴ME∥NF∴四边形MFNE为平行四边形.7、解答:证明:连接AC交BD于点O,∵四边形ABCD为平行四边形,∴OA=OC,OB=OD.∵BE=DF,∴OE=OF.∴四边形AECF为平行四边形.8、解答:证明:∵四边形ABCD是平行四边形,∴CD=AB,AD=CB,∠DAB=∠BCD.又∵△ADE和△CBF都是等边三角形,∴DE=BF,AE=CF.∠DAE=∠BCF=60°.∵∠DCF=∠BCD﹣∠BCF,∠BAE=∠DAB﹣∠DAE,∴∠DCF=∠BAE.∴△DCF≌△BAE(SAS).∴DF=BE.∴四边形BEDF是平行四边形.9、解答:证明:∵E是AC的中点,∴EC=AC,又∵DB=AC,∴DB=EC.又∵DB∥EC,∴四边形DBCE是平行四边形.∴BC=DE.10、解答:解:设P,Q同时出发t秒后四边形PDCQ或四边形APQB是平行四边形,根据已知得到AP=t,PD=24﹣t,CQ=2t,BQ=30﹣2t.(1)若四边形PDCQ是平行四边形,则PD=CQ,∴24﹣t=2t∴t=8∴8秒后四边形PDCQ是平行四边形;(2)若四边形APQB是平行四边形,则AP=BQ,∴t=30﹣2t∴t=10∴10秒后四边形APQB是平行四边形11、解答:证明:∵D、E、F分别是△ABC各边的中点,根据中位线定理知:DE∥AC,DE=AF,EF∥AB,EF=AD,∴四边形ADEF为平行四边形.故AE与DF互相平分.12、解答:证明:∵▱ABCD中,对角线AC交BD于点O,∴OB=OD,又∵四边形AODE是平行四边形,∴AE∥OD 且AE=OD,∴AE∥OB且AE=OB,∴四边形ABOE是平行四边形,同理可证,四边形DCOE也是平行四边形.13、解答:证明:连接EG、GF、FH、HE,点E、F、G、H分别是AB、CD、AC、BD的中点.在△ABC中,EG=BC;在△DBC中,HF=BC,∴EG=HF.同理EH=GF.∴四边形EGFH为平行四边形.∴EF与GH互相平分.14、解答:证明:∵四边形ABCD是平行四边形,∴AM∥QC,AP∥NC.又∵MN∥AC,∴四边形AMQC为平行四边形,四边形APNC为平行四边形.∴AC=MQ AC=NP.∴MQ=NP.15、解答:证明:如答图所示,∵点O为平行四边形ABCD对角线AC,BD的交点,∴OA=OC,OB=OD.∵G,H分别为OA,OC的中点,∴OG=OA,OH=OC,∴OG=OH.又∵AB∥CD,∴∠1=∠2.在△OEB和△OFD中,∠1=∠2,OB=OD,∠3=∠4,∴△OEB≌△OFD,∴OE=OF.∴四边形EHFG为平行四边形.16、解答:(1)证明:∵四边形ABCD是平行四边形,17、∴AB=CD,AB∥CD,∴∠GBE=∠HDF.又∵AG=CH,∴BG=DH.又∵BE=DF,∴△GBE≌△HDF.∴GE=HF,∠GEB=∠HFD,∴∠GEF=∠HFE,∴GE∥HF,∴四边形GEHF是平行四边形.(2)解:仍成立.(证法同上)17、解答:(1)证明:∵AF∥EC,∴∠DFA=∠DEC,∠DAF=∠DCE,∵D是AC的中点,∴DA=DC,∴△DAF≌△DCE,∴AF=CE;(2)解:四边形AFCE是正方形.理由如下:∵AF∥EC,AF=CE,∴四边形AFCE是平行四边形,又∵AC=EF,∴平行四边形AFCE是矩形,∴∠FCE=∠CFA=90°,而∠ACB=135°,∴∠FCA=135°﹣90°=45°,∴∠FAC=45°,∴FC=FA,∴矩形AFCE是正方形.18、解答:(1)证明:在平行四边形ABCD中,AB∥CD,且AB=CD,又∵AE∥BD,∴四边形ABDE是平行四边形,∴AB=DE,∴CD=DE,即D是EC的中点;(2)解:连接EF,∵EF⊥BF,∴△EFC是直角三角形,又∵D是EC的中点,∴DF=CD=DE=2,在平行四边形ABCD中,AB∥CD,∵∠ABC=60°,∴∠ECF=∠ABC=60°,∴△CDF是等边三角形,∴FC=DF=2.故答案为:2.19、解答:证明:(1)∵△ABC是等边三角形,∴∠ABC=60°,∵∠EFB=60°,∴∠ABC=∠EFB,∴EF∥DC (内错角相等,两直线平行),∵DC=EF,∴四边形EFCD是平行四边形;(2)连接BE∵BF=EF,∠EFB=60°,∴△EFB是等边三角形,∴EB=EF,∠EBF=60°∵DC=EF,∴EB=DC,∵△ABC是等边三角形,∴∠ACB=60°,AB=AC,∴∠EBF=∠ACB,∴△AEB≌△ADC,∴AE=AD..22、解答:解:四边形AFED是平行四边形.证明如下:在△BED与△BCA中,BE=BC,BD=BA(均为同一等边三角形的边)∠DBE=∠ABC=60°﹣∠EBA∴△BED≌△BCA(SAS)∴DE=AC又∵AC=AF∴DE=AF在△CBA与△CEF中,CB=CE,CA=CF∠ACB=∠FCE=60°+∠ACE∴△CBA≌△CEF(SAS)∴BA=EF又∵BA=DA,∴DA=EF故四边形AFED为平行四边形(两组对边分别相等的四边形是平行四边形).26、解答:解:(1)过点A作AM⊥CD于M,根据勾股定理,AD=10,AM=BC=8,∴DM==6,∴CD=16;(2)当四边形PBQD为平行四边形时,点P在AB上,点Q在DC上,如图,由题知:BP=10﹣3t,DQ=2t∴10﹣3t=2t,解得t=2此时,BP=DQ=4,CQ=12∴∴四边形PBQD的周长=2(BP+BQ)=;(3)①当点P在线段AB上时,即时,如图∴.②当点P在线段BC上时,即时,如图BP=3t﹣10,CQ=16﹣2t∴化简得:3t2﹣34t+100=0,△=﹣44<0,所以方程无实数解.③当点P在线段CD上时,若点P在Q的右侧,即6≤t≤,则有PQ=34﹣5t,<6,舍去若点P在Q的左侧,即,则有PQ=5t﹣34,,t=7.8.综合得,满足条件的t存在,其值分别为,t2=7.8.28、解答:解:设AB=x,则BC=18﹣x,由AB•DE=BC•DFF得:,解之x=10,所以平行四边形ABCD的面积为.30、解答:证明:在平行四边形ABCD中,AD ∥BC,∴∠DAF=∠F,又AF平分∠BAD,∴∠DAF=∠BAF,∴∠BAF=∠F,∴AB=BF,又AF平分∠BAD,DE⊥AF,∴∠AOD=∠ADO,又∠BOE=∠AOD=∠EDC,∠ADO=∠E,∴∠EDC=∠E,∴CE=CD,又AB=CD,∴BE=CF.。
八下数学第十八章平行四边形证明题专项·练习
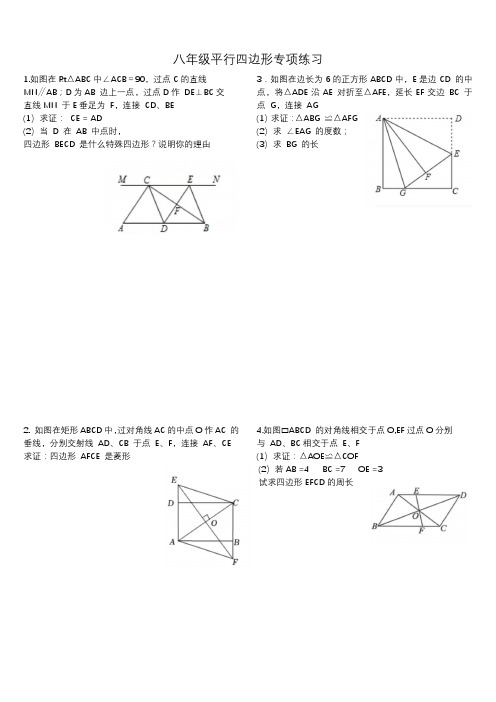
八年级平行四边形专项练习1.如图在Rt△ABC中∠ACB=90,过点C的直线MN∥AB;D为AB 边上一点,过点D作DE⊥BC交直线MN 于E垂足为F,连接CD、BE(1)求证:CE = AD(2)当D 在AB 中点时,四边形BECD 是什么特殊四边形?说明你的理由2. 如图在矩形ABCD中,过对角线AC的中点O作AC 的垂线,分别交射线AD、CB 于点E、F,连接AF、CE 求证:四边形AFCE 是菱形3.如图在边长为6的正方形ABCD中,E是边CD 的中点,将△ADE沿AE 对折至△AFE,延长EF交边BC 于点G,连接AG(1)求证:△ABG ≌△AFG(2)求∠EAG 的度数;(3)求BG 的长4.如图▭ABCD 的对角线相交于点O,EF过点O分别与AD、BC相交于点E、F(1)求证:△AOE≌△COF(2)若AB =4 BC =7 OE =3试求四边形EFCD的周长5如图BD 是△ABC 的角平分线,过点D作DE∥BC交AB于点E,DF∥AB 交BC 于点F(1)求证:四边形BEDF是菱形;(2)若∠ABC =60°∠ACB =45°CD =6√2求菱形BEDF的面积6.如图在△ABC中中线BE、CD 交于点O,F、G 分别是OB、OC 的中点求证:(1) DE ∥FG(2) DG 和EF 互相平分.7. 如图在△ABC 中AB=AC ,D为BC上一点以AB、BD 为邻边作平行四边形ABDE连接AD、EC(1)求证:△ADC ≌△ECD ;(2)若BD =CD 求证:四边形ADCE 是矩形8.如图在Rt△ABC 中∠ACB =90°,过点C 的直线MN ∥AB , D为AB 边上一点,过点D作DE⊥BC ,交直线MN于E,垂足为F,连接CD、BE(1)求证:CE = AD(2)当D在AB中点时,四边BECD是什么特殊四边形?说明你的理由9.如图四边形ABCD是正方形,点E在BC延长线上,DF ⊥AE 于点F 点G在AE 上且∠ABG =∠E求证:AG = DF10. 如图是直角三角尺△ABC 和等腰直角三角尺△ BCD放置在同一平面内,斜边BC重合在一起∠A =∠BDC =90°∠ABC =30°BD = CD DE⊥AB 交AB 于点E 作DF⊥AC 交AC 的延长线于点F (1)求证:四边形AEDF 是正方形(2)当AC =4时,求正方形AEDF 的边长11.如图点0是口ABCD 对角线的交点,过点0作直线分别交AB、CD 的延长线于点E、F求证:BE = DF12. 如图,四边形ABCD是平行四边形,∠BAD的角平分线AE交CD 于点F,交BC的延长线于点E(1)求证:BE = CD(2)若BF 恰好平分∠ABE ,连接AC、DE求证:四边形ACED 是平行四边形13.如图1在正方形ABCD 中,E、F分别是边AD、DC 上的点且AF⊥BE(1)求证:AF = BE(2)如图2在正方形ABCD 中,M、N、P、Q 分别是边AB、BC、CD、DA 上的点且MP⊥NQ 判断MP 与NQ 是否相等?并说明理由14.如图在平行四边形ABCD中,0为对角线交点,DP 平分∠ADC,CP 平分∠BCD,AB =6 AD =10则OP的长是多少?15. 如图矩形ABCD中延长AB至E,延长CD至F . BE = DF连接EF与BC、AD 分别相交于P、Q两点(1)求证:CP = AQ(2)若BP =1 PQ =2 ∠AEF =45°求矩形ABCD 的面积16.如图在Rt△ABC中∠BAC =90° AD⊥BC于D BG 平分∠ABC EF∥BC交AC 于F求证:AE = CF17.如图将矩形纸片ABCD沿对角线AC 折叠,使点B 落到点B '的位置,AB '与CD 交于点E(1)试找出一个与△AED 全等的三角形,并加以证明;(2)若AB =8 DE =3 , P为线段AC上的任意一点PG⊥AE 于G PH⊥EC于H 试求PG + PH的值并说明理由18.如图在△ABC 中AB = BC ,BD 平分∠ABC 四边形ABED 是平行四边形,DE 交BC 于点 F 连接CE求证:四边形BECD 是矩形19.如图1将边长为4cm的正方形纸片ABCD沿EF折叠(点E、F 分别在边AB、CD上,使点B 落在AD 边上的点M 处,点C落在点N处,MN与CD交于点P,连接EP (1)如图②若M 为AD 边的中点①△AEM 的周长=cm②求证:EP = AE + DP(2)随着落点M 在AD 边上取遍所有的位置(点M 不与A、D 重合),△PDM的周长是否发生变化?若发生变化,直接写出△ PDM 的周长,若发生变化,请说明理由。
平行四边形经典证明题例题讲解
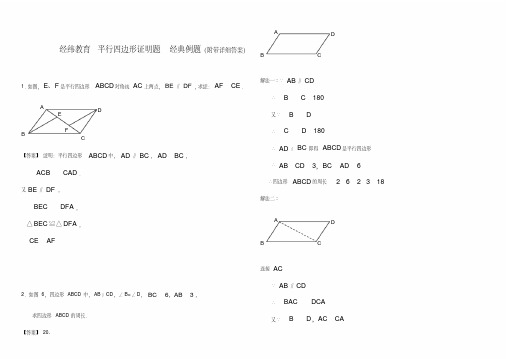
【关键词】平行四边形的性质 , 判定
【答案】 证明:(1)Q DF ∥ BE , DFE BEF .Q AFD DFE 180°, CEB BEF 180°, AFD CEB . 又 Q AF CE,DF BE , △ AFD ≌△ CEB(SAS) .
求四边形 ABCD 的周长. 【答案】 20、
连接 AC ∵ AB ∥ CD ∴ BAC DCA 又∵ B D,AC CA
∴ △ ABC ≌ △CDA ∴ AB CD 3,BC AD 6 ∴四边形 ABCD 的周长 2 6 2 3 18
解法三 :
Байду номын сангаас根据四边形内角和定理得, x ( x 20) 2x 60 360 . 解得, x 70 . ∴ A 70 , B 90 , C 140 .
D
C
E
F
A
B
∴ AD ∥ BC 即 ABCD 是平行四边形 ∴ AB CD 3,BC AD 6 ∴四边形 ABCD 的周长 2 6 2 3 18
3. (在四边形 ABCD 中,∠ D=60°,∠ B 比∠ A 大 20°,∠ C 是∠ A 的 2 倍,求∠ A,∠ B,∠ C 的大小.
【关键词】多边形的内角和
A B
D C
4 . ( 如 图 , E,F 是 四 边 形 ABCD 的 对 角 线 AC 上 两 点 , AF CE, DF BE,DF ∥ BE .
连接 BD ∵ AB ∥ CD ∴ ABD CDB 又∵ ABC CDA ∴ CBD ADB
求证:(1) △ AFD ≌△CEB . (2)四边形 ABCD 是平行四边形.
A
经纬教育 平行四边形证明题 经典例题(附带详细答案)
平行四边形专题证明题33道-含答案

图1 平行四边形专题练习1.如果边长分别为4cm 和5cm 的矩形与一个正方形的面积相等,那么这个正方形的边长为______cm .2.(08贵阳市)如图1,正方形ABCD 的边长为4cm ,则图中阴影部分的面积为 cm 2.3.若四边形ABCD 是平行四边形,请补充条件 (写一个即可),使四边形ABCD 是菱形.4.在平行四边形ABCD 中,已知对角线AC 和BD 相交于点O ,△ABO 的周长为17,AB =6,那么对角线AC +BD =5.以正方形ABCD 的边BC 为边做等边△BCE ,则∠AED 的度数为 .6.已知菱形ABCD 的边长为6,∠A =60°,如果点P 是菱形内一点,且PB =PD =2那么AP 的长为 .7.在平面直角坐标系中,点A 、B 、C 的坐标分别是A(-2,5),B(-3,-1),C(1,-1),在第一象限内找一点D ,使四边形ABCD 是平行四边形,那么点D 的坐标是 .二、选择题(每题3分,共30分)8.如图2在平行四边形ABCD 中,∠B=110°,延长AD 至F ,延长CD 至E ,连结EF ,则∠E +∠F =( )A .110°B .30°C .50°D .70°图2 图3 图49.菱形具有而矩形不具有的性质是 ( )A .对角相等B .四边相等C .对角线互相平分D .四角相等10.如图3所示,平行四边形ABCD 中,对角线AC 、BD 交于点O ,点E 是BC 的中点.若OE=3 cm ,则AB 的长为 ( )A .3 cmB .6 cmC .9 cmD .12 cm11.已知:如图4,在矩形ABCD 中,E 、F 、G 、H 分别为边AB 、BC 、CD 、DA 的中点.若AB =2,AD =4,则图中阴影部分的面积为 ( )A .8B .6C .4D .3E AF D C B H G12.将两块能完全重合的两张等腰直角三角形纸片拼成下列图形:①平行四边形(不包括菱形、矩形、正方形)②矩形③正方形④等边三角形⑤等腰直角三角形( )A.①③⑤B.②③⑤C.①②③D.①③④⑤13.如图5所示,是一块电脑主板的示意图,每一转角处都是直角,数据如图所示(单位:mm),则该主板的周长是( )A.88 mm B.96 mm C.80 mm D.84 mm图5 图614、(08甘肃省白银市)如图6所示,把矩形ABCD沿EF对折后使两部分重合,若150∠=,∠=()则AEFA.110° B.115°C.120° D.130°15、四边形ABCD,仅从下列条件中任取两个加以组合,使得ABCD是平行四边形,一共有多少种不同的组合?()AB∥CD BC∥AD AB=CD BC=ADA.2组B.3组C.4组D.6组16、下列说法错误的是()A.一组对边平行且一组对角相等的四边形是平行四边形.B.每组邻边都相等的四边形是菱形.C. 对角线互相垂直的平行四边形是正方形.D.四个角都相等的四边形是矩形.三、解答题17、如图7,四边形ABCD是菱形,对角线AC=8 cm ,BD=6 cm, DH⊥AB于H,求:DH的长。
(完整版)平行四边形典型证明题(已分类)
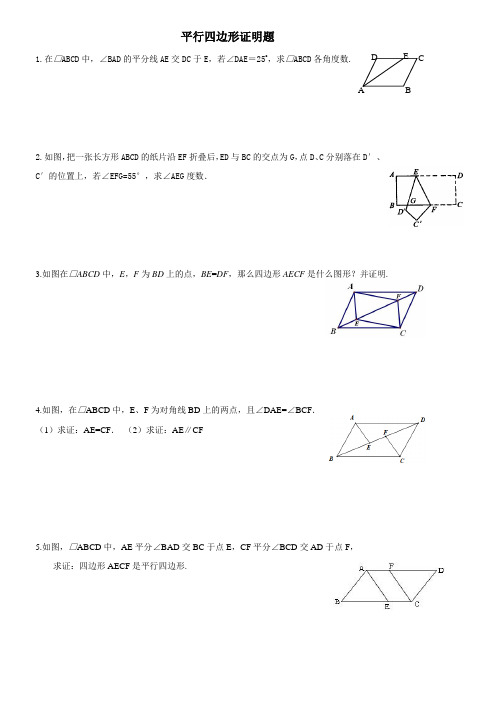
平行四边形证明题1.在□ABCD 中,∠BAD 的平分线AE 交DC 于E ,若∠DAE =25o,求□ABCD 各角度数.2.如图,把一张长方形ABCD 的纸片沿EF 折叠后,ED 与BC 的交点为G ,点D 、C 分别落在D ′、C ′的位置上,若∠EFG=55°,求∠AEG 度数.3.如图在□ABCD 中,E ,F 为BD 上的点,BE =DF ,那么四边形AECF 是什么图形?并证明.4.如图,在□ABCD 中,E 、F 为对角线BD 上的两点,且∠DAE=∠BCF . (1)求证:AE=CF . (2)求证:AE ∥CF5.如图,□ABCD 中,AE 平分∠BAD 交BC 于点E ,CF 平分∠BCD 交AD 于点F ,求证:四边形AECF 是平行四边形.DA CBE6. 如图,点D 、E 、F 分别是△ABC 各边中点. (1)求证:四边形ADEF 是平行四边形.(2)若AB=AC=10,BC=12,求四边形ADEF 的周长和面积.7.如图,在ABC △中,点D E ,分别是AB AC ,边的中点,若把ADE △绕着点E 顺时针旋转180°得到CFE △. 求证:四边形DBCF 是平行四边形。
8.如图,一张矩形纸片ABCD ,其中AD =8cm ,AB =6cm ,先沿对角线BD 对折,点C 落在点C ′的位置,BC ′交AD 于点G .(1)求证:AG =C′G .(2) 求△BDG 的面积9.如图,矩形ABCD 中,AC 与BD 相交于点O.若 AO=3, ∠OBC=30°,求矩形的周长和面积。
10.如图,在矩形ABCD中,AE平分∠BAD,∠1=15°.(1)求∠2的度数.(2)求证:BO=BE.11. 如图,O为矩形ABCD对角线的交点,DE∥AC,CE∥BD.(1)试判断四边形OCED的形状,并证明(2)若AB=6,BC=8,求四边形OCED的面积.12.在△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠ACD的平分线于点F,求证:(1)EO=FO(2)当点O运动到何处时,四边形AECF是矩形?13.如图,BD是菱形ABCD的对角线,点E,F分别在边CD,DA上,且CE=AF.求证:∠DBF=∠DBE.14.如图,在菱形ABCD 中,E 为AD 中点,EF ⊥AC 交CB 的延长线于F.求证:AB 与EF 互相平分.15.如图,在平行四边形ABCD 中,O 是对角线AC 的中点,过点O 作AC 的垂线与边AD 、BC 分别交于E 、F . 求证:四边形AFCE 是菱形.16.在□ABCD 中,对角线AC 与BD 相交于点O ,过点O 作EF ⊥AC 交BC 于点E ,交AD 于点F ,连接AE 、CF . 四边形AECF 是什么形状?并证明.17.已知:如图所示,△ABC 中,E 、F 、D 分别是AB 、AC 、BC 上的点,且DE ∥AC ,DF ∥AB ,要使四边形AEDF 是菱形,在不改变图形的前提下,你需添加的一个条件是_____ 试证明:这个多边形是菱形. ABDCF EDCFEBA HG18.如图,在正方形ABCD 中,点G 是BC 上任意一点,连接AG ,过B ,D 两点分别作BE ⊥AG ,DF ⊥AG , 垂足分别为E ,F 两点,求证:△ADF ≌△BAE .19.如图,已知点E 为正方形ABCD 的边BC 上一点,连结AE ,过点D 作DG ⊥AE ,垂足为G ,延长DG 交AB 于点F .求证:①BF =CE .②DF ⊥AE20.如图, 在正方形ABCD 中, M 为AB 的中点,MN ⊥MD ,BN 平分∠CBE 并交MN 于N .试说明:MD=MN .21.在Rt △ABC 中,∠ACB=90°,CD 平分∠ACB ,过点D 分别作DE ⊥BC,DF ⊥AC ,垂足分别为E,F.求证:四边形DECF 为正方形AF BE CDG 图6A M DBCEN22.在△ABC中,∠BAC=45°,AD⊥BC于点D,将△ABD沿AB所在的直线折叠,使点D落在点E处,将△ADC沿AC所在的直线折叠,使点D落在点F处,分别延长EB,FC使其交于点M,判断四边形AEMF的形状并证明.23.如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.(1)求证:四边形AEBD是矩形.(2)当△ABC满足什么条件时,矩形AEBD是正方形,并证明.24.已知菱形ABCD的两条对角线分别为6和8,M、N分别是边BC、CD的中点,P是对角线BD上一点,则PM+PN的最小值为多少?25.如图,在直角梯形ABCD中,∠ABC=90°,AD∥BC,AD=4,AB=5,BC=6,点P是AB上的一个动点,当PC+PD的值最小时,最小值为 .。
八年级平行四边形几何证明汇总
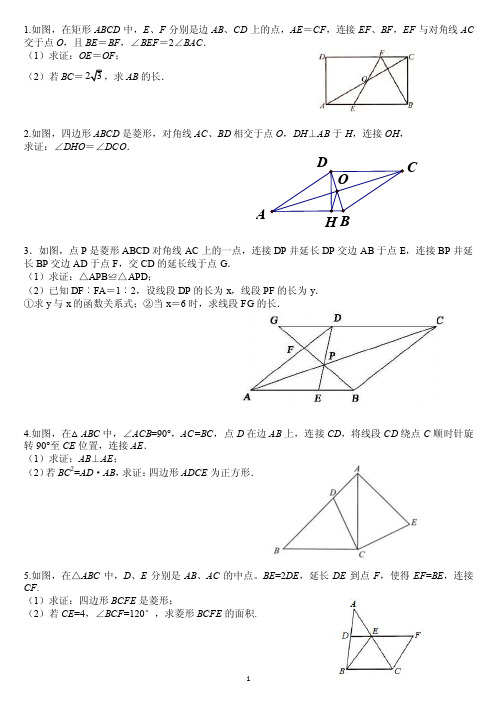
1.如图,在矩形ABCD 中,E 、F 分别是边AB 、CD 上的点,AE =CF ,连接EF 、BF ,EF 与对角线AC 交于点O ,且BE =BF ,∠BEF =2∠BAC . (1)求证:OE =OF ;(2)若BC =AB 的长.2.如图,四边形ABCD 是菱形,对角线AC 、BD 相交于点O ,DH ⊥AB 于H ,连接OH , 求证:∠DHO =∠DCO.3.如图,点P 是菱形ABCD 对角线AC 上的一点,连接DP 并延长DP 交边AB 于点E ,连接BP 并延长BP 交边AD 于点F ,交CD 的延长线于点G . (1)求证:△APB ≌△APD ;(2)已知DF ︰FA =1︰2,设线段DP 的长为x ,线段PF 的长为y . ①求y 与x 的函数关系式;②当x =6时,求线段FG 的长.4.如图,在△ABC 中,∠ACB =90°,AC=BC ,点D 在边AB 上,连接CD ,将线段CD 绕点C 顺时针旋转90°至CE 位置,连接AE . (1)求证:AB ⊥AE ; (2)若BC 2=AD ·AB ,求证:四边形ADCE 为正方形.5.如图,在△ABC 中,D 、E 分别是AB 、AC 的中点。
BE =2DE ,延长DE 到点F ,使得EF =BE ,连接CF .(1)求证:四边形BCFE 是菱形;(2)若CE =4,∠BCF =120°,求菱形BCFE 的面积. C A6.如图,在△ABC 中,AD 是BC 边上的中线,E 是AD 的中点,过点A 作BC 的平行线交BE 的延长线于点F ,连接CF .(1)求证:AF =DC ;(2)若AB ⊥AC ,试判断四边形ADCF 的形状,并证明你的结论.7.如图8,四边形ABCD 是菱形,对角线AC 与BD 相交于O,AB=5,AO=4,求BD 的长. 8.(1)如图1,已知△ABC ,以AB 、AC 为边向△ABC 外做等边△ABD 和等边△ACE ,连接BE ,CD 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
平行四边形的证明题一.解答题(共30小题)1.如图,已知四边形ABCD为平行四边形,AE⊥BD于E,CF⊥BD于F.(1)求证:BE=DF;(2)若M、N分别为边AD、BC上的点,且DM=BN,试判断四边形MENF 的形状(不必说明理由).2.如图所示,▱AECF的对角线相交于点O,DB经过点O,分别与AE,CF交于B,D.求证:四边形ABCD是平行四边形.3.如图,在四边形ABCD中,AB=CD,BF=DE,AE⊥BD,CF⊥BD,垂足分别为E,F.(1)求证:△ABE≌△CDF;(2)若AC与BD交于点O,求证:AO=CO.4.已知:如图,在△ABC中,∠BAC=90°,DE、DF是△ABC的中位线,连接EF、AD.求证:EF=AD.5.如图,已知D是△ABC的边AB上一点,CE∥AB,DE交AC于点O,且OA=OC,猜想线段CD与线段AE的大小关系和位置关系,并加以证明.6.如图,已知,▱ABCD中,AE=CF,M、N分别是DE、BF的中点.求证:四边形MFNE是平行四边形.7.如图,平行四边形ABCD,E、F两点在对角线BD上,且BE=DF,连接AE,EC,CF,FA.求证:四边形AECF是平行四边形.8.在▱ABCD中,分别以AD、BC为边向内作等边△ADE和等边△BCF,连接BE、DF.求证:四边形BEDF是平行四边形.9.如图所示,DB∥AC,且DB=AC,E是AC的中点,求证:BC=DE.10.已知:如图,在梯形ABCD中,AD∥BC,AD=24cm,BC=30cm,点P自点A向D以1cm/s的速度运动,到D点即停止.点Q自点C向B以2cm/s的速度运动,到B点即停止,直线PQ截梯形为两个四边形.问当P,Q同时出发,几秒后其中一个四边形为平行四边形?11.如图:已知D、E、F分别是△ABC各边的中点,求证:AE与DF互相平分.12.已知:如图,在▱ABCD中,对角线AC交BD于点O,四边形AODE是平行四边形.求证:四边形ABOE、四边形DCOE都是平行四边形.13.如图,已知四边形ABCD中,点E,F,G,H分别是AB、CD、AC、BD 的中点,并且点E、F、G、H有在同一条直线上.求证:EF和GH互相平分.14.如图:▱ABCD中,MN∥AC,试说明MQ=NP.15.已知:如图所示,平行四边形ABCD的对角线AC,BD相交于点O,EF经过点O并且分别和AB,CD相交于点E,F,点G,H分别为OA,OC的中点.求证:四边形EHFG是平行四边形.16.如图,已知在▱ABCD中,E、F是对角线BD上的两点,BE=DF,点G、H 分别在BA和DC的延长线上,且AG=CH,连接GE、EH、HF、FG.(1)求证:四边形GEHF是平行四边形;(2)若点G、H分别在线段BA和DC上,其余条件不变,则(1)中的结论是否成立?(不用说明理由)17.如图,在△ABC中,D是AC的中点,E是线段BC延长线一点,过点A作BE的平行线与线段ED的延长线交于点F,连接AE、CF.(1)求证:AF=CE;(2)如果AC=EF,且∠ACB=135°,试判断四边形AFCE是什么样的四边形,并证明你的结论.18.如图平行四边形ABCD中,∠ABC=60°,点E、F分别在CD、BC的延长线上,AE∥BD,EF⊥BF,垂足为点F,DF=2(1)求证:D是EC中点;(2)求FC的长.19.如图,已知△ABC是等边三角形,点D、F分别在线段BC、AB上,∠EFB=60°,DC=EF.(1)求证:四边形EFCD是平行四边形;(2)若BF=EF,求证:AE=AD.20.如图,四边形ABCD,E、F、G、H分别是AB、BC、CD、DA的中点.(1)请判断四边形EFGH的形状?并说明为什么;(2)若使四边形EFGH为正方形,那么四边形ABCD的对角线应具有怎样的性质?21.如图,△ACD、△ABE、△BCF均为直线BC同侧的等边三角形.(1)当AB≠AC时,证明:四边形ADFE为平行四边形;(2)当AB=AC时,顺次连接A、D、F、E四点所构成的图形有哪几类?直接写出构成图形的类型和相应的条件.22.如图,以△ABC的三边为边,在BC的同侧分别作三个等边三角形即△ABD、△BCE、△ACF,那么,四边形AFED是否为平行四边形?如果是,请证明之,如果不是,请说明理由.23.在△ABC中,AB=AC,点P为△ABC所在平面内一点,过点P分别作PE ∥AC交AB于点E,PF∥AB交BC于点D,交AC于点F.若点P在BC边上(如图1),此时PD=0,可得结论:PD+PE+PF=AB.请直接应用上述信息解决下列问题:当点P分别在△ABC内(如图2),△ABC外(如图3)时,上述结论是否成立?若成立,请给予证明;若不成立,PD,PE,PF与AB之间又有怎样的数量关系,请写出你的猜想,不需要证明24.如图1,P为Rt△ABC所在平面内任意一点(不在直线AC上),∠ACB=90°,M为AB边中点.操作:以PA、PC为邻边作平行四边形PADC,连续PM并延长到点E,使ME=PM,连接DE.探究:(1)请猜想与线段DE有关的三个结论;(2)请你利用图2,图3选择不同位置的点P按上述方法操作;(3)经历(2)之后,如果你认为你写的结论是正确的,请加以证明;如果你认为你写的结论是错误的,请用图2或图3加以说明;(注意:错误的结论,只要你用反例给予说明也得分)(4)若将“Rt△ABC”改为“任意△ABC”,其他条件不变,利用图4操作,并写出与线段DE有关的结论(直接写答案).25.在一次数学实践探究活动中,小强用两条直线把平行四边形ABCD分割成四个部分,使含有一组对顶角的两个图形全等;(1)根据小强的分割方法,你认为把平行四边形分割成满足以上全等关系的直线有无数组;(2)请在图中的三个平行四边形中画出满足小强分割方法的直线;(3)由上述实验操作过程,你发现所画的两条直线有什么规律?26.如图,在直角梯形ABCD中,AB∥CD,∠BCD=Rt∠,AB=AD=10cm,BC=8cm.点P从点A出发,以每秒3cm的速度沿折线ABCD方向运动,点Q 从点D出发,以每秒2cm的速度沿线段DC方向向点C运动.已知动点P、Q 同时发,当点Q运动到点C时,P、Q运动停止,设运动时间为t.(1)求CD的长;(2)当四边形PBQD为平行四边形时,求四边形PBQD的周长;(3)在点P、点Q的运动过程中,是否存在某一时刻,使得△BPQ的面积为20cm2?若存在,请求出所有满足条件的t的值;若不存在,请说明理由.27.已知平行四边形的三个顶点的坐标分别为O(0,0)、A(2,0)、B(1,1),则第四个顶点C的坐标是多少?28.已知平行四边形ABCD的周长为36cm,过D作AB,BC边上的高DE、DF,且cm,,求平行四边形ABCD的面积.29.如图,在平面直角坐标系中,已知O为原点,四边形ABCD为平行四边形,A、B、C的坐标分别是A(﹣3,),B(﹣2,3),C(2,3),点D在第一象限.(1)求D点的坐标;(2)将平行四边形ABCD先向右平移个单位长度,再向下平移个单位长度所得的四边形A1B1C1D1四个顶点的坐标是多少?(3)求平行四边形ABCD与四边形A1B1C1D1重叠部分的面积?30.如图所示.▱ABCD中,AF平分∠BAD交BC于F,DE⊥AF交CB于E.求证:BE=CF.1、解答:(1)∵四边形ABCD是平行四边形,∴AB=CD,AB∥CD,∴∠ABD=∠CDB,∵AE⊥BD于E,CF⊥BD于F,∴∠AEB=∠CFD=90°,∴△ABE≌△CDF(A.A.S.),∴BE=DF;(2)四边形MENF是平行四边形.证明:有(1)可知:BE=DF,∵四边形ABCD为平行四边行,∴AD∥BC,∴∠MDB=MBD,∵DM=BN,∴△DNF≌△BNE,∴NE=MF,∠MFD=∠NEB,∴∠MFE=∠NEF,∴MF∥NE,∴四边形MENF是平行四边形.2、解答:证明:∵四边形AECF是平行四边形∴OE=OF,OA=OC,AE∥CF,∴∠DFO=∠BEO,∠FDO=∠EBO,∴△FDO≌△EBO,∴OD=OB,∵OA=OC,∴四边形ABCD是平行四边形.3、解答:证明:(1)∵BF=DE,∴BF﹣EF=DE﹣EF,即BE=DE,∵AE⊥BD,CF⊥BD,∴∠AEB=∠CFD=90°,∵AB=CD,∴Rt△ABE≌Rt△CDF(HL);(2)∵△ABE≌△CDF,∴∠ABE=∠CDF,∴AB∥CD,∵AB=CD,∴四边形ABCD是平行四边形,∴AO=CO.4、解答:证明:∵DE,DF是△ABC的中位线,∴DE∥AB,DF∥AC,∴四边形AEDF是平行四边形,又∵∠BAC=90°,∴平行四边形AEDF是矩形,∴EF=AD.5、解答:解:猜想线段CD与线段AE的大小关系和位置关系是:平行且相等.证明:∵CE∥AB,∴∠DAO=∠ECO,∵OA=OC,∴△ADO≌△ECO,∴AD=CE,∴四边形ADCE是平行四边形,∴CD AE.6、解答:证明:由平行四边形可知,AD=CB,∠DAE=∠FCB,又∵AE=CF,∴△DAE≌△BCF,∴DE=BF,∠AED=∠CFB又∵M、N分别是DE、BF的中点,∴ME=NF又由AB∥DC,得∠AED=∠EDC∴∠EDC=∠BFC,∴ME∥NF∴四边形MFNE为平行四边形.7、解答:证明:连接AC交BD于点O,∵四边形ABCD为平行四边形,∴OA=OC,OB=OD.∵BE=DF,∴OE=OF.∴四边形AECF为平行四边形.8、解答:证明:∵四边形ABCD是平行四边形,∴CD=AB,AD=CB,∠DAB=∠BCD.又∵△ADE和△CBF都是等边三角形,∴DE=BF,AE=CF.∠DAE=∠BCF=60°.∵∠DCF=∠BCD﹣∠BCF,∠BAE=∠DAB﹣∠DAE,∴∠DCF=∠BAE.∴△DCF≌△BAE(SAS).∴DF=BE.∴四边形BEDF是平行四边形.9、解答:证明:∵E是AC的中点,∴EC=AC,又∵DB=AC,∴DB=EC.又∵DB∥EC,∴四边形DBCE是平行四边形.∴BC=DE.10、解答:解:设P,Q同时出发t秒后四边形PDCQ或四边形APQB是平行四边形,根据已知得到AP=t,PD=24﹣t,CQ=2t,BQ=30﹣2t.(1)若四边形PDCQ是平行四边形,则PD=CQ,∴24﹣t=2t∴t=8∴8秒后四边形PDCQ是平行四边形;(2)若四边形APQB是平行四边形,则AP=BQ,∴t=30﹣2t∴t=10∴10秒后四边形APQB 是平行四边形11、解答:证明:∵D、E、F分别是△ABC各边的中点,根据中位线定理知:DE∥AC,DE=AF,EF∥AB,EF=AD,∴四边形ADEF为平行四边形.故AE与DF互相平分.12、解答:证明:∵▱ABCD中,对角线AC交BD于点O,∴OB=OD,又∵四边形AODE是平行四边形,∴AE∥OD且AE=OD,∴AE∥OB且AE=OB,∴四边形ABOE是平行四边形,同理可证,四边形DCOE也是平行四边形.13、解答:证明:连接EG、GF、FH、HE,点E、F、G、H分别是AB、CD、AC、BD的中点.在△ABC中,EG=BC;在△DBC中,HF=BC,∴EG=HF.同理EH=GF.∴四边形EGFH为平行四边形.∴EF与GH互相平分.14、解答:证明:∵四边形ABCD是平行四边形,∴AM∥QC,AP∥NC.又∵MN∥AC,∴四边形AMQC为平行四边形,四边形APNC为平行四边形.∴AC=MQ AC=NP.∴MQ=NP.15、解答:证明:如答图所示,∵点O为平行四边形ABCD对角线AC,BD的交点,∴OA=OC,OB=OD.∵G,H分别为OA,OC的中点,∴OG=OA,OH=OC,∴OG=OH.又∵AB∥CD,∴∠1=∠2.在△OEB和△OFD中,∠1=∠2,OB=OD,∠3=∠4,∴△OEB≌△OFD,∴OE=OF.∴四边形EHFG为平行四边形.16、解答:(1)证明:∵四边形ABCD是平行四边形,17、∴AB=CD,AB∥CD,∴∠GBE=∠HDF.又∵AG=CH,∴BG=DH.又∵BE=DF,∴△GBE≌△HDF.∴GE=HF,∠GEB=∠HFD,∴∠GEF=∠HFE,∴GE∥HF,∴四边形GEHF是平行四边形.(2)解:仍成立.(证法同上)17、解答:(1)证明:∵AF∥EC,∴∠DFA=∠DEC,∠DAF=∠DCE,∵D是AC的中点,∴DA=DC,∴△DAF≌△DCE,∴AF=CE;(2)解:四边形AFCE是正方形.理由如下:∵AF∥EC,AF=CE,∴四边形AFCE是平行四边形,又∵AC=EF,∴平行四边形AFCE是矩形,∴∠FCE=∠CFA=90°,而∠ACB=135°,∴∠FCA=135°﹣90°=45°,∴∠FAC=45°,∴FC=FA,∴矩形AFCE是正方形.18、解答:(1)证明:在平行四边形ABCD中,AB∥CD,且AB=CD,又∵AE∥BD,∴四边形ABDE是平行四边形,∴AB=DE,∴CD=DE,即D是EC的中点;(2)解:连接EF,∵EF⊥BF,∴△EFC是直角三角形,又∵D是EC的中点,∴DF=CD=DE=2,在平行四边形ABCD中,AB∥CD,∵∠ABC=60°,∴∠ECF=∠ABC=60°,∴△CDF是等边三角形,∴FC=DF=2.故答案为:2.19、解答:证明:(1)∵△ABC是等边三角形,∴∠ABC=60°,∵∠EFB=60°,∴∠ABC=∠EFB,∴EF∥DC(内错角相等,两直线平行),∵DC=EF,∴四边形EFCD是平行四边形;(2)连接BE∵BF=EF,∠EFB=60°,∴△EFB是等边三角形,∴EB=EF,∠EBF=60°∵DC=EF,∴EB=DC,∵△ABC是等边三角形,∴∠ACB=60°,AB=AC,∴∠EBF=∠ACB,∴△AEB≌△ADC,∴AE=AD.20、解答:解:(1)如图,四边形EFGH是平行四边形.连接AC,∵E、F分别是AB、BC的中点,∴EF∥AC,EF=AC同理HG∥AC,∴EF∥HG,EF=HG∴EFGH是平行四边形;(2)四边形ABCD的对角线垂直且相等.∵假若四边形EFGH为正方形,∴它的每一组邻边互相垂直且相等,∴根据中位线定理得到四边形ABCD的对角线应该互相垂直且相等.21、解答:(1)证明:∵△ABE、△BCF为等边三角形,∴AB=BE=AE,BC=CF=FB,∠ABE=∠CBF=60°.∴∠CBA=∠FBE.∴△ABC≌△EBF.∴EF=AC.又∵△ADC为等边三角形,∴CD=AD=AC.∴EF=AD.同理可得AE=DF.∴四边形AEFD是平行四边形.(2)解:构成的图形有两类,一类是菱形,一类是线段.当图形为菱形时,∠BAC≠60°(或A与F不重合、△ABC不为正三角形)当图形为线段时,∠BAC=60°(或A与F重合、△ABC为正三角形).22、解答:解:四边形AFED是平行四边形.证明如下:在△BED与△BCA中,BE=BC,BD=BA(均为同一等边三角形的边)∠DBE=∠ABC=60°﹣∠EBA∴△BED≌△BCA(SAS)∴DE=AC又∵AC=AF∴DE=AF在△CBA与△CEF中,CB=CE,CA=CF∠ACB=∠FCE=60°+∠ACE∴△CBA≌△CEF(SAS)∴BA=EF又∵BA=DA,∴DA=EF故四边形AFED为平行四边形(两组对边分别相等的四边形是平行四边形).23、解答:解:图2结论:PD+PE+PF=AB.证明:过点P作MN∥BC分别交AB,AC于M,N两点,由题意得PE+PF=AM.∵四边形BDPM是平行四边形,∴MB=PD.∴PD+PE+PF=MB+AM=AB,即PD+PE+PF=AB.图3结论:PE+PF﹣PD=AB.24、解答:解:(1)DE∥BC,DE=BC,DE⊥AC.(2)如图4,如图5.(3)方法一:如图6,连接BE,∵PM=ME,AM=MB,∠PMA=∠EMB,∴△PMA≌△EMB.∵PA=BE,∠MPA=∠MEB,∴PA∥BE.∵平行四边形PADC,∴PA∥DC,PA=DC.∴BE∥DC,BE=DC,∴四边形DEBC是平行四边形.∴DE∥BC,DE=BC.∵∠ACB=90°,∴BC⊥AC,∴DE⊥AC.方法二:如图7,连接BE,PB,AE,∵PM=ME,AM=MB,∴四边形PAEB是平行四边形.∴PA∥BE,PA=BE,余下部分同方法一:方法三:如图8,连接PD,交AC于N,连接MN,∵平行四边形PADC,∴AN=NC,PN=ND.∵AM=BM,AN=NC,∴MN∥BC,MN=BC.又∵PN=ND,PM=ME,∴MN∥DE,MN=DE.∴DE∥BC,DE=BC.∵∠ACB=90°,∴BC⊥AC.∴DE⊥AC.(4)如图9,DE∥BC,DE=BC.25、解答:解:(1)无数;(2)作图的时候要首先找到对角线的交点,只要过对角线的交点,任画一条直线即可.如图有:AE=BE=DF=CF,AM=CN.(3)这两条直线过平行四边形的对称中心(或对角线的交点).26、解答:解:(1)过点A作AM⊥CD于M,根据勾股定理,AD=10,AM=BC=8,∴DM==6,∴CD=16;(2)当四边形PBQD为平行四边形时,点P在AB上,点Q在DC上,如图,由题知:BP=10﹣3t,DQ=2t∴10﹣3t=2t,解得t=2此时,BP=DQ=4,CQ=12∴∴四边形PBQD的周长=2(BP+BQ)=;(3)①当点P在线段AB上时,即时,如图∴.②当点P在线段BC上时,即时,如图BP=3t﹣10,CQ=16﹣2t∴化简得:3t2﹣34t+100=0,△=﹣44<0,所以方程无实数解.③当点P在线段CD上时,若点P在Q的右侧,即6≤t≤,则有PQ=34﹣5t,<6,舍去若点P在Q的左侧,即,则有PQ=5t﹣34,,t=7.8.综合得,满足条件的t存在,其值分别为,t2=7.8.27、解答:解:当BC∥OA,BC=OA时,C和B的纵坐标相等,若选择AB为对角线,则C1(3,1);若选择OB为对角线,则C2(﹣1,1);当AB∥OC,AB=OC时,选择OA为对角线,则C3(1,﹣1).故第四个顶点坐标是:C1(3,1),C2(﹣1,1),C3(1,﹣1).28、解答:解:设AB=x,则BC=18﹣x,由AB•DE=BC•DFF得:,解之x=10,所以平行四边形ABCD的面积为.29、解答:解:(1)由B、C的坐标可知,AD=BC=4,则可得点D的横坐标为1,点D的纵坐标与点A的纵坐标相等,为,可得点D的坐标为(1,).(2)依题意得A1、B1、C1、D1的坐标分别为A(﹣3+,0),B(﹣2+,2)C(2+,2),D(1+,0).(3)如图,平行四边形ABCD与四边形A1B1C1D1重叠部分的面积为平行四边形DEFG的面积,由题意可得GD=AD﹣AG=4﹣,平行四边形DEFG的高为2﹣=,∴重叠部分的面积为(4﹣)•=4﹣2.30、解答:证明:在平行四边形ABCD中,AD∥BC,∴∠DAF=∠F,又AF平分∠BAD,∴∠DAF=∠BAF,∴∠BAF=∠F,∴AB=BF,又AF平分∠BAD,DE⊥AF,∴∠AOD=∠ADO,又∠BOE=∠AOD=∠EDC,∠ADO=∠E,∴∠EDC=∠E,∴CE=CD,又AB=CD,∴BE=CF.。
