固体物理基础第三章晶格振动
合集下载
固体物理学:第3章 晶格振动

2 2
21 2
cos
qa
1 2
光学支
2 o
1
m
2 1 m
1
2 1
2 2
21
2
cos
qa
2
声学支
2A
1
m
2 1 m
12 22 21 2 cos qa
1 2
三、色散关系
UESTC
ω
当 q=0
ωO
ωA = 0 ωo = 21 2
m
ωA
当
q=
a
a
o
q
a
A
21
m
o
2 2
m
四、格波数
q 2 m
Na
2
Na
m 0 , 1, 2
q
o
波矢q 的取值是分立的,相邻q的“距离”N2a
五、格波数
UESTC
此前研究的晶格原子集体的波动运动就是格波。
晶体中所有原子以相同的频率和振幅在 平衡位置附近作简谐振动,原子的运动状 态在晶体中以波的形式传播,这种简谐波 称为格波。
五、格波数
UESTC
3.1 一维单原子链的振动
一. 物理模型 二. 运动方程 三. 色散关系 四. 波恩-卡曼周期性边界条件 五. 格波数 六. 小结
UESTC
一、物理模型
UESTC
一维简单晶格的振动
平衡位置 振动时偏离 平衡位置
un :第n个原子偏离平衡位置的位移 m :原子质量
一、物理模型
UESTC
V (r) V (0) dV (r) r 1 d 2V (r) r2
UESTC
❖ 对于一维原子链,简约区中波数q的取值总
固体物理第三章总结

时以比T3更快的速度趋于零。 温度越低,与实验吻合的越好。
kBE
局限性
E
kB
D
D
kB
晶体的非简谐效应
1.非简谐效应:
U(
R0
)
U(
R0
)
1 2!
2U R2
R0
2
1 3!
3U R3
R0
3
c 2 g 3
im jm
b1
b2
1010 i 1010 j
m 1 m 1
3.14 1010 i m 1 3.14 1010 j m1
a3 21010 km b3 1010 k m1 3.141010 k m1
S
TO 0,
3.极化声子和电磁声子
0
因为长光学波是极化波,且只有长光学纵波才伴随着宏观
的极化电场,所以长光学纵波声子称为极化声子。 长光学横波与电磁场相耦合,它具有电磁性质,称长光学
横波声子为电磁声子。
1.已知模式密度 ( ) 求:
(1)~+d间隔内的振动模式数;
(2) ~+d间隔内的声子数及晶体中总的声子数;
2
2
2
中的 振~ 动模d式数目:2Lc
2 d ,
v
Sc
2
v2
d ,
Vc
2 2
2
v3
d
一维有一支纵波,二维有一支纵波一支横波,三维有
一支纵波两支横波,纵波与横波速度相等
:
Lc 2 d , 2 v
《固体物理基础》晶格振动与晶体的热学性质

一、三维简单格子
二、三维复式格子
三、第一布里渊区
四、周期性边界条件
◇一个原胞内有P
个不同原子,则
有3P个不同的振
动模式,其中3支 声学波。
◇具有N个原胞的 晶体中共有3PN个
振动模式,其中
3N个声学波, 3N(P-1)个光学波。
四、周期性边界条件 总结
§ 3.4 声子
声子:晶格振动中格波的能量量子
二、一维单原子链的振动
格波
二、一维单原子链的振动
色散关系
二、一维单原子链的振动
色散关系
二、一维单原子链的振动
第一布里渊区
二、一维单原子链的振动
第一布里渊区
二、一维单原子链的振动
第一布里渊区
二、一维单原子链的振动
周期性边界条件
玻恩—卡曼边界条件
二、一维单原子链的振动
周期性边界条件
即q有N个独立的取值—晶格中的原胞数第一布
◇非弹性X射线散射、非弹性中子散射、可见光 的非弹性散射。
§ 3.4 声子
§ 3.4 声子
90K下钠晶体沿三个方向的色散关系
§ 3.5 晶格热容
一、晶格振动的平均能量
热力学中,固体定容热容:
根据经典理论,每一个自由度的平均能量是kBT, kBT/2为平均动能,kBT/2为平均势能,若固体有
N个原子,总平均能量: 取N=1摩尔原子数,摩尔热容是:
二、一维单原子链的振动
一维单原子链的振动
二、一维单原子链的振动
简谐近似下的运动方程
二、一维单Hale Waihona Puke 子链的振动简谐近似下的运动方程
在简谐近似下,原子的相互作用像一个弹 簧振子。一维原子链是一个耦合谐振子,各原 子的振动相互关联传播,形成格波。
固体物理05-晶格振动

周期性边界条件(Born-Karman边界条件)
包含N个原子的环状链。当系统移动N个原子后,振动情况完全复原。
i t naq u ( q ) Ae 格波解: n
周期性边界条件要求: e
iNaq
1
或
2 qn Na
n 为整数
周期性边界条件(Born-Karman边界条件)
b1 b 2 b 3 * N1 N 2 N 3 N
每个q 点有3n支模式,总共有3nN支模,正好是nN个 原子的全部自由度,即已包含所以得振动模式。
Pb的格波谱
无光学模 Why?
Cu的格波谱
光学支 金刚石的振动谱
声学支
作
业
1.分别画出 M=m, 1.5m, 2m 的一维双原子链的色散关系图。
上述方程有 解的条件是:
m 2 2 2 cos aq
2 cos aq M 2
2
0
最后解得方程:
2
( M m) Mm
( M m ) 2 4 Mm sin 2 aq
β(M m) 4 Mm 2 sin aq 1 1 2 Mm ( M m)
u ( x, q ) Ae i t qx
连续介质波中的x表示为空间中的任意一点,而晶格中的格波只 能取na格点的位置。在格波中将aq改变2π的整数倍,原子的实 际振动没有任何不同。可以将q的取值范围限制在:
a
q
a
第一布里渊区
q 取第一布里渊区外的值,不能提供新的波解。
对于格波白色和黑色的这两种波动解是等价的(只在离散 的晶格上有振动),但对连续介质波来说,这两个波是不 一样的。
固体物理基础第3章 晶格振动理论

第3章 晶格振动理论
第3章 晶格振动理论
3.1 一维单原子链 3.2 一维双原子链 3.3 三维晶格的振动 3.4 声子 3.5 晶格振动谱的实验测定 3.6 晶格热容的量子理论 3.7 晶体的非简谐效应 热膨胀和热传导
1
第3章 晶格振动理论
2
第3章 晶格振动理论
3
第3章 晶格振动理论
图3.1 一维单原子链模型
6
第3章 晶格振动理论 将μ(x-Δx,t)和μ(x+Δx,t)在x处泰勒展开,并且只保留到二 阶项,这种假设称为简谐近似,于是有
(x-x, t)(x, t)-12dd(xt,t)x-12d2d(t2x,t)x2 (x+x, t)(x, t)+12dd(xt,t)x+12d2d(t2x,t)x2
把这些连续量带入方程(3.1)整理后即可得到:
率。
根据这种长波近似的极限情形,就可以设想,当长波近
似的条件λ>>a不成立时,方程(3.1)的解仍应具有类似的形式,
即只需在式(3.4)的简谐波的解中用na替代x即可,也就是式
(3.2)
8
第3章 晶格振动理论
3.1.3 色散关系 为了进一步研究一维单原子链振动的特点,可以将式
(3.2)所示的格波ห้องสมุดไป่ตู้式的解代入振动方程(3.1),得:
10
第3章 晶格振动理论
-π<qa≤π
即
-π q π
(3.6)
a
a
而
-
π a
,π a
正好是一维单原子链的第一布里渊区。该范围以
外的q并不能提供其他不同的波。晶体中的格波之所以具有
这样的特点,可以用图3.2来说明。为了便于图示,图中把
第3章 晶格振动理论
3.1 一维单原子链 3.2 一维双原子链 3.3 三维晶格的振动 3.4 声子 3.5 晶格振动谱的实验测定 3.6 晶格热容的量子理论 3.7 晶体的非简谐效应 热膨胀和热传导
1
第3章 晶格振动理论
2
第3章 晶格振动理论
3
第3章 晶格振动理论
图3.1 一维单原子链模型
6
第3章 晶格振动理论 将μ(x-Δx,t)和μ(x+Δx,t)在x处泰勒展开,并且只保留到二 阶项,这种假设称为简谐近似,于是有
(x-x, t)(x, t)-12dd(xt,t)x-12d2d(t2x,t)x2 (x+x, t)(x, t)+12dd(xt,t)x+12d2d(t2x,t)x2
把这些连续量带入方程(3.1)整理后即可得到:
率。
根据这种长波近似的极限情形,就可以设想,当长波近
似的条件λ>>a不成立时,方程(3.1)的解仍应具有类似的形式,
即只需在式(3.4)的简谐波的解中用na替代x即可,也就是式
(3.2)
8
第3章 晶格振动理论
3.1.3 色散关系 为了进一步研究一维单原子链振动的特点,可以将式
(3.2)所示的格波ห้องสมุดไป่ตู้式的解代入振动方程(3.1),得:
10
第3章 晶格振动理论
-π<qa≤π
即
-π q π
(3.6)
a
a
而
-
π a
,π a
正好是一维单原子链的第一布里渊区。该范围以
外的q并不能提供其他不同的波。晶体中的格波之所以具有
这样的特点,可以用图3.2来说明。为了便于图示,图中把
固体物理基础第3章-晶格振动与晶体的热学性质

3-2 一维单原子链模型
格波的色散关系 4 2 2 aq sin ( )
m 2 • ω取正值,则有 (3)
(q)
aq 2 sin( ) m 2 • 频率是波数的偶函数
• 色散关系曲线具有周期性, 仅取简约布里渊区的结果即可 • 由正弦函数的性质可知,只有满足 0 2 / m 的格波 才能在一维单原子链晶体中传播,其它频率的格波将被强
原子n和原子n+1间的距离
非平衡位置
原子n和原子n+1间相对位移
a n1 n
n1 n
3-2 一维单原子链模型
• 忽略高阶项,简谐近似考虑原子 振动,相邻原子间相互作用势能 1 d 2v v(a ) ( 2 ) a 2 2 dr • 相邻原子间作用力 dv d 2v f , ( 2 )a d dr • 只考虑相邻原子的作用,第n个原 子受到的作用力
• 连续介质中的波(如声波)可表示为 Ae ,则可看出 • 格波和连续介质波具有完全类似的形式 • 一个格波表示的是所有原子同时做频率为ω的振动 • 格波与连续介质波的主要区别在于(2)式中,aq取值任意加减 2π的整数倍对所有原子的振动没有影响,所以可将波数q取值 限制为 q a a
V
O
a
r
• 第n个原子的运动方程
(n1 n ) (n n1 ) (n1 n1 2n )
(1)
平衡位置
d 2 n m 2 ( n1 n 1 2n ) dt
非平衡位置
——牛顿第二定律F=ma
3-2 一维单原子链模型
• 上述(1)式的解(原子振动位移)具有平面波的形式
a
)
固体物理 第三章 晶格振动
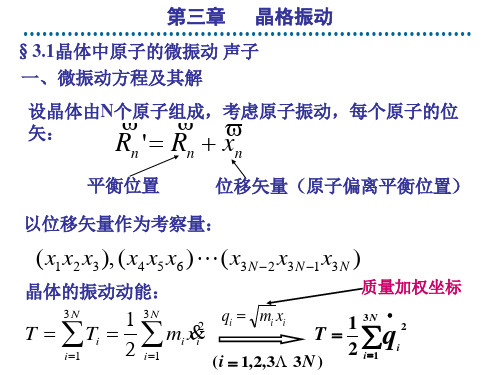
1 2 T = ∑q 2 i =1 i
3N •
3.1晶体中原子的微振动 3.1晶体中原子的微振动 声子 晶体振动势能U (qi ) 按 qi 的幂将势能在平衡位置附近展开为泰勒级数 ∂U 1 ∂ 2U U = U0 + ∑ ( ) 0 qi + ∑ ( ) 0 qi q j + 高阶项 ∂q i 2 ij ∂qi ∂q j i 其中 U 0 = 0 平衡位置处的势能为零势能点
xn = x N + n
又 : xn = Ae
i ( kna − ωt )
又 − π < k ≤ π s = − N + 1,− N + 2⋯⋯ N 共有N个取值 : a a 2 2 2
=1 e ⇒ 2π ⋅ s, = N+ 2π ,− π + 2 2π ,..., π 有N种均匀分布的分立取值 种均匀分布的分立取值 a L a L a 2π L 间隔∆k = ,密度 ,第一布里渊区倒格点数N。 L 2π
, ( l =1, 2, ⋯ 3N )
Ql = Ql0 sin(ωl t + α 1 )
1 ε l = (Q l + ωl2Ql2 ) 2
• 2
能量量子化
1 εl = (nl + )hυl 2
3.2 一维布拉菲格子的晶格振动 一、简谐近似
du 1 d 2u u( x) ≈ u( x0 ) + ∆x + (∆x)2 2 dx r0 2 dx x
3.1晶体中原子的微振动 声子 3.1晶体中原子的微振动 晶格振动模式
质量加权坐标下: 质量加权坐标下:
•• 3N
↔
独立的谐振子
↔
声子
固体物理第三章

LOGO
Click to edit Master text styles
qa qa sin m sin 或者: 2 m 2 2
m 2
m
2 a
——色散关系
为截止频率
2 i a
由上可见,ω与q的关系具有明显的周期性, ω是q的周
期函数,周期为 ,q与 q q (i为整数)对应于 ,q与 q 相应 同样的角频率ω,而且由
相邻原子的位相差:
格波2(绿色标示)的波矢: 相邻原子的位相差:
—— 两种波矢下,格波描述的原子振动是完全相同。
所以,为了保证 un 的单值性,只须将q限制在 , a a (a为晶格常数),这恰好是一维布拉菲格子的第一布里渊区。
LOGO
Click to edit Master text styles
m
2
2
q
弹q
在长波极限下,一维单原子晶 格格波的色散关系和连续介质中 弹性波的色散关系一致。
LOGO
Click to edit Master text styles
下面再比较一下长波近似下,格波与弹性波的相速度
弹性波的相速度: 弹 C
C——弹性模量 ρ——连续介质密度
晶格振动与格波的传播是不可分割的物理现象。
LOGO
Click to edit Master text styles
模型:一维无限长的单原子链,原子间距(晶格常量)为a,
原子质量为m.
u n 代表第n个原子离开平衡位置的位移。
第n个原子和第n+1个原子间的相对位移是
un 1 un
LOGO
Click to edit Master text styles
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Trapping-detrapping
X
D DAP A
Conduction band NRC Valence band
eA0
Excitation photon(PL) electron (CL) …
b-b
exciton
h
浙江大学硅材料国家重点实验室 黄靖云
Why with LO?
• Polariton concept ZnO: ionic binding, charge carrier polarize the lattice lattice distortion Charge carrier accompanied by “phonon cloud”---polaron • Phonon cloud: preferentially LO phonon
频率为j的特解: nj Aje
方程的一般解: n
i jt naqj
j
Ae
j
i jt naqj
1 Nm
Q q, t einaq
q
浙江大学硅材料国家重点实验室 黄靖云
20赫兹---20000赫兹,高于20000赫兹的叫超声波
能量(eV)
声子
0.01
Q(q, t)代表一个新的空间坐标,它已不再是描述某个原
子运动的坐标了,而是反映晶体中所有原子整体运动的
坐标,称为简正坐标。
浙江大学硅材料国家重点实验室 黄靖云
运动方程:
2 Qj q, t j q Qj q, t 0
晶体中所有原子共同参与的同一频率的简谐振动称为 一种振动模式。 能量本征值: 声子的概念: • 声子是晶格振动的能量量子 j • 一种格波即一种振动模式称为一种声子, nj:声子数。 • 当电子或光子与晶格振动相互作用时,总是以 j 为 单元交换能量。 浙江大学硅材料国家重点实验室 黄靖云
浙江大学硅材料国家重点实验室 黄靖云
在q轴上,每一个q的取值所占的空间为
2 Na
q的分布密度:
Na L q 2 2
L=Na ——晶体链的长度
2 Na 2 简约区中波数q的取值总数 q a 2 a
=N=晶体链的原胞数
晶格振动格波的总数=N· =晶体链的自由度数 1
:极化率(电子极化率)
感应的偶极矩将向空间辐射电磁波,形成散射光 电子极化矩会被晶格振动所调制,从而导致频率改 变的非弹性散射 立方晶体: 电子极化率为标量 设: = 0+
0 cos t q r
浙江大学硅材料国家重点实验室 黄靖云
1930诺贝尔物理学奖
浙江大学硅材料国家重点实验室 黄靖云
Quantum theory of phonon-assisted transition • K. Huang and A. Rhys, Proc. Roy. Soc., A204 (1950), 406 • Importance of phonon-assisted PL: affect line width of exciton emission affect decay of exciton affect near band edge emission …
浙江大学硅材料国家重点实验室 黄靖云
第n个原子的运动方程:
mn n 1 n 1 2n
试解
n Ae
2
i t naq
—— 格波方程
m Ae
i t naq
Ae
i t naq iaq
Ae
i t naq iaq
简约区 由6个{100}面 围成的立方体 由12个{110}面 围成的正12面体
2 a
bcc
a
fcc
4 a 4 a
fcc
a
bcc
由8个{111}面和6个 {100}面围成的14面体
浙江大学硅材料国家ห้องสมุดไป่ตู้点实验室 黄靖云
体心立方晶格的倒格子与简约区
浙江大学硅材料国家重点实验室 黄靖云
面心立方晶格的倒格子与简约区
浙江大学硅材料国家重点实验室 黄靖云
四、格波的简谐性、声子概念
1 2 晶体链的动能: T mn 2 n 2 1 晶体链的势能: U n n 1 2 n 2 1 1 2 n n n 1 系统的总机械能: H m 2 n 2 n
一、中子的非弹性散射(单声子过程) 中子的非弹性散射是确定晶格振动谱最有效的实验方法 E1和 p(E2和 p 2) :入射(出射)中子的能量与动量; 1
{
2 p2 p12 E2 E1 q 2M n 2M n p 2 p1 q G
的形式在整个晶体中传播,称为格波。
浙江大学硅材料国家重点实验室 黄靖云
q取不同的值,相邻两原子间的振动位相差不同,则 晶格振动状态不同。 2 q 则 q 与 q描述同一晶格振动状态 若 q a 2 q1 1 4a 1 2a 2 例: q2 q1 4 2 5 a q2 2 a 2 2a 5
浙江大学硅材料国家重点实验室 黄靖云
3 2 Ⅱ 1 3 Ⅱ 2
可以证明,每个布里渊区的体积均相等,都等于第 一布里渊区的体积,即倒格子原胞的体积b 。
浙江大学硅材料国家重点实验室 黄靖云
浙江大学硅材料国家重点实验室 黄靖云
浙江大学硅材料国家重点实验室 黄靖云
正格子 格常数 倒格子 格常数 sc a sc
1 E n j j 2 j=1
N
• 声子可以通过热激发产生,也可以通过光子或其他粒子
与晶格的相互作用过程产生,在相互作用的过程中,声
子数不守恒。 浙江大学硅材料国家重点实验室 黄靖云
布里渊区的边界面是倒格矢的垂直平分面。 布里渊区的几何作图法: 根据晶体结构,作出该晶体的倒易空间点阵,任取一 个倒格点为原点; 由近到远作各倒格矢的垂直平分面; 在原点周围围成一个包含原点在内的最小封闭体积, 即为简约区或第一布里渊区。 简约区就是倒易空间中的Wigner-Seitz原胞。
—— 色散关系
a
q
a
—— 简约区
- 2a - a
0
a
2 a
q
浙江大学硅材料国家重点实验室 黄靖云
格
波:
Ae
i t naq
连续介质弹性波: Ae
i t xq
对于确定的n:第n个原子的位移随时间作简谐振动 对于确定时刻t:不同的原子有不同的振动位相 q的物理意义:沿波的传播方向(即沿q的方向)上,单 位距离两点间的振动位相差。 格波解:晶体中所有原子共同参与的一种频率相同的振 动,不同原子间有振动位相差,这种振动以波
{
k 1 和1:入射光的波矢与频率 k 2 和2:散射光的波矢与频率
2 1 q k 2 k 1 q G
浙江大学硅材料国家重点实验室 黄靖云
Raman散射:
入射光较弱时: p E
浙江大学硅材料国家重点实验室 黄靖云
理解
§3.2 确定晶格振动谱的实验方法
晶格振动谱可以利用中子、可见光光子或X光光
子受晶格的非弹性散射来测定。
中子(或光子)与晶格的相互作用即中子(或光子) 与晶体中声子的相互作用。中子(或光子)受声子的非
弹性散射表现为中子吸收或发射声子的过程。
只讨论单声子过程
浙江大学硅材料国家重点实验室 黄靖云
“+”:吸收声子的散射过程, “-”:发射声子散射过程; Mn:中子质量; G :倒格矢
浙江大学硅材料国家重点实验室 黄靖云
能量的转化与守恒
• • • • • • • 动能 势能 电能 光能 热能 核能 化学能 1/2mv2 mgh Pt(UIt) hc/λ kT mc2 反应能
浙江大学硅材料国家重点实验室 黄靖云
浙江大学硅材料国家重点实验室 黄靖云
Pb
Cu
浙江大学硅材料国家重点实验室 黄靖云
Si
GaAs
浙江大学硅材料国家重点实验室 黄靖云
金刚石
浙江大学硅材料国家重点实验室 黄靖云
NaI
浙江大学硅材料国家重点实验室 黄靖云
二、可见光的非弹性散射
发射或吸收光学声子的散射称为Raman散射
发射或吸收声学声子的散射称为Brillouin散射 能量守恒和准动量守恒(单声子过程):
q G q
有
2 2 p p p2 p1 1 2 2M n 2M n
慢中子的能量:0.020.04 eV,与声子的能量同数量级; 中子的de Broglie波长:2 3×10-10 m(2 3 Å),与晶 格常数同数量级,可直接准确地给出晶格振动谱的信息。 中子的非弹性散射被广泛地用于研究晶格振动谱。 局限性:不适用于原子核对中子有强俘获能力的情况
2 Ae
i t n aq
m 2 eiaq eiaq 2 2 cos aq 1
解得
1 2 sin aq m 2
—— 色散关系
浙江大学硅材料国家重点实验室 黄靖云
二、格波的简约性质、简约区
1 2 sin aq m 2
(q)
浙江大学硅材料国家重点实验室 黄靖云
三、周期性边界条件(Born-Karman边界条件)
N+1
1 2
n
N N+2
N+n
Ae
N n
