汉明码编译码及纠错能力验证实验
QPSK解调与汉明码

通信原理实验报告实验题目:QPSK解调与汉明码实验成绩:学生姓名:学号:指导教师:杨俊东学院名称:信息学院专业:通信工程年级: 2013级一、实验目的1.掌握汉明码编译码原理2.掌握汉明码纠错检错原理3.通过纠错编解码实验,加深对纠错编解码理论的理解二、实验原理三、实验步骤项目一汉明码编码规则验证实验:编码输入输出(CH1为编码输入CH2编码输出)项目二汉明码检纠错性能实验译码输入与译码输出 32K编码输入与56K编码输出(CH1为译码输入CH2译码输出)(CH1为32K编码输入 CH2为56K编码输出)延时输出与译码输出插错指示与误码指示(CH1为延时输出 CH2为译码输出)(CH1为插错指示 CH2为误码指示)帧同步信号与插错指示(CH1为帧同步信号 CH2为插错指示)项目三QPSK相干解调实验DIN1与DOUT 原始时钟信号与解调恢复时钟信号(CH1为DIN1 CH2 DOUT)(CH1为原始时钟信号 CH2为解调恢复时钟信号)四、实验小结经实验可以得出:由图一可按一定的规律即以延时输出为参考点,从后向前读出7位的位出错,实验书上的α2α1编码输出,得出汉明码的编码规则,发现此实验中一直都是α6α0 冗余位。
填表结果与通信原理课本一致。
分析图二可知汉明码具有纠错能力,汉明码是一种效率较高的线性编码分组,它的监督关系以及编码规则见下图所示:编码输入部分受32KHz的时钟信号控制,汉明码编码输出部分受56KHz时钟信号控制。
这样可以保证信号传输4个码元的同时汉明码编码7个码元,实现汉明码的监督。
分析图三,对比编码时钟和串并转换后出来的时钟可以看出4/7的占用率,多出了三bit的信号用于冗余编码。
所以信号编码速率加快了。
观察图七可得,通过天线接收译码输出,可发现输入与输出之间存在延时,所谓时钟同步就是指时钟的上升沿在波形的中间位置进行采样判决,所以出现延时。
五、实验思考题及解答1.汉明码编码效率?纠检错与码距的关系。
汉明码编译码实验

汉明码编译码实验一、实验目的1.掌握汉明码2的编解码原理。
掌握汉明码的纠错和检测原理二、实验内容1.汉明码编码实验。
2.汉明码译码实验。
3、汉明码纠错检错能力验证实验。
三、实验设备lte-tx-02e通信原理综合实验系统----------------------------------------------模块8四、实验原理在随机信道中,错码的出现是随机的,且错码之间是统计独立的。
例如,由高斯白噪声引起的错码就具有这种性质。
因此,当信道中加性干扰主要是这种噪声时,就称这种信道为随机信道。
由于信息码元序列是一种随机序列,接收端是无法预知的,也无法识别其中有无错码。
为了解决这个问题,可以由发送端的信道编码器在信息码元序列中增加一些监督码元。
这些监督码元和信码之间有一定的关系,使接收端可以利用这种关系由信道译码器来发现或纠正可能存在的错码。
在信息码元序列中加入监督码元就称为差错控制编码,有时也称为纠错编码。
不同的编码方法有不同的检错或纠错能力。
有的编码就只能检错不能纠错。
那么,为了纠正一个错位码,至少应该向块码中添加多少监督位?编码效率可以提高吗?基于这一思想的研究催生了汉明码。
汉明码是一种线性分组码,它能纠正位错码,编码效率高。
接下来,我们介绍了汉明码的构造原理。
一般说来,若码长为n,信息位数为k,则监督位数r=n?k。
如果希望用r个监督位构造出r个监督关系式来指示一位错码的n种可能位置,则要求2r?1.≥ n或2R≥ K+R+1下面我们通过一个例子来说明如何具体构造这些监督关系式。
在分组码(n,k)中设k=4。
为了纠正错位代码,从公式(14-1)中可以看出,监管数字R需要≥ 3.如果r=3,那么n=K+r=7。
我们用α6α5?α0代表这七个符号,S1、S2和S3代表三种监督关系中的校正器。
然后可以指定s1s2s3的值与错误代码位置之间的对应关系,如表14-1所示。
表14-1(14-1)s1s2s3001010100011错码位置αααα0123s1s2s3101110111000错码位置α4α5α6无错由表中规定可见,仅当一错码位置在α2、α4、α5或α6时,校正子s1为1;否则s1为0。
汉明码编译码及纠错能力验证实验

汉明码编译码及纠错能力验证实验课程名称通信原理实验序号实验8实验名称汉明码编译码及纠错能力验证实验实验地点 B702实验学时 2 实验类型验证性指导教师实验员专业 _电子信息工程__ 班级 14电信一班学号姓名2021年 12月15日一、实验目的及要求 1.学习汉明码编译码的基本概念; 2.掌握汉明码的编译码方法; 3.验证汉明码的纠错能力。
二、实验原理与内容实验原理:(一)汉明码编码采用?7,4?汉明码,信息位数k?4,监督位数r?n?k?3,可以纠一位错码,生成?1?0矩阵G???0??0表格 1010000100001111011011?0??,编码情况见表格 1。
1??1??7,4? Hamming 编码表信息位监督位信息位监督位 a6a5a4a3 0000 0001 0010 0011 0100 0101 0110 0111 (二)汉明码译码 a2a1a0 000 011 101 110 110 101 011 000 a6a5a4a3 1000 1001 1010 1011 1100 1101 1110 1111 a2a1a0 111 100 010 001 001 010 100 111 计算校正子S??S1,S2,S3?,其中 S1?a6?a5?a4?a2 S2?a6?a5?a3?a1 S3?a6?a4?a3?a0 校正子S的值决定了接收码元中是否有错码,并且指出错码的位置,见表格 2。
表格 2 错码位置示意 S1S2S3 001 010 100 011 实验内容: 1.插入有关实验模块: 2.信号线连接: 3.加电 4.编码模块设置:错码位置 S1S2S3 101 110 111 000 错码位置 a0 a4a5 a1 a2 a3 a6 无错 5.使用双踪示波器CH1观察帧同步输出TP01,CH2观察编码输出TP03,结合实验原理验证汉明编码是否正确(最后一位0为冗余位)。
6.信道误码设置:7.译码模块设置: 8.验证分析汉明码的规则及纠错能力: 9.关机拆线:实验结束,关闭电源,拆除信号连线,并按要求放置好实验模块。
实验三 汉明码编码与译码
实验三汉明码编码与译码一、实验题目1、写一个错误生成器模块,在给定的一个比特流作输入时,它的输出流的每个比特流都以概率p发生了改变,即比特错误概率为p。
2、对m=3,将汉明码编码后的比特流输入到上述模块,然后对收到的字用译码器进行译码。
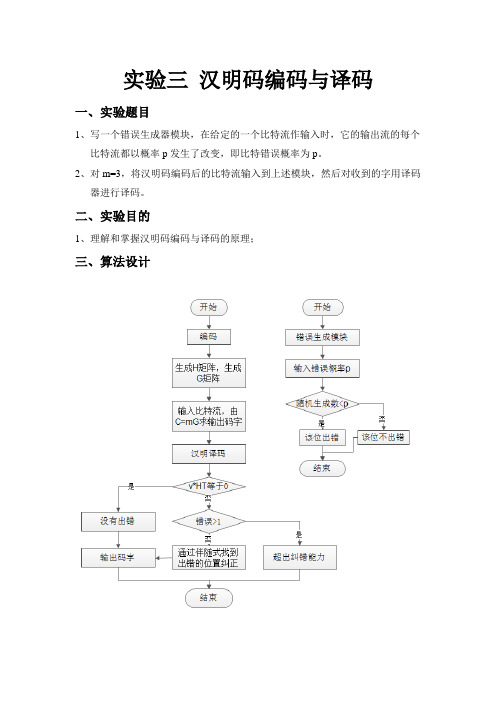
二、实验目的1、理解和掌握汉明码编码与译码的原理;三、算法设计四、程序分析1、错误生成模块:任一给以p,系统任意生成一数,若比p小则让其出错,否则不出错。
2、编码:首先随机生成H矩阵,由H矩阵生成G矩阵,利用C=mG编码。
3、解码:若v*H’=0,则没有出错,直接输出v中前k位;若v*H’!=0,列出所有的e和e*H’得到伴随阵s,若能在s中找到s=v*H则c0=v-e,输出c0中前k位;若找不到s,则输出“错误位数大于纠错能力,无法解码”。
五、程序代码#include <iostream>#include <string> // 字符串处理头文件#include <iomanip> // 输入输出控制头文件#include <math.h>#include <stdlib.h>#include <time.h>using namespace std;void Err_Pro();void Hamming_Decode();intm,n,k,t,err,r,R[100],N[100],COUNT[100],num[100][100],Th[100][100],PT_S[100][100],PT_D[1 00][100];intH[100][100],HT[100][100],Ig[100][100],P[100][100],G[100][100],Ibit[100],Cbit[100],Err_Cbit[1 00],V[100];/**************************************************************************//*函数名:void Binary_Conversion(int i) *//*功能:十-二进制转换*//*说明:该函数输出二进制数为低位在前,高位在后*//**************************************************************************/ void Binary_Conversion(int i){int j=0,temp=0;do // 生成完整n个二进制{temp = i % 2; // 判断相应最低位为0或1(若为2的倍数则为0,否则为1)i = i / 2; // 为考虑前一位为0或1做准备if(j < m) // m确定二进制的位数{N[j] = temp;j++;}}while(i != 0); // 等待i等于0(即等待十进制数为0时不进行二进制转换)}/**************************************************************************/ /*函数名:void Random_Array() */ /*功能:将数组的列随机排放*/ /**************************************************************************/ void Random_Array(){srand(unsigned(time(NULL))); // 随机生成条件(抵消rand函数伪随机效果)cout << endl << "产生随机数为:" << endl;for(int j=0;j<n;j++){loop:r= rand() % n; // 随机生成范围为0~n-1的正整数for(int i=0;i<j;i++){if(R[i] == r) // 如果随机产生的数与已产生的数相等,则重新随机产生数{goto loop;}}R[j] = r; // 产生不重复的随机数cout << setw(4) << r + 1;for(int i=0;i<m;i++){PT_D[i][j] = PT_S[i][r]; // 顺序转置系数矩阵->随机转置系数矩阵}}}/**************************************************************************/ /*函数名:void Creat_H() */ /*功能:创建系统型奇偶校验矩阵H */ /*说明:系统型奇偶校验矩阵H由转置负系数矩阵和单位矩阵组成*/ /**************************************************************************/ void Creat_H(){int i,j,count0=0,count1=0,count2=0,count3=0;/*************生成单位矩阵Ih************/ //教材P101for(i=0;i<m;i++) //i表示行j表示列{for(j=0;j<n;j++){if((j >= k) && (i+k == j))Ih[i][j] = 1;elseIh[i][j] = 0;}}/*********生成转置负系数矩阵PT**********/for(i=0;i<m;i++) // 转置二进制转换数组到PT_S{for(j=0;j<n;j++){PT_S[i][j] = num[j][i]; // 生成顺序转置系数矩阵}}Random_Array();//将数组的列随机排放for(j=0;j<n;j++){for(i=0;i<m;i++){if(PT_D[i][j] == 0)count0 ++;}count1 = count0; // count1记录每一列1的个数count0 = 0;if(count1 == (m-1)) // 将只有一位为1其余位为0的列的所有位置0{for(i=0;i<m;i++){PT_D[i][j] = 0;}}else// COUNT数组记录只有一位为1其余位为0的列为0,其余位的值为PT_D列的位置值+1 COUNT[count2] = j + 1;count2 ++;}for(int q=0;q<n;q++) // 将PT_D的至少有两个1的列赋给PT{if(COUNT[q] > 0){for(i=0;i<m;i++)PT[i][count3] = PT_D[i][q];count3 ++;}}cout << endl;/********生成系统型奇偶校验矩阵H********/for(i=0;i<m;i++){for(j=0;j<n;j++){H[i][j] = PT[i][j] + Ih[i][j];}}cout << endl << "系统型奇偶校验矩阵H为:" << endl;for(i=0;i<m;i++) // 显示系统型奇偶校验矩阵H{for(j=0;j<n;j++){cout << setw(2) << H[i][j] << setw(2);}cout << endl;}}/**************************************************************************/ /*函数名:void Creat_G() *//*功能:创建系统型生成矩阵G */ /*说明:系统型生成矩阵G由单位矩阵和系数矩阵组成*/ /**************************************************************************/ void Creat_G(){int i,j;/*************生成单位矩阵Ig************/for(i=0;i<k;i++){for(j=0;j<n;j++){if(i == j)Ig[i][j] = 1;elseIg[i][j] = 0;}}/*************生成系数矩阵P*************/for(j=0;j<n;j++){for(i=0;i<k;i++){if(j>k-1)P[i][j] = PT[j-k][i];}}/**********生成系统型生成矩阵G**********/for(i=0;i<k;i++){for(j=0;j<n;j++){G[i][j] = P[i][j] + Ig[i][j];}}cout << endl << "系统型生成矩阵G为:" << endl;for(i=0;i<k;i++) // 显示系统型奇偶校验矩阵H{for(j=0;j<n;j++){cout << setw(2) << G[i][j] << setw(2);}cout << endl;}}/*******************************主函数*************************************/ int main(){int i,j;cout << setw(30) << "汉明码" << endl;cout << "请输入校验元位数m = ";cin >> m;n = pow(2,m) - 1; //码长k = pow(2,m) - 1 -m; //信息源位数cout << "提示:" << setw(10) << "您输入的为(" <<n<< "," <<k<< ")汉明码,可纠正" << t << "个错误" << endl;cout << endl;for(i=0;i<n;i++) // 将n个转换二进制数组存入二维数组{Binary_Conversion(i+1);for(j=0;j<m;j++){num[i][j] = N[j];//num[i][m-j-1] = N[j]; // m-j-1意义在于将二进制高位在前,低位在后}}cout << "n个二进制转换表为:" << endl;for(i=0;i<n;i++) // 输出二进制转换对应表低位在前高位在后{for(j=0;j<m;j++){cout << num[i][j] << setw(2);}cout << setw(4);}cout << endl;Creat_H();Creat_G();cout << endl << "请输入" << k << "位信息比特流:" << endl;for(i=0;i<k;i++)cin >> Ibit[i];for(i=0;i<n;i++){for(j=0;j<k;j++){Cbit[i] += (Ibit[j] * G[j][i]); // 十进制加法Cbit[i] = Cbit[i] % 2; // 将十进制转换二进制}}cout << endl << "输出" << n << "位码字比特流:" << endl;for(i=0;i<n;i++) //输出编码后的码字cout << setw(3) << Cbit[i];cout << endl;Err_Pro(); //错误概率函数Hamming_Decode(); //汉明译码return 0;}/**************************************************************************/ /*函数名:void Err_Pro() */ /*功能:产生错误概率函数*/ /**************************************************************************/ void Err_Pro(){float p;cout << endl << "请输入错误概率p = ";cin >> p;for(int x=0;x<n;x++){if((float)((rand() % 1001) * 0.001) < p) // 如果小于概率,则原码0与1互换{err ++;Err_Cbit[x] = (Cbit[x] + 1) % 2;}elseErr_Cbit[x] = Cbit[x]; // 如果大于错误概率,则赋值原码}cout << endl << "输出" << n << "位码字比特流(每位等概出错):" << endl;for(int y=0;y<n;y++)cout << setw(3) << Err_Cbit[y];cout << endl;}/**************************************************************************/ /*函数名:void Hamming_Decode() */ /*功能:汉明译码函数*//**************************************************************************/ void Hamming_Decode(){int i,j,flag=0,d;for(i=0;i<n;i++) // 得到H的转置矩阵HT{for(j=0;j<m;j++){HT[i][j] = H[j][i];}cout << endl << "输出转置奇偶校验矩阵HT为:" << endl;for(i=0;i<n;i++){for(j=0;j<m;j++){cout << setw(3) << HT[i][j] << setw(3);}cout << endl;}for(i=0;i<m;i++) // 计算伴随矩阵{for(j=0;j<n;j++){V[i] += Err_Cbit[j] * HT[j][i];}if(V[i] % 2 == 0) // 将十进制转换二进制V[i] = 0;elseV[i] = 1;}cout << endl << "输出伴随矩阵为:" << endl;for(i=0;i<m;i++)cout << V[i] << setw(2);cout << endl;for(i=0;i<m;i++){if(V[i] == 0) // 如果伴随矩阵为零矩阵,则直接输出原码流{if(i == m-1){cout << endl << "<译码正确!>输出码流为:" << endl;for(j=0;j<n;j++)cout << Err_Cbit[j] << setw(3);cout << endl;}}else{flag ++; // 如果伴随矩阵为非零矩阵,则标志位自加1break;}if(flag != 0){if(err == 1) // 伴随矩阵为非零矩阵时执行{for(i=0;i<n;i++){for(j=0;j<m;j++){if(V[j] == HT[i][j]){if(j == (m-1)) d = i;//d记录行}elsebreak;}}cout << endl << "<译码正确!>输出码流为:"<< endl;Err_Cbit[d] = (Err_Cbit[d] + 1) % 2;for(i=0;i<n;i++)cout << setw(3) << Err_Cbit[i] << setw(3);cout << endl;}elsecout << endl << "由于本次编码有" << err << "个错误位,大于纠错能力" << t << ",故<译码错误!>" << endl;}}六、程序运行结果。
Hamming码实验报告(孙鹏跃)

信息论与编码基础实验报告学院:电子科学与工程学院队别:四院二队专业: 2006级通信工程专业姓名:孙鹏跃学号: 200604015002国防科学技术大学电子科学与工程学院实验三 汉明码编译码一、【设计思想】1948年,Bell 实验室的C.E.Shannon 发表的《通信的数学理论》,是关于现代信息理论的奠基性论文,它的发表标志着信息与编码理论这一学科的创立。
Shannon 在该文中指出,任何一个通信信道都有确定的信道容量C,如果通信系统所要求的传输速率R 小于C,则存在一种编码方法,当码长n 充分大并应用最大似然译码(MLD ,MaximumLikelihoodDecdoding)时,信息的错误概率可以达到任意小。
从Shannon 信道编码定理可知,随着分组码的码长n 或卷积码的约束长度N 的增加,系统可以取得更好的性能(即更大的保护能力或编码增益),而译码的最优算法是MLD,MLD 算法的复杂性随n 或N 的增加呈指数增加,因此当n 或N 较大时,MLD 在物理上是不可实现的。
因此,构造物理可实现编码方案及寻找有效译码算法一直是,信道编码理论与技术研究的中心任务。
信息传输的可靠性是所有通信系统努力追求的首要目标。
要实现高可靠性的传输,可采用诸如增大发射功率、增加信道带宽、提高天线增益等传统方法,但这些方法往往难度比较大,有些场合甚至无法实现。
而香农信息论指出:对信息序列进行适当的编码后可以提高信道传输的可靠性,这种编码即是信道编码。
信道编码是在著名的信道编码定理指导下发展起来的,几十年来已取得了丰硕的成果。
现将信道编码定理简述如下:每一个信道都具有确定的信道容量C,对于任何小于C 的信息传输速率R,总存在一个码长为n,码率等于R 的分组码,若采用最大似然译码,则其译码错误概率Pe 满足: )(R nE E Ae P −≤其中A 为常数,E(R )为误差函数。
香农编码定理仅仅是一个存在性定理,他只是告诉我们确实存在这样的好码,但并没有说明如何构造这样的码,但定理却为寻找这种码指明了方向。
通信原理实验 汉明编码和译码实验 实验报告

姓名:学号:班级:
第周星期第大节
实验名称:汉明编码和译码实验
一、实验目的
1.掌握汉明码编译码原理。
2.掌握汉明码纠错检错原理。
3.通过纠错编解码实验,加深对纠错编解码理论的理解。
二、实验仪器
1.ZH5001A通信原理综合实验系统
2.20MHz双踪示波器
三、实验内容
2.编码规则验证
(1)输入数据为0011
(2)输入数据为1100
3.译码数据输出观测
(1)m序列方式为11
(1)不加错
♦观测加错指示TPC03与错码检测指示输出波形TPW03波形
(2)加1位错
♦观测加错指示TPC03与错码检测指示输出波形TPW03波形
(4)加3位错
(1)不加错
加2位错不能全部正确译码
(4)加3位错
四、思考题
2.汉明编码器模块的使能开关,译码器模块的使能模块(H_EN断路器)起什么作用?
从电路图中可以看出,没有插入H_EN时,汉明编码器被短路,输出数据没有经过汉明编码。
插入H_EN时,输出数据经过汉明编码。
汉明码编译码及纠错性能验证

汉明码编译码及纠错性能验证目录一、实验目的 (2)二、实验原理 (2)1.汉明编译码介绍 (2)2.汉明编译码原理 (2)3.举例说明 (3)4.实验框图说明 (3)5.框图中各个测量点说明 (4)三、实验任务 (5)四、实验步骤 (5)1. 实验准备 (5)2.汉明码编码原理验证 (5)3.汉明译码观测及纠错能力验证 (8)4.实验结束 (10)五、实验分析 (11)一、实验目的1.学习汉明码编译码的基本概念;2.掌握汉明码的编译码方法;3.验证汉明码的纠错能力。
二、实验原理1.汉明编译码介绍汉明码(Hamming Code)是一个可以有多个校验位,具有检测并纠正一位错误代码的纠错码,所以它也仅用于信道特性比较好的环境中,如以太局域网中,因为如果信道特性不好的情况下,出现的错误通常不是一位。
汉明码的检错、纠错基本思想是将有效信息按某种规律分成若干组,每组安排一个校验位进行奇偶性测试,然后产生多位检测信息,并从中得出具体的出错位置,最后通过对错误位取反(也是原来是 1 就变成 0,原来是 0 就变成 1)来将其纠正。
2.汉明编译码原理●汉明码编码采用(4,7)汉明码,信息位数k=4,监督位数r=n-k=3,可以纠一位错码,生成矩阵G=[1 0 0 0 1 1 10 1 0 0 1 1 00 0 1 0 1 0 10 0 0 1 0 1 1],编码情况见表格1。
表格1 (7,4)Hamming编码表●汉明码译码计算校正子S=[S1,S2,S3],其中S1=a6⨁a5⨁a4⨁a2S2=a6⨁a5⨁a3⨁a1S3=a6⨁a4⨁a3⨁a0校正子S 的值决定了接收码元中是否有错码,并且指出错码的位置,见表格 2。
表格 2 错码位置示意3.举例说明信息位a6a5a4a3=1001,根据表格 1(4,7) Hamming 编码表,编码为1001100,如果在信道传输的过程中产生一位误码,编码接收时变为1101100 ,我们计算校正子:S1=a6⨁a5⨁a4⨁a2=1S2=a6⨁a5⨁a3⨁a1=1S3=a6⨁a4⨁a3⨁a0=0校正子S=110,查找表格 2 错码位置示意,a5产生误码,则译码输出信息位1001。
汉明码编码实验报告

汉明码实验报告一、实验目的实现汉明码纠错编码算法二、实验步骤1、判断是否执行程序2、输入要查错的码字3、分析输入的码字并输出码字4、继续判断三、源代码#include<iostream>using namespace std;void input(int *a){cout<<"请输入7位要查错的码字(输入一个数(0或1)就空格):"<<endl;for(int i=0;i<7;i++)cin>>a[i];}void analyze(int *a,int ht[7][3]){ //二维数组ht[7][3]调用之前一定要明确定义int p[3]={0};int q=0; //数据要初始化int h[3][7];int out[7];for(int k=0;k<3;k++){for(int i=0, j=0;j<7;i++,j++){p[k]=p[k]+a[i]*ht[j][k];p[k]=p[k]%2; //使数值小于2}if(p[k]==1){q++;}}cout<<"伴随式为:"<<p[0]<<p[1]<<p[2]<<endl;if(q==2||q==3){cout<<"一共有"<<q<<"位错误,超越了纠错范围"<<endl; }if(q==0){cout<<"码字没有错误!!"<<endl;cout<<"输出的码字为:";for(int i=0;i<7;i++){out[i]=a[i];cout<<out[i];}cout<<endl;}if(q==1){for(int i=0;i<3;i++){for(int j=0;j<7;j++){if((h[i][j]==p[0])&&(h[i+1][j]==p[1])&&(h[i+2][j]==p[2])){cout<<"要查错的码字的第"<<j+1<<"位出错"<<endl;a[j]=(a[j]+1)%2;cout<<"输出的码字应为";for(i=0;i<7;i++){out[i]=a[i];cout<<a[i];}cout<<endl;}}}}}void main(){int H[4][7]={{1,0,0,0,0,1,1}, //生成矩阵{0,1,0,0,1,0,1},{0,0,1,0,1,1,0},{0,0,0,1,1,1,1}};int h[3][7]={{0,0,0,1,1,1,1}, // 校验矩阵{0,1,1,0,0,1,1},{1,0,1,0,1,0,1}};int ht[7][3]={{0,0,1}, //ht (h的转置矩阵) {0,1,0},{0,1,1},{1,0,0},{1,0,1},{1,1,0},{1,1,1}};int in[7];int c;while(c){cout<<"是否需要查错(是请输入1不是输入0): ";cin>>c;switch(c){case 1: input(in);analyze(in,ht);break;case 0: break; }}}四、运行结果。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课程名称通信原理
实验序号实验8
实验名称汉明码编译码及纠错能力验证实验实验地点B702
实验学时 2 实验类型验证性
指导教师实验员
专业 _电子信息工程__ 班级14电信一班
学号姓名
2016年12 月15 日
五、测试/调试及实验结果分析
图片说明:CH1(黄色)帧同步信号
CH2(浅蓝色)编码后信号
CH3(粉红色)编码前信号
CH4(深蓝色)译码后信号
保护位
无加错的时候设置的原始信号是:1100,编码后的信号是:1100001,译码后的信号为:1100。
对照图片的波形图,无误输出,汉明码正确。
有延时的现象。
1位加错的时候:设置的原始信号是:1100,编码后的信号是:1101001
译码后的信号是:1100 通过计算S1、S2、S3可知错误位为:a3 对照译码后的波形与编码前的波形,可知已经纠错成功。
汉明码的一位纠错功能实现。
有延时的现象。
2位加错的时候:设置的原始信号是:1100,编码后的信号是:1111001
码后的信号是:0111 对照无错的编码后序列,可知错误位为:a3、a4 对照译码后的波形与编码前的波形,可知译码后的波形与编码前的波形对不上。
(7,4)汉明码的2位纠错功能无法实现。
3位加错的时候:设置的原始信号是:1100,编码后的信号是:1011001
码后的信号是:0111 对照无错的编码后序列,可知错误位为:a3、a4、a5 ,对照译码后
的波形与编码前的波形,可知译码后的波形与编码前的波形对不上。
(7,4)汉明码的3位纠错功能无法实现。
4位加错的时候:设置的原始信号是:1100,编码后的信号是:0011001
码后的信号是:0111 对照无错的编码后序列,可知错误位为:a3、a4、a5 、a6 ,对照译码后的波形与编码前的波形,可知译码后的波形与编码前的波形对不上。
(7,4)汉明码的4位纠错功能无法实现。
六、实验结论与体会
1.课堂上对汉明码的理解不够深入,经过本次实验明显加深了我对汉明码的理论的认识和
理解,实际动手才是关键
2.经过编码后的编码序列,在加错码的时候,对a0、a1、a2位没有影响,也就是说这三位
不会在无错的时候编码是什么,加错后这三位的编码还是一样
3.一位加错时,(7,4)汉明码有检错以及纠错的功能,两位加错的时候,只有检错的功能,
却没有纠错的功能,三位或三位以上加错时,既没有检错的功能,也没有纠错的功能;
4.(7,4)汉明码作为一种信道编码的方式,具有一定的纠错检错能力。
