人教版数学七年级下册辅导资料7
(word完整版)人教版数学七年级下册辅导资料7
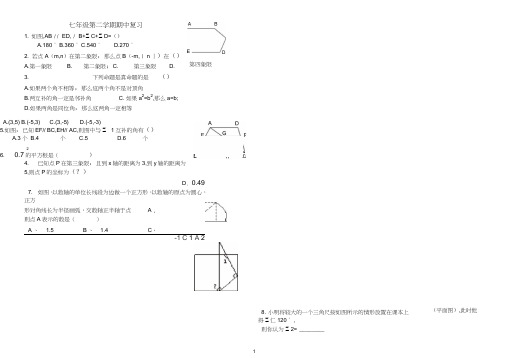
七年级第二学期期中复习1. 如图,AB // ED, / B+Z C+Z D=()A.180 °B.360 °C.540 °D.270 °2. 若点A (m,n )在第二象限,那么点B (-m, | n 丨)在() A.第一象限 B.第二象限;C.第三象限D.3.下列命题是真命题的是()A.如果两个角不相等,那么这两个角不是对顶角B.两互补的角一定是邻补角C. 如果a 2=b 2,那么a=b;D.如果两角是同位角,那么这两角一定相等4.已知点P 在第三象限,且到x 轴的距离为3,到y 轴的距离为5,则点P 的坐标为(?)D . 0.497. 如图,以数轴的单位长线段为边做一个正方形,以数轴的原点为圆心,正方形对角线长为半径画弧,交数轴正半轴于点 A , 则点A 表示的数是( ) A 、 1.5B 、 1.4C 、-1 C 1 A 28. 小明将较大的一个三角尺按如图所示的情形放置在课本上 得Z 仁120 ° ,则你认为Z 2= ________A.(3,5)B.(-5,3)C.(3,-5)D.(-5,-3)5.如图,已知EF// BC,EH// AC,则图中与Z 1互补的角有()A.3个B.4 个C.5D.6 个 26. 0.7的平方根是()(平面图),此时他量第四象限9. 在x轴上表示距离原点.2的点是____________________10.已知、、1.72011 .311,J7 .201 4.147 ,那么0.001720111.大于■ 17小于,11的所有整数的和是12.一个正数x的平方根是2a 3 与 5 a,贝U x= .13.点A在数轴上表示的数为 3 ••• 5 ,点B在数轴上对应的数为5则A B两点的距离为 __________、解答题:(19-22每题9分,23题10分,共46分)15.化简:16.已知,且x是正数,求代数的值14.比较大小'- 5 1 _________21.如图,AB // CD,探讨下面图形中/ APC与/ PAB, / PCD的关系并加以说明17.平面直角坐标系中,顺次连结(-2,1), (-2,-1),(2,-2),(2,3) 各点,你会得到一个什么图形?试求出该图形的面积.4,3<2<1-4 -3 -2 -1 ----------- »-ST ------------->---------------- - ------------------- ----------------- «-----------h-1「1 2 34X18.如图,AB // DE,试问/ B、/ E、/ BCE有什么关系. 解:/ B+/ E=/ BCE过点C作CF // AB, 则 B (又••• AB // DE , AB / CF , 二 (.•./ E=/ ______ (•••/ B +/ E = / 1 + / 2 即/ B +/ E = / BCE .——B19.如图,已知直线AB CD被直线EF所截,如果/ BMN=/ D NF, / 1 = / 2,那么MQ/ NP试写出推理过程20.如图,已知ABC , AD BC于D, E为AB上一点,EF BC于 F , DG//BA 交CA 于G。
七年级下第七章数学知识点(人教版)

第七章七年级下第七章数学知识点(人教版)本章重点讲解:一个距离(点到特殊直线的距离);两个平移(点的平移、图形的平移);三个概 念(有序数对、平面直角坐标系、象限点的对称);五个特征平面直角坐标系、1⑴有序数对 有顺序的两个数a 与b 组成的数对;叫做有序数对;记作(a ; b ) 注:当a ^b 时;(a ;匕)和(b ; a )是不同的两个有序数对.⑵平面直角坐标系 在平面内画两条互相垂直、原点重合的数轴就构成了平面直角坐标系;通常把其中水平的一条数轴称为横轴或x 轴;取向右的方向为正方向;竖直的数轴称为纵轴或 两条数轴的交点叫做原点;x 轴和y 轴统称为坐标轴.⑶象限如右图所示:x 轴和y 轴把坐标平面分成四个部分;称为四个象限; 按逆时针顺序依次叫做第一象限;第二象限;第三象限;第四象限 注:①两条坐标轴不属于任何一个象限.②如果所表示的平面直角坐标系具有实际意义时;要在表示横 轴;纵轴的字母后附上单位.⑷点的坐标 对于坐标平面内的一点 A ;过点A 分别向x 轴、y 轴作垂线;垂足在x 轴、y 轴上对应的数a 、b 分别叫做点A 的横坐标和纵坐标;有序数对(a ; b )叫做 A 的坐标;记作 A (a ; b ). 坐标平面内的点与有序数对是 对应的.注:横坐标写在纵坐标前面;中间用“;”号隔开;再用小括号括起来.2、坐标平面内特殊点的坐标特征⑴ 各象限内点的坐标特征点 P (x ; y )在第一象限 <=> x >0; y >0;点 P (x ; y )在第二象限 <=> x v 0; y >0;点P (x ; y )在第三象限<=> x v 0; y v 0;点P (x ; y )在第四象限<=> x >0; y v 0.⑵坐标轴上点的坐标特征 点P (x ; y )在x 轴上<=> y = 0; x 为任意实数;点P (x ; y )在y 轴上<=> x = 0; y 为任意实数;点P (x ; y )即在x 轴上;又在y 轴上<=> x = 0; y = 0;即点P 的坐标为(0; 0) ⑶两坐标轴夹角平分线上点的坐标特征点P (x ; y )在第一、三象限夹角的角平分线上 <=> x = y ;点P (x ; y )在第二、四象限夹角的角平分线上 <=> x + y = 0. y 轴;取向上的方向为正方向; 厂 --------- ■ ------ ―■ -------------- -------- ■ 1 幫二舉限;策•皐ft!⑷ 平行于坐标轴的直线上的点的坐标特征平行于x 轴直线上的两点;其纵坐标相等;横坐标为两个不相等的实数;平行于y 轴直线上的两点;其横坐标相等;纵坐标为两个不相等的实数.⑸ 坐标平面内对称点的坐标特征点P (a,b )关于x轴的对称点是P'(a;-b );即横坐标不变;纵坐标互为相反数;点P(a,b )关于y轴的对称点是P'(-a ;b);即纵坐标不变;横坐标互为相反数;点P(a,b )关于原点的对称点是P'(-a ;-b);即横坐标互为相反数;纵坐标也互为相反数. 注:点P (a,b)关于点Q(m,n)的对称点是M(2m-a,2n-b).3、用坐标表示地理位置⑴ 直角坐标系法先确定原点;然后画出x轴和y轴;建立平面直角坐标系;再确定它的横坐标及纵坐标;点的坐标可以由横坐标和纵坐标唯一确定.⑵ 方位角法从一定点出发;测量出被侧点到定点的距离;即相对于定点的距离及相对于定点所处的方位角. 点的位置由距离和方位角唯一确定.4、用坐标表示距离点P (x;y)到x轴的距离是I y I;点P (x ;y)到直线y = m的距离是I y—ml;点P (x;y)到y轴的距离是I x I;点P (x;y)到直线x = n的距离是I x—n I ;当P1P2平行于x 轴时;P i(x i ;y i);P2 (X2;y2);I P1P2 I = I x i —x? I ;(y i = y2);当P1P2平行于y 轴时;I P i F2 I = I y i —y2 I;(x i = X2).5、用坐标表示平移⑴ 点的平移将点(x,y)向右(或向左)平移 a 个单位;可得对应点(x+a;y){或(x—a;y)} ;可记为“右加左减;纵不变”;将点(x,y)向上(或向下)平移b 个单位;可得对应点(x;y+b){或(x;y—b)} ;可记为“上加下减;横不变” .⑵ 图形的平移把一个图形的各个点的横坐标都加上(或减去)一个正数向左)平移 a 个单位得到的.把一个图形的各个点的纵坐标都加上(或减去)一个正数向下)平移a个单位得到的.a;相应的新图形就是把原图形向右(或a;相应的新图形就是把原图形向上(或。
人教版数学七年级下 第7章《三角形》复习ppt课件

基础过关
1.下列条件中能组成三角形的是( C ) A、5cm,7cm,13cm B、3cm,5cm,9cm C、6cm,9cm,14cm D、5cm,6cm,11cm 2.三角形的两边为7cm和5cm,则第三边x的范 围是 2cm<X <12cm ; 3.等腰三角形的两边为7cm和5cm,则三角形 的周长是x是 ;
A
100°
敢来应战吗?
D
C
B
这个图形好熟悉哦~
变式(一)、如图:
∠A=100°,∠ABD=30°,∠ACD=35° 求∠BDC的度数。
A
100°
D
35°
30°
C
B
噫~好像有点不一样~
变式(二)、如图:
∠A=50°,BD、CD分别平分两个外角 求∠BDC的度数。 A
50 °
C B
E F D
怎么变来变去都是这种类型哦~
B
基础过关
8.(06,江西)如图,则ABC的形状是( A、锐角三角形 B、钝角三角形 C、直角三角形 D、等腰三角形
C )
9.如图, ∠A+∠B+∠C+∠D+∠E+∠F=
F
360° ;
E D
B 2a C 3a
a
A
A
B C
基础过关
9、如果一个三角形的各内角与一个外角的 和是225°,则与这个外角相邻的内角是____度. 10.AB∥CD, ∠A=45°∠C=80°,求∠M的度数. 11.如图,直线DE与△ABC的三边所在直线交与D、 E、F,A=40°,D=25°,DE⊥AB,求ACB的度数.
A
A E
E O
D
B
C
B
人教版数学七年级下册 7课件

新课讲解
分析:本题主要考查平面直角坐标系的概念.根据平 面直角坐标系的概念可知A,B,C项正确.D 项不正确,因为平面直角坐标系必须由数轴构 成,且构成平面直角坐标系的两条数轴互相垂 直、原点重合.
新课讲解
练一练
1 下列说法错误的是( A ) A.平面内两条互相垂直的数轴就构成了平面直 角坐标系 B.平面直角坐标系中两条数轴是互相垂直的 C.坐标平面被两条坐标轴分成了四个部分,每 个部分称为象限 D.坐标轴上的点不属于任何象限
拓展与延伸
若点P(a,b)在第二象限,则点M(b-a,a-b)
在( D )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
布置作业
请完成对应习题
坐标特征 在x轴正半轴上:M(正,0) 在x轴负半轴上:M(负,0) 在y轴正半轴上:M(0,正) 在y轴负半轴上:M(0,负)
新课讲解
拓展: 平行于x轴的直线上的点的纵坐标相等; 平行于y轴的直线上的点的横坐标相等.
新课讲解
典例分析
例 已知点P(x+6,x-4)在y轴上,则点P的坐标是 _(_0_,__-__1_0_)_.
当堂小练
1.在平面直角坐标系中,若点A(a,-b)在第一象限
内,则点B(a,b)所在的象限是( D )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
当堂小练
2.在一次科学探测活动中,探测人员发现一目标在如 图所示的阴影区域内,则目标的坐标可能是( C ) A.(-3,300) B.(7,-500) C.(9,600) D.(-2,-800)
新课讲解
知识点2 平面直角坐标系内点的坐标
1、直角坐标系的横轴和纵轴将平面分成 __四__ 部分, 从右上方的部分说起,按逆时针方向,各部分 依次是_第__一__象__限___、 _第__二__象__限__ 、 _第__三__象__限__ 和_第__四__象__限___.
人教版数学七年级下册7课件

M点在x 轴上为 5
3, 3叫点M的 4
横坐标;
3
M22
1
-4 -3 -2 -1 0 -1
M点在y 轴上 -2 的为2, 2叫 -3 点M的纵坐 -4 标。
M点在平面直角坐标系中的坐标为(3, 2)
记作:M(3,2)
·N ·M
X轴上的坐标 写在前面
M1
12345
x 横轴
N点在平面直角坐标系中 的坐标为(2, 3)
是
;
• (3)点P(-2,-4)关于原点对称点的坐标
是
.
练习1:
y
指出图中点A,B,C,D,
7•F(0,7)
6
E,F,G,H,O各在哪一
•B(-6,5)5
4
•A(3,5)
3
象限,并写出各点的
2
坐标。
(-5,0)
-6 -•5H-4 -3 -2
-1-11(O01,203)4(55•,E60)x
-2
-3
1、在电影票上“6排3号”与“3排6号”中的 “6”的含义有什么不同?
2、如果将“8排3号”简记作(8,3),那么 “3排8号”如何表示?(5,6)表示什么含义?
问题2 在教室里,怎样确定一 个同学的座位?
• 解 例如,××同学在第3行第4排.这样教 室里座位也可以用一对实数表示.
王敏 讲台
行
10
(-2,-5)•C--45•G(0,-4)
-6
-7
•D
(5,-7)
练习2:
在直角坐标系中画 出下列各点:
A(3 ,6) B(-1.5 ,3.5) C(-4 ,-1) D(2 ,-3) E(3 ,0) F(-2 ,0) G(0 ,5) H(0 ,-4)
人教版数学七年级下册第7章复习课教案

人教版数学七年级下册第7章复习课教案第七章平面直角坐标系小结一、本章知识结构图:二、平面直角坐标系1、平面内有公共原点且互相垂直的两条数轴,构成平面直角坐标系.平面直角坐标系,水平的数轴叫做x轴或横轴(正方向向右),铅直的数轴叫做y轴或纵轴(正方向向上),两轴交点O是原点.这个平面叫做坐标平面.x轴和y把坐标平面分成四个象限(每个象限都不包括坐标轴上的点),要注意象限的编号顺序及各象限内点的坐标的符号:由坐标平面内一点向x轴作垂线,垂足在x轴上的坐标叫做这个点的横坐标,由这个点向y轴作垂线,垂足在y轴上的坐标叫做这个点的纵坐标,这个点的横坐标、纵坐标合在一起叫做这个点的坐标(横坐标在前,纵坐标在后).一个点的坐标是一对有序实数,对于坐标平面内任意一点,都有唯一一对有序实数和它对应,对于任意一对有序实数,在坐标平面都有一点和它对应,也就是说,坐标平面内的点与有序实数对是一一对应的.2、不同位置点的坐标的特征:(1)、各象限内点的坐标有如下特征:点P(x, y)在第一象限 x >0,y>0;点P(x, y)在第二象限 x<0,y>0;点P(x, y)在第三象限 x<0,y<0;点P(x, y)在第四象限 x>0,y<0.(2)、坐标轴上的点有如下特征:点P(x, y)在x轴上 y为0,x为任意实数.点P(x,y)在y轴上 x为0,y为任意实数.3、点P(x, y)坐标的几何意义:(1)点P(x, y)到x轴的距离是| y |;(2)点P(x, y)到y袖的距离是| x |;(3)点P(x, y)到原点的距离是4、关于坐标轴、原点对称的点的坐标的特征:(1)点P(a, b)关于x轴的对称点是;(2)点P(a, b)关于x轴的对称点是;(3)点P(a , b)关于原点的对称点是;〖考查重点与常见题型〗1、考查各象限内点的符号,有关试题常出选择题,如:若点P (a,b)在第四象限,则点M(b-a,a-b)在()(A)第一象限(B)第二象限(C)第三象限(D)第四象限2、考查对称点的坐标,有关试题在中考试卷中经常出现,习题类型多为填空题或选择题,如:点P(-1,-3)关于y轴对称的点的坐标是()(A)(-1,3)(B)(1,3)(C)(3,-1)(D)(1,-3)3、考查自变量的取值范围,有关试题出现的频率很高,重点考查的是含有算术平方根中自变量的取值范围,题型多为填空题,如:2x -3的自变量x的取值范围是4、取值范围:(1)1x-1中自变量x的取值范围是(2)x+2+ 5-x中自变量x的取值范围是(3)x-2(2-x)2-1中自变量x的取值范围是5、已知点P(a,b),a·b>0,a+b<0,则点P在()(A)第一象限(B)第二象限(C)第三象限(D)第四象限6、在直角坐标系中,点P(-1,-12 )关于x轴对称的点的坐标是()(A)(-1,-12 )(B)(1,-12 )(C)(1,12 )(D)(-1,12 )7、已知点P(x,y)的坐标满足方程|x+1|+y-2 =0,则点P在()(A)第一象限(B)第二象限(C)第三象限(D)第四象限考点训练:1、点A(x,y)是平面直角坐标系中的一点,若xy<0,则点A在象限;若x=0则点A在;若x<0,y≠0则点A在 ; 若xy>0,且x=y, 则点A在2、已知点A(a,b), B(a,-b), 那么点A,B关于对称,直线AB平行于轴3、点P(-4,-7)到x轴的距离为,到y轴的距离为,到原点距离为4、已知P是第二象限内坐标轴夹角平分线上一点,点P到原点距离为4,那么点P坐标为5、某音乐厅有20排座位,第一排有18个座位,后面每排比前一排多一个座位,每排座位数m与这排的排数n的函数关系是,自变量n的取值范围是6、求下列函数中自变量的取值范围:(1)y= 132x+1 ( ) (2)y=--3x--1∣x∣--2 ( )解题指导1、点P(x,y)在第二象限,且│x│=2 , │y│=3 ,则点P的坐标是,点P到原点O的距离OP= .2、已知点P(x,4), Q(--3,y).若P,Q关于y轴对称,则x= , y= ;若P,Q关于x轴对称,则x= , y= ;若P,Q关于原点O对称,则x= , y= .3.以A(0,2), -4,0), C(3,0)为三个顶点画三角形,则S△ABC= .4、依此连结A(-6,-1), B(-3,-4), C(2,1), D(-1,4)四点,则四边形ABCD是形.5、当x=-2 时,则2x--1x+1 的值是;6、--xx--1 中x的取值范围是 .7、等腰三角形的底角的度数为x,顶角的度数为y,写出以x表示y的关系式,并指出自变量x的取值范围 .8、多边形的内角和a与边数n(n≥3)的关系式是;多边形的对角线条数m与边数n(n ≥3)的关系式是独立训练1、已知A(-3 ,2 )与点B关于y轴对称,则点B的坐标是,与点B关于原点对称的点C的坐标是,这时点A与点C关于对称.2、在xx2--1 中,自变量x的取值范围是 .3、若点M(a,b)在第二象限,则点N(a-1,b)在第象限.4、所有横坐标为零的点都在上,所有纵坐标为零的点都上5、若点P(a,--3)在第三象限内两条坐标轴夹角的平分线上,则a=6、若A(a,b), B(b,a)表示同一点,则这一点在7、求下列x的取值范围:(1)3x-1x-2 () (3) 32+x-1 ()2x-3 +9-3x()三、坐标方法的简单应用(一)、表示地理位置:(注意点)1、建立坐标系,选择一个适当的参照点为原点,确定x轴、y轴的正方向.(说清楚以什么为原点,什么所在的方向为x轴的正方向,什么所在的方向为y轴的正方向).2、根据具体问题确定适当的比例尺,在坐标轴上标出单位长度.(比例尺不能漏,单位长度不要忘记).3、在坐标平面内画出这些点,写出各点的坐标和各个点的名称.(二)、用坐标表示平移1、图形的平移:在平面内,将一个图形沿某个方向移动一定距离,这种图形的运动称为平移.2、图形的移动引起坐标变化的规律:(1)、将点(x,y)向右平移a个单位长度,得到的对应点的坐标是:(x+a,y)(2)、将点(x,y)向左平移a个单位长度,得到的对应点的坐标是:(x-a,y)(3)、将点(x,y)向上平移b个单位长度,得到的对应点的坐标是:(x,y+b)(4)、将点(x,y)向下平移b个单位长度,得到的对应点的坐标是:(x,y-b)3、点的变化引起图形移动的规律:(1)、将点(x,y)的横坐标加上一个正数a,纵坐标不变,即(x+a,y),则其新图形就是把原图形向右平移a个单位.(2)、将点(x,y)的横坐标减去一个正数a,纵坐标不变,即(x-a,y),则其新图形就是把原图形向左平移a个单位.(1)、将点(x,y)的纵坐标加上一个正数b,横坐标不变,即(x,y+b),则其新图形就是把原图形向上平移a个单位.(1)、将点(x,y)的纵坐标加上一个正数b,横坐标不变,即(x,y+b),则其新图形就是把原图形向下平移b个单位.4、平移的性质:(1)、平移后,对应点所连的线段平行且相等;(2)、平移后,对应线段平行且相等;(3)、平移后,对应角相等;(4)、平移后,只改变图形的位置,不改变图形的形状与大小.5、决定平移的因素:平移的方向和距离.6、画平移图形,必须找出平移的方向和距离、画平移图形的依据是平移的性质.7、在实际生活中,同一个图案往往可以由不同的基本图案经过平移形成的,选取了不同的基本图案之后,分析这个图案的形成过程就有所不同.。
新人教版七年级数学下册全套课件第七章 平面直角坐标系全章课件汇总
y 4 3 2 1
-3 -2 -1-1 O1 2 3 -2 -3 -4
两条数轴:(一般性特征)
(1)互相垂直 (2)原点重合 x (3)通常取向上、向右为正方向 (4)单位长度一般取相同的
选择:下面四个图形中,是平面直角坐标系的是( D )
Y
Y
2
1
-3 -2 -1 O1 2 3
X
X
3 2 1 O -1 -2 -3 -1
E (b,9) √
游戏:
走亲戚
规则:
老师点到哪位同学,表示老师想去他家作客,
为了表示欢迎,这位同学要马上站起来并大声说出
代表他的座位的有序数对。我们约定“列数在前, 排数在后”。如王明:“我家是(2,3),欢迎光 临!”
写出学校里各个地点表示的有序数对.
8
实验楼(3,7)
●
教学楼(6,8)
7
●
6
小刚家(1 500,2 000), 小强家(-1 500,3 500), 小敏家(3 000,-1 750).
自主探究
问题2 追问3 选取学校所在位置为原点,并以正东, 正北方向为x轴、y轴的正方向有什么优点?
选取学校所在位置为原点,并以正东,正北 方向为x轴,y轴正方向,可以容易地写出三位同 学家的位置的坐标.
ABCDE
(1)(A,5 ) (A,3) (C,4 ) (E,5 ) (B,1) (C,2) (E,4)
我
非 常 喜 欢数学
(2)(B,4) (C,1) (D,4) (C,5) (A,1) (D,3) (E,1)
有序 数 对 很 有趣
如图是中国象棋一次对局时的部分示意图,若”帅” 所在的位置用有序数对(5,1)表示, (1)请你用有序数对表示其它棋子的位置。 (2)我们知道马行“日”字,图中的“马”下一步可 以走到的位置有几个?分别如何表示?
数学人教版七年级下册新人教版七年级下第七章全章复习
B(0,-2) y轴上
❖ C(-3,-2)第三象限 D(-3,0) x轴上
❖ E(-1.5,3.5)第二象限 F(2,-3) 第四象限
2.点P(x,y)的坐标x,y,满足xy=0,则点P在
.
3.点A(1+m,2m+1)在x轴上,则m=___,此时A的坐标_______
4.甲同学从A(1,0)出发,向东走2个单位,再向北走3个单位
-1
-1
-2
-2
-3
-3
3.第一次将⊿OAB变成⊿OA1B1,第二次将 ⊿OA1B1变换成⊿OA2B2,再将⊿OA2B2变换成 ⊿OA3B3,已知 A(1,3),A1(2,3),A2(4,3),A3(8,3);B(2,0),B1(4,0), B2(8,0),B3(16,0).
3 A A1 A2
A3
与x轴
.与y轴
.
2.若不同的两点A(2,a),B(b,-4), 直线AB与x轴平行,
则a=
,b=
.
3. 若不同的两点A(2,a),B(b,-4), 直线AB与y轴平
行,则a=
,b=
.
4.A(a,-2),B(4,-2)且AB=6,由条件写出a= .
5.A(a,b),B(4,-2),线段平行于y轴,且AB=6,由条件
O
B B1
B2
B3
A4的坐标
, B4的坐标
.
An的坐标
, Bn的坐标
.
写在最后
成功的基础在于好的学习习惯
The foundation of success lies in good habits
13
谢谢大家
人教版数学七年级下册 7课件
课堂小结
点的平移与点的坐标变化规律: 左、右平移,横变纵不变,“右加左减”; 上、下平移,纵变横不变,“上加下减”.
当堂小练
1.如图,线段AB经过平移得到线段A′B′,其中点A,B的对应点 分别为点A′,B′,这四个点都在格点上.若线段AB上有一个点 P(a,b),则点P在A′B′上的对应点P′的坐标为( A ) A.(a-2,b+3) B.(a-2,b-3) C.(a+2,b+3) D.(a+2,b-3)
A. (-3,0)
B. (-1,6)
C. (-3,-6)
D. (-1,0)
分析:根据平移规律点P(-2,-3)向左平移1个单位,
再向上平移3个单位,则所得到的点的坐标为
(-3,0),故选A.
新课讲解
练一练
在平面直角坐标系中,将点P(3,2)向右平移2个单
位长度,所得到的点的坐标是( D )
A.(1,2)
新课讲解
议一议 在平面直角坐标系中,一个点沿y轴方向平移a
(a>0)个单位长度后的点的坐标是什么?
新课讲解
上下点的平移
如图,将点A(-2, -3)向上平移 6个单位长度,得到点A1,在图上 标出这个点,并写出它的坐标.
y
A1 (-2, 343)
平移前后的 坐标有什么
2
关系?
1
把点A向下平移4个单位呢?
新课讲解
知识点1 坐标系中点的平移
议一议 在平面直角坐标系中,一个点沿x轴方向平移a
(a>0)个单位长度后的坐标是什么?
新课讲解
左右点的平移
y
如图,将点A(-2, -3)向右平
4 平移前后的 3 坐标有什么
移5个单位长度,得到点A1,在图上
人教版数学七年级下册第七章知识点(精编版)
人教版数学七年级下册第七章知识点在学习数学时,老师们总是通过已有知识自然而然过渡到新知识,水到渠成,亦即所谓“温故而知新”。
所以我们要多复习学过的数学知识。
下面是整理的人教版数学七年级下册第七章知识点,仅供参考希望能够帮助到大家。
人教版数学七年级下册第七章知识点1、有序数对:有顺序的两个数a与b组成的数对叫做有序数对,记做(a,b)。
2、平面直角坐标系:在平面内,两条互相垂直且有公共原点的数轴组成平面直角坐标系。
3、横轴、纵轴、原点:水平的数轴称为x轴或横轴;竖直的数轴称为y轴或纵轴;两坐标轴的交点为平面直角坐标系的原点。
4、坐标:对于平面内任一点P,过P分别向x轴,y轴作垂线,垂足分别在x轴,y轴上,对应的数a,b分别叫点P的横坐标和纵坐标,记作P(a,b)。
5、象限:两条坐标轴把平面分成四个部分,右上部分叫第一象限,按逆时针方向依次叫第二象限、第三象限、第四象限。
坐标轴上的点不在任何一个象限内。
6、各象限点的坐标特点①第一象限的点:横坐标0,纵坐标0;②第二象限的点:横坐标0,纵坐标0;③第三象限的点:横坐标0,纵坐标0;④第四象限的点:横坐标0,纵坐标0。
7、坐标轴上点的坐标特点①x轴正半轴上的点:横坐标0,纵坐标0;②x轴负半轴上的点:横坐标0,纵坐标0;③y轴正半轴上的点:横坐标0,纵坐标0;④y轴负半轴上的点:横坐标0,纵坐标0;⑤坐标原点:横坐标0,纵坐标0。
(填“>”、“<”或“=”)8、点P(a,b)到x轴的距离是|b|,到y轴的距离是|a|。
9、对称点的坐标特点①关于x轴对称的两个点,横坐标相等,纵坐标互为相反数;②关于y轴对称的两个点,纵坐标相等,横坐标互为相反数;③关于原点对称的两个点,横坐标、纵坐标分别互为相反数。
10、点P(2,3)到x轴的距离是;到y轴的距离是;点P(2,3)关于x轴对称的点坐标为(,);点P(2,3)关于y轴对称的点坐标为(,)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
H
1
F
E
D
C
B
A
G
七年级第二学期期中复习
1.如图,AB∥ED,∠B+∠C+∠D=( )
A.180°
B.360°
C.540°
D.270°
2.若点A(m,n)在第二象限,那么点B(-m,│n│)在( )
A.第一象限
B.第二象限;
C.第三象限
D.第四象限
3.下列命题是真命题的是( )
A.如果两个角不相等,那么这两个角不是对顶角;
B.两互补的角一定是邻补角
C.如果a2=b2,那么a=b;
D.如果两角是同位角,那么这两角一定相等
4.已知点P在第三象限,且到x轴的距离为3,到y轴的距离为5,则点P的坐标为( • )
A.(3,5)
B.(-5,3)
C.(3,-5)
D.(-5,-3)
5.如图,已知EF∥BC,EH∥AC,则图中与∠1互补的角有( )
A.3个
B.4个
C.5个
D.6个
6.()2
0.7
-的平方根是()
A.0.7
-B.0.7
±C.0.7D.0.49
7.如图,以数轴的单位长线段为边做一个正方形,以数轴的原点为圆心,正方
形对角线长为半径画弧,交数轴正半轴于点A,
则点A表示的数是()
A、1.5
B、1.4
C、
D、
8. 小明将较大的一个三角尺按如图所示的情形放置在课本上(平面图),此时他量
得∠1=120°,
则你认为∠2=
9.在x轴上表示距离原点2的点是。
D
A
E
C
B
10.
的平方根是
那么已知0017201.0,147.4201.17,311.17201.1==
11.
大于
的所有整数的和是 . 12. 一个正数x 的平方根是2a -3与5-a ,则x= .
13. 在数轴上表示的数为点A 53,在数轴上对应的数为点B 5-
,
两点的距离为,则B A .
14.比较大小
1+
2
-
三、解答题:(19-22每题9分,23题10分,共46分)
15.化简:
16. 已知 ,且x 是正数,求代数
式的值
y
x
1
234-1-2-3-4
-4
-3-2
-1
04
3
21
17.平面直角坐标系中,顺次连结(-2,1), (-2,-1),(2,-2),(2,3)各点,你会得到一 个什么图形?试求出该图形的面积.
18.如图,AB ∥DE ,试问∠B 、∠E 、∠BCE 有什么关系. 解:∠B +∠E =∠BCE
过点C 作CF ∥AB ,
则B ∠=∠____( ) 又∵AB ∥DE ,AB ∥CF ,
∴____________( ) ∴∠E =∠____( ) ∴∠B +∠E =∠1+∠2 即∠B +∠E =∠BCE .
19.如图,已知直线AB 、CD 被直线EF 所截,如果∠BMN =∠D NF ,∠1=∠2,那么MQ ∥NP ,试写出推理过程
20.如图,已知ABC ∆,AD BC ⊥于D ,E 为AB 上一点,
EF BC ⊥于F ,//DG BA 交CA 于G 。
.求证12∠=∠.
21.如图,AB ∥CD,探讨下面图形中∠APC 与∠PAB,∠PCD 的关系并加以说明.
(3)
P
D
C
B
A
方程组部分
1、方程组⎩
⎨⎧=-=+.134,
723y x y x 的解是( )
A 、⎩⎨
⎧=-=;3,1y x B 、⎩⎨⎧-==;1,3y x C 、⎩⎨⎧-=-=;1,3y x D 、⎩⎨⎧-=-=.
3,
1y x
2、设⎩⎨
⎧=+=.
04,
3z y y x ()0≠y 则=z x ( )
A 、12
B 、12
1-
C 、12-
D 、.121
3、设方程组()⎩⎨
⎧=--=-.433,1by x a by ax 的解是⎩⎨⎧-==.
1,
1y x 那么b a ,的值分别为( )
A 、;3,2-
B 、;2,3-
C 、;3,2-
D 、.2,3- 4、方程82=+y x 的正整数解的个数是( )
P
Q
M N 21
F
E D C B A
A 、4
B 、3
C 、2
D 、1
5、在等式n mx x y ++=2
中,当3.5,3;5,2=-=-===x y x y x 则时时时, =y ( )。
A 、23 B 、-13 C 、-5 D 、13 6、关于关于
y x 、的方程组⎩⎨
⎧-=+-=-5m
212y 3x 4m
113y 2x 的解也是二元一次方程2073=++m y x 的解,则m 的值是( )
A 、0
B 、1
C 、2
D 、
2
1 7、由==--y y x y x 得表示用,,06911_______,=x x y 得表示,_______。
8、如果⎩
⎨⎧=-=+.232,12y x y x 那么=-+-+3962242y
x y x _______。
9、如果103216
231
2=--+--b a b a y
x
是一个二元一次方程,那么数a =__ _,
b = 。
10、购面值各为20分,30分的邮票共27枚,用款6.6元。
购20分邮票_____枚,30
分邮票_____枚。
11、已知⎩⎨
⎧==⎩⎨⎧=-=310y 2x y x 和是方程02
2=--bx ay x 的两个解,那么a = ,b = 12、如果b a a b y x y x 4222542-+-与是同类项,那么 a = ,b = 。
三、用适当的方法解下列方程(每题4分,共24分)
⎩⎨
⎧=--=523
x y x y ⎩
⎨
⎧+==-130
2y x y x
⎩⎨
⎧=+=-1
5
2y x y x ⎩⎨
⎧-=+=-1
43
29m n n m
⎩⎨
⎧=+=-9
245
23n m n m ⎩⎨
⎧=-=+-6
430
524m n n m
⎩⎨
⎧=+-=-q p q p 4513
32 ⎪⎪⎩⎪⎪⎨
⎧=--=-323
113
121
y x y x
⎩⎨
⎧=+=-524753y x y x ⎪⎩⎪⎨⎧=-=
+2
.03.05.0523151
y x y x
四、列方程解应用题(每题7分,共28分)
1、初一级学生去某处旅游,如果每辆汽车坐45人,那么有15个学生没有座位;如果每辆汽车坐60人,那么空出1辆汽车。
问一工多少名学生、多少辆汽车。
2、某校举办数学竞赛,有120人报名参加,竞赛结果:总平均成绩为66分,合格
生平均成绩为76分,不及格生平均成绩为52分,则这次数学竞赛中,及格的学生有多少人,不及格的学生有多少人。
3、有一个两位数,其数字和为14,若调换个位数字与十位数字,就比原数大18则这
个两位数是多少。
4、甲乙两地相距20千米,A从甲地向乙地方向前进,同时B从乙地向甲地方向前进,
两小时后二人在途中相遇,相遇后A就返回甲地,B仍向甲地前进,A回到甲地时,B离甲地还有2千米,求A、B二人的速度。
阅读下面列题的“换元法”解方程组,并利用此方法解例题后所给方程组
例 解方程组
解:设 , .
原方程组可化为 解得
∴ ,解得
⎪⎪⎩⎪⎪⎨⎧=---=-+-152223*********y
x y x y x y x y x a 231-=
y x b 521-=
⎩⎨⎧=-=+12510
34b a b a ⎩⎨⎧==2
1b a ⎪⎩⎪⎨⎧=-=-2152123y x y x ⎪⎩⎪⎨⎧==.221,114y x
解方程组⎪⎩⎪⎨⎧-=--+=-++.
1106
,
3106y x y x y x y x
解:。
