【名师点睛】高中数学北师大版必修2 第一章 立体几何初步双基限时练4(含解析)
北师大版高中数学必修2双基限时练:第一章++立体几何初步(16套,含解析)双基限时练6

双基限时练(六)一、选择题1.下列说法错误的是()A.若一条直线与平面有无数个公共点,则这条直线在平面内B.若两个平面没有公共点,则两个平面互相平行C.直线与平面的位置关系有两种:相交、平行D.如果一条直线与平面只有一个公共点,那么这条直线和平面相交答案 C2.下列表示正确的是()A.直线l在平面α内,用符号表示为“l∈α”B.点A在直线l上,直线l在平面α内,用符号表示为“A∈l,lα”C.点A在平面α内,用符号表示为“Aα”D.直线l与平面α外,用符号表示为“l∉α”答案 B3.如果两条直线a和b没有公共点,那么a与b的位置关系是() A.共面B.平行C.异面D.平行或异面解析由两条直线的位置关系,可知答案为D.答案 D4.下面空间图形画法错误的是()解析画立体图时,被平面遮住的部分画成虚线或不画.答案 D5.分别在两相交平面内的两条直线的位置关系是()A.异面B.平行C.相交D.以上皆有可能答案 D6.一条直线与两条异面直线中的一条相交,则它与另一条的位置关系是()A.异面B.平行C.相交D.可能相交、平行,也可能异面解析一条直线与两条异面直线中的一条相交,它与另一条的位置关系有三种:平行、相交、异面,如图所示.答案 D二、填空题7.点A在直线l上,用符号表示为________;直线AB在平面β内,用符号可表示为________;平面α与平面β相交于直线l可表示为________.答案A∈l ABβα∩β=l8.如图是一个正方体表面的一种展开图,图中的四条线段AB,CD,EF,GH在原正方体中相互异面的有________对.解析如图所示,AB与GH异面,AB与CD异面,EF与GH异面.答案三9.若直线a,b都平行于平面α,则直线a,b的位置关系是________.解析直线a,b的位置关系有三种:相交、平行、异面,如图所示.三、解答题10.按照给出的要求,完成下面两个相交平面的作图,如图①②③④⑤⑥中的线段AB,分别是两个平面的交线.答案11.如图,在四棱锥P-ABCD中,写出互相异面的直线.解由异面直线的判定定理可知,互为异面的直线有AB与PD,AB与PC,AD与PB,AD与PC,DC与P A,DC与PB,BC与P A,BC与PD异面.12.如图,已知P∉平面ABC,P A≠PB,CM是AB上的中线,PN⊥AB 于N,求证:CM和PN是异面直线.证明证法1:假设CM和PN共面,则有下列两种情况:(1)若M、N重合,可得AN=BN,∴PN是线段AB的中垂线,∴P A=PB,与题设P A≠PB矛盾.(2)若M、N不重合,CM和PN共面,即PC与MN共面,可得P∈平面ABC,与题设P∉平面ABC矛盾.所以CM和PN是异面直线.证法2:∵CM是AB上的中线,∴CM平面ABC.又∵PN⊥AB于N,∴N∈平面ABC.∵P A≠PB,∴AN≠BN.∴N与M不重合,即N∉CM.又∵P∉平面ABC,∴CM和PN是异面直线.思维探究13.若a与b异面,c与b异面,试举例说明a与c的位置关系.解a与c可能相交、平行、异面,说明如下:在正方体ABCD-A1B1C1D1中,A1D1与AB异面,B1C1与AB异面,而A1D1∥B1C1;A1D1与AB异面,DD1与AB异面,而A1D1与DD1相交;A1D1与AB异面,CC1与AB异面,而CC1与A1D1异面,故与b异面的两条直线a,c可能相交、平行、异面.。
北师大版高中数学必修2双基限时练:第一章++立体几何初步(16套,含解析)双基限时练5
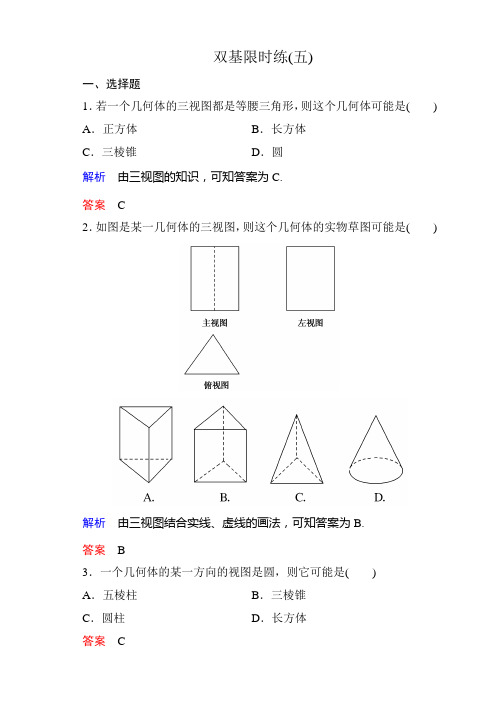
双基限时练(五)一、选择题1.若一个几何体的三视图都是等腰三角形,则这个几何体可能是() A.正方体B.长方体C.三棱锥D.圆解析由三视图的知识,可知答案为C.答案 C2.如图是某一几何体的三视图,则这个几何体的实物草图可能是()解析由三视图结合实线、虚线的画法,可知答案为B.答案 B3.一个几何体的某一方向的视图是圆,则它可能是()A.五棱柱B.三棱锥C.圆柱D.长方体答案 C4.某几何体的三视图如图所示,则该几何体是()A.棱台B.棱柱C.棱锥D.以上均不对解析由相似比,可知几何体的侧棱相交于一点.答案 A5.如果一个几何体的主视图和左视图都是矩形,则这个几何体可能是()A.长方体B.圆柱或正方体C.长方体或圆台D.长方体或圆柱解析正方体的三视图都是正方形;圆台的主视图、左视图都是等腰梯形,长方体和圆柱的主视图和左视图都是矩形.答案 D6.某几何体的主视图和左视图均如图所示,则该几何体的俯视图不可能是()解析若俯视图是A,则原几何体是两个圆柱的组合体;若俯视图是B,则原几何体是一个圆柱和一个四棱柱的组合体;若俯视图为D,则原几何体是一个底面为等腰直角三角形的直三棱柱和一个四棱柱的组合体,故选C.答案 C二、填空题7.如图所示,①②③是三个几何体的三视图,其中①对应的几何体为________,②对应的几何体为________,③对应的几何体为________.解析由三视图的知识,可知甲对应的几何体为圆柱,乙对应的几何体为三棱锥,丙对应的几何体为圆锥.答案圆柱三棱锥圆锥8.桌上放着一个半球,如图所示,则在它的三视图及右面看到的图形中,有三个图相同,这个不同的图应该是________.解析俯视图为圆,主视图与左视图均为半圆.答案俯视图9.如图是长和宽分别相等的两个矩形.给定下列三个命:①存在三棱柱,其主视图、俯视图如图;②存在四棱柱,其主视图、俯视图如图;③存在圆柱,其主视图、俯视图如图.其中是真命题的是________(只填写序号).解析如图①②③的主视图和俯视图都与原题相同.答案①②③三、解答题10.如图是简单组合体的三视图,想象它们表示的组合体的结构特征,并作适当描述.解由三视图可知该几何体是体育器材杠铃.11.根据下列几何体的三视图,画出该几何体的直观图.该几何体上面是一个圆锥,下面是一个倒置的圆台,如图②所示.9题解析图12.某建筑由相同的若干房间组成,该楼房的三视图如图所示,问:(1)该楼房有几层?从前往后最多要经过几个房间?(2)最高一层的房间在什么位置?请画出此楼房的大致形状.解(1)由主视图和左视图可以知道,该楼房有3层;由俯视图知道,从前往后最多要经过3个房间;(2)从主视图和左视图可以知道,最高一层的房间在左侧的最后一排的房间.楼房大致形状如图所示.思维探究13.如图所示,已知几何体的三视图,用斜二测画法画出它的直观图.解由三视图可知,该几何体下方是一个长方体,上方是以长方体的上底面为底面的四棱锥,其直观图的画法如下:(1)作出长方体的直观图ABCD-A1B1C1D1,如图a所示;(2)再以上底面A1B1C1D1的对角线交点为原点建立x′,y′,z′轴,如图b所示,在z′上取点V′,使得V′O′的长度为棱锥的高,连接V′A1,V′B1,V′C1,V′D1,得到四棱锥的直观图,如图b;(3)擦去辅助线和坐标轴,遮住部分用虚线表示,得到几何体的直观图,如图c.。
高中数学北师大版必修2习题:第一章立体几何初步 1.5.1.1 Word版含解析

§5平行关系5.1平行关系的判定第1课时直线与平面平行的判定1.若直线a∥平面α,直线b∥平面α,则a与b的位置关系是()A.平行B.相交C.异面D.以上都有可能答案:D2.在五棱台ABCDE-A1B1C1D1E1中,若F,G分别是AA1和BB1上的点,且,则FG与平面ABCDE的位置关系是()A.平行B.相交C.异面D.FG在平面ABCDE内答案:A3.点E,F,G,H分别是空间四边形ABCD的边AB,BC,CD,DA的中点,则空间四边形的四条边与两条对角线中与平面EFGH平行的条数为()A.0B.1C.2D.3解析:由线面平行的判定定理可知,BD∥平面EFGH,AC∥平面EFGH.答案:C4.下列四个正方体图形中,A,B为正方体的两个顶点,M,N,P分别为其所在棱的中点,能得出AB∥平面MNP的图形的序号是()A.①②B.①④C.①③D.②④答案:B5.如图所示,在长方体ABCD-A1B1C1D1中,E为AA1的中点,F为BB1的中点,与EF平行的长方体的面有()A.1个B.2个C.3个D.4个解析:∵在长方体ABCD-A1B1C1D1中,E为AA1的中点,F为BB1的中点,∴EF∥CD,EF∥AB,EF∥A1B1,∴由直线与平面平行判定定理得,与EF平行的长方体的面有面CDD1C1,面ABCD,面A1B1C1D1,共3个.故选C.答案:C6.已知两条直线a,b,a∥平面α,b⫋α,则直线a与b的位置关系是.答案:平行或异面7.在空间四边形ABCD中,E,F分别为AB和BC上的点,且AE∶EB=CF∶FB=1∶3,则对角线AC和平面DEF的位置关系是.解析:∵,∴EF∥AC.又AC⊈平面DEF,EF⫋平面DEF,∴AC∥平面DEF.答案:平行8.如图所示,在三棱柱ABC-A1B1C1中,D是AB的中点.求证:BC1∥平面CA1D.证明如图所示,连接AC1交A1C于点O,连接OD,则O是AC1的中点.∵D是AB的中点,∴OD∥BC1.又OD⫋平面CA1D,BC1⊈平面CA1D,∴BC1∥平面CA1D.9.如图所示,在三棱柱ABC-A1B1C1中,点D1是A1C1上的一点,当等于何值时,BC1∥平面AB1D1? 解当=1时,BC1∥平面AB1D1.证明如下:如图所示,此时D1为线段A1C1的中点,连接A1B交AB1于点O,连接OD1.由棱柱的定义,知四边形A1ABB1为平行四边形,所以点O为A1B的中点.在△A1BC1中,点O,D1分别为A1B,A1C1的中点,所以OD1∥BC1.又因为OD1⫋平面AB1D1,BC1⊈平面AB1D1,所以BC1∥平面AB1D1.所以当=1时,BC1∥平面AB1D1.★10.如图所示,四边形ABCD是梯形,四边形CDEF是矩形,M是AE上的动点.试确定定点M的位置,使AC∥平面MDF,并说明理由.解当点M是线段AE的中点时,AC∥平面MDF.证明如下:连接CE,交DF于点N,连接MN,因为M,N 分别是AE,CE的中点,所以MN∥AC.又因为MN⫋平面MDF,AC⊈平面MDF,所以AC∥平面MDF.。
新北师大版高中数学必修二第一章《立体几何初步》检测(包含答案解析)(4)

一、选择题1.已知正方体1111ABCD A B C D -,E 、F 分别是正方形1111D C B A 和11ADD A 的中心,则EF 和BD 所成的角的大小是( )A .30B .45C .60D .902.已知三棱锥P ABC -的三条侧棱两两垂直,且,,PA PB PC 的长分别为,,a b c ,又2()a b c +=,侧面PAB 与底面ABC 成45︒角,当三棱锥体积最大时,其外接球的表面积为( )A .10πB .40πC .20πD .18π3.设m ,n 为两条不同的直线,α,β为两个不同的平面,给出下列命题: ①若//m α,//m n ,则//n α;②若m α⊥,//m β,则αβ⊥;③若αβ⊥,n αβ=,m n ⊥,则m β⊥;④若//m n ,//αβ,则m 与α所成的角和n 与β所成的角相等.其中正确命题的序号是( ))A .①②B .①④C .②③D .②④ 4.已知三棱柱111ABC A B C -的所有顶点都在球O 的表面上,侧棱1AA ⊥底面111A B C ,底面111A B C △是正三角形,1AB 与底面111A B C 所成的角是45°.若正三棱柱111ABC A B C -的体积是O 的表面积是( )A .28π3B .14π3C .56π3D .7π 35.已知三棱锥A BCD -的各棱长都相等,E 为BC 中点,则异面直线AB 与DE 所成角的余弦值为( )A B C D6.如图,正三棱柱111ABC A B C -的高为4,底面边长为D 是11B C 的中点,P 是线段1A D 上的动点,过BC 作截面AP α⊥于E ,则三棱锥P BCE -体积的最小值为( )A .3B .23C .43D .127.已知正四棱锥的高为2,底面正方形边长为4,其正视图为如图所示的等腰三角形,正四棱锥表面点M 在正视图上的对应点为腰的中点A ,正四棱锥表面点N 在正视图上对应点为B ,则||MN 的取值范围为( ).A .[10,19]B .[11,19]C .[10,25]D .[11,25] 8.在下面四个正方体ABCD A B C D ''''-中,点M 、N 、P 均为所在棱的中点,过M 、N 、P 作正方体截面,则下列图形中,平面MNP 不与直线A C '垂直的是( ) A . B .C .D . 9.设有直线m ,n ,l 和平面α,β,下列四个命题中,正确的是( )A .若//,//m n αα,则//m nB .若//,//,//l m αβαβ,则//l mC .若,m αβα⊥⊂,则m β⊥D .若,,m m αββα⊥⊥⊄,则//m α 10.某三棱锥的三视图如图所示,已知网格纸上小正方形的边长为1,则该三棱锥的体积为( )A .43B .83C .3D .4 11.已知四面体ABCD ,AB ⊥平面BCD ,1AB BC CD BD ====,若该四面体的四个顶点都在球O 的表面上,则球O 的表面积为( )A .73πB .7πC .712πD .79π 12.如果一个水平放置的平面图形的斜二测直观图是如图所示的直角梯形,其中2O A ''=,45B A O '''∠=,//B C O A ''''.则原平面图形的面积为( )A .32B .62C .322D .34二、填空题13.在边长为3的菱形ABCD 中,对角线3AC =,将三角形ABC 沿AC 折起,使得二面角B AC D --的大小为2π,则三棱锥B ACD -外接球的体积是_________________.14.已知等腰直角三角形ABC 中,2C π∠=,22CA =,D 为AB 的中点,将它沿CD 翻折,使点A 与点B 间的距离为22,此时三棱锥C ABD -的外接球的表面积为____.15.如图,正方形BCDE 的边长为a ,已知3AB BC =,将ABE △沿边BE 折起,折起后A 点在平面BCDE 上的射影为D 点,则翻折后的几何体中有如下描述:①AB 与DE 2;②//AB CE ;③B ACE V -体积是316a ;④平面ABC ⊥平面ADC .其中正确的有______.(填写你认为正确的序号)16.如图,已知一个八面体的各条棱长均为2,四边形ABCD 为正方形,给出下列说法:①该八面体的体积为83;②该八面体的外接球的表面积为8π; ③E 到平面ADF 的距离为3;④EC 与BF 所成角为60°.其中正确的说法为__________.(填序号)17.如图,在直角梯形ABCD 中,//,,2,3,60AB CD AB AD CD AB ABC ⊥==∠=°,将此梯形以AD 所在直线为轴旋转一周,所得几何体的表面积是_________________.18.表面积为16π的球与一个正三棱柱各个面都相切,则这个正三棱柱的体积为___________.19.如下图所示,三棱锥P ABC -外接球的半径为1,且PA 过球心,PAB △围绕棱PA 旋转60︒后恰好与PAC △重合.若3PB =,则三棱锥P ABC -的体积为_____________.20.如图,已知正四面体D ABC -,P 为线段AB 上的动点(端点除外),则二面角D PC B --的平面角的余弦值的取值范围是___________.三、解答题21.如图,ABC 是边长为2的正三角形,ABD △是以AB 为斜边的等腰直角三角形,且2CD =.(1)求证:平面ABC ⊥平面ABD ;(2)求二面角A-BC-D 的余弦值.22.如图,正四棱锥P ABCD -中,底面ABCD 的边长为4,4PD =,E 为PA 的中点.(1)求证://PC 平面EBD .(2)求三棱锥E ABD -的体积.23.如图,AB 是O 的直径,PA 垂直于O 所在的平面,C 是圆周上不同于A ,B 的一动点.(1)证明:BC ⊥面PAC ;(2)若PA =AC =1,AB =2,求直线PB 与平面PAC 所成角的正切值.24.已知四棱锥S ABCD -中,底面ABCD 是边长为2的菱形,60BAD ∠=︒,6SA SD ==,22SB =,点E 是棱AD 的中点,点F 是棱SC 上靠近S 的一个三等分点.(1)求证:平面SBE ⊥平面ABCD ;(2)求三棱锥F SEB -的体积.25.如图,矩形ABCD 所在平面与半圆弧CD 所在平面垂直,M 是CD 上异于C D ,的点.(1)证明:平面AMD ⊥平面BMC ;(2)在线段AM 上是否存在点P ,使得//MC 平面PBD ?若不存在,说明理由,若存在请证明你的结论并说明P 的位置.26.在四棱锥P ABCD -中,90ABC ACD ∠=∠=,60BAC CAD ∠=∠=,PA ⊥平面ABCD ,E 为PD 的中点,M 为AD 的中点,24PA AB ==.(1)取PC 中点F ,证明:PC ⊥平面AEF ;(2)求点D 到平面ACE 的距离.【参考答案】***试卷处理标记,请不要删除一、选择题1.C解析:C【分析】作出图形,连接1AD 、11B D 、1AB ,推导出1//EF AB ,11//BD B D ,可得出异面直线EF 和BD 所成的角为11AB D ∠,分析11AB D 的形状,即可得出结果.【详解】如下图所示,连接1AD 、11B D 、1AB ,设正方体1111ABCD A B C D -的棱长为1,则11112AD AB B D ===,所以,11AB D 为等边三角形,则1160AB D ∠=,因为E 、F 分别是正方形1111D C B A 和11ADD A 的中心,则E 、F 分别是11B D 、1AD 的中点,所以,1//EF AB ,在正方体1111ABCD A B C D -中,11//BB DD 且11BB DD =,所以,四边形11BB D D 为平行四边形,则11//BD B D ,所以,异面直线EF 和BD 所成的角为1160AB D ∠=.故选:C.【点睛】思路点睛:平移线段法是求异面直线所成角的常用方法,其基本思路是通过平移直线,把异面直线的问题化归为共面直线问题来解决,具体步骤如下:(1)平移:平移异面直线中的一条或两条,作出异面直线所成的角;(2)认定:证明作出的角就是所求异面直线所成的角;(3)计算:求该角的值,常利用解三角形;(4)取舍:由异面直线所成的角的取值范围是0,2π⎛⎤ ⎥⎝⎦,当所作的角为钝角时,应取它的补角作为两条异面直线所成的角. 2.A解析:A【分析】将三棱锥体积用公式表示出来,结合均值不等式和2()a b c +=a b =,进而得到2c a =,带入体积公式求得2,a b c ===24S R π=求出外接球的表面积.【详解】解:211166()643V abc ab ab a b ab ==⋅⋅=+,当且仅当a b =时取等号, 因为侧面PAB 与底面ABC 成45︒角,则2PC a c ==,21623V a a ∴=⨯=2,a b c ∴===所以2222410R a b c =++=,故外接球的表面积为10π.故选:A.【点睛】易错点睛:利用基本不等式求最值时,要注意其必须满足的三个条件:(1)“一正二定三相等”“一正”就是各项必须为正数;(2)“二定”就是要求和的最小值,必须把构成和的二项之积转化成定值;要求积的最大值,则必须把构成积的因式的和转化成定值;(3)“三相等”是利用基本不等式求最值时,必须验证等号成立的条件,若不能取等号则这个定值就不是所求的最值,这也是最容易发生错误的地方.3.D解析:D【分析】①根据//n α或n ⊂α判断;②利用面面垂直的判定定理判断;③根据m β⊂,或//m β,或m 与β相交判断;④利用线面角的定义判断.【详解】①若//m α,//m n ,则//n α或n ⊂α,因此不正确;②若//m β,则β内必存在一条直线//m m ',因为m α⊥,所以m α'⊥,又因为m β'⊂,所以αβ⊥,正确;③若αβ⊥,n αβ=,m n ⊥,则m β⊂,或//m β,或m 与β相交,因此不正确;④若//m n ,//αβ,则m 与α所成的角和n 与β所成的角相等,正确.其中正确命题的序号是②④.故选:D .【点睛】空间直线、平面平行或垂直等位置关系命题的真假判断,除了利用定理、公理、推理判断外,还常采用画图(尤其是画长方体)、现实实物判断法(如墙角、桌面等)、排除筛选法等;另外,若原命题不太容易判断真假,可以考虑它的逆否命题,判断它的逆否命题真假,原命题与逆否命题等价. 4.A解析:A【分析】首先得到11AB A ∠是1AB 与底面111A B C 所成的角,再通过三棱柱的体积得到三棱柱的底面等边三角形的边长,最后通过球的半径,球心到底面距离,底面外接圆半径的关系计算.【详解】因为侧棱1AA ⊥底面111A B C ,则11AB A ∠是1AB 与底面111A B C 所成的角,则1145AB A ∠=︒. 故由11111tan tan 451AA AB A A B ∠=︒==,得111AA A B =.设111AA A B a ==,则111312ABC A B C V a a -=⨯==三棱柱 解得2a =.所以球O的半径22232722233 R⎛⎫⎛⎫+⨯⨯=⎪⎪ ⎪⎝⎭⎝=⎭,所以球O的表面积22728π4π4π33S R⎛⎫==⨯=⎪⎪⎝⎭.故选:A.【点睛】解决球与其他几何体的切、接问题,关键在于仔细观察、分析,弄清相关元素的关系和数量关系,选准最佳角度作出截面(要使这个截面尽可能多地包含球、几何体的各种元素以及体现这些元素之间的关系),达到空间问题平面化的目的.5.B解析:B【分析】取AC中点F,连接,EF DF,证明FED∠是异面直线AB与DE所成角(或其补角),然后在三角形中求得其余弦值即可得.【详解】取AC中点F,连接,EF DF,∵E是BC中点,∴//EF AB,12EF AB=,则FED∠是异面直线AB与DE所成角(或其补角),设1AB=,则12EF=,32DE DF==,∴在等腰三角形DEF中,11324cos63EFFEDDE∠===.所以异面直线AB与DE所成角的余弦值为36.故选:B.【点睛】思路点睛:平移线段法是求异面直线所成角的常用方法,其基本思路是通过平移直线,把异面直线的问题化归为共面直线问题来解决,具体步骤如下:(1)平移:平移异面直线中的一条或两条,作出异面直线所成的角; (2)认定:证明作出的角就是所求异面直线所成的角; (3)计算:求该角的值,常利用解三角形; (4)取舍:由异面直线所成的角的取值范围是0,2π⎛⎤⎥⎝⎦,当所作的角为钝角时,应取它的补角作为两条异面直线所成的角.6.C解析:C 【分析】因为P BCE P ABC E ABC V V V ---=-则当E ABC V -取最大值时,三棱锥P BCE -体积有最小值,建立坐标系求得当点E 的高为3时,问题得解. 【详解】以点O 为原点,,,OA OD OB 分别为,,x y z 轴建立空间直角坐标系,如图所示:设点(),0,E x z ,依题意得()6,0,0A ,则()6,0,AE x z =- ,(),0,OE x z = 因为过BC 作截面AP α⊥于E ,所以AE OE ⊥则0AE OE ⋅=, 故()2600x x z -++= 所以()6z x x =-3x =时max 3z =又()143P BCE P ABC E ABC ABCV V V S z ---=-=-因为max 3z =所以三棱锥P BCE -体积的最小值()1114343643332P BCE ABC V S-=-=⋅⋅=故选:C 【点睛】关键点点晴:本题的解题关键是将问题转化为求E ABC V -的最大值,通过建系求得三棱锥E ABC -的高的最大值即可.7.A解析:A 【分析】由题意画出如图正四棱锥,可得M 点在GK 上运动,N 点在CD 上运动,且四边形KCDG 是等腰梯形,则||MN 的取值范围的最小值就是等腰梯形的高,最大值就是梯形的对角线长,作KH ED ⊥,在直角三角形中求KJ KD 、的长可得答案. 【详解】如图正四棱锥P ECDF -,PO ⊥平面ECDF ,O 是底面中心,G K 、分别是PF PE 、的中点,由题意知,M 点在GK 上运动,N 点在CD 上运动,所以////GK FE DC ,且11222GK FE DC ===, 所以四边形KCDG 是梯形,在ECK 与FDG △中,,,EC FD EK FG KEC GFD ==∠=∠,所以ECK ≅FDG △,所以KC GD =,所以四边形KCDG 是等腰梯形,则||MN 的取值范围的最小值就是等腰梯形的高, 最大值就是梯形的对角线长,且22PO EC CD ===,,1222EO ED == 作KH ED ⊥于H ,所以//KH PO ,KH ⊥平面ECDF ,112KH PO ==,且H 是EO 的中点,122EH EO ==,32DH =,45EDC ∠=,作KJ CD ⊥于J ,连接HJ ,12CD KGCJ -==, 所以3DJ =, 由余弦定理得2222cos 9HJ DH DJ DH DJ EDC =+-⋅∠=, 所以2221910KJ KH HJ =+=+=,10KJ =22211819DK EH HD =+=+=,19DK =故选:A. 【点睛】本题考查了正四棱锥的性质及线段的取值范围问题,关键点是画出正四棱锥分析出问题的实质,考查了学生的空间想象力.8.A解析:A 【分析】利用线面垂直的判定定理可判断BCD 选项,利用假设法推出矛盾,可判断A 选项. 【详解】对于A 选项,连接B C ',假设A C '⊥平面MNP ,在正方体ABCD A B C D ''''-中,A B ''⊥平面BB C C '',B C '⊂平面BB C C '',A B B C '''∴⊥,所以,A B C ''为直角三角形,且A CB ''∠为锐角,因为M 、N 分别为BB '、BC 的中点,则//MN B C ',所以,MN 与A C '不垂直, 这与A C '⊥平面MNP 矛盾,故假设不成立,即A C '与平面MNP 不垂直; 对于B 选项,连接B D ''、A C '',如下图所示:因为四边形A B C D ''''为正方形,则A C B D ''''⊥,CC '⊥平面A B C D '''',B D ''⊂平面A B C D '''',CC B D '''∴⊥, A C CC C ''''=,B D ''∴⊥平面A CC '',A C '⊂平面A CC '',A CB D '''∴⊥,M 、P 分别为A B ''、A D ''的中点,则//MN B D '',可得MP A C '⊥, 同理可证A C MN '⊥,MP MN M ⋂=,A C '∴⊥平面MNP ;对于C 选项,连接C D '、A N '、CN 、A P '、PC ,取A B ''的中点E ,连接C E '、PE ,因为四边形CC D D ''为正方形,则CD C D ''⊥,A D ''⊥平面CC D D '',C D '⊂平面CC D D '',C D A D '''∴⊥,CD A D D ''''=,C D '∴⊥平面A CD '',A C '⊂平面A CD '',A C C D ''∴⊥,M 、N 分别为DD '、C D ''的中点,//MN C D '∴,A C MN '∴⊥,在正方形A B C D ''''中,E 、N 分别为A B ''、C D ''的中点,//A E C N ''∴且A E C N ''=, 所以,四边形A EC N ''为平行四边形,所以,//A N C E ''且A N C E ''=, 同理可证四边形CC EP '为平行四边形,//C E CP '∴且C E CP '=, 所以,//A N CP '且A N CP '=,所以,四边形A PCN '为平行四边形, 易得A N CN '=,所以,四边形A PCN '为菱形,所以,A C PN '⊥,MN PN N =,A C '∴⊥平面MNP ;对于D 选项,连接AC 、BD ,因为四边形ABCD 为正方形,则AC BD ⊥,AA '⊥平面ABCD ,BD ⊂平面ABCD ,AA BD '∴⊥, AC AA A '⋂=,BD ∴⊥平面AA C ',A C '⊂平面AA C ',AC BD '∴⊥,M 、N 分别为CD 、BC 的中点,则//MN BD ,A C MN '∴⊥,同理可证A C MP '⊥,MN MP M ⋂=,A C '∴⊥平面MNP .故选:A. 【点睛】方法点睛:证明线面垂直的方法: 一是线面垂直的判定定理; 二是利用面面垂直的性质定理;三是平行线法(若两条平行线中一条垂直于这个平面,则另一条也垂直于这个平面),解题时,注意线线、线面与面面关系的相互转化;另外,在证明线线垂直时,要注意题中隐含的垂直关系,如等腰三角形的底边上的高、中线和顶角的角平分线三线合一、矩形的内角、直径所对的圆周角、菱形的对角线互相垂直、直角三角形(或给出线段长度,经计算满足勾股定理)、直角梯形等等.9.D解析:D 【分析】在A 中,m 与n 相交、平行或异面; 在B 中,l 与m 不一定平行,有可能相交; 在C 中,m ⊥β或m ∥β或m 与β相交;在D 中,由直线与平面垂直的性质与判定定理可得m ∥α.【详解】由直线m 、n ,和平面α、β,知:对于A ,若m ∥α,n ∥α,则m 与n 相交、平行或异面,故A 错误; 对于B ,若//,//,//l m αβαβ,l 与m 不一定平行,有可能相交,故B 错误; 对于C ,若α⊥β,m ⊂α,则m ⊥β或m ∥β或m 与β相交,故C 错误;对于D ,若α⊥β,m ⊥β,m ⊄α,则由直线与平面垂直的性质与判定定理得m ∥α,故D 正确.故选:D . 【点睛】本题考查了命题真假的判断问题,考查了空间线线、线面、面面的位置关系的判定定理及推论的应用,体现符号语言与图形语言的相互转化,是中档题.10.A解析:A 【分析】首先由三视图还原几何体,然后由几何体的空间结构特征求解三棱锥的体积即可. 【详解】由三视图可知,在棱长为2的正方体中,其对应的几何体为棱锥P ABC -,该棱锥的体积:11142223323V Sh ⎛⎫==⨯⨯⨯⨯= ⎪⎝⎭. 故选:A. 【点睛】方法点睛:(1)求解以三视图为载体的空间几何体的体积的关键是由三视图确定直观图的形状以及直观图中线面的位置关系和数量关系,利用相应体积公式求解;(2)若所给几何体的体积不能直接利用公式得出,则常用等积法、分割法、补形法等方法进行求解.11.A解析:A 【分析】本题首先可根据题意将四面体ABCD 看作底面是等边三角形的直三棱柱的一部分,然后求出直三棱柱的外接球的半径,最后根据球的表面积计算公式即可得出结果. 【详解】因为AB ⊥平面BCD ,1AB BC CD BD ====,所以可将四面体ABCD 看作底面是等边三角形的直三棱柱的一部分,如图所示:则四面体ABCD 的外接球即直三棱柱的外接球,因为底面三角形BCD 的外心到三角形BCD 的顶点的长度为222131323,所以直三棱柱的外接球的半径221372312r, 则球O 的表面积2277π4π4π123S r , 故选:A. 【点睛】关键点点睛:本题考查四面体的外接球的表面积的计算,能否将四面体ABCD 看作底面是等边三角形的直三棱柱的一部分是解决本题的关键,考查直三棱柱的外接球的半径的计算,是中档题.12.A解析:A 【分析】作出原平面图形,然后求出面积即可. 【详解】45B A O '''∠=B O A '''=∠,则O A B '''△是等腰直角三角形,∴2A B OB '''==,又O C C B ''''⊥,45C O B '''∠=︒,∴1B C ''=, 在直角坐标系中作出原图形为:梯形OABC ,//OA BC ,2,1OA BC ==,高22OB = ∴其面积为1(21)22322S =+⨯= 故选:A 【点睛】方法点睛:本题考查斜二测法画平面图形直观图,求原图形的面积,可能通过还原出原平面图形求得面积,也可以通过直观图到原图形面积的关系求解:直观图面积为S ',原图形面积为S ,则24S S '=. 二、填空题13.;【分析】分析菱形的特点结合其翻折的程度判断其外接球球心的位置放到相应三角形中利用勾股定理求得半径利用球的体积公式求得外接球的体积【详解】根据题意画出图形根据长为的菱形中对角线所以和都是正三角形又因解析:556π; 【分析】分析菱形的特点,结合其翻折的程度,判断其外接球球心的位置,放到相应三角形中,利用勾股定理求得半径,利用球的体积公式求得外接球的体积. 【详解】根据题意,画出图形,3的菱形ABCD 中,对角线3AC = 所以ABC 和DBC △都是正三角形, 又因为二面角B AC D --的大小为2π, 所以分别从两个正三角形的中心做面的垂线,交于O , 则O 是棱锥B ACD -外接球的球心,且11,2GD OG GE ===, 所以球的半径2252R GD OG =+=, 所以其体积为3344555(3326V R ππ==⋅=, 55π.【点睛】思路点睛:该题考查的是有关几何体外接球的问题,解题思路如下: (1)根据题中所给的条件,判断菱形的特征,得到两个三角形的形状;(2)根据直二面角,得到两面垂直,近一倍可以确定其外接球的球心所在的位置; (3)利用勾股定理求得半径; (4)利用球的体积公式求得结果;(5)要熟知常见几何体的外接球的半径的求解方法.14.12【分析】根据题意可判断出两两垂直即可求出外接球半径得出表面积【详解】等腰直角三角形中为的中点满足两两垂直设外接球的半径为则即三棱锥的外接球的表面积为故答案为:【点睛】本题考查三棱锥外接球问题解题 解析:12π【分析】根据题意可判断出,,DC DA DB 两两垂直,即可求出外接球半径,得出表面积. 【详解】等腰直角三角形ABC 中,2C π∠=,22CA CB ==,D 为AB 的中点,2CD AD BD ∴===,,CD AD CD BD ∴⊥⊥,22AB =,满足222AD BD AB +=,AD BD ∴⊥, ,,DC DA DB ∴两两垂直,设外接球的半径为R ,则222222223R =++=,即3R =,∴三棱锥C ABD -的外接球的表面积为2412R ππ=.故答案为:12π.【点睛】本题考查三棱锥外接球问题,解题的关键是得出,,DC DA DB 两两垂直.15.①③④【分析】作出折叠后的几何体的直观图由题中条件得到是异面直线与所成的角求出其正切可判断①正确;根据线面垂直的的判定定理先证明平面可判断②错;根据等体积法由体积公式求出可判断③正确;根据面面垂直的解析:①③④【分析】作出折叠后的几何体的直观图,由题中条件,得到ABC ∠是异面直线AB 与DE 所成的角,求出其正切,可判断①正确;根据线面垂直的的判定定理,先证明CE ⊥平面ABD ,可判断②错;根据等体积法,由体积公式求出B ACE V -,可判断③正确;根据面面垂直的判定定理,可判断④正确.【详解】作出折叠后的几何体直观图如图所示:由题意,3AB a =,BE a =,∴2AE a =; ∴22AD AE DE a =-=,222AC CD AD a ∴=+=,∵//BC DE ,∴ABC ∠是异面直线AB 与DE 所成的角,在Rt ABC 中, tan 2AC ABC BC∠==①正确; 连结BD ,CE ,则CE BD ⊥,又AD ⊥平面BCDE ,CE ⊂平面BCDE ,∴CE AD ⊥,又BD AD D ,BD ⊂平面ABD ,AD ⊂平面ABD ,∴CE ⊥平面ABD ,又AB 平面ABD ,∴CE AB ⊥.故②错误.三棱锥B ACE -的体积2311113326B ACE A BCE BCE V V S AD a a a --===⨯⨯=⋅⨯. 故③正确.∵AD ⊥平面BCDE ,BC ⊂平面BCDE ,∴BC AD ⊥,又BC CD ⊥,CD AD D =,CD ⊂平面ADC ,AD ⊂平面ADC , ∴BC ⊥平面ADC ,∵BC ⊂平面ABC ,∴ABC ⊥平面ADC .故④正确.故答案为:①③④.【点睛】思路点睛:判断空间中线线、线面、面面位置关系时,一般根据相关概念,结合线面平行、垂直的判定定理及性质,以及面面平行、垂直的判定定理及性质,根据题中条件,进行判断或证明. 16.②④【分析】①求出该八面体的体积即可判断;②可得球心为正方形ABCD 对角线交点即可得出半径求出表面积;③取AD 的中点G 连接EGFGEF 过E 作求出即可;④可得为所成角【详解】①八面体的体积为;②八面体 解析:②④【分析】①求出该八面体的体积即可判断;②可得球心为正方形ABCD 对角线交点,即可得出半径求出表面积;③取AD 的中点G ,连接EG ,FG ,EF ,过E 作EH FG ⊥,求出EH 即可;④可得DEC ∠为所成角.【详解】①八面体的体积为21822(22)33⨯⨯⨯=; ②八面体的外接球球心为正方形ABCD 对角线交点,易得外接球半径为2,表面积为8π;③取AD 的中点G ,连接EG ,FG ,EF ,易得3EG FG ==AD ⊥平面EGF ,过E 作EH FG ⊥,交FG 的延长线于H ,又EH AD ⊥,AD FG G ⋂=,故EH ⊥平面ADF ,解得26EH =,所以E 到平面ADF 的距离为263; ④因为//ED BF ,所以EC 与BF 所成角为60︒.故答案为:②④.【点睛】解本题的关键是正确理解正八面体的性质,根据线面垂直关系得到点到平面的垂线段. 17.【分析】此梯形以AD 所在直线为轴旋转一周得到的是圆台然后根据圆台的侧面积和表面积公式进行计算【详解】将此梯形以AD 所在直线为轴旋转一周得到的是圆台其中圆台的上底半径为r =CD =2下底半径为R =AB = 解析:23π【分析】此梯形以AD 所在直线为轴旋转一周,得到的是圆台,然后根据圆台的侧面积和表面积公式进行计算.【详解】将此梯形以AD 所在直线为轴旋转一周,得到的是圆台,其中圆台的上底半径为r =CD =2,下底半径为R =AB =3,母线BC =2,∴圆台的上底面积为πr 2=4π,下底面积为πR 2=9π,圆台的侧面积为(πr +πR )•BC =π(2+3)×2=10π,∴圆台的表面积为4π+9π+10π=23π,故答案为23π.【点睛】本题考查圆台表面积的计算,利用旋转体的定义确定该几何体是圆台是解决本题的关键. 18.【分析】求出正三棱柱的高底面三角形的边长和高即可求出正三棱柱的体积【详解】设球的半径为r 由得则球的半径为2正三棱柱的高为正三棱柱底面正三角形的内切圆的半径是2所以正三角形的边长是高是6正三棱柱的体积解析:【分析】求出正三棱柱的高、底面三角形的边长和高,即可求出正三棱柱的体积.【详解】设球的半径为r ,由2416r π=π,得2r ,则球的半径为2,正三棱柱的高为24r =,正三棱柱底面正三角形的内切圆的半径是2,所以正三角形的边长是6,正三棱柱的体积为1642⨯⨯=故答案为:【点睛】本题考查正三棱柱的内切球、正三棱柱的体积,考查空间想象能力与计算能力. 19.【分析】作于可证得平面得得等边三角形利用是球的直径得然后计算出再应用棱锥体积公式计算体积【详解】∵围绕棱旋转后恰好与重合∴作于连接则∴又过球心∴而∴同理由得平面∴故答案为:【点睛】易错点睛:本题考查解析:8【分析】作BH PA ⊥于H ,可证得PA ⊥平面BCH ,得60BHC ∠=︒,得等边三角形BCH ,利用PA 是球的直径,得PB AB ⊥,然后计算出BH ,再应用棱锥体积公式计算体积.【详解】∵PAB △围绕棱PA 旋转60︒后恰好与PAC △重合,∴PAB PAC ≅△△,作BH PA ⊥于H ,连接CH ,则,CH PA CH BH ⊥=,60BHC ∠=︒,∴BC BH CH ==.又PA 过球心,∴PB AB ⊥,而2,3PA PB ==,∴1AB =,同理1AC =,31322PB AB BH PA ⋅⨯===,2233333BCH S BH ⎛⎫=⨯=⨯= ⎪ ⎪⎝⎭△, 由BH PA ⊥,CH PA ⊥,CHBH H =,得PA ⊥平面BCH , ∴11333233P ABC BCH V S PA -=⋅=⨯⨯=△. 故答案为:3.【点睛】易错点睛:本题考查求棱锥的体积,解题关键是作BH PA ⊥于H ,利用旋转重合,得PA ⊥平面BCH ,这样只要计算出BCH 的面积,即可得体积,这样作图可以得出60BHC ∠=︒,为旋转所形成的二面角的平面角,这里容易出错在误认为旋转60︒,即为60CAB ∠=︒.旋转60︒是旋转形成的二面角为60︒.应用作出二面角的平面角. 20.【分析】当点从点运动到点时二面角的平面角逐渐增大二面角的平面角最小趋于二面角的平面角最大趋于二面角的平面角的补角求出二面角的平面角和二面角的平面角即可【详解】当点从点运动到点时二面角的平面角逐渐增大解析:11,33⎛⎫- ⎪⎝⎭【分析】当点P 从点A 运动到点B 时,二面角D PC B --的平面角逐渐增大,二面角D PC B --的平面角最小趋于二面角D AC B --的平面角,最大趋于二面角D BC A --的平面角的补角,求出二面角D AC B --的平面角和二面角D BC A --的平面角即可.【详解】当点P 从点A 运动到点B 时,二面角D PC B --的平面角逐渐增大,二面角D PC B --的平面角最小趋于D AC B --的平面角,最大趋于二面角D BC A --的平面角的补角,设正四面体的棱长为2a ,如图所示,取AC 的中点E ,连接DE 、BE ,易知DEB ∠为二面角D AC B --的平面角,3DE BE a ==,所以((()()()2223321cos 3233a a a DEB a a +-∠==⨯⨯, 同理可得:二面角D BC A --的平面角的补角的余弦值为13-,故二面角D PC B --的平面角的余弦值的取值范围是11,33⎛⎫- ⎪⎝⎭,故答案为:11,33⎛⎫- ⎪⎝⎭【点睛】本题主要考查了二面角的平面角的求解,考查空间想象能力,属于中档题.三、解答题21.(1)证明见解析;(2)217. 【分析】(1)取AB 中点O ,连OC 、OD ,即可得到COD ∠是二面角C AB D --的平面角,再由勾股定理逆定理得到222OC OD CD +=,即可得到二面角是直二面角,即可得证; (2)过O 作OM ⊥BC 交BC 于M ,连DM ,即可证明BC ⊥平面DOM ,从而得到ODM ∠为二面角A-BC-D 的平面角,再利用锐角三角函数计算可得;【详解】(1)证明:取AB 中点O ,连OC 、OD ,因为ABC 是边长为2的正三角形,ABD △是以AB 为斜边的等腰直角三角形,所以OC AB ⊥,⊥OD AB ,所以COD ∠是二面角C AB D --的平面角.在OCD 中,因为3OC =1OD =,2CD =,所以222OC OD CD +=所以90COD ∠=︒.所以平面ABC ⊥平面ABD .(2)过O 作OM ⊥BC 交BC 于M ,连DM ,由(1)可知DO ⊥面ABC ,又BC ⊂面ABC ,所以BC DO ⊥,由OM DO O =,,OM DO ⊂面DOM所以BC ⊥平面DOM因为DM ⊂面DOM ,所以BC ⊥DM ,则ODM ∠为二面角A-BC-D 的平面角.在Rt OMD 中,1OD =,3OM =,由勾股定理:7DM =, ∴二面角A-BC-D 的余弦值为21cos 7OM OMD DM ∠==.【点睛】本题考查了立体几何中的面面垂直的判定和二面角的求解问题,意在考查学生的空间想象能力和逻辑推理能力;解答本题关键在于能利用直线与直线、直线与平面、平面与平面关系的相互转化,通过严密推理,同时对于立体几何中角的计算问题,往往可以利用空间向量法,通过求解平面的法向量,利用向量的夹角公式求解.22.(1)证明见解析;(2)823. 【分析】(1)连接AC 交BD 于点O ,连接EO ,利用三角形中位线定理可得//EO PC ,再由线面平行的判定定理可得结论;(2)先证明PO ⊥面ABCD ,由E 是PA 的中点,可得E 到面ABCD 的距离12PO =,再利用棱锥的体积公式可得答案.【详解】(1)连接AC 交BD 于点O ,连接EO .四边形ABCD 为正方形,所以O 为AC 中点,又E 为PA 中点,//EO PC ∴,又EO ⊂面EBD ,PC ⊄面EBD ,//PC ∴面EBD .(2)正四棱锥P ABCD -中,PA PC =,O 是AC 的中点PO AC ∴⊥,PD PB =,O 是BD 的中点PO BD ∴⊥,又AC 与BD 在平面ABCD 内相交,所以PO ⊥面ABCD E 是PA 的中点,E ∴到面ABCD 的距离12PO =, 221822,2ABD S AB AD PO PD DO ∆=⋅⋅==-= 182323E ABD ABD PO V S -∆=⋅⋅= 【点睛】方法点睛:证明线面平行的常用方法:①利用线面平行的判定定理,使用这个定理的关键是设法在平面内找到一条与已知直线平行的直线,可利用几何体的特征,合理利用中位线定理、线面平行的性质或者构造平行四边形、寻找比例式证明两直线平行.②利用面面平行的性质,即两平面平行,在其中一平面内的直线平行于另一平面.23.(1)证明见解析;(2)62【分析】(1)证明AC ⊥BC 和PA ⊥BC ,BC ⊥面PAC 即得证;(2)先证明∠BPC 为PB 与平面PAC 所成的角,再通过解三角形求出,BC PC 即得解.【详解】证明:(1) AB 为圆O 直径 ∴∠ACB =90°即AC ⊥BCPA ⊥面ABC ,∴PA ⊥BC。
北师大版高中数学必修2双基限时练:第一章++立体几何初步(16套,含解析)双基限时练8

双基限时练(八)一、选择题1.在正方体ABCD—A1B1C1D1中,E,F,G,H分别为AB,BC,A1B1,B1C1的中点,下列结论错误的是()A.GH∥EFB.GH∥ACC.GE∥HFD.GB∥B1F解析GB与B1F异面.答案 D2.如图,点P,Q,R,S分别在正方体的四条棱上,且是所在棱的中点,则直线PQ与RS不平行的两个图是()A.①②B.②③C.③④D.①④解析③中的PQ与RS异面,④中的PQ与RS相交于一点,故选C.答案 C3.在四棱柱ABCD—A1B1C1D1中,底面ABCD为平行四边形(称这样的几何体为平行六面体),与AB共面也与CC1共面的棱的条数为() A.3 B.4C.5 D.6解析根据两条平行直线、两条相交直线确定一个平面,可得CD,BC,BB1,AA1,C1D1符合条件.答案 C4.在正方体ABCD—A1B1C1D1中,E,F,M,N分别为A1D1,A1B1,DC,BC的中点,下列说法中错误的是()A.EF∥MN B.AF∥C1MC.AF∥C1N D.AE∥C1N解析∵B1D1∥BD,MN∥BD,∴MN∥B1D1.又EF∥B1D1,∴MN∥EF,故A正确,如图取AD的中点G,连接D1G,GN,则D1C1綊GN,∴D1G∥C1N,而E,G为A1D1,AD的中点,∴AE∥D1G,∴AE∥C1N,故D正确,同理可证AF∥C1M,故B正确,而AF与C1N 异面.答案 C5.在正方体ABCD—A1B1C1D1中,E,F,M分别为A1B1,B1C1,BB1的中点,下列说法中错误的是()A .∠BA 1C 1=∠MEFB .∠A 1BC 1=∠EMF C .∠B 1EM =∠EA 1BD .∠EFM =∠A 1C 1F解析 由等角定理,可知A 、B 、C 均正确. 答案 D6.在三棱柱ABC -A 1B 1C 1中,E ,F 分别在AB ,AC 上,且AE =13AB ,AF =13AC ,则下列说法正确的是( )A .EF ⊥BB 1 B .EF ∥A 1B 1C .EF ∥B 1C 1D .EF ∥AA 1解析 ∵AE =13AB ,AF =13AC ,∴EF ∥BC ,又ABC -A 1B 1C 1为棱柱,∴BC ∥B 1C 1,∴EF ∥B 1C 1.答案 C 二、填空题7.如图所示,在空间四边形ABCD 中,E ,H 分别为AB ,AD 的中点,F ,G 分别是BC ,CD 上的点,且CF CB =CG CD =23,若BD =6 cm ,梯形EFGH 的面积为28 cm 2,则平行线EH ,FG 间的距离为________.解析 EH =3,FG =6×23=4,S EFGH =(EH +FG )h 2=28,得h =8(cm). 答案 8 cm8.用一个平面去截一个正方体,截面可能是________. 解析(注:这儿画了其中的特例来说明有这几种图形) 答案 三角形、四边形、五边形、六边形9.空间中两个角α,β且α,β的角的两边分别平行,且α=60°,则β=________.答案 60°或120° 三、解答题10.在正方体ABCD -A 1B 1C 1D 1中,E ,F 分别为棱CC 1和AA 1的中点.画出平面BED 1F 与平面ABCD 的交线.解 如图,在平面AA 1D 1D 内,延长D 1F ,DA .∵D 1F 与DA 不平行,∴D 1F 与DA 必相交于一点,设为P ,则P ∈D 1F ,P ∈DA .又∵D 1F ⊂平面BED 1F ,DA ⊂平面ABCD , ∴P ∈平面BED 1F ,且P ∈平面ABCD . 又∵B 为平面ABCD 与平面BED 1F 的公共点,∴连接PB ,则PB 即为平面BED 1F 与平面ABCD 的交线.11.如图,两个三角形ABC 和A ′B ′C ′的对应顶点的连线AA ′,BB ′,CC ′交于同一点O ,且AO OA ′=BO OB ′=CO OC ′=23.(1)求证:A ′B ′∥AB ,A ′C ′∥AC ,B ′C ′∥BC ; (2)求S △ABCS △A ′B ′C ′的值.解 (1)证明:∵AA ′与BB ′交于点O ,且 AO OA ′=BO OB ′=23,∴AB ∥A ′B ′.同理AC ∥A ′C ′,BC ∥B ′C ′.(2)∵A ′B ′∥AB ,AC ∥A ′C ′,且AB 和A ′B ′,AC 和A ′C ′方向相反,∴∠BAC =∠B ′A ′C ′. 同理∠ABC =∠A ′B ′C ′. 因此△ABC ∽△A ′B ′C ′,且AB A ′B ′=AO OA ′=23.∴S △ABCS △A ′B ′C ′=⎝ ⎛⎭⎪⎫232=49. 12.如图,E ,F ,G ,H 分别是三棱锥ABCD 的边AB ,BC ,CD ,DA 上的点,且AE EB =AH HD =λ,CF FB =CGGD =μ.(1)若λ=μ,判断四边形EFGH 的形状; (2)若λ≠μ,判断四边形EFGH 的形状; (3)若λ=μ=12,且EG ⊥HF ,求ACBD 的值.解 (1)∵AE EB =AHHD =λ,∴EH ∥BD ,且EH =λ1+λBD .①又∵CF FB =CG GD =μ,∴FG ∥BD ,且FG =μ1+μBD .②又λ=μ,∴EH 綊FG (公理4).因此λ=μ时,四边形EFGH 为平行四边形.(2)若λ≠μ,由①②,知EH ∥FG ,但EH ≠FG ,因此λ≠μ时,四边形EFGH 为梯形.(3)∵λ=μ,∴四边形EFGH 为平行四边形. 又∵EG ⊥HF ,∴四边形EFGH 为菱形. ∴FG =HG .∴BD =1+μμFG =3FG , AC =(λ+1)HG =32HG =32FG . ∴AC BD =12.思 维 探 究13.如图,一个梯形纸片ABCD ,AB ∥CD ,E ,F 分别是AD ,BC 的中点,将四边形ABFE 绕EF 旋转到A ′B ′FE 的位置,G ,H 分别为A ′D ,B ′C 的中点.求证:(1)四边形A ′B ′CD 是梯形; (2)四边形EFHG 是平行四边形.证明(1)∵四边形ABCD是梯形,AB∥CD,∴AB≠CD. ∵E,F分别为AD,BC的中点,∴EF∥AB,EF∥CD,旋转后A′B′∥EF.∴A′B′∥CD,且A′B′=AB≠CD.∴四边形A′B′CD是梯形.(2)由(1)知四边形A′B′CD是梯形,∴GH=12(A′B′+CD).又GH∥CD,∴EF∥GH.∵EF=12(AB+CD),∴EF綊GH. ∴四边形EFHG是平行四边形.。
北师大版高中数学必修2双基限时练:第一章++立体几何初步(16套,含解析)双基限时练1

双基限时练(一)一、选择题1.下面几何体的截面一定是圆面的是()A.圆柱B.圆锥C.球D.圆台答案 C2.下列说法正确的是()A.圆锥是直角三角形绕其一边旋转而成B.在圆台上、下底面圆周上各取一点,则这两点的连线是圆台的母线C.圆柱的任意两条母线所在直线互相平行D.用一平面截圆锥,截面与底面之间的部分为圆台解析由旋转的过程,可知圆柱的任意两条母线所在直线互相平行.答案 C3.如图所示,观察下面四个几何体,其中判断正确的是()A.①是圆台B.②是圆台C.③是圆锥D.④是圆台答案 C4.如图①是由下面哪个平面旋转得到的()解析由旋转的知识,可知答案为C.答案 C5.一个圆锥的母线长为20 cm,母线与轴的夹角为30°,则圆锥的高为()A.10 3 cm B.20 3 cmC.20 cm D.10 cm解析由图可知,h=20cos30°=103(cm),答案为A.答案 A6.有下列四个命题:①圆柱是将矩形旋转一周所得的几何体;②以直角三角形的一边为旋转轴,旋转所得几何体是圆锥;③圆台的任意两条母线的延长线可能相交也可能不相交;④圆锥的轴截面是等腰三角形.其中错误命题的个数是( ) A .1 B .2 C .3D .4解析 ①错,以矩形某一边为轴旋转才是圆柱,以对角线为轴旋转则不是圆柱;②错,以其直角边为轴旋转才是圆锥;③错,一定相交;④正确.答案 C 二、填空题7.圆台的两底面半径分别为2 cm 和5 cm ,母线长为310 cm ,则它的轴截面面积为________.解析 圆台的高h =(310)2-(5-2)2=9(cm), S 轴截面=(4+10)×92=63(cm 2). 答案 63 cm 28.用一张4 cm ×8 cm 的矩形硬纸卷成圆柱的侧面,接头忽略不计,则轴截面面积是________.解析 若圆柱的高为8 cm ,则2πr =4(cm), 2r =4π,轴截面面积S =8·4π=32π(cm 2), 若圆柱的高为4 cm ,则2πr =8(cm), 2r =8π,轴截面面积S =4·8π=32π(cm 2), 故答案为32π cm 2.答案 32π cm 29.一直角梯形上底长为1,下底长为3,高为2,现绕着直角梯形的下底旋转一周,所围成的几何体的轴截面的面积为________.解析 其轴截面由两部分组成其中一个为矩形,一个为三角形,S =4×1+12×4×2=8.答案 8 三、解答题 10.如图所示,已知梯形ABCD 中,AD ∥BC ,且AD <BC ,当梯形ABCD 绕AD 所在直线旋转一周时,其他各边旋转围成一个几何体,试描述该几何体的结构特征.解 如图所示,旋转所得的几何体是一个圆柱挖去两个圆锥后剩余部分而成的组合体.11.如果一个圆锥的侧面展开图是半圆,求这个圆锥的轴截面的顶角.解 设圆锥的底面半径为r ,母线长为l ,由题意,可得πl =2πr ,∴r =l2. ∴轴截面的顶角α满足 sin α2=r l =12,∴α2=30°.∴α=60°,即圆锥轴截面的顶角为60°.12.已知一个圆台的母线长是5 cm ,上、下底面的面积分别是9π cm 2和16π cm 2,求:(1)圆台的高;(2)截得此圆台的圆锥的母线长.解 (1)设圆台的上、下底面半径为r 、R ,高为h , 则r =3,R =4,h =l 2-(R -r )2=52-12= 26(cm);(2)设圆锥母线长为l ′,则l ′-l l ′=r R ,即l ′-5l ′=34,l ′=20(cm).思 维 探 究13.一个圆锥的底面直径为4,高为8,在其中有一个高为x 的内接圆柱.(1)用x 表示圆柱的轴截面面积; (2)当x 为何值时,S 最大.解 作出圆锥和内接圆柱的轴截面,设圆柱的底面半径为r . 由三角形相似可得x 8=2-r 2,得r =2-x4.(1)圆柱的轴截面面积S =2rx =2⎝ ⎛⎭⎪⎫2-x 4x =-12x 2+4x ,x ∈(0,8) (2)∵S =-12x 2+4x =-12(x -4)2+8,x ∈(0,8), ∴当x =4时,S 取得最大值8.。
北师大版高中数学必修2双基限时练:第一章++立体几何
双基限时练(二)一、选择题1.下列说法中正确的是()A.棱柱的各个面中,至少有两个面互相平行B.棱柱中两个互相平行的平面一定是棱柱的底面C.棱柱中侧棱的长叫做棱柱的高D.棱柱的侧面是矩形,但它的底面一定不是矩形解析据棱柱的概念,知答案为A.答案 A2.若棱台上、下底面的对应边之比为1:2,则上、下底面的面积之比为()A.1:2 B.1:4C.2:1 D.4:1解析面积之比等于对应边之比的平方,可知答案为B.答案 B3.棱台不一定具有的性质是()A.侧面都是梯形B.侧棱都相等C.两底面相似D.侧棱延长后交于一点解析据棱台的性质,知答案为B.答案 B4.以下命题正确的是()A.棱锥的各侧棱长相等B.棱柱的各侧面都是矩形C.棱台的各侧棱延长线相交于一点D.圆锥的母线长等于底面圆的周长答案 C5.一个正棱锥的底面边长与侧棱长相等,则该棱锥一定不是() A.三棱锥B.四棱锥C.五棱锥D.六棱锥解析由于正六边形的中心到顶点的距离与边长都相等,故正六棱锥的侧棱长大于底面边长.答案 D6.给出下列命题:①有两个面平行,其余各面都是平行四边形所围成的几何体一定是棱柱;②有一个面是多边形,其余各面都是三角形所围成的几何体是棱锥;③用一个平行于棱锥底面的平面去截棱锥,得到的几何体叫棱台.以上命题中真命题的个数为()A.0 B.1C.2 D.3解析对于①②不符合棱柱、棱锥的定义;对于③,用一个平行于棱锥底面的平面去截棱锥,得的几何体一个是棱台,另一个是棱锥,故③不正确.答案 A二、填空题7.四棱柱有________条侧棱;________个顶点;________个侧面.答案48 48.给出下列几个命题:①棱柱的侧面都是平行四边形;②棱锥的侧面为三角形,且所有侧面都有一个公共点;③棱台的侧棱所在直线均相交于一点;④将直角梯形绕着它的一条腰所在的直线旋转一周所得的几何体为圆台.其中正确的是________.解析①②③显然正确,对于④,只有当直角梯形绕着它的一条垂直于底边的腰所在的直线旋转一周时,所形成的几何体才是圆台,故④不正确.答案①②③9.已知正四棱锥V—ABCD,底面面积为16,一条侧棱长为211,则它的斜高为________.解析由S底=16,知底面边长为4,又侧棱长为211,故斜高h′=(211)2-22=210.答案210三、解答题10.如图所示的棱柱ABCD—A1B1C1D1为正四棱柱,用平面BCEF把该棱柱分成两部分后,各部分的几何体还是棱柱吗?如果是,是几棱柱?如果不是,说明理由.解∵ABCD—A1B1C1D1为正四棱柱,∴截面BCEF右边的部分是三棱柱BFB1—CEC1,截面BCEF左边的部分也是棱柱,是一个四棱柱ABF A1—DCED1.11.如图所示的几何体所有的棱长都相等,分析此几何体的面数,顶点数和棱数,并判断该几何体是不是棱柱、棱锥、棱台的一种.解该几何体有8个面,6个顶点,12条棱,它不满足棱柱、棱锥、棱台的定义,故不是棱柱,也不是棱锥,也不是棱台,但它是一个多面体.12.已知正三棱柱ABC-A1B1C1的底面边长为1,高为4,一动点从A 点出发,沿着三棱柱的侧面绕行一周到达点A1,求动点所经过的最短路程长.解将三棱柱沿AA1将侧面展开,如图所示其中AA′=3,A′A′1=4,∴AA′1=AA′2+A′A′21=32+42=5.∴动点所经过的最短路程长为5.思维探究13.已知底面是正方形,侧棱都相等的棱锥的高为3,侧棱长为7,求侧面等腰三角形底边上的高.解如图,在棱锥S-ABCD中,高OS=3,侧棱SA=SB=SC=SD =7,解Rt△SOA,得OA=2,则AC=4,∴AB=BC=CD=DA=2 2.作OE⊥AB于E,则E为AB中点.连接SE,则SE即为所求.由于SO⊥OE,在Rt△SOE中,∵OE=12BC=2,SO=3,∴SE= 5.∴棱锥侧面等腰三角形底边上的高为 5.。
北师大版高中数学必修2双基限时练:第一章++立体几何
双基限时练(十五)一、选择题1.已知正四棱锥的侧棱长为23,高为3,则该棱锥的体积为( ) A .3 B .6 C .9D .18解析 设棱锥的底面边长为a ,则(23)2=32+⎝ ⎛⎭⎪⎫22a 2,∴a 22=3,∴a 2=6,V 锥=13a 2h =13×6×3=6. 答案 B2.已知一正四棱台的三视图如图所示,则该几何体的体积为( )A .624B .208C .131D .1313解析 由图可知,棱台的上底面边长为4,下底面边长为10,高为4,所以棱台的体积为V =13(S 上+S下+S 上·S 下)h =13×(16+100+40)×4=6243=208.答案 B3.直角梯形的一个内角为45°,下底为上底长的32倍,这个梯形绕下底所在的直线旋转一周所成的旋转体的全面积为(5+2)π,则旋转体的体积为( )A .2πB .4+23πC .5+23πD .73π解析 设该直角梯形的上底长为r ,下底长则为32r.该几何体为圆柱与圆锥的组合体.S 全=π×⎝ ⎛⎭⎪⎫r 22+πr 2+π2r ×22r =⎝ ⎛⎭⎪⎫54π+24πr 2=(5+2)π,∴r =2,∴V =V 圆柱+V 圆锥=73π. 答案 D4.在棱长为1的正方体上,分别用过公共顶点的三条棱的中点的平面截该正方体,则截去8个三棱锥后,剩下的多面体的体积是( )A .23B .76C .45D .56解析 V =1-8V 锥=1-8×13×12×12×12×12=56. 答案 D5.已知某个几何体的三视图如图所示,根据图中标明的尺寸(单位:cm )可得这个几何体的体积是( )A .40003 cm 3 B .80003 cm 3 C .2000 cm 3D .4000 cm 3解析 由三视图得几何体S -ABCD ,且面SCD ⊥面ABCD ,四边形ABCD 为正方形,作SE ⊥CD 于E ,得SE ⊥面ABCD ,SE =20 cm .∴V S -ABCD =13S ABCD ·SE =80003(cm 3). 答案 B6.图中的三个直角三角形是一个体积为20 cm 3的几何体的三视图,则该几何体的高为( )A .4B .12C .43D .24解析 由三视图可知该几何体为一个三棱锥S -ABC ,其中SA ⊥面ABC ,AB ⊥AC ,∴V =13S △ABC ·h =13×12×5×6×h =5h ,得h =4.答案 A 二、填空题7.用一张圆弧长为12π,半径为10的扇形纸片制作一个圆锥体,则这个圆锥体的体积是________.解析 由2πr =12π,得r =6,h =102-r 2=8,∴V 锥=13S 底·h =13π×62×8=96π. 答案 96π8.正四棱台的斜高与上、下底面边长之比为,体积为14 cm 3,则棱台的高为________.解析 设正四棱台上底为2a ,下底为8a ,斜高为5a ,则(5a)2=h 2+9a 2, ∴h 2=16a 2,∴h =4a ,又由棱台的体积公式求得h =2(cm ). 答案 2 cm9.在三棱锥P —ABC 中,三条侧棱PA ,PB ,PC 两两垂直,设PA =x ,PB =y ,PC =1,若x +y =4,则此三棱锥体积的最大值是________.解析 V =13×12xy =16xy =16x(4-x)=16(4x -x 2)=16×[-(x -2)2+4], ∴当x =2即x =y 时,V max =46=23. 答案 23 三、解答题10.将边长为a 的正方形ABCD 沿对角线AC 折起,使BD =a ,求三棱锥D —ABC 的体积.解取AC的中点M,连接BM,DM,∵BD=a,BM=22a,DM=22a,∴DM2+BM2=BD2.∴∠DMB=90°,又AD=DC,∴DM⊥AC.又AC∩BM=M,∴DM⊥面ABC.∴V=13S底·h=13×a22×22a=212a3.11.在下图所示的三个图中,上面的是一个长方体截去一个角所得多面体的直观图,它的正视图和侧视图在下面画出(单位:cm).(1)在正视图下面,按照画三视图的要求画出该多面体的俯视图; (2)按照给出的尺寸,求该多面体的体积. 解 (1)俯视图如下图所示.(2)所求多面体的体积V =V 长方体-V 三棱锥=4×4×6-13×⎝ ⎛⎭⎪⎫12×2×2×2=2843(cm 3).12.在正方体ABCD —A 1B 1C 1D 1中,O 为底面ABCD 的中心,若正方体的棱长为a.(1)求三棱锥O —AB 1D 1的体积; (2)求O 到平面AB 1D 1的距离. 解 (1)∵V O -AB 1D 1=V A —B 1D 1O , S △B 1D 1O =12B 1D 1·a =22a 2, 又AO ⊥面BDD 1B 1, 且AO =22a ,∴V A —B 1D 1O =V O —AB 1D 1=13×22a 2×22a =a 36. (2)∵AB 1=B 1D 1=AD 1=2a , ∴S △AB 1D 1=12B 1D 1·AB 1 sin 60°=32a 2, 设O 到平面AB 1D 1的距离为h. 由等积转化得13×32a 2h =a 36, ∴h =33a.思 维 探 究13.如图所示,在△ABC 中,∠ACB =90°,∠B =30°,AC =2,M 是AB 的中点,将△ACM 沿CM 折起,使A ,B 间的距离为22,求三棱锥A -BCM 的体积.解 由题意知在Rt △ABC 中,AB =4,BC =2 3. 又∵CM 为中线,∴MA =MB =MC =12AB =2.∴在三棱锥A -BCM 中,M 在面ABC 上的射影为△ABC 的外心. 又∵在折叠后的△ABC 中,AC =2,AB =22,BC =23, ∴AC 2+AB 2=BC 2,即折叠后的△ABC 也为直角三角形.取BC 的中点E ,连接ME ,则E 为点M 在面ABC 上的射影,即ME 的长为三棱锥M -ABC 的高.∵ME 为△MBC 的高,MB =MC =2,∠MBE =30°, ∴ME =12MB =1.∴V A -BCM =V M -ABC =13S △ABC ·ME =223.。
北师大版高中数学必修2双基限时练:第一章++立体几何初步(16套,含解析)双基限时练10
双基限时练(十)一、选择题1.在空间中,下列命题正确的是()A.若a∥α,b∥a,则b∥αB.若a∥α,b∥α,aβ,bβ,则α∥βC.若α∥β,b∥α,则b∥βD.若α∥β,aα,则a∥β解析对于A,当a∥α,b∥a时,b可能在α内,故A不正确;对于B,a,b有可能平行,此时α∥\β,故B不正确;对于C,α∥β,b∥α,此时b 有可能在平面β内,故C不正确.答案 D2.平面α∥平面β,平面γ∥平面δ,且α∩γ=a,α∩δ=b,β∩γ=c,β∩δ=d,则交线a,b,c,d的位置关系是()A.互相平行B.交于一点C.相互异面D.不能确定解析由面面平行的性质定理,可知答案为A.答案 A3.给出下列命题:①一条直线与另一条直线平行,它就和经过另一条直线的任何平面平行;②一条直线和一个平面平行,它就和这个平面内的所有直线平行;③经过两条异面直线a,b外一点,必有一个平面与a,b都平行;④经过两条异面直线中的一条,有且只有一个平面平行于另一条直线.其中正确的命题有()A.0个B.1个C.2个D.3个解析①因为两条平行直线可确定一个平面,其中的一条直线可能在另一条直线所在的平面内,故①不对;对于②,一条直线和一个平面平行,它和这个平面内的直线有的平行,有的异面,故②不对;③中,经过两条异面直线外一点P,可作a′∥a,b′∥b,a′∩b′=P,可确定一个平面,但有可能aα或bα,故③不正确;④显然正确,故选B.答案 B4.在正方体ABCD—A1B1C1D1中,E,F,G,H分别为棱AA1,BB1,CC1,DD1上的点,且E,F,G,H四点共面,则四边形EFGH一定是() A.平行四边形B.菱形C.不是菱形D.不一定是平行四边形解析据两平面平行的性质定理,可知EFGH一定为平行四边形.答案 A5.过长方体ABCD—A1B1C1D1任意两条棱的中点作直线,其中与平面DBB1D1平行的直线共有()A.4条B.6条C.8条D.12条解析与面BDD1B1平行的平面有EFGH,MNPQ,其中E,F,G,H,M,N,P,Q分别为棱的中点,每一个平面由中点构成的线有6条,据面面平行的性质定理,可知与面BDD1B1平行的线共有12条.答案 D6.过三棱柱ABC-A1B1C1的任意两条棱的中点作直线,其中与面ABB1A1平行的直线的条数有()A.4 B.5C.6 D.7解析画出图形,结合图形作出判断.如图所示,E,F,G,H分别是所在棱的中点,显然EF,EH,HG,GF,EG,FH都与平面ABB1A1平行.答案 C二、填空题7.在正方体ABCD—A1B1C1D1中,M,N分别在AB1,BC1上,且AM=BN,那么①AC∥MN;②MN∥面ABCD;③MN∥面A1B1C1D1.其中正确的是________.解析如图,过M ,N 分别作MG ∥BB 1,NH ∥BB 1,分别交AB ,BC 于G ,H 两点.∴MG BB 1=AM AB 1=AG AB ,又NH CC 1=BN BC 1=BH BC ,又ABCD —A 1B 1C 1D 1为正方体,∴AB 1=BC 1,又AM=BN ,∴MG =NH ,AG =BH .故当G ,H 不是AB ,BC 的中点时,GH AC , 故①不正确,由MG 綊NH ,知MN ∥GH ,∴MN ∥面ABCD ,同理可得MN ∥面A 1B 1C 1D 1. 答案 ②③8.如图a ∥α,A 是α的另一侧的点,B ,C ,D ∈a ,线段AB ,AC ,AD 交α于E ,F ,G ,若BD =4,CF =4,AF =5,则EG =________.解析 由相似比EG BD =AF AC ,∴EG =AF ·BD AC =5×49=209. 答案 2099.如图,在四面体ABCD 中,若截面PQMN 是正方形,则在下列命题中,正确的是________.①AC ∥面PQMN ;②AC =BD ;③BD ∥面PQMN ;④AC ⊥BD 解析 由PQMN 为正方形,知PQ ∥MN , ∴PQ ∥面ADC .又PQ面ABC ,面ABC ∩面ADC =AC ,∴PQ ∥AC . ∴AC ∥面PQMN ,同理BD ∥面PQMN .故①③正确,又AC ∥MN ,BD ∥MQ ,MN ⊥MQ , ∴AC ⊥BD ,故④正确.∴正确的有①③④.答案①③④三、解答题10.如图,正三棱柱ABC—A1B1C1中,D是BC的中点.判断直线A1B 与平面ADC1的关系.解A1B∥面ADC1,证明如下:证法1:如图①,连接A1C交AC1于F,则F为A1C的中点.连接FD.∵D是BC的中点,∴DF∥A1B.又DF平面ADC1,A1B平面ADC1,∴A1B∥平面ADC1.证法2:如图②,取C1B1的中点D1,则AD∥A1D1,C1D∥D1B,∴AD∥平面A1D1B,且C1D∥平面A1D1B.又AD∩C1D=D,∴平面ADC1∥平面A1D1B.∵A1B平面A1D1B,∴A1B∥平面ADC1.11.如图,在直四棱柱ABCD—A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AB=4,DC=2,E,E1分别为AD,AA1的中点,F为AB的中点.求证:EE1∥面FCC1.证明∵ABCD—A1B1C1D1为直棱柱,∴DD1∥CC1.又CC1面ADD1A1,DD1面ADD1A1,∴CC 1∥面ADD 1A 1.又ABCD 为梯形,AB ∥CD ,AB =4,DC =2, F 为AB 的中点, ∴AF ∥DC ,且AF =DC .故四边形AFCD 为平行四边形,故FC ∥AD . 又AD面ADD 1A 1,FC面AD 1,∴FC ∥面ADD 1A 1. 又FC ∩CC 1=C , ∴面FCC 1∥面ADD 1A 1. 又EE 1面ADD 1A 1,∴EE 1∥面FCC 1.12.在四棱锥P —ABCD 中,底面ABCD 为矩形,E 为线段PD 上的点,F 为线段AB 上的点,且PE ED =BFF A ,试判断EF 与平面PBC 的关系,并证明.证明 EF ∥平面PBC .证明如下: 如图作FG ∥BC 交CD 于点G ,连接EG , 则BF F A =CGGD .∵PE ED =BF F A ,∴PE ED =CG GD . ∴PC ∥EG .又FG ∥BC ,BC ∩PC =C ,FG ∩GE =G , ∴平面PBC ∥平面EFG .又EF 平面PBC , ∴EF ∥平面PBC .思 维 探 究13.在三棱柱ABC -A 1B 1C 1中,点D 为AC 的中点,点D 1是A 1C 1上的一点.(1)当A 1D 1D 1C 1等于何值时,BC 1∥平面AB 1D 1?(2)当BC 1∥平面AB 1D 1时, 求证:平面BC 1D ∥平面AB 1D 1.解(1)A1D1D1C1=1.证明如下:如图,此时D1为线段A1C1的中点,连接A1B交AB1于O,连接OD1.由棱柱的定义知四边形A1ABB1为平行四边形,∴点O为A1B的中点.在△A1BC1中,点O,D1分别为A1B,A1C1的中点,∴OD1∥BC1.又∵OD1平面AB1D1,BC1平面AB1D1,∴BC1∥平面AB1D1,∴当A1D1D1C1=1时,BC1∥平面AB1D1.(2)证明:由(1)知,当BC1∥平面AB1D1时,点D1是线段A1C1的中点,则有AD∥D1C1,且AD=D1C1,∴四边形ADC1D1是平行四边形.∴AD1∥DC1.又∵DC1平面AB1D1,AD1平面AB1D1,∴DC1∥平面AB1D1.又∵BC1∥平面AB1D1,BC1平面BC1D,DC1平面BC1D,DC1∩BC1=C1,∴平面BC1D∥平面AB1D1.。
新北师大版高中数学必修二第一章《立体几何初步》测试题(含答案解析)(4)
一、选择题1.正三棱锥(底面为正三角形,顶点在底面的射影为底面中心的棱锥)的三视图如图所示,俯视图是正三角形,O是其中心,则正视图(等腰三角形)的腰长等于()A.5B.2 C.3D.22.已知三棱锥A BCD的各棱长都相等,E为BC中点,则异面直线AB与DE所成角的余弦值为()A.13B.3C.33D.1163.某几何体的三视图(单位:cm)如图所示,则该几何体的体积(单位:3cm)为()A.43B.2C .4D .64.如图,正三棱柱111ABC A B C -的高为4,底面边长为43,D 是11B C 的中点,P 是线段1A D 上的动点,过BC 作截面AP α⊥于E ,则三棱锥P BCE -体积的最小值为( )A .3B .23C .43D .125.某几何体的三视图如图所示(单位:cm ),则该几何体的体积(单位:3cm )是( )A .24B .30C .47D .676.如图正三棱柱111ABC A B C -的所有棱长均相等,O 是1AA 中点,P 是ABC 所在平面内的一个动点且满足//OP 平面11A BC ,则直线OP 与平面ABC 所成角正弦值的最大值为( )A .2 B .255C .32D .2777.如图,在四棱锥P ABCD -中,底面ABCD 是矩形.其中3AB =,2AD =,PAD △是以A ∠为直角的等腰直角三角形,若60PAB ∠=︒,则异面直线PC 与AD 所成角的余弦值是( )A .2211B .2211-C .77D .211118.已知球O 的半径为5,球面上有,,A B C 三点,满足214,27AB AC BC ===,则三棱锥O ABC -的体积为( ) A .77B .142C .714D .1479.在正方体1111ABCD A BC D -中,M 是棱1CC 的中点.则下列说法正确的是( ) A .异面直线AM 与BC 5B .BDM 为等腰直角三角形C .直线BM 与平面11BDD B 10D .直线1AC 与平面BDM 相交10.如图,正方形ABCD 的边长为4,点E ,F 分别是AB ,B C 的中点,将ADE ,EBF △,FCD 分别沿DE ,EF ,FD 折起,使得A ,B ,C 三点重合于点A ',若点G 及四面体A DEF '的四个顶点都在同一个球面上,则以FDE 为底面的三棱锥G -DEF 的高h 的最大值为( )A .263+B .463+C .4263-D .2263- 11.在四棱锥P -ABCD 中,//AD BC ,2AD BC =,E 为PD 中点,平面ABE 交PC 于F ,则PFFC=( ) A .1B .32C .2D .312.如图,长、宽、高分别为2、1、1的长方体木块上有一只小虫从顶点A 出发沿着长方体的外表面爬到顶点B ,则它爬行的最短路程是( )A .10B .5C .22D .3二、填空题13.如图,在三棱锥P ABC -中,点B 在以AC 为直径的圆上运动,PA ⊥平面,ABC AD PB ⊥,垂足为,D DE PC ⊥,垂足为E ,若23,2PA AC ==,则三棱锥P ADE -体积的最大值是_________.14.如图,点E 是正方体1111ABCD A BC D -的棱1DD 的中点,点M 在线段1BD 上运动,则下列结论正确的有__________. ①直线AD 与直线1C M 始终是异面直线②存在点M ,使得1B M AE ⊥ ③四面体EMAC 的体积为定值④当12D M MB =时,平面EAC ⊥平面MAC15.正方体1111ABCD A BC D -棱长为点1,点E 在边BC 上,且满足2BE EC =,动点P 在正方体表面上运动,满足1PE BD ⊥,则动点P 的轨迹的周长为__________. 16.在三棱锥P ABC -中,4PA PB ==,42BC =,8AC =,AB BC ⊥.平面PAB ⊥平面ABC ,若球O 是三棱锥P ABC -的外接球,则球O 的半径为_________.17.在三棱锥P ABC -中,P 在底面ABC 的射影为ABC 的重心,点M 为棱PA 的中点,记二面角P BC M --的平面角为α,则tan α的最大值为___________. 18.在三棱锥D ABC -中,AD ⊥平面ABC ,3AC =,17BC =,1cos 3BAC ∠=,若三棱锥D ABC -的体积为27,则此三棱锥的外接球的表面积为______19.如图,在三棱锥A BCD -,,AB AD BC ⊥⊥平面ABD ,点E 、F (E 与A 、D 不重合)分别在棱AD 、BD 上,且EF AD ⊥.则下列结论中:正确结论的序号是______.①//EF 平面ABC ;②AD AC ⊥;③//EF CD20.将底面直径为8,高为23为______.三、解答题21.在所有棱长均为2的直棱柱1111ABCD A BC D -中,底面ABCD 是菱形,且60BAD ∠=︒,O ,M 分别为1,BD B C 的中点.(Ⅰ)求证:直线//OM 平面11DB C ; (Ⅱ)求二面角1D AC D --的余弦值.22.如图(1)在ABC 中,AC BC =,D 、E 、F 分别是AB 、AC 、BC 边的中点,现将ACD △沿CD 翻折,使得平面ACD ⊥平面BCD .如图(2)(1)求证://AB 平面DEF ; (2)求证:BD AC ⊥.23.如图,在四棱锥P ABCD -中,底面ABCD 是正方形,32,3,PB PD PA AD ====点,E F 分别为线段,PD BC 的中点.(1)求证://EF 平面ABP ; (2)求证:平面AEF ⊥平面PCD ;(3)求三棱锥C AEF -的体积24.如图,圆柱的轴截面ABCD 是长方形,点E 是底面圆周上异于A ,B 的一点,AF DE ⊥,F 是垂足.(1)证明:AF DB ⊥;(2)若2AB =,3AD =,当三棱锥D ABE -体积最大时,求点C 到平面BDE 的距离. 25.如图,在平面四边形A ABC '中,90CAB CA A '∠=∠=,M 在直线AC 上,A A A C ''=,AB AM MC ==,A AC '绕AC 旋转.(1)若A AC '所在平面与ABC 所在平面垂直,求证:A C '⊥平面A AB '. (2)若二面角A AC B '--大小为60,求直线A B '与平面ABM 所成角的正弦值. 26.如图,四边形ABCD 为矩形,且4=AD ,22AB =PA ⊥平面ABCD ,2PA =,E 为BC 的中点.(1)求证:PC DE ⊥;(2)若M 为PC 的中点,求三棱锥M PAB -的体积.【参考答案】***试卷处理标记,请不要删除一、选择题 1.B 解析:B 【分析】可得原几何体如图所示正三棱锥A BCD -,取BD 中点E ,连接,AE CE ,设底面边长为2x ,表示出2522x AO OE -===1333xOE CE ==,即可求出x ,进而求出腰长. 【详解】根据三视图可得原几何体如图所示正三棱锥A BCD -,取BD 中点E ,连接,AE CE ,则底面中心O 在CE 上,连接AO ,可得AO ⊥平面ABC ,由三视图可知5AB AC AD ===45AEC ∠=, 设底面边长为2x ,则DE x =,则25AE x =-则在等腰直角三角形AOE 中,2522xAO OE -===O 是底面中心,则133xOE CE ==,则253 23x x-=,解得3x=,则1AO=,底面边长为23,则正视图(等腰三角形)的腰长为()22312+=.故选:B.【点睛】本题考查根据三视图计算原几何体的相关量,解题的关键是根据正三棱锥中的关系求出底面边长.2.B解析:B【分析】取AC中点F,连接,EF DF,证明FED∠是异面直线AB与DE所成角(或其补角),然后在三角形中求得其余弦值即可得.【详解】取AC中点F,连接,EF DF,∵E是BC中点,∴//EF AB,12EF AB=,则FED∠是异面直线AB与DE所成角(或其补角),设1AB=,则12EF=,32DE DF==,∴在等腰三角形DEF中,11324cos3EFFEDDE∠===.所以异面直线AB与DE3故选:B.【点睛】思路点睛:平移线段法是求异面直线所成角的常用方法,其基本思路是通过平移直线,把异面直线的问题化归为共面直线问题来解决,具体步骤如下: (1)平移:平移异面直线中的一条或两条,作出异面直线所成的角; (2)认定:证明作出的角就是所求异面直线所成的角; (3)计算:求该角的值,常利用解三角形; (4)取舍:由异面直线所成的角的取值范围是0,2π⎛⎤⎥⎝⎦,当所作的角为钝角时,应取它的补角作为两条异面直线所成的角.3.B解析:B 【分析】根据三视图判断出几何体的结构,利用椎体体积公式计算出该几何体的体积. 【详解】根据三视图可知,该几何体为如图所示四棱锥,该棱锥满足底面是直角梯形,且侧棱ED ⊥平面ABCD , 所以其体积为11(12)22232V =⨯⨯+⨯⨯=, 故选:B. 【点睛】方法点睛:该题考查的是有关根据几何体三视图求几何体体积的问题,解题方法如下:(1)首先根据题中所给的几何体的三视图还原几何体;(2)结合三视图,分析几何体的结构特征,利用体积公式求得结果.4.C解析:C 【分析】因为P BCE P ABC E ABC V V V ---=-则当E ABC V -取最大值时,三棱锥P BCE -体积有最小值,建立坐标系求得当点E 的高为3时,问题得解. 【详解】以点O 为原点,,,OA OD OB 分别为,,x y z 轴建立空间直角坐标系,如图所示:设点(),0,E x z ,依题意得()6,0,0A ,则()6,0,AE x z =- ,(),0,OE x z = 因为过BC 作截面AP α⊥于E ,所以AE OE ⊥则0AE OE ⋅=, 故()2600x x z -++= 所以()6z x x =-3x =时max 3z =又()143P BCE P ABC E ABC ABCV V V S z ---=-=-因为max 3z =所以三棱锥P BCE -体积的最小值()1114343643332P BCE ABC V S-=-=⋅⋅=故选:C 【点睛】关键点点晴:本题的解题关键是将问题转化为求E ABC V -的最大值,通过建系求得三棱锥E ABC -的高的最大值即可.5.D解析:D 【分析】先找到几何体的原图,再求出几何体的高,再求几何体的体积得解.【详解】由三视图可知几何体为图中的四棱锥1P CDD E -, 由题得22437AD =-=,所以几何体的高为7. 所以几何体的体积为11(24)676732⋅+⋅⋅=. 故选:D 【点睛】方法点睛:通过三视图找几何体原图常用的方法有:(1)直接法;(2)拼凑法;(3)模型法.本题利用的就是模型法.要根据已知条件灵活选择方法求解.6.D解析:D 【分析】先找到与平面11A BC 平行的平面OEFG ,确定点P 在直线FG 上,作出线面角,求出正弦,转化为求AP 的最小值. 【详解】分别取1,,CC BC BA 的中点,连接,,,OE EF FG GO ,并延长FG ,如图,由中位线性质可知11//OE AC , 1//EF BC ,且OEEF E =,故平面11//A BC 平面OGFE ,又P 是ABC 所在平面内的一个动点且满足//OP 平面11A BC 则点P 在直线FG 上,OA ⊥平面ABC ,OPA ∴∠是直线OP 与平面ABC 所成角,sin OAOPA OP∴∠=, OA 为定值,∴当OP 最小时,正弦值最大,而OP所以当AP 最小时,sin OPA ∠最大, 故当AP FG ⊥时,sin OPA ∠最大, 设棱长为2, 则1212AG =⨯=,而30GAP ∠=︒,AP ∴=, 又1212OA =⨯=,sin OAOPA OP∴∠===故选:D 【点睛】关键点点睛:由P 是ABC 所在平面内的一个动点且满足//OP 平面11A BC ,转化为找过O 的平面与平面11A BC 平行,P 在所找平面与平面ABC 的交线上,从而容易确定出线面角,是本题解题的关键所在.7.D解析:D 【分析】在图形中找到(并证明)异面直线所成的角,然后在三角形中计算. 【详解】因为//AD BC ,所以PCB ∠是异面直线PC 与AD 所成角(或其补角), 又PA AD ⊥,所以PA BC ⊥,因为AB BC ⊥,AB PA A ⋂=,,AB PA ⊂平面PAB ,所以BC ⊥平面PAB , 又PB ⊂平面PAB ,所以PB BC ⊥. 由已知2PA AD ==,所以PB==cos11BCPCBPC∠===,所以异面直线PC与AD所成角的余弦值为11.故选:D.【点睛】思路点睛:平移线段法是求异面直线所成角的常用方法,其基本思路是通过平移直线,把异面直线的问题化归为共面直线问题来解决,具体步骤如下:(1)平移:平移异面直线中的一条或两条,作出异面直线所成的角;(2)认定:证明作出的角就是所求异面直线所成的角;(3)计算:求该角的值,常利用解三角形;(4)取舍:由异面直线所成的角的取值范围是0,2π⎛⎤⎥⎝⎦,当所作的角为钝角时,应取它的补角作为两条异面直线所成的角.8.A解析:A【分析】利用正弦定理求出ABC的外接圆半径,则可求出三棱锥的高,进而求出三棱锥体积.【详解】设ABC的外接圆的圆心为D,半径为r,在ABC中,cos ABC∠==sin4ABC∴∠=,由正弦定理可得28sinACrABC==∠,即4r=,则3OD==,11133324O ABC ABCV S OD-∴=⨯⨯=⨯⨯=故选:A.【点睛】本题考查球内三棱锥的相关计算,解题的关键是利用正弦定理求出ABC 的外接圆半径,利用勾股关系求出高.9.C解析:C 【分析】A 通过平移,找出异面直线所成角,利用直角三角形求余弦即可. B.求出三角形的三边,通过勾股定理说明是不是直角三角形.C.求出点M 到面11BB D D 的距离,再求直线BM 与平面11BDD B 所成角的正弦.D.可通过线线平行证明线面平行. 【详解】 设正方体棱长为2A. 取1BB 的中点为N ,则//BC MN ,则AM 与BC 所成角为AMN ∠ 由BC ⊥面11ABB A ,故MN ⊥面11ABB A ,故MN AN ⊥,在Rt ANM △中,5tan AMN ∠=,故2cos 3AMN ∠=B. BDM 中,5BM =22BD =5DM =C. AC BD ⊥,1AC BB ⊥,故AC ⊥面11BB D D ,1//CC 面11BB D D ,故M 到面11BB D D 的距离等于C 到面11BB D D 的距离,即为122d AC =直线BM 与平面11BDD B 所成角为θ210sin 5d BM θ===直线BM 与平面11BDD B 所成角的正弦值等于105D.如图ACBD O =OM 为1ACC △的中位线,有1//OM AC故直线1AC 与平面BDM 平行故选:C 【点睛】本题考查了空间几何体的线面位置关系判定与证明:(1)对于异面直线的判定要熟记异面直线的概念:把既不平行也不相交的两条直线称为异面直线;(2)对于线面位置关系的判定中,熟记线面平行与垂直、面面平行与垂直的定理是关键.10.A解析:A 【分析】先求出'A FDE -外接球的半径和外接圆的半径,再利用勾股定理求出外接球的球心到外接圆的圆心的距离,可得高h 的最大值. 【详解】因为A ,B ,C 三点重合于点A ',原来A B C ∠∠∠、、都是直角,所以折起后三条棱'''A F A D A E 、、互相垂直,所以三棱锥'A FDE -可以看作一个长方体的一个角,它们有相同的外接球,外接球的直径就是长方体的体对角线,即为2R==R=,DE DF====EF=在DFE△中,222cos2DE EF DFDEFDE EF+-∠===⨯,所以DEF∠为锐角,所以sin DEF∠==,DEF的外接圆的半径为2sinDFrDEF===∠则球心到DEF23,以FDE为底面的三棱锥G-DEF的高h的最大值为1R OO+23.故选:A.【点睛】本题考查了翻折问题和外接球的问题,关键点翻折前后量的变化及理解外接球和三棱锥的关系,考查了学生的空间想象力和计算能力.11.C解析:C【分析】首先通过延长直线,DC AB,交于点G,平面BAE变为GAE,连结PG,EG交于点F,再根据三角形中线的性质,求PFFC的值.【详解】延长,DC AB,交于点G,连结PG,EG交PC于点F,//AD BC,且2AD BC=,可得点,B C分别是,AG DG的中点,又点E是PD的中点,PC∴和GE是△PGD的中线,∴点F是重心,得2PFFC=故选:C 【点睛】关键点点睛:本题的关键是找到PC 与平面BAE 的交点,即将平面BAE 转化为平面GAE 是关键.12.C解析:C 【分析】小虫有两种爬法,一种是从点A 沿着侧面ACGF 和上底面BHFG 爬行,另一种是从点A 沿着侧面ACGF 和侧面BDCG 爬行,将两种情况下的两个面延展为一个面,计算出平面图形的对角线长,比较大小后可得结果. 【详解】由于长方体ACDE FGBH -的长、宽、高分别为2、1、1,则小虫从点A 沿着侧面AEHF 和上底面FHBG 爬行,以及小虫从点A 沿着侧面ACGF 和侧面BDCG 爬行,这两条线路的最短路程相等.①若小虫从点A 沿着侧面ACGF 和上底面BHFG 爬行,将侧面ACGF 和上底面BHFG延展为一个平面,如下图所示:则2AC BC ==,最短路程为2222AB AC BC +=②若小虫从点A 沿着侧面ACGF 和侧面BDCG 爬行,将面ACGF 和侧面BDCG 延展为一个平面,如下图所示:则3AD AC CD =+=,1BD =,最短路程为2210AB AD BD =+因为2210,因此,小虫爬行的最短路程为22 故选:C. 【点睛】方法点睛:(1)计算多面体或旋转体的表面上折线段的最值问题时,一般采用转化的方法进行,即将侧面展开化为平面图形,即“化折为直”或“化曲为直”来解决,要熟练掌握多面体与旋转体的侧面展开图的形状;(2)对于几何体内部折线段长的最值,可采用转化法,转化为两点间的距离,结合勾股定理求解.二、填空题13.【分析】由已知证明再由三角形相似列比例式可得证明利用基本不等式求得的最大值可得三棱锥体积的最大值【详解】由平面得又平面得又平面得而平面可得在中由得由得则由得又得即(当且仅当时等号成立)三棱锥体积的最解析:34【分析】由已知证明AE PC ⊥,再由三角形相似列比例式可得PE ,证明AD DE ⊥,利用基本不等式求得AD DE ⋅的最大值,可得三棱锥P ADE -体积的最大值. 【详解】由PA ⊥平面ABC ,得PA BC ⊥,又BC AB ⊥,PAAB A =,BC ∴⊥平面PAB ,得BC AD ⊥,又AD PB ⊥,PB BC B ⋂=, AD ∴⊥平面PBC ,得AD PC ⊥,而DE PC ⊥,AD DE D ⋂=,PC ∴⊥平面ADE ,可得AE PC ⊥.在Rt PAC △中,由23,2PA AC ==,得4PC =.由Rt PEA Rt PAC ∽,得PE PA PA PC =,则21234PA PE PC ===, 由3PE =,23PA =23AE =,又AD DE ⊥,2223AD DE AE ∴+==,得2232AD DE AD DE =+≥⋅, 即32AD DE⋅(当且仅当AD DE =时等号成立), ∴三棱锥P ADE -体积的最大值是1111333323224AD DE PE ⨯⨯⨯=⨯⨯⨯=.故答案为:34. 【点睛】方法点睛:解答空间几何体中垂直关系时,一般要根据已知条件把空间中的线线、线面、面面之间垂直关系进行转化,转化时要正确运用有关的定理,找出足够的条件进行推理.14.②③④【分析】取点为线段的中点可判断①建立空间直角坐标系假设存在点使得利用解出的值即可判断②;连接交于点证明线段到平面的距离为定值可判断③;求出点的坐标然后计算平面和平面的法向量即可判断④【详解】对解析:②③④. 【分析】取点M 为线段1BD 的中点可判断①,建立空间直角坐标系假设存在点M ,使得1B M AE ⊥,利用()1110AE B M AE B B BD λ⋅=⋅+=解出λ的值即可判断②;连接AC 、BD 交于点1O ,证明11//EO BD ,线段1BD 到平面AEC 的距离为定值,可判断③;求出点M 的坐标,然后计算平面AEC 和平面MAC 的法向量,即可判断④. 【详解】对于①:连接1AC 交1BD 于点O ,当点M 在O 点时直线AD 与直线1C M 相交,故①不正确,以D 为坐标原点,建立如图所示的空间直角坐标系,设正方体的边长为2,则()0,0,0D ,()10,0,2D ,()2,0,0A ,()0,2,0C ,()0,0,1E ,()2,2,0B ,()12,2,2B ,对于②:()2,0,1AE =-,假设存在点M ,使得1B M AE ⊥,()()()1110,0,22,2,22,2,22B M B B BD λλλλλ=+=-+--=---,[]0,1λ∈,所以14220AE B M λλ⋅=+-=,解得13λ=,所以当12D M MB =时1B M AE ⊥, 故②正确; 对于③:连接AC 、BD 交于点1O ,因为点E 是棱1DD 的中点,此时11//EO BD ,故线段1BD 到平面AEC 的距离为定值,所以四面体EMAC 的体积为定值,故③正确; 对于④:当12D M MB =时,442,,333M ⎛⎫⎪⎝⎭,()2,0,1AE =-,()2,2,0AC =-,设平面AEC 的法向量为()111,,m x y z =,由111120220m AE x z m AC x y ⎧⋅=-+=⎪⎨⋅=-+=⎪⎩令12z =,可得11x =,11y =,可得()1,1,2m =,设平面MAC 的法向量为()222,,n x y z =,242,,333MA ⎛⎫=-- ⎪⎝⎭,由222222202420333n AC x y n MA x y z ⎧⋅=-+=⎪⎨⋅=--=⎪⎩解得:20y =,令 21x =可得22z =,所以1,1,1n ,因为1111120m n ⋅=⨯+⨯-⨯=,m n ⊥所以平面EAC ⊥平面MAC ,故④正确;故答案为:②③④.【点睛】方法点睛:证明面面垂直的方法(1)利用面面垂直的判定定理,先找到其中一个平面的一条垂线,再证明这条垂线在另外一个平面内或与另外一个平面内的一条直线平行即可;(2)利用性质://,αββγαγ⊥⇒⊥(客观题常用);(3)面面垂直的定义(不常用);(4)向量方法:证明两个平面的法向量垂直,即法向量数量积等于0.15.【分析】根据题意得平面在上取使得连接证得平面平面将空间中的动点轨迹的周长问题转化为求三角形边周长问题又代入计算即可【详解】解:如图正方体中连接:易得平面在上取使得连接易得根据线面平行判定定理证得平面【分析】根据题意得1BD ⊥平面1ABC ,在1,BB AB 上取,F G使得12,2BF FB AG GB ==连接,,GE EF GF 证得平面1//AB C 平面EFG ,将空间中的动点P 轨迹的周长问题转化为求三角形EFG 边周长问题,又GE EF GF ===,代入计算即可. 【详解】解:如图正方体中连接11,,AC B C B A :易得1BD ⊥平面1ABC ,在1,BB AB 上取,F G 使得12,2BF FB AG GB ==连接,,GE EF GF ,易得1//,//GE AC EF BC根据线面平行判定定理证得平面1//AB C 平面EFG所以1BD ⊥平面EFG所以线段,,GE EF GF 就是点P 的运动轨迹, 因为1223GE EF GF ==== 所以动点P 的运动轨迹周长为232GE EF GF ++==2【点睛】关键点点睛:本题考查线面垂直,面面平行的概念,解题的关键是借助图形将空间问题转化为平面问题.本题中根据1BD ⊥平面1ABC 及平面1//ABC 平面EFG 得到线段,,GE EF GF 就是点P 的运动轨迹,代值计算即可.16.4【分析】取中点连接再根据题意依次计算进而得球的球心即为(与重合)【详解】解:因为所以又因为所以所以因为平面平面平面平面平面所以平面取中点连接所以所以平面所以此时所以即球的球心球心即为(与重合)半径 解析:4【分析】取,AB AC 中点,D E ,连接DE ,DP ,再根据题意依次计算4EA EB EC EP ====,进而得球O 的球心O 即为E (O 与E 重合)【详解】 解:因为42BC =8AC =,AB BC ⊥, 所以42AB =4PA PB ==,所以222PA PB AB +=,所以PA PB ⊥,因为平面PAB ⊥平面ABC ,平面PAB ⋂平面ABC AB =,AB BC ⊥,BC ⊂平面ABC ,所以BC ⊥平面PAB ,取,AB AC 中点,D E ,连接DE ,DP所以//DE BC ,22DE =,22DP =所以DE ⊥平面PAB ,所以DE PD ⊥,此时,142EB AC EA EC ====, 224EP DP DE =+=, 所以4EA EB EC EP ====,即球O 的球心球心O 即为E (O 与E 重合),半径为4EA =.故答案为:4.【点睛】本题解题的关键在于寻找球心,在本题中,,PAB ABC △△均为直角三角形,故易得AC 中点即为球心.考查空间思维能力,运算求解能力,是中档题.17.【分析】取中点为过分别作底面的垂线根据题中条件得到;过分别作的垂线连接由二面角的定义结合线面垂直的判定定理及性质得到为二面角的平面角;为二面角的平面角得出令进而可求出最值【详解】取中点为过分别作底面解析:34【分析】取BC 中点为E ,过P 、M 分别作底面的垂线PO 、MN ,根据题中条件,得到AN NO OE ==,2PO MN =;过O 、N 分别作BC 的垂线OG 、NH ,连接MH ,PG ,由二面角的定义,结合线面垂直的判定定理及性质,得到MHN ∠为二面角M BC A--的平面角;PGO ∠为二面角A BC P --的平面角,得出tan 4tan PGO MHN ∠=∠,()23tan tan tan 14tan MHN PGO MHN MHNα∠=∠-∠=+∠,令tan 0x MHN =∠>,进而可求出最值.【详解】取BC 中点为E ,过P 、M 分别作底面的垂线PO 、MN ,则O 为ABC 的重心,MN ⊥平面ABC ;PO ⊥平面ABC ;由于点M 为棱PA 的中点,所以有AN NO OE ==,2PO MN =;过O 、N 分别作BC 的垂线OG 、NH ,连接MH ,PG ,因为BC ⊂平面ABC ,所以MN BC ⊥,同理PO BC ⊥;又MN NH N ⋂=,MN ⊂平面MNH ,NH ⊂平面MNH ,所以BC ⊥平面MNH ;因为MH ⊂平面MNH ,所以BC MH ⊥,所以MHN ∠为二面角M BC A --的平面角;同理BC PG ⊥,所以PGO ∠为二面角A BC P --的平面角,所以tan PO PGO OG ∠=,tan MN MHN HN∠=, 因为NO OE =,//OG NH ,所以12OG NH =; 因此2tan 4tan 12PO MN PGO MHN OG HN ∠===∠, 所以()2tan tan 3tan tan tan 1tan tan 14tan PGO MHN MHN PGO MHN PGO MHN MHN α∠-∠∠=∠-∠==+∠⋅∠+∠, 令tan 0x MHN =∠>,则2333tan 1444x x x x α=≤=+,当且仅当214x =,即12x =时,等号成立. 故答案为:34. 【点睛】关键点点睛: 求解本题的关键在于确定二面角M BC A --、A BC P --以及P BC M --三者之间的关系,由题中条件得出二面角A BC P --是二面角MBC A --的4倍,进而可求得结果. 18.【分析】设出外接球的半径球心的外心半径r 连接过作的平行线交于连接如图所示在中运用正弦定理求得的外接圆的半径r 再利用的关系求得外接球的半径运用球的表面积公式可得答案【详解】设三棱锥外接球的半径为球心为 解析:20π【分析】设出外接球的半径R 、球心O ,ABC 的外心1O 、半径 r , 连接1AO ,过O 作的平行线OE 交AD 于 E ,连接OA ,OD ,如图所示,在ABC 中,运用正弦定理求得 ABC 的外接圆的半径r ,再利用1,,R r OO 的关系求得外接球的半径,运用球的表面积公式可得答案.【详解】设三棱锥外接球的半径为R 、球心为O ,ABC 的外心为1O 、外接圆的半径为r ,连接1AO ,过O 作平行线OE 交AD 于E ,连接OA ,OD ,如图所示,则OA OD R ==,1O A r =,OE AD ⊥,所以E 为AD 的中点.在ABC中,由正弦定理得2sin BC r BAC ==∠r =. 在ABC 中,由余弦定理2222cos BC AB AC AB AC BAC =+-⋅⋅∠,可得2117963AB AB =+-⋅⋅,得4AB =.所以11sin 34223ABC S AB AC BAC =⋅⋅∠=⨯⨯⨯=△因为11333D ABC ABC V S AD AD -=⋅⋅=⨯=△,所以4AD =.连接1OO ,又1//OO AD ,所以四边形1EAOO 为平行四边形,1128EA OO AD ===,所以R ===所以该三棱锥的外接球的表面积()224π4π520πS R ===.故答案为:20π.【点睛】本题考查三棱锥的外接球,及球的表面积计算公式,解决问题的关键在于利用线面关系求得外接球的球心和球半径,属于中档题.19.①②【分析】采用逐一验证法根据线面平行线面垂直的判定定理以及线面距离判断可得结果【详解】由共面所以因为平面平面所以平面;故①正确;平面平面所以又因为平面平面所以故②正确;若则平面或EF 在平面ACD 内 解析:①②【分析】采用逐一验证法,根据线面平行,线面垂直的判定定理,以及线面距离,判断可得结果.【详解】由AB AD ⊥,,,EF AD AD EF AB ⊥,共面 ,所以//EF AB ,因为EF ⊄平面ABC ,AB 平面ABC ,所以//EF 平面ABC ;故①正确; BC ⊥平面ABD ,AD ⊂平面ABD ,所以BC AD ⊥,又因为AB AD ⊥,AB BC B ⋂=,AD ⊥平面ABC ,AC ⊂平面ABC ,所以AD AC ⊥,故②正确;若//EF CD ,则//EF 平面ACD ,或EF 在平面ACD 内,如图EF 与平面ACD 相交于点E ,显然不成立,故③不正确,故答案为:①②【点睛】本题主要考查了线线、线面之间的位置关系,考查了线面平行的判断以及由线面垂直证明线线垂直,属于中档题. 20.【分析】欲使圆柱侧面积最大需使圆柱内接于圆锥设圆柱的高为h 底面半径为r 用r 表示h 从而求出圆柱侧面积的最大值【详解】欲使圆柱侧面积最大需使圆柱内接于圆锥;设圆柱的高为h 底面半径为r 则解得;所以;当时取 解析:43π【分析】欲使圆柱侧面积最大,需使圆柱内接于圆锥,设圆柱的高为h ,底面半径为r ,用r 表示h ,从而求出圆柱侧面积的最大值.【详解】欲使圆柱侧面积最大,需使圆柱内接于圆锥;设圆柱的高为h ,底面半径为r , 23423h r -=,解得323h =; 所以()23222334S rh r r r πππ⎛⎫===- ⎪ ⎪⎝⎭圆柱侧; 当2r 时,S 圆柱侧取得最大值为43π 故答案为:43π.【点睛】本题考查了求圆柱侧面积的最值,考查空间想象能力,将问题转化为函数求最值,属于中档题.三、解答题21.(Ⅰ)证明见解析;(Ⅱ5 【分析】(Ⅰ)由中位线定理证明1//OM C D ,即可得线面平行;(Ⅱ)连1D O ,证明1D OD ∠为二面角1D AC D --的平面角, 在直角1D DO △中计算可得.【详解】解:(Ⅰ)连1BC ,则M 也为1BC 的中点,又M 为BD 的中点,所以1//OM C D ,因为OM ⊄平面11DB C ,1C D ⊂平面11DC B ,所以直线//OM 平面11DB C ;(Ⅱ)连1D O ,因为ABCD 是菱形,所以DO AC ⊥,又1111ABCD A BC D -为直棱柱,底面为菱形,所以11D A D C =,而O 为AC 中点,所以1D O AC ⊥,所以1D OD ∠为二面角1D AC D --的平面角,因为ABCD 是边长为2的菱形,且60BAD ∠=︒,所以1DO =,又12DD =, 由直棱柱知1DD DO ⊥,所以15DO =,所以115cos DO D OD D O ∠==.【点睛】方法点睛:本题考查证明线面平行,考查求二面角角,求二面角常用方法:(1)定义法:作出二面角的平面角并证明,然后在三角形中计算可得;(2)向量法:建立空间直角坐标系,求出两个平面的法向量夹角的余弦即可得二面角的余弦(注意判断二面角是锐角还是钝角).22.(1)证明见解析;(2)证明见解析.【分析】(1)根据三角形中位线的性质,得到//EF AB ,利用线面平行的判定定理证得结果; (2)根据面面垂直的性质定理,得到BD ⊥平面ACD ,进而证得BD AC ⊥.【详解】证明:(1)如图(2):在ABC 中,E 、F 分别是AC 、BC 中点,得//EF AB , 又AB ⊄平面DEF ,EF ⊂平面DEF ,//AB ∴平面DEF .(2)∵平面ACD ⊥平面BCD 且交线为CD ,BD CD ⊥,且BD ⊂平面BCD , ∴BD ⊥平面ACD ,又AC ⊂平面ACD∴BD AC ⊥.【点睛】方法点睛:该题考查的是有关空间关系的证明问题,解题方法如下:(1)熟练掌握线面平行的判定定理,在解题过程中,一定不要忘记线在面内、线在面外的条件;(2)根据面面垂直的条件,结合线线垂直,利用面面垂直的性质定理,得到线面垂直,进而证得线线垂直.23.(1)证明见解析;(2)证明见解析;(3)98. 【分析】(1)取PA 的中点G ,连接,BG EG ,证明四边形EFBG 为平行四边形,得出//EF BG ,再由线面平行的判定定理证明即可;(2)先证明PA ⊥平面ABCD ,从而得出PA CD ⊥,再由等腰三角形的性质得出AE PD ⊥,最后由面面垂直的判定定理证明即可;(3)以AFC △为底,12PA 为高,由棱锥的体积公式得出答案. 【详解】(1)如图,取PA 的中点G ,连接,BG EG .因为点,E G 分别为,PD PA 的中点,所以1//,2EG AD EG AD = 又因为F 是BC 的中点,四边形ABCD 是正方形,所以//BF EG 且BF EG = 故四边形EFBG 为平行四边形,所以//EF BG因为BG ⊂平面,ABP EF 不在平面ABP 内,所以//EF 平面ABP .(2)由条件知32,3PB PD PA AD AB =====,所以PAB △和PAD △都是等腰直角三角形,,PA AB PA AD ⊥⊥又因为,,AB AD A AB AD =⊂平面,ABCD 所以PA ⊥平面ABCD因为CD ⊂平面ABCD ,所以PA CD ⊥又因为,,AD CD PA AD A ⊥⋂=所以CD ⊥平面PAD ,所以CD AE ⊥因为E 是PD 的中点,所以AE PD ⊥又因为,,PD CD D PD CD ⋂=⊂平面PCD ,所以AE ⊥平面PCD因为AE ⊂平面,AEF 所以平面AEF ⊥平面PCD .(3)由图可知C AEF E ACF V V --=,1111319333232228E ACF ACF V S PA -=⨯=⨯⨯⨯⨯⨯=△, 即三棱锥C AEF -的体积为98 【点睛】 关键点睛:在证明线线平行时,关键是证明四边形EFBG 为平行四边形,从而得出//EF BG .24.(1)证明见解析;(232211【分析】。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
双基限时练(四)
一、选择题
1.如图所示的三棱锥的主视图为( )
解析由三视图的画法,可知答案为B.
答案 B
2.下列说法正确的是( )
A.任何物体的三视图都与物体的摆放位置有关
B.任何物体的三视图都与物体的摆放位置无关
C.有的物体的三视图与物体摆放位置无关
D.正方体的三视图一定是三个全等的正方形
解析球的三视图与物体的摆放位置无关.
答案 C
3.若一几何体的主视图和左视图均为等腰梯形,则这个几何体可能是( ) A.圆锥B.圆柱
C.圆台D.球
答案 C
4.
四个正方体按如图所示的方式放置,其中阴影部分为我们观察的正面.则该物体的三视图正确的为( )
解析由三视图的画法,可知答案为B.
答案 B
5.如图,已知正三棱柱ABC-A1B1C1的底面边长为2,高为3,则其左视图的面积为( )
A.6 B.3
C.3 3 D.6 3
解析由三视图的画法可知,该几何体的左视图是一个矩形,其底面边长为2sin60°
=3,高为3,∴面积S=3 3.
答案 C
6.如图所示的几何体是一个四棱柱截去一个角后剩余的几何体,则此几何体的主视图正确的是( )
解析由三视图的画法,可知答案为C.
答案 C
二、填空题
7.给出下列命题:
①如果一个几何体的三个视图是完全相同的,则这个几何体是正方体;②如果一个几何体的主视图和俯视图都是矩形,则这个几何体是长方体;③如果一个几何体的三个视图都是矩形,则这个几何体是长方体;④如果一个几何体的主视图和左视图都是等腰梯形,则这个几何体是圆台.
其中正确的是________.(将正确的全都写在横线上)
解析对于①由于球的三个视图也是完全相同的,故①不对;对于④,主视图与左视图都是等腰梯形的除圆台之外,还有棱台,故④不对;对于②,当圆柱倒置时,如图,其主视图与俯视图均为矩形,故②不正确.
答案③
8.下列几何体各自的三视图中,有且仅有两个视图相同的是( )
A.①②B.②④
C.①③D.①④
解析①中的三个视图均相同,③中主视图为与左视图不同,只有②④中的左视图与主视图相同.
答案 B
9.如图是4个三视图和4个实物图,请将三视图与实物图正确配对________________.
解析由三视图的画法可知.
答案(1)→B,(2)→A,(3)→C,(4)→D
三、解答题
10.观察下列实物体,画出它们的三视图.
解(1)三视图如下:
(2)三视图如下:
11.如图所示,是一个长方体截去一个角所得多面体的直观图和它的主视图和左视图(单位: cm).请在正视图下面,按照画三视图的要求画出该多面体的俯视图.
解依据三视图的绘图原则,可作出该几何体的俯视图如图.
12.如图,直角梯形ABCD绕底边AD所在直线EF旋转,在旋转前,非直角的腰的端点A可以在DE上选定.当点A选在射线DE上的不同位置时,形成的几何体的大小、形状不同,分别画出它的三视图并比较其异同点.
解(1)当点A在图①射线DE的位置时,绕EF旋转一周所得几何体为底面半径为CD 的圆柱和圆锥拼成,其三视图如图②.
(2)当点A位于如图③所示位置时,其旋转所得几何体为圆柱中挖去一个同底的圆锥,其三视图如图④所示.
思 维 探 究
13.已知一个正三棱锥S -ABC 的棱长均为a ,分别求出它的三个视图的面积.
解 ∵S -ABC 为正三棱锥,∴S 在底面ABC 上的射影为△ABC 的中心O ,又BO =a sin60°×23=3
3
a ,∴SO =SB 2-BO 2=
a 2
-a 2
3
=
6
3
a .∴S 主视图
=12×a ×63a =66
a 2
,S 左视图=12×a ×sin60°×63a =24
a 2
,S 俯视图
=1
2
×a 2
sin60°=34
a 2
.。
