高考数学分类题库考点41 双曲线()理新人教版(1)

合集下载

2017高考数学必考点【双曲线的标准方程及图象】整理.doc

2017高考数学必考点【双曲线的标准方程及图象】整理高考数学一直是很多考生头疼的科目，考生难以取得数学高分是因为没有掌握好考点，为了帮助大家掌握好数学考点，下面为大家带来2017高考数学必考点【双曲线的标准方程及图象】整理，希望大家用心记住这些数学考点。

高考数学知识点：双曲线的标准方程及图象双曲线的标准方程：(1)中心在原点，焦点在x轴上：,复习方法;(2)中心在原点，焦点在y轴上：。

双曲线的图像：(1)焦点在x轴上的双曲线的图像;(2)焦点在y轴上的双曲线的图像。

判断双曲线的焦点在哪个轴上：判断双曲线的焦点在哪个轴上的方法看未知数前的系数，哪一个为正，焦点就在哪一个轴上.定义法求双曲线的标准方程:求动点的轨迹方程时，可利用定义先判断动点的轨迹，再写出方程.平面几何中的定理性质在解决解析几何问题时起着简化运算的作用，一定要注意应用，根据双曲线的定义，到两个定点的距离之差的绝对值是一个常数的点的轨迹是双曲线，可以求双曲线的标准方程，待定系数法求双曲线的标准方程:在求双曲线标准方程时，可先设出其标准方程，再根据双曲线的参数a，b，c，e的取值及相互之间的关系，求出a，b的值，已知双曲线的渐近线方程，求双曲线方程时，可利用共渐近线双曲线系方程,再由其他条件求.若焦点不确定时，要注意分类讨论.利用双曲线的性质求解有关问题:要解决双曲线中有关求离心率或求离心率范围的问题，应找好题中的等量关系或不等关系，构造出离心率的关系式，这里应和椭圆中a，b，c的关系区分好，即几种特殊的双曲线：等轴双曲线实轴和虚轴相等的双曲线叫做等轴双曲线.离心率两条渐近线互相垂直共轭双曲线共渐近线的双曲线2017高考数学必考点【双曲线的标准方程及图象】整理是为大家精心总结的，希望大家能够在复习数学考点的时候多下功夫，这样就能在高考数学考试中取得满意的成绩。

2020年人教版高考数学(理)一轮复习第53讲双曲线

听课正文第53讲双曲线1.双曲线的定义平面内与两个定点F1,F2的等于常数(小于|F1F2|)的点的轨迹叫作双曲线.这两个定点叫作,两焦点间的距离叫作.集合P={M|||MF1|-|MF2||=2a},|F1F2|=2c,其中a,c为常数且a>0,c>0.(1)当时,P点的轨迹是双曲线;(2)当时,P点的轨迹是两条射线;(3)当时,P点不存在.2.标准方程(1)中心在坐标原点,焦点在x轴上的双曲线的标准方程为x2a2-y2b2=1(a>0,b>0);(2)中心在坐标原点,焦点在y轴上的双曲线的标准方程为y2a2-x2b2=1(a>0,b>0).3.双曲线的性质标准方程x2a2-y2b2=1(a>0,b>0)y2a2-x2b2=1(a>0,b>0)图形(续表)标准方程x2a2-y2b2=1(a>0,b>0)y2a2-x2b2=1(a>0,b>0)性质范围,y∈R ,x∈R对称性对称轴:坐标轴.对称中心:原点顶点A1,A2A1,A2渐近线y= y=离心率e=ca,e∈a ,b ,c的关系c 2= (c>a>0,c>b>0)实、虚轴线段A 1A 2叫作双曲线的实轴,它的长|A 1A 2|= ;线段B 1B 2叫作双曲线的虚轴,它的长|B 1B 2|= ;a 叫作双曲线的实半轴长,b 叫作双曲线的虚半轴长常用结论双曲线的几个常用结论: (1)与双曲线x 2a2-y 2b 2=1(a>0,b>0)有共同渐近线的双曲线系的方程为x 2a2-y 2b2=λ(λ≠0).(2)双曲线上的点P (x 0,y 0)与左(下)焦点F 1或右(上)焦点F 2之间的线段叫作双曲线的焦半径,分别记作r 1=|PF 1|,r 2=|PF 2|,则①x 2a2-y 2b 2=1(a>0,b>0),若点P 在右支上,则r 1=ex 0+a ,r 2=ex 0-a ;若点P 在左支上,则r 1=-ex 0-a ,r 2=-ex 0+a.②y 2a2-x 2b2=1(a>0,b>0),若点P 在上支上,则r 1=ey 0+a ,r 2=ey 0-a ;若点P 在下支上,则r 1=-ey 0-a ,r 2=-ey 0+a.题组一常识题1.[教材改编] 若双曲线E :x 29-y 225=1的左、右焦点分别为F 1,F 2,点P 在双曲线E 上,且|PF 1|=5,则|PF 2|= .2.[教材改编] 已知双曲线经过点P (4,-2√2)和点Q (-4√2,2√3),则该双曲线的标准方程为 .3.[教材改编] 双曲线C :4x 2-10y 2=100的离心率是 ,渐近线方程是 .题组二常错题◆索引:忽视双曲线定义中的条件“2a<|F 1F 2|”;忽视定义中的条件“差的绝对值”;忽视双曲线焦点的位置;忽视双曲线上的点的位置.4.平面内到点F 1(5,0),F 2(-5,0)距离之差的绝对值等于10的点P 的轨迹是 .5.已知A (-5,0),B (5,0),动点P 满足|PA |-|PB |=6,则点P 的轨迹是 .6.已知双曲线的实轴长为8,离心率为2,则双曲线的标准方程为 .7.P 是双曲线x 216-y 281=1上任意一点,F 1,F 2分别是它的左、右焦点,且|PF 1|=9,则|PF 2|= .探究点一双曲线的定义及标准方程例1 (1)已知双曲线x 2a 2-y 2b 2=1(a>0,b>0)的右焦点为F ,点A 在双曲线的渐近线上,△OAF是边长为2的等边三角形(O 为原点),则双曲线的方程为 ( )A .x 24-y 212=1B .x 212-y 24=1 C .x 23-y 2=1D .x 2-y 23=1(2)[2018·辽宁朝阳一模] 设中心在原点、焦点在x 轴上的双曲线的焦距为12,圆(x-6)2+y 2=20与该双曲线的渐近线相切,点P 在双曲线上,若点P 到焦点F 1的距离是9,则点P 到F 2的距离是 ( ) A .17或1 B .13或5 C .13 D .17[总结反思] (1)应用双曲线的定义,可判定平面内动点的轨迹是否为双曲线,进而求出曲线方程;可在“焦点三角形”中,利用正弦定理、余弦定理,并结合||PF 1|-|PF 2||=2a ,运用配方法,建立与|PF 1|·|PF 2|的联系.应用双曲线的定义时,若去掉绝对值,则点的轨迹是双曲线的一支.(2)待定系数法求双曲线方程时,一要注意焦点位置的判断,二要注意c 2=a 2+b 2,a ,b ,c 的关系不要弄错.变式题 (1)[2018·合肥三模] 已知双曲线C :y 2a 2-x 2b 2=1(a>0,b>0)的上焦点为F ,M 是双曲线虚轴的一个端点,过F ,M 的直线交双曲线的下支于A 点.若M 为AF 的中点,且|AF|=6,则双曲线C 的方程为 ( ) A .y 22-x 28=1 B .y 28-x 22=1 C .y 2-x 24=1D .y 24-x 2=1(2)双曲线C的渐近线方程为y=±2√33x,一个焦点为F(0,-√7),点A(√2,0),点P为双曲线在第一象限内的点,则当点P的位置变化时,△PAF周长的最小值为()A.8B.10C.4+3√7D.3+3√7(3)已知双曲线的虚轴长为12,离心率为54,则其方程为.探究点二双曲线的几何性质有关问题微点1已知离心率求渐近线方程例2[2018·辽宁凌源二中月考]已知圆E:(x-3)2+(y+m-4)2=1(m∈R),当m变化时,圆E上的点与原点O的最短距离与双曲线C:x 2a2-y2b2=1(a>0,b>0)的离心率相等,则双曲线C的渐近线方程为()A.y=±2xB.y=±12xC.y=±√3xD.y=±√33x[总结反思]已知离心率求渐近线方程,即e=ca ⇒c2=e2·a2=a2+b2⇒e2=1+b2a2,即得渐近线方程为y=±√e2-1x.微点2已知渐近线方程求离心率例3[2018·赣州模拟]若双曲线y2a2-x2b2=1(a,b>0)的一条渐近线方程为y=34x,则该双曲线的离心率为()A.43B.53C.169D.259[总结反思]已知渐近线方程y=±kx,若焦点位置不明确要分k=ba 和k=ab两种情况讨论.已知渐近线方程为y=±ba ·x,可由c2=a2+b2⇒c2a2=1+b2a2,从而求得离心率e=√1+(ba)2.微点3由离心率研究渐近线夹角问题例4定义平面上两条相交直线的夹角为:两条相交直线交成的不超过90°的正角.已知双曲线E:x2 a2-y2b2=1(a>0,b>0),当其离心率e∈[√2,2]时,对应双曲线的渐近线的夹角的取值范围为()A.[0,π6]B.[π6,π3]C.[π4,π3]D.[π3,π2][总结反思]已知离心率可得出双曲线的渐近线方程,即得出渐近线的斜率,从而可解决与渐近线夹角有关的问题.微点4利用渐近线与已知直线的位置关系求离心率范围例5已知双曲线C:x2a2-y2b2=1(a>0,b>0)的左、右焦点分别为F1,F2,过点F1且与双曲线C的一条渐近线垂直的直线l与C的两条渐进线分别交于M,N两点,若|NF1|=2|MF1|,则双曲线C的离心率为.[总结反思]一般可以先求解已知直线与渐近线的交点,再结合相关条件得到关于a与b的方程(或不等式),利用c2=a2+b2,转化为关于a与c的方程(或不等式),从而得离心率的值(或范围).应用演练1.【微点1】[2018·永州模拟]双曲线x2-y2b2=1(b>0)的离心率e=√5,则双曲线的渐近线方程为 ( ) A .y=±12x B .y=±15xC .y=±2xD .y=±5x2.【微点2】[2018·合肥一模] 若双曲线x 2a 2-y 2b 2=1(a>0,b>0)的一条渐近线方程为y=-2x ,则该双曲线的离心率是 ( )A .√52B .√3C .√5D .2√33.【微点3】已知双曲线x 2a2-y 2b2=1的离心率为2√33,则双曲线的两条渐近线的夹角为 ( )A .π6B .π4C .π3D .π24.【微点4】[2018·珠海三模] 双曲线x 2a2-y 2b2=1的一条渐近线与直线x+2y-1=0垂直,则双曲线的离心率为( ) A .√52B .√5C .√3+12 D .√3+15.【微点2】已知双曲线C :x 2a 2-y 2b 2=1(a>0,b>0)的渐近线经过圆E :x 2+y 2-2x+4y=0的圆心,则双曲线C 的离心率为 ( )A .√5B .√52C .2D .√26.【微点4】过双曲线x 2a2-y 2b2=1(a>0,b>0)的右焦点F 作渐近线的垂线,垂足为P ,且该直线与y 轴的交点为Q ,若|FP|<|OQ|(O 为坐标原点),则双曲线的离心率的取值范围为 .探究点三直线与双曲线的位置关系例6 [2018·安阳一模] 如图8-53-1所示,在平面直角坐标系xOy 中,直线l 1:y=x 与直线l 2:y=-x 之间的阴影部分记为W ,区域W 中动点P (x ,y )到l 1,l 2的距离之积为1.(1)求点P 的轨迹C 的方程;(2)动直线l 穿过区域W ,分别交直线l 1,l 2于A ,B 两点,若直线l 与轨迹C 有且只有一个公共点,求证:△OAB的面积恒为定值.图8-53-1[总结反思]解决直线与双曲线的位置关系问题的常用方法:(1)将直线方程代入双曲线方程得到关于x(或y)的方程,利用根与系数的关系及整体代入的思想解题,设直线与双曲线交于A(x1,y1),B(x2,y2)两点,直线的斜率为k,则|AB|=√1+k2·|x1-x2|;(2)比较直线的倾斜角(或斜率)与渐近线的倾斜角(或斜率)的大小,得到直线与双曲线的交点情况;(3)与中点有关的问题常用点差法.变式题已知双曲线C以F1(-2,0),F2(2,0)为焦点,且过点P(7,12).(1)求双曲线C与其渐近线的方程;(2)若斜率为1的直线l与双曲线C相交于A,B两点,且OA⃗⃗⃗⃗⃗ ⊥OB⃗⃗⃗⃗⃗ (O为坐标原点),求直线l的方程.。

高考数学专题复习：双曲线(含解析)

高考数学专题复习：双曲线(含解析)本文存在大量的格式错误和段落问题，需要进行修正和删减。

修正后的文章如下：研究目标：1.理解双曲线的定义、几何图形、标准方程以及简单几何性质。

2.理解数形结合的思想。

3.了解双曲线的实际背景及其简单应用。

一、单选题1.设 $F_1,F_2$ 分别是双曲线 $C: \frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ 的左右焦点，点 $P$ 在双曲线 $C$ 的右支上，且 $F_1P=F_2P=c$，则 $\frac{c^2}{a^2-b^2}$ 的值为：A。

$1$B。

$\frac{1}{2}$C。

$\frac{1}{3}$D。

$\frac{1}{4}$答案】B解析】根据双曲线的性质求出 $c$ 的值，结合向量垂直和向量和的几何意义进行转化求解即可。

点睛】本题主要考查双曲线性质的意义，根据向量垂直和向量和的几何意义是解决本题的关键。

2.设 $F_1(-1,0),F_2(1,0)$ 是双曲线 $C: \frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ 的左右焦点，$A(0,b)$ 为左顶点，点$P$ 为双曲线右支上一点，且 $AP=\frac{a}{2}$，则$\frac{b^2}{a^2}$ 的值为：A。

$1$B。

$\frac{1}{2}$C。

$\frac{1}{3}$D。

$\frac{1}{4}$答案】D解析】先求出双曲线的方程为 $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$，再求出点 $P$ 的坐标，最后求$\frac{b^2}{a^2}$。

点睛】本题主要考查双曲线的几何性质和向量的数量积运算，考查双曲线方程的求法，意在考查学生对这些知识的掌握水平和分析推理计算能力。

双曲线的通径为 $2a$。

3.已知直线$l$ 的倾斜角为$\theta$，且$l: y=x\tan\theta$，直线 $l$ 与双曲线 $C: \frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ 的左、右两支分别交于 $A,B$ 两点，$OA\perp$轴，$OB\perp$轴（其中 $O$、$F_1,F_2$ 分别为双曲线的坐标原点、左、右焦点），则该双曲线的离心率为：A。

2020版高考理科数学(人教版)一轮复习讲义：第九章第六节双曲线 Word版含答案

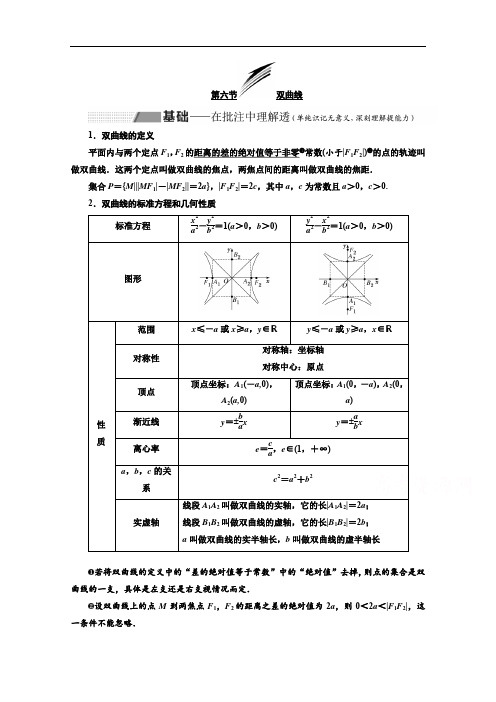
第六节双曲线1．双曲线的定义平面内与两个定点F 1，F 2的距离的差的绝对值等于非零❶常数(小于|F 1F 2|)❷的点的轨迹叫做双曲线．这两个定点叫做双曲线的焦点，两焦点间的距离叫做双曲线的焦距．集合P ＝{M |||MF 1|－|MF 2||＝2a }，|F 1F 2|＝2c ，其中a ，c 为常数且a ＞0，c ＞0. 2．双曲线的标准方程和几何性质若将双曲线的定义中的“差的绝对值等于常数”中的“绝对值”去掉，则点的集合是双曲线的一支，具体是左支还是右支视情况而定．设双曲线上的点M 到两焦点F 1，F 2的距离之差的绝对值为2a ，则0＜2a ＜|F 1F 2|，这一条件不能忽略．①若2a ＝|F 1F 2|，则点M 的轨迹是分别以F 1，F 2为端点的两条射线； ②若2a ＞|F 1F 2|，则点M 的轨迹不存在；③若2a ＝0，则点M 的轨迹是线段F 1F 2的垂直平分线.[熟记常用结论]1．双曲线的焦点到其渐近线的距离为b .2．若P 是双曲线右支上一点，F 1，F 2分别为双曲线的左、右焦点，则|PF 1|min ＝a ＋c ，|PF 2|min＝c －a .3．同支的焦点弦中最短的为通径(过焦点且垂直于长轴的弦)，其长为2b 2a ；异支的弦中最短的为实轴，其长为2a .4．若P 是双曲线上不同于实轴两端点的任意一点，F 1，F 2分别为双曲线的左、右焦点，则S △PF 1F 2＝b 2tan θ2，其中θ为∠F 1PF 2.5．若P 是双曲线x 2a 2－y 2b 2＝1(a ＞0，b ＞0)右支上不同于实轴端点的任意一点，F 1，F 2分别为双曲线的左、右焦点，I 为△PF 1F 2内切圆的圆心，则圆心I 的横坐标为定值a .6．等轴双曲线(1)定义：中心在原点，以坐标轴为对称轴，实半轴长与虚半轴长相等的双曲线叫做等轴双曲线．(2)性质：①a ＝b ；②e ＝2；③渐近线互相垂直；④等轴双曲线上任意一点到中心的距离是它到两焦点距离的等比中项．7．共轭双曲线(1)定义：如果一条双曲线的实轴和虚轴分别是另一条双曲线的虚轴和实轴，那么这两条双曲线互为共轭双曲线．(2)性质：①它们有共同的渐近线；②它们的四个焦点共圆；③它们的离心率的倒数的平方和等于1.[小题查验基础]一、判断题(对的打“√”，错的打“×”)(1)平面内到点F 1(0,4)，F 2(0，－4)距离之差的绝对值等于8的点的轨迹是双曲线．( ) (2)方程x 2m －y 2n ＝1(mn ＞0)表示焦点在x 轴上的双曲线．( )(3)双曲线方程x 2m 2－y 2n 2＝λ(m ＞0，n ＞0，λ≠0)的渐近线方程是x 2m 2－y 2n 2＝0，即x m ±yn ＝0.( ) (4)若双曲线x 2a 2－y 2b 2＝1(a ＞0，b ＞0)与x 2b 2－y 2a 2＝1(a ＞0，b ＞0)的离心率分别是e 1，e 2，则1e 21＋1e22＝1.()答案：(1)×(2)×(3)√(4)√二、选填题1．双曲线2x2－y2＝8的实轴长是()A．2B．2 2C．4 D．4 2解析：选C双曲线2x2－y2＝8的标准方程为x24－y28＝1，故实轴长为4.2．若双曲线方程为x2－2y2＝1，则它的右焦点坐标为()A.⎝⎛⎭⎫22，0B.⎝⎛⎭⎫52，0C.⎝⎛⎭⎫62，0D．(3，0)解析：选C∵原方程可化为x21－y212＝1，∴a2＝1，b2＝12，∴c2＝a2＋b2＝32，∴右焦点坐标为⎝⎛⎭⎫62，0.3．若方程x22＋m－y2m＋1＝1表示双曲线，则m的取值范围是________.解析：因为方程x22＋m－y2m＋1＝1表示双曲线，所以(2＋m)(m＋1)＞0，即m＞－1或m＜－2.答案：(－∞，－2)∪(－1，＋∞)4．若双曲线x2－y2m＝1的离心率为3，则实数m＝________.解析：由已知可得a＝1，c＝1＋m，所以e＝ca＝1＋m＝3，解得m＝2.答案：25．双曲线C的焦点分别为(－6,0)，(6,0)，且经过点(－5,2)，则该双曲线的标准方程为____________________．解析：由题意得2a＝|(－5＋6)2＋22－(－5－6)2＋22|＝45，所以a＝25，又c＝6，所以b2＝c2－a2＝36－20＝16，所以双曲线的标准方程为x 220－y 216＝1.答案：x 220－y 216＝1考点一双曲线的标准方程[基础自学过关][题组练透]1．(2019·绵阳联考)已知双曲线C ：x 2a 2－y 2b 2＝1(a ＞0，b ＞0)的渐近线方程为y ＝±34x ，且其右焦点为(5,0)，则双曲线C 的标准方程为( )A.x 29－y 216＝1 B.x 216－y 29＝1 C.x 23－y 24＝1 D.x 24－y 23＝1 解析：选B 由题意得b a ＝34，c 2＝a 2＋b 2＝25，所以a ＝4，b ＝3，所以所求双曲线的标准方程为x 216－y 29＝1.2．与椭圆x 24＋y 2＝1共焦点且过点P (2,1)的双曲线标准方程是( )A.x 24－y 2＝1 B.x 22－y 2＝1 C.x 23－y 23＝1 D ．x 2－y 22＝1解析：选B 法一：椭圆x 24＋y 2＝1的焦点坐标是(±3，0)．设双曲线标准方程为x 2a 2－y 2b 2＝1(a ＞0，b ＞0)，因为双曲线过点P (2,1)，所以4a 2－1b2＝1，又a 2＋b 2＝3，解得a 2＝2，b 2＝1，所以所求双曲线标准方程是x 22－y 2＝1.法二：设所求双曲线标准方程为x 24－λ＋y 21－λ＝1(1＜λ＜4)，将点P (2,1)的坐标代入可得44－λ＋11－λ＝1，解得λ＝2(λ＝－2舍去)，所以所求双曲线标准方程为x 22－y 2＝1.3．过双曲线C ：x 2a 2－y 2b 2＝1(a ＞b ＞0)的右顶点作x 轴的垂线，与C 的一条渐近线相交于点A .若以C 的右焦点F 为圆心、半径为4的圆经过A ，O 两点(O 为坐标原点)，则双曲线C 的标准方程为( )A.x 24－y 212＝1 B.x 27－y 29＝1 C.x 28－y 28＝1 D.x 212－y 24＝1 解析：选A 因为渐近线y ＝ba x 与直线x ＝a 交于点A (a ，b )，c ＝4且(4－a )2＋b 2＝4，解得a 2＝4，b 2＝12，因此双曲线的标准方程为x 24－y 212＝1.4．经过点P (3,27)，Q (－62，7)的双曲线的标准方程为____________．解析：设双曲线方程为mx 2＋ny 2＝1(mn ＜0)，因为所求双曲线经过点P (3,27)，Q (－62，7)，所以⎩⎪⎨⎪⎧9m ＋28n ＝1，72m ＋49n ＝1，解得⎩⎨⎧m ＝－175，n ＝125.故所求双曲线标准方程为y 225－x 275＝1.答案：y 225－x 275＝15．焦点在x 轴上，焦距为10，且与双曲线y 24－x 2＝1有相同渐近线的双曲线的标准方程是________________．解析：设所求双曲线的标准方程为y 24－x 2＝－λ(λ＞0)，即x 2λ－y 24λ＝1，则有4λ＋λ＝25，解得λ＝5，所以所求双曲线的标准方程为x 25－y 220＝1.答案：x 25－y 220＝1[名师微点]求双曲线标准方程的2种方法(1)待定系数法：设出双曲线方程的标准形式，根据已知条件，列出参数a ，b ，c 的方程并求出a ，b ，c 的值．与双曲线x 2a 2－y 2b 2＝1有相同渐近线时，可设所求双曲线方程为x 2a 2－y 2b 2＝λ(λ≠0)．(2)定义法：依定义得出距离之差的等量关系式，求出a 的值，由定点位置确定c 的值． [提醒] 求双曲线的标准方程时，若焦点位置不确定，要注意分类讨论．也可以设双曲线方程为mx 2＋ny 2＝1(mn ＜0)求解．(如第4题)考点二双曲线的定义及其应用 [师生共研过关][典例精析](1)已知圆C 1：(x ＋3)2＋y 2＝1和圆C 2：(x －3)2＋y 2＝9，动圆M 同时与圆C 1及圆C 2相外切，则动圆圆心M 的轨迹方程为____________________．(2)已知F 1，F 2为双曲线C ：x 2－y 2＝2的左、右焦点，点P 在C 上，|PF 1|＝2|PF 2|，则cos ∠F 1PF 2＝________.(3)已知F 是双曲线x 24－y 212＝1的左焦点，A (1,4)，P 是双曲线右支上的一动点，则|PF |＋|PA |的最小值为________．[解析] (1)如图所示，设动圆M 与圆C 1及圆C 2分别外切于点A 和点B ，根据两圆外切的充要条件，得|MC 1|－|AC 1|＝|MA |， |MC 2|－|BC 2|＝|MB |. 因为|MA |＝|MB |，所以|MC 2|－|MC 1|＝|BC 2|－|AC 1|＝3－1＝2＜6.这表明动点M 到两定点C 2，C 1的距离的差是常数2且小于|C 1C 2|.根据双曲线的定义知，动点M 的轨迹为双曲线的左支(点M 到C 2的距离大，到C 1的距离小)，且a ＝1，c ＝3，则b 2＝8，设点M 的坐标为(x ，y )，则其轨迹方程为x 2－y 28＝1(x ≤－1)．(2)∵由双曲线的定义有|PF 1|－|PF 2|＝2a ＝22， |PF 1|＝2|PF 2|，∴|PF 1|＝42，|PF 2|＝22，则cos ∠F 1PF 2＝|PF 1|2＋|PF 2|2－|F 1F 2|22|PF 1|·|PF 2|＝(42)2＋(22)2－422×42×22＝34.(3)因为F 是双曲线x 24－y 212＝1的左焦点，所以F (－4,0)，设其右焦点为H (4,0)，则由双曲线的定义可得|PF |＋|PA |＝2a ＋|PH |＋|PA |≥2a ＋|AH |＝4＋(4－1)2＋(0－4)2＝4＋5＝9.[答案] (1)x 2－y 28＝1(x ≤－1) (2)34(3)9[解题技法]双曲线定义的应用策略(1)根据动点与两定点的距离的差判断动点的轨迹是否为双曲线．(2)利用双曲线的定义解决与双曲线的焦点有关的问题，如最值问题、距离问题．(3)利用双曲线的定义解决问题时应注意三点：①距离之差的绝对值；②2a ＜|F 1F 2|；③焦点所在坐标轴的位置．[过关训练]1．(2019·唐山模拟)已知F 1，F 2是双曲线x 24－y 2＝1的两个焦点，P 在双曲线上，且满足∠F 1PF 2＝90°，则△F 1PF 2的面积为( )A ．1 B.52C ．2D. 5解析：选A 不妨设|PF 1|＝m ，|PF 2|＝n ，则由双曲线的定义可知||PF 1|－|PF 2||＝|m －n |＝4.又因为∠F 1PF 2＝90°，所以|PF 1|2＋|PF 2|2＝(2c )2＝20，即m 2＋n 2＝20.又||PF 1|－|PF 2||2＝|m －n |2＝16，所以mn ＝2.所以△F 1PF 2的面积为S ＝12mn ＝1，故选A.2．已知△ABC 的顶点A (－5,0)，B (5,0)，△ABC 内切圆的圆心在直线x ＝2上，则顶点C 的轨迹方程是( )A.x 24－y 221＝1(x ＞2) B.y 24－x 221＝1(y ＞2) C.x 221－y 24＝1 D.y 24－x 22＝1解析：选A 如图，△ABC 与内切圆的切点分别为G ，E ，F . |AG |＝|AE |＝7，|BF |＝|BG |＝3，|CE |＝|CF |，所以|CA |－|CB |＝7－3＝4.根据双曲线定义，所求轨迹是以A ，B 为焦点，实轴长为4的双曲线的右支，方程为x 24－y 221＝1(x ＞2)．考点三双曲线的几何性质[全析考法过关][考法全析]考法(一) 求双曲线的离心率(或范围)[例1] (1)已知点F 是双曲线x 2a 2－y 2b 2＝1(a ＞0，b ＞0)的左焦点，点E 是该双曲线的右顶点，过F 作垂直于x 轴的直线与双曲线交于A ，B 两点，若△ABE 是锐角三角形，则该双曲线的离心率e 的取值范围是( )A ．(1，＋∞)B ．(1,2)C ．(2,1＋2)D ．(1,1＋2)(2)设双曲线C ：x 2a 2－y 2b 2＝1(a ＞0，b ＞0)的左焦点为F ，直线4x －3y ＋20＝0过点F 且与双曲线C 在第二象限的交点为P ，O 为原点，|OP |＝|OF |，则双曲线C 的离心率为( )A ．5 B. 5 C.53D.54[解析] (1)若△ABE 是锐角三角形，只需∠AEF ＜45°，在Rt △AFE 中，|AF |＝b 2a ，|FE |＝a ＋c ，则b 2a ＜a ＋c ，即b 2＜a 2＋ac ，即2a 2－c 2＋ac ＞0，则e 2－e －2＜0，解得－1＜e ＜2，又e ＞1，则1＜e ＜2，故选B.(2)根据直线4x －3y ＋20＝0与x 轴的交点F 为(－5,0)，可知半焦距c ＝5，设双曲线C 的右焦点为F 2，连接PF 2，根据|OF 2|＝|OF |且|OP |＝|OF |可得，△PFF 2为直角三角形，如图，过点O 作OA 垂直于直线4x －3y ＋20＝0，垂足为A ，则易知OA 为△PFF 2的中位线，又原点O 到直线4x －3y ＋20＝0的距离d ＝4，所以|PF 2|＝2d ＝8，|PF |＝|FF 2|2－|PF 2|2＝6，故结合双曲线的定义可知|PF 2|－|PF |＝2a ＝2，所以a ＝1，故e ＝ca＝5.[答案] (1)B (2)A考法(二) 求双曲线的渐近线[例2] (2019·武汉调研)已知双曲线C ：x 2m 2－y 2n 2＝1(m ＞0，n ＞0)的离心率与椭圆x 225＋y 216＝1的离心率互为倒数，则双曲线C 的渐近线方程为( )A ．4x ±3y ＝0B ．3x ±4y ＝0C ．4x ±3y ＝0或3x ±4y ＝0D ．4x ±5y ＝0或5x ±4y ＝0[解析] 由题意知，椭圆中a 2＝25，b 2＝16，∴椭圆的离心率e ＝ 1－b 2a 2＝35， ∴双曲线的离心率为 1＋n 2m 2＝53，∴n m ＝43，∴双曲线的渐近线方程为y ＝±n m x ＝±43x ，即4x ±3y ＝0.故选A.[答案] A考法(三) 求双曲线的方程[例3] 已知双曲线x 2a 2－y 2b 2＝1(a ＞0，b ＞0)的左焦点为F ，离心率为 2.若经过F 和P (0,4)两点的直线平行于双曲线的一条渐近线，则双曲线的方程为( )A.x 24－y 24＝1 B.x 28－y 28＝1C.x 24－y 28＝1 D.x 28－y 24＝1 [解析] 由离心率为2，可知a ＝b ，c ＝2a ，所以F (－2a ,0)，由题意知k PF ＝4－00－(－2a )＝42a ＝1，所以2a ＝4，解得a ＝22，所以双曲线的方程为x 28－y 28＝1.[答案] B[规律探求][过关训练]1．(2018·全国卷Ⅱ)双曲线x 2a 2－y 2b 2＝1(a ＞0，b ＞0)的离心率为3，则其渐近线方程为( )A ．y ＝±2xB ．y ＝±3xC ．y ＝±22xD ．y ＝±32x解析：选A ∵e ＝ca ＝a 2＋b 2a ＝3， ∴a 2＋b 2＝3a 2，∴b ＝2a . ∴渐近线方程为y ＝±2x .2．(2018·全国卷Ⅲ)设F 1，F 2是双曲线C ：x 2a 2－y 2b 2＝1(a ＞0，b ＞0)的左、右焦点，O 是坐标原点．过F 2作C 的一条渐近线的垂线，垂足为P .若|PF 1|＝6|OP |，则C 的离心率为( )A. 5B.2C. 3D. 2解析：选C 不妨设一条渐近线的方程为y ＝ba x ，则F 2到y ＝ba x 的距离d ＝|bc |a 2＋b 2＝b . 在Rt △F 2PO 中，|F 2O |＝c ，所以|PO |＝a ，所以|PF 1|＝6a ，又|F 1O |＝c ，所以在△F 1PO 与Rt △F 2PO 中，根据余弦定理得cos ∠POF 1＝a 2＋c 2－(6a )22ac ＝－cos ∠POF 2＝－ac ，即3a 2＋c 2－(6a )2＝0，得3a 2＝c 2，所以e ＝ca＝ 3.3．已知M (x 0，y 0)是双曲线C ：x 22－y 2＝1上的一点，F 1，F 2是双曲线C 的两个焦点．若MF 1―→·MF 2―→＜0，则y 0的取值范围是( )A.⎝⎛⎭⎫－33，33 B.⎝⎛⎭⎫－36，36 C.⎝⎛⎭⎫－223，223D.⎝⎛⎭⎫－233，233解析：选A 由题意知a ＝2，b ＝1，c ＝3，设F 1(－3，0)，F 2(3，0)，则MF 1―→＝(－3－x 0，－y 0)， MF 2―→＝(3－x 0，－y 0)． ∵MF 1―→·MF 2―→＜0，∴(－3－x 0)(3－x 0)＋y 20＜0，即x 20－3＋y 20＜0.∵点M (x 0，y 0)在双曲线C 上， ∴x 202－y 20＝1，即x 20＝2＋2y 20， ∴2＋2y 20－3＋y 20＜0，∴－33＜y 0＜33.。

高考数学分类题库考点42 曲线与方程、圆锥曲线的综合应用理

考点42 曲线与方程、圆锥曲线的综合应用一、选择题1.（2020·山东高考理科·Ｔ8）已知双曲线22221x y a b-=（a>0,b>0）的两条渐近线均和圆C ：x 2+y 2-6x+5=0相切，且双曲线的右核心为圆C 的圆心，那么该双曲线的方程为( )（A ）22154x y -= （B ）22145x y -=（C ）221x y 36-= （D ）221x y 63-= 【思路点拨】先求出圆C 的圆心坐标（3,0），半径r=2，再求出渐近线方程，由圆心到渐近线的距离等于半径即可取得a,b 的关系，再由双曲线的右核心为圆C 的圆心知c=3，即可求出结果.【精讲精析】选A.双曲线的渐近线方程为bx+ay=0和bx-ay=0，圆心为（3,0），半径r=2.由圆心到直线的距离为223r ba b +=，得4a 2=5b 2，又因为双曲线的右核心为圆C 的圆心，因此c=3，即9=a 2+b 2，因此，a 2=5，b 2=4因此该双曲线的方程为22154x y -=. 2．（2020·福建卷理科·Ｔ7）设圆锥曲线Γ的两个核心别离为F 1，F 2，假设曲线Γ上存在点P 知足1122::PF F F PF =4:3:2，那么曲线Γ的离心率等于( )（A ）1322或（B ）23或2 （C ）12或2 （D ）2332或【思路点拨】依照1122::PF F F PF =4:3:2，设出1122PF F F PF ｜｜，｜｜，｜｜，然后按曲线Γ为椭圆或双曲线，在12PF F ∆中别离利用概念求离心率. 【精讲精析】选A.1122::PF F F PF =4:3:2，11224,||3,||2,PF k F F k PF k ∴==可设｜｜＝其中12||23F F c k ==，32kc ∴=.假设圆锥曲线Γ为椭圆，那么12||||26PF PF a k +==，3a k ∴=，312.32∴===k c e a k 假设圆锥曲线Γ为双曲线，那么12||||22,PF PF a k -==3. （2020·福建卷文科·Ｔ11）设圆锥曲线C 的两个核心别离为F 1， F 2，假设曲线C 上存在点P 知足1PF ：12F F ：2PF = 4:3:2，那么曲线C 的离心率等于（）（A ）1322或（B ）223或（C ）122或（D ）2332或【思路点拨】依照1122::PF F F PF =4:3:2，设出1122PF F F PF ｜｜，｜｜，｜｜的值，然后按曲线C 为椭圆或双曲线，在12PF F ∆中别离利用概念求离心率. 【精讲精析】选A.1122::PF F F PF =4:3:2，11224,||3,||2,PF k F F k PF k ==设｜｜＝其中12||23F F c k ==，32kc ∴=.假设圆锥曲线C 为椭圆，那么12||||26PF PF a k +==，3a k ∴=，312,32k c e a k ∴===假设圆锥曲线C 为双曲线，那么12||||22,PF PF a k -==,∴=a k二、填空题4.（2020·山东高考文科·Ｔ15）已知双曲线22221(0b 0)x y a a b -=＞，＞和椭圆22x y =1169+有相同的核心，且双曲线的离心率是椭圆离心率的两倍，那么双曲线的方程为 .【思路点拨】先求椭圆核心，即双曲线的核心，再由双曲线的离心率是椭圆离心率的两倍求出b ，然后写出双曲线的方程.【精讲精析】由题意知双曲线的核心为（-7，0），（7，0），即c=7，又因为双曲线的离心率为c 27e a 4==，因此a=2,故b 2=3，因此双曲线的方程为13422=-y x . 【答案】13422=-y x 5.（2020·北京高考理科·T14）曲线C 是平面内与两个定点1(1,0)F -和2(1,0)F 的距离的积等于常数2(1)a a >的点的轨迹.给出以下三个结论：①曲线C 过坐标原点； ②曲线C 关于坐标原点对称；③假设点P 在曲线C 上，那么12F PF ∆的面积不大于212a . 其中所有正确的结论的序号是 .【思路点拨】写出曲线C 的方程，再逐个验证三个结论.【精讲精析】设P(x,y)为曲线C 上任意一点，那么由212||||PF PF a ⋅=，得C:22222(1)(1)x y x y a ++⋅-+= ，把（0，0）代入方程可得21a =，与1a >矛盾，故①不正确；当M(x,y)在曲线C 上时，点M 关于原点的对称点'(,)M x y --，也知足方程，故曲线C 关于原点对称，故②正确；122212121111||||sin sin 222F PF S PF PF F PF a F PF a ∆=∠=∠≤，故③正确. 【答案】②③ 三、解答题6．（2020·安徽高考理科·Ｔ21）假设0>λ，点A 的坐标为（1,1），点B 在抛物线2x y =上运动，点Q知足BQ QA λ=，通过点Q 与x 轴垂直的直线交抛物线于点M ，点P 知足MP QM λ=,求点P 的轨迹方程.【思路点拨】设出Ｐ点坐标，通过Ｑ，Ｂ等中间量成立方程，消去中间量，求出点Ｐ的轨迹方程．【精讲精析】由MP QM λ=知Q,M,P 三点在同一条垂直于x 轴的直线上，故可设P(x,y),Q(x,0y ),M(x,x 2),那么).(202x y y x -=-λ即.)1(20y x y λλ-+= ①再设),,(11y x B 由BQ QA λ=，即),1,1(),(0101y x y y x x --=--λ解得110x (1)x ,y (1)y .=+λ-λ⎧⎨=+λ-λ⎩ ② 将①式代入②式，消去0y ，得1221x (1)x ,y (1)x (1)y .=+λ-λ⎧⎨=+λ-λ+λ-λ⎩ ③ 又点B 在抛物线2x y =上，因此211x y =，再将③式代入211x y =，得因为0>λ，两边同时除以),1(λλ+得故所求点P 的轨迹方程为12-=x y .7. （2020·新课标全国高考理科·Ｔ20）在平面直角坐标系xOy 中，已知点A(0,-1)，B 点在直线y = -3上，M 点知足//MB OA ， MA AB MB BA ⋅=⋅，M 点的轨迹为曲线C .（1）求C 的方程；（2）P 为C 上的动点，l 为C 在P 点处的切线，求O 点到l 距离的最小值.【思路点拨】第（1）问，求M 点的轨迹，可设M 点坐标为(,)x y ，然后利用条件//MB OA 取得点B 的坐标，最后将条件MA AB MB BA ⋅=⋅转化为坐标关系，取得,x y 知足的关系式，化简整理即得C 的方程；第（2）问，设出点P 的坐标，利用导数求出切线l 的斜率，表示出l 的方程，再利用点到直线的距离公式求得O 点到l 距离的函数，然后利用函数的知识求出最值即可. 【精讲精析】(1)设M(x,y ),由已知得B(x ,-3),A(0,-1). 因此MA =（-x,-1-y ）, MB =(0,-3-y), AB =(x ,-2).再由题意可知（MA +MB ）• AB =0, 即（-x,-4-2y ）• (x,-2)=0. 因此曲线C 的方程式为y=14x 2-2. (2)设P(x 0,y 0)为曲线C ：y=14x 2-2上一点，因为y '=12x,因此l 的斜率为12x 0, 因此直线l 的方程为0001()2y y x x x -=-，即2000220x x y y x -+-=. 则O 点到l 的距离20020|2|4y x d x -=+.又200124y x =-，因此当20x =0时取等号，因此O 点到l 距离的最小值为2. 8.（2020·山东高考理科·Ｔ22）已知直线l 与椭圆C: 22132x y +=交于P （x 1,y 1），Q(x 2,y 2)两不同点，且△OPQ 的面积62∆=OPQ S ,其中O 为坐标原点.（1）证明x 12+x 22和y 12+y 22均为定值；（2）设线段PQ 的中点为M ，求PQ OM ⋅的最大值；（3）椭圆C 上是不是存在点D,E,G ，使得ODE ODG OEG S S S ∆∆∆===假设存在，判定△DEG 的形状；假设不存在，请说明理由.【思路点拨】此题重点考查学生的计算能力，相较较去年的圆锥曲线题目，今年的题目难度要大一些，是一道较好的选拔优秀学生的题目.（1）分斜率存在和不存在两种情形讨论.（2）利用第一问的结论，再应用大体不等式容易患出结论.（3）利用反证法，假设存在如此的点，经推理得出矛盾，从而证明原结论成立.【精讲精析】（1）当直线l 的斜率不存在时，,P Q 两点关于x 轴对称，那么1212,x x y y ==-，由()11,P x y 在椭圆上，那么2211132x y +=，而11OPQ S x y ∆==，那么111x y ==.于是22123x x +=，22122y y +=.当直线l 的斜率存在，设直线l 为y kx m =+，代入22132x y +=可得2223()6x kx m ++=，即222(23)6360+++-=k x kmx m ，由0∆>得，222236k m 4(23k )(3m 6)0-+->，化简得2232+>k m ，2121222636,2323km m x x x x k k-+=-=++.12PQ x =-==，0=l d 到的距离，1122POQS d PQ ∆=⋅⋅==，整理得22322k m +=，知足0∆>，222221212122263(2)()2()232323km m x x x x x x k k -+=+-=--⨯=++，222222*********(3)(3)4()2333y y x x x x +=-+-=-+=，综上可知22123x x +=，22122y y +=.（2）当直线l 的斜率不存在时，由（1）知1622==⨯=OM PQ x PQ 当直线l 的斜率存在时，由（1）知12322x x km+=-， 2121231()222y y x x k k m m m m++=+=-+=，222212122229111()()(3)2242++=+=+=-x x y y k OM m m m， 22222222224(32)2(21)1(1)2(2)(23)k m m PQ k k m m+-+=+==++， 22221125(3)(2)4OMPQ m m =-+≤，当且仅当221132m m-=+，即m =综上可知OM PQ ⋅的最大值为52.（3）假设椭圆上存在三点,,D E G ，使得ODE ODG OEG S S S ∆∆∆===由（1）知2222223,3,3D E E G G D x x x x x x +=+=+=，2222222,2,2D E E G G D y y y y y y +=+=+=.解得22232D E G x x x ===,2221D E G y y y ===，因此,,D E G x x x 只能从当选取，,,D E G y y y 只能从1±当选取，因此,,D E G 只能从(1)±当选取三个不同点，而这三点的两两连线必有一个过原点，这与ODE ODG OEG S S S ∆∆∆===故椭圆上不存在三点,,D E G ，使得2ODE ODG OEG S S S ∆∆∆===. 9.（2020·山东高考文科·Ｔ22）在平面直角坐标系xOy 中，已知椭圆22:13x C y +=.如下图，斜率为(0)k k ＞且只是原点的直线l 交椭圆C 于A ，B 两点，线段AB 的中点为E ，射线OE 交椭圆C 于点G ，交直线3x =-于点(3,)D m -. （Ⅰ）求22m k +的最小值；（Ⅱ）假设2OG OD =·OE ，（i ）求证：直线l 过定点；（ii ）试问点B ，G 可否关于x 轴对称？假设能，求出现在ABG ∆的外接圆方程；假设不能，请说明理由. 【思路点拨】此题重点考查学生的计算能力，相较较去年的圆锥曲线题目，今年的题目难度要大一些，是一道较好的选拔优秀学生的题目.（I ）设直线:(0)l y kx n n =+≠，联立方程，再由韦达定理得出中点E 的坐标，由三点共线，可知OE k K =OD ，k 解得1m k=，由大体不等式得出最小值.（II ）（i ）注意先求出k 和n 的关系，再由交点直线系方程得出l 过定点. （ii ）可先假设对称，然后通过运算验证如此的圆是不是存在. 【精讲精析】（Ⅰ）由题意:设直线:(0)l y kx n n =+≠,由22y=kx x 13+⎧⎪⎨+=⎪⎩n y 消y 得:222(13)6330k x knx n +++-=, 2222364(13)3(1)∆=-+-k n k n ×2212(31)0k n =+->，设A 11(,)x y ，B 22(,)x y ,AB 的中点E 00(,)x y ,那么由韦达定理得:12x x +=2613kn k -+,即02313kn x k -=+,002313kn y kx n k n k -=+=⨯+=+213nk+, 因其中点E 的坐标为23(,13kn k -+2)13nk +,因为O ，E ，D 三点在同一直线上，因此OE k K =，OD k 即133mk -=-，解得1m k=，因此22m k +=2212k k+≥,当且仅当1k =时取等号, 即22m k +的最小值为2.（Ⅱ）（i ）证明:由题意知:n>0,因为直线OD 的方程为3my x =-, 因此由得交点G 的纵坐标为223G m y m =+又因为213E n y k=+,D y m =,且2OG OD =·OE ，因此222313m n m m k =⋅++, 又由（Ⅰ）知: 1m k=,因此解得k n =,因此直线l 的方程为:l y kx k =+, 即有:(1)l y k x =+,x=-得y=0,与实数k无关,令1因此直线l 过定点(-1,0).（ii ）假设点B ，G 关于x 轴对称,那么有△ABG 的外接圆的圆心在x 轴上, 又在线段AB 的中垂线上, 由（i ）知点G 23(,3m -+2)3m m +,因此点B 23(,3m -+2)3m m -+,又因为直线l 过定点(-1,0),因此直线l 的斜率为223313mm k m -+=-++，又因为1m k=，因此解得21m =或26m =，又因为230m ->,因此26m =舍去,即21m =，现在k=1，m=1，E （31,44-），31(,)22G -. AB 的中垂线为2x+2y+1=0，圆心坐标为1(,0)2-，圆半径为52，圆的方程为2215()24x y ++=. 综上所述, 点B ，G 关于x 轴对称,现在△ABG 的外接圆的方程为: 2215()24x y ++=. 10.（2020·辽宁高考理科·Ｔ20）如图，已知椭圆C 1的中心在原点O ，长轴左、右端点M ，N 在x 轴上，椭圆C 2的短轴为MN ，且C 1，C 2的离心率都为e ，直线l ⊥MN ，l 与C 1交于两点，与C 2交于两点，这四点按纵坐标从大到小依次为A ，B ，C ，D ．（I ）设12e =，求BC 与AD 的比值；（II ）当e 转变时，是不是存在直线l ，使得BO ∥AN ，并说明理由．【思路点拨】（I ）先利用离心率相同设出21,C C 的方程和直线l 的方程)(a t t x <=，再求出B A ,的坐标，然后计算BC 与AD 的长度就可求出比值；（II ）先考虑直线过原点的情形，再考虑直线只是原点的情形，现在利用斜率相等（即BO k ＝AN k ）成立等式关系，再考虑a t <的因素，可取得关于e 的不等式，求讲解明即可．【精讲精析】(Ⅰ)因为21,C C 的离心率相同，故依题意可设1C ：1222=+b y a x ，2C ：122422=+ax a y b ，（)0>>b a ，设直线l ：)(a t t x <=，别离与1C ，2C 的方程联立，求得当21=e 时，a b 23=，别离用B A y y ,表示A ，B 的纵坐标，可知 BC :AD =432222==ab y y AB .（Ⅱ）0=t 时，l 不符合题意．0≠t 时，BO ∥AN 当且仅当BO 的斜率BO k 与AN 的斜率AN k 相等，即=-t t a a b 22at ta ba --22，解得222b a ab t --= a e e ⋅--=221，因为a t <，又10<<e ，因此1122<-e e ，解得122<<e ，因此当220≤<e 时，不存在直线l ，使得BO ∥AN ；当122<<e 时，存在直线l ，使得BO ∥AN .11．（2020·湖南高考理科·T21）如下图，椭圆,23)0(122221的离心率为：>>=+b a by a x C x 轴被曲线2C ：2x y =-b 截得的线段长等于1C 的长半轴长.（Ⅰ）求21,C C 的方程；（Ⅱ）设2C 与y 轴的交点为M ，过坐标原点O 的直线l 与2C 相交于点A ，B ，直线MA ，MB 别离与1C 相交于点D ，E.（i ）证明：MD ME ⊥；（ii ）记MDE MAB ，∆∆的面积别离为21，SS .问：是不是存在直线l ，使得321721=S S ？请说明理由.【思路点拨】此题以椭圆和抛物线为载体，考查两曲线的大体知识.题中第一问通过求曲线的方程考查两曲线的大体知识点的关系.第二问通过证明考查逻辑思维能力和探讨参数的存在.解决此题需要较强的综合运用知识的能力.考查了数形结合思想、等价转化思想和方程思想. 【精讲精析】（I）由题意知2c e a ==，从而2a b =，又a =，解得2,1a b ==. 故1C ，2C 的方程别离为2221,14x y y x +==-. （II ）（i ）由题意知，直线l 的斜率存在，设为k ，那么直线l 的方程为y kx =.由2,1,=⎧⎨=-⎩y kx y x 得210x kx --=，设1122(,),(,)A x y B x y ，那么12,x x 是上述方程的两个实根，于是1212,1x x k x x +==-. 又A ，B 在直线上，∴y 1=kx 1,y 2=kx 2, 又点M 的坐标为(0,1)-，因此故MA MB ⊥，即MD ME ⊥.（ii ）设直线MA 的斜率为1k ，那么直线的方程为11y k x =-，由121,1,=-⎧⎨=-⎩y k x y x 解得0,1,=⎧⎨=-⎩x y 或121,1,=⎧⎨=-⎩x k y k 那么点A 的坐标为211(,1)k k -,点M 的坐标为（0，-1）.又直线MB 的斜率为11k -，同理可得点B 的坐标为21111(,1)k k --.于是211111111||||||||.22||k S MA MB k k k +=⋅=-= 由1221,440,=-⎧⎨+-=⎩y k x x y 得2211(14)80k x k x +-=，解得0,1,=⎧⎨=-⎩x y 或12121218,1441,14⎧=⎪+⎪⎨-⎪=⎪+⎩k x k k y k 那么点D 的坐标为2112211841(,)1414k k k k -++；又直线ME 的斜率为11k -，同理可得点E 的坐标211221184(,),44--++k k k k于是2112221132(1)||1||||2(14)(4)k k S MD ME k k +⋅=⋅=++.因此21122114(417)64=++S k S k . 由题意知，21211417(417)6432++=k k ,解得214k = 或2114k =. 又由点,A B 的坐标可知，21211111111k k k k k k k -==-+，因此3.2k =± 故知足条件的直线l 存在，且有两条，其方程别离为32y x =和32y x =-. 12．（2020·湖南高考文科T21）已知平面内一动点P 到点F(1,0)的距离与点P 到y 轴的距离的差等于1. （Ⅰ）求动点P 的轨迹C 的方程；（Ⅱ）过点F 作两条斜率存在且相互垂直的直线l 12l ，，设l 1与轨迹C 相交于点A ，B ，l 2与轨迹C 相交于点D ，E ，求AD EB ·的最小值.【思路点拨】此题考查求曲线的方程，考查利用代数方式研究几何问题的大体方式，考查数形结合思想.考查运算能力，考查分析问题、解决问题的能力. 【精讲精析】（I ）设动点P 的坐标为(,)x y ，由题意知22(1)|| 1.x y x -+-=化简得222||,y x x =+当20,4;0x y x x ≥=<时当时,y=0.因此动点P 的轨迹C 的方程为2,4(0)0)y x x x =≥<和y=0(. （II ）由题意知，直线1l 的斜率存在且不为0，设为k ，那么1l 的方程为(1)y k x =-．由得2222(24)0.k x k x k -++=∴21616k 0,k R∆=+>∈即设1122(,),(,),A x y B x y 则12,x x 是上述方程的两个实根，于是1212242,1x x x x k +=+=．因为12l l ⊥，因此2l 的斜率为1k-．设那么同理可得2343424,1x x k x x +=+=，当且仅当221k k =时，即1k =±时，AD EB •取最小值16． 13．（2020·陕西高考理科·T17）如图，设P 是圆2225x y +=上的动点，点D 是P 在x 轴上投影， M 为PD 上一点，且4||||5MD PD =．（Ⅰ）当P 在圆上运动时，求点M 的轨迹C 的方程；（Ⅱ）求过点（3，0）且斜率为45的直线被C 所截线段的长度．【思路点拨】（Ⅰ）动点M 通过点P 与已知圆相联系，因此把点P 的坐标用点M 的坐标表示，然后代入已知圆的方程即可；（Ⅱ）直线方程和椭圆方程组成方程组，能够求解，也能够利用根与系数的关系，结合两点的距离公式计算．【精讲精析】（Ⅰ）设点M 的坐标是(,)x y ，点P 的坐标是(,)p p x y ，因为点D 是P 在x 轴上投影， M 为PD 上一点，且4||||5MD PD =，因此p x x =，且54p y y =， ∵P 在圆2225x y +=上，∴225()254x y +=，整理得2212516x y +=，即C 的方程是2212516x y +=．（Ⅱ）过点（3，0）且斜率为45的直线方程是4(3)5y x =-，设此直线与C 的交点为11(,)A x y ，22(,)B x y ，将直线方程4(3)5y x =-代入C 的方程2212516x y +=得：22(3)12525x x -+=，化简得2380x x --=，∴1x =，2x =，因此线段AB 的长度是||AB ==415==，即所截线段的长度是415．。

新高考数学复习考点知识讲解与专题训练31---双曲线的方程及几何性质(解析版)

新高考数学复习考点知识讲解与专题训练专题31、双曲线的方程及几何性质一、双曲线的定义平面内与两个定点F 1，F 2的距离之差的绝对值等于非零常数(小于||F 1F 2)的点的轨迹叫做双曲线．这两个定点叫做双曲线的焦点，两焦点间的距离叫做双曲线的焦距．集合P ＝{M ⎪⎪⎪⎪| ||MF 1－||MF 2＝2a }，||F 1F 2＝2c ，其中a ，c 为常数，且a >0，c >0.(1)当a ＜c 时，点P 的轨迹是双曲线； (2)当a ＝c 时，点P 的轨迹是两条射线； (3)当a ＞c 时，点P 不存在．二、双曲线的标准方程和几何性质一、常用结论1、过双曲线的一个焦点且与实轴垂直的弦的长为2b 2a，也叫通径．2、与双曲线x 2a 2－y 2b 2＝1(a >0，b >0)有共同渐近线的方程可表示为x 2a 2－y 2b2＝t (t ≠0)．3、双曲线的焦点到其渐近线的距离为b .4、若P 是双曲线右支上一点，F 1，F 2分别为双曲线的左、右焦点，则|PF 1|min ＝a ＋c ，|PF 2|min ＝c －a .题型一、双曲线的方程与渐近线的方程例1、【2020年高考天津】设双曲线C 的方程为22221(0,0)x y a b a b-=>>，过抛物线24y x =的焦点和点(0,)b 的直线为l ．若C 的一条渐近线与l 平行，另一条渐近线与l 垂直，则双曲线C 的方程为A ．22144x y -=B ．2214y x -= C ．2214x y -=D ．221x y -=【答案】D【解析】由题可知，抛物线的焦点为()1,0，所以直线l 的方程为1yx b+=，即直线的斜率为b -，又双曲线的渐近线的方程为b y x a=±，所以b b a-=-，1b b a-⨯=-，因为0,0a b >>，解得1,1a b ==．故选：D ．变式、【2018年高考天津卷理数】已知双曲线22221(0,0)x y a b a b-=>>的离心率为2，过右焦点且垂直于x 轴的直线与双曲线交于A ，B 两点. 设A ，B 到双曲线的同一条渐近线的距离分别为1d 和2d ，且126d d +=，则双曲线的方程为A ．221412x y -=B ．221124x y -=C ．22139x y -=D ．22193x y -=【答案】C【解析】设双曲线的右焦点坐标为(),0F c （c >0），则A B x x c ==，由22221c y a b -=可得：2b y a=±，不妨设：22,,,b b A c B c a a ⎛⎫⎛⎫- ⎪ ⎪⎝⎭⎝⎭，双曲线的一条渐近线方程为：0bx ay -=，据此可得：21bc b d c -==，22bc b d c +==，则12226bcd d b c+===，则23,9b b ==，双曲线的离心率：2c e a ====，据此可得：23a =，则双曲线的方程为22139x y -=.本题选择C 选项.例2、【2018年高考全国Ⅱ理数】双曲线22221(0,0)x y a b a b-=>>的离心率A．y =B．y =C．2y x =±D．2y x =±【答案】A【解析】因为c e a ==，所以2222221312b c a e a a-==-=-=，所以b a =因为渐近线方程为by x a=±，所以渐近线方程为y =，故选A ．变式、（2020届山东省济宁市高三上期末）已知12,F F 是双曲线22221(0,0)x y a b a b -=>>的左、右焦点，若点2F 关于双曲线渐近线的对称点A 满足11F AO AOF ∠=∠（O 为坐标原点），则双曲线的渐近线方程为（）A ．2y x =±B ．y =C ．y =D ．y x =±【答案】B【解析】如图所示：由对称性可得：M 为2AF 的中点，且2AF OM ⊥，所以12F A AF ⊥，因为11F AO AOF ∠=∠，所以11AF FO c ==，故而由几何性质可得160AFO ∠=，即260MOF ∠=，故渐近线方程为y =，故选B.题型二、双曲线的离心率例3、【2018年高考全国III 理数】设1F ，2F 是双曲线2222:1(0,0)x y C a b a b-=>>的左、右焦点，O 是坐标原点．过2F 作C 的一条渐近线的垂线，垂足为P ．若1|||PF OP =，则C 的离心率为AB ．2CD 【答案】C【解析】由题可知2PF b =，2OF c =，PO a ∴=，在2Rt POF △中，222cos PF b PF O OF c∠==，在12Rt PF F △中，22221212212cos 2PF F F PF b PF O PF F F c∠+-==，b c=，即223c a =，e ∴=C ．变式1、（2020届山东省潍坊市高三上期末）已知点P 为双曲线()2222:10,0x y C a b a b -=>>右支上一点，12,F F 分别为C 的左，右焦点，直线1PF 与C 的一条渐近线垂直，垂足为H ，若114PF HF =，则该双曲线的离心率为（）A B C ．53D ．73【答案】C【解析】取1PF 的中点M ，连接2MF ,由条件可知1111142HF PF MF ==， O 是12F F 的中点，2//OH MF ∴又1OH PF ⊥，21MF PF ∴⊥1222F F PF c ∴==,根据双曲线的定义可知122PF a c =+，12a cHF +∴=，直线1PF 的方程是：()a y x c b=+ ，即0ax by ac -+= ，原点到直线的距离OH a ==，1OHF ∴∆中，2222a c a c +⎛⎫+= ⎪⎝⎭，整理为：223250c ac a --= ，即23250e e --= ，解得：53e = ，或1e =-（舍）故选：C变式2、【2020年高考全国I 卷理数】已知F 为双曲线2222:1(0,0)x y C a b a b -=>>的右焦点，A 为C 的右顶点，B 为C 上的点，且BF 垂直于x 轴.若AB 的斜率为3，则C 的离心率为 .【答案】2【解析】联立22222221x cx y a b a b c=⎧⎪⎪-=⎨⎪⎪=+⎩，解得2x c b y a =⎧⎪⎨=±⎪⎩，所以2bBF a =.依题可得，3BF AF =，AF c a =-，即()2223b c a a c a a c a -==--，变形得3c a a +=，2c a =,因此，双曲线C 的离心率为2. 故答案为：2．变式3、【2019年高考全国Ⅰ卷理数】已知双曲线C ：22221(0,0)x y a b a b-=>>的左、右焦点分别为F 1，F 2，过F 1的直线与C 的两条渐近线分别交于A ，B 两点．若1F A AB =，120FB F B ⋅=，则C 的离心率为____________．【答案】2 【解析】如图，由1,F A AB =得1.F A AB =又12,OF OF =得OA 是三角形12F F B 的中位线，即22,2.BF OA BF OA =∥由120FB F B ⋅=，得121,,F B F B OA F A ⊥∴⊥∴1OB OF =，1AOB AOF ∠=∠，又OA 与OB 都是渐近线，∴21,BOF AOF ∠=∠又21πBOF AOB AOF ∠+∠+∠=，∴2160,BOF AOF BOA ∠=∠=∠=又渐近线OB 的斜率为tan 60ba=︒=，∴该双曲线的离心率为2c e a ====．题型三、双曲线的综合问题例4、【2020年高考全国Ⅱ卷理数】设O 为坐标原点，直线x a =与双曲线2222:1(0,0)x y C a b a b -=>>的两条渐近线分别交于,D E 两点，若ODE 的面积为8，则C 的焦距的最小值为 A ．4B ．8C ．16D ．32【答案】B 【解析】2222:1(0,0)x y C a b a b-=>>， ∴双曲线的渐近线方程是by x a=±，直线x a =与双曲线2222:1(0,0)x y C a b a b -=>>的两条渐近线分别交于D ，E两点不妨设D 为在第一象限，E 在第四象限，联立x ab y x a =⎧⎪⎨=⎪⎩，解得x a y b =⎧⎨=⎩，故(,)D a b ，联立x ab y x a =⎧⎪⎨=-⎪⎩，解得x a y b =⎧⎨=-⎩，故(,)E a b -，∴||2ED b =，∴ODE 面积为：1282ODE S a b ab =⨯==△，双曲线2222:1(0,0)x y C a b a b -=>>，∴其焦距为28c ===，当且仅当a b ==∴C 的焦距的最小值：8.故选：B ．变式1、（2020届山东省临沂市高三上期末）已知P 为双曲线C ：2214y x -=右支上一点，1F ，2F 分别为C 的左、右焦点，且线段12A A ，12B B 分别为C 的实轴与虚轴.若12A A ，12B B ，1PF 成等比数列，则2PF =______.【答案】6【解析】2214y x -=1222A A a ∴==，1224B B b ==，12A A ，12B B ，1PF 成等比数列212112A A PFB B ∴⋅=，解得18PF =，2826PF a ∴=-=故答案为：6变式2、【2020年高考全国Ⅲ卷理数】.设双曲线C ：22221x y a b-=（a >0，b >0）的左、右焦点分别为F1，F 2，P 是C 上一点，且F 1P ⊥F 2P ．若△PF 1F 2的面积为4，则a =A ． 1B ． 2C ． 4D ． 8【答案】A【解析】5ca=，c ∴=，根据双曲线的定义可得122PF PF a -=， 12121||42PF F PF F S P =⋅=△，即12||8PF PF ⋅=， 12F P F P ⊥，()22212||2PF PF c ∴+=，()22121224PF PF PF PF c ∴-+⋅=，即22540a a -+=，解得1a =，故选：A ．1、【2019年高考浙江卷】渐近线方程为x ±y =0的双曲线的离心率是A ．2B ．1C D ．2【答案】C【解析】因为双曲线的渐近线方程为0x y ±=，所以a b =，则c =，所以双曲线的离心率ce a==故选C. 2、【2018年高考浙江卷】双曲线2213x y -=的焦点坐标是A ．(0)，0) B ．(−2，0)，(2，0) C ．(0，，(0 D ．(0，−2)，(0，2) 【答案】B【解析】设2213x y -=的焦点坐标为(,0)c ±，因为222314c a b =+=+=，2c =，所以焦点坐标为(2,0)±，故选B ．3、（2020届山东省烟台市高三上期末）若双曲线()222210,0x y a b a b-=>>的，则其渐近线方程为（）A ．230x y ±=B ．320x y ±=C ．20x y ±=D ．230x y ±=【答案】C【解析】由题,离心率c e a ===,解得12b a =,因为焦点在x 轴上,则渐近线方程为12y x =±,即20x y ±=故选：C4、【2019年高考全国Ⅲ卷理数】双曲线C ：2242x y -=1的右焦点为F ，点P 在C 的一条渐近线上，O 为坐标原点，若=PO PF ，则△PFO 的面积为A ．4B ．2C ．D ．【答案】A【解析】由2,,a b c ====,2P PO PF x =∴=，又P 在C 的一条渐近线上，不妨设为在by x a=上，则P P b y x a =⋅==1122PFO P S OF y ∴=⋅==△，故选A ． 5、【2018年高考全国I 理数】已知双曲线22:13x C y -=，O 为坐标原点，F 为C 的右焦点，过F 的直线与C 的两条渐近线的交点分别为M ，N ．若OMN △为直角三角形，则||MN =A ．32B ．3C ．D ．4【答案】B【解析】由题可知双曲线C 的渐近线的斜率为3±，且右焦点为(2,0)F ，从而可得30FON ∠=︒，所以直线MN 的倾斜角为60︒或120︒，根据双曲线的对称性，设其倾斜角为60︒，可以得出直线MN 的方程为2)y x =-，分别与两条渐近线y x =和y x =联立，求得M ，3(,2N ，所以||3MN ==，故选B ．6、（2020届山东省德州市高三上期末）双曲线22221x y a b-=（0a >，0b >）的右焦点为()1F ，点A 的坐标为()0,1，点P 为双曲线左支上的动点，且1APF ∆周长的最小值为8，则双曲线的离心率为（）AB C ．2 D ．【答案】D【解析】如下图所示：设该双曲线的左焦点为点F ，由双曲线的定义可得12PF PF a =+，所以，1APF ∆的周长为11123262AP AF PF AF AP PF a AF a a ++=+++≥++=+，当且仅当A 、P 、F 三点共线时，1APF ∆的周长取得最小值，即628a +=，解得1a =.因此，该双曲线的离心率为e == 故选：D.7、【2020年高考北京】已知双曲线22:163x y C -=，则C 的右焦点的坐标为_________；C 的焦点到其渐近线的距离是_________．【答案】()3,0【解析】在双曲线C 中，a =b =3c ==，则双曲线C 的右焦点坐标为()3,0，双曲线C 的渐近线方程为2y x =±，即0x =，所以，双曲线C=.故答案为：()3,08、【2019年高考江苏卷】在平面直角坐标系xOy 中，若双曲线2221(0)y x b b-=>经过点（3，4)，则该双曲线的渐近线方程是 ▲ .【答案】y =【解析】由已知得222431b-=，解得b =b =，因为0b >，所以b =因为1a =，所以双曲线的渐近线方程为y =.9、【2020年高考江苏】在平面直角坐标系xOy 中，若双曲线222105()x y a a -=>的一条渐近线方程为y =，则该双曲线的离心率是 ▲ ．【答案】32【解析】双曲线22215x y a -=，故b =由于双曲线的一条渐近线方程为2y x =，即22b a a =⇒=，所以3c ==，所以双曲线的离心率为32c a =.故答案为：3221/ 21。

2024年高考真题分类专项(解析几何)(学生版)

2024年高考真题分类专项（解析几何）一、单选题1．（2024年北京高考数学真题）圆22260x y x y +-+=的圆心到直线20x y -+=的距离为（）A B ．2C ．3D ．2．（2024年天津高考数学真题）双曲线22221()00a x y a b b >-=>，的左、右焦点分别为12.F F P、是双曲线右支上一点，且直线2PF 的斜率为2．12PF F △是面积为8的直角三角形，则双曲线的方程为（）A ．22182y x -=B ．22184x y -=C ．22128x y -=D ．22148x y -=3．（2024年新课标全国Ⅱ卷数学真题）已知曲线C ：2216x y +=（0y >），从C 上任意一点P 向x 轴作垂线段PP '，P '为垂足，则线段PP '的中点M 的轨迹方程为（） A ．221164x y +=（0y >）B ．221168x y +=（0y >）C ．221164y x +=（0y >）D ．221168y x +=（0y >）4．（2024年高考全国甲卷数学（文）真题）已知直线20ax by a b +-+=与圆2241=0C x y y ++-：交于,A B 两点，则AB 的最小值为（）A ．2B ．3C ．4D ．65．（2024年高考全国甲卷数学（理）真题）已知双曲线的两个焦点分别为()()0,4,0,4-，点()6,4-在该双曲线上，则该双曲线的离心率为（）A．4 B ．3C ．2D6．（2024年高考全国甲卷数学（理）真题）已知b 是,a c 的等差中项，直线0ax by c 与圆22410x y y ++-=交于,A B 两点，则AB 的最小值为（） A ．1B ．2C ．4D．二、多选题7．（2024年新课标全国Ⅱ卷数学真题）抛物线C ：24y x =的准线为l ，P 为C 上的动点，过P 作22:(4)1A x y +-=⊙的一条切线，Q 为切点，过P 作l 的垂线，垂足为B ，则（） A ．l 与A 相切B ．当P ，A ，B三点共线时，||PQ = C ．当||2PB =时，PA AB ⊥D ．满足||||PA PB =的点P 有且仅有2个8．（2024年新课标全国Ⅱ卷数学真题）设计一条美丽的丝带,其造型可以看作图中的曲线C 的一部分.已知C 过坐标原点O .且C 上的点满足:横坐标大于2-，到点(2,0)F 的距离与到定直线(0)x a a =<的距离之积为4，则（）A ．2a =- B．点在C 上C ．C 在第一象限的点的纵坐标的最大值为1D ．当点()00,x y 在C 上时，0042y x ≤+三、填空题9．（2024年上海夏季高考数学真题）已知抛物线24y x =上有一点P 到准线的距离为9，那么点P 到x 轴的距离为．10．（2024年北京高考数学真题）抛物线216y x =的焦点坐标为．11．（2024年北京高考数学真题）若直线()3y k x =-与双曲线2214x y -=只有一个公共点，则k 的一个取值为．12．（2024年天津高考数学真题）圆22(1)25-+=x y 的圆心与抛物线22(0)y px p =>的焦点F 重合，A 为两曲线的交点，则原点到直线AF 的距离为．13．（2024年新课标全国Ⅱ卷数学真题）设双曲线2222:1(0,0)x y C a b a b-=>>的左右焦点分别为12F F 、，过2F 作平行于y 轴的直线交C 于A ，B 两点，若1||13,||10F A AB ==，则C 的离心率为．四、解答题14．（2024年上海夏季高考数学真题（网络回忆版））已知双曲线222Γ:1,(0),y x b b-=>左右顶点分别为12,A A ，过点()2,0M -的直线l 交双曲线Γ于,P Q 两点. (1)若离心率2e =时，求b 的值．(2)若2b MA P =△为等腰三角形时，且点P 在第一象限，求点P 的坐标． (3)连接OQ 并延长，交双曲线Γ于点R ，若121A R A P ⋅=，求b 的取值范围．15．（2024年北京高考数学真题）已知椭圆E ：()222210x y a b a b +=>>，以椭圆E 的焦点和短轴端点为顶点的四边形是边长为2的正方形.过点()(0,t t >且斜率存在的直线与椭圆E 交于不同的两点,A B ，过点A 和()0,1C 的直线AC 与椭圆E 的另一个交点为D ． (1)求椭圆E 的方程及离心率； (2)若直线BD 的斜率为0，求t 的值．16．（2024年天津高考数学真题）已知椭圆22221(0)x y a b a b+=>>椭圆的离心率12e =．左顶点为A ，下顶点为B C ，是线段OB 的中点，其中ABC S △． (1)求椭圆方程．(2)过点30,2⎛⎫- ⎪⎝⎭的动直线与椭圆有两个交点P Q ，．在y 轴上是否存在点T 使得0TP TQ ⋅≤．若存在求出这个T 点纵坐标的取值范围，若不存在请说明理由．17．（2024年新课标全国Ⅱ卷数学真题）已知(0,3)A 和33,2P ⎛⎫ ⎪⎝⎭为椭圆2222:1(0)x y C a b a b+=>>上两点.(1)求C 的离心率;(2)若过P 的直线l 交C 于另一点B ，且ABP 的面积为9，求l 的方程．18．（2024年高考全国甲卷数学（理）真题）已知椭圆2222:1(0)x y C a b a b+=>>的右焦点为F ，点31,2M ⎛⎫⎪⎝⎭在C 上，且MF x ⊥轴．(1)求C 的方程；(2)过点()4,0P 的直线交C 于,A B 两点，N 为线段FP 的中点，直线NB 交直线MF 于点Q ，证明：AQ y ⊥轴．。

2024年新高考版数学专题1_9.3 双曲线及其性质(分层集训)

A. 22
2
B. 4 10
5
答案 D
C. 7
D. 10
4.(2017课标Ⅲ理,5,5分)已知双曲线C:
x a
2 2
-
y2 b2
=1(a>0,b>0)的一条渐近线方
程为y= 5 x,且与椭圆 x2 + y2 =1有公共焦点,则C的方程为 ( )
2
12 3
A. x2 - y2 =1
8 10
B. x2 - y2 =1
C.互为共轭的双曲线的离心率为e1、e2,则e1e2≥2
D.互为共轭的双曲线的4个焦点在同一圆上
答案 CD
7.(多选)(2021广东揭阳4月联考,9)已知一组直线x±2y=0,则以该组直线为
渐近线的双曲线的方程可能是 ( )
A.x2-4y2=1 B.4y2-x2=1
C.x2- y2 =1
4
答案 ABD
y
k1
x2 y2 16
x
1 2
m,
1(x 1),
得
(16-
k12
)x2+(
k12
-2k1m)x-
1 4
k12
+k1m-m2-16=0,
设A(x1,y1),B(x2,y2),
则x1+x2=
k12 2k1m k12 16
,x1x2=
1 4
k12
m2 k1m k12 16
16
,
则|TA|=
设其方程为 x2 - y2 =1(a>0,b>0,x≥a),
a2 b2
则2a=2,2c=2 17 ,解得a=1,c= 17 ,
则b2=c2-a2=( 17 )2-12=16,

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

考点41 双曲线一、选择题
1.（2012·浙江高考理科·Ｔ8）如图，F1,F2分别是双曲线C
：
22
22
1
x y
a b
-=
（a,b＞0）的左、右焦点，B
是虚轴的端点，直线F1B与C的两条渐近线分别交于P,Q两点，线段PQ的垂直平分线与x轴交于点M，若|MF2|=|F1F2|,则C的离心率
是( )
(A)23
3(B)
6
2 (C)2 (D)3
【解题指南】关键是通过中垂线的性质与坐标间的关系建立
,,
a b c的等式.
【解析】选B．由可解得
,
ac bc
x y
c a c a
==
--，即
(,)
ac bc
Q
c a c a
--.
由可解得
,
ac bc
x y
c a c a
=-=
++，即
(,)
ac bc
P
c a c a
-
++.
∴PQ的中点
22
2222
(,)
a c bc
N
c a c a
--
而
(3,0)
M c∴
1
MN
b
k
c
⋅=-
，即
2
23
43
bc c
a c c b
=-
-，整理得32
23
c a c
=，即
2
3
2
e=
，解得
6
e=
．
2.（2012·湖南高考文科·Ｔ6）与（2012·湖南高考理科·Ｔ5）相同
已知双曲线C：
2
2
x
a-
2
2
y
b=1的焦距为10 ，点P （2,1）在C 的渐近线上，则C的方程为（）
(A)220x -25y =1 (B)25x -220y =1 (C)280x -220
y =1 (D)220x -280y =1
【解题指南】根据双曲线的性质，由焦距为10可以求出c=5，再将P （2,1）代入渐近线求出方程中的参数.
【解析】选A. 由焦距为10，知2c=10，c=5.将P （2,1）代入y=b
x a 得a=2b.
2222222,525,5,420a b c b b a b +=====，所以方程为22
1
205x y -=.
3.（2012·福建高考理科·Ｔ8）已知双曲线22
214x y b -=的右焦点与抛物线
2
12y x =的焦点重合，则该双曲线的焦点到其渐近线的距离等于（） (A)5
(B)42
(C)3
(D)5
【解题指南】利用抛物线的标准形式来求解焦点，可将一次项系数直接除4获得数值；对于双曲线的标准方程，只要注意到c 最大，同时也满足一个平方关系式即可，同时要熟识渐近线的方程，焦点在x 轴上时，
方程是
b
y x a =±
.
【解析】选A.
212y x =的焦点(3,0)，由题意知，249b +=，25b =，双曲线的焦点到其渐近线的距离为5b =．
4.（2012·福建高考文科·Ｔ5）已知双曲线22
2
15x y a -=的右焦点为(3,0)，则该双曲线的离心率等于（） (A)314
14
(B)324
(C)32 (D)4
3
【解题指南】对于双曲线的标准方程，只需注意到c 最大，而且也满足一个平方关系式即可，同时还要明
确离心率
c e a =
.
【解析】选C . 由题意知2
59a +=，解得2a =，
32c e a =
=.
5.（2012·新课标全国高考文科·Ｔ10）与（2012·新课标全国高考理科·Ｔ8）相同
等轴双曲线C 的中心在原点，焦点在x 轴上，C 与抛物线2
16y x =的准线交于A ，B 两点，43
AB =
则C 的实轴长为（）
(A)2 (B)22 (C)4 (D)8
【解题指南】注意到双曲线为等轴双曲线，可先设出曲线C 的方程，然后利用AB 的长及抛物线的准线方程，得到A 、B 两点的坐标，代入所设的曲线C 方程，可求得曲线C 的方程，最后求得实轴长.
【解析】选C.设双曲线的方程为22
221x y a a -=（a>0），抛物线的准线为4x =-，且43AB =，故可得
()(
)4,23,4,23
A B ---，将点A 坐标代入双曲线方程得2
4a
=，故2a =，故实轴长为4.
二、填空题
6.（2012·辽宁高考文科·Ｔ15）已知双曲线x 2
- y 2
=1,点F 1,F 2为其两个焦点，点P 为双曲线上一点，若P F 1⊥PF 2,则∣P F 1∣+∣P F 2∣的值为___________________. 【解题指南】利用双曲线定义得122,
PF PF a -=利用已知条件12PF PF ⊥，由勾股定理得2
2
2
2
1212(2)PF PF F F c +==，即可解得
12
,PF PF .
【解析】不妨设12
PF PF >.由双曲线方程22
1x y -=知1,2a b c ===
由双曲线定义得
1222,
PF PF a -==
由已知条件12PF PF ⊥及勾股定理得2
2
2
21
2
12(2)8
PF PF F F c +===，上述两式联立，解得1231,31
PF PF =+=-，故
1223
PF PF +=.
【答案】23
7.（2012·湖北高考理科·Ｔ14）如图，双曲线的
两顶点为A 1，A 2，虚轴两端点为B 1，B 2，两焦点为F 1，F 2.若以A 1A 2为直径的圆内切于菱形F 1B 1F 2B 2，切点分别为A ，B ，C ，D.则（1）双曲线的离心率e=______；
（2）菱形F 1B 1F 2B 2的面积S 1与矩形ABCD 的面积S 2的比值
1
2
S S =__________. 【解题指南】本题主要考查双曲线的基本性质,解答本题（1）可利用22
OF B V 的面积求解;本题（2）中可
将所求面积的比值转化成离心率的关系.
【解析】（1）
化简得: 220a ac c +-=,即2
10e e --=.又1e >,
则
15e +=
.
（2）由题意知: S 1=2bc,在22
OF B V 中连接OA ，则A F 2=b, 矩形ABCD 边长
AD=2
ab c
AB=22
a c ，S 2=43
2a b c
，则
【答案】（1）15+ （2）25
+
8.（2012·江苏高考·Ｔ8）在平面直角坐标系xOy 中，若双曲线22
21
4x y m m -=+5m
的值为 .
【解题指南】应从焦点的位置入手，确定长半轴长.
【解析】由题意，双曲线的焦点在x 轴上，所以24
5
++=
=m m e m
，所以2=m .
【答案】2。