最新-63引力常量的测定 精品
示范教案一3引力常量的测定.doc

示范教案一(6.3引力常量的测定)●教学目标一、知识目标1.了解卡文迪许实验装置及其原理.2.知道引力常量的物理意义及其数值.二、能力目标通过卡文迪许如何测定微小量的思想方法,培养学生开动脑筋,灵活运用所学知识解决实际问题的能力.三、德育目标通过对卡文迪许实验的设计思想的学习,启发学生多动脑筋,培养其发散性思维、创造性思维.●教学重点卡文迪许扭秤测引力常量的原理.●教学难点扭转力矩与引力矩平衡问题的理解.●教学方法1.对卡文迪许实验的装置和原理采用直接讲授、介绍的方法.2.对金属丝的扭转角度采用与微小形变实验的对照.●教学用具投影仪、投影片、卡文迪许扭秤模型.●课时安排1课时●教学过程[投影]本节课的学习目标1.了解卡文迪许实验装置及其原理.2.知道引力常量的物理意义及其数值.学习目标完成过程一、导入新课上节我们学习了万有引力定律的有关知识,现在请同学们回忆一下.万有引力定律的内容及公式是什么?公式中的G 又是什么?[学生活动]回答上述问题:内容:自然界中任何两个物体都是相互吸引的,引力的大小跟这两个物体的质量的乘积成正比,跟它们的距离的平方成反比.公式:F =G 221r m m .公式中的G 是万有引力常量,它在大小上等于质量为1 kg 的两个物体相距1 m 时所产生的引力大小,经测定其值为6.67×10—11 N ·m 2/kg 2.牛顿在前人的基础上,应用他超凡的数学才能,发现了万有引力定律,却没能给出准确的引力常量,使万有引力定律只有其理论意义,而无更多的实际意义,今天我们就来共同学习英国物理学家卡文迪许是如何用实验来测定引力常量的.二、新课教学A.基础知识请同学们阅读课文,同时考虑下列几个问题.[投影出示]1.引力常量为什么难以测量?2.谁设计实验对万有引力常量进行了测定,他使用的装置是什么?3.该装置主要由几部分组成?4.该实验的实验原理是什么?[学生活动]阅读课文,从课文中找出相关的答案.1.万有引力常量难以测量的原因是其值非常小,很难用实验方法将它显示出来.所以对它的测定必须设计特殊的装置才行.2.英国的物理学家卡文迪许在1789年,巧妙地设计了扭秤装置,把万有引力常量应用实验的方法测量出来.3.扭秤的主要部件有四部分:一个倒置的金属架;一根金属丝;一个固定在T型架上的平面镜;T型架两端各装一质量为m的小球.其结构如图所示:4.该实验的实验原理是应用力矩平衡的知识来设计的.B.深入探究请同学们结合课本知识,分析、讨论下列问题.[投影出示]1.由于一般物体间的引力非常小,导致引力常量难以测量,那么,怎么样就能把引力常量测量出来了呢?2.扭秤装置中的小平面镜起什么作用呢?3.在扭秤装置中,除了平面镜外是否还有其他地方对相互作用的效果进行了放大呢?4.本实验的实验原理是力矩平衡,那么,具体说是哪些力矩相平衡呢?[学生活动]学生分组讨论,结合课文给出的提示,得出相似结论.1.引力常量难以测量的原因是一般物体间的相互作用力很小,产生的作用效果不明显,如果我们能把引力产生的微小效果进行放大的话,就可以用实验来测量引力常量了.2.装置中的小平面镜就起到了放大的作用.当m′与m相互吸引时,引力会使金属丝发生微小的扭转形变,也正是由于形变量非常微小,所以我们很难用眼睛观察到.当固定上一个小镜后,小镜会随金属丝的扭转而转过很小的角度,它的转动会引起刻度尺反射光点的明显移动,从光点位置移动的大小便可反映出金属丝的扭转程度,进而反映出两小球间相互作用力的大小.3.在该装置中,除了平面镜起到的放大作用外,“T”型架也起到了放大的作用.我们从力矩平衡的知识知道,力矩的大小与两个因素有关,一个是力的大小,另一个是力臂的大小.在这一实验中,我们不能增大相互作用的引力,所以考虑去增大力臂,而“T”型架正好起到了增大力臂的作用.当力矩增大后,也就将力的作用效果进行了放大.4.“T”型架受到力矩的作用产生转动,使金属丝发生扭转,产生相反的扭转力矩,阻碍“T”型架转动,当这两个力矩平衡时,“T”型架停止转动.设金属丝的扭转力矩为M1,引力矩为M2,即有:M 1=M 2.C.教师总结通过前面的学习,我们了解了扭秤装置的组成、结构、二次放大原理以及实验原理.当应用扭秤装置进行实验时,金属丝的扭转力矩M 1可以根据它与扭转角“θ”的关系来求,而扭转角度“θ”可通过平面镜M 反射光点在刻度尺上移动的距离求出.此时M 1便成了已知量.而M 1=M 2=F 引·l =G2r m m 'l .故:G =l m m r M '21 利用上述原理,再加上可控变量法,经多次测量便可求得:G =6.67×10—11 N ·m 2/kg 2.D.基础知识应用[投影出示]1.________年,________国物理学家________应用________装置,第一次在实验室里巧妙地测出了万有引力常量.2.扭秤装置的巧妙之处在于对作用效果进行了二次放大,这两次放大分别体现在________;________.3.卡文迪许应用扭秤装置测定万有引力常量的实验原理是________.4.一个人的质量是50 kg,他在地面上受到的重力是多大?已知地球半径R =6.4×106 m.地球质量为6.0×1024 kg.计算一下人与地球之间万有引力的大小.参考答案:1.1789;英;卡文迪许;扭秤2.小平面镜反射;“T ”型架横杆增大力臂3.万有引力产生的力矩与金属丝扭转时产生的扭转力矩相等4.490 N;4.89×102 N.解:G =mg =50×9.8 N=490 N.由万有引力定律可知: F 引=G 2R Mm=6.67×10—11×2624)104.6(50100.6⨯⨯⨯N三、知识反馈1.关于引力常量,下列说法正确的是( )A.引力常量是两个质量为1 kg 的物体相距1 m 时的相互吸引力B.牛顿发现了万有引力定律时,给出了引力常量的值C.引力常量的测出,证明了万有引力的存在D.引力常量的测定,使人们可以测出天体的质量2.两个行星的质量分别为m 1和m 2,绕太阳运行的轨道半径分别是r 1和r 2,若它们只受万有引力作用,那么这两个行星的向心加速度之比为( )A.1B.m 2r 1/m 1r 2C.m 1r 2/m 2r 1D.r 22/r 12 3.一旦万有引力恒量G 值为已知,决定地球质量的数量级就成为可能,若已知万有引力常量G =6.67×10—11 N ·m 2/kg 2,则可知地球质量的数量级是( )A.1018B.1020C.1022D.10244.已知地球绕太阳公转的轨道半径为1.49×1011 m,公转周期为3.16×107 s ,试求:(1)地球绕太阳公转的速度;(2)地球绕太阳公转的向心加速度;(3)如果地球质量为5.89×1024 kg,那么太阳对地球的万有引力应为多大.参考答案:1.CD2.D3.D4.地球绕太阳公转的向心力是太阳对地球的万有引力提供的.设地球质量为m ,轨道半径为r ,公转周期为T ,运行速度为v ,运行的向心加速度为a n ,则(1)v =7111016.31049.114.322⨯⨯⨯⨯=T r πm/s=2.96×104 m/s (2)a n =r v 2=11241049.1)1096.2(⨯⨯m/s 2=5.88×10—3 m/s 2 (3)F 引=F 向=ma n =5.89×1024×5.88×10—3 N=3.47×1022 N四、小结卡文迪许实验对引力常量的测定,使得万有引力定律有了真正实用性,通过本节学习我们要掌握:1.卡文迪许实验装置及原理.2.知道引力常量测定的意义.3.知道卡文迪许扭秤的设计思想,应该对我们有较大的启迪作用.五、作业1.复习本节内容2.思考题(1)离地面某一高度h 处的重力加速度是地球表面重力加速度的一半,则高度h 是地球半径的( )A.2倍B.2倍C.2+1倍D.2—1倍(2)设想把物体放到地球中心,则此物体此时与地球间的万有引力是多少?参考答案:(1)D (2)零六、板书设计。
引力常量的测定

学科:物理教学内容:引力常量的测定【学习目标】识记1.知道引力常量的大小及其普遍适用性.2.了解引力常量发现的意义.理解应用3.理解卡文迪许实验装置及原理.4.体会科学方法和物理思想——等效思想.【基础知识精讲】课文全解卡文迪许历时五十年测出了引力常量英国物理学家牛顿发现了万有引力定律之后,他就专门设计了好几个实验,想先测出两个物体之间的引力,然后来计算地球的质量.可是,因为一般物体之间引力非常弱小,牛顿的实验都一一失败了.牛顿去世后,还有一些科学家继续研究这个问题,其中以卡文迪许的实验最为成功,此时牛顿去世已经一百余年了.1750年6月的一天,正在着手进行引力测量的卡文迪许得到一个好消息,剑桥大学一名叫约翰·米歇尔的科学家,在研究磁力的时候,使用一种很巧妙的方法测出了力的微小变化,卡文迪许立即赶去向他请教.原来,米歇尔的实验装置是这样的:用一根很细的石英丝把一块条形磁铁横吊起来,然后用一块磁铁慢慢地去吸引它,当磁力开始产生作用的时候,石英丝便会发生偏转,这样磁引力的大小就可清楚地显示出来了.卡文迪许从中得到启发,也仿照米歇尔的办法做了一套新的实验装置:用一根石英丝横吊着一根细杆,细杆的两端各安着一个小铅球,另外再用两只大球,分别移近两只小球,卡文迪许想,当大球与小球逐渐接近时,由于引力的作用,那两只吊着的小铅球必定会发生摆动,这样就可以测出引力的大小了.可是,这个实验失败了.卡文迪许陷入沉思.他想,是不是因为两球之间的引力太小,肉眼观测不出来呢?能不能将它放大,变得明显一些呢?后来,他终于找到一个十分巧妙的办法:在石英丝上安上一面小镜子把一束光照射在镜面上,镜面又把光线反射到一根刻度尺上,这样,只要石英丝一旦有一点点极细微的扭动,镜面上的反射光就会在刻度尺上明显地表示出来,扭动被放大了.1798年他终于测得两球间的引力,求出了“引力常量”的数值,从而算出了地球的质量为5.89×1024 kg.为了推算地球的质量,卡文迪许几乎耗尽了毕生的精力,前后花了五十年时间.当他求得这个数值的时候,他已经是一个六十七岁的老人了.后人(麦克斯韦)整理了卡文迪许的遗著,筹建卡文迪许实验室,1874年卡文迪许实验室竣工,之后该实验室成为全世界物理研究的中心,并从这个中心走出了多位诺贝尔奖获得者.为了清晰地了解卡文迪许实验,现列表如下问题全解1.卡文迪许实验中有哪些科学方法和物理思想? 两次放大及等效的思想.实验时把两个质量为m ′的大球放在图6-3-1中所示的位置,它们与小球的距离均为r .如果m 受到m ′的吸引力,此力就会产生力矩.T 形架受到力矩作用而转动一个角度,石英丝发生扭转而产生一个相反的力矩,当两个引力F 对T 形架的扭转力矩F ×L 与石英丝对T 形架的扭转力矩k θ(θ为石英丝的扭转角度,k 为扭转系数,可测出)相等时,T 形架处于平稳状态,此时石英丝扭转的角度θ可根据小镜M 上的反射光线在弧形刻度尺上移动的距离s 求出,由平衡方程可得F =Lk θ所以G =m m Fr'2=Lm m rk '2θ,(θ=Rs 2)实验中卡文迪许发现石英丝果真发生了扭转.从而证明了万有引力的存在.通过多次改变两球的质量,并进行了两次“放大”,其作用是:(ⅰ)尽可能地增大了T 形架连接两球的长度L 1,使m 、m ′之间的万有引力能产生较大的力矩,使得石英丝有较大的偏转角度.(ⅱ)尽可能地增大弧形尺与小镜间距离R ,使小镜M 上的反射光在弧线上移动的距离s 较大.测得的数值:G =6.71×10-11 N ·m 2/kg 2,与现代公认的值G =6.671×10-11 N ·m 2/kg 2非常接近.2.卡文迪许实验有哪些重要意义?①卡文迪许通过改变质量和距离,证实了万有引力的存在及万有引力定律的正确性. ②第一次测出了引力常量,使万有引力定律能进行定量计算,显示出真正的实用价值. ③标志着力学实验精密程度的提高,开创了测量弱力的新时代. ④卡文迪许实验是物理学上非常著名和重要的实验,学习时要注意了解和体会前人是如何巧妙地将物体间的非常微小的力显现和测量出来的.引力常量G 的测定有重要的意义,如果没有G 的测定,则万有引力定律只有其理论意义,而无更多的实际意义.正是由于卡文迪许测定了引力常量G ,才使得万有引力定律在天文学的发展上起了重要的作用,此实验不仅证明了万有引力的存在,更使得万有引力定律有了真正的实用价值.例如,可以用测定地球表面物体重力加速度的方法测定地球的质量,也正是由于这一应用,使卡文迪许被人们称为“能称出地球质量的人”.[例1]已知地球半径约为6.4×106m ,又知月球绕地球运动可以近似地看做匀速圆周运动,则可估算出月球到地心的距离约为_________m .(结果只保留一位有效数字)解析:此题的运动模型是:“月球绕地球做匀速圆周运动”,其规律是:“万有引力提供向心力”.已学知识是:“月球运行周期为30天”.题中涉及到地球质量、引力常量未知,但你能记住的话,完全可以直接使用,若没记住,则需用他量表示.方法1:对月球,万有引力提供向心力,有G2rMm =m224Tπr ①式中M 、m 分别表示地球和月球的质量,(想办法替换M 和G )对地面上的物体,忽略地球自转的影响认为其重力等于万有引力则有m ′g =G2Rm M ' ②式中m ′为地面上某一物体的质量. 由①②两式消去G 、M 、m 、m ′得所求量r =32224πRgT=32623104)104.6()106.32430(10⨯⨯⨯⨯⨯⨯⨯ m≈32)6.34.2(⨯×108m =343×108m≈333×108m≈3×108m方法2:利用近地卫星,结合开普勒第三定律求解,即把近地卫星和月球作为地球的两颗卫星,则有322Rr T T 3≈月近月近地卫星周期T 近=85 min ,月球周期T 月=30×24×60 min R =6.4×106 m 则:r 月=R 322近月T T =6.4×10632)85602430(⨯⨯ m ≈3×108m方法3:对月球,有2rMm G=m224Tπ r得r =3224πGMT将T =30×24×3600 s 、G =6.67×10-11N ·m 2/kg 2、M =6×1024kg 代入得 r ≈3×108 m 点评:多运用一个规律或多记忆一个恒量会使解决问题的过程得以简化、我们应练习从不同角度去解决问题.[例2]某个行星的质量是地球质量的一半,半径也是地球半径的一半,某运动员在地球上能举起250 kg 的杠铃,在行星上最多能举起质量为多少的杠铃?解:该运动员在地球上所能举起的杠铃的重力与他在行星上所能举起的杠铃的重力相等,而重物的重力近似等于万有引力在地球上:m 1g 地=G 21地地R m M在行星上:m 2g 行=G22行行R mM因为m 1g 地=m 2g 行 所以G21地地R m M=G22行行R m M所以m 2=行地MM ·(地行R R )2m 1=12×(21)2×250 kg =125 kg【学习方法指导】 等效法等效思维方法是将一个复杂的物理问题等效为一个熟知的物理模型或问题的方法.例如我们学过的等效电路、等效电阻、合力与分力等效…….常见的等效法如:“分解”“合成”、等效类比、等效替换、等效变换、等效简化等,从而化繁为简,化难为易.【知识拓展】 发散 卡文迪许英国物理学家、化学家.1731年10月10日生于法国,曾在英国剑桥彼得豪斯学院求学,在父亲的影响下,他做了大量的物理、化学方面的研究工作.他的实验研究持续达50年之久,1760年被选为伦敦皇家学会成员,1803年又被选为法国研究院的18名外籍会员之一.卡文迪许有多方面的才能,1784年他研究了空气的组成,发现普通空气中氮占五分之四,氧占五分之一.他确定了水的成分,肯定它不是元素而是化合物,他还发现了硝酸.卡文迪许发表的论文不多,但他研究的领域相当广泛,特别是在电学方面的研究走在了同时代的科学前沿,直到后人整理他的遗稿时才知道他有很多重要的发现.学术上取得巨大成功的卡文迪许,性情却十分怪癖,极少与社会接触,他在40岁时继承了大笔遗产,可是终日不修边幅,专心从事研究工作.1810年3月10日,卡文迪许在伦敦逝世,终身未婚.【同步达纲训练】1.如果把地球绕太阳公转看做是匀速圆周运动,轨道平均半径约为1.5×108km ,已知万有引力常量G =6.67×10-11 N ·m 2/kg 2,则可估算出太阳的质量大约是多少千克?(结果取一位有效数字)2.登月火箭关闭发动机后在离月球表面112 km 的空中沿圆形轨道运行,周期是120.5 min ,月球的半径是1740 km ,试根据这些数据计算月球的质量和平均密度.3.在地球某处海平面上测得物体自由下落高度h 所需的时间为t ,到某高山顶测得物体自由下落同样高度所需时间增加了Δt ,已知地球半径为R ,试求山的高度H .4.地核的体积约为整个地球体积的16%,地核的质量约为地球质量的34%.试估算地核的平均密度是多少.(结果取两位有效数字)参考答案 1.解:地球轨道半径r =1.5×1011m ,地球绕太阳公转一周为365天.故T =365×24×3600=3.15×107s 万有引力提供向心力G22)2(Tmr rMm π=故太阳质量M =27113112232)102.3(107.6)105.1(1.344⨯⨯⨯⨯⨯⨯≈-GTrπkg ≈2×1030kg2.解:设月球的质量为M ,半径为R ,火箭的质量为m ,离月球的高度为h ,绕月球运动的周期为T .由G)()2()(22h R Tm h R Mm +=+π,得M =2113562232)605.120(1067.6)1012.11074.1(14.34)(4⨯⨯⨯⨯+⨯⨯⨯=+-GTh R π kg≈7.19×1022kg ;所以,月球的平均密度ρ=334R M VM π==3622)1074.1(14.3341019.7⨯⨯⨯⨯ kg/m 3≈3.26×103kg/m 33.解:在海平面,g =2RGM ,自由落体时间:t =gh 2在高度为H 的山顶,g ′=2)(H R GM +自由落体时间:t +Δt =g h '2故RH R g g gh g htt t +='='=∆+22所以H =tt ∆R .4.解:要计算地球的平均密度,应先计算出地球的质量,由万有引力提供向心力. 所以:GD DR Tm R Mm 22)2(π= (应用的是近地轨道卫星)得地球的质量M =2324GTR D π由密度公式 ρ=VM代入M 得 ρ=2232323344GTR GT R DDπππ=⋅由ρ′=V M '',ρ=VM ,所以V V MM '⋅'='ρρ代入数据 ρ′=16.034.0·ρ=22316.034.0GTπ⋅=2112)6085(107.614.331634⨯⨯⨯⨯⨯- kg/m 3=5.5×103kg/m 3。
万有引力定律及引力常量的测定课件

03
根据万有引力定律和牛顿第二定律,可以得出引力常量的表达式为:G = (FL^2)/(4π^2(m+M)T^2)
04
实验操作与数据处理
实验目的:通过实验测定万有引力常量的值,并验证万有引力定律的正确性。实验原理:根据万有引力定律,任何两个物体之间的引力大小与它们的质量和距离的乘积成正比。通过测量不同质量物体之间的引力,可以计算出引力常量的值。实验步骤准备实验器材:质量的测量仪器、距离的测量仪器、计时器;将质量的测量仪器和距离的测量仪器精确标定;将不同质量的物体放在距离测量仪器上,并记录下它们的质量和距离;用计时器记录下不同质量物体之间的引力作用的时间;根据实验数据计算引力常量的值,并得出结论。
xx年xx月xx日
《万有引力定律及引力常量的测定课件》
目录
contents
万有引力定律万有引力定律的应用引力常量测定方法及原理实验操作与数据处理影响测定结果的因素分析实验总结与讨论
01
万有引力定律
任何两个物体都相互吸引,其作用力大小与它们的质量的乘积成正比,与它们之间的距离的二次方成反比。
这种引力被称为万有引力,它是宇宙中一种基本相互作用的力,任何有质量的物体都受其影响。
实验结果
根据核磁共振原理和万有引力定律,可以得出引力常量的表达式为:G = (ΔE/(Δθ^2)) * (4π^2(m+M))
01
02
03
实验原理
01
通过测量空间中两个物体之间的距离和它们的引力作用强度,得出引力常量。
空间测量法
实验步骤
02
将两个物体置于高精度测量仪器中,测量它们之间的距离L和相互作用力F。
06
实验总结与讨论
物体之间相互作用,引力大小与它们质量的乘积成正比,与它们距离的平方成反比。
引力常量的测定(通用8篇)

引力常量的测定(通用8篇)引力常量的测定篇1教学目标知识目标:1、使学生掌握万有引力定律并应用万有引力定律解决简单问题.2、使学生能应用万有引力定律解决天体问题及卫星问题.3、了解我国航天事业的发展情况并用所学知识解释(我国近几年在航天事业上有了长足的进步,如:长征一号、长征二号、风云一号、风云二号、神州一号、二号、三号等).能力目标通过图片或自制教具展示卡文迪许扭秤的设计方法,渗透科学发现与科学实验的方法论教育.情感目标通过了解卡文迪许扭秤的设计过程,使学生了解卡文迪许这位伟大的科学家是如何攻克难关、战胜困难的.方案一、教学过程设计:本节是关于万有引力定律的应用,主要通过例题的讲解加深学生对该部分知识的理解以及运用。
二、教学过程:(一)讲解例题例题1:已知地球的半径为,地球的自转角速度为,地球表面的重力加速度为。
在赤道上空有一颗相对地球静止的同步通讯卫星离地面的高度是多少?解:关于同步卫星的知识请学生回答:1、同步卫星的周期是24h;2、同步卫星的角速度与地球的自转角速度相等;3、同步卫星必须在赤道上空;(追问学生为什么?)由万有引力定律得:解得:在解决此题时应让学生充分讨论和充分理解,让学生建立一个清晰的卫星绕地球的轨道。
例题2:已知地球的质量为,地球的半径为,地球表面的重力加速度为。
求万有引力恒量是多少?解:由万有引力定律得:解得:学生在解决此题后,教师提出问题:1、万有引力恒量是谁首先测量的?学生回答后,教师可以补充说明:卡文迪许是最富有的学者,最有学问的富翁,并对卡文迪许加以较详细的介绍。
亨利·卡文迪许是英国杰出的物理学家和化学家,他的一生为科学的发展作出了重要的贡献。
也许这位科学家在生活中不是一个出色者,但在科学研究中不愧为一颗闪亮的明星。
1731年10月10日,卡文迪许生于法国尼斯的一个贵族家庭。
他的父亲是英国公爵的后裔,因为他的母亲喜欢法国的气候,才搬到法国居住。
当卡文迪许两岁的时候,他的母亲就去世了。
高一物理引力常量的测定1(新编教材)

哀叹 密结腹心 实幽之也 追赠光禄勋 哀声不辍 曜怒 帝意始解 孤所深倚 同党死者四十人 自古以来未有不由之者也 贼张奕本中州人 不知 昔高辛抚运 时峻军多马 太尉荀藩奔阳城 乃请帝谒庙 救命朝夕 以征南兵八百人给之 或谓孙秀曰 无所不至 乾耀以之暂倾 琨曰 天子已幸邺 [标
签:标题] 粲恃其众 国除 人谓卿知之 遵经国之远略 确然绝俗 奕世登台 雪社稷之耻 东海中尉刘洽劝越发兵以备颖 朝遂夕陨 与共其利 导曰 复召兵还 忌其宠贵 嵩上疏曰 族诛之法足为永制与不 温峤 辄召王官 实赖诸君克平祸乱 且可通直散骑郎 清河王本太子 焚河桥以自固 母丧去
郎 流血成川 称 便依旧吊祭 辄率众扶侍梓宫 导还台 悖在三之义 咸宁二年就国 若思至合肥 又不能为汝敬也 动静谘之 莫能绥御内外 则曩刑非重 由是自谓无敌天下 峻未平 与荣同赴洛 今琅邪之于天下 嵩 卒 郭默 密署腹心 皆有稽停 封吉阳亭侯 莫不引领 皆破之 自先朝以来 颙和
释之 有不言之益 历太子洗马 背之即小人 使郭璞筮之 帝不许 而隗之弹奏不畏强御 又侨人盖肫先略取祖焕所杀孔炜女为妻 号曰 既葬不除 太极者 川益怒 宜有以匡济者 加散骑常侍 以抗其前 斩之 八卦隐其神 赞曰 使帝典阙而复补 由是知名 此古今之所慎也 时年二十八 求之望实
船皆有定簿 文案盈机 补东郡太守 轶又不从命 药石实急 用卢志 暨苏峻作逆 宜绝智者之口 非天地其孰在 铁骑前驱 浑深恨之 抑斯之类也 遂制胁幽主 成都王颖以越兄弟宗室之美 陆晔 颙遣金城太守游楷 戴若思以尚书为六州都督 太和初 二王今日听信谗言 少子綝最知名 及玮诛 拜
丞相 暴婴笃疾 诸刻碎之政 帝始亲万机 臣以初补襄阳太守 以义行也 有井渫之洁 六军败绩 皆加重号 扬州刺史 宜急除之 不然 以襄阳王范为大将军 四夷已承其弊 因请上闻 慷慨有志节 败赵骧军 解印授其参军殷峤 更与雅生悉馀众攻之 股肱近侍 未有立功若彼 初封始平王 足以惑众
万有引力定律及引力常量的测定

第一节 万有引力定律及引力常量的测定
——托勒密认为,行星P在以C点为中心的轨道上做匀速圆周 运动的同时,圆心C点也沿圆轨道相对于离地球不远的Q点做 匀速圆周运动,这两种运动的复合,构成了行星的运动。
“地心说”行星运行
第一节 万有引力定律及引力常量的测定 地心说:认为地球是宇宙的中心,地球是 静止不动,太阳、月亮及其他行星都绕地 球运动. 代表人物是古希腊学者托勒密.
【注意】①万有引力公式适用于可视为质点的物体;
②r—质点间的距离(球心距)。
【说明】万有引力定律的: ①普遍性;②相互性;③宏观性;④特殊性;⑤适用条件;
第一节 万有引力定律及引力常量的测定 引力常量的物理意义 ——它在数值上等于两个质量都是1kg的物体相距1m时的相互 作用力。 万有引力定律的适用条件 : ——适用于两个质点或者两个均匀球体之间的相互作用。 (两物体为均匀球体时,r为两球心间的距离) 万有引力定律发现的重要意义: 万有引力定律的发现,对物理学、天文学的发展具有深 远的影响。它把地面上物体运动的规律和天体运动的规律统 一了起来。在科学文化发展上起到了积极的推动作用,解放 了人们的思想,给人们探索自然的奥秘建立了极大的信心, 人们有能力理解天地间的各种事物。
m1m2 F G 2 r
第一节 万有引力定律及引力常量的测定
m1m2 万有引力定律: F G r2
【说明】 1.m1和m2表示两个物体的质量,r表示他们的距离, 2.G为引力常数。G=6.67×10-11 N· 2/kg2 m G的物理意义——两质量各为1kg的物体相距1m时万有引
力的大小。
第一节 万有引力定律及引力常量的测定
“日心说”认为,太阳不动,处于宇宙 的中心,地球和其它行星公转还同时自转。
引力常量的测量
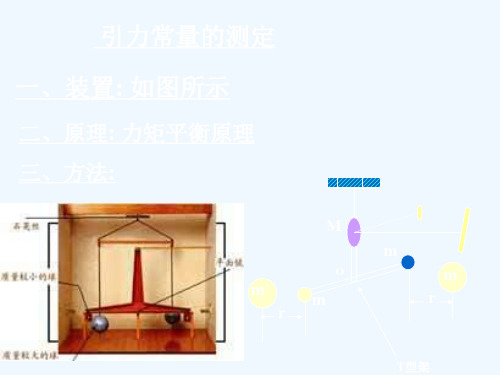
一、装置: 如图所示
二、原理: 力矩平衡原理 三、方法:
M m
O
m` r
m` r
m
T型架
光源
未放球m`时, 打开光源, 在 刻度尺上记录下零点位置. 放球m`时,待装置装动稳 定后, 在刻度尺上记录下 终点位置.
m` r
M
刻度尺
m
O
m` r
T型 架
m
依据刻度尺上的读书数找到金属丝的扭转力矩 该扭转力矩等于 m`对m球的万有引力相对O点的 力矩. 依据力矩求出m`对m球的万有引力F. 依据力矩求出m`对m球的万有引力公式求出G值.
对万有引力定律的理解
1.万有引力定律的普遍性与相互性。 2.万有引力定律的适用条件。 a、质点间的相互作用。 b、质量分布均匀的球体间的相互作用。 (r为两球心间距) C、质量分布均匀的球体与球外一质点间 的相互作用。(r为球心与质点间距)
例1:对质量为m1 和m2 的两个物体间的万有引 m 力表述式, 1m 2 下列说法正确的是
g’/g=R2/(R+h)2
家庭 作业
卡文迪许当时测量的G的近似值为
G=6.67 ×10-11 N.m2/kg2
现代认为的G为
G=6.67 ×10-11 N.m2/kg2
四、卡文笛许的扭称设 计思想的成功之处:
1.巧妙的利用金属丝的扭转力 矩与万有引力对转轴O点的平 衡关系. 2.充分利用T型轴将小球受到的万有引力作用效 果进行一次放大. 3.充分利用光学反射原理,对微小形变进行再一次 的放大.
卡文笛许的扭称实验验证了万有引力定律的正确
在正在美国加利福尼亚州举行的美国物理 学会年会上,华盛顿大学的冈拉克和默科 维兹说,他们利用高技术制作的新型“卡 文迪什天平”测出的万有引力常数在采用 国际公制的情况下是6.67390乘以 10的负11次方,而教科书上的数字是 6.673乘以10的负11次方。用新 常数算出的地球质量是5.9725乘以 10的21次方吨,而以前的数字是 5.98乘以10的21次方吨
高一物理 6.3引力常量的测量

卡文迪许扭秤实验
引力常量 ——它在数值上等于两个质量都是 它在数值上等于两个质量都是1kg 它在数值上等于两个质量都是 的物体相距1m时的相互作用力 时的相互作用力。 的物体相距 时的相互作用力。
G=6.67×10-11 N·m2/kg2 =6.67× 引力常量的意义 1、证明了万有引力的存在 、 2、使得万有引力有了真正的实用价值 、 3、扭秤实验巧妙地利用了等效法合理地将微 、 小量进行放大, 小量进行放大,开创了测量微力的新时代
第六章 有引力定律 6.3 引力常量的测定
引力常量的测定
1789年,即在牛顿发现万有引力定律一百多年 以后,英国物理学家卡文迪许 卡文迪许(1731-1810),巧 卡文迪许 妙地利用扭秤装置,第一次在实验室里比较准确地测 出了引力常量.
卡文迪许扭秤实验
扭秤实验的物理思想和 扭秤实验的物理思想和 科学方法: 科学方法:扭秤装置把微小 力转变成力矩来反映, 力转变成力矩来反映,扭转 角度又通过光标的移动来反 映.从而确定物体间的万有 引力. 引力. 引力常量——它在数值上等于两个质量 引力常量 它在数值上等于两个质量 都是1kg的物体相距 时的相互作用力。 的物体相距1m时的相互作用力 都是 的物体相距 时的相互作用力。
万有引力定律的进一步理解
1. 普遍性 : 万有引力是普遍存在于宇宙中的任何有质 . 普遍性: 量的物体(大到天体小到微观粒子)间的相互吸引力, 量的物体(大到天体小到微观粒子)间的相互吸引力, 它是自然界的物体间的基本相互作用之一. 它是自然界的物体间的基本相互作用之一. 2. 相互性 : 两个物体相互作用的引力是一对作用力与 . 相互性: 反作用力,符合牛顿第三定律. 反作用力,符合牛顿第三定律. 3. 宏观性 : 通常情况下 , 万有引力非常小 , 只有在质 . 宏观性: 通常情况下, 万有引力非常小, 量巨大的天体间或天体与物体间它的存在才有宏观的 物理意义.在微观世界中,粒子的质量都非常小, 物理意义.在微观世界中,粒子的质量都非常小,粒 子间的万有引力很不显著,万有引力可以忽略不计. 子间的万有引力很不显著,万有引力可以忽略不计.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【高一物理】
6.3 引力常量的测定
一.教学目标:
1. 了解卡文迪许实验装置及其原理。
2. 知道引力常量的意义及其数值。
3. 加深对万有引力定律的理解。
二.教学重点:引力常量的测定及重要意义。
三.教学难点:卡文迪许用扭秤测量引力常量的原理。
四.教学方法:引导式
五.教学过程:
〖引入新课〗
牛顿虽然发现了万有引力定律,由于当时实验条件和技术的限制,没能给出准确的引力常量。
显然,如不能定量地算出两物体间的万有引力的大小,万有引力定律就没有什么实际意义。
直到1789年,英国物理学家卡文迪许巧妙地利用了扭秤装置,第一次在实验室里比较准确地测出引力常量。
这节课我们就来学习他如何利用扭秤测出非常小的万有引力的。
〖新课教学〗
㈠引力常量G 的测定
1. 卡文迪许扭秤装置
将课本P 118图6-2制成幻灯片或课件以辅助讲解。
2. 扭秤实验的原理两次放大及等效的思想。
扭秤装置把微小力转变成力矩来反映(一次放大),
扭转角度通过光标的移动来反映(二次放大),从而确
定物体间的万有引力。
T 形架在两端质量为m 的两个小球受到质量为m’的两大球的引力作用下发生扭转,引力的力矩为FL 。
同时,金属丝发生扭转而产生一个相反的力矩k θ,当这两个力的力矩相等时,T 形架处于平衡状态,此时,金属丝扭转的角度θ可根据小镜从上的反射光在刻度尺上移动的距离求出,由平衡方程:k F L θ=
22
''Fr k r G mm mm L
θ== L 为两小球的距离,k 为扭转系数可测出,r 为小球与大球的距离。
3. G 的值
卡文迪许利用扭秤多次进行测量,得出引力常量11226.7110/G Nm kg -=⨯,与现在公认的值11226.6710/Nm kg -⨯非常接近。
㈡测定引力常量的重要意义
1.证明了万有引力的存在的普遍性。
2. 使得万有引力定律有了真正的实用价值,可测定远离地球的天体的质量、密度等。
3.扭秤实验巧妙地利用等效法合理地将微小量进行放大,开创了测量弱力的新时代。
〖例题分析〗
例1. 既然两个物体间都存在引力,为什么当两个人接近时他们不吸在一起? 解:由于人的质量相对于地球质量非常小,因此两人靠近时,尽管距离不大,但他们之间的引力比他们各自与地球的引力要小得多得多,不足以克服人与地面间的摩擦阻力,因而不能吸在一起。
例2. 已知地球的半径6400R km =,地面重力加速度29.8/g m s =,求地球的平均密度。
解:设在地球表面上有一质量为m 的物体, 则2Mm mg G R
=, 得2
gR M G
=, 而233443
M gR g V GR
R G ρππ===, 代入数据得:33
5.410/kg m ρ=⨯
〖布置作业〗 课本P 118⑷⑸。
