(整理)spss因素分析教程.
使用SPSS软件进行多因素方差分析

使用SPSS软件进行多因素方差分析使用SPSS软件进行多因素方差分析一、引言多因素方差分析是一种重要的统计方法,用于分析多个自变量对因变量的影响。
它可以帮助研究人员确定不同因素对研究对象的差异产生的影响,以及这些因素之间是否存在交互作用。
SPSS软件是一款功能强大且易于使用的统计分析工具,可以帮助用户在进行多因素方差分析时快速、准确地得出结果。
本文将介绍使用SPSS软件进行多因素方差分析的步骤,并通过一个案例来具体说明。
二、SPSS软件介绍SPSS(Statistical Package for the Social Sciences)是一款专业的统计分析软件,被广泛应用于社会科学、医学、商业等领域。
它提供了丰富的统计方法和分析工具,并具备数据清洗、可视化、报告生成等功能。
在多因素方差分析中,SPSS 可以帮助用户进行方差分析表的生成、方差分析的可视化、方差齐性检验和事后比较等操作,大大简化了分析过程。
三、多因素方差分析的步骤1. 数据准备:将需要分析的数据录入SPSS软件,并确定自变量和因变量的测量水平。
一般自变量为定类变量,而因变量可以是定量或定类变量。
2. 方差分析表的生成:选择“分析”菜单中的“一元方差分析”选项,然后将因变量添加到依赖变量框中,将自变量添加到因子框中。
接下来,点击“选项”按钮设置参数,如设定显著性水平和置信区间。
点击“确定”后,SPSS会生成方差分析表。
3. 方差分析的可视化:在方差分析表中,用户可以查看各个因素的主效应和交互作用,以及统计指标如F值、p值等。
此外,SPSS还提供了绘制效应图、交互作用图等功能,帮助用户更直观地理解分析结果。
4. 方差齐性检验:方差齐性检验用于验证因变量的变异是否在各组间具有相同的方差。
SPSS软件可以通过选择“分析”菜单中的“Compare Means”选项,进而进行多个组间方差齐性检验。
5. 事后比较:当发现方差分析存在显著差异时,需要进一步进行事后比较以确定差异所在。
数据统计分析及方法SPSS教程完整版

Cumulative Percent 76.6 82.3 100.0
二、程序方式
在Syntax编辑窗口中键入以下程序: Get file=‘c:\program files\spss\employee data.sav’. Frequencies variables = jobcat/order = analysis。
(3)定矩尺度(Interval Measurement):定矩尺度是对事物类 别或次序之间间距的测度。
特点:不仅能将事物区分为不同类型并进行排序,而且可能准确指 出类别之间的差距是多少;定居变量通常以自然或物理单位为计量 尺度,因此测量结果往往表现为数值,所以计量结果可以进行加减 运算。
(4)定比尺度(Scale Measurement):定比尺度是能够测算 两个测度值之间比值的一种计量尺度,它的测量结果同定距变 量一样表现为数值。
SPSS Categories SPSS Complex Sample SPSS Conjoint SPSS Exact Test SPSS Maps SPSS Missing Value
Analysis SPSS Regression
SPSS Tables
SPSS Trends
功能 一般线性模型、混合线性模型、对数线性模型、
注意:在输入数据时不应输入引号,否则双引号将会作为字 符型数据的一部分。
日期型:日期型数据是用来表示日期或时间的。日期型数据 的显示格式有很多,SPSS以菜单方式列出日期型数据的显 示格式以供用户选择。事实上,SPSS存储中的日期型变量 是该实践与1582年10月14日零点相差的秒数。
关于日期型格式的几点说明:
1.2.2 SPSS的5个窗口
(1)数据编辑窗口(SPSS Data Editor)
使用SPSS进行探索式因素分析的教程

使用SPSS进行探索式因素分析的教程探索性因素分析是一种统计方法,用于确定一组变量之间的潜在结构。
SPSS是一种常用于数据分析的软件工具,它提供了强大的因素分析功能。
以下是一个使用SPSS进行探索性因素分析的简单教程,该教程可以帮助您了解如何使用SPSS来执行因素分析并对结果进行解释。
步骤1:导入数据步骤2:准备数据确保您的数据符合因素分析的前提条件。
确定您要进行因素分析的变量是否具有线性关系,并进行必要的数据转换(例如,对数转换)以满足这个条件。
步骤3:执行因素分析在SPSS的“分析”菜单下,选择“数据准备”和“因子”。
在弹出的对话框中,选择您要进行因素分析的变量并将其移动到“因子”框中。
选择“萃取方法”(如主成分分析或最大似然估计)并指定要提取的因素的数量。
您还可以选择执行因子旋转以获得更简单和解释性更强的因子结构。
步骤4:解读结果SPSS将生成一个因素分析的输出报告,其中包含多个表格和图形。
以下是一些常见的解读步骤:-总体解释:观察“总体解释”表,了解因子数量和提取方法的解释力度。
查看“因素”的特征值,了解提取的因子解释的总方差比例。
-因子负荷:查看“因子负荷”表,该表显示了原始变量与提取的因子之间的相关性。
较高的因子负荷表示原始变量与特定因子之间的较强关联。
-因子旋转:如果您选择了因子旋转,则查看“旋转因子载荷矩阵”表,该表显示了旋转后的因子负荷。
查看这些旋转后的因子负荷以确定是否存在更简单的因子结构。
-因子得分:根据选定的因子分析方法,可以生成每个观测值的因子得分。
这些得分表示了每个观测值在每个因子上的得分情况,可以用于后续的分析和解释。
步骤5:解释因子根据因子负荷和因子名称,解释每个因子代表的潜在结构。
结合领域知识和因子负荷,您可以确定每个因子是否与特定概念或潜在维度相关联。
步骤6:结果报告根据您的研究目的和需要,将因子分析的结果写入报告中。
确保清楚地描述因子数量、命名以及每个因子代表的结构或概念。
SPSS-多因素方差分析

④在Univariate对话框中,单击Options…按钮。在Options对话框中, 把Factor(s) and Factor Interations栏中的变量“保存时间”、 “保存温度”、 和“保存时间*保存温度”放入Display Means for栏;并在Display多选项中,选择Descriptive statistics, Estimates of effect size,Homogeneity tests。单击Model…,选择 默认项,即Full factorial项(全析因模型),单击Continue按钮返 回。
⑤在Univariate对话框,单击OK按钮得到Univariate过程的运行结果。
7
结果
8
均数分布图
9
例2, 用5×2×2析因设计研究5种 类型的军装在两种环境、两种活动状 态下的散热效果,将100名受试者随 机等分20组,观察指标是受试者的主 观热感觉(从“冷”到“热”按等级评 分),结果见下表。试进行方差分析。
多因素方差分析
1
一、析因设计资料的方差分析 两因素两水平 三因素多水平
2
析因设计的特点
必须是: 两个以上(处理)因素(factor)(分 类变量)。 两个以上水平(level)。 两个以上重复(repeat)。 每次试验涉及全部因素,即因素同时 施加观察指标(观测值)为计量资料 (独立、正态、等方差)。
24
25
SPSS数据分析问题提出与实例导学 第11章 效度检验因素分析.ppt

(第十一部分)
主讲:赵小军(安庆师范学院) 祁禄(广州大学)
第十一章 效度检验――因素分析
第一节 因素分析统计知识简介
一、R型因子分析与Q型因子分析
R型因子分析是针对变量所做的因子分析,其 基本思想是通过对变量的相关系数矩阵内部结构 的研究,找出能够控制所有变量的少数几个随机 变量去描述多个随机变量之间的相关关系。但这 少数几个随机变量是不能直接观测的,通常称为 因子。然后再根据相关性的大小把变量分组,使 同组内的变量之间的相关性较高,不同组变量之 间的相关性较低。Q型因子分析是针对样品所做 的因子分析。
具体来讲,探索性因素分析与验证性因素分析模型假设有一些区分: 【探索性因素分析的假设】
(1)所有的公共因素都相关(或都无关); (2)所有的公共因素直接影响所有的观测变量; (3)特殊因素之间相互独立; (4)所有观测变量只受一个特殊因素的影响; (5)公共因素和特殊因素相互独立 ; (6) 观测变量与潜在变量之间的关系不是事先假定的; (7)潜在变量的个数不是在分析前确定的; (8)模型通常是不可识别的。 【验证性因素分析的假设】
correlation matrix框: coefficients:相关系数矩阵 significance level:显著性水平 determinant:相关系数矩阵的行列式 inverse:相关系数矩阵的逆矩阵 reproduced:由k(k≤m)个主成分再生的原变量相关系数矩阵 anti-image:反映象相关矩阵 KMO and Bartlett’s test of sphericity :KMO检验和Bartlett检 验,它是对分析模型的适宜程度的检验。(必选)
(1)正交旋转:正交,指旋转过程中,因子之间 的轴线夹角为90度,即因子之间的相关设定为0。 有最大变异法,四方最大法,均等变异法。 (2)斜交旋转:先求得在正交因素模型下的因素 负荷矩阵B,然后对因素负荷矩阵A作斜交变换T*, 求得斜交负荷矩阵A*=BT*。这种方法因子与因子 之间具有一定的相关性。有最小斜交法,最大斜 交法和四方最小法。 至于采用何种转轴法,研究者可以根据文献探究 与理论基础分析结果作为依据,如果相关理论上 显示共同因素层面间是彼此独立,没有关系存在 的,则应采取正交转轴法;如果依理论研究所得, 因素层面间,彼此有相关并且非独立的,则应采 取斜交转轴法。在心理学与教育学中,更多的可 能应该选择斜交旋转。
(整理)使用SPSS进行探索式因素分析的教程.

第4章探索式因素分析在社会与行为科学研究中,研究者经常会搜集实证性的量化资料來做验证,而要证明这些资料的可靠性与正确性,则必须依靠测量或调查工具的信度或效度(杨国枢等,2002b)。
一份好的量表应该要能够将欲研究的主题构念(Construct,它是心理学上的一种理论构想或特质,无法直接观测得到)清楚且正确的呈现出来,而且还需具有「效度」,即能真正衡量到我们欲量测的特性,此外还有「信度」,即该量表所衡量的结果应具有一致性、稳定性,因此为达成「良好之衡量」的目标,必须有以下两个步骤:第一个步骤是针对量表的题项作项目分析,以判定各项目的区别效果好坏;第二步骤则是建立量表的信度与效度。
量表之项目分析、信度检验已于第2、3章有所说明,本章将探讨量表之效度问题。
4-1 效度效度即为正确性,也就是测量工具确实能测出其所欲测量的特质或功能之程度。
一般的研究中最常使用「内容效度」(Content Validity)与「建构效度」(Construct Validity)来检视该份研究之效度。
所谓「内容效度」,是指该衡量工具能足够涵盖主题的程度,此程度可从量表内容的代表性或取样的适切性来加以评估。
若测量内容涵盖所有研究计划所要探讨的架构及内容,就可说是具有优良的内容效度。
在一般论文中,常使用如下的描述来「交代」内容效度:本研究问卷系以理论为基础,参考多数学者的问卷内容及衡量项目,并针对研究对象的特性加以修改,并经由相关专业人员与学者对其内容审慎检视,继而进行预试及修正,因此本研究所使用之衡量工具应能符合内容效度的要求。
本研究之各研究变项皆经先前学者之实证,衡量工具内容均能足够地涵盖欲探讨的研究主题。
另外,本研究于正式施测前,亦针对问卷之各题项与相关领域的学者、专家进行内容适切度之讨论,因此,研究采用之衡量工具应具内容效度。
在内容效度方面,主要是根据文献探讨及专家研究者的经验。
然因本研究问卷设计之初,考虑目前相关的文献中,尚未对本研究议题提出实证性问卷,故只能自行设计量表,对于内容效度是否达成,尚有疑虑。
(整理)spss因素分析教程.
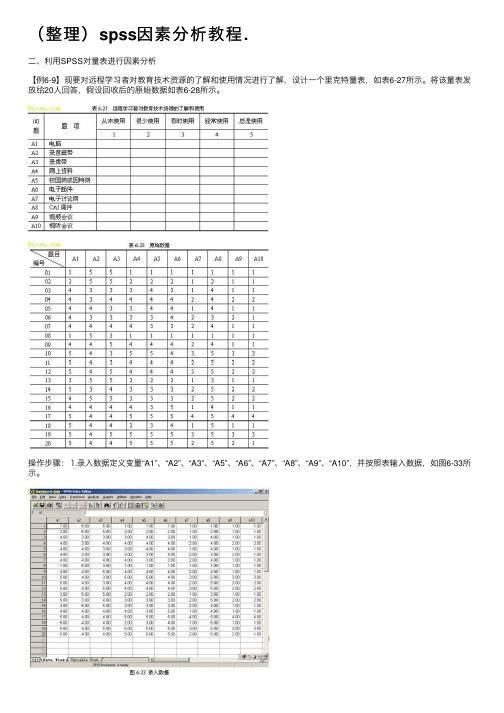
(整理)spss因素分析教程.⼆、利⽤SPSS对量表进⾏因素分析【例6-9】现要对远程学习者对教育技术资源的了解和使⽤情况进⾏了解,设计⼀个⾥克特量表,如表6-27所⽰。
将该量表发放给20⼈回答,假设回收后的原始数据如表6-28所⽰。
操作步骤:⒈录⼊数据定义变量“A1”、“A2”、“A3”、“A5”、“A6”、“A7”、“A8”、“A9”、“A10”,并按照表输⼊数据,如图6-33所⽰。
⒉因素分析(1)选择“AnalyzeData ReductionFactor…”命令,弹出“Factor Analyze”对话框,将变量“A1”到“A10”选⼊“Variables”框中,如图6-34所⽰。
(2)设置描述性统计量单击图6-34对话框中的“Descriptives…”按钮,弹出“Factor Analyze:Desc riptives”(因素分析:描述性统计量)对话框,如图6-35所⽰。
①“Statistics”(统计量)对话框A “Univariate descriptives”(单变量描述性统计量):显⽰每⼀题项的平均数、标准差。
B “Initial solution”(未转轴之统计量):显⽰因素分析未转轴前之共同性、特征值、变异数百分⽐及累积百分⽐。
②“Correlation Matric”(相关矩阵)选项框A “Coefficients”(系数):显⽰题项的相关矩阵B “Significance levels”(显著⽔准):求出前述相关矩阵地显著⽔准。
C “Determinant”(⾏列式):求出前述相关矩阵地⾏列式值。
D “KMO and Bartlett’s test of sphericity”(KMO与Bartlett的球形检定):显⽰KMO抽样适当性参数与Bartlett’s的球形检定。
E “Inverse”(倒数模式):求出相关矩阵的反矩阵。
F “Reproduced”(重制的):显⽰重制相关矩阵,上三⾓形矩阵代表残差值;⽽主对⾓线及下三⾓形代表相关系数。
SPSS数据分析教程因子分析(共36张PPT)

12.2 因子分析的统计理论
因子分析假设每一个原始变量都可以表示成不 可观测的公共因子的线性组合和一个特殊因子 之和。
X11 a11F1a12F2 a1qFq1
X2
2
a21F1a22F2
a2qFq 2
Xpp ap1F1ap2F2 apqFqp
因子分析模型(1)
这里q为公共因子的个数 ,F1,…,Fq表示公共
它衡量公共因子的重要性。
因子分析模型的求解方法 (1)
SPSS中给出了7种求解因子分析模型的方法
主成分 未加权的最小平方法 综合最小平方法 最大似然(K) 主轴因子分解 α因子分解 映像因子分解法。
因子分析模型的求解方法(2)
这7种求解因子分析模型的方法都可以基于相 关系数矩阵 。
因子分析选项设置(1)
因子分析选项设置(2)
如果因子分析的结果输出错误信息“解不收敛” ,可以考虑更改 “最大收敛性迭代次数”为一个 较大的值,然后重新进行因子分析。
因子分析选项设置(3)
因子分析结果(1)
因子分析结果(2)
因子分析结果(3)
旋转后的因子载荷矩阵
因子的解释
第一个因子上载荷较大的原始变量有Fibre、Nutritious、 Health、Natural、Regular、Filling、Quality、Energy和 Satisfying,所有这些变量都描述了谷物产品的自然健康属 性,我们称之为“健康因子”。
结பைடு நூலகம்分析(1):相关系数矩阵
KMO和Bartlett检验
特征值、方差贡献率和累积方差贡献率
初始因子载荷矩阵
旋转因子载荷矩阵
碎石图
因子载荷图
案例2:因子分析在市场调查中的应用
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二、利用SPSS对量表进行因素分析【例6-9】现要对远程学习者对教育技术资源的了解和使用情况进行了解,设计一个里克特量表,如表6-27所示。
将该量表发放给20人回答,假设回收后的原始数据如表6-28所示。
操作步骤:⒈录入数据定义变量“A1”、“A2”、“A3”、“A5”、“A6”、“A7”、“A8”、“A9”、“A10”,并按照表输入数据,如图6-33所示。
⒉因素分析(1)选择“AnalyzeData ReductionFactor…”命令,弹出“Factor Analyze”对话框,将变量“A1”到“A10”选入“Variables”框中,如图6-34所示。
(2)设置描述性统计量单击图6-34对话框中的“Descriptives…”按钮,弹出“Factor Analyze:Desc riptives”(因素分析:描述性统计量)对话框,如图6-35所示。
①“Statistics”(统计量)对话框A “Univariate descriptives”(单变量描述性统计量):显示每一题项的平均数、标准差。
B “Initial solution”(未转轴之统计量):显示因素分析未转轴前之共同性、特征值、变异数百分比及累积百分比。
②“Correlation Matric”(相关矩阵)选项框A “Coefficients”(系数):显示题项的相关矩阵B “Significance levels”(显著水准):求出前述相关矩阵地显著水准。
C “Determinant”(行列式):求出前述相关矩阵地行列式值。
D “KMO and Bartlett’s test of sphericity”(KMO与Bartlett的球形检定):显示KMO抽样适当性参数与Bartlett’s的球形检定。
E “Inverse”(倒数模式):求出相关矩阵的反矩阵。
F “Reproduced”(重制的):显示重制相关矩阵,上三角形矩阵代表残差值;而主对角线及下三角形代表相关系数。
G “Anti-image”(反映像):求出反映像的共变量及相关矩阵。
在本例中,选择“Initial solution”与“KMO and Bartlett’s test of sphericity”二项,单击“Continue”按钮确定。
(3)设置对因素的抽取选项单击图6-34对话框中的“Extraction…”按钮,弹出“Factor Analyze:Extraction”(因素分析:抽取)对话框,如图6-36所示。
①“Method”(方法)选项框:下拉式选项内有其中抽取因素的方法:A “Principal components”法:主成份分析法抽取因素,此为SPSS默认方法。
B “Unweighted least squares”法:未加权最小平方法。
C “Generalized least square”法:一般化最小平方法。
D “Maximum likelihood”法:最大概似法。
E “Principal-axis factoring”法:主轴法。
F “Alpha factoring”法:α因素抽取法。
G “Image factoring”法:映像因素抽取法。
②“Analyze”(分析)选项框A “Correlation matrix”(相关矩阵):以相关矩阵来抽取因素B “Covariance matrix”(共变异数矩阵):以共变量矩阵来抽取因素。
③“Display”(显示)选项框A “Unrotated factor solution”(未旋转因子解):显示未转轴时因素负荷量、特征值及共同性。
B “Scree plot”(陡坡图):显示陡坡图。
④“Extract”(抽取)选项框A “Eigenvalues over”(特征值):后面的空格默认为1,表示因素抽取时,只抽取特征值大于1者,使用者可随意输入0至变量总数之间的值。
B “Number of factors”(因子个数):选取此项时,后面的空格内输入限定的因素个数。
在本例中,设置因素抽取方法为“Principal components”,选取“Correlation matrix”、“Unr otated factor solution”、“Principal components”选项,在抽取因素时限定在特征值大于1者,即SPSS的默认选项。
单击“Continue”按钮确定。
(4)设置因素转轴单击图6-34对话框中的“Rotation…”按钮,弹出“Factor Analyze: Rotation”(因素分析:旋转)对话框,如图6-37所示。
①“Method”(方法)选项方框内六种因素转轴方法:A “None”:不需要转轴B “Varimax”:最大变异法,属正交转轴法之一。
C “Quartimax”:四次方最大值法,属正交转轴法之一。
D “Equamax”:相等最大值法,属正交转轴法之一。
E “Direct Oblimin”:直接斜交转轴法,属斜交转轴法之一。
F “Promax”:Promax转轴法,属斜交转轴法之一。
②“Display”(显示)选项框:A “Rotated solution”(转轴后的解):显示转轴后的相关信息,正交转轴显示因素组型矩阵及因素转换矩阵;斜交转轴则显示因素组型、因素结构矩阵与因素相关矩阵。
B “Loading plots”(因子负荷量):绘出因素的散步图。
③“Maximum Iterations for Convergence”:转轴时之行的叠代最多次数,后面默认得数字为25,表示算法之行转轴时,执行步骤的次数上限。
在本例中,选择“Varimax”、“Rotated solution”二项。
研究者要选择“Rotated solution”选项,才能显示转轴后的相关信息。
单击“Continue”按钮确定。
(5)设置因素分数单击图6-34对话框中的“Scores…”按钮,弹出“Factor Analyze:Factor Scores”(因素分析:因素分数)对话框,如图6-38所示。
①“Save as variable”(因素存储变量)框勾选时可将新建立的因素分数存储至数据文件中,并产生新的变量名称(默认为fact_1、fact_2、fact_3、fact_4等)。
在“Method”框中表示计算因素分数的方法有三种:A “Regression”:使用回归法。
B “Bartlett”:使用Bartlette法C “Anderson-Robin”:使用Anderson-Robin法。
②“Display factor coefficient matrix”(显示因素分数系数矩阵)选项勾选时可显示因数分数系数矩阵。
在本例中,取默认值。
单击“Continue”按钮确定。
(6)设置因素分析的选项单击图6-34对话框中的“Options…”按钮,弹出“Factor Analyze:Options”(因素分析:选项)对话框,如图6-39所示。
①“Missing Values”(遗漏值)选项框:遗漏值的处理方式。
A “Exclude cases listwise”(完全排除遗漏值):观察值在所有变量中没有遗漏值者才加以分析。
B “Exclude cases pairwise”(成对方式排除):在成对相关分析中出现遗漏值得观察值舍弃。
C “Replace with mean”(用平均数置换):以变量平均值取代遗漏值。
②“Coefficient Display Format”(系数显示格式)选项框:因素负荷量出现的格式。
A “Sorted by size”(依据因素负荷量排序):根据每一因素层面的因素负荷量的大小排序。
B “Suppress absolute values less than”(绝对值舍弃的下限):因素负荷量小于后面数字者不被显示,默认的值为0.1。
在本例中,选择“Exclude cases listwise”、“Sorted by size”二项,并勾选“Suppress absol ute values less than”,其后空格内的数字不用修改,默认为0.1。
如果研究者要呈现所有因素负荷量,就不用选取“Suppress absolute values less than”选项。
在例题中为了让研究者明白此项的意义,才勾选了此项,正式的研究中应呈现题项完整的因素负荷量较为适宜。
单击“Cont inue”按钮确定。
设置完所有的选项后,单击“OK”按钮,输出结果。
⒊结果分析(1)KMO及Bartlett’检验如图6-40所示,显示KMO及Bartlett’检验结果。
KMO是Kaiser-Meyer-Olkin的取样适当性量数,当KMO值愈大时,表示变量间的共同因素愈多,愈适合进行因素分析,根据专家Kaiser(1974)观点,如果KMO的值小于0.5时,较不宜进行因素分析,此处的KMO值为0.695,表示适合因素分析。
此外,从Bartlett’s球形检验的值为234.438,自由度为45,达到显著,代表母群体的相关矩阵间有共同因素存在,适合进行因素分析。
(2)共同性如图6-41所示,显示因素间的共同性结果。
共同性中显示抽取方法威主成份分析法,最右边一栏为题项的共同性。
(3)陡坡图如图6-42所示,显示因素的陡坡图。
从陡坡图中,可以看出从第三个因素以后,坡线甚为平坦,因而以保留3个因素较为适宜。
(4)整体解释的变异数——未转轴前的数据如图6-43所示,显示的是未转轴前整体解释的变异数。
从图中可以看出,左边10个成份因素的特征值总和等于10。
解释变异量为特征值除以题项数,如第一个特征值得解释变异量为6.358÷10 63.579%。
将左边10个成份的特征值大于1的列于右边。
特征值大于1的共有三个,这也是因素分析时所抽出的共同因素数。
由于特征值是由大到小排列,所以第一个共同因素的解释变异量通常是最大者,其次是第二个1.547,再是第三个1.032。
转轴后的特征值为4.389、3.137、1.411,解释变异量为43.885%、31.372%、14.108%,累积的解释变异量为43.885%、75.257%、89.366%。
转轴后的特征值不同于转轴前的特征值。
(5)未转轴的因素矩阵如图6-44所示,显示的是未转轴的因素矩阵。
从图中可以看出,有3个因素被抽取,并且因素负荷量小鱼0.1的未被显示。
(6)转轴后的因素矩阵如图6-45所示,显示了转轴后的因素矩阵。
从图中可以看出A1、A8、A6、A5、A4为因素一,A10、A9、A7为因素二,A3、A2为因素三。
题项在其所属的因素层面顺序是按照因素负荷量的高低排列。
