蚂蚁在圆柱体上爬行的最短路径探究
勾股定理的应用——立体图形中最短路程问题教案

《勾股定理的应用——立体图形中最短路程问题》教案(总4页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--教学过程分析第一环节:情境引入创设情景:如图一圆柱体底面周长为32cm,高AB为12cm,BC是上底面的直径。
一只蚂蚁从A点出发,沿着圆柱的表面爬行到C点,试求出蚂蚁爬行的最短路线长。
意图:创设引入新课,从学生熟悉的生活场景引入,提出问题,学生探究热情高涨,激发学生探究热情.第二环节:合作探究内容:引导学生分析题意,明确已知信息,明确题目问题,引导学生合作探究蚂蚁爬行的最短路线,充分讨论汇总方案,在全班范围内讨论每种方案的路线计算方法,四种方案:A A A(1)(2)(3)(4)通过具体分析,得出最短路线,并计算出最短路线长。
让学生发现:沿圆柱体母线剪开后展开得到矩形,研究“蚂蚁怎么走最近”就是研究两点连线最短问题,引导学生体会利用数学解决实际问题的方法.意图:通过学生的合作探究,找到解决“蚂蚁怎么走最近”的方法,将曲面最短距离问题转化为平面最短距离问题并利用勾股定理求解.在活动中体验数学建摸,培养学生与人合作交流的能力,增强学生探究能力,分析能力,发展空间观念.就此问题的解决进行思路小结:将立体图形问题转化为平面图形问题,构建直角三角形利用勾股定理解决此问题,渗透了建模思想。
练习:1.有一圆形油罐底面圆的周长为16m,高为7m,一只蚂蚁从距底面1m的A处爬行到对角B处吃食物,它爬行的最短路线长为多少?2. 如图是一个三级台阶,它的每一级的长、宽和高分别为20dm、3dm、2dm,A和B是这个台阶两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物,则蚂蚁沿着台阶面爬到B点最短路程是多少?第三环节:拓展一:正方体内容:如果圆柱换成如图的棱长为10cm的正方体盒子,蚂蚁沿着表面从A点爬行到B点的最短路线长又是多少呢?1.如图,在棱长为10 cm的正方体的一个顶点A处有一只蚂蚁,现要向顶点B处爬行,已知蚂蚁爬行的速度是1 cm/s,且速度保持不变,问蚂蚁能否在20 s内从A爬到BBA渗透解题思路:即 1、展 -----(立体图形转为平面图形)2、找-----起点A,终点B或B′3、连-----最短路线AB和AB ′4、算-----利用勾股定理总结:对于正方体展开任意两个面连接起点和终点线段即最短的路线大小相等。
初二数学蚂蚁绕圆柱问题

初二数学蚂蚁绕圆柱问题蚂蚁绕圆柱问题是一道经典的数学问题,可以用于帮助学生理解几何形体的性质和解决实际问题。
这个问题是这样的:假设我们有一个半径为r的圆柱体,蚂蚁位于圆柱的侧表面上,蚂蚁可以以固定的速度向上或向下爬行。
蚂蚁的速度足够慢,所以我们可以忽略重力的影响。
问题是,当蚂蚁从圆柱的侧表面出发,沿着圆柱的侧边爬行一圈,最后能够回到初始位置的最短时间是多少?为了解决这个问题,我们首先需要了解圆柱体的性质。
圆柱体由两个平行的圆面和一个侧表面组成。
当我们将圆柱体展开时,侧表面呈现为一个长方形,其中的长度等于圆周的长度,而宽度等于圆柱的高度。
所以,蚂蚁需要爬行的距离就等于这个长方形的周长。
现在,假设蚂蚁的速度为v,圆柱的半径为r,圆柱的高度为h。
我们知道周长等于2πr,所以蚂蚁需要爬行的总时间等于周长除以速度:2πr/v。
为了找到最短时间,我们需要确定速度的方向。
如果蚂蚁以速度v1向上爬行,可以定义向上为正方向,我们可以将速度表示为v1=|v|,即速度的绝对值。
那么,蚂蚁相对圆柱体运动的速度为v2=v1-2πr/t,其中t为蚂蚁绕圆柱体行走一圈需要的时间。
蚂蚁需要爬行的距离等于圆柱侧面的周长,所以蚂蚁相对圆柱体运动的时间为t=2πr/|v|。
将这个时间代入上一个公式中,我们可以得到蚂蚁相对圆柱体运动的速度为v2=|v|-2πr/(2πr/|v|)=|v|-|v|=0。
所以,蚂蚁相对圆柱体的运动速度等于0,即蚂蚁相对圆柱体保持静止。
这意味着蚂蚁绕圆柱体行走一圈的最短时间是0,因为蚂蚁只需要保持静止就可以回到初始位置。
这个问题的答案看起来有些奇怪,蚂蚁绕圆柱体行走一圈的最短时间竟然是0。
但这个答案是正确的,因为我们在问题的设定中忽略了重力的影响,并假设蚂蚁的速度足够慢,所以蚂蚁可以保持静止,而不会从圆柱体上掉下来。
这道题目给了我们一个启示:在解决数学问题时,我们需要仔细思考问题的设定和前提条件。
在这个问题中,我们忽略了可能存在的其他因素,如重力的影响,这导致了最终的答案可能与我们的直觉不一致。
勾股定理的应用(1)----蚂蚁爬行的最短路径
1 2
A
3
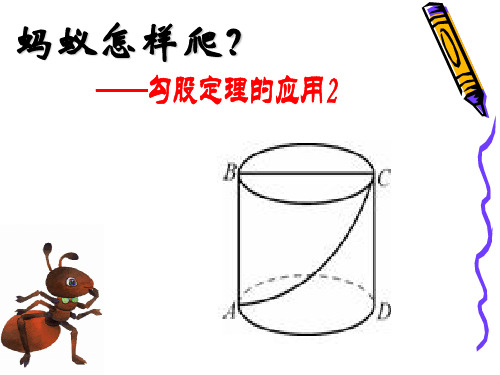
分析:蚂蚁由A爬到B过程中较短的路线有多 少种情况?
(1)经过前面和上底面; 18 (2)经过前面和右面; 26 20 (3)经过左面和上底面 . 3
2 1 1 3 2 2
2
B
1 1
A
利用勾股定理解决问题,关键是 建立数学模型
找出问题中隐藏的直角三角形 或自己构造合适的直角三角形,
尝试把立体图形转换为平面图形。
9 15
B
B
Байду номын сангаас
B C
12
A
A
r=3,π=3
2πr =2×3×3=18
A
要把立体图形转化为平面图形哦!
拓展1
如果圆柱换成如图的棱长为10cm的正方 体盒子,蚂蚁沿着表面需要爬行的最短路 程又是多少呢?
B
A
10
B
B
10
A
10
A
10
10
C
拓展2
如果盒子换成如图长为3cm,宽为 2cm,高为1cm的长方体,蚂蚁沿着 表面需要爬行的最短路程又是多少呢?
2.如图,是一个三级台阶,它的每一级的长、宽、 高分别为2m、0.3m、0.2m,A和B是台阶上两个 相对的顶点,A点有一只蚂蚁,想到B点去吃可口 的食物,问蚂蚁沿着台阶爬行到B点的最短路程 是多少? B B
0.3
0.2 0.3
0.2
0.3 0.2
A
2
A
C
2m
(0.2×3+0.3×3)m
小结
• 通过本节课的学习,你学会解决什么问 题?
选作: 如图,长方形中AC=3,CD=5,DF=6, 求蚂蚁沿表面从A爬到F的最短距离.
蚂蚁行程问题
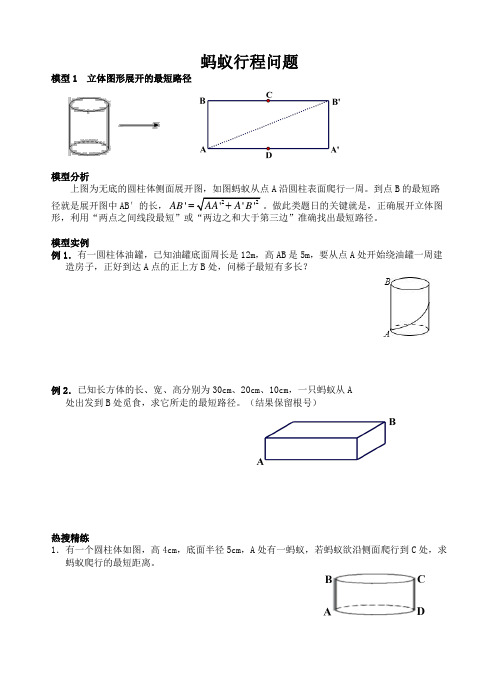
蚂蚁行程问题模型1 立体图形展开的最短路径模型分析 上图为无底的圆柱体侧面展开图,如图蚂蚁从点A 沿圆柱表面爬行一周。
到点B 的最短路径就是展开图中AB ′的长,22''''AB AA A B =+。
做此类题日的关键就是,正确展开立体图形,利用“两点之间线段最短”或“两边之和大于第三边”准确找出最短路径。
模型实例例1.有一圆柱体油罐,已知油罐底面周长是12m ,高AB 是5m ,要从点A 处开始绕油罐一周建造房子,正好到达A 点的正上方B 处,问梯子最短有多长?例2.已知长方体的长、宽、高分别为30cm 、20cm 、10cm ,一只蚂蚁从A处出发到B 处觅食,求它所走的最短路径。
(结果保留根号)热搜精练1.有一个圆柱体如图,高4cm ,底面半径5cm ,A 处有一蚂蚁,若蚂蚁欲沿侧面爬行到C 处,求蚂蚁爬行的最短距离。
2.如图,圆锥体的高为8cm,底面周长为4cm,小蚂蚁在圆柱表面爬行,从A点到B点,路线如图,则最短路程为。
3.桌上有一个圆柱形无盖玻璃杯,高为12厘米,底面周长18厘米,在杯口内壁离杯口距离3厘米的A处有一滴蜜糖,一只小虫从杯子外壁,当它正好在蜜糖相对方向离桌面3厘米的B处时,突然发现了蜜糖,问小虫至少爬多少厘米才能到达蜜糖所在的位置。
4.如图,一只蚂蚁沿着边长为2的正方体表面从点A出发,经过3个面爬行到点B,如果它运动的路径是最短的,则最短距离为。
5.如图,是一个三级台阶,它的每一级的长、宽和高分别等于5cm、3cm和1cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物。
请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点的最短路程是多少?。
数学人教版九年级上册圆柱体表面蚂蚁爬行最短路线问题探讨

蚂蚁在圆柱表面爬行的最短路线问题的探究教学目标:(1)让学生学会转化,把空间问题转化为平面问题;(2)线段公理与勾股定理的应用;教学难点:如何把空间问题转化为平面问题;教学重点:线段公理与勾股定理的应用;教学设计探究一:请看题目:我国古代有这样一道数学问题:“枯木一根直立地上,高二丈,周三尺,有葛藤自根缠绕而上,五周而达其顶,问葛藤之长几何?”题意是:如图所示把枯木看作一个圆柱体,因一丈是十尺,则该圆柱的高为20尺,底面周长为3尺,有葛藤自点A处缠绕而上,绕五周后其末端恰好到达点B处,则问题中葛藤的最短长度是尺。
解题思路:要解决这道题首先应解决好缠绕一圈时最短长度是多少尺;探究二:有一圆柱,底面圆的周长为24cm,高为6cm,一只蚂蚁从底面的A处爬行到对角B处吃食物,它爬行的最短路线长为多少?分析:由于蚂蚁是沿着圆柱的表面爬行的,故需把圆柱展开成平面图形.根据两点之间线段最短,可以发现A、B分别在圆柱侧面展开图的宽6cm处和长24cm 中点处,即AB长为最短路线.(如图)如果蚂蚁从距底面1cm的A处爬行到对角B处吃食物,它爬行的最短路线长为多少?分析:探究三:如图,圆柱形容器高18cm,底面周长为24cm,在杯内壁离杯底4cm的点B处有一滴蜂蜜,此时已知蚂蚁正好在杯外壁,离杯上沿2cm与蜂蜜相对的A处,则蚂蚁从外壁A处到达内壁B处的最短距离为cm。
设计意图:1、体会转化思想(1)把空间问题转化成平面问题(2)把复杂问题转化成简单问题2、提高综合利用数学知识能力如线段公理、勾股定理、对称的性质等3、体会三个探究问题中的联系与区别(1)探究一与探究二目的地不同,展开图对应点位置也不同。
(2)探究三是探究二的拓展。
蚂蚁行程问题

蚂蚁行程问题◐名师点金◑蚂蚁行程问题主要是讲蚂蚁沿立体图形表面行走的最短距离问题,解题技巧是将立体图形展开为平面图形,在平面图形中将路程转化为两点间的距离,然后借助勾股定理等知识求出最短路程.模型分析上图为无底的圆柱体侧面展开图,如图蚂蚁从点A 沿圆柱表面爬行一周。
到点B 的最短路径就是展开图中AB ′的长,22''''AB AA A B =+。
做此类题日的关键就是,正确展开立体图形,利用“两点之间线段最短”或“两边之和大于第三边”准确找出最短路径。
类型1:圆柱中的最短问题例1.有一只蚂蚁要从一个圆柱形玻璃杯的点A 爬到点B 处(点A,B 均在玻璃杯外部),如图所示,已知杯子高8cm,点B 距杯口3cm,杯子底面半径为4cm.蚂蚁从A 点爬到B 点的最短路程为多少(π取3)?拓展1:例1中的B 若改为在玻璃杯内部时,这时蚂蚁从A 点爬到B 点的最短路程又为多少(π取3)?例2.如图,圆锥体的高为8cm ,底面周长为4cm ,小蚂蚁在圆柱表面爬行,从A 点到B 点,路线如图,则最短路程为 。
类型2:长方体中表面的最短问题例3.如图,长方体盒子的长、宽、高分别是12 cm,8 cm,30 cm,在外表面AB的中点C 处有一滴蜜糖,一只小虫从E处沿盒子表面爬到C处去吃.求小虫爬行的最短路程.例4.有一个如图所示的长方体的透明玻璃鱼缸,假设其长AD=80cm,高AB=60cm,水深为AE=40cm,在水面上紧贴内壁G处有一鱼饵,G在水面线EF上,且EG=60cm.一小虫想从鱼缸外的A点沿壁爬进鱼缸内G处吃鱼饵.(1)小虫应该走怎样的路线才能使爬行的路线最短呢?请你在图中画出它爬行的路线,并用箭头标注.(2)求小虫爬行的最短路线长.八年级《蚂蚁行程问题》演练题1.如图,一只蚂蚁沿着边长为2的正方体表面从点A出发,经过3个面爬行到点B,如果它运动的路径是最短的,则最短距离为。
也说圆柱台表面蚂蚁爬行最短路径

直观简析蚂蚁爬行最短路径----- 几何画板应用案例探微江苏省扬州市高邮市司徒镇初级中学杨万元摘要:通过几何画板的动态效果直观反映探究内容,并利用其公式功能拓展问题本身关键词:建模函数质疑数学实验现代教育技术分类思想—.提出冋题:在与学生一起学习勾股定理相应章节时,遇到蚂蚁在圆柱体表面爬行的问题,总是心存疑虑。
出题者的本意,是关乎侧面的化曲为直,以及勾股定理的运用;可是将问题生活化了,就很难最贴切的仅仅化为侧面的事情。
不能总说,蚂蚁在没有上底的油桶,或没有上底纸筒上爬行,略嫌生活化不够。
一般会说在圆柱型木桩上,或是圆柱型石凳上。
但这样一来,蚂蚁到对应点就多了选择,可以经底面到达。
而有时,特别是圆柱较扁平时,经底面的路径,比单纯经侧面更短。
例如:圆柱的半径为1,高也为1•则单纯在侧面最短路径二\/彳2经c点的最短路径=3 进一步提问:什么情况下,什么样的路径是最短的?二•解析问题:为使问题简洁,可令圆柱的半径为单位 1.①高为h, E为上底边缘点,弧CE的长度为X, / COE的度数也为x (弧度制),最短路径长为y.则经E 点到最短路径二侧面上AE 的距离+底面上EB 的距离由此可知,在半径一定的情况下最短路径长 y 受x,h 两变量影响在几何画板中,建立直角坐标系,设立 h 为动画参数,②绘制函数图 像通过观察发现,在0-3.14160范围内,h 从小到大的变化过程中, 左点先是最低,后与右点相平,再后来右点一直最低。
也可通过创建此函数的导函数,③并绘制导函数图像。
图像在 x 轴上下的位置能帮助我们判定原函数的增减性,进一步印证其上感性B 为使核心问题在动态图形中体现出来,过图形与 y 轴交点作x 轴认识。
接下来,我们再来看看左右点相平这个关键点。
经反复实验, h 的值确定在1.5上下。
我们不妨推导一番。
左点的横坐标为0,则y=h+2右点的横坐标为,则y= ■. h 2 ~2左右相等,则h+2二h 2二22综上所述,当匕<4时,过c 点路径最短;r 4 当h = 4时,过C 点或单纯在侧面最短路径一样;r 4 2h 二 一 4即-= 4④解之得h=二2 -4 4当h> 4时,单纯在侧面路径最短r 4三•问题小结:与纯理论(高等数学)分析相比,虽显粗糙,却形象直观。
蚂蚁怎样走最近圆柱PPT课件

回顾与思考
A
从A到B的最短路径为 。
①
②
B
③
两点之间,线段最短。
圆柱的侧面展开图为 长方形 ,
且长方形的长等于 圆柱的底面周长 ;宽圆柱的高
为
。
回顾与思考
勾股定理:
形→数 Rt∆→ a²+b²=c²
直角三角形两直角边的平方和等于斜边的平方。
勾股定理的逆定理:
A
A
60
B ②把正面和上面展开成平面如图, 连接AB,由题意得:AC=60cm, BC=80cm
AB2=AC2+BC2=602+802=1002
B
∴蚂蚁爬行的最短路程为100厘米。
80
c
C A
B
③把左面和上面展开成平面如图, 连接AB,由题意得:AC=60cm, BC=80cm
B
AB2=AC2+BC2=402+1002=11600
60 ∴综上所述,蚂蚁爬行的最短路程为 100厘米。
40
A
c
40
1.有一只蚂蚁从一个正方体的顶点A沿表面 爬到顶点C,如果底面是一个边长为4厘米的 正方形,高为6厘米,则蚂蚁所爬的最短路 径是多少厘米?
C
A
D BC
A E BC
如图,长方体的长、宽、高分别为 3cm、2cm、4cm,点B离点C的1cm, 一只蚂蚁如果要沿着长方体的表面 从点A爬到点B,需要爬行的最短路 程是多少?
x尺
x = 12
5尺
SUCCESS
THANK YOU
•
解:①把正面和右面展开成平面
D
如图,连接AB,由题意得:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一类蚂蚁在圆柱体上爬行的最短路径探究
一、请阅读下列材料:
问题:如图(1),一圆柱的底面半径、高均为5cm,BC是底面直径,求一只蚂蚁从A点出发沿圆柱表面爬行到点C的最短路线.小明设计了两条路线:
路线1:侧面展开图中的线段AC.如下图(2)所示:
设路线1的长度为l1,则l12=AC2=AB2+2=52+(5π)2=25+25π2
路线2:高线AB+底面直径BC.如上图(1)所示:
设路线2的长度为l2,则l22=(AB+BC)2=(5+10)2=225
l12-l22=25+25π2-225=25π2-200=25(π2-8)>0
∴l12>l22,∴l1>l2
所以要选择路线2较短.
(1)小明对上述结论有些疑惑,于是他把条件改成:“圆柱的底面半径为1cm,高AB为5cm”继续按前面的路线
进行计算.请你帮小明完成下面的计算:
(2)路线1:l12=AC2=_____;
(3)路线2:l22=(AB+BC)2=_____
(4)∵l12_____l22,
(5)∴l1_____l2(填>或<)
(6)∴选择路线_____(填1或2)较短.
(7)(2)请你帮小明继续研究:在一般情况下,当圆柱的底面半径为r,高为h时,应如何选择上面的两条路线才
能使蚂蚁从点A出发沿圆柱表面爬行到C点的路线最短.
二、如图所示,一圆柱高AB为5cm,BC是底面直径,设底面半径长度为acm,求点P从A点出发沿圆柱表面移动到点C的最短路线.
方案设计
某班数学兴趣小组设计了两种方案:
图1是方案一的示意图,该方案中的移动路线的长度为l1,则l1=5+2a(cm);
图2是方案二的示意图,设l2是把圆柱沿AB侧面展开的线段AC的长度,则l2=________cm(保留π).
计算探究
① 当a=3时,比较大小:l 1________ l 2(填“>”“=”或“<”);
② ②当a=4时,比较大小:l 1________ l 2(填“>”“=”或“<”);
③ 延伸拓展:
④ 在一般情况下,设圆柱的底面半径为rcm .高为hcm .
⑤ ①若l 12=l 22,求h 与r 之间的关系;
⑥ ②假定r 取定值,那么h 取何值时,l 1<l 2?
⑦ ③假定r 取定值,那么h 取何值时,l 1>l 2?
三、1.有一圆柱体如图,高4cm ,底面半径5cm ,A 处有一蚂蚁,若蚂蚁欲爬行到C 处,求蚂蚁爬行的最短距离 .
2.如图,已知圆柱体底面圆的半径为π
4,高为1,AB 、CD 分别是两底面的直径,AD 、BC 是母线,若一只小虫从A 点出发,(沿圆柱表面)爬行到点C ,则小虫爬行的最短的路线的长度是 (结果精确到0.01).
3.如图,已知圆柱体底面圆的半径为π
2,高为2,AB 、CD 分别是两底面的直径,AD 、BC 是母线,若一只小虫从A 点出发,从圆柱侧面爬行到点C ,则小虫爬行的最短的路线的长度是 (结果保留根式).。
