人口预测实验报告材料
人口预测实验报告

3、一元线性回归模型法预测
(1)数据分析
根据府谷县10年的数据的数据散点图如下图1。
图1:府谷县10年人口数据散点图
并对其进行一元线性回归分析得下表2、表3、表4、
表2:SUMMARY OUTPUT
回归统计
Multiple R
1.457422
10
24.88956
1.168435
1.145483
由人口数和年份的散点图可以看出人口随年份基本上呈线性排列的。再由回归分析结果可知相关系数r=0.850,说明人口数和年份是高度相关的,比较适合用一元线性回归模型进行预测。
(2)原理分析
一元线性回归模型利用历史的人口时间序列数据, 建立一元线性回归方程,以此预测一定时期内的人口规模。具体步骤是:
0.270949
0.265626
4
21.57724
-0.00424
-0.00416
5
22.05043
-0.50643
-0.49648
6
22.52362
-0.89162
-0.8741
7
23.47
-1.787
-1.75189
8
23.94319
-0.89419
-0.87662
9
24.41638
1.486624
0.850013
R Square
0.722522
Adjusted R Square
0.687838
标准误差
1.081913
观测值
10
表3:方差分析
df
SS
MS
人口预测 matlab

数学建模第一次实验报告一.实验目的学习有关人口预测的模型,了解有关混沌的基本理论,建立人口预报模型,并完成人口总量的预报,能够用软件完成数据计算。
二.实验内容1.下表为我国自1949年至2000年的人口数据,请根据人口模型,预测出2010、2015年我国的人口总数,并根据中国统计局的全国人口普查公报的1%调查数据,计2.谈谈你所认识的混沌三. 实验步骤1. 查阅资料选择模型通过查阅资料,发现在考虑算法复杂度以及预测效果等综合因素时,阻滞增长模型(Logistic 模型)要优于其他模型,所以我们选用阻滞增长模型进行本次实验。
2. 建立模型阻滞增长模型(Logistic 模型)是考虑到自然资源、环境条件等因素对人口增长的阻滞作用,对指数增长模型的基本假设进行修改后得到的。
阻滞作用体现在对人口增长率r 的影响上,是的r 随着人口数量x 的增加而下降。
若将r 表示为x 的函数()r x ,则它应是减函数,于是有:()()0,0dxr x x x x dt== (1) 对于()r x 的一个最简单的假设是()r x 为x 的线性函数,即:()(),0,0r x r sx r s =->> (2)设自然资源和环境所能容纳的最大人口数量为m x ,当m x x =时人口不在增长,即增长率()0m r x =,代入(2)式可得mrs x =,所以有: ()(1)mrr x r x =-(3) 将(3)式代入(1)式得:()0(1)0m dxr rx dt x x x⎧=-⎪⎨⎪=⎩(4) 解(4)可得(5)式:()01(1)e mrtm x x t xx -=+- (5)3. 根据模型原理进行编程程序见第五部分。
4. 运行结果采用1949年到2000年的人口调查结果作为数据,计算得到的模型参数()r x 和m x 为:()0.0296r x =,()204.5537m x =千万人。
1949年到2000年的预测结果与人口调查结果对比图如图1所示。
人口预测数学实验报告
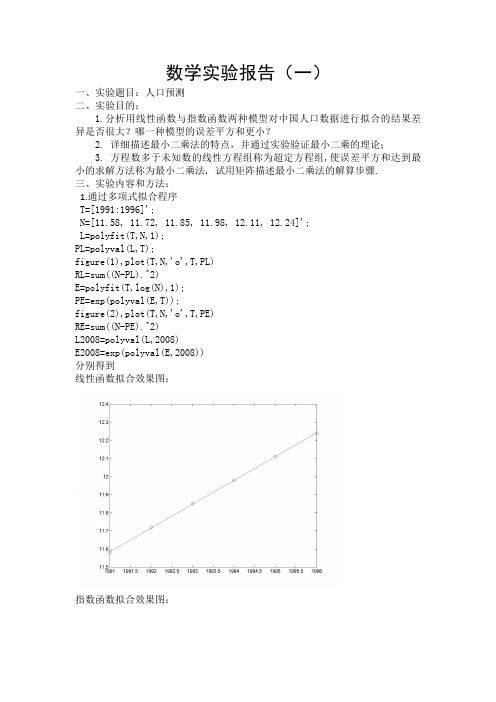
数学实验报告(一)一、实验题目:人口预测二、实验目的:1.分析用线性函数与指数函数两种模型对中国人口数据进行拟合的结果差异是否很大?哪一种模型的误差平方和更小?2. 详细描述最小二乘法的特点,并通过实验验证最小二乘的理论;3. 方程数多于未知数的线性方程组称为超定方程组,使误差平方和达到最小的求解方法称为最小二乘法, 试用矩阵描述最小二乘法的解算步骤.三、实验内容和方法:1.通过多项式拟合程序T=[1991:1996]';N=[11.58, 11.72, 11.85, 11.98, 12.11, 12.24]';L=polyfit(T,N,1);PL=polyval(L,T);figure(1),plot(T,N,'o',T,PL)RL=sum((N-PL).^2)E=polyfit(T,log(N),1);PE=exp(polyval(E,T));figure(2),plot(T,N,'o',T,PE)RE=sum((N-PE).^2)L2008=polyval(L,2008)E2008=exp(polyval(E,2008))分别得到线性函数拟合效果图:指数函数拟合效果图:由图可以看出两种方式的结果差异并不是很大其次,由程序可以得出,线性函数的误差平方和为:4.7619e-005指数函数的误差平方和为:1.1549e-004可见线性函数的误差平方和更小。
2.曲线拟合的实际含义是寻求一个函数y=f(x),使f(x)在某种准则下与所有数据点最为接近。
最小二乘法就是使所有散点到曲线的距离平方和最小。
这就类似于概率中的标准差,也是用距离的方式来定义,以求得误差最小。
通过有实际意义的数值来判断比较并最终得到最好的拟合方法。
编写程序,将实际折线图分别与线性拟合和指数拟合在同一个图中显示:折线图与线性拟合图:T=[1991:1996]';N=[11.58, 11.72, 11.85, 11.98, 12.11, 12.24]';plot(T,N,'O',T,N)hold onL=polyfit(T,N,1);PL=polyval(L,T);plot(T,N,'*',T,PL)hold of折线图与指数拟合图:T=[1991:1996]';N=[11.58, 11.72, 11.85, 11.98, 12.11, 12.24]'; plot(T,N,'O',T,N)hold onE=polyfit(T,log(N),1);PE=exp(polyval(E,T));plot(T,N,'*',T,PE)hold off由此可见,误差平方和更小些的线性拟合方法拟合出的图形与原图更加接近。
人口预测实验报告

南京信息工程大学实验报告实验名称:人口预测日期:2009年12月26日指导老师:吕红学院:计算机与软件学院专业:网络工程年级:2008 班次:1姓名:王欣然学号:20081346005一、实验目的:学习有关人口预测的模型,根据所给的数据,能够建立合理模型,并完成计算,能够用数学软件(比如Mathematica、Matlab)绘制出计算结果的简单图形,了解混沌系统的特征。
二、实验内容:1.下表为我国自1949年至2000年的人口数据,请根据人口模型,预测出2005-2010年我国的人口总数。
年份年末总人口(万人)出生率(‰)死亡率(‰)自然增长率1949 54167 36.00 20.00 16.00 1950 55196 37.00 18.00 19.00 1951 56300 37.80 17.80 20.00 1952 57482 37.99 17.00 20.99 1953 58796 37.00 14.00 23.00 1954 60266 38.19 13.18 25.00 1955 61465 32.18 12.28 19.90 1956 62780 33.67 11.40 21.39 1957 64238 34.03 10.80 23.23 1958 65346 29.22 11.98 17.24 1959 66012 24.78 14.59 10.19 1960 66207 20.86 17.91 2.95 1961 66457 18.02 14.24 3.78 1962 67295 22.63 10.02 12.61 1963 69172 40.00 12.11 27.89 1964 70499 30.68 11.50 19.18 1965 72538 38.42 9.50 28.92 1966 74206 31.82 8.83 22.99 1967 76032 33.04 8.43 24.61 1968 78198 36.70 8.21 28.49 1969 80335 35.35 8.03 27.32 1970 82542 35.07 7.60 27.47 1971 84779 34.42 7.32 27.10 1972 86727 30.59 7.61 22.98 1973 88761 30.49 7.04 23.45 1974 90409 25.91 7.34 18.57 1975 91970 24.59 7.32 17.27 1976 93267 21.35. 7.25 14.10 1977 94774 23.03 6.87 16.161978 96159 20.86 6.25 14.611979 97542 20.59 6.21 14.381980 98705 18.26 6.34 11.921981 100072 20.21 6.36 13.851982 101654 22.28 6.60 15.681983 103008 20.19 6.90 13.291984 104357 19.90 6.82 13.081985 105851 21.04 6.78 14.261986 107507 22.43 6.86 15.571987 109300 23.33 6.72 16.611988 111026 22.37 6.64 15.731989 112704 21.58 6.54 15.041990 114333 21.06 6.67 14.391991 115823 19.68 6.70 12.981992 117171 18.24 6.64 11.601993 118517 18.09 6.64 11.451994 119850 17.70 6.49 11.211995 121121 17.12 6.57 10.551996 122389 16.98 6.56 10.421997 123626 16.57 6.51 10.061998 124761 15.64 6.50 9.141999 125786 14.64 6.46 8.182000 126743 14.03 6.45 7.582. 用数学软件绘制我国人口增长率随着人口总量的曲线,以及人口总量随着时间变化的曲线;3. 举例说明你所认识的混沌。
(完整word版)数学建模-人口预测实验报告

数学与计算科学学院实验报告实验项目名称人口预报所属课程名称数学模型实验类型综合型实验日期班级信计1001班学号201053100127姓名徐超成绩129207 129735 130137)得人口预测方程:0.022552ˆ()176060.7575988.75t Xt e -=- 将各个年份分别代入上面的方程即得各个年份的人口数据预测值,然后将其分别与实际值比较,并计算出其误差.实际值与预测值的比较图[1]该模型对于中短期的人口预测,所得结果较为准确,大部分预测数据与实际数据的误差率都在2%以内,较好地估计出了最近几十年的人口数量。
根据我们的模型所预测出的结果,到本世纪中叶我国的人口数量将超过15亿,但是根据国内的本课题专家研究,随着我国经济社会发展和计划生育工作加强,可以预测我国的总人口将于2010年、2020年分别达到13.6亿人和14。
5亿人,2033年前后达到峰值15亿人左右,即我国人口的上限不会超过15亿人。
这一结论与我们的模型所得到的数据有所出入。
于是我们将模型进行改进,选择在长期预测方面比较精准的模型(2)Logistic 人口模型来求解. B 、模型(2)这个问题是典型的伯努利方程初值问题,其解为:()-(-)01(-1)0w mw t t t w m ew μ=+分析上式可知:(1)当t →∞时,()m w t w →,即无论人口初值如何随着时间推移而变化,人口总数总是趋向于一个确定的值m w ;(2)222(1)md w wdt w μ=-,所以当人口达到极限值的一半2m w 时,属于加速增长,超过一半属于减速增长,但是增长率仍为正的,并且其增长率随时间的增加而减少。
根据1981年~2005年的全国人口统计数据,利用计算机Matlab 编程得,0.0422μ=,150000Wm =从而得到全国总人口数的Logistic 模型方程为:0.0422(1981)150000()1500001(1)100072t w t e --=+-利用该模型对1981年~2005年的人口数据进行检验并对2006年~2050年的人口数据进行预测。
人口预测报告

人口预测报告
报告摘要:
本报告基于当前世界各地的人口普查和其他相同类型的数据,
预测世界各地区的人口发展趋势。
我们发现,在全球范围内,人
口增长率已经逐渐下降,而人口老龄化的趋势则不断加剧。
此外,由于大量的人口迁移,尤其是从发展中国家向发达国家的迁移,
正在改变世界各地的人口构成。
I. 人口增长的趋势
全球人口的增长率已经逐渐下降。
预计到2050年,全球人口
增长率将从现在的1.2%降至0.5%左右。
而在发展中国家,由于生育率的下降,人口增长率将降至极低水平,部分地区甚至将出现
人口负增长。
II. 人口老龄化的现状
与此同时,人口老龄化的趋势正在全球范围内不断加剧。
预计
到2050年,全球65岁以上的老年人口将达到2.1亿人。
这将对世
界各国的经济、社会和医疗保健等方面带来巨大的挑战。
III. 人口迁移的影响
人口迁移一直是影响全球人口构成的重要因素之一。
目前,越
来越多的人从发展中国家向发达国家进行迁移,这将会对人口分
布和结构产生深远影响。
结论:
世界各国政府需要注意人口变化趋势,并采取相应措施,来应
对人口老龄化、人口迁移和人口集中等问题。
政府需要积极推动
人口结构和经济发展相适应,确保新一代人口的健康成长和发展。
人口预测方法总结材料
1. 人口总量预测(1)人口总量趋势外推模型图 1 永康市1985年以来历年的人口变化(2)人口增长率预测模型人口增长率预测模型是根据计划生育有关指标而进行的一种人口预测方法。
数学公式表示为:+1(=)+P n∆kPP(3-2)0式中: P表示规划期总人口(人),P表示规划基期总人口(人),ΔP表示规划期间人口机械增长数(人),n表示规划年期,k表示规划期间人口自然增长率。
人口自然增长率k可用出生率b和死亡率d表示:=(3-3)k-db图 2 永康市1989年以来历年的人口出生率、死亡率和自然增长率图 3 永康市1989年以来历年的户籍人口迁移数量(3)人口离散预测模型人口离散预测模型也即人口差分方程预测模型,又称“宋健模型”,是我国自行提出的比较成功的人口发展预测模型,能较好的运用人口普查资料对未来人口进行预测。
该模型是根据分年龄的人口结构递推公式进行预测,模型的数学表达如下:1,...,2,1,0)()()](1[)1()()()()()](1[)(100021-=+⋅-=+⋅⋅⋅⋅-=+∑m i t f t X t t X t X t k t h t t t X i i i i r r i i i μβμ (3-6)式中:X 0(t)为t 年代0岁出生婴儿数,X i (t)为t 年代之年龄组人口数,μ00(t)为t 年出生婴儿当年死亡率,β(t)为妇女总和生育率,即社会人中平均意义下一个妇女在整个育龄时期的生育总数(r 2,r 1即为生育年龄的上下限),h i (t)为生育模式,反映某一地区某一个育龄妇女生育状态分布,k i (t)为t 年代之年龄组女性性别比,μi (t)为t 年代之年龄组人口死亡率,f i (t)为t 年代之年龄组净迁移数。
在模型的具体应用中,课题组工作的重点是如何确定公式3-6中的各种参数。
①第五次人口普查资料中的数据是2000年11月1日的数据,而规划所需的数据是年末的数据,课题组将普查的户籍人口分龄人口数按比例修正到2000年底的统计人口总数作为X i (t);②从普查资料来看45岁以下的性别比比较稳定,为了简化模型,t 年代之年龄组女性性别比k i (t)用常量 k 表示,即采用普查资料中的45岁以下的男女性别比=104.85(女性=100)推算,故k= 0.488326;③根据普查资料,妇女总和生育率取2000年的数据β(t)= 0.8795;④模型中出生婴儿当年死亡率μ00(t)假定与2000年出生婴儿当年死亡率的80%,即采用μ00=3.88‰。
人口数据分析报告及预测(3篇)
第1篇一、引言人口是社会发展的重要基础,对国家、地区乃至全球的经济、政治、文化等方面都有着深远的影响。
随着我国经济的快速发展,人口问题日益凸显,如何科学地分析人口数据,准确预测未来人口发展趋势,对于制定合理的政策、优化资源配置、促进社会和谐稳定具有重要意义。
本报告将对我国人口数据进行分析,并预测未来人口发展趋势。
二、我国人口现状分析1. 人口总量截至2020年底,我国总人口为14.1亿,占世界总人口的18.1%。
在过去几十年里,我国人口总量持续增长,尤其是改革开放以来,人口增长速度加快。
2. 人口结构(1)年龄结构:我国人口年龄结构呈现“老龄化”趋势。
据国家统计局数据显示,2019年我国60岁及以上人口占比为18.1%,比2018年提高0.6个百分点。
预计未来老龄化程度将不断加深。
(2)性别结构:我国性别比例失衡问题突出。
据国家统计局数据显示,2019年我国男性人口为7.23亿,女性人口为6.88亿,性别比为104.6。
这一现象对婚姻、生育、教育等方面产生了一定影响。
(3)城乡结构:我国城乡人口差距较大。
据国家统计局数据显示,2019年我国城镇常住人口为8.48亿,占总人口的59.6%;农村常住人口为5.62亿,占总人口的40.4%。
城乡人口结构不合理,导致城市人口压力增大,农村人口流失严重。
3. 人口素质我国人口素质不断提高,受教育程度逐渐提高。
据国家统计局数据显示,2019年我国人均受教育年限为9.77年,比2018年提高0.16年。
然而,地区之间、城乡之间的人口素质差距仍然较大。
三、我国人口发展趋势预测1. 人口总量根据联合国人口预测数据,我国人口总量将在2030年达到峰值,约为14.8亿。
此后,人口总量将逐渐下降,预计2050年左右降至14亿以下。
2. 人口结构(1)年龄结构:随着生育政策的调整和老龄化程度的加深,我国人口年龄结构将呈现“老龄化、少子化”趋势。
预计2030年左右,我国60岁及以上人口占比将超过20%。
微分方程模型—人口模型与预测实验报告
20 12 ——20 13 学年第 2 学期合肥学院数理系实验报告课程名称:数学模型实验项目:微分方程模型—人口模型与预测实验类别:综合性□设计性□验证性□专业班级:10级数学与应用数学(2)班姓名:王倩学号:1007022039 实验地点:数理系机房实验时间:2013年5月2日指导教师:闫晓辉成绩:一.实验目的:掌握常微分方程模型的建模方法,并能用数值算法或MATLAB 库函数求解。
二.实验内容:下表列出了中国1982-1998年的人口统计数据,取1982年为起始年(0=t ),1016540=N 万人,200000=m N 万人。
实验要求:1、建立中国人口的指数增长模型,并用该模型进行预测,与实际人口数据进行比较。
2、建立中国人口的Logistic 模型,并用该模型进行预测,与实际人口数据进行比较。
3、绘图,在图中标出中国人口的实际统计数据,并画出两种模型的预测曲线。
三. 实验方案(程序设计说明)模型一:指数增长模型(马尔萨斯(Malthus )模型)假设:人口净增长率r 是一常数符号:x(t )t --时刻时的人口,可微函数00x t --=时的人口 则()()()x t t x t r x t t+∆-=∆于是x (t )满足如下微分方程:00()dxrxdt x x ⎧=⎪⎨⎪=⎩解为:0()rt x t x e = 模型二:Logistic 模型人口净增长率应当与人口数量有关,即: r =r (x )从而有:00()()dxr x xdt x x ⎧=⎪⎨⎪=⎩对马尔萨斯模型引入一次项(竞争项),令 r (x )=r -ax 此时得到微分方程:()dxr ax x dt=-或(1)m dx x r x dt x =-可改写成:()m mdx rx x x dt x =- 分离变量:11m dx rdt x x x ⎛⎫+= ⎪-⎝⎭两边积分并整理得: 1mrtx x Ce-=+ 令x (0)=0x ,求得: 0001m mx x x C x x -==- 满足初始条件x (0)=0x 的解为: 011()()mrtm x x t xe x -=+-易见: lim ()m t x t x →+∞=四. 实验步骤或程序(经调试后正确的源程序)1、matlab 源程序%以1982-1998年共计17个数据为例进行拟合: t=0:16; %输入数据s=[101654 103008 104357 105851 107507 109300 111026 112704 114333 115823 117171 118517 119850 121121 122389 123626 124810];y=log(s); p=polyfit(t,y,1)2、matlab 源程序 t=0:16;s=101654*(1+0.0131).^t; plot(t,s,'r') hold on t=0:16;s=[101654 103008 104357 105851 107507 109300 111026 112704 114333 115823 117171 118517 119850 121121 122389 123626 124810]; plot(t,s,'o') hold on t=0:16;s=200000./(1+(200000/101654-1)*exp(-0.029*t)); plot(t,s,'c')五.程序运行结果1、运行结果p = 0.0131 11.534200131115342..y t =+001153421021502451ln ..x x ∴=⇒= 0013110215024514.().t x t e ∴=预测公式预测1991--1998年的人口数量可得,1998年的由指数增长模型预测出的人口数于实际人口数相差最小,而其他年份的真实值与预测值之间有差别:由1991年开始,指数增长模型预测的结果很好的反映了实际情况。
MATLAB实验-9 (2) 河南省人口预测模型 马尔萨斯人口模型
结果
functionf=fun6(x,t);
f=7285*x(1)./((x(1)-7285)*exp(-x(2)*(t-1980))+7285);
t=[1980:2010];
y=[7285 7397 7519 7632 7737 7847 7985 8148 8317 8491 8649 8763 8861 8946 9027 9100 9172 9243 9315 9387 9488 9555 9613 9667 9717 9768 9820 9869 9918 9967 10437];
由图可以看出,拟合图与真实值有较大的误差,可以推测出人口增长率不是一个固定数,人口增长与已有人口数有关,由生物学角度来说,当一种生物数量达到环境的最大容纳量时,就不会再增加了,所以我们就认为随着人口数量的增加,增长率在减小,设最大人口容纳量为Nm,则增长率为r*(1-N/Nm),就有微分方dN/dt=r*(1-N/Nm)*N,得到方程N=Nm*N0/((Nm-N0)*exp(-r*t)+N0)
x0=[1000000,0.001];
x=lsqcurvefit('fun6',x0,t,y)
f=fun6(x,t);
y0=fun6(x,2013)
plot(t,y,'*',t,f,2013,y0,'r+')
x = 1.0e+005 *
9.9993 0.0000y0 = 1.0966e+004
三、实验小结
新乡学院
数学与信息科学系实验报告
实验名称河南省人口预测模型
所属课程数学软件与实验
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数学与计算科学学院实验报告
实验项目名称人口的控制与预测
所属课程名称数学建模
实验类型综合
实验日期2014年4月15日
班级数学1201班
学号2012641001
姓名何兴
成绩
附录1:源程序
附录2:实验报告填写说明
1.实验项目名称:要求与实验教学大纲一致。
2.实验目的:目的要明确,要抓住重点,符合实验教学大纲要求。
3.实验原理:简要说明本实验项目所涉及的理论知识。
4.实验环境:实验用的软、硬件环境。
5.实验方案(思路、步骤和方法等):这是实验报告极其重要的容。
概括整个实验过程。
对于验证性实验,要写明依据何种原理、操作方法进行实验,要写明需要经过哪几个步骤来实现其操作。
对于设计性和综合性实验,在上述容基础上还应该画出流程图、设计思路和设计方法,再配以相应的文字说明。
对于创新性实验,还应注明其创新点、特色。
6.实验过程(实验中涉及的记录、数据、分析):写明具体实验方案的具体实施步骤,包括实验过程中的记录、数据和相应的分析。
7.实验结论(结果):根据实验过程中得到的结果,做出结论。
8.实验小结:本次实验心得体会、思考和建议。
9.指导教师评语及成绩:指导教师依据学生的实际报告容,给出本次实验报告的评价。
