系统的模拟图与框图
信号与系统第三版教案第6章课件

零、极点的表示:
图1
阻抗函数的意义: H (s) U (s) 1
s
I (s) C (s s1)(s s2 )
图2
二、零极点分布与时域特性
例
h( t ) = £1[H( s )]
H (s)
1 s
s
1
0
s2
2 0
(s
0 )2
02
h(t) (t) et sin 0t et sin 0t
图3
结论:
• 极点位于S平面原点,h( t )对应为阶跃函数; • 极点位于S平面负实轴上, h( t )对应为衰减指数函数; • 共轭极点位于虚轴上, h( t )对应为正弦振荡; • 共轭极点位于S的左半平面, h( t )对应为衰减的正弦振荡; • H( s )的零点只影响h( t )的幅度和相位, H( s )的极点才决定
时域特性的变化模式。
三、H(s)与频域特性
由H(s)可以决定系统的频率特性H(j),即
H ( j) H (s) s j
二阶系统的四种频域特性:
低通函数: 高通函数: 带通函数: 带阻函数:
H
(
j )
K
s2
a bs
a
s
j
H
(
j
)
K
s2
s2 bs
a
s j
H
(
j )
K
s2
s bs
a
s
j
H
(
j )
K
a1a2 a0a3
例 导弹跟踪系统
H (s)
s3
34.5s2 119.7s 98.1 35.714s2 119.741s 98.1
N (s) D(s)
1.3系统的框图

§ 1.3 系统框图
二、时不变性
1.系统的输入和输出之间的关系不随时间而改变。
若 f(t)→yf(t) 则 f (t-t0)→yf (t-t0)
f[k]→yf[k] f[k-n]→yf[k-n]
式中,n为任意整数
f (t)
yf(t)
1
oT
t
f (t-td) 1
时不变 系统
o
t
yf(t-td)
o
td td+T
t
o
td
t
蚌埠坦克学院电子教研室
§ 1.3 系统框图
2.时不变系统的判断 根据定义:参数不随时间变化的系统;
根据描述系统的数学方程,若为常系数微分 (差分)方程,系统是时不变系统; 系统激励延迟,系统零状态响应也作同样的 延迟。
若 f(t)→yf(t) 则 f (t-t0)→yf (t-t0)
稳定系统的判断: 根据定义; 稳定性判据。第七章
蚌埠坦克学院电子教研室
§ 1.3 系统框图
例 1.6-4 试判断以下系统是否为稳定系统?
yk f k f k 1 稳定系统
y
f
t
t
0
f
( x)dx
y
f
(t
)
df t
dt
y f k k 2 f k
不稳定系统 不稳定系统 不稳定系统
蚌埠坦克学院电子教研室
蚌埠坦克学院电子教研室
§ 1.3 系统框图
变换域分析法: 将时间变量函数变换成相应变换域 的某种变量函数. 常用变换域分析法:傅里叶变换(Fபைடு நூலகம்)、拉普拉斯变 换(LT)、 z变换(ZT)
傅里叶变换以频率为独立变量,以频域特性为主要 研究对象.
2.3系统的方框图及其简化
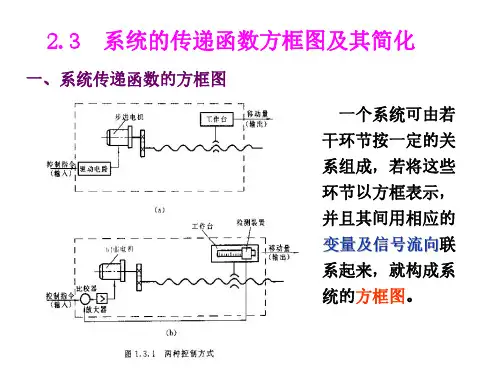
例:求系统传递函数。
Xi(s) + E(+s)
分
+
支
B(s)
点
前
移 Xi(s) + E(+s)
+
B(s)
G1 +
H2
G2
G3
H1
H2G3
G1 +
G2
G3
H1
Xo(s) Xo(s)
Xi(s) + E(+s)
+
B(s)
G1 +
H2G3 G2
H1
Xo(s) G3
Xi(s) + E(+s) G1
+
B(s)
纲也要相同。 相加点可以有多个输入,
但输出是唯一的。
C
A + A-B+C +
B
(3) 分支点
分支点表示同一信号向不同方向的传递。只传递信号, 不传递能量。
在分支点引出的信号不仅量纲相同,而且数值也相 等。
X(s) X(s) X(s)
2、系统方框图的建立步骤
(1) 建立系统(或元件)的
;
(2) 对这些原始微分方程进行
函数无量纲,而且H(s)的量纲是G(s)的量纲的倒数。
小小总结:
前述三种基本连接形式:串联、并联、反馈
G(s)
①两个环 Xi(s)
节相串联
G1(Gs) 1 ( sX)1G(s)2 (Gs)2(s)
Xo(s)
②两个环节 G(s)
相并联
G1(s) Xo1(s)
Xi(s)
G1(s)
G2
+
(s) +_
G2 (s) Xo2(s)
系统的信号流图

例3
H (z)
z2 z3+3z2
2z
,画出直接形式、
串联形式和并联形式信号流图。
解:(1)
H (z)
z3 z3+3z2
= z2 3z3 2z 1 3z1 2z2
(2)
H (z)
z3 z3+3z2
2z
z(z
z3 2)(z
1)
1 z
z z
3 2
1 z 1
z 1
1 1
3z 1 2 z 1
1
z
1 s1
1 s1
根据梅森公式分别画出 2
1 3s1
2 1 s1
的流图,并联起来
1 F(s)
1
s-1
1/2 -3
Y(s)
s-1
1/2
-1
系统的状态变量分析
例2
H
(s)
s(s
2s 3 3)(s
2)
,画出直接形式、串联
形式和并联形式信号流图。
解:(1)
H (s)
s(s
2s 3 3)(s
2)
s3
1
1
z-1
z-1
z-1
F(z)
Y(s)
-3
4
2
H(z)
z2 2
Y(z)
z3 2z2 3z 4
-3
1 s-1 s-1 1
F(s)
-2
s-1 1 Y(s)
-1
H
(s)
1
s 1
s 3 5s 2
2 s 3
系统的状态变量分析
三、系统函数计算
1.列节点方程(由加法器输出端)
2.梅森公式
H 1
k
系统模型及其分类

第
d t 2 3 d t 2r(t) d t 2
e(t )
r(t)
3
2
X
13
三.系统的分类
第
页
1.连续时间系统与离散时间系统
a.定义 连续时间系统:输入信号与输出信号都连续,
并且其内部也未转换为离散信号。 离散时间系统:输入信号与输出信号都离散。 混合系统:连续系统与离散系统组合运用
b.数学模型 连续时间系统:微分方程 离散时间系统:差分方程
X
14
第 页
2.即时系统与动态系统
a.定义 即时系统(无记忆系统): 系统的输出只由相同时刻的激励信号决 定,而与过去的工作状态无关。 动态系统(记忆系统): 系统的输出信号不仅与同时刻的激励信 号有关,还与它过去的工作状态有关。
X
15
5
第
系统模拟:
页
实际系统→方程→模拟框图 →实验室实现(模拟系统)→指导实际系统设计
例1-6-1:已知y”(t) + ay’(t)+ by(t) = f(t),画框图。 解:将方程写为 y”(t) = f(t) –ay’(t) –by(t)
y"(t) ∑
∫ y'(t)
∫
y(t)
f(t)
a b
X
6
y(t) = 4x’(t)+ 3x(t)
根据前面,逆过程,得
y”(t) + 2y’(t) + 3y(t) = 4f’(t)+ 3f(t)
X
11
练习
第
页
请用积分器画出如下微分方程所代表的系统的系统框图。
d2 r(t) dt2
系统方框图的组成及其绘制(共7张PPT)

Q2为系统的干扰量
气动阀门:执行机构
被控对象:水箱
作业
• 1-1,1-5,1-8,1-12
Байду номын сангаас
控制器:比较、放大的作用 元4、件按方信框息:流方动框的中方写向入将元各、个部环件节的用名元称件,方进框入和箭连头线表连示接其输入信号;
重系点统及 方难框点图:系由统许方多框对图信及号其〔绘量制〕进行单向传递的元件方框和一些连线组成,表示系统信息传递的框图。
浮子:液面高度的反馈元件 元引件出方 箭框头:表方示框其中输写出入信元号、. 部件的名称,进入箭头表示其输入信号;
重点及难点:系统方框图及其绘制 系统方框图:由许多对信号〔量〕进行 单向传递的元件方框和一些连线组成, 表示系统信息传递的框图。它包括三个 基本的单元,即
1.引出点〔u分支点):表u 示信号的引出 或信号的分支,箭头表示u 信号的传递方 向,线上标记信号的名称。
2. 比较点〔相加点):表示两个或以上的信号进行相加 或相减运算。“+”表示信号相加;“-”表示信号相减.
例题:
下图是一个液位控制系统原理图。在这里, 自动控制器通过比较实际液位与希望液位,并 通过调整气动阀门的开度,对误差进行修正, 从而保持液位不变。说明系统的工作原理,试 画出该控制系统的方框图。
引3、出按点照〔控分制支系点统)各:环表节示的信定号义的,引找出出或相信应号的的各分个支环,节箭头表示信号的传递方向,线上标记信号的名称。 下引图出是 箭一头个表液示位其控输制出系信统号原. 理图。 2系、统分方清框系图统:的由输许入多量对、信输号出〔量量〕进行单向传递的元件方框和一些连线组成,表示系统信息传递的框图。 系下统图方 是框一图个:液由位许控多制对系信统号原〔理量图〕。进行单向传递的元件方框和一些连线组成,表示系统信息传递的框图。 2说、明分系清统系的统工的作输原入理量,、试输画出出量该控制系统的方框图。 比它较包点 括〔三相个加基点本)的:单表元示,两即个或以上的信号进行相加或相减运算。 引出点〔分支点):表示信号的引出或信号的分支,箭头表示信号的传递方向,线上标记信号的名称。 Q2、2为分系清统系的统干的扰输量入量、输出量 下引图出是 箭一头个表液示位其控输制出系信统号原. 理图。 1元、件分方析框控:制方系框统中的写工入作元原、理部,件找的出名被称控,对进象入箭头表示其输入信号; 说明系统的工作原理,试画出该控制系统的方框图。
《现代控制理论》刘豹著(第3版)课后习题答案(最完整版)
第一章习题答案1-1 试求图1-27系统的模拟结构图,并建立其状态空间表达式。
11K s K K p +sK s K p 1+s J 11sK n 22s J K b -++-+-)(s θ)(s U 图1-27系统方块结构图解:系统的模拟结构图如下:)(s U )(s θ---+++图1-30双输入--双输出系统模拟结构图1K pK K 1pK K 1+++pK n K ⎰⎰⎰11J ⎰2J K b ⎰⎰-1x 2x 3x 4x 5x 6x系统的状态方程如下:u K K x K K x K K x X K x K x x x x J K x J x J K x J K x x J K x x x pp p p n p b1611166131534615141313322211+--=+-==++--===∙∙∙∙∙∙令y s =)(θ,则1x y =所以,系统的状态空间表达式及输出方程表达式为[]⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-----=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡∙∙∙∙∙∙654321165432111111112654321000001000000000000010010000000000010x x x x x x y uK K x x x x x x K K K K K K J K J J K J K J K x x x x x x p p pp n p b1-2有电路如图1-28所示。
以电压)(t u 为输入量,求以电感中的电流和电容上的电压作为状态变量的状态方程,和以电阻2R 上的电压作为输出量的输出方程。
R1L1R2L2CU---------Uc---------i1i2图1-28 电路图解:由图,令32211,,x u x i x i c ===,输出量22x R y =有电路原理可知:∙∙∙+==+=++3213222231111x C x x x x R x L ux x L x R 既得22213322222131111111111x R y x C x C x x L x L R x u L x L x L R x =+-=+-=+--=∙∙∙写成矢量矩阵形式为:[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡----=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡32121321222111321000*********x x x R y u L x x x CC L L R L L R x x x 。
CH10-8离散系统的方框图
k 0 N
k
1 1 ak z k
k 1 N
. bk z k
k 0
M
H1(z):只含系统的极点
H2(z) :只含系统的零点
1. 直接型结构
系统可以看成两个子系统的级联
H1 ( z ) 1 1 ak z k
k 1 N
W (z) X (z)
H 2 ( z ) bk z
x[n 1]
ax[n]
乘常数: x[n]
a
相加:
x1[n] x2 [n]
x1 [n]
x 2 [ n]
y[n] a1 y[n 1] a2 y[n 2] b0 x[n]
x[n]
b0 x[n]
b0
y[n]
z 1
a1 y[n 1]
a1
y[n 1]
z 1
a2 y[n 2]
a2
y[n 2]
用信号流图法表示LTI系统的结构
三种基本的运算:
单位延时: 乘常数:
z
1
a
相加:
y[n] a1 y[n 1] a2 y[n 2] b0 x[n]
x[n] b0
y[n]
z 1
a1
a2 y[n 2]
y[n 1]
z 1
a2
y[n 2]
2. 级联型结构
将系统函数分解为一阶因式或二阶因式相乘
的形式,即
H(z) = H1(z) H2(z) ….. Hn(z)
1
1 b1 z 一阶:A 1 1 a1 z
1 b1 z b2 z 二阶:A 1 2 1 a1 z a2 z
信号与系统参考答案(第二版)电子工程出版 徐亚宁 苏启常
第一章1.8 系统的数学模型如下,试判断其线性、时不变性和因果性。
其中()0X -为系统的初始状态。
(2)()()2f t y t e= (5)()()cos 2y t f t t = (8)()()2y t f t =解:(2)()()2f t y t e =① 线性: 设 ()()()()1122,f t y t f t y t →→,则 ()()()()122212,f t f t y t ey t e==那么 ()()()()()()()112211222221122a f t a f t a f t a f t a f t a f t y t eee +⎡⎤⎣⎦+→==,显然,()()()1122y t a y t a y t ≠+,所以系统是非线性的。
② 时不变性设()()11,f t y t →则 ()()()()10122110,f t t f ty t e y t t e-=-=设()()102,f t t y t -→则()()()102210f t t y t e y t t -==-,所以系统是时不变的。
③ 因果性因为对任意时刻 1t ,()()121f ty t e =,即输出由当前时刻的输入决定,所以系统是因果的。
(5)()()cos 2y t f t t = ① 线性: 设 ()()()()1122,f t y t f t y t →→,则 ()()()()1122cos 2,cos 2y t f t t y t f t t ==那么()()()()()()()112211221122cos 2cos 2cos 2a f t a f t y t a f t a f t t a f t t a f t t +→=+=+⎡⎤⎣⎦,显然()()()1122y t a y t a y t =+,所以系统是线性的。
② 时不变性设()()11,f t y t →则 ()()()()()1110100cos 2,cos 2y t f t t y t t f t t t t =-=--设()()102,f t t y t -→则()()()21010cos 2y t f t t t y t t =-≠-,所以系统是时变的。
数字信号处理课后习题答案
(修正:此题有错,
(3)系统的单位脉冲响应 而改变,是两个复序列信号之和)
(4)
(修正: 随上小题答案
(修正:此图错误,乘系数应该为 0.5,输出端 y(n)应该在两个延迟器 D 之间)
1-25 线性移不变离散时间系统的差分方程为
(1)求系统函数 ; (2)画出系统的一种模拟框图; (3)求使系统稳定的 A 的取值范围。 解:(1)
(2)
(3)
解:(1)
(2)
(3)
1-7 若采样信号 m(t)的采样频率 fs=1500Hz,下列信号经 m(t)采样后哪些信号不 失真? (1) (2) (3) 解:
(1)
采样不失真
(2)
采样不失真
(3)
,
采样失真
1-8 已知
,采样信号 的采样周期为 。
(1) 的截止模拟角频率 是多少?
(2)将 进行 A/D 采样后, 如何?
(3)最小阻带衰减 5-4
由分式(5.39)根据 A 计算 ,如下: 由表 5.1 根据过度带宽度 计算窗口:
单位脉冲响应如下:
单位脉冲响应如下:
其中 为凯泽窗。 5-5 答:减小窗口的长度 N,则滤波器的过度带增加,但最小阻带衰减保持不变。 5-6:图 5.30 中的滤波器包括了三类理想滤波器,包括了低通,带通和高通,其响应的单位
(1)
,
(2)
1-18 若当 时
;时
(1)
,其中
(2) 证明:
,收敛域
,其中 N 为整数。试证明: ,
(1) 令 其中
,则 ,
(2)
,
1-19 一系统的系统方程及初时条件分别如下: ,
(1)试求零输入响应 ,零状态响应 ,全响应 ; (2)画出系统的模拟框图 解: (1)零输入响应
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
6-4 系统的模拟图与框图一、 三种运算器系统模拟中应用的运算器有三种:加法器、数乘器(也称标量乘法器)和积分器。
三种运算器的表示符号及其时域、s 域中输入与输出的关系,如表6 - 3中所示。
二、 系统模拟的定义与系统的模拟图在实验室中用三种运算器:加法器、数乘器和积分器来模拟给定系统的数学模型——微分方程或系统函数H(s),称为线性系统的模拟,简称系统模拟。
经过模拟而得到的系统称为模拟系统。
从系统模拟的定义可看出,所谓系统模拟,仅是指数学意义上的模拟。
模拟的不是实际的系统,而是系统的数学模型——微分方程或系统函数H(s)。
这就是说,不管是任何实际系统,只要它们的数学模型相同,则它们的模拟系统就一样,就可以在实验室里用同一个模拟系统对系统的特性进行研究。
例如当系统参数或输入信号改变时,系统的响应如何变化,系统的工作是否稳定,系统的性能指标能否满足要求,系统的频率响应如何变化,等等。
所有这些都可用实验仪器直接进行观测,或在计算机的输出装置上直接显示出来。
模拟系统的输出信号,就是系统微分方程的解,称为模拟解。
这不仅比直接求解系统的微分方程来得简便,而且便于确定系统的最佳参数和最佳工作状态。
这正是系统模拟的重要实用意义和理论价值。
在工程实际中,三种运算器:加法器、数乘器和积分器,都是用含有运算放大器的电路来实现,这在电路基础课程中已进行了研究,不再赘述。
系统模拟一般都是用模拟计算机或数字计算机实现,也可在专用的实验设备上实现。
由加法器、数乘器和积分器连接而成的图称为系统模拟图,简称模拟图。
模拟图与系统的微分方程(或系统函数H(s))在描述系统特性方面是等价的。
三、 常用的模拟图形式常用的模拟图有四种形式:直接形式、并联形式、级联形式和混联形式。
它们都可以根据系统的微分方程或系统函数H(s)画出。
在模拟计算机中,每一个积分器都备有专用的输入初始条件的引入端,当进行模拟实验时,每一个积分器都要引入它应有的初始条件。
有了这样的理解,下面画系统模拟图时,为简明方便,先设系统的初始状态为零,即系统为零状态。
此时,模拟系统的输出信号,就只是系统的零状态响应了。
1.直接形式设系统微分方程为二阶的,即'''10()()()()y t a y t a y t f t ++= (6 - 15)为了画出其直接形式的模拟图,将式(6 - 15) 改写为'''10()()()()y t a y t a y t f t =--+根据此式即可画出时域直接形式的模拟图,如图6-18(a)所示。
可见图中有两个积分器(因为微分方程是二阶的),有两个数乘器和一个加法器。
图中各变量之间的关系,一目了然,无需赘述。
若将式(6 - 15)进行拉普拉斯变换即有210()()()()s Y s a sY s a Y s F s ++= (6- 16)或210()()()()s Y s a sY s a Y s F s =--+ (6- 17)根据此式即可画出s 域直接形式的模拟图,如图6 – 18 (b)所示。
'''()y t (F s ()Y s (a)(b)图 6 - 18将图6 – 18 (a)和 (b)对照,可看出两者的结构完全相同,仅是两者的变量表示形式不同。
图(a)中是时域变量,图(b)中则是s 域变量,而且两者完全是对应的。
所以,为简便,以后就不必要将两种图都画出了,而只需画出二者之一即可。
根据式(6 - 16)可求出系统函数为22121010()1()()1Y s s H s F s s a s a a s a s ---===++++ (6 - 18)将式(6 - 18)与图6 - 18(b)进行联系对比,不难看出,若系统函数H(s)已知,则根据H(s)直接画出s 域直接形式模拟图的方法也是一目了然的。
若系统的微分方程为如下的形式:''''''10210()()()()()()y t a y t a y t b f t b f t b f t ++=++ (6 - 19)则其系统函数 (这里取m=n=2)为2122102102121010()()()1b s b s b b b s b s Y s H s F s s a s a a s a s ----++++===++++ (6 - 20)为了画出与此微分方程或H(s)相对应的直接形式的模拟图,可引入中间变量x(t),使之满足下式,即 '''10()()()()x t a x t a x t f t ++=(6 - 21)故有'''10()()()()x t a x t a x t f t =--+ (6 - 22)与此式相对应的模拟图如图6-19(a)的下面部分所示。
将式(6 - 21)分别相继乘以012,,b b b 系数,即有'''010000()[()][()]()b x t a b x t a b x t b f t ++= (6 - 23)'''111011()[()][()]()b x t a b x t a b x t b f t ++= (6 - 24)'''212022()[()][()]()b x t a b x t a b x t b f t ++= (6 - 25)将式(6 - 24)求导一次,将式(6 - 25)求导两次,即有 '''''''111011[()][()][()]()b x t a b x t a b x t b f t ++='''''''''''212022[()][()][()]()b x t a b x t a b x t b f t ++=此两式又可写为 '''''''111011[()][()][()]()b x t a b x t a b x t b f t ++= (6 - 26)'''''''''''212022[()][()][()]()b x t a b x t a b x t b f t ++= (6 - 27)将式(6 - 23),式(6 - 26),式(6 - 27)相加并归并同类项即得'''''''''2101210[()()()][()()()]b x t b x t b x t a b x t b x t b x t ++++++''''''0210210[()()()]()()()a b x t b x t b x t b f t b f t b f t ++=++ (6 - 28)将式(6 - 28)与式(6 - 19)比较,可看出必有'''210()()()()y t b x t b x t b x t =++ (6 - 29)根据式(6 - 29)即可画出与之对应的模拟图,如图6 – 19 (a)中的上面部分所示。
这样,就得到了与式(6 - 19)相对应的完整的直接形式的模拟图,如图6 – 19 (a)所示。
与式(6 - 19)相对应的s 域直接形式的模拟图如图6 – 19 (b)所示。
此图也可根据系统函数H(s)的表示式(6 - 20)直接画出,其步骤和方法一目了然,也无需赘述。
从图6 - 19中看出,图中有两个积分器(因微分方程是二阶的)、两个加法器(因式(6 - 19)中等号左端和右端各有一个求和式)和五个数乘器。
推广 若系统的微分方程为n 阶的,且设m=n ,即1'110()()()()n n n y t a y t a y t a y t --++⋅⋅⋅++=1'110()()()()m m m m b f t b f t b f t b f t --++⋅⋅⋅++ (6 – 30a )则其系统函数为11101110()()()m m m m nn n b s b s b s b Y s H s F s s a s a s a ----++⋅⋅⋅++==++⋅⋅⋅++ (6 – 30b ) 或1(1)1101(1)110()()()1m mm m n n n b b s b s b s Y s H s F s a s a s a s ----------++⋅⋅⋅++==++⋅⋅⋅++(6 – 30c )仿照上面的结论,可以很容易地画出与上两式相对应的时域和s 域直接形式的模()f t ()y t (a)()F s ()Y s (b)图 6- 19 (a )时域,(b )s 域 拟图。
请读者自己画出。
需要指出,直接形式的模拟图,只适用于m ≤n 的情况。
因当m >n 时,就无法模拟了。
2.并联形式设系统函数仍为式(6 - 20),即2210210()b s b s b H s s a s a ++=++ (6 – 31a )将式(6 - 31a)化成真分式并将余式0()N s 展开成部分分式,即00122222101212()()()()()N s N s K K H s b b b s a s a s p s p s p s p =+=+=++++---- (6 – 31b )式中12,p p 为H(s)的单阶极点12,K K 为部分分式的待定系数,它们都是可以求得的。
根据式(6 - 31b)即可画出与之对应的并联形式的模拟图,如图6 - 20所示。
特例:若2b =0,则图中最上面的支路即断开了。
若系统函数H(s)为n 阶的,则与之对应的并联形式的模拟图,也可如法炮制。
请读者研究。
并联模拟图的特点是,各子系统之间相互独立,互不干扰和影响。
()F s ()s图 6 - 20并联模拟图也只适用于m ≤n 的情况。
3.级联形式设系统函数仍为式(6 - 20),即22102121222101212()()()()()b s b s b b s z s z s z s z H s b s a s a s p s p s p s p ++----===++---- (6 - 32)式中,12,p p 为H(s)的单阶极点;1z ,2z 为H(s)的单阶零点。
