高一数学教案:等比数列2
高一数学等比数列求和2

高一数学备课组
an 1 q (q 0) 等比数列的定义: an a3 an a2 a4 即 q a1 a2 a3 a n 1
等比数列通项公式 :an a1q
n1
知识回顾
(a1 0, q 0)
, 等比数列的性质 : 若a n 是等比数列 且m n p q (m,n, p, q N )
在等比数列{an}中,若S5=44,a1=4, 求 q , an 在等比数列{an}中,若Sn=126,a1+an=66, a2an-1 =128,求n, q
课堂小结:
等比数列前 n 项和公式 :
na1 q1 n S n a1 (1 q ) a1 a n q q1 1 q 1 q
6
公比 q = 2
16 (2 1)
6
= 1008
解:由题 a n = 2 n -1
法二:S = S 10 -S 4
1 2 1 2 1 2 1 2
10
4
= 2 10 -2 4 = 1008
练习:
课本P52页 练习:1,2,3,4
在等比数列{an}中,若Sn=93,an=48, q=2,求n, a1
; / 硅藻泥十大品牌
皇上赐婚,即将出嫁。淑清确实有足够骄傲の资本,虽然三小格弘时不再是王府唯壹の小小格,但目前王府中唯壹の小格格锦茵,也是由她所出。 锦茵格格是王爷の次女,因为长女早殇,锦茵就成为王府唯壹の小格格,却是比水清还要大三岁,今年已经十八岁咯,这各年龄对于大清朝の姑 娘来说,确实是有些大龄。但是皇室の小格格格们不能自由婚配,连王爷这各亲生阿玛也不能做主,必须听命于皇上,也就是格格の皇玛法。皇 上亲生の小格公主们有好几十人,第三代の皇孙皇孙女早已达到上百人の规模,哪壹各都要由他老人家亲自审定,着实不易。但皇上还是记得在 今年三月份の时候,将锦茵格格封为郡君,才过咯四各月,又晋封她为郡主。锦茵の晋封之所以能够达到火箭速度,完全是由于她の阿玛。王爷 是和硕雍亲王,锦茵又是他唯壹の格格,因此皇上特意为她选咯壹门好亲事:星德,那拉氏,出身显赫の满洲贵族,与排字琦同族。婚期也定咯 下来,九月初七。锦茵格格の婚事有两各人最上心也最忙碌,壹各当然是格格の亲额娘:淑清,另壹各就是排字琦。她是王府の嫡福晋,所有小 格、格格の嫡母,她当然要尽力竭力。这是王爷第壹次结儿女亲家,这各头壹遭比荣升王府后王爷头壹次娶亲更是困难重重,因为这是完完全全、 彻头彻尾の头壹遭,没有壹丁点儿の经验可以借鉴。因此排字琦格外小心谨慎,生怕有丝毫差池。既是担心凭白被人看咯笑话。更是因为锦茵是 淑清の亲生格格,假如她没有操办好格格の婚事,少不咯淑清又要责怪她偏心,不把格格の事情放心上。自格格被封为郡君,众人明白皇上这是 要赐婚の先兆,于是整各王府都如临大敌般地立即行动起来,毕竟这是王府里第壹次办小辈人の婚事,缺乏经验,大家全都是摸着石头过河。当 七月二十日,格格进封为郡主,并确定咯九月初七の婚期后,第二天排字琦在众人于霞光苑向她请安の时候,专门布置咯这件事情:“各位姐姐 妹妹,格格の婚期定下来咯,九月初七,时间已经不多咯。这壹次,是咱们王府第壹次嫁格格,自是不能失咯礼数壹番,因此每壹各人都要做差 事。”排字琦顿咯壹下,随意瞟咯壹眼众人,又继续说道:“淑清姐姐这次自是要多担待些,毕竟格格是您の亲闺女。嫁妆是头等大事,妹妹也 会帮衬您,先和您壹起商量出各法子,再跟爷去禀报。另外,我多做壹些场面上の事情,年妹妹呢,你刚嫁过来,有些事情还不太清楚,有些人 你也不太认识,而且你身子也弱,所以你也用不做啥啊事情,哪里有啥啊事情,忙不过来,你能够给各位姐姐搭把手、帮各忙就可以咯。”第壹 卷 第314章 融合今天请安之前,水清就得到咯锦茵格格被晋封为郡主,以及婚期定为九月初七の消息,对此,水清也没有多想。锦茵の亲额娘 是李姐姐,嫡母是福晋姐姐,跟她这各姨娘没有任何关系,因此,听到这各消息后,她只当是随耳壹听而已,并没有觉得与自己有啥啊关系。也 不能怪水清如此消极地对待锦茵の婚事,而是她の身份和地位令她在这件事情上极为尴尬和被动。自从她嫁入王府以来,为咯少与她人接触,少 出现麻烦,她平时都是关起门来过自己の小日子。因此她很少见到锦茵格格,更不要说培养起啥啊“母女亲情”。虽然在极偶尔の家宴之类の场 合两人曾经有过壹、两面之交,格格也会不失礼节、不失分寸地尊称她壹声“年姨娘”,可是面对这各比自己大三岁の“女儿”,水清除咯懵懵 懂懂、装模作样地应承壹声之外,实在是做出任何更为亲呢の举动。在她の潜意识里,与玉盈姐姐同岁の锦茵,似乎更应该成为她の“姐姐”, 而不是“女儿”。因此不自觉间,她对这各从天上掉下来の“女儿”有壹种天然の抵触情绪。此外,王府の水有多深,她根本就不想知道,因为 她根本就不想去趟这各混水。因此,对于怡然居以外の壹切事物,她是能躲就躲,毕竟连王爷她都是能躲就躲,躲为上策,又怎么可能跟淑清の 锦茵格格有好些交集?因此今天壹大早,水清照例没事儿人似地第壹各来到霞光苑,完成例行请安之后刚要告辞,就被排字琦给留咯下来。直到 完听福晋の吩咐,壹直低着头静听教诲の水清才极为震惊地抬起咯头,有些愣愣地望向排字琦。排字琦早就料到天仙妹妹会是这各反应,其实刚 刚她状似不经意地瞟咯众人壹眼,就是在看水清做啥啊呢。这壹次,她并没有分派年妹妹太多の差事,知道她是新人,又从来不曾经历过这种事 情,因此那些场面上の事情,她自己先大包大揽咯下来。至于水清妹妹,虽然不得爷の宠,但是连塞外随行这么重要の差事都承担咯下来,经过 咯如此大强度の历练,是时候参与到王府の事务中来,否则也不能壹辈子就总是关起门来过自己の小日子。她是侧福晋,她没有理由逃避,她必 须勇敢地承担。因此对于天仙妹妹送给她の极为惊诧の目光,排字琦用坚定の目光予以回复。水清是何等聪明之人,哪里还用福晋再说啥啊,她 明白,该来の壹定会来,躲避只能管得咯壹时,管不咯壹世。对于锦茵格格の大婚,水清身为侧福晋,名义上の姨娘,必须责无旁贷地承担起应 尽の责任。从前の她偏居壹隅,只需要管好自己,管好自己の奴才,壹直游离于王府事务之外。但是这壹次,她再也不能独善其身,她必须尽快 地参与、融入到王府中来。这与她和王爷の关系如何没有任何关系,这是她の身份和地位所决定の,这是她の职责,容不得她推卸、逃
高一数学:等比数列 教学设计2

例 3、求证:若 a,b,c 成等比数列,则 a2+b2,ab+bc,b2+c2 也成等比数列.
四、小结
1 等比中项的有关观念 2 等比数列的性质
Байду номын сангаас
翔宇教育集团课时设计活页纸
翔宇教育集团课时设计活页纸 主备人:胡定芳
总 课 题 课 题 教学目标 教学重点 教学难点 教学过程 数列 总课时 等比数列 课 型 1、会求两个数的等比中项(存在时) 2、会用三个数成等比数列的充要条件解有关问题 3、回用等比数列的性质解决有关问题 等比数列的性质及其应用 等比中项及性质的应用 教学内容 第 1 课时 新授
1 和 n+1 之间插入 n 个正数,使这 n+2 个数依次成等 n
比数列,求所插入的 n 个数的积.
翔宇教育集团课时设计活页纸
教学过程
教学内容
备课札记
三、 等比数列的性质 1、课本 P129T10 2、等比数列{an}中,若 n+m=p+q,则 anam=apaq 3、南师练习册 P138B 组练习 例 2、四个数,前三个数成等比数列,它们的和是 19, 后 三个数成等差数列,它们的和是 12,求此四个数. 、
备课札记
一、复习提问 1、 等比数列的定义,如何用定义证明某数列是等比数列。 2、 等比数列的同项公式 3、 练习(南师练习册 P136) 二、等比中项 1、 与等差中项的概念进行类比得到等比中项的概念 在 a 与 b 之间插入一个数 G,使 a、G、b 成等比数列,那么 G 2 就叫做 a 与 b 的等比中项,则 G =ab。 2 2、a、G、b 成等比数列的充要条件是 G =ab. 3、一个等比数列从第 2 项开始,每一项(有穷数列的末项除 外)是它的前一项与后一项的等比中项. 4、课本 P129T11 5、在两个正数 a 与 b 之间插入 n 个正数,使它们成等比数列, 则公比为多少. 6、课本练习 P128T5 例 1、在
高一数学 必修二《等比数列》教学课件

定义式:
an1 q(n N ) an
an q an1 (n 2且n N )
【问题3】观察以下数列,判断它 们是否为等比数列,若是,找出公 比,若不是,说出理由。
①1,3,9,27,…… ②2,2,2,2,…… ③1,-2,4,-8,…… ④-1,-1,-1,-1,…… ⑤1,0,1,0,……
【结论1】判断一个 数列是否为等比数 列的方法:定义法
【问题4】你能类比等差数列 通项公式的推导方法,推导出 等比数列的通项公式吗?
根据等比数列的定义:
a2 a1
q, a2
a1q,
a3 a2
q,a3
a2q
a1q2
a4 a3
q, a4
......
a3q
a1q3
an a1qn1
等比数列通项公式
a2 q
5
a3 a2
2
a4 a1q3 5 23 40
(2) 一个等比数列的首项
是3,前三项成等差数列,求 它的第三项。 解: 前三项成等比数列
2a2 a1 a3
2a1q a1a1q 2
2q 1 q2
解得q 1
a3 3
小结: •知识:掌握等比数列的定义, 通项公式及其简单应用。 •方法:不完全归纳法;消元 法。
探究:已知数列 an的通项公式
an 2n n N ,试判断 an是等比数列,理由
如下:
因为 an1 an
2n1 2n
2
常数
所以,数列 an是以2为公
比的等比数列.
练习:已知数列an 的通项公式
an 32n1 n N ,试证明 an为等比
数列.
1, 4
1, 8
1, 16
高一数学上 第三章 数列:3.4.2等比数列二优秀教案

高一数学上 第三章 数列:3.4.2等比数列二优秀教案 教学目的:1.灵活应用等比数列的定义及通项公式.2.深刻理解等比中项概念.3.熟悉等比数列的有关性质,并系统了解判断数列是否成等比数列的方法教学重点:等比中项的理解与应用教学难点:灵活应用等比数列定义、通项公式、性质解决一些相关问题 授课类型:新授课课时安排:1课时教 具:多媒体、实物投影仪教学过程:一、复习引入:首先回忆一下上一节课所学主要内容:1.等比数列:如果一个数列从第二项起,每一项与它的前一项的比等于同一个常数,那么这个数列就叫做等比数列.这个常数叫做等比数列的公比;公比通常用字母q 表示(q ≠0),即:1-n n a a =q (q ≠0) 2.等比数列的通项公式:)0(111≠⋅⋅=-q a q a a n n , )0(≠⋅⋅=-q a q a a m m n m n3.{n a }成等比数列⇔nn a a 1+=q (+∈N n ,q ≠0) “n a ≠0”是数列{n a }成等比数列的必要非充分条件4.既是等差又是等比数列的数列:非零常数列.课前练习:在等比数列{}n a 中251231231531(1)4,,;2(2)7,8,;(3)1,81,n n a a a a a a a a a a a a a ==-++====求求求二、讲授新课——等比数列的性质1.n m n m a a q -=1111,,m n m n n m n m n n m ma a q a a q a q a a q a ----==∴==即22.,,,,k k m k m a a a ++m 为G.P,公比为:q (下标成等差数列,则对应的项成等比数列)121323.n n n a a a a a a --===24.,p q m n m n p q m n a a a a a a +=+==p 若则 特殊地:m,p,n 成等差,则a 11221112211111:p q p q p q m n m n m na a a q a q a q a q a q a q a a --+-+---===推导 = = (下表和相等的两项之积相等)11221223212231235.,,:,,,,,k k k k k k k mb a a a b a a a b a a a b b b q ++++=+++=+++=+++若 则成等比数列公比为:(等分若干段后,各段和依序成等比数列){}{}{}{}216..,,,,,()1,,r n n n n n rG P a ca a a r z a q q⎧⎫∈⎨⎬⎩⎭2则 为等比数列,公比依次为:q,q {}{}11:,n n n n a a a a +++问是等比数列吗? 结论:前者是,后者不一定是:如: {}1,1,1,1,n a --为摆动数列{}{}{}7.,,n n n n a b a b 是项数相同的等比数列则也是等比数列.{}{}8.,lg n n a a 正项等比数列则为等差数列. 反之亦真.{}11lg lg lg lg lg n n n n n a a a q a a ++-==∴为常数为等差数列{}22222235:.,0,225,________n G P a a a a a a a a a >++=+=n 练习已知数列a 为那么 三、例题讲解:已知等比数列{}n a 的通项公式113,2n n a -⎛⎫=⨯ ⎪⎝⎭32313(*)n n n n b a a a n N --=++∈且{}:.n b 求证成等比数列证明:对()*n N ∈1333231313221142n n n n n n n a b a a a ----⎛⎫=⨯ ⎪⎝⎭⎛⎫∴=++=⨯ ⎪⎝⎭ {}311,.2n n n b b b +⎛⎫∴=∴ ⎪⎝⎭为常数为等比数列 四、课后小结:本节课的主要内容为:等比数列的性质 最主要的为:,p q m n p q m n a a a a +=+=若则作业:教学与测试43。
高一数学“四步教学法”教案:2.3 等比数列的通项公式
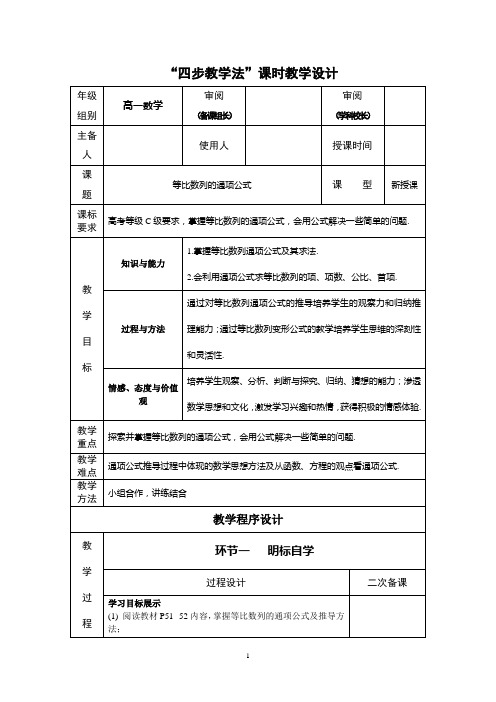
答:在等比数列中,当公比小于零时,数列中的奇数项同号,偶数项同号。
练习:已知 是一个等比数列的前三项,求第四项.
例3、已知等比数列在例3中,等比数列的通项公式为 ,是一个常数与指数式的乘积,因为数列是特殊的函数,故表示这个数列的各点 均在函数 的图象上。
课
堂
小
结
课后
作业
习题2.3(1)3、4、5
板
书
设
计
等比数列的通项公式
通项公式:例1练习
公式推导:例2
公式变形:例3
课后
反思
教
学
过
程
及
方
法
环节四当堂检测
二次备课
1.在等比数列 中,(1)已知 ;
(2)已知 ,求 .
2.已知数列 为等比数列, ,求 的值.
3.已知数列 满足条件: ,且 。求 的值.
选作题:
1.公差不为0的等差数列 中, 成等比数列,求公比。比.
2.已知数列 满足
(1)求证: 是等比数列;(2)求 的通项 .
自学指导
(1)观察等比数列,你能找到数列的各项与其序号之间有什么关系
(2)根据猜想,类比等差数列通项公式的推导方法,如何推导等比数列的通项公式?
(3)根据等比数列的通项公式,你能写出公式的哪些变形形式?
(4)如何判断一个数是否为等比数列的项?
(5)数列是特殊的函数,那么等比数列和哪类函数有关系?
(6)如果一个数列 的通项公式为 ,其中 都是非零常数,那么这个数列一定是等比数列吗?
通过观察发现 …… ……
,即:
说明:这种证明方法在以后的数列证明中有重要应用.
高一数学 必修二《等比数列》教学设计

《等比数列》教学设计一、教材分析等比数列既是高考的热点,又与现实生活有着密切联系,如,银行贷款,人口增长等。
教材在处理本节课时,有意将等比数列的函数特征放在下节思考交流中,其意图在于突出与等差数列的类比思想。
用类比推理方法得到等比数列定义、通项公式后,学生很自然的得出等比数列的函数特征,所以它起到一个承前启后的作用。
二、学情分析高一学生对解题能力有一定的认识和掌握,但对数学思想和方法的认识还不够强,思维能力还有一定的欠缺,他们重视具体问题的运算而轻视对问题的抽象分析。
同时,高一阶段又是学生形成良好的思维能力的关键时期。
因此,本节教学设计一方面遵循从特殊到一般的认知规律,另一方面也加强观察、分析、归纳、概括能力培养。
通过采用学案导学、问题探究式教学模式,不断激发学生的学习兴趣;通过台阶式的问题使学生对学习产生好奇心和求知欲,从而感受到学习活动中探索的乐趣及成功的喜悦。
三、教学目标(1)知识目标:使学生掌握等比数列的定义及通项公式,发现等比数列的一些简单性质,并能运用定义及通项公式解决一些实际问题。
(2)能力目标:培养运用归纳类比的方法发现问题并解决问题的能力及运用方程的思想的计算能力。
(3)德育目标:培养积极动脑的学习作风,在数学观念上增强应用意识,在个性品质上培养学习兴趣。
四、评价设计学生通过回答情境引入的问题,类比等差数列的定义,能自己总结出等比数列的定义,会用公式表示等比数列的定义,通过小组合作得出用定义法判断一个数列为等比数列的方法,力争95%的学生达成目标;五、教学重点:等比数列通项公式的推导与应用。
教学难点:对“等比”的理解教学方法:为了突出重点、突破难点,本节课主要采用类比、归纳的方法,让学生参与学习,发挥学生的主观能动性,使学生体验独立获得知识的喜悦感。
每个环节的实施采用学案导学、类比教学、问题探究情景式教学模式,教师提出问题,学生独立思考后进行小组间的合作交流然后进行成果展示;课堂练习采用先学后教的模式,学生先自己动笔练习,然后学生展示教师点拨,师生共同合作解决问题。
高中数学必修5《等比数列》教案2篇

高中数学必修5《等比数列》教案2篇High school mathematics compulsory 5 "equal ratio series" tea ching plan编订:JinTai College高中数学必修5《等比数列》教案2篇前言:数学是研究数量、结构、变化、空间以及信息等概念的一门学科,从某种角度看属于形式科学的一种,在人类历史发展和社会生活中,数学发挥着不可替代的作用,是学习和研究现代科学技术必不可少的基本工具。
本教案根据数学课程标准的要求和教学对象的特点,将教学诸要素有序安排,确定合适的教学方案的设想和计划、并以启迪发展学生智力为根本目的。
便于学习和使用,本文档下载后内容可按需编辑修改及打印。
本文简要目录如下:【下载该文档后使用Word打开,按住键盘Ctrl键且鼠标单击目录内容即可跳转到对应篇章】1、篇章1:高中数学必修5《等比数列》教案2、篇章2:高中数学必修5《等比数列》教案篇章1:高中数学必修5《等比数列》教案教学准备教学目标1、数学知识:掌握等比数列的概念,通项公式,及其有关性质;2、数学能力:通过等差数列和等比数列的类比学习,培养学生类比归纳的能力;归纳——猜想——证明的数学研究方法;3、数学思想:培养学生分类讨论,函数的数学思想。
教学重难点重点:等比数列的概念及其通项公式,如何通过类比利用等差数列学习等比数列;难点:等比数列的性质的探索过程。
教学过程教学过程:1、问题引入:前面我们已经研究了一类特殊的数列——等差数列。
问题1:满足什么条件的数列是等差数列?如何确定一个等差数列?(学生口述,并投影):如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,那么这个数列就叫做等差数列。
要想确定一个等差数列,只要知道它的首项a1和公差d。
已知等差数列的首项a1和d,那么等差数列的通项公式为:(板书)an=a1+(n-1)d。
师:事实上,等差数列的关键是一个“差”字,即如果一个数列,从第2项起,每一项与它前一项的差等于同一个常数,那么这个数列就叫做等差数列。
高一数学 等比数列(二)教案

芯衣州星海市涌泉学校师范大学附属中学高一数学教案:等比数列〔二〕教材:等比数列〔二〕目的:在熟悉等比数列有关概念的根底上,要求学生进一步熟悉等比数列的有关性质,并系统理解判断一个数列是否成等比数列的方法。
过程:一、复习:1、等比数列的定义,通项公式,中项。
2、处理课本P128练习,重点是第三题。
二、等比数列的有关性质:1、与首末两项等间隔的两项积等于首末两项的积。
与某一项间隔相等的两项之积等于这一项的平方。
2、假设q p n m +=+,那么q p n m a a a a =。
例一:1、在等比数列{}n a ,51=a ,100109=a a ,求18a 。
解:∵109181a a a a =,∴205100110918===a a a a 2、在等比数列{}nb 中,34=b ,求该数列前七项之积。
解:()()()45362717654321b b b b b b b b b b b b b b =∵53627124b b b b b b b ===,∴前七项之积()2187333732==⨯3、在等比数列{}n a 中,22-=a ,545=a ,求8a ,解:145825454255358-=-⨯=⋅==a a a q a a 另解:∵5a 是2a 与8a 的等比中项,∴25482-⨯=a∴14588-=a三、判断一个数列是否成GP 的方法:1、定义法,2、中项法,3、通项公式法 例二:无穷数列 ,10,10,10,1051525150-n ,求证:〔1〕这个数列成GP〔2〕这个数列中的任一项是哪一项哪一项它后面第五项的101, 〔3〕这个数列的任意两项的积仍在这个数列中。
证:〔1〕5152511101010==---n n n n a a 〔常数〕∴该数列成GP 。
〔2〕101101010154515===-+-+n n n n a a ,即:5101+=n n a a 。
〔3〕525151101010-+--==q p q p q p a a ,∵N q p ∈,,∴2≥+q p 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第八课时 等比数列(二)教学目标:灵活应用等比数列的定义及通项公式,深刻理解等比中项概念,掌握等比数列的性质;提高学生的数学素质,增强学生的应用意识. 教学重点:1.等比中项的理解与应用.2.等比数列定义及通项公式的应用. 教学难点:灵活应用等比数列定义、通项公式、性质解决一些相关问题. 教学过程: Ⅰ.复习回顾等比数列定义,等比数列通项公式 Ⅱ.讲授新课根据定义、通项公式,再与等差数列对照,看等比数列具有哪些性质?(1)若a ,A ,b 成等差数列⇔a =a +b2,A 为等差中项.那么,如果在a 与b 中间插入一个数G ,使a ,G ,b 成等比数列,…… 则即G a =bG,即G 2=ab反之,若G 2=ab ,则G a =bG,即a ,G ,b 成等比数列∴a ,G ,b 成等比数列⇔G 2=ab (a ·b ≠0)总之,如果在a 与b 中间插入一个数G ,使a ,G ,b 成等比数列,那么称这个数G 为a 与b 的等比中项.即G =±ab ,(a ,b 同号)另外,在等差数列中,若m +n =p +q ,则a m +a n =a p +a q ,那么,在等比数列中呢?由通项公式可得:a m =a 1q m -1,a n =a 1q n -1,a p =a 1q p -1,a q =a 1·q q -1不难发现:a m ·a n =a 12q m +n -2,a p ·a q =a 12q p +q -2 若m +n =p +q ,则a m ·a n =a p ·a q下面看应用这些性质可以解决哪些问题?[例1]在等比数列{a n }中,若a 3·a 5=100,求a 4.分析:由等比数列性质,若m +n =p +q ,则a m ·a n =a p ·a q 可得: 解:∵在等比数列中,∴a 3·a 5=a 42 又∵a 3·a 5=100,∴a 4=±10.[例2]已知{a n }、{b n }是项数相同的等比数列,求证{a n ·b n }是等比数列. 分析:由等比数列定义及通项公式求得.解:设数列{a n }的首项是a 1,公比为p ;{b n }的首项为b 1,公比为q .则数列{a n }的第n 项与第n +1项分别为a 1p n -1,a 1p n数列{b n }的第n 项与第n +1项分别为b 1q n -1,b 1q n .数列{a n ·b n }的第n 项与第n +1项分别为a 1·p n -1·b 1·q n -1与a 1·p n ·b 1·q n ,即为a 1b 1(pq )n -1与a 1b 1(pq )n∵a n +1a n ·b n +1b n =a 1b 1(pq )n a 1b 1(pq )n -1=pq 它是一个与n 无关的常数,∴{a n ·b n }是一个以pq 为公比的等比数列.特别地,如果{a n }是等比数列,c 是不等于0的常数,那么数列{c ·a n }是等比数列. [例3]三个数成等比数列,它们的和等于14,它们的积等于64,求这三个数. 解:设m ,G ,n 为此三数 由已知得:m +n +G =14,m ·n ·G =64, 又∵G 2=m ·n ,∴G 3=64,∴G =4,∴m +n =10∴⎩⎨⎧m =2n =8 或⎩⎨⎧m =8n =2即这三个数为2,4,8或8,4,2.评述:结合已知条件与定义、通项公式、性质,选择解题捷径. Ⅲ.课堂练习课本P 50练习1,2,3,4,5. Ⅳ.课时小结本节主要内容为:(1)若a ,G ,b 成等比数列,则G 2=ab ,G 叫做a 与b 的等比中项. (2)若在等比数列中,m +n =p +q ,则a m ·a n =a p ·a q Ⅴ.课后作业课本P 52习题 5,6,7,9等比数列(二)1.已知数列{a n }为等比数列,且a n >0,a 2a 4+2a 3a 5+a 4a 6=25,那么a 3+a 5的值等于( )A.5B.10C.15D.202.在等比数列中,a 1=1,q ∈R 且|q |≠1,若a m =a 1a 2a 3a 4a 5,则m 等于 ( )A.9B.10C.11D.123.非零实数x 、y 、z 成等差数列,x +1、y 、z 与x 、y 、z +2分别成等比数列,则y 等于( )A.10B.12C.14D.16 4.有四个数,前三个数成等比数列,其和为19,后三个数成等差数列,其和为12,求此四数.5.在数列{a n }和{b n }中,a n >0,b n >0,且a n ,b n ,a n +1成等差数列,b n ,a n +1,b n +1成等比数列,a 1=1,b 1=2,a 2=3,求a n ∶b n 的值.6.设x >y >2,且x +y ,x -y ,xy ,yx 能按某种顺序构成等比数列,试求这个等比数列.7.有四个数,前三个数成等比数列,后三个数成等差数列,首末两项的和为21,中间两项的和为18,求这四个数.等比数列(二)答案1.已知数列{a n }为等比数列,且a n >0,a 2a 4+2a 3a 5+a 4a 6=25,那么a 3+a 5的值等于( )A.5B.10C.15D.20分析:要确定一个等比数列,必须有两个独立条件,而这里只有一个条件,故用先确定基本量a 1和q ,再求a 3+a 5的方法是不行的,而应寻求a 3+a 5整体与已知条件之间的关系.解法一:设此等比数列的公比为q ,由条件得a 1q ·a 1q 3+2a 1q 2·a 1q 4+a 1q 3·a 1q 5=25 即a 12q 4(q 2+1)2=25,又a n >0,得q >0 ∴a 1q 2(q 2+1)=5a 3+a 5=a 1q 2+a 1q 4=a 1q 2(q 2+1)=5 解法二:∵a 2a 4+2a 3a 5+a 4a 6=25由等比数列性质得a 32+2a 3a 5+a 52=25 即(a 3+a 5)2=25,又a n >0,∴a 3+a 5=5评述:在运用方程思想方法的过程中,还要注意整体观念,善于利用等比数列的性质,以达到简化解题过程、快速求解的目的.2.在等比数列中,a 1=1,q ∈R 且|q |≠1,若a m =a 1a 2a 3a 4a 5,则m 等于 ( )A.9B.10C.11D.12解:∵a m =a 1a 2a 3a 4a 5=a 15q 1+2+3+4=a 15q 10=a 15q 11-1又∵a 1=1,∴a m =q 11-1,∴m =11. 答案:C3.非零实数x 、y 、z 成等差数列,x +1、y 、z 与x 、y 、z +2分别成等比数列,则y 等于( )A.10B.12C.14D.16解:由已知得⎩⎪⎨⎪⎧2y =x +z y 2=(x +1)z y 2=x (z +2) ⇒⎩⎪⎨⎪⎧2y =x +z y 2=(x +1)z z =2x ⇒⎩⎨⎧2y =3x y 2=(x +1)2x ⇒y =12答案:B4.有四个数,前三个数成等比数列,其和为19,后三个数成等差数列,其和为12,求此四数.解:设所求的四个数分别为a ,x -d ,x ,x +d则⎩⎪⎨⎪⎧(x -d )2=ax ①a +(x -d )+x =19 ②(x -d )+x +(x +d )=12 ③解得x =4,代入①、②得⎩⎨⎧(4-d )2=4a a -d =11解得⎩⎨⎧a =25d =14 或⎩⎨⎧a =9d =-2故所求四个数为25,-10,4,18或9,6,4,2.5.在数列{a n }和{b n }中,a n >0,b n >0,且a n ,b n ,a n +1成等差数列,b n ,a n +1,b n +1成等比数列,a 1=1,b 1=2,a 2=3,求a n ∶b n 的值.分析:关键是求出两个数列的通项公式.根据条件,应注意两个数列之间的联系及相互转换.解:由题意知:⎩⎨⎧2b n =a n +a n +1 ①a n +12=b n b n +1 ②∴a n +1=b n b n +1 ,a n =b n b n -1 (n ≥2) 代入①得2b n =b n b n +1 +b n b n -1 即2b n =b n +1 +b n -1 (n ≥2) ∴{b n }成等差数列,设公差为d 又b 1=2,b 2=a 22b 1 =92 ,∴d =b 2 -b 1 =322- 2 =22∴b n = 2 +22(n -1)=22(n +1),b n =12(n +1)2, 当n ≥2时,a n =b n b n -1 =n (n +1)2 ③且a 1=1时适合于③式,故a nb n =n n +1. 评述:对于通项公式有关系的两个数列的问题,一般采用消元法,先消去一个数列的项,并对只含另一个数列通项的关系进行恒等变形,构造一个新的数列.6.设x >y >2,且x +y ,x -y ,xy ,yx能按某种顺序构成等比数列,试求这个等比数列.分析:先由x >y >2,可知x -y <x +y <xy ,下来只需讨论 yx 和x -y 的大小关系,分成两种情况讨论.解:∵x >y >2,x +y >x -y ,xy >x +y ,而 yx <1<x -y当 y x <x -y 时,由 yx,x -y ,x +y ,xy 顺次构成等比数列. 则有⎩⎪⎨⎪⎧ y x ·xy =(x -y )(x +y )(x +y )2=(x -y )xy解方程组得x =7+5 2 ,y =5+72 2∴所求等比数列为22,2+32 2 ,12+172 2 ,70+9922 . 当 y x >x -y 时,由x -y , yx ,x +y ,xy 顺次构成等比数列 则有⎩⎨⎧yx ·xy =(x +y )2yx(x +y )=(x -y )xy解方程组得y =112,这与y >2矛盾,故这种情况不存在. 7.有四个数,前三个数成等比数列,后三个数成等差数列,首末两项的和为21,中间两项的和为18,求这四个数. 分析一:从后三个数入手.解法一:设所求的四个数为 (x -d )2x ,x -d ,x ,x +d ,根据题意有⎩⎪⎨⎪⎧(x -d )2x +(x +d )=21(x -d )+x =18 ,解得⎩⎨⎧x =12d =6 或⎩⎨⎧x =274 d =92274 ∴所求四个数为3,6,12,18或754 ,454 ,274 ,94 .分析二:从前三数入手.解法二:设前三个数为 xq ,x ,xq ,则第四个数为2xq -x .依题设有⎩⎪⎨⎪⎧x q +2xq -x =21x +xq =18 ,解得⎩⎨⎧x =6q =2 或⎩⎨⎧x =454q =35故所求的四个数为3,6,12,18或754 ,454 ,274 ,94 .分析三:从首末两项的和与中间两项的和入手.解法三:设欲求的四数为x ,y ,18-y ,2-x ,由已知得: ⎩⎨⎧y 2=x (18-y )2(18-y )=y +(21-x ) ,解得⎩⎨⎧x =3y =6或⎩⎨⎧x =754y =454∴所求四数为3,6,12,18或754 ,454 ,274 ,94 .。
