第二章 控制系统的数学模型习题讲解
第二章控制系统的数学模型-2007

16
y=x2
14
y=(2x)2
12
10
8
6
4
2
0 0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2
2
0
-2
0
0.5
1
1.5
1
0
-1
-100 -80 -60 -40 -20
0
20 40 60 80 100
1
0
-1
-100 -80 -60 -40 -20
0
20 40 60 80 100
2.若L[ f (t)] 1 ,求f (0), f () f (0) lim 1 0
s 3
s s 3
f () lims 1 0 s0 s 3
26
答案
3.求F(s)s2(s11),F(s)s(sa1)(sb),F(s)s(s2
1 的反变换 s1)
L1[s2(s11)]L1[1ss12
• 延迟定理 L[f(t) ]esF(s)
• 初值定理 lim f(t)lim sF (s)
t 0
s
• 终值定理 lim f(t)lim sF (s)
t
s 0
位移定理
clear clc t=0:0.1:5; y=t; f=exp(-2*t).*y; plot(t,f,'r','LineWidth',2) hold on %plot(t,y) grid on
2.1 拉普拉斯变换与反变换
1. 拉氏变换的定义 2. 拉氏变换的基本定理 3. 拉氏反变换
2.1 拉普拉斯变换与反变换
1. 拉氏变换的定义 函数f(t),t 为实变量,如果线性积分
第二章控制系统的数学模型例题全

L ddt
Ac ost
L
Asint
A 2 S2
2
另一种解法:
设xt Acost, xs A s
s2 2
x0 Acost A t0
Lddt xt sx(s) x0
Lddt Acost
s s2
s
2
A
A 2
S2 2
7已知f t cost- cos2t,求Fs。 8已知f t 2e-tsin2t,求Fs。 9已知f t te-2t ,求Fs。 10已知f t t n ,求Fs。
dt
2已知Fs
ss
4
2
, 求f
t
。
3已知Fs 1 ,求f 0、f 。
sa
3已知Fs 1 ,求f 0、f 。
sa
f 0
lims Fs s
lims s
s
1 a
1
f
lims s0
s
1 a
0
• Using the laplace transform methodes solve the differential equations
第二章控制系统的数学模型 例题
1已知f t d Acost,求Fs。
dt
2已知f t 3t 4e2t ,求Fs。
3已知f t e3tsin4t,求Fs。
t
4已知f t Acostdt,求Fs。
0
5已知f t sint ,求Fs。
6已知f t 8e-100t - 5e-200t ,求Fs。
G1
-1
- G2
N1
C
G2
C 1 G 2 G 3
N1 1 G 2 G1G 2G3
自动控制原理C作业(第二章)答案
4 3
0.1
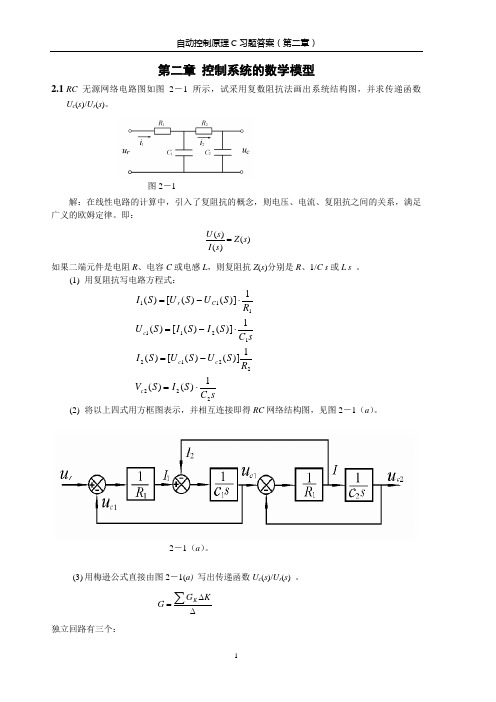
图 3-1 二阶控制系统的单位阶跃响应
解 在单位阶跃作用下响应的稳态值为 3,故此系统的增益不是 1,而是 3。系统模型为
(s)
s2
3
2 n
2n s
2 n
然后由响应的 p % 、 t p 及相应公式,即可换算出 、 n 。
p%
c(t p ) c() c()
4
3
3
33%
t p 0.1(s)
P1 G1G2
1 1
P2 G2G4
2 1
因此,传递函数为
C(s) P11 P2 2
R(s)
G2G1 G4G2 1 G1G2G3
3
自动控制原理 C 习题答案(第二章)
2.4 用梅森公式求系统传递函数。
R(S)
-
_
+ G1(s)
- _
G2(s)
+ C(S)
+
图 2-4 解: 单独回路 5 个,即
L1
1 R
1 C1S
1 R1C1S
11
1
L2
R2
C2S
R2C2 S
L3
1 C1S
1 R2
1 R2C1S
回路相互不接触的情况只有 L1 和 L2 两个回路。则
L12
L1L2
1 R1C1R2C2S 2
由上式可写出特征式为:
1
( L1
L2
L3 )
L1 L2
1
1 R1C1S
1 R2C2 S
1 R2C1S
1 R1C1R2C2S 2
益 K1 和速度反馈系数 Kt 。同时,确定在此 K1 和 Kt 数值下系统的延迟时间、上升时间和调节时间。
自动控制原理简明教程 第二章控制系统的数学模型 习题答案

互不接触回路:L1L3 G1(S )G3 (S ) 2) 系统特征式
1 G1(S) G2 (S) G3(S) G3(S)G2 (S)G1(S)H (S)
G1(S)G2 (S)G3(S) G1(S)G3(S)
3) 前向通道
P1 G1(S )G2 (S )G3 (S ) 1 1
则: (S) C(S) G1G2G3
u(S)
1 SC2
[I1(S )
I2 (S)]
I2 (S )
1 R2
[u(S ) uc (S )]
1 uc (S ) ur (S ) SC1 I2 (S )
其中 R1, R2,C1,C2 为数值恒定的网络参数,要求。
1.以 ur (t) 为输入,uc (t) 为输出,依次选取 i1(t),
1 G1 G2 G3 G1G2G3 G1G2 G1G3 G2G3 G1G2G3
P1 G1G2G3
1 1
P2 G4G5
2 1 G1 G2 G1G2
P3 G4G3 3 1 G1
则:
(S) C(S) G1G2G3 G4G5 (1 G1 G2 G1G2 ) G4G3 (1 G1)
e(t) r(t) C(t)
d (t) m(t) C(t)
1) 绘制以求传递函数 C(S) R(S) 及E(S) R(S)
解:拉氏变换:
(S 3 6S 2 2S )C(S ) D(s) (S 1)E(S) 0.05M (S) E(S) R(S) C(S) D(S) M (S) C(S)
故选A
三.已知描述某电网络动态特性的微分方程组为:
ur (t) R1i1(t) u(t)
i1 (t )
i2 (t)
C2
d dt
自动控制原理-胡寿松-第二版-答案全解参考word

第二章控制系统的数学模型习题及参考答案自动控制原理胡寿松第二版课后答案2-2 由牛顿第二运动定律,在不计重力时,可得整理得将上式拉氏变换,并注意到运动由静止开始,即初始条件全部为零,可得于是传递函数为②其上半部弹簧与阻尼器之间,取辅助点A,并设A点位移为x,方向朝下;而在其下半部工。
引出点处取为辅助点B。
则由弹簧力与阻尼力平衡的原则,从A和B两点可以分别列出如下原始方程:消去中间变量x,可得系统微分方程对上式取拉氏变换,并计及初始条件为零,得系统传递函数为③以引出点作为辅助点,根据力的平衡原则,可列出如下原始方程:移项整理得系统微分方程对上式进行拉氏变换,并注意到运动由静止开始,即则系统传递函数为2-3(b)以k1和f1之间取辅助点A,并设A点位移为x,方向朝下;根据力的平衡原则,可列出如下原始方程:所以2-6解:2-7 解:2-8 解:2-9解:2-10解:系统的结构图如下:系统的传递函数为:2-11 解:(a)(b)(c)(d)(e)(f)2-12 解:第三章线性系统的时域分析习题及参考答案自动控制原理胡寿松第二版课后答案3-1解:3-2 解:3-3 解:3-4 解:3-5 解:3-6 解:3-7 解:3-8 解:3-9 解:列劳斯表如下:系统不稳定3-10 解:(略)3-11 解:系统的特征方程为:化简得;列劳斯表如下:0<k<1.73-12 解:系统的开环传递函数为:特征方程为:列劳斯表如下:所以τ>03-13 解:(1)、(2)(3)3-14 解:(1)(2)(3)3-15 解:(1)系统的开环传递函数为:而(2)系统的开环传递函数为:而(3)系统的开环传递函数为:而同时作用下的系统误差为:第四章线性系统的根轨迹法习题及参考答案自动控制原理胡寿松第二版课后答案4-1 解:系统的开环传递函数为根轨迹如图所示4-2 解:4-3 解:(1)系统的开环传递函数为概略的根轨迹如下图所示:(2)系统的开环传递函数为根轨迹如下图所示4-4 解:(1)系统的开环传递函数为(2)系统的开环传递函数为有三个极点一个零点:(-20,j0)。
控制系统的数学模型例题和习题

= =
G2 [X
(s)[X1(s) - G6 (s)X3(s)] 2 (s) - C(s)G5 (s)]G3(s)
试绘制系统结构图,并求闭环传递函数
C(s) R(s)
。
C(s) = G4 (s)X3 (s)
解 系统结构图如图解2-11所示。 利用结构图等效化简或梅逊增益公式可求出系统的闭环传递函数为
微分方程为
Uc (s) = R2C 2s2 + 2RCs + 1 Ur (s) R2C 2s2 + 3RCs + 1
duc2 dt 2
+
3 CR
duc dt
+
1 C 2R2
uc
=
dur2 dt 2
+
2 CR
dur dt
+
1 C 2R2
ur
红河学院自动所示的力学系统(a)和电路 系统(b)是相似系统(即有相同形式的数学模 型)。 解:(a)取A、B两点分别进行受力分析,如图
解 系统的微分方程为:
d 2c(t) dt 2
3
dc(t) dt
2c(t)
2r(t)
考虑初始条件,对式(1)进行拉氏变换,得
(1)
s2C(s) s 3sC(s) 3 2C(s) 2
(2)
C(s) s2 3s 2 1 4 2 s(s2 3s 2) s s 1 s 2
s
c(t) 1 4et 2e2t
K1
红河学院自动化系
30 10 3 10 10 3
3
K2
20 10 3 10 10 3
2
自动控制原理
(2) 可画出系统结构如图解2-9所示:
K 0 K1K 2 K 3 K m
【推荐】自动控制习题-参考答案
0
0
3-19单位反馈系统的开环传递函数 ,试求:
(1)系统稳定的 值;
(2)系统所有特征根的实部均小于-1之 值;
(3)有根(-1,0)时之 值。
解:
1
16
5
0
1
9
2
0
3-21某单位反馈系统的开环传递函数 ,若系统以 的频率特性持续振荡,试确定相应的 和 值
解:
1
2
0
3-25系统如图所示,N(s)为阶跃干扰信号,哪一个系统对于消除或减少误差更好?
整理得
2-28
解一:
解二:
第三章控制系统的时域分析
3-2假设温度计可用1/(Ts+1)传递函数描述其特性。现用该温度计测量某容器中的水温,发现经1min后才能指示出实际水温的96%,问:
(1)该温度计的指示从实际水温的10%变化到90%所需的时间是多少?
(2)如果给该容器加热,使容器内水温以0.1℃/s的速度均匀上升,当定义误差 时,温度计的稳态指示误差有多大?
第一章绪论
第二章控制系统的数学模型
2-2求下列拉氏变换(假定t<0, f(t)=0)
(5)
解:
(6)
解:
(7)
解:
(8)
解:
2-4求所示信号的象函数
ห้องสมุดไป่ตู้解:
解:
2-5求图所示信号的象函数。
解:
解:
解:
解:
2-6求下列函数的拉氏反变换
(2)
解:
(5)
解:
运用性质:
(6)
(8)
解:
2-8设f(t)是以T为周期的周期函数,即f(t+T)=f(t),试证:
自动控制原理
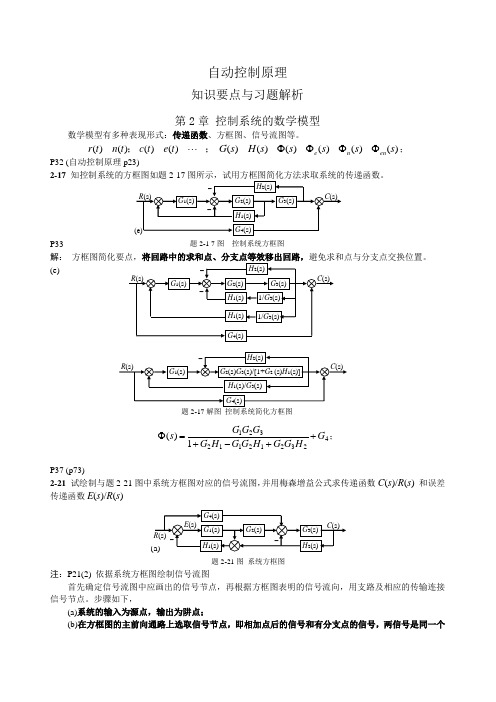
自动控制原理知识要点与习题解析第2章 控制系统的数学模型数学模型有多种表现形式:传递函数、方框图、信号流图等。
;; )()()()(t e t c t n t r )()()()()()(s s s s s H s G en n e ΦΦΦΦ; P32 (自动控制原理p23)2-17P33解:(e)4232121123211)(G H G G H G G H G G G G s ++-+=Φ;P37 (p73)2-21 试绘制与题2-21图中系统方框图对应的信号流图,并用梅森增益公式求传递函数C (s )/R (s ) 和误差传递函数E (s )/R (s )注:P21(2) 依据系统方框图绘制信号流图首先确定信号流图中应画出的信号节点,再根据方框图表明的信号流向,用支路及相应的传输连接信号节点。
步骤如下,(a)系统的输入为源点,输出为阱点;(b)在方框图的主前向通路上选取信号节点,即相加点后的信号和有分支点的信号,两信号是同一个题2-21图 系统方框图 题2-1 7图 控制系统方框图 题2-17解图 控制系统简化方框图信号时只作为一个节点;(c)其它通路上,仅反馈结构求和点后的信号选作节点; (d)最后,依据信号关系,用支路连接这些节点。
解:图(a)信号流图如题2-21解图(a)所示。
计算C (s )/R (s )和E (s )/R (s )过程中,关于回路和特征式的计算是完全相同,可统一计算。
回路111H G L -=,232H G L -=,213213H H G G G L -=;特征式 21312132123111H H G G H H G G G H G H G ++++=∆。
计算C (s )/R (s ):前向通路 3211G G G P =,342G G P =; 特征子式 11=∆,1121H G +=∆;2131223111134321)1(1)1()()(H H G G G H G H G H G G G G G G s R s C ++++++=; 计算E (s )/R (s ):前向通路 11=P ;21342H H G G P -=; 特征子式 2311H G +=∆,12=∆;213122311213423)1(11)()(H H G G G H G H G H H G G H G s R s E ++++-+=;P38 (p73)2-22 试用梅森增益公式求题2-22图中各系统信号流图的传递函数)(/)(s R s C 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
X o(s) G3 G3 = = G2 H2 Xi 2 (s) 1+ G G (G H + H2 ) 1+ G3 (G1H1 + ) 3 4 1 1 G2 1+ G2H3 G2
X o(s) G3 (1+ G2H3 ) = Xi 2 (s) 1+ G2H3 + G3H2 + G1G2G3H1
证明题图2 13中(a)与(b)表示的系统是 2-13 证明题图2-13中(a)与(b)表示的系统是 相似系统( 相似系统(即证明两个系统的传递函数具有相似 的形式)。 的形式)。
H2 Xi (s) G1
G2
A
Xo (s) G3
H1 G4
-
06-7-20
控制工程基础
11
G5 (s) H2 Xi (s) G1
G7 (s) G6 (s)
G2
A
Xo (s) G3
H1 H1 G4
1 G3
-
G2 G5G3 G2G3 G5 = G6 = = 1 + G2 H1 1 + G5G3 H 2 1 + G2 H1 + G2G3 H 2
a2 = [F (s)(s +1) ] s=−1 = −1 d 2 a1 = [F (s)(s +1) ] s=−1 = 2 ds a3 = [F (s)(s + 2)] s=−2 = −2
2
f (t ) = ( − t • e + 2 • e − 2 • e
06-7-20 控制工程基础
−t
−t
−2 t
6
π
s
06-7-20
2 5 9•e = + +2+ 2 2 s + 20 ( s + 20 ) s +9
6
控制工程基础
−
π
s
3
试求下列函数的拉氏反变换: 2-2 试求下列函数的拉氏反变换: ( 5)
s F (s) = ( s + 2 )( s + 1 ) 2
a3 s a2 a1 = + + 解:F ( s ) = 2 2 ( s + 2 )( s + 1) ( s + 1) s +1 s + 2
06-7-20 控制工程基础 18
R1
D2 K2 Xi
R2 Ui Uo C1 C2
D1
Xo K1
( a) ( b)
06-7-20
控制工程基础
19
( a) U ( s ) o
U i ( s)
=
1 R2 + sC2 1 R1 • 1 sC1 R2 + + sC2 R + 1 1 sC1
2
R1R2C1C2 s + ( R1C1 + R2C2 )s + 1 = R1R2C1C2 s 2 + ( R1C1 + R2C2 + R1C2 )s + 1
1 e − πs 1 + e − πs = F (s) = 2 + 2 s +1 s +1 s2 +1
( 4) 解:
06-7-20
f ( t ) = [ 4 cos( 2 t − f ( t ) = [ 4 cos 2 ( t −
π
3
)] • 1 ( t − )] • 1 ( t −
π
6
) + e − 5 t • 1( t ) ) + e − 5 t • 1( t )
a1 =
也可以用初值定理和终值定理: 也可以用初值定理和终值定理: 值定理
2s + 3 1 2 yo (0) = lim sYo ( s) = lim s • • = 3s + 2 s 3 s →∞ s →∞ 2s + 3 1 3 yo (∞) = lim sYo (s) = lim s • • = 3s + 2 s 2 s →0 s →0
) • 1(t )
4
4 ( 6) F ( s ) = s 2 + s + 4 8 15 • 2 15 解: F ( s ) = 1 2 15 2 (s + ) + ( ) 2 2
8 f (t ) = e 15
1 − t 2
15 sin( t) 2
= 0;
用拉氏变换法解下列微分方程: 2-3 用拉氏变换法解下列微分方程:
k1 D1 s X o (s) = F (s) k1 + D1 s
(k 2
06-7-20
k1D1s + D 2 s )[ X i ( s ) − X o ( s )] = X o (s) k1 + D1s
控制工程基础 21
X o( s ) k 2 + D2 s = X i( s ) ( k + D s ) + k1 D1 s 2 2 k 1 + D1 s
) 之间的闭环传递函数。 (2)求X o (s) 和 X i 2 (s之间的闭环传递函数。
解 : ( 1) 令 X i 2 ( s ) = 0
06-7-20
控制工程基础
14
Xi1 G1
H3
Xi 2 Xo (s)
G2
H1
-
A H2
G3
B
G5 Xi1 G1 H3
1 G3
G2
G4 Xo (s) B
H1
-
(2) f2(t) =sin t •1 t −t0) =sin[ (t −t0) +ω 0]•1 t −t0) ω ( ω t (
=[sin (t −t0)cos t0 +cos (t −t0)sin t0]•1(t −t0) ω ω ω ω
代入初始条件, 代入初始条件,得:
a3 s2 + 6s + 1 a1 a2 X (s) = = + + 2 s ( s + 6 s + 8) s s+2 s+4
1 a1 = [ X (s)s] s=0 = 7 8 a2 = [ X (s)(s + 2)] s=−2 = 47 a3 = [ X (s)(s + 4)] s=−2 = − 8 1 7 − 2t 7 − 4t x (t ) = ( + • e − • e ) • 1(t ) 8 4 8
控制工程基础
06-7-20
6
dyo (t ) dxi (t ) + 2 yo (t ) = 2 + 3xi (t ) 2-5 某系统微分方程为 3 dt dt
已知: 已知:y o ( 0 − ) = x i ( 0 − ) = 1 ,当输入为1( t ) 出的终值和初值各为多少? 出的终值和初值各为多少? 解:方程两边同时进行拉氏反变换
d 2 x (t ) dx (t ) dx ( t ) 其中: (1) dt 2 + 6 dt + 8 x(t ) = 1 其中:x ( 0 ) = 1, dt
06-7-20 控制工程基础
t=0
5
解:
2
方程两边同时进行拉氏反变换
•
1 [ s X ( s ) − sx ( 0 ) − x ( 0 )] + 6[ sX ( s ) − x ( 0 )] + 8 X ( s ) = s
2
π
6
π
6
控制工程基础
s•e 6 1 4s • e 6 1 + + F (s) = 4 • 2 = 2 s +4 s+5 s +4 s+5
−
πs
−
πs
( 5) 解:
f (t) = (15t + 4t + 6) • δ (t) +1(t − 2)
2
e −2 s F (s) = 6 + s
π
2 )] • 1 ( t −
06-7-20 控制工程基础 7
a2 = − 2 62 3 5 −3t y o (t ) = ( − e ) • 1( t ) 2 6 2 3 y o (0) = y o (∞ ) = 3 2
a2 2s + 3 2 s + 3 1 a1 Yo ( s ) = • X i (s) = • = + 2 s 3s + 2 3s + 2 s s+ 3 5 3
G1 e1
G2 − H1 H1 e2 − G4
G3
1
Xo
前向通路 回路
P = G1G2G3 1
P2 = −G4 L3 = G1G2 H1
L1 = −G2 H1 L2 = −G2G3 H 2
∆ = 1 − ( L1 + L2 + L3 ) = 1 + G2 H1 + G2G3H 2 −G1G2 H1
06-7-20 控制工程基础 13
f ( t ) = e − 20 t • ( 2 + 5 t ) • 1 ( t ) + ( 7 t + 2 ) • δ ( t ) ( 8) + [ 3 sin( 3 t −
π
6
)
−
2 d 1 3•e 解:F ( s ) = −5• ( )+ 2 + 3• 2 s + 20 ds s + 20 s +9
X o(s) D1D2 s + (k2 D1 + k1D2 )s + k1k2 = 2 X i(s) D1D2 s + (k2 D1 + k1D2 +k1D1 )s + k1k2
