第四章 三元合金相图
三元合金相图
我游览过的一个地方作文400字•相关推荐大坦克，两辆大坦克屹立在大道中间，向东走就会有一座精美的小桥，过了小桥，就是儿童乐园了，那里有碰碰车、有疯狂老鼠……我高兴地玩了疯狂老鼠和套圈，疯狂老鼠十分刺激，和我一起坐在老鼠上的妈妈吓得大叫，可我觉得非常好玩。
爸爸还给我买了10元的套圈，可惜我一个也没有套着，好失望哦！我们又到了山上，山上树的枝叶长的非常茂盛，碧绿的枝条摇晃着欢迎我们的到来。
一阵微风拂过，山上的瀑布微波粼粼，一缕淡淡的薄雾，好像一只只美丽的蝴蝶在花间飞舞。
短短的游览结束了，我的眼里流动了一丝留恋，啊！碧绿的小草让我再看看你吧！啊！雄伟的瀑布让我在和你照张相吧！啊！这美丽的濮上园让我在看看你的花草树木，让我把你记在我的心中吧！我游览过的一个地方作文400字篇2我从小到大，游览过许多地方，不过有一次游览让我终身难忘。
那就是游览丽江古城。
一天晚上，我游览着丽江古城的商店街，看见了商店街的屋子都是一层楼制作而成商店，商品真是玲琅满目。
有卖织品的，手工艺品的，乐器的……，让我目不暇接，样样都大感兴趣。
我走着走着，来到了桥上，桥的两旁是用木头造成的看起来古朴而有韵味，地上铺的红色角砾岩干净整齐，让人感觉十分舒服。
桥下的这条小溪清澈见底，冰凉刺骨，古城的人们爱把它当成天然的冰箱，把水果、饮料等用篮子装着浸在水中。
过了一会，我看见了屋子，屋子上写着平安屋，我很好奇就进了这个平安屋，进去一看天花板上挂满了风铃，风铃上写着游客们的想要说的话和心愿。
风轻轻地吹过，叮叮当当的声音清脆悦耳，余音不绝，像在进行一场美妙的风铃合奏。
我观赏完了平安屋后，来到了丽江古城的美食街那里有着各式各样的小吃，阵阵香味扑鼻而来，让我不得不去尝尝。
唉！时间一分一秒的过去了我要回宾馆了。
看着这无以媲美的美景，看着这平静如镜的河面，看着这轻如薄纱的雾，我还真有点依依不舍呢！我游览过的一个地方作文400字篇3在我的家乡——山西，有着许多的古建筑，四大佛教圣地之一五台山，蔚为壮观的黄河壶口瀑布还有风景秀丽的绵山。
三元相图
L+ A+ B
L+A+C L+A+B+C
C C B+ B+ L+ L+
C B
A+B+C
A
L+B L+ A+ B
L+A+C L+ A C L+ L
C C B+ B+ L+ L+
e1
四、变温截面图
TA A3 A2 A1 TB E1 E3 TC E C3 C2 C1 E2 B3 B2 B1
A e
e3 e2
L
L+α
α
20
4. 垂直截面
类型一：
B
C
C
A
类型二：
B
C
A
• 从变温截面图可知： • （1）合金冷却过程中相变次序； • （2）转变温度范围； • （3）不同温度下相组成。
第三节 固态互不溶解的三元共晶相图 • 液态无限互溶，固态互不溶解，并且其中 任意两个组元具有共晶转变的三元相图。
一、相图空间模型
B
C
L L+A L+B L+A+C A+B+C L+B+A
A
B
C
34
e1
A e
TA A3 A2 A1 TB E1 TC E3 C3 C2 C1 E B3 B2 B1 E2
B
e2
e3
C
L L+A L+B L+A+C L+A+B L+B+C A+B+C
三元相图
© meg/aol ‘02
3. 合金的平衡凝固过程
如图8.6所示的相图中，成分为O点的合金，在液相面以上处于液
态，当温度下降至与液相面相交于1时，开始结晶出 α，并随着温度 降低， α相增多，L相减少，当温度降至与固相面相交于2时，则液相 L全部结晶，合金呈单相α固溶体，如图8.6（b）所示。 根据以上分析，可以进一步讨论合金O的凝固过程。在凝固过程 中，如下图所示，当固相和液相的成分分别沿着ss1s2•••O和Ol1l2 •••l曲线发生变化，注意： 1)连接线一定通过合金成分点； 2）随着温度的降低，连结线以原合金成分轴线为中心旋转并平行下 移，旋转的方向是液相成分点逐渐向低熔点组元A方向偏转（这可从 二元相图可知），形成了蝴蝶形的轨迹； 3），只有在知道凝固过程中某一相的成分变化情况之后（由相律可 知），才能得出另一相的成分变化规律。
© meg/aol ‘02
8.2 固态不溶解的三元共晶相图
1. 相图的空间模型
Q G M o
b NLeabharlann ApaC
© meg/aol ‘02
© meg/aol ‘02
3)推论：位于三角形高BH上任一点的合金，其两边组元的含量相等。 4）背向规则——从任一三元合金M中不断取出某一组元B，那么合金 浓度三角形位置将沿BM的延长线背离B的方向变化，这样满足B量不断 变化减少，而A、C含量的比例不变。 C
于是，Ca，Ab，Bc线段分别代 表S相中
三组元A，B，C的各自质量分数。 反之，如已知3个组元质量分数时，
也可求出S点 在成分三角形中的位置。
确定合金某组元（如B)成分的方法： 通过合金成分点作B组元对边的平行线
与另两边中任一边相交于（如 b点），则Ab长度就是B组元的成分。 © meg/aol ‘02
三元相图
90
10 20 30 40 50 C% 60 70 80 90
60
50 40 ← A%
30 20 10
C
课堂练习
90
B 10 20 30 40 50 C% 60 70 80 90 90 80 70 60 50 40 ← A% 30 20 10 C
第 四 章
第四章 三元相图-第九节三元相图 三元相图三、三元共晶相图
（ 一） 组元在固态互不 相溶的共晶相图
组元在液态完全互溶、固 态完全不溶、具有共晶转变的 三元相图。
章 例题4.9.1
第 九 节 三 元 相 图 之 基 本 知 识
第 四 章
第四章 三元相图-第九节三 三元相图二、匀晶相图 元相图
匀晶转变：由液相直接结晶出单相固溶体的转变（相变） 匀晶转变
T （℃）
第 九 节 三 元 相 图 之 匀 晶 相 图
形成匀晶相图的条件 1.组元在液相、固相 均可完全互溶 2组元晶体结构相同、 原子尺寸、电负性相似 液相线 固相线 单相区 双相区
2）若两个平衡相的成分点已知，合金的成分点必然位 若两个平衡相的成分点已知， 于两个已知成分点的连线上。 于两个已知成分点的连线上。
第 四 章
第四章 三元相图-第九节三元相图 三元相图(4) 重心定律 在一定温度下，三元合金三相平衡时，合金的成分点为 在一定温度下，三元合金三相平衡时， 三个平衡相的成分点组成的三角形的质量重心。（ 。（由相率可 三个平衡相的成分点组成的三角形的质量重心。（由相率可 此时系统有一个自由度，温度一定时， 知，此时系统有一个自由度，温度一定时，三个平衡相的成 分是确定的。） 分是确定的。）
物理化学三元相图
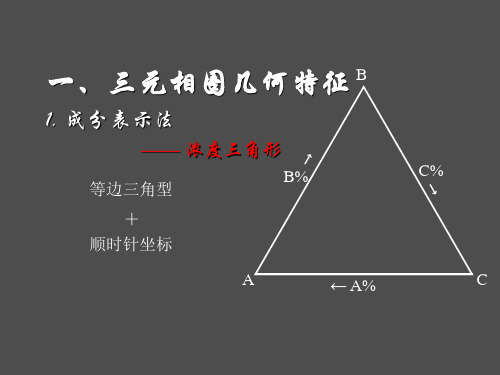
A3
A2 A1
TA E A3 A2 A1
E1
B2
B1
LA+ B
——
TB E1 B3 B2 E2 B1
A
A1 E3 E
E3
TC E C3 C2 C1
B
E2
B3
B1 E
C3 C1
C
C2 C1
L B +C
LA+ C
LA+ C
LA+ B
A
L A+B
e
B
C
L B +C
LA+ B + C
50
C%
60 70 80 90 IV 50 40 ← A% 30 20 10 C
课堂练习
90 2. 标出 75%A+10%B+15%C 80 的合金 70 60 B% 50 40 30 20 10 A 90 80 70 60
B 10 20 30 40
50
C%
60 70 80 90 50 40 ← A% 30 20 10 C
两相区 三相区 四相区 同析三角台
单相区 (1个液相区，固溶体相、、的单相区)
3个液相面以上 的区域——1个 液相区
单相区 (1个液相区，固溶体相、、的单相区)
课堂练习
90 3. 标出 50%A+20%B+30%C 80 的合金 70 60 B% 50 40 30 20 10 A 90 80 70 60
B 10 20 30 40
50
C%
60 70 80 90 50 40 ← A% 30 20 10 C
B 2. 浓度三角形中具有特定意义的直线 90 II点：20%A- 50%B- 30%C III 点：20%A- 20%B- 60%C IV 点：40%A- 0%B- 60%C 80 70 II 10 20 30
三元合金相图
• 三维空间立体图 • 多元可作伪三元处理
内容
5.1
5.2 5.3 5.4 5.5 5.6
表示方法
相平衡定量法则 三元匀晶相图 三元共晶相图 三元相图总结 三元相图举例
5.1 表示方法
一、浓度三角形
三元合金有三个组元A、B、C，需满足一个约束条件： XA+XB+XC=100% 两个组元独立可变，需用一个平面表示 ——浓度三角形。 (1)直角三角形 B xB A C A
相 图 发 展 而 来 。
e1
β e3
TC E B
e2
α
γ
A C
TA> TB >TC >e1>e2>e3>TE
相 区：
• 单相区：L、α、β、γ f=3 任意形状空间区域。 与三个两相区衔接。
α
L+α
A
α+β α+γ
双相区： L+α L+β L+γ e1 e2 α
E
L→α L→β L→γ
TA
一对成分共轭面包围的空间区域， 两平衡相的浓度在共轭面上 按蝴蝶规律变化。 f=2
Fe-13%Cr-0.2%C 合金： — 2Cr13成分点 O，在1150℃位 于γ区，为单相奥 氏体。
Fe-13%Cr-2%C 合金：
C
C1
1150℃
C2 b C3
L + γ+ C1
C
γ a
Fe
o
α
Cr
3、Fe-C-Si系垂直截 面图
• 1-2 L→γ
• 2-3 L→γ+C
L +δ
L +δ+γ
三元合金相图和凝固
2．固态有限溶解三元共晶合金的凝固过程和组织
合金IV L→α，L→α+γ，α→γ， 合金VI：L→α，L→α + γ，
L→β+α+γ α → β 同析反应
→ γ →
固态有限溶解三元共晶合金的凝固过程和 组织
2 4
3
3．
固态有限溶解三元共晶合金的等温截面
4．
固态有限溶解三元共晶合金的变温截面
三元相图
一、三元相图的成分表示法 二、杠杆定律及重心法则 三、匀晶三元相图 四、简单三元共晶相图 五、固态有限溶解的三元共晶相图 六、有包共晶反应的三元相图 七、 三元包晶相图 八、形成稳定化合物的三元相图 九、三元相图分析法总结 十、三元相图实例
必要性：工业材料为多元合金 本章主要内容： 1. 三元相图的表达方式，使用方法 2．几种基本的三元相图立体模型 3．各种等温截面，变温截面及各相区在浓 度三角形上的投影图 4．典型合金的凝固过程及组织，各种相变过程及 相平衡关系。
一、三元相图的成分表示法
1．浓度等边三角形：
三个顶点为纯组元，三条边为二元合金，三角形内任一点为三 元合金
一．三元相图的成分表示法：等腰三角形
一．三元相图的成分表示法：直角坐标系
三、匀晶Байду номын сангаас元相图
1． 立体模型 液相区，固相区，液、固两相区
匀晶三元相图---合金凝固过程及组织 a.平衡凝固 b.蝶形法则：如图
L→A+B+C， 练习：分析p-f之间合金的结晶过程
五、固态有限溶解的三元共晶相图
1． 固态有限溶解三元共晶立体模型 三个液相面，三个固溶体相面，一个三元共晶固相面 三个二元共晶完毕固相面， 三组二元共晶开始面
三元合金相图
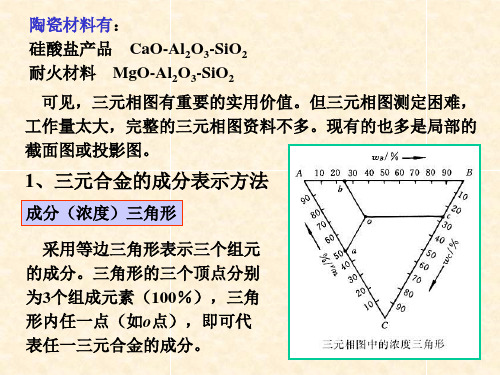
2、Fe-C-Cr三元系的水平截面
当投影图只有靠近成分三角形一个角的一部分时，可以用直 角坐标表示成分。
Fe-C-Cr系三元合金在工业上被广泛应用，如不锈钢0Cr13、 1Cr13、 2Cr13、高碳高铬模具钢Cr12等。
陶瓷材料有： 硅酸盐产品 CaO-Al2O3-SiO2 耐火材料 MgO-Al2O3-SiO2
可见，三元相图有重要的实用价值。但三元相图测定困难， 工作量太大，完整的三元相图资料不多。现有的也多是局部的 截面图或投影图。
1、三元合金的成分表示方法
成分（浓度）三角形
采用等边三角形表示三个组元 的成分。三角形的三个顶点分别 为3个组成元素（100％），三角 形内任一点（如o点），即可代 表任一三元合金的成分。
确定o点合金成分的具体方法： 通过o点分别作三角形3 个边的3 条平行线，则Ca = wA，即o点合 金中A组元的含量；同样， Ab = wB， Bc = wC。
证明：根据等边三角形的性质 Ca +Ab +Bc =AB = BC = CA=1 所以，wA+wB+wC =1=100%
例：在成分三角形ABC中确定三元合金40％A-30%B-30%C的 成分点。
对于三元合金两相平衡共存时，只有 测得其中一相的成分，才能确定另一相 得成分。
4、垂直（变温）截面图分析
为了方便通常取通过两条特殊直线的垂直截面。
垂直截面的用途
分析成分在该垂直截面上的合金在一定温度时的状态。 说明： ➢在垂直截面上不能应用杠杆定律计算相的相对量。 ➢垂直截面与水平截面图都是由实验测得的，并非由立体相图 截得。相反，三元立体相图则是由一系列的水平截面和垂直截 面作出的。
5 三元合金相图
2、等温截面 、
三相区都是直边三角形，顶点是平衡相成 分点，三个顶点与三个单相区接触； 两相区和三相区之间的分界线是直线，实 际上是两个相区分界的连接线； 两相区和单相区之间的分界线是曲线。
3、变温截面(平行于浓度三角形 边的变温截面 、变温截面 平行于浓度三角形 边的变温截面) 平行于浓度三角形AB边的变温截面
材料科学基础
武汉科技大学材料与冶金学院 吴志方 E-mail：wuzhifang@ ： Tel：63596309 ：
5 三元相图
必要性：工业材料为多元(三元或三元以 上)合金。 三元合金举例如下：轴承钢中的Fe-C-Cr 合金；高锰耐磨钢中的Fe-C-Mn合金；不 锈钢中的Fe-Cr-Ni合金；铸铁中的Fe-CSi合金；铝合金中的Al-Mg-Si合金，AlCu-Mg合金等。
五、投影图
1、全方位投影图 把空间相图的所有相区间的交线都投影到 成分三角形中。 分析合金在冷却或加热过程中的相变过程 和室温组织，并可标出组织。 匀晶相图不必要。
2、等温线投影图 、
把一系列等温截面中的相界线都投影到成 分三角形中，在每一条线上都注明相应的 温度。 可确定合金结晶开始、结束温度。 等温线反映了液相面和固相面的倾斜走向 和陡度(温度的高低)。
2、变温截面中的四相平衡 、
四相平衡区：上下都有三相区邻接。 判断转变类型：共晶(析)、包共晶(析)、 包晶(析)。四相-水平线；三上一下，共晶 (析)；二上二下，包共晶(析)；一上三下， 包晶(析)。
3、投影图中的四相平衡 、
根据12根单变量线的位置和走向来判断 四相平衡反应的类型：四相平衡平面和四 个三相区相连，每一个三相区都有三根单 变量线，四相平衡平面必然与12根单变量 线相连； 根据3根液相单变量线来判断四相平衡反 应的类型：指向结点单变量线数为产物数。
金属学与热处理5.三元合金相图(下)
相组成
A+B+C A+B+C A+B+C A+B+C A+B+C A+B+C A+B+C
组织组成
( A+B )+( A+B+C ) ( B+C )+( A+B+C )
( C+A )+( A+B+C ) A初+( A+B+C ) B初+( A+B+C ) C初+( A+B+C ) ( A+B+C ) A e
意义
三相平衡共晶开始
四相平衡共晶
TB E1 B3 B2 E2 B1
A
E3
TC
B
E
C3 C2 C1
C
48
(2)结晶过程 1） E点合金
L
L A+B+C
e1
A e
e3
TA
B
e2
C
A3 A2 A1 E1 E3 TC E C3 C2 C1 E2
TB B3 B2 B1
A+ B +C
A
B
相组成： A + B + C 组织组成： ( A + B + C )
二元相图 （二维平面图）
＋ 1维 ＋ 1维
三元相图 （三维立体图）
平面相区
线 点
立体相区
面 线
9
＋ 1维 ＋ 1维
结晶过程
L t1
L→
B
t2
C
A
10
三元相图
计算方法同杠杆定律。
W Rd w % 100% WR ad W Re w % 100% WR e W Rf A w % 100% WR f
B%
C%
f
R d
e
← A% C
4. 其它浓度三角形
1） 等腰浓度三角形
组元B的含量很少 成分点靠近AC边
B
按比例放大AB、BC边
三、 三元共晶相图
共晶转变：
一个液相 ，同时结晶出两个（或三个）固相 —— 共同结晶
共晶线：
M-E-N
T（℃） TA
L
L＋
M 183℃ E
液相线：
线：
TA——E——TS
L＋
N
TS
固相线：
TA—M—E—N—TS
＋
F Pb G Sn
固溶度曲线：
MF、NG
共晶点：
点：
E
最大溶解度点：
M、N
II点： A%=20% B%=50% C%=30% 70 60 B% 50 40 30 20 10 A 90 80 70 60 90 80
B 10 20 30 40 II C% 60 70 80 90 50 40 ← A% 30 20 10 C
50
课堂练习
1. 确定合金I、II、 III、IV的成分
3. 等温截面及其投影
B
C
A
B
L+
C
L
A
L+
相区变化方向 L
随着等温温度的降低， 液相线投影向液相区移 动，即液相区缩小；固 相区增大，两相区向液 相区一方移动
匀晶三元系的等温截面
三元合金相图ppt
选取具有代表性的三元合金试样，进行化学成分分析。
根据实验数据，确定三元合金中各相的化学成分、晶体结构、物理性质等。
数据处理与分析
比较不同三元合金之间的性能差异，为实际应用提供参考。
分析各成分的含量对三元合金相变温度、力学性能、物理性能等的影响。
为研究其他多元合金相图提供了方法和思路，推动了材料科学的发展。
丰富了材料科学研究领域的基础理论，为后续研究提供了参考。
研究不足与展望
由于实验条件和时间的限制，本研究仅针对部分三元合金进行了研究，未来可以进一步拓展三元合金相图的研究范围。
在研究过程中，虽然采用了先进的检测和分析手段，但仍有可能存在误差和不足之处，敬请批评指正。
例如，三元合金相图的测定和计算模型不够精确，缺乏足够的实验数据支持等等。
01
02
03
发展趋势与展望
发展三元合金相图的实验和计算技术，提高相图的精确性和可靠性。
利用三元合金相图优化设计和制备高性能材料，发展新型功能材料和能源材料。
针对三元合金相图的复杂性，开展多尺度模拟和智能化预测研究。
加强国内外学术交流和合作，推动三元合金相图研究领域的快速发展。
三元合金相图可以提供合金在不同环境条件下的稳定性信息，有助于我们评估材料的可靠性。
评估材料的力学性能
材料的可靠性评估
金属材料的性能预测与评估
05
三元合金相图的发展趋势
研究现状及问题
三元合金相图在材料科学、能源、电子等领域具有广泛应用前景。
目前，国内外研究者已经开展了很多关于三元合金相图的研究，但仍然存在很多问题需要解决。
06
结论
Байду номын сангаас
三元相图
三元相图工业上所使用的金属材料，如各种合金钢和有色合金，大多由两种以上的组元构成，这些材料的组织，性能和相应的加工，处理工艺等通常不同于二元合金，因为在二元合金中加入第三组元后，会改变原合金组元间的溶解度，甚至会出现新的相变,产生新的组成相。
目录1释义2正文3表示方法4特定意义图5-101oa+ob+oc=AB=BC=CA由于oa=bC=WAob=Ac=WBoc=Ba=WC因此,可用oa代表A组元的含量,ob代表B组元的含量,oc代表C组元的含量.直角成分坐标表示法当三元系成分以某一组元为主,其他两个组元含量很少时,合金成分点将靠近等边三角形某一顶点.若采用直角坐标表示成分,则可使该部分相图更为清楚的表示出来,一般用坐标原点代表高含量组元,而两个互相垂直的坐标轴代表其他两个组元的成分。
等腰成分三角形当三元系中某一组元含量较少,而另两组元含量较大时,合金成分点将靠近等边成分三角形的某一边.为了使该部分相图清晰的表示出来,常采用等腰三角形,即将两腰的刻度放大,而底边的刻度不变.如图5-103所示.对于O点成分的合金,其成分的确定方法与前述等边三角形的确定方法相同,即过O点分别引两腰的平行线与AC边相交于a和c 点,则:Ca=WA=30%Ac=WC=60%Ab=WB=10%.虽然,上述成分表示方法在三元相图中都有应用,但应用最为广泛的还是等边三角形.4特定意义等边成分三角形中特定意义的线平行于三角形某一边的直线凡成分位于该线上的所有合金,它们所含的由这条边对应顶点所代表的组元的含量为一定值。
通过三角形顶点的任一直线凡成分位于该直线上的所有合金，它们所含的由另两个顶点所代表的两组元的含量之比为一定值。
定量法则应用相律f=c-p+1当三元系时f=4-p故当两相平衡共存时,有f=4-2=2即两个平衡相的成分只有一个独立改变,当一个平衡相的成分发生变化时,另一相的成分随之而改变,即两相的成分之间具有一定的关系,此关系称为直线法则.①直线法则和杠杆定律直线法则:三元合金中两相平衡时,合金的成分点和两个平衡相的成分点,必须在同一直线上.如图5-105所示,当合金O在某一温度处于α+β两相平衡时,这两个相的成分点便定为a和b,则aob三点必位于同一条直线上，且o点位于a，b两点之间，此时α，β两相的质量比为:由直线法则可得到以下规律:a：当温度一定时，若已知两平衡相的成分,则合金的成分必位于两平衡相成分的连线上；b：当温度一定时，若已知一相的成分及合金的成分，则另一平衡相的成分必位于两已知成分点的连线的延长线上；c：当温度变化时，两平衡相的成分变化时，其连线一定绕合金的成分点而转动；1 相图分析a,b,c为三组元A,B,C的熔点,且Tb>Ta>Tc.液相面：abc黄色面；固相面：abc蓝色面；液相区L：abc黄色面以上空间；固相区α：abc蓝色面以下空间；液固两相共存区L+α:abc黄色面和蓝色面之间区域。
三元合金相图
三元合金相图1、三元合金相图三元系相图简介相图基本学问三元相图的主要特点——立体图形，主要由曲面构成三元系相图简介垂直轴表示温度。
成分表示在棱柱底，通常是一等边三角形。
棱柱的每个侧面表示三个二元系统，如AB，BC，AC。
三元系相图简介相律：f=C-P+1=3-P+1=4-PP1234f3210完好的三元相图是三维的。
在三元系统中可能存在四相平衡。
在三元系统中存在三相平衡区域。
〔1〕是立体图形，主要由曲面构成；〔2〕可发生四相平衡转变；〔3〕单、两、三相区均占有肯定空间，是变温转变，四相区为恒温水平面。
第一节三元合金相图的表示方法一、成分三角形三角形中特别的点和线〔1〕三个顶点：代表三个纯组元〔2〕三个边：二元系合金〔3〕三个边2、上的点：二元系合金的成分点三角形内任意一点都代表一个三元合金。
第一节三元合金相图的表示方法1〕过O作A角对边的平行线↗2〕求平行线与A 坐标的截距B%C%↘得组元A的含量3〕同理求组元B、C的含量O←A%C第一节三元合金相图的表示方法CBAOa+Ob+Oc=AB=AC=BC=100%A浓度:Oa=Of=CbA浓度:55%B浓度:Ob=Od=AcB浓度:20%C浓度:Oc=BaC浓度:25%?确定合金的成分9010点：IA%=60%8020B%=30%30C%=10%70II点：↗6040A%=20%IIC%B%=50%B%5050↘C%=30%4060III点：I3070A%=40%2080B%=0%C%=60%3、1090III908070605040302021←A%9010?标出802075%A+10%B+15%C30的合金70↗6040C%B%5050↘4060307020801090908070605040302021←A%9010?标出802050%A+20%B+30%C的合金7030↗6040C%B%5050↘4060307020801090908070605040302021←A%第一节三元合金相图的表示方法二、在成分三角形中具有特定意义的直线成分三角形中特别的点和线〔1〕平行于某条边的直线：↗凡成分位于该线上的材料，C%B%↘其合金所含由此边对应顶点所代表的组元的含量相等。
材料科学基础.第四章
(1)平衡凝固溶质分布 冷却时固相的溶质分布
这种情况下,冷速极其缓慢， 固体、液体中溶质原子充
分扩散。凝固结束时，各部分成分都为Co，无偏析产生，如图
中的Co水平线。
（2）实际凝固（正常凝固）溶质分布 溶质分布及表达式见图。 ①液体中溶质完全混合--偏析严重,左端纯化； ②液体中溶质完全不混合—比较符合实际凝固； ③液体中溶质部分混合。
f=c-p+1(←f=c-p+2，温度、压力) 自由度数是指在木改变系统平衡相的数目的条件厂，可独立改变
的，不影响（影响/决定体系状态）合金状态的因素(如温度、压 力、平衡相成分)的数目。
自由度数的最小值为零，f =0时发生恒温转变，例如纯金属结 晶、二元合金的三相平衡转变、三元合金的四相平衡转变等。
1
4( 3
h2 hk k 2 a2
)(
l c
)2
六方系
对复杂点阵(体心立方，面心立方等)，要考虑晶面层数的增加。 体心立方(001)面之间还有一同类的晶面（002），因此间距减半。
1.2.4 晶体的极射赤面投影
通过投影图可将立体图表现于平面上。晶体投影方法很多， 包括球面投影和极射赤面投影。
不平衡凝固的冷速越快，平均成分线的偏离越大。合金内部成分
不均匀现象称为偏析，晶粒内部成分不均匀称为“晶内偏析”， 树
枝晶内的偏析称为“枝晶偏析”。生产中用扩散退火(均匀化退 火)
4.固溶体合金凝固时的溶质量分布 合金凝固时的溶质重新分布，导致宏观偏析和微观偏析并对 晶体的生长形态产生很大影响。 匀晶合金冷却时，固相浓度CS与液相浓度CL的比值K0= CS/CL, 称为平衡分配系数,如图示。 讨论图4.7水平放置的圆 棒容器中，合金液体的定
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
边对应顶点所代表的组元的含量为一定值。
平行于AC的直线上的 P与Q合金所含B组元的 数量相等（b%B），但 是，它们所含A与C组元 的数量不同。
含B组元相等的直线
7
（二）通过三角形顶点的任一直线 凡成分位于该直线上的三元合金，其所含的、由
13
成分为R点的合 金分解为、、 三相。
d点相当于、两相混 合物的成分点，当计算出 相含量后，、两相的 含量也可以利用 — 作 杠杆进行计算。
三元相图的重心法则
% = Rd/d100% % = d/(1-%) = d/R/d100% % = d/(1-%) = d/R/d100%
14
第三节 三元匀晶相图
5
（2）直角成分三角形
当三元系成分以某一组 元为主、其它两个组元成 分很少时，合金成分点将 靠近等边三角形某一顶角 。若采用直角坐标表示成 分，则可使该部分相图清 楚地表示出来。
例如，左图中的P点是 成 分 为 wMn=0.8% ， wSi=0.6% ， 余 量 为 Fe 的 合金。
6
二、在成分三角形中具有特定意义的直线
二元共晶线： E1E、E2E、E3E
31
三相平衡区和两相共晶面
32
三元共晶相图的三相区是以三条单变量线作为棱边的 空间三棱柱体。在水平截面上三相区一定是直边三角形， 三个顶点是三个平衡相的成分。每个三角形内是该温度下 的三相平衡区。
33
三元共晶点：E 四相平衡转变：
（三元共晶转变） 四相区：△A1B1C1
变温截面与二元匀晶相图的区别
两者成分坐标的含义不同。 变温截面两相区的形状与二元匀晶相图的不同。 当变温截面中的纵坐标不是纯组元时，液相线与固 相线不闭合。 变温截面中的液相线和固相线不代表相图中合金 的液相和固相的平衡成分随温度变化的轨迹，不能 根据液相线和固相线应用直线法则和杠杆定律计算 相的含量。
第四章 三元合金相图
第一节 三元合金相图的表示方法
一、成分三角形（ 浓度三角形）
在三元相图中，通常采 用等边三角形表示成分， 这种三角形通常称为成分 三角形（或浓度三角形）。
图中O合金所含A、B、 C三个组元的浓度分别为 a%A、b%B、c%C。
2
等边三角形的三个顶点，分别表示A、B、C三 个纯组元。 等边三角形的三条边AB、BC、CA，分别表示 A-B、B-C、C-A简单二元合金的浓度坐标。凡是 位于三角形边上的合金，都是二元合金。 位于等边三角形内任意一点的合金，都是三元 合金。
% = P/100% % = P/100%
11
规律：
当给定合金在一定温度下处于两相平衡状态时， 若其中一相的成分给定，则根据直线法则，另一相 的成分点必定位于两个已知成分点的延长线上。 若两个平衡相的成分点已知，合金的成分点必然 位于两个已知成分点的连线上。
12
二、重心法则
成分为R点的合 金分解为、、 三相。
直线法则（共线法则）：三 元合金在两相平衡时，合金 的成分点和两个平衡相的成 分点必定在同一条直线上。
三元相图的两相区中两平 衡相成分点的连线称为共轭 线。
10
成分为P点的 合金分解为、 两相。
设相和相的成分点分别 为和，根据直线法则，、 P、三点必在同一直线上。 然后应用杠杆定律计算平衡 两相的相对量。
27
五、投影图
液相面投影图
固相面投影图
匀晶相图投影图
28
第四节 三元共晶相图
一、组元在固态完全不溶的共晶相图 （一）相图分析
三组元在液态能 无限互溶，在固态几 乎完全互不溶解，并 且其中任两个组元具 有共晶转变，形成简 单的三元共晶相图。
29
组元在固态完全不互溶的三元共晶相图 30
三个液相面： tAE1EE3tA：L A tBE1EE2tB： L B tCE2EE3tC： L C
律
三元固溶体在结晶过程中液、固相成分的变化
21
三、等温截面（水平截面）
B A
C
22
三元匀晶相图的等温截面
合金O在t1温度下固相和液相L的含量分别为：
w= nO/mn100%
wL= mO/mn100%
23
四、变温截面（垂直截面）
类型一：
L
L+
B
C
D
D
C
A
24
类型二：
L
L+
B
E
F
E C
F
A
25
26
另两个顶点所代表的两组元的量之比是恒定的。
A%/C%=常数的直线
BD线上的合金E与F， 分别含A、C两个组元 的浓度比值保持不变，
即
(A%/C%)E= Ba1/Bc1
=Ba2/Bc2=(A%/C%)F
=(A%/C%)D=CD/AD
=常数
8
9
第二节 三元系平衡相的定量法则
一、直线法则和杠杆定律
成分为P点的 合金分解为、 两相。
三元相图的成分的平衡相、 和时，合金成分点R必定 位于△的重心（三相的 质量重心，不是三角形的 几何重心）位置上。、 和三个相的质量分数可以 按以下公式进行计算：
%=Rd/d100%；%=Re/e100%；%=Rf/f100% 这就是三元系的重心法则（重心定律）。
3
实际三元相图的成分三角形有时会标上网格。一 般均沿顺时针（有时也沿逆时针）一个方向标注组 元的浓度。
有网格的成分三角形
4
其它的成分三角形
（1）等腰成分三角形
等腰成分三角形
当三元系中某一组元含量 较少，而另两个组元含量较 多时，合金成分点将靠近等 边三角形的某一边。可将成 分三角形两腰放大，成为等 腰三角形。左图中，由于成 分点O靠近底边，所以在实 际应用中只取等腰梯形部分 即可。
34
相区
35
单相区：一个 L
双相区：三个 L + A、L + B、L + C
三相区：四个 L + A + B、L + B +C、 L + A + C、A + B + C
四相区：一个 L+A+B+C
36
（二）投影图及合金的结晶过程
A
E3
E1
B
E
E2
C 三元共晶相图的投影图
一、相图分析
三个组元在液态 及固态均无限溶解 的相图称为三元匀 晶相图。
15
B
C
A
16
液相面
L
固相面
单相区：
L、
B
双相区：
L＋
L+ C
A
17
三元匀晶相图的空间模型
18
二、三元固溶体合金的结晶过程
L
t1
L→ B
t2
t1
t2
C
A
19
三元匀晶相图及合金的凝固
20
固
溶
体
合
金
结
晶
过
程
的
蝴
蝶
形
规