双曲线标准方程的推导
双曲线的推导过程

双曲线的推导过程双曲线是一种重要的数学曲线,它的形状类似于两个相交的直线。
在数学中,双曲线是由两个相交的直线沿着它们的渐近线旋转而形成的。
在本文中,我们将介绍双曲线的推导过程。
我们来看一下双曲线的定义。
双曲线是由以下方程定义的:x^2/a^2 - y^2/b^2 = 1其中,a和b是常数,且a>b。
这个方程描述了一个横轴为x,纵轴为y的平面上的曲线。
这个方程的图像看起来像两个相交的直线,但它们并不相交,而是在无限远处相交。
接下来,我们来推导一下双曲线的方程。
我们从一个标准的双曲线开始,它的方程是:x^2/a^2 - y^2/b^2 = 1我们将这个方程变形为:y^2/b^2 = x^2/a^2 - 1然后,我们将两边都乘以b^2,得到:y^2 = b^2(x^2/a^2 - 1)接下来,我们将x^2/a^2 - 1写成(x/a + 1)(x/a - 1),得到:y^2 = b^2(x/a + 1)(x/a - 1)我们可以将这个方程进一步简化,得到:y^2/a^2 - x^2/b^2 = -1这就是双曲线的标准方程。
我们可以看到,这个方程与最初的方程非常相似,只是x和y的系数被交换了。
我们来看一下双曲线的性质。
双曲线有两条渐近线,它们分别是y = bx/a和y = -bx/a。
双曲线的中心位于原点,它的焦点位于x = a 和x = -a处。
双曲线还有一个重要的性质,就是它的离心率为c/a,其中c是焦点到中心的距离。
双曲线是一种重要的数学曲线,它的推导过程相对简单,但它的性质却非常丰富。
通过学习双曲线,我们可以更好地理解数学中的曲线和几何形状。
双曲线方程abc关系公式推导

双曲线方程abc关系公式推导双曲线的标准方程为$\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1$,其中$a$和$b$分别是双曲线的横轴和纵轴的半轴长度。
要推导$a$、$b$和$c$之间的关系公式,我们首先需要了解双曲线的几何定义:1. 双曲线的焦点:设焦点为$F_1(-c,0)$和$F_2(c,0)$,其中$c$是双曲线的焦距。
2. 双曲线的顶点:设顶点为$V(0,0)$,也就是双曲线的两个分支的交点所在的位置。
根据几何定义,可以得到以下关系:1. 双曲线的半焦距:$ae=c$,其中$e$是双曲线的离心率。
2. 双曲线的焦点到顶点的距离:$VF_1 = VF_2 = c$。
3. 双曲线的直线渐近线方程:$y = \pm \frac{b}{a}x$。
下面我们来推导$a$、$b$和$c$之间的关系公式:首先,根据双曲线的半焦距定义,我们可以解出$c =\frac{ae}{2}$。
然后,根据双曲线的顶点和焦点的距离定义,容易发现焦点到原点的距离是$VF_1 - 0 = c - 0 = c$。
利用勾股定理,我们可以求出焦点到原点的距离:$$\sqrt{c^2} = \sqrt{(\frac{ae}{2})^2} = \frac{ae}{2} $$由此可得,$$c = \frac{ae}{2}$$将$c = \frac{ae}{2}$代入双曲线方程,得到:$$\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1$$于是,我们得到了$a$、$b$和$c$之间的关系公式:$$c = \frac{ae}{2}$$。
双曲线标准方程的推导过程

双曲线标准方程的推导过程双曲线是一种二次曲线,与椭圆和抛物线类似,具有一些特殊的性质和形态。
双曲线的标准方程是一个关于x和y的方程,其推导过程较为复杂,需要从基本定义开始逐步推导。
首先介绍一下双曲线的定义:设点F_1(-c,0)和F_2(c,0)是平面上固定的两个点,点P(x,y)是平面上动态的点。
双曲线是满足PF_1 - PF_2 = 2a (a>0)的动点P所构成的图形。
根据定义推导双曲线的标准方程:1.根据两点之间的距离公式,可以得到PF_1和PF_2的距离公式:PF_1² = (x + c)² + y²PF_2² = (x - c)² + y²2.根据定义中的等式PF_1 - PF_2 = 2a,可以得到:(x + c)² + y² - (x - c)² - y² = 4a²化简后可得:4cx = 4a²化简后可得:x = a²/c3.将x = a²/c代入PF_1² = (x + c)² + y²中,得到:(a²/c + c)² + y² = PF_1²化简后可得:(a² + c²) / c² + y² = PF_1² / c²4.根据双曲线的性质PF_1² - PF_2² = 4a²,可以得到:PF_1² - PF_2² = 4a²(a² + c²) / c² - [(a² - c²) / c² + y²] = 4a² / c²化简后可得:2c² / c² - y² / c² = 4a² / c²化简后可得:2 - y² / c² = 4a² / c²化简后可得:y² / c² - 2 = 4a² / c²化简后可得:y² / c² - 4a² / c² = 2通过上述推导过程,我们得到了双曲线的标准方程:y² / c² - x² / a² = 1其中,c是双曲线的焦点到中心的距离,a是双曲线的半轴长度。
双曲线标准方程的推导
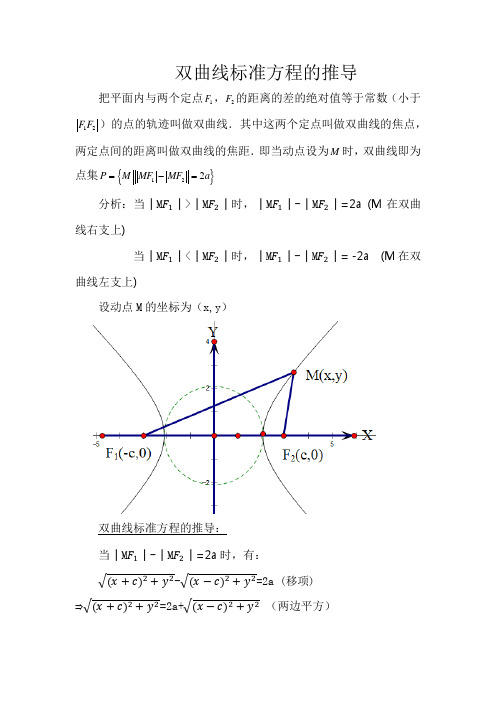
双曲线标准方程的推导把平面内与两个定点1F ,2F 的距离的差的绝对值等于常数(小于12F F )的点的轨迹叫做双曲线.其中这两个定点叫做双曲线的焦点,两定点间的距离叫做双曲线的焦距.即当动点设为M 时,双曲线即为点集P ={}122M MF MF a -=分析:当│M │>│M │时,│M │-│M │=2a (M 在双曲线右支上)当│M │<│M │时,│M │-│M │= -2a (M 在双曲线左支上)设动点M 的坐标为(x,y )双曲线标准方程的推导:当│M │-│M │=2a 时,有:- =2a (移项)⇒ =2a+ (两边平方)⇒=4+4a+(展开)⇒+2cx+=4+4a+-2cx+(移项)⇒+2cx+2cx +-=4+4a(合并同类项)⇒4cx=4+4a(两边除以4)⇒cx=+a(移项)⇒cx-(两边平方)⇒-2+=[(展开)⇒-2+=[-2++(展开)⇒-2+=-2++(移项)⇒-2+---(合并同类项)⇒---(按x,y顺序提取公因式)⇒(---)(=+,等量代替)-(两边除以)⇒-=1(a>0,b>0)当│M│-│M│=-2a时,有:-=-2a (移项)⇒=-2a+(两边平方)⇒=4-4a+(展开)⇒+2cx+=4-4a+-2cx+(移项)⇒+2cx+2cx +-=4-4a(合并同类项)⇒4cx=4-4a(两边除以4)⇒cx=-a(移项)⇒cx-(两边平方)⇒-2+=[(展开)⇒-2+=[-2++(展开)⇒-2+=-2++(移项)⇒-2+---(合并同类项)⇒---(按x,y顺序提取公因式)⇒(---)(=+,等量代替)-(两边除以)⇒-=1(a>0,b>0)通过以上推导可知,一个方程-=1(a>0,b>0)涵盖了动点M左右两支运动轨迹,而不是一支运动轨迹。
故称其为“双曲线标准方程”。
圆锥曲线(抛物线、椭圆、双曲线)标准方程推导

圆锥曲线(抛物线、椭圆、双曲线)标准方程推导几何定义是在平面中,由所有满足到一定点与到一定直线距离相等的点所组成的图形,把这个定点称为焦点(focus)、定直线称为准线(directrix)。
为了方便推导,把这一定点放在x轴正方向上,定直线垂直x 轴放在x轴负半轴上,且原点刚好在两者中间。
上面这些都仅仅是为了推导方便而已。
设曲线上的点坐标为(x,y),于是,\begin{aligned} d(F, P) &=d(P, D) \\ \sqrt{(x-a)^{2}+(y-0)^{2}} &=|x+a| \\ (x-a)^{2}+y^{2}&=(x+a)^{2} \\ x^{2}-2 a x+a^{2}+y^{2} &=x^{2}+2 ax+a^{2} \\ y^{2} &=4 a x \end{aligned}四种不同开口的标准型:二、椭圆(Ellipse)几何意义是在平面中,由所有到两个顶点距离之和为定值的点所组成的图形,把这两个定点称为焦点(foci),也是为了推导的方便,把这两个焦点对称放在x轴正负半轴上,令两段距离之和为2a,根据两点之间距离公式进行如下推导:\begin{aligned} d\left(F_{1}, P\right)+d\left(F_{2}, P\right) &=2 a \\ \sqrt{(x+c)^{2}+y^{2}}+\sqrt{(x-c)^{2}+y^{2}} &=2 a \\ \sqrt{(x+c)^{2}+y^{2}}=& 2 a-\sqrt{(x-c)^{2}+y^{2}} \\ (x+c)^{2}+y^{2}=& 4 a^{2}-4 a \sqrt{(x-c)^{2}+y^{2}} \\ &+(x-c)^{2}+y^{2} \\x^{2}+2 c x+c^{2}+y^{2}=& 4 a^{2}-4 a \sqrt{(x-c)^{2}+y^{2}} \\ &+x^{2}-2 c x+c^{2}+y^{2} \\ 4 c x-4 a^{2}=&-4 a \sqrt{(x-c)^{2}+y^{2}} \\ c x-a^{2}=&-a\sqrt{(x-c)^{2}+y^{2}} \\ \left(c x-a^{2}\right)^{2}=& a^{2}\left[(x-c)^{2}+y^{2}\right] \\ c^{2} x^{2}-2a^{2} c x+a^{4}=& a^{2}\left(x^{2}-2 cx+c^{2}+y^{2}\right) \\ \left(c^{2}-a^{2}\right)x^{2}-a^{2} y^{2} &=a^{2} c^{2}-a^{4} \\ \left(a^{2}-c^{2}\right) x^{2}+a^{2} y^{2} &=a^{2}\left(a^{2}-c^{2}\right) \end{aligned}令 b^2=a^2-c^2 (根据三角形两边之和大于第三边推出c<a)所以,\begin{aligned} b^{2} x^{2}+a^{2} y^{2} &=a^{2} b^{2} \\ \frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}} &=1\end{aligned}常见的两种椭圆标准方程,一种是横躺在x轴上,一种是“站立”着,关键就是看x和y下面哪个数值比较大,哪个大,那么长的对称轴就在哪个方向上。
双曲线的标准方程公式

双曲线的标准方程公式双曲线是代数曲线中的一种,在数学和物理学中都有着重要的应用。
双曲线的标准方程公式是描述双曲线的基本形式,通过标准方程我们可以更好地理解双曲线的性质和特点。
本文将详细介绍双曲线的标准方程公式及其相关知识。
首先,我们来看一下双曲线的定义。
双曲线是平面上的一种曲线,其定义为到两个给定点的距离之差等于常数的点的轨迹。
这两个给定点称为焦点,常数称为双曲线的离心率。
根据焦点的位置关系,双曲线可以分为两种类型,横向双曲线和纵向双曲线。
横向双曲线的焦点在x轴上,而纵向双曲线的焦点在y轴上。
接下来,我们来推导双曲线的标准方程公式。
以横向双曲线为例,设焦点为F1(c,0),F2(-c,0),离心率为e,点P(x,y)为双曲线上的任意点。
根据双曲线的定义,我们可以得到以下关系式:PF1 PF2 = 2a。
其中,a为双曲线的半焦距,即焦点到双曲线的距离。
根据点到两点的距离公式,我们可以得到:√((x-c)²+y²) √((x+c)²+y²) = 2a。
整理化简后得到双曲线的标准方程公式:(x²/a²) (y²/b²) = 1。
其中,a²= c²+ b²,b²= a²(e²-1)。
这就是横向双曲线的标准方程公式。
同理,对于纵向双曲线,其标准方程公式为:(y²/a²) (x²/b²) = 1。
通过标准方程公式,我们可以更好地理解双曲线的性质。
首先,双曲线在坐标系中是关于两条直线(称为渐近线)对称的。
其次,双曲线有两条渐近线,分别与双曲线的两支相切,并且渐近线的斜率分别为±b/a。
另外,双曲线的两支分别位于两条渐近线的两侧。
双曲线在数学和物理学中有着广泛的应用。
在数学中,双曲线是代数曲线的一种,研究双曲线可以帮助我们更好地理解曲线的性质和特点。
双曲线及其标准方程课件

音乐艺术
双曲线在音乐艺术中用于 创作优美的音乐旋律和和 声,特别是在处理音高和 音程时。
交通工程
双曲线在交通工程中用于 设计道路和轨道,特别是 在处理弯道和交叉口时。
04
双曲线的图像绘制
使用数学软件绘制双曲线
使用Ge双曲 线。用户只需在软件中输入双曲线的标准方程,即可自动生 成对应的双曲线图像。
05
双曲线的性质与方程 的关联
双曲线的性质与标准方程的关系
焦点距离
双曲线的标准方程中的系数与焦 点距离有关,决定了双曲线的开
口大小和方向。
渐近线
双曲线的标准方程中的系数决定了 渐近线的斜率和截距,反映了双曲 线的形状和位置。
离心率
双曲线的标准方程中的系数与离心 率有关,离心率决定了双曲线的开 口程度和形状。
推导结果
01
双曲线的标准方程为
$frac{x^2}{a^2}
-
frac{y^2}{b^2} = 1$。
02
其中$a > 0, b > 0$,且满足 $c^2 = a^2 + b^2$。
推导结论
双曲线是一种特殊的二次曲线,其标 准方程反映了双曲线的几何特性。
双曲线的焦点到曲线上任意一点的距 离之差为常数,这个常数等于两焦点 之间的距离的一半。
绘制双曲线
在工具箱中选择“双曲线”工具,然 后在绘图区域单击并拖动鼠标,即可 绘制出双曲线。用户可以根据需要调 整双曲线的参数和位置。
使用手工绘制双曲线
准备工具
准备一张纸、一支笔和一把直尺。
绘制过程
首先在纸上确定双曲线的中心和焦点,然后使用直尺和笔绘制出双曲线的渐近线。接着,使用笔和直尺在纸上绘 制出双曲线的上半部分。最后,使用对称性画出双曲线的下半部分。这种方法虽然比较传统,但对于理解双曲线 的几何意义非常有帮助。
双曲线abc关系推导过程

双曲线abc关系推导过程
双曲线方程中abc的关系式是c的平方等于a的平方加b的平方,双曲线是指与平面上到两个定点的距离之差的绝对值为定值的点的轨迹,也可以定义为到定点与定直线的距离之比是一个大于1的常数的点之轨迹。
双曲线是圆锥曲线的一种,即圆锥面与平行于中轴的平面的交截线。
椭圆和双曲线标准方程的推导方法大致有两种:一种是教材上移项平方的方法,另一种是资料上常见的构造对偶式的方法.这两种方法的运算量都比较大,尤其前一种方法需要两次移项平方。
最近,在进行椭圆的教学时,又发现了一种运算量较小的办法,即根据圆和椭圆的方程都具备“二元二次”的特征,可通过构造圆的方程能简化椭圆标准方程的推导过程,而该方法也同样适用于双曲线标准方程的推导双曲线中,a,b,c的关系,即c的平方等于a的平方加b的平方,不是利用什么知识点证明的。
它是在利用定义推导双曲线方程时,为了简化方程,令b的平方等于c的平方减a的平方得到的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
双曲线标准方程的推导
把平面内与两个定点1F ,2F 的距离的差的绝对值等于常数(小于
12F F )的点的轨迹叫做双曲线.其中这两个定点叫做双曲线的焦点,
两定点间的距离叫做双曲线的焦距.即当动点设为M 时,双曲线即为点集P ={}122M MF MF a -=
分析:当│M F 1│>│M F 2│时,│M F 1│-│M F 2│=2a (M 在双曲线右支上)
当│M F 1│<│M F 2│时,│M F 1│-│M F 2│= -2a (M 在双曲线左支上)
设动点M 的坐标为(x,y )
双曲线标准方程的推导:
当│M F 1│-│M F 2│=2a 时,有:
√(x +c)2+y 2-√(x −c)2+y 2=2a (移项)
⇒√(x +c)2+y 2=2a+√(x −c)2+y 2 (两边平方)
⇒(x+c)2+y2=4a2+4a√(x−c)2+y2+(x−c)2+y2(展开)
⇒x2+2cx+c2+y2=4a2+4a√(x−c)2+y2+x2-2cx+c2+y2(移项) ⇒x2−x2+2cx+2cx +c2−c2+y2-y2=4a2+4a√(x−c)2+y2(合并同类项)
⇒4cx=4a2+4a√(x−c)2+y2(两边除以4)
⇒cx=a2+a√(x−c)2+y2(移项)
⇒cx-a2=a√(x−c)2+y2(两边平方)
⇒c2x2-2a2cx+a4=a2[(x−c)2+y2](展开)
⇒c2x2-2a2cx+a4=a2[x2-2 cx+c2+y2](展开)
⇒c2x2-2a2cx+a4=a2x2-2a2 cx+a2c2+a2y2(移项)
⇒-2a2cx+2a2cx+c2x2-a2x2-a2y2=a2c2-a4(合并同类项)
⇒c2x2-a2x2-a2y2=a2c2-a4(按x,y顺序提取公因式)
⇒(c2-a2)x2-a2y2=a2(c2-a2)(c2=a2+b2,等量代替)
⇒b2x2-a2y2=a2b2(两边除以a2b2)
⇒x 2
a2-y
2
b2
=1(a>0,b>0)
当│M F1│-│M F2│=-2a时,有:
√(x+c)2+y2-√(x−c)2+y2=-2a (移项)
⇒√(x+c)2+y2=-2a+√(x−c)2+y2(两边平方)
⇒(x+c)2+y2=4a2-4a√(x−c)2+y2+(x−c)2+y2(展开)
⇒x2+2cx+c2+y2=4a2-4a√(x−c)2+y2+x2-2cx+c2+y2(移项)
⇒x2−x2+2cx+2cx +c2−c2+y2-y2=4a2-4a√(x−c)2+y2(合并同类项)
⇒4cx=4a2-4a√(x−c)2+y2(两边除以4)
⇒cx=a2-a√(x−c)2+y2(移项)
⇒cx-a2=−a√(x−c)2+y2(两边平方)
⇒c2x2-2a2cx+a4=a2[(x−c)2+y2](展开)
⇒c2x2-2a2cx+a4=a2[x2-2 cx+c2+y2](展开)
⇒c2x2-2a2cx+a4=a2x2-2a2 cx+a2c2+a2y2(移项)
⇒-2a2cx+2a2cx+c2x2-a2x2-a2y2=a2c2-a4(合并同类项)⇒c2x2-a2x2-a2y2=a2c2-a4(按x,y顺序提取公因式)
⇒(c2-a2)x2-a2y2=a2(c2-a2)(c2=a2+b2,等量代替)
⇒b2x2-a2y2=a2b2(两边除以a2b2)
⇒x 2
a2-y
2
b2
=1(a>0,b>0)
通过以上推导可知,一个方程x
2
a2
-y
2
b2
=1(a>0,b>0)涵盖了动点M左
右两支运动轨迹,而不是一支运动轨迹。
故称其为“双曲线标准方程”。
