《统计学》 第六章 统计指数(补充例题)
(完整版)统计基础6第六章统计指数测试卷8K

(完整版)统计基础6第六章统计指数测试卷8K统计基础知识测试题第六章统计指数⼀、判断题:本⼤题共20⼩题,每⼩题1分,共20分。
下列命题你认为正确的在题后括号内打“√”,错误的打“×”。
1.⼴义的指数是指反映同类现象在不同条件下数量变动的相对数。
√2.个体指数是综合指数的⼀种形式。
×3.指数体系可以测定各因素的变动对总变动的影响,进⾏因素分析。
√4.统计指数简称指数,是反映现象变动和进⾏因素分析的基本⽅法;主要⽤于分析研究现象的动态变化,如物价变动、产量变动、劳动⽣产率变动、股价变动、成本变动等。
√5.平均数指数是综合指数的⼀种形式。
×6.综合法总指数需要研究总体的全⾯资料,对起综合作⽤的同度量因素的资料要求也⽐较严格,⼀般采⽤与指数化有明确经济联系的指标,且应有⼀⼀对应的全⾯实际资料。
⽽平均法总指数则既适⽤于全⾯的资料,也适⽤于⾮全⾯资料。
√7.如果零售物价上升2%,商品销售量增长5%,则商品销售额增长10%。
×8.某企业按1990年不变价格编制的2004年⼯业总产值指数为134.8%,这表明该企业2004年的产量是1990年的1.348倍。
√9.编制质量指标指数,⼀般⽤报告期的数量指标作同度量因素。
√10.综合指数可以同时研究⼏个因素的变动⽅向和变动程度。
×11.综合指数是根据全⾯资料计算的,平均数指数是根据⾮全⾯资料计算的。
√12.在编制质量指标指数时,⼀般把作为同度量因素的数量指标固定在报告期。
√13.物价综合指数的分⼦减去分母后的差额综合反映由于物价变动⽽增减的销售额。
√14.同度量因素时期选择⼀般原则是:数量指标综合指数的同度量因素时期固定在报告期,质量指标综合指数的同度量因素时期固定在基期。
×15.狭义的指数是指反映总体现象中不能直接加总与不能直接对⽐的不同事物在不同时间条件下的数量综合变动的⼀种特殊相对数。
√16.总指数最主要的作⽤是综合反映社会经济现象总体的变动⽅向和变动程度。
《统计学概论》第六章课后练习题答案

8.什么是指数体系?它与因素分析有什么关系?
9.平均指标变动的因素分析应编制哪几种平均指标指数?如何分析?
Hale Waihona Puke 10.综合指数或平均指标指数因素分析的对象如何分辨?
二、单项选择题
1.在统计实践中,通常人们所说的指数一词的含义指的是( )。
A.广义的指数
B.狭义的指数
C.广义和狭义的指数
D.拉氏和派氏指数
2.从指数包括的范围不同,可以把指数分为( )。
C.一个固定在基期,另一个固定在报告期
D.采用基期和报告期的平均
7.拉氏指数所采用的同度量因素是固定在( )。
A.基期
B.报告期
C.假定期
D.任意时期
8.因素分析法的依据是( )。
A.指标体系
B.指数体系
C.拉氏指数
D.派氏指数
9.∑p1q1-∑p0q1 表明( )。
A.由于销售量的变化对销售额的影响
解:(1)拉式公式下的工业品出口价格总指数为:
∑∑ ∑∑ kp =
p1q0 = p0q0
k p p0q0
=
926 × 3880 + 583 × 3890 +
935
550
520 × 3300 + 515
450 × 2500 422
= 102.90%
p0q0
2880 + 3890 + 3300 + 2500
∑ ∑ 全部商品价格变动使得居民增加支出的金额= p1q1 − p0q1 =12006(万)
(4)四种商品零售量总指数为:
∑∑ kq =
q1 p0 = (5.20 × 2.0 + 5.52 ×17.0 +1.15× 5.2 +1.30×16.5) ×1000 = 118.58% q0 p0 (5.00× 2.0 + 4.46 ×17.0 +1.20× 5.2 +1.15×16.5) ×1000
第六章 统计指数含答案

第六章统计指数分析习题一、填空题1.指数按其指标的作用不同,可分为和。
2.狭义指数是指反映由不能同度量的事物所构成的特殊总体变动或差异程度的特殊。
3.总指数的编制方法,其基本形式有两种:一是,二是。
4.平均指数是的加权平均数。
5.因素分析法的基础是。
6.在含有两个因素的综合指数中,为了观察某一因素的变动,则另一个因素必须固定起来。
被固定的因素通常称为,而被研究的因素则称为指标。
7.平均数的变动同时受两个因素的影响:一是各组的变量值水平,二是。
8.编制综合指数,确定同度量因素的一般原则是:数量指标指数宜以作为同度量因素,质量指标指数宜以作为同度量因素。
9.已知某厂工人数本月比上月增长6%,总产值增长12%,则该企业全员劳动生产率提高。
10.综合指数的重要意义,在于它能最完善地显示出所研究对象的经济内容,即不仅在相对数,而且还能在方面反映事物的动态。
二、单项选择1.统计指数按其反映的对象范围不同分为( )。
A简单指数和加权指数B综合指数和平均指数C个体指数和总指数D数量指标指数和质量指标指数2.总指数编制的两种形式是( )。
A算术平均指数和调和平均指数B个体指数和综合指数C综合指数和平均指数D定基指数和环比指数3.综合指数是一种( )。
A简单指数B加权指数C个体指数D平均指数4.某市居民以相同的人民币在物价上涨后少购商品15%,则物价指数为( )。
A 17.6%B 85%C 115%D 117.6%5.在掌握基期产值和各种产品产量个体指数资料的条件下,计算产量总指数要采用( )。
A综合指数B可变构成指数C加权算术平均数指数D加权调和平均数指数6.在由三个指数组成的指数体系中,两个因素指数的同度量因素通常( )。
A都固定在基期B都固定在报告期C一个固定在基期,另一个固定在报告期D采用基期和报告期的平均数7.某商店报告期与基期相比,商品销售额增长6.5%,商品销售量增长6.5%,则商品价格( )。
A增长13%B增长6.5%C增长1%D不增不减8.单位产品成本报告期比基期下降6%,产量增长6%,则生产总费用( )。
《统计学》第六章统计指数(补充例题)
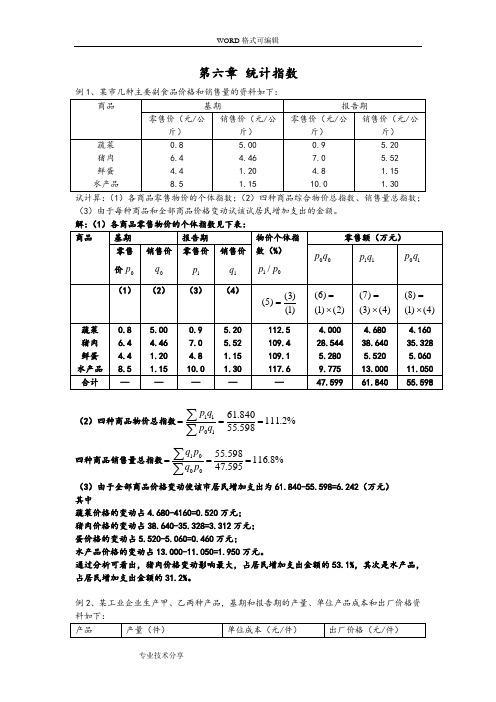
第六章 统计指数(3)由于每种商品和全部商品价格变动试该试居民增加支出的金额。
解:(1)各商品零售物价的个体指数见下表:(2)四种商品物价总指数%2.111598.55840.611011===∑∑qp q p四种商品销售量总指数%8.116595.47598.55001===∑∑pq p q(3)由于全部商品价格变动使该市居民增加支出为61.840-55.598=6.242(万元) 其中蔬菜价格的变动占4.680-4160=0.520万元; 猪肉价格的变动占38.640-35.328=3.312万元; 蛋价格的变动占5.520-5.060=0.460万元;水产品价格的变动占13.000-11.050=1.950万元。
通过分析可看出,猪肉价格变动影响最大,占居民增加支出金额的53.1%,其次是水产品,占居民增加支出金额的31.2%。
例2、某工业企业生产甲、乙两种产品,基期和报告期的产量、单位产品成本和出厂价格资试计算:(1)以单位成本为同度量因素的产量总指数 (2)以出厂价格为同度量因素的产量总指数 (3)单位成本总指数 (4)出厂价格总指数(1)以单位成本为同度量因素的产量总指数%7.1193100037100001===∑∑zq z q(2)以出厂价格为同度量因素的产量总指数%6.115550006360001===∑∑pq p q(3)单位成本总指数%2.14837100550001011===∑∑qz q z(4)出厂价格总指数%8.9963600635001011===∑∑qp q p例3、试根据例2的资料,从相对数和绝对数方面分析: (1)总成本变动受产量和单位成本变动的影响程度 (2)销售额变动受产量和出厂价格变动的影响程度 解:(1)总成本变动:总成本指数%4.1773100055000011===∑∑qz q z增加总成本∑∑=-=-2400031000550000011qz q z (元)其中由于产量变动的影响:产量指数%7.1193100037100001===∑∑zq z q由于产量增长而引起总成本增加:∑∑=-=-610031000371000001zq z q (元)由于单位成本变动的影响: 单位成本指数%2.1483710055000111===∑∑zq z q由于单位成本增长而引起总成本增加:∑∑=-=-1790037100550000111zq z q (元)177.4%=119.7%×148.2% 24000元=6100元+17900元计算表明,该厂两种产品总成本报告期比基期增长77.4%,是由于产品产量增加19.7%和单位成本提高48.2%两因素造成的。
统计学判断补充题目

第一章.总论1.统计学是一门实质性学科。
(×)2.统计学是一门方法论学科。
(√)3.某企业职工人数为1200人,这里的“职工人数1200人”是标志值。
(√)4.标志是指总体单位的特征和属性的名称。
(√)5.产品质量等级是数量标志。
(×)6.平均工资是质量指标。
(√)7.职工人数和职工工资都是连续型变量。
(×)8.变异是指标和标志各不相同。
(×)9.变量按其计数特点不同可以分为连续变量和离散变量。
(√)10.指标按其数值变现形式不同可以分为总量指标和相对指标。
(×)第二章.统计数据的搜集、整理和显示1.统计调查中的填报单位与报告单位是一致的。
(×)2.在统计调查中,调查单位是调查标志的承担者。
(√)3.普查和全面统计报表都是全面调查,所以两者的功能是相同的。
(×)4.对于有限总体进行调查时只能采取全面调查。
(×)5.调查时间就是调查人员进行调查工作所需要的时间。
(×)6.抽样调查和普查的目的相同,两者在调查中可以相互取代。
(×)7.当调查任务只要求掌握总体的基本情况,而该总体中又有部分单位能比较集中地反映研究项目的数量特征时,运用重点调查是比较合适的。
√8.统计调查所搜集的资料有原始资料和次级资料两种。
(√)9.确定调查对象是为了解决向谁调查的问题。
(√)10.确定调查方案的首要问题是明确调查目的。
(√)11.统计整理仅仅是对统计调查所得到的原始资料进行加工整理。
(×)12.在组距数列中,组数等于数量标志所包含的变量值的个数。
(×)13.统计分组中的“分”是针对总体单位而言的,而“合”则是针对总体而言的。
(×)14.对一个既定的统计总体而言,合理的分组标志只有一个。
(×)15.凡是按两个或两个以上标志进行的层叠分组都叫复合分组。
(√)16.在异距分组数列中,计算频数密度主要是为了消除组距因素对次数分布的影响。
统计学 第六章 统计指数

K p
p1
q0
2
q1
p0
q0
q1 2
p1 q0 q1 p0 q0 q1
Kq
q1
p0
2
p1
q0
p0 p1 2
q1 p0 p1 q0 p0 p1
将例1资料带入公式,可得:
k p
p1q0 p0q0
p1q1 26120 38600 64720 108.59% p0q1 23800 35800 59600
在选择指数形式时,主要考虑指数的经济意义,还要考虑 实际编制工作的可能性及对指数分析性质的特殊要求。
(一)工业生产指数 编制过程:
首先,对各种工业产品分别制定相应的不变价格标准,记为P0 然后,逐项计算各种产品的不变价格产值,加总起来就得到全部工 业产品的不变价格总产值 最后将不同时期的不变价格总产值加以对比,就得到相应时期的工 业生产指数
与马埃公式一样,虽然从数量上不偏不倚,但缺乏经济意义,所 用资料较多,计算困难。
是对拉氏指数和帕氏指数直接进行平均(型交叉)的结果,公式 为:
kp
p1q0
p1q1
p0 q0
p0 q1
kq
q1 p0
q1 p1
q0 p0
q0 p1
将例1资料带入公式,可得:
k p
p1q0 p0q0k p
统计学原理第六章 统计指数_OK

2021/7/22
28
其他权数形式的综合指数的编制
在指数编制理论的发展和实践过程中,除了拉斯贝尔和派许 提出了以基期和报告期为权数以外,还有不少统计学家曾提出 或采用过其他形式的权数计算总指数的综合形式。
2021/7/22
29
(1) 采用平均权数。即在研究数量指标指数时,其同度量 因素质量指标以拉式和派式指数分析法中的基期和报告期 的质量指标的简单算数平均数为权数;而在研究质量指标指 数时,其同度量因素数量指标也以拉式和派式指数分析法中 的基期和报告期的数量指标的简单算术平均数为权数。
2021/7/22
20
(1) 采用基期权数。即把同度量因素固定在基期,以基期的 数量指标作为权数。则销售单价的综合指数公式为:
这个指数公式是由德国经济学家拉斯贝尔(Laspeyres)在 1864年提出的,简称拉氏指数公式。从以上公式可以看出:p1q0 为基期的销售量(数量指标)按报告期销售单价(质量指标)计算 所得的销售额,分母∑p0q0是基期的销售额。
2021/7/22
5
指数分析法在实际工作中有着极其重要的作用
1) 综合反映复杂的社会经济现象总体的变动方向和程度 2) 分析和测定现象的各个构成因素对现象发展变动的影响程度和
绝对效果 3) 研究事物在长时间内的变动趋势
2021/7/22
6
6.1.3 统计指数的种类
由于划分的标准不同,统计指数有很多种类: 按照研究对象的范围不同,可分为个体指数和总指数
2021/7/22
16
从上表可知,可以编制三个总指数,即销售量总指数、价格 总指数和销售额总指数。
在分析该商店三种商品的销售额变动时,只要把报告期的 销售额与基期销售额直接进行对比。
第六章 统计指数

计算题:试计算(1)各商品零售物价的个体指数; (2)四种商品物价总指数;(3)由于每种商品和全部商品价格变动使该市居民增加支出的金额; (4)四种商品零售量总指数。
解:(1)各商品零售物价的个体指数: 蔬菜:%00.1100.22.201===p p k p 猪肉:%71.1040.178.1701===p p k p 鲜蛋:%92.1762.52.901===p p k p 水产品:%09.1095.160.1801===p p k p(2)物价总指数:109.12%131.67143.67630.15.1615.12.552.50.1720.50.230.10.1815.12.952.58.1720.52.21011__==⨯+⨯+⨯+⨯⨯+⨯+⨯+⨯==∑∑qp q p k p(3)每种商品价格变动影响的绝对额:蔬菜:p 1q 1-p 0q 1=2.2×5.20-2.0×5.20=1040(万元) 猪肉:p 1q 1-p 0q 1=17.8×5.52-17.0×5.52=4416(万元) 鲜蛋:p 1q 1-p 0q 1=9.2×1.15-5.2×1.15=4600(万元) 水产品:p 1q 1-p 0q 1=18.0×1.30-16.5×1.30=1950(万元) 全部商品价格变动影响的绝对额:∑∑==)(1200667.131676.1431011万元-qp -q p(4)零售量总指数:%58.11804.11167.1315.1615.12.520.10.1746.40.200.55.1630.12.515.10.1752.50.220.50001__==⨯+⨯+⨯+⨯⨯+⨯+⨯+⨯==∑∑pq pq k q2、某工业企业生产甲、乙两种产品,基期和报告期的产量、单位成本和出厂价格资料如下:(2)以出厂价格为同度量因素的产量总指数; (3)单位成本总指数; (4)出厂价格总指数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第六章 统计指数(3)由于每种商品和全部商品价格变动试该试居民增加支出的金额。
解:(1)各商品零售物价的个体指数见下表:(2)四种商品物价总指数%2.111598.55840.611011===∑∑qp q p四种商品销售量总指数%8.116595.47598.55001===∑∑pq p q(3)由于全部商品价格变动使该市居民增加支出为61.840-55.598=6.242(万元) 其中蔬菜价格的变动占4.680-4160=0.520万元; 猪肉价格的变动占38.640-35.328=3.312万元; 蛋价格的变动占5.520-5.060=0.460万元;水产品价格的变动占13.000-11.050=1.950万元。
通过分析可看出,猪肉价格变动影响最大,占居民增加支出金额的53.1%,其次是水产品,占居民增加支出金额的31.2%。
例2、某工业企业生产甲、乙两种产品,基期和报告期的产量、单位产品成本和出厂价格资试计算:(1)以单位成本为同度量因素的产量总指数 (2)以出厂价格为同度量因素的产量总指数 (3)单位成本总指数 (4)出厂价格总指数(1)以单位成本为同度量因素的产量总指数%7.1193100037100001===∑∑zq z q(2)以出厂价格为同度量因素的产量总指数%6.115550006360001===∑∑pq p q(3)单位成本总指数%2.14837100550001011===∑∑qz q z(4)出厂价格总指数%8.9963600635001011===∑∑qp q p例3、试根据例2的资料,从相对数和绝对数方面分析: (1)总成本变动受产量和单位成本变动的影响程度 (2)销售额变动受产量和出厂价格变动的影响程度 解:(1)总成本变动:总成本指数%4.1773100055000011===∑∑qz q z增加总成本∑∑=-=-2400031000550000011qz q z (元)其中由于产量变动的影响:产量指数%7.1193100037100001===∑∑zq z q由于产量增长而引起总成本增加:∑∑=-=-610031000371000001zq z q (元)由于单位成本变动的影响: 单位成本指数%2.1483710055000111===∑∑zq z q由于单位成本增长而引起总成本增加:∑∑=-=-1790037100550000111zq z q (元)177.4%=119.7%×148.2% 24000元=6100元+17900元计算表明,该厂两种产品总成本报告期比基期增长77.4%,是由于产品产量增加19.7%和单位成本提高48.2%两因素造成的。
因此总成本增加24000元,是由于产量增加而增加6100元,单位成本提高而增加17900元。
(2)销售额变动:%4.1155500063500011==∑∑qp q p增加销售额∑∑=-=-850055000635000011qp q p (元)其中由于产量变动的影响: 产量指数%6.1155500063600010===∑∑qp q p由于产量提高而增加销售额:∑∑=-=-860055000636000010qp q p (元)出厂价格变动的影响: 出厂价格指数%8.9963600635001011===∑∑qp q p由于出厂价格降低而减少销售额:∑∑-=-=-10063600635001011qp q p (元)115.4%=115.6%×99.8% 8500元=8600元-100元计算结果表明,该厂两种产品销售额报告期比基期增长15.4%,是由于产品产量增加15.6%和出厂价格降低0.2%两因素造成的。
销售额增加8500元,是由于产量增长而增加8600元和出厂价格下降减少销售额100元所共同造成的。
例4、某市2003年社会商品零售额12000万元,2002年增加为15600万元,这年零售物价指数提高4%。
试计算零售量指数,并分析零售量和零售物价两因素变动对零售总额变动影响的绝对值。
解:已知零售物价指数%1041011==∑∑qp q p可得15000%1041560010==∑q p零售量指数%1251200015000010===∑∑qp q p由于零售量增加而增加的零售额:15000-12000=3000(元) 零售物价指数%10415000156001011===∑∑qp q p由于物价上涨而增加零售额:∑∑=-=-60015000156001011qp q p (万元)报告期比基期零售总额增加3600万元(15600-12000)是因为零售量增长25%而增加3000万元,零售物价上涨4%而增加600万元两因素共同造成的。
例5、某厂2003年产量比2002年增长了13.6%,生产费用增加了12.9%。
问该厂2003年产品成本的变动情况。
解:生产费用总指数=产量指数×单位成本指数单位成本指数=生产费用总指数÷产量指数=112.9%÷113.6%=99.4% 单位成本降低0.6%。
例6、某年我国城市消费品零售额12389亿元,比上年增长28.2%;农村消费品零售额8290亿元,增长24.3%,扣除价格因素,实际分别增长13%和6.8%。
试问城乡消费价格分别上涨多少? 解:零售价格指数=零售额指数÷零售量指数 城市消费品价格指数=128.2%÷113%=113.5% 农村消费品价格指数=124.3%÷106.8%=116.4%即城市、农村消费品价格分别上涨13.5%和16.4%。
例7、某印刷厂2003年职工的工资水平提高3.2%,职工工人数增加2%,问该厂工资总额的变动情况如何?解:工资总额指数=工资水平指数×职工工人数指数=103.2%×102%=105.3%试分析该企业2002年比2000年总产值增长中受职工人数、生产工人占职工人数的比重及工人劳动生产率三因素影响的相对程度和绝对值。
对总产值变动进行分析的三个因素关系如下:总产值=职工人数×工人数占职工总数的比重×工人劳动生产率 计算如下: 总产值总数%4.1449001300000111===c b a c b a4009001300000111=-=-c b a c b a (万元)其中: 职工人数总数%1059009454062.1%808004062.1%80840000001==⨯⨯⨯⨯==c b a c b a工人数占职工总数的比重45900945000001=-=-c b a c b a (万元)劳动生产率指数%5.1291004130054062.1%8580082072.1%85840011111==⨯⨯⨯⨯==c b a c b a 29610041300011111=-=-c b a c b a (万元)三因素变动影响的关系为:144.4%=105%×106.2%×129.5% 400万元=45万元+59万元+296万元该企业2002年比2000年劳动生产率提高29.5%,使总产值增加296万元;工人数占职工总数的比重从2000你的80%上升到2002年的85%,增长6.2%,增加总产值59万元;职工人数增加5%,使总产值增加45万元。
三个因素共同作用,使该企业总产值2002年比2000年增长44.4%,绝对值增长400万元。
(1)根据上表资料,分别计算三个工厂生产这种产品的报告期和基期的总平均成本,进一步计算总平均成本指数,并分析由于总平均成本下降所节约的总成本金额。
(2)在这平均成本的变动中,分析各工厂成本水平变动及个工厂产量结构变动的影响程度和影响绝对值。
基期总平均成本37.2307100===∑∑qz q (元/件) 报告期总平均成本2.250110111===∑∑qz q (元/件) 总平均成本指数∑∑=111q z q ÷%8.9237.22.2000===∑∑qz q 由于总平均成本下降所节约的总成本金额为:-∑∑111(q z q 5.850)37.22.2()100-=⨯-=∑∑∑q qz q (万元)(2)固定构成成本指数÷=∑∑111q z q %4.94505.1162.211=÷=∑∑q z q 由于各工厂成本水平下降而节约的总成本为:-∑∑111(q z q 5.650)33.22.2()100-=⨯-=∑∑∑q qz q (万元) 产量结构变动指数÷=∑∑101qz q %3.9837.233.200=÷=∑∑qz q由于工厂产品产量结构变动而节约的总成本额为:-∑∑11(q z q 250)37.233.2()100-=⨯-=∑∑∑q qz q (万元)92.8%=94.4%×98.3%-8.5%万元=(-6.5)万元+(-2)万元从上面的计算可以看出,该管理局产品成本降低工作取得了一定的成效。
总平均成本从基期的2.37元/件降到报告期的2.2元/件,降低程度为7.2%。
由于总平均成本下降节约总成本金额8.5万元,究其原因,有两方面因素造成:首先原因各个企业成本水平综合下降了5.6%,节约总成本6.5万元;其次各个企业产量结构也发生变化,单位成本低的企业产量比重提高,从而影响总平均成本下降了1.7%,节约总成本2万元。
要求:(1)计算总平均劳动生产率指数(2)对总平均劳动生产率变动及总产值的影响进行因素分析。
总平均劳动生产率指数%5.157150450200945000111=÷=÷=∑∑∑∑TT q T T q 总平均劳动生产率变动导致总产值增加:345200)3725.4()(100111=⨯-=-∑∑∑∑∑T T T q T T q (万元) 其中由于各厂劳动生产率水平的变动对总平均劳动生产率的影响为: 固定指数%2.111200850200945110111=÷=÷=∑∑∑∑TTq T T q 使总产值增加:95200)25.4725.4()(1110111=⨯-=-∑∑∑∑∑T T T q T T q (万元) 由于各工厂工人数所占比重(即结构)的变动对总平均劳动生产率影响为: 结构指数%7.141150450200850000110=÷=÷=∑∑∑∑TTq T T q 使总产值增加为:250200)325.4()(00110=⨯-=÷∑∑∑∑T T q T T q (万元) 以上各指数及其各绝对值的关系为:157.5%=111.2%×141.7% 345万元=95万元+250万元以上分析说明,两工厂综合劳动生产率从每人3万元提高到每人4.725万元,提高程度57.5%,增加总产值345万元。
