九年级中考数学复习《平移知识点梳理+过关练习》)专题复习讲义
初中数学平移的知识点复习

I just walked along the road of life. I suddenly encountered a wall. All the grievances I encountered unexpectedly spread like air. I was overwhelmed and didn't have the strength to break free.同学互助一起进步(页眉可删)初中数学平移的知识点复习其实我们可以通过简单的平移可以构造精美的图形,这也是平移的作用体现。
平移经过平移,对应线段平行(或共线)且相等,对应角相等,对应点所连接的线段平行且相等;平移变换不改变图形的形状、大小和方向(平移前后的两个图形是全等形)。
(1)图形平移前后的形状和大小没有变化,只是位置发生变化;(2)图形平移后,对应点连成的线段平行且相等(或在同一直线上)(3)多次平移相当于一次平移。
(4)多次对称后的图形等于平移后的图形。
(5)平移是由方向,距离决定的。
(6)经过平移,对应线段平行(或共线)且相等,对应角相等,对应点所连接的线段平行且相等。
这种将图形上的所有点都按照某个方向作相同距离的位置移动,叫做图形的平移运动,简称为平移平移的条件:确定一个平移运动的条件是平移的方向和距离。
三个要点:1 原来的物体2 平移的方向。
3 平移的距离。
大家要知道平移前后图形的形状、大小不变,只是位置发生改变。
初中数学知识点总结:平面直角坐标系下面是对平面直角坐标系的内容学习,希望同学们很好的掌握下面的内容。
平面直角坐标系平面直角坐标系:在平面内画两条互相垂直、原点重合的数轴,组成平面直角坐标系。
水平的数轴称为x轴或横轴,竖直的数轴称为y轴或纵轴,两坐标轴的交点为平面直角坐标系的原点。
平面直角坐标系的要素:①在同一平面②两条数轴③互相垂直④原点重合三个规定:①正方向的规定横轴取向右为正方向,纵轴取向上为正方向②单位长度的规定;一般情况,横轴、纵轴单位长度相同;实际有时也可不同,但同一数轴上必须相同。
九年级数学讲义二次函数的图像及平移变换讲解

九年级数学讲义二次函数的图像及平移变换讲解一、基础知识图像的平移:(1)平移:将图像F 每个点,都沿着同一个方向,移动相同的距离,得到一个新图像F ', 我们称这个过程为一次平移;常见的平移有向左(右)平移,向上(下)平移;(2)以二次函数的顶点式来说明二次函数的平移:020)(y x x a y +-=−−−−−→−个单位向左平移h 020))((y x h x a y +-+=; 020)(y x x a y +-=−−−−−→−个单位向上平移k k y x x a y ++-=020)(;归纳为:左加右减,上加下减**(3)对称:此处只学习关于x 轴、y 轴、原点对称;图形对称前后,形状、大小均保持不变。
20)(y x x a y +-=−−−−−→关于x 轴对称200()y a x x y -=-+, 即200()y a x x y =--- 020)(y x x a y +-=−−−−−→关于y 轴对称200()y a x x y =--+, 即200()y a x x y =++ 020)(y x x a y +-=−−−−−→关于原点对称200()y a x x y -=--+,即200()y a x x y =-+-二、例题解析与跟进训练:练习:求下列函数的图象的对称轴、顶点坐标及与x 轴的交点坐标.(1)y=4x 2+24x+35; (2)y=﹣3x 2+6x+2;(3)y=x2﹣x+3;(4)y=2x2+12x+18.例1 已知抛物线y=ax2+bx经过点A(﹣3,﹣3)和点P(t,0),且t≠0.(1)若该抛物线的对称轴经过点A,如图,请通过观察图象,指出此时y的最小值,并写出t的值;(2)若t=﹣4,求a、b的值,并指出此时抛物线的开口方向;(3)直接写出使该抛物线开口向下的t的一个值.例2 已知抛物线C1的解析式是y=2x2﹣4x+5,抛物线C2与抛物线C1关于x轴对称,求抛物线C2的解析式.例3 已知二次函数y=﹣2x2,怎样平移这个函数的图象,才能使它经过(0,1)和(1,6)两点?写出平移后的函数解析式.例4 已知抛物线y=ax2+bx+c经过A,B,C三点,当x≥0时,其图象如图所示.(1)求抛物线的解析式,写出抛物线的顶点坐标;(2)画出抛物线y=ax2+bx+c当x<0时的图象;(3)利用抛物线y=ax2+bx+c,写出x为何值时,y>0.当堂练习1.已知抛物线y=4x2﹣11x﹣3.(Ⅰ)求它的对称轴;(Ⅱ)求它与x轴、y轴的交点坐标.2.(1)请在坐标系中画出二次函数y=﹣x2+2x的大致图象;(2)在同一个坐标系中画出y=﹣x2+2x的图象向上平移两个单位后的图象;(3)直接写出平移后的图象的解析式.注:图中小正方形网格的边长为1.3.已知点A(﹣2,﹣c)向右平移8个单位得到点A′,A与A′两点均在抛物线y=ax2+bx+c上,且这条抛物线与y轴的交点的纵坐标为﹣6,求这条抛物线的顶点坐标.4.如图,抛物线y1=﹣x2+2向右平移1个单位得到抛物线y2,回答下列问题:(1)抛物线y2的顶点坐标;(2)阴影部分的面积S=______________;(3)若再将抛物线y2绕原点O旋转180°得到抛物线y3,求抛物线y3的解析式.5.已知二次函数的图象经过点(0,3),(﹣3,0),(2,﹣5),且与x轴交于A、B两点.(1)试确定此二次函数的解析式;(2)判断点P(﹣2,3)是否在这个二次函数的图象上?如果在,请求出△PAB的面积;如果不在,试说明理由.6.已知二次函数的图象过坐标原点,它的顶点坐标是(1,﹣2),求这个二次函数的解析式.7.推理运算:二次函数的图象经过点A(0,﹣3),B(2,﹣3),C(﹣1,0).(1)求此二次函数的关系式;(2)求此二次函数图象的顶点坐标;(3)填空:把二次函数的图象沿坐标轴方向最少平移_________个单位,使得该图象的顶点在原点.8.一次函数y=x﹣3的图象与x轴,y轴分别交于点A,B.一个二次函数y=x2+bx+c的图象经过点A,B.(1)求点A,B的坐标,并画出一次函数y=x﹣3的图象;**(2)求二次函数的解析式及它的最小值.课后挑战1.已知二次函数y=x2+bx+c中,函数y与自变量x的部分对应值如下表:(1)求该二次函数的关系式;(2)当x为何值时,y有最小值,最小值是多少?(3)若A(m,y1),B(m+1,y2)两点都在该函数的图象上,试比较y1与y2的大小.2.在直角坐标平面内,二次函数图象的顶点为A(1,﹣4),且过点B(3,0).(1)求该二次函数的解析式;(2)将该二次函数图象向右平移几个单位,可使平移后所得图象经过坐标原点?并直接写出平移后所得图象与x轴的另一个交点的坐标.3.二次函数图象过A、C、B三点,点A的坐标为(﹣1,0),点B的坐标为(4,0),点C在y 轴正半轴上,且AB=OC.(1)求C的坐标;(2)求二次函数的解析式,并求出函数最大值.。
人教版九年级下册数学中考综合复习:第29讲《图形的平移》

第29讲《图形的平移》要点梳理知识点1.平移的概念把一个图形整体沿某一方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同;新图形中的每一点,都是由原图形中的某一点移动后所得到的,这两个点是对应点.连接各组对应点的线段____________.图形的这种移动叫做平移变换,简称_________________.知识点2.平移的条件确定一个平移运动的条件是平移的_________________和__________________.知识点3.平移的规则图形上的每一个点都沿同一个方向移动相同的距离.知识点4.平移的性质(1) 平移不改变图形的形状与大小;(2)连接各组对应点的线段平行且相等;(3)对应线段________________;(4)对应角__________________________.知识点5.画平移图形画平移图形,必须找出平移方向和距离,其依据是平移的性质.1.平移的作图以局部带整体,先找出图形的关键点,将原图中的关键点与移动后的对应点连接起来,确定平移距离和平移方向,再过其他关键点分别作线段与前面所连接的线段平行且相等,得到关键点的对应点,将对应点连接,所得的图形就是平移后的新图形.2.图形经过两次轴对称(两对称轴相互平行)得到的图形,可以看作是由原图形经过平移得到的,也就是说两次翻折相当于一次平移.命题点1:平移的性质1.(台州)如图,把三角板的斜边紧靠直尺平移,一个顶点从刻度“5”平移到刻度“10”,则顶点C 平移的距离CC ′=_______________.2.(东营)如图,把△ABC 沿着BC 的方向平移到△DEF 的位置,它们重叠部分的面积是△ABC 面积的一半,若BC=3 ,则△ABC 移动的距离是( )A.23 B.33 C.26 D.26-3命题点2:坐标系中的平移3.(西宁)在平面直角坐标系中,将点A(-1,-2)向右平移3个单位长度得到点B,则点B 关于x 轴的对称点B'的坐标为( )A.(-3,-2)B.(2,2)C.(-2,2)D.(2,-2)4.(安顺)如图,将△PQR 向右平移2个单位长度,再向下平移3个单位长度,则顶点P 平移后的坐标是( )A .(-2,-4)B .(-2,4)C .(2,-3)D .(-1,-3)命题点3:利用平移设计图案5.(本溪)下列各网格中的图形是用其图形中的一部分平移得到的是( )典例精析考点1.判断图形的平移【例1】(济南)如图,在6×6方格中有两个涂有阴影的图形M,N,①中的图形M 平移后位置如②所示,以下对图形M 的平移方法叙述正确的是( )A .向右平移2个单位,向下平移3个单位B . B .向右平移1个单位,向下平移3个单位C .向右平移1个单位,向下平移4个单位D .向右平移2个单位,向下平移4个单位点考点2.求平移变换后对应点的坐标【例2】(海南)如图,在平面直角坐标系中,△ABC 位于第二象限,点A 的坐标是(-2,3),先把△ABC 向右平移4个单位长度得到111C B ΔA ,再作与111C B ΔA 关于x 轴对称的222C B ΔA ,则点A 的对应点A2的坐标是( )A .(-3,2)B .(2,-3)C.(1,-2) D .(-1,2)【例3】(雅安)已知△ABC 顶点坐标分别是A(0,6),B(-3,-3),C(1,0),将△ABC 平移后顶点A 的对应点A 1的坐标是(4,10),则点B 的对应点B 1的坐标为( )A .(7,1)B .(1,7)C .(1,1)D .(2,1)考点3.作已知图形的平移图形【例3】(临夏州)如图,在平面直角坐标系中,△ABC 的顶点A(0,1),B(3,2),C(1,4)均在正方形网格的格点上.(1) 画出△ABC 关于x 轴的对称图形111C B ΔA(2) 将111C B ΔA 沿x 轴方向向左平移3个单位后得到222C B ΔA ,写出顶点A 2,B 2,C 2的坐标.【达标测试】 1.如图,在10×6的网格中,每个小方格的边长都是1个单位,将△ABC 平移到△DEF 的位置,下面正确的平移步骤是( )A .先把△ABC 向左平移5个单位,再向下平移2个单位;B .先把△ABC 向右平移5个单位,再向下平移2个单位C .先把△ABC 向左平移5个单位,再向上平移2个单位D .先把△ABC 向右平移5个单位,再向上平移2个单位2.如图,在平面直角坐标系:xOy 中,已知点,0)2A(,B(1,1)。
初中数学知识点精讲精析 平移知识讲解

5·4 平移
1. 平移的性质
①把一个图形整体沿某一方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同.
②新图形中的每一个点,都是由原图形中的某一点移动后得到的,这两个点是对应点,连接各组对应点的线段平行且相等.
2.平移的概念
一个图形沿着某个方向..移动一定的距离..
,图形的这种移动,叫做平移变换,简称平移. 注意:图形平移的方向,不一定是水平的,也不一定是竖直的。
平移在我们日常生活中是很常见的.利用平移可以制作出很多美丽的图案
例1:如图(4)-1,平移三角形ABC,使点A 移动到点A′.画出平移后的三角形A′B′C′.
分析:“点A 移到点A′”这句话告诉我们图形平移的方向是A 到A′的方向, 平移的距离为线段AA′的长,根据这两个要素就可以确定点B 、C 的对应点B′、C′,从而画出△A′B′C′.
(4)-1 (4)-2
解:如图(4)-2,连接AA′,分别过B 、C 作AA′的平行线L 、L′,在L 上截取BB ′=AA′,在L′上截取CC′=AA′,连接A′C′,A′B′,B′C′.则△A′B′C ′为所求画的三角形.
例2. 下图中,图形(2)可以通过图形(1)平移得到吗? A 'C B
A
C '
B 'A '
C
B
A
(1)(2)(1)(2)
(1)(2)(1)(2)
答:都不可以。
例3.在下面的六幅图案中,(2)(3)(4)(5)(6)中的哪个图案可以通过平移图案(1)得到?
答:图案(3)。
初中数学总复习《几何三大变化—平移》讲义

教师辅导讲义学员姓名:辅导课目:数学年级:九年级学科教师:汪老师授课日期及时段课题初中数学总复习——几何三大变化——平移学习目标教学内容初中数学总复习——几何三大变化——平移轴对称、平移、旋转是平面几何的三大变换。
平移变换是指在同一平面内,将一个图形(含点、线、面)整体按照某个直线方向移动一定的距离,这样的图形变换叫做图形的平移变换,简称平移。
平移由移动的方向和距离决定。
经过平移,平移前后图形的形状、大小不变,只是位置发生改变;平移前后图形的对应点所连的线段平行且相等;平移前后图形的对应线段平行且相等,对应角相等。
在初中数学以及日常生活中有着大量的平移变换的知识,是中考数学的必考内容。
结合2011和2012年全国各地中考的实例,我们从下面七方面探讨平移变换:(1)构造平移图形;(2)点的平移;(3)直线(线段)的平移;(4)曲线的平移;(5)三角形的平移;(6)四边形的平移;(7)圆的平移。
【一、构造平移图形:】例1、(2012江苏泰州10分)如图,在边长为1个单位长度的小正方形组成的网格中,△ABC的顶点A、B、C在小正方形的顶点上,将△ABC向下平移4个单位、再向右平移3个单位得到△A1B1C1,然后将△A1B1C1 绕点A1顺时针旋转90°得到△A1B2C2.(1)在网格中画出△A1B1C1和△A1B2C2;(2)计算线段AC在变换到A1C2的过程中扫过区域的面积(重叠部分不重复计算)1、(2012福建泉州9分)如图,在方格纸中(小正方形的边长为1),反比例函数ky x=与直线的交点A 、B 均 在格点上,根据所给的直角坐标系(点O 是坐标原点),解答下列问题: (1)分别写.出点A 、B 的坐标后,把直线AB 向右平移平移5个单位, 再在向上平移5个单位,画.出平移后的直线A ′B ′. (2)若点C 在函数ky x=的图像上,△ABC 是以AB 为底边的等腰三角形, 请写出点C 的坐标.【二、点的平移:】例1、(2012辽宁鞍山3分)在平面直角坐标系中,将点P (﹣1,4)向右平移2个单位长度后,再向下平移 3个单位长度,得到点P 1,则点P 1的坐标为 .例2、(2012安徽省4分)如图,A 点在半径为2的⊙O 上,过线段OA 上的一点P 作直线 ,与⊙O 过A 点的 切线交于点B ,且∠APB=60°,设OP= x ,则△PAB 的面积y 关于x 的函数图像大致是【 】例3、(2012浙江嘉兴、舟山4分)如图,正方形ABCD 的边长为a ,动点P 从点A 出发, 沿折线A →B →D →C →A 的路径运动,回到点A 时运动停止.设点P 运动的路程长为 长为x ,AP 长为y ,则y 关于x 的函数图象大致是【 】A .B .C .D .例4、(2012湖北黄石3分)如图所示,已知A 11(,y )2,B 2(2,y )为反比例函数1y x=图像上的两点,动点 P (x,0)在x 正半轴上运动,当线段AP 与线段BP 之差达到最大时,点P 的坐标是【 】A. 1(,0)2B. (1,0)C. 3(,0)2D. 5(,0)2例5、(2012辽宁大连3分)如图,一条抛物线与x轴相交于A、B两点,其顶点P在折线C-D-E上移动,若点C、D、E的坐标分别为(-1,4)、(3,4)、(3,1),点B的横坐标的最小值为1,则点A的横坐标的最大值为【】A.1B.2C.3D.4例6、(2012江苏常州9分)已知,在矩形ABCD中,AB=4,BC=2,点M为边BC的中点,点P为边CD上的动点(点P异于C、D两点)。
九年级函数平移知识点

九年级函数平移知识点在九年级的数学学习中,我们将接触到函数的平移。
平移是指将函数的图像沿着坐标轴进行移动,而不改变函数的形状。
在本文中,我们将探讨函数平移的概念、平移的规律以及一些习题训练,帮助大家更好地理解和掌握这一知识点。
1. 平移的概念函数的平移是指将函数图像沿着横轴或纵轴进行移动,其实质是改变了函数中的相应自变量或因变量的值。
在进行平移时,函数的形状、增减性和单调性等特点都不发生改变,只是在坐标平面上移动位置。
2. 平移的规律2.1 沿横轴平移当我们将函数沿横轴右移(正向平移)或左移(负向平移)时,只需改变函数中的自变量的值。
设函数为y = f(x),平移后的函数可以表示为y = f(x ± a),其中a为平移的单位长度。
具体而言,右移a个单位长度可以表示为x - a,左移a个单位长度可以表示为x + a。
2.2 沿纵轴平移当我们将函数沿纵轴上移(正向平移)或下移(负向平移)时,只需改变函数中的因变量的值。
同样设函数为y = f(x),平移后的函数可以表示为y ± a = f(x),其中a为平移的单位长度。
具体而言,上移a个单位长度可以表示为y - a,下移a个单位长度可以表示为y + a。
3. 平移的效果3.1 横轴平移的效果当函数沿横轴平移时,平移方向的相反方向(右移与左移、上移与下移)将导致函数图像的相应部分的位置发生变化。
右移使整个函数图像向左移动,而左移使图像向右移动;上移使整个函数图像向下移动,而下移使图像向上移动。
但是,平移后函数的形状、增减性和单调性等特点保持不变。
3.2 纵轴平移的效果当函数沿纵轴平移时,平移方向的相反方向(上移与下移、右移与左移)将导致函数图像整体上移或下移。
上移会使整个函数图像向上平移,下移会使图像向下平移。
同样地,平移后函数的形状、增减性和单调性等特点不发生改变。
4. 习题训练4.1 横轴平移的习题训练A. 设函数y = f(x) = x^2,将其向右平移3个单位长度,写出平移后的函数表达式。
九年级数学中考知识点归纳复习 第24讲 平移、对称、旋转与位似 视图和投影
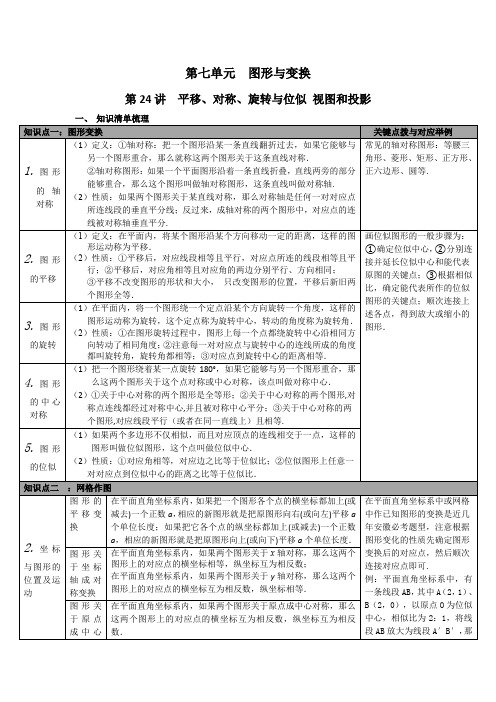
在平面直角坐标系内,如果两个图形的位似中心为原点,相似比为k,那么这两个位似图形对应点的坐标的比等于k或-k.
视图与投影
二、知识清单梳理
知识点一:三视图内容
关键点拨
1.三视图
主视图:从正面看到的图形.
俯视图:从上面看到的图形.
左视图:从左面看到的图形.
例:长方体的主视图与俯视图如图所示,则这个长方体的体积是36 .
4.图形的中心对称
(1)把一个图形绕着某一点旋转180°,如果它能够与另一个图形重合,那么这两个图形关于这个点对称或中心对称,该点叫做对称中心.
(2)①关于中心对称的两个图形是全等形;②关于中心对称的两个图形,对称点连线都经过对称中心,并且被对称中心平分;③关于中心对称的两个图形,对应线段平行(或者在同一直线上)且相等.
2.三视图的对应关系
(1)长对正:主视图与俯视图的长相等,且相互对正;
(2)高平齐:主视图与左视图的高相等,且相互平齐;
(3)宽相等:俯视图与左视图的宽相等,且相互平行.
3.常见几何体的三视图常见几何体的三视图
正方体:正方体的三视图都是正方形.
圆柱:圆柱的三视图有两个是矩形,另一个是圆.
圆锥:圆锥的三视图中有两个是三角形,另一个是圆.
第七单元图形与变换
第24讲平移、对称、旋转与位似视图和投影
一、知识清单梳理
知ห้องสมุดไป่ตู้点一:图形变换
关键点拨与对应举例
1.图形的轴对称
(1)定义:①轴对称:把一个图形沿某一条直线翻折过去,如果它能够与另一个图形重合,那么就称这两个图形关于这条直线对称.
②轴对称图形:如果一个平面图形沿着一条直线折叠,直线两旁的部分能够重合,那么这个图形叫做轴对称图形,这条直线叫做对称轴.
人教版初中数学中考考点系统复习 第31讲 图形的平移、旋转与位似

(3)拓展延伸:如图3,△AO'E是将图1中的△AOB绕点A按逆时针方向旋转 45°得到的,连接BO',P,Q分别为CE,BO'的中点,连接PQ,PB.若正方形 ABCD的边长为1,求△PQB的面积. 解:延长O'E,交边BC于点G,连接PG,O'P. ∵四边形ABCD是正方形,AC是对角线, ∴∠DAB=∠ABC=90°,∠ECG=45°. 由旋转的性质,得∠AO'E=90°,∴四边形O'ABG是矩形, ∴O'G=AB=BC,∠EGC=90°. ∵O'E=O'A=BG,∴EG=CG,
△ABC内一点,∠BAD=15°,AD=6 cm,连接BD,将△ABD绕点A按逆时针方
向旋转,使AB与AC重合,点D的对应点为点E,连接DE,DE交AC于点F,则CF
的长为
cm.
第(2)题图
【思路分析】(1)易证∠ABE+∠ADE=180°,推出∠BAD+∠BED=180°即 可解决问题. (2)过点A作AG⊥DE于点G,由旋转的性质推出∠AED=∠ADG=45°, ∠AFD=60°,利用锐角三角函数分别求出AG,GF,AF的长,即可求出CF的 长.
(1)D
解决有关旋转的问题,关键是利用旋转的性质,旋转变换的作用如下: (1)把分散的几何图形进行集中和整合; (2)添加辅助线易构造等腰三角形、全等三角形.
对点训练
2.(齐齐哈尔中考)有两个直角三角形纸板,一个含45°角,另一个含30°角,
如图1所示叠放,先将含30°角的纸板固定不动,再将含45°角的纸板绕顶点A
A
5.(2022·六盘水)如图,将△ABC绕点A旋转得到△ADE.若∠B=90°,∠C= 30°,AB=1,则AE的长为 2 .
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中考数学复习《平移知识点梳理+过关练习》)专题复习讲义
一.知识点回顾
1.定义:在平面内,将一个图形沿某个方向移动一定的距离,图形的这种变化称为平移.
2.性质:一个图形和它经过平移得到的图形中,对应点所连的线段平行(或在同一条直线上)且;
对应线段平行(或在同一条直线上)且,对应角相等.
3.用坐标表示平移:
在平面直角坐标系中,将点(x,y)向右或向左平移a个单位长度,可得到对应点;
将点(x,y)向上或向下平移b个单位长度,可得到对应点; 即“左减右加横坐标,上加下减纵坐标”.
4.平移前后的两个图形形状和大小完全相同(即全等),则对应线段相等,对应角相等.
二.规律总结:利用平移的性质解题:把图形进行平移,图形的大小和形状不发生改变,正确找到变换前后的对应角和对应线段,是解决这类题目的关键.
三.过关练习
1. 下列四个图形中,可以由上图通过平移得到的是 ()
2. 已知三角形ABC在平面直角坐标系中的位置如图所示,将三角形ABC向右平移6个单位,则平移后A点的坐标是( )
A.(-2,1)
B.(2,1)
C.(2,-1)
D.(-2,-1)
3.如图,将△ABC沿BC边上的中线AD平移到△A'B'C'的位置.已知△ABC的面积为16,阴影部分三角形的面积9.若AA'=1,则A'D等于()
A.2
B.3
C.4
D.5
4. 如图,在平面直角坐标系中,将点A(-2,3)向右平移3个单位长度,那么平移后对应的点A′的坐标是 ( )
A.(-2,-3)
B.(-2,6)
C.(1,3)
D.(-2,1)
4. 如图,如果将△ABC的顶点A先向下平移3格,再向左平移1格到达A′点,连接A′B,则线段A′B与线段AC的关系是( )
A.垂直
B.相等
C.平分
D.平分且垂直
5. 在平面直角坐标系中,△A
1B
1
C
1
是由△ABC平移后得到的,△ABC中任意一点
P(x
0,y
)经平移后对应点为P
1
(x
+6,y
+1).若点A
1
的坐标是(5,-3),则它对应
的点A的坐标为.
A.(-1,-4) B.(-1,4) C.(1,-4) D.(1,4)
6.如图,在直角坐标系中,△ABC的顶点都在方格线的格点上,如果将△ABC先
向右平移4个单位长度,再向下平移1个单位长度,得到△A
1B
1
C
1
,那么点A的
对应点A
1
的坐标为( )
A.(4,3)
B.(2,4)
C.(3,1)
D.(2,5)
7. 如图,在正方形OABC中,O为坐标原点,点C在y轴正半轴上,点A的坐标为
(2,0),将正方形OABC沿着OB方向平移1
2
OB个单位,则点C的对应点坐标为( )
A.(0,3)
B.(0,4)
C.(0,1)
D.(0,2)
8. 如图,在△ABC中,∠ACB=90°,边BC在x轴上,顶点A,B的坐标分别为(-2,6)和(7,0).将正方形OCDE沿x轴向右平移,当点E落在AB边上时,点D的坐标为( )
A.(3
2,2) B.(2,2) C.(11
4
,2) D.(4,2)
9. 如图,O为坐标原点,△OAB是等腰直角三角形,∠OAB=90°,点B的坐标为(0,2√ 2 ),将该三角形沿x轴向右平移得到Rt△O'A'B',此时点B'的坐标为(2√ 2 ,2√ 2 ),则线段OA在平移过程中扫过部分的图形面积为.
10. 如图,将△ABE向右平移2 cm得到△DCF,如果△ABE的周长是14 cm,那么四边形ABFD的周长是cm.
11. 如图,在△ABC中,AB=AC,BC=12 cm,点D在AC上,DC=4 cm,将线段DC沿CB 方向平移7 cm得到线段EF,点E,F分别落在边AB,BC上,则△EBF的周长为cm.
12. 把经过点(-1,1)和(1,3)的直线向右移动2个单位后过点(3,a),则a的值为 .
13. 在平面直角坐标系中,有一条线段AB,已知点A(-2,0)和B(0,2),平移
线段AB得到线段A
1B
1
.若点A的对应点A
1
的坐标为(1,3),则线段A
1
B
1
的中点坐
标是__ __.
14. 如图,两个全等的直角三角形重叠在一起,将其中的一个三角形沿着点B到C 的方向平移到△DEF的位置,AB=10,DO=4,平移距离为6,则阴影部分面积为__ _.
15. 如图,在网格中,每个小正方形的边长均为1个单位长度.我们将小正方形的顶点叫做格点,△ABC的三个顶点均在格点上.
(1)将△ABC先向右平移6个单位长度,再向上平移3个单位长度,得到△A1B1C1,
画出平移后的△A1B1C1;
(2)建立适当的平面直角坐标系,使得点A的坐为(-4,3);
(3)在(2)的条件下,直接写出点A1的坐标.
16. 在平面直角坐标系中,把点向右平移2个单位,再向上平移1个单位记为一次
“跳跃”.点A(-6,-2)经过第一次“跳跃”后的位置记为A
1,点A
1
再经过一次“跳
跃”后的位置记为A
2
,…,以此类推.
(1)写出点A
3的坐标:A
3
.
(2)写出点A
n 的坐标:A
n
(用含n的代数式表示).
17.如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A′C′D′.
(1)证明△A′AD′≌△CC′B;
(2)若∠ACB=30°,试问当点C′在线段AC上的什么位置时,四边形ABC′D′是菱形,并请说明理由.
18. 在平面直角坐标系中,把点向右平移2个单位,再向上平移1个单位记为一次
“跳跃”.点A(-6,-2)经过第一次“跳跃”后的位置记为A
1,点A
1
再经过一次“跳
跃”后的位置记为A
2
,…,以此类推.
(1)写出点A
3的坐标:A
3
.
(2)写出点A
n 的坐标:A
n
(用含n的代数式表示).。
