三等分角仪证明过程
阿基米德三等分角的证明

阿基米德三等分角的证明
阿基米德三等分角的证明是通过构造一个特殊的逆时针旋转等边三角形来实现的。
以下是详细的证明过程:
证明过程:
1.首先,构造一个等边三角形ABC,其中AB=BC=AC。
2.然后,以A为圆心,AB为半径画一条圆弧,与AC相交于D点。
3.再以B为圆心,BC为半径画一条圆弧,与AB相交于E点。
4.连接DE,延长DE与BC相交于F点。
5.观察三角形DEF,可以发现DF与BC平行,并且由于DE与AC相交,根据平行线的性质可知∠BDE=∠C。
6.接下来我们需要证明∠B=∠CDF。
7.由于DF与BC平行,△FBC与△DCF相似。
根据相似三角形的性质,可得BD/BC = CD/CF。
8.由三角形ABC的等边性质可知BD=CD=BC,代入上述等式可得BC/BC = CD/CF。
9.进一步化简可得,1 = CD/CF,即CD=CF。
10.由三角形CDF的等腰性质可知∠CDF=∠CDF,即∠B=∠CDF。
11.通过以上证明可以得出,∠C=∠B=∠CDF。
12.所以,由三角形DEF的角度平分定理可知
∠CDE=∠EDF=∠FDC=1/3∠C。
综上所述,通过构造特殊的逆时针旋转等边三角形,我们成功地证明了阿基米德三等分角。
数学 三等分角 标定直尺

数学三等分角标定直尺在数学中,三等分角是指将一个角分成三个相等的部分。
标定直尺则是通过直尺上的刻度来测量或绘制线段、角度等。
下面将分别介绍三等分角和标定直尺的相关内容。
一、三等分角:要将一个角三等分,可以采用以下方法之一:1.作图法:-步骤1:画出所给角的两条边。
-步骤2:以其中一条边为半径,作一个圆弧,与另一条边交于点A。
-步骤3:以点A为中心,再作一个圆弧,使其与第一条边交于点B。
-步骤4:以点B为中心,再作一个圆弧,使其与第一条边交于点C。
-步骤5:连接点A和点C,即可将原始角分为三等分。
2.角平分器法:使用角平分器工具可以更加准确地进行三等分角的操作。
按照角平分器的使用说明,设置角平分器的两臂长度,并将一个臂放在所给角的顶点上,然后旋转角平分器使其另一个臂与角的一条边对齐。
再次旋转角平分器,使其另一个臂与角的另一条边对齐。
最后,将角平分器旋转三次,每次旋转1/3的角度,即可完成三等分角。
需要注意的是,无论使用何种方法进行三等分角,都需要保持精确和准确性,并在实践中多加练习。
二、标定直尺:标定直尺是为了能够在直尺上准确地测量或绘制线段、角度等,需要对直尺进行刻度。
下面是一种常见的标定直尺的方法:1.制作基准:首先,确定一个已知长度的线段(如10厘米),将其作为基准线段。
2.分割等分:使用一个精确的测量工具(如卡尺),将基准线段等分为若干份(如10份)。
3.标记刻度:在直尺上的每个等分点上进行标记,以表示相应的刻度。
例如,在第一个等分点上标记1毫米,第二个等分点上标记2毫米,以此类推。
根据实际需要,可以选择适当的刻度单位,如毫米、厘米、英寸等。
4.连接刻度:使用细长的笔或刻度刀,在每个标记处刻下一个垂直的刻痕,以便更清晰地看到刻度。
5.校准检查:完成标定后,应该进行校准检查以确保刻度的准确性。
可以使用已知长度的线段或其他测量工具,将其放在直尺上进行比较和对齐,以验证刻度的准确性。
需要注意的是,在进行标定直尺时,要使用精确的测量工具,并尽可能保持手稳定和垂直。
磬折形尺如何三等分一个角
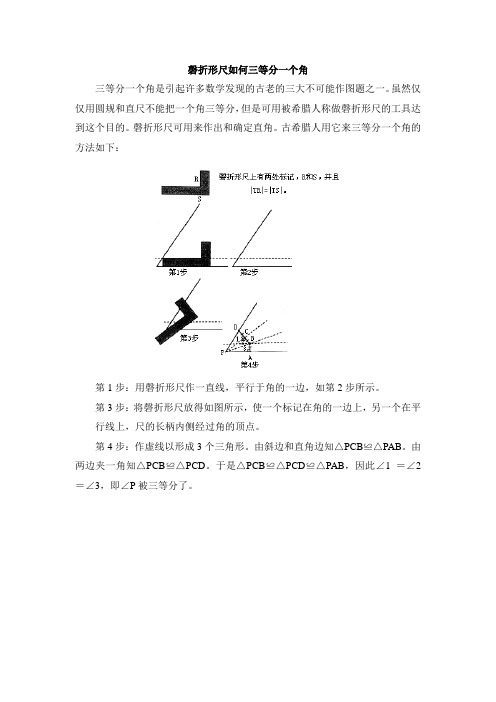
磬折形尺如何三等分一个角
三等分一个角是引起许多数学发现的古老的三大不可能作图题之一。
虽然仅仅用圆规和直尺不能把一个角三等分,但是可用被希腊人称做磬折形尺的工具达到这个目的。
磬折形尺可用来作出和确定直角。
古希腊人用它来三等分一个角的方法如下:
第1步:用磬折形尺作一直线,平行于角的一边,如第2步所示。
第3步:将磬折形尺放得如图所示,使一个标记在角的一边上,另一个在平行线上,尺的长柄内侧经过角的顶点。
第4步:作虚线以形成3个三角形。
由斜边和直角边知△PCB≌△PAB。
由两边夹一角知△PCB≌△PCD。
于是△PCB≌△PCD≌△PAB,因此∠1 =∠2=∠3,即∠P被三等分了。
阿基米德原理公式推导过程三等分角器

阿基米德原理公式推导过程三等分角器阿基米德原理是物理学中非常重要的一个原理,而三等分角器则是数学中一个有趣的工具。
让咱们先来聊聊阿基米德原理的公式推导过程。
话说有一天,我正在教室里给学生们讲阿基米德原理。
我拿了一个装满水的大玻璃缸,还有一个金属块。
我先问学生们:“你们猜猜把这个金属块放进水里,会发生啥?”学生们七嘴八舌地说开了,有的说水会溢出来,有的说金属块会沉下去。
然后我就把金属块慢慢地放进水里,果然,水溢出来了一些。
这时候我就告诉他们,溢出来的水的体积就等于金属块的体积。
这就是阿基米德原理的一个小起点。
咱们再深入一点,假设一个物体浸没在液体中。
这个物体受到了向下的重力 G 物,还受到了向上的浮力 F 浮。
根据力的平衡原理,如果物体处于静止状态,那么重力 G 物就等于浮力 F 浮。
那浮力 F 浮到底咋算呢?这就得从液体对物体的压力说起啦。
液体内部的压强是随着深度增加而增大的。
所以物体在液体中不同深度的表面受到的压力是不一样的。
想象一下,这个物体是一个规则的长方体。
它的上下表面面积相等,深度不同。
下表面受到的压力 F 下就比上表面受到的压力 F 上大。
那浮力 F 浮不就是这两个压力的差嘛!经过一番推导,咱们就能得出阿基米德原理的公式:F 浮= ρ 液 gV 排。
其中,ρ 液是液体的密度,g 是重力加速度,V 排是物体排开液体的体积。
再来说说三等分角器。
有一次我在办公室里研究三等分角器,想得那叫一个入神。
旁边的老师都笑我,说我太较真儿了。
三等分角器的原理其实挺巧妙的。
它利用了一些几何图形的特性和比例关系。
比如说,通过构建特定的三角形或者线段比例,来实现角的三等分。
但是呢,三等分角问题在只用尺规作图的情况下是没法完成的。
可这并不妨碍我们通过其他工具或者方法来实现它。
就像在学习和生活中,有时候我们觉得一个问题没法解决,可能只是我们的思路被限制住了。
当我们换个角度,或者借助一些新的工具和方法,说不定就能找到答案。
三等分角器

“三等分角器”是利用阿基米德原理做出的。
如图,∠AOB为要三等分的任意角,图中AC,OB两滑块可在角的两边内滑动,始终保持有OA=OC=PC.求证:∠APB=13∠AOB.考点:等腰三角形的性质已知如图,在△ABC中,AB=AC,O是△ABC内一点,且OB=OC,求证:AO⊥BC.考点:等腰三角形的性质,线段垂直平分线的性质如图所示,在△ABC中,AB=AC,O是△ABC内一点,且OB=OC,求证:AO⊥BC.证明:延长AO交BC于D在△ABO和△ACO中⎧⎩⎨⎪⎪AB=AC()OB=OC()AO=AO()∴△ABO≌△ACO(___)∴∠BAO=∠CAO即∠BAD=∠CAD(___)∴AD⊥BC,即AO⊥BC(___)考点:全等三角形的判定如图,已知△ABC的面积为12,AD平分∠BAC,且AD⊥BD于点D,则△ADC的面积是()A. 10B. 8C. 6D. 4考点:[角平分线的性质]如图,在△ABC中,AB的垂直平分线EF交BC于点E,交AB于点F,D为线段CE的中点,BE=AC.(1)求证:AD⊥BC.(2)若∠BAC=75∘,求∠B的度数。
考点:等腰三角形的性质,线段垂直平分线的性质如图,在△ABC中,∠BAC=120∘,AB=AC,点D在BC上,且BD=BA,点E在BC 的延长线上,且CE=CA.(1)试求∠DAE的度数。
(2)如果把题中“AB=AC”的条件去掉,其余条件不变,那么∠DAE的度数会改变吗?(3)若∠BAC=α∘,其它条件与(2)相同,则∠DAE的度数是多少?考点:[等腰三角形的性质, 三角形内角和定理, 三角形的外角性质]。
三等分角仪的用法

使用三等分角仪的方法如下:
1.准备卡片:首先,需要在塑料卡片上找到中心点,并在卡片上画出两条彼此
垂直的线段,这些线段应在中心的交点相遇。
为了更精确地找到中心点,可以使用直角三角尺。
2.标记角度:接下来,需要根据想要三等分的角度大小,在卡片上标出相应的
短、中、长三个线段。
例如,如果角度为60度,则应使用尺子在卡片上画出20度、40度、和60度标记,每个标记应对应一段不同的长度。
为了区分不同线段,可以使用不同颜色的笔(如红色代表60度标记,蓝色代表40度标记,绿色代表20度标记)。
3.剪切卡片:完成角度标记后,使用剪刀将卡片剪下,留下带有标记的条形卡
片。
4.折叠卡片:将剪下的卡片折成特定的形状,即所谓的“哈夫曼板”。
在这个
过程中,20度和40度标记处的卡片将对折,使得它们之间形成60度的夹角。
然后,剩余的标记可以相互对折,最终形成一个类似梯形的结构。
5.使用三等分角仪:现在,我们可以使用三等分角仪进行角度测量。
将三等分
角仪的短刻度与所画的边重合,并将卡板的中心对准角点。
两条对称的线将分别与该边的接缝对齐,帮助确定其他角度的方向。
苏科版-数学-九年级上册-知识拓展 “三等分角仪”的制作原理是什么?

初中-数学-打印版
初中-数学-打印版
“三等分任意角”属于几何作图三大名题(也是难题)之一.
数学上已经证明,仅用圆规、直尺三等分任意角是不可能的.使用量角器三等分任意角的方法简便易行,但准确性太差.
在工程作图中,为了提高工作效率,适应施工的需要,制图的工具不受圆规、直尺的限制.利用圆的切线的有关性质,可以制作一个三等分任意角的工具——三等分角仪,能把任意一个角分成三等分.
把板材(纸板、木板、金属板、塑料板等)制成图中阴影部分的形状,使AB 与半圆的半径CB 、CD
相等,PB 垂直于AD (即PB 与半圆相切,切点为B ).这便做成了一个“三等分角仪”.
如果要把∠MPN 三等分时,可将三等分角仪放在∠MPN 上,适当调整它的位置,使PB 通过角的顶点P ,使A 点落在角的PM 边上,使角的另一边与半圆相切于E 点.最后通过B 、C 两点分别作两条射线PB 、PC ,则∠MPB =∠BPC =∠CPN .
证明:连结CE ,则CE ⊥PN .
∵Rt △PAB ≌Rt △PCB ≌Rt △PCE ,
∴∠APB =∠BPC =∠CPE =13
∠MPN . 注:在“三等分角仪”的制作和应用过程中,涉及了圆的切线的下列性质:(1)切线和圆只有一个公共点;(2)切线和圆心的距离等于圆的半径;(3)切线垂直于过切点的半径;
(4)经过圆心垂直于切线的直线必经过切点;(5)经过切点垂直于切线的直线必经过圆心;
(6)从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角.。
一线三等角证明过程

一线三等角证明过程
嘿,朋友们!今天咱来聊聊“一线三等角”这个神奇的玩意儿!
你看啊,这“一线三等角”就像是一个隐藏在几何世界里的小秘密。
想象一下,一条直线上,三个角整整齐齐地排着,是不是有点像三个好兄弟站成一排呀!
咱们先来说说它的特点。
这三个角啊,那可是有特殊关系的呢!它们就像商量好了似的,有着某种奇妙的联系。
你说神奇不神奇?
那怎么用它来解题呢?这可就有讲究啦!当你看到那一条直线上出现了三个角,嘿嘿,那你就得留个心眼啦!这说不定就是“一线三等角”在向你招手呢。
比如说,在一个图形里,你突然瞅见了这样的情况,那你就得赶紧开动脑筋啦。
想想看,这三个角能给你带来什么线索?它们能让你找到哪些边之间的关系?
就好比是你在走迷宫,突然发现了一个特别的标记,那你不就得顺着这个标记找路嘛!这“一线三等角”就是那个特别的标记呀。
你再想想,要是没有它,你可能就得在那一堆线条和角里瞎转悠,找不到头绪。
但有了它,就像有了一盏明灯,指引着你找到正确的方向。
而且啊,这“一线三等角”还特别实用呢!在好多几何问题里都能派上大用场。
它能让那些看起来很复杂的图形一下子变得清晰起来。
不信你试试,下次遇到几何题,先找找有没有“一线三等角”,然后再根据它提供的线索去解题,看看是不是容易多了。
哎呀呀,这“一线三等角”可真是几何世界里的宝贝呀!它能让我们更轻松地理解和解决那些复杂的几何问题。
所以啊,大家可千万别小瞧了它,要好好去研究研究,把它的奥秘都给挖出来!让我们在几何的海洋里畅游,利用“一线三等角”这个神奇的工具,攻克一个又一个难题!这“一线三等角”,真的是太有意思啦!。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三等分角仪证明过程
引言
三等分角仪是一种用于将一个角度等分为三等份的测量工具。
在几何学中,角度的等分是一项重要的任务,它可以帮助我们在建筑、制图、天文学等领域中进行精确的角度划分。
本文将详细介绍三等分角仪的证明过程,帮助读者理解该工具的原理和使用方法。
证明过程
为了证明三等分角仪的原理,我们需要借助一些基本的几何定理和概念。
下面将逐步介绍证明过程。
步骤1:构造等边三角形
首先,我们需要构造一个等边三角形ABC作为基础。
在平面上选择一个点O作为三角形的中心,然后以O为圆心,OA为半径画一个圆。
再以O为圆心,OB为半径画
第二个圆。
最后以O为圆心,OC为半径画第三个圆。
这样我们就得到了一个等边
三角形ABC,其中AO、BO、CO分别为三角形的边。
步骤2:构造三等分角仪
接下来,我们需要构造一个三等分角仪。
在等边三角形ABC的边上,分别取三个点D、E、F,使得AD=BE=CF。
然后连接OC、OF和OE。
这样就构造出了一个三等分角仪,其中OC是三等分角仪的基线,OF和OE是三等分角仪的刻度线。
步骤3:证明三等分角仪的原理
现在我们来证明三等分角仪的原理。
首先,我们知道在等边三角形ABC中,角A、
角B和角C的度数都是60度。
我们可以通过测量角A来验证三等分角仪的准确性。
我们先测量角AOC的度数,假设为x度。
然后通过三等分角仪的刻度线OF和OE来测量角AOF和角AOE的度数,假设分别为y度和z度。
根据三等分角仪的设计,我们可以得到以下等式:
x = y + z
接下来,我们需要证明角AOC的度数是角A的三分之一。
根据等边三角形ABC的性质,我们知道角AOC的度数是60度。
因此,我们需要证明以下等式成立:
x = 3 * y
将之前的等式代入上述等式中,可以得到:
y + z = 3 * y
化简后得到:
z = 2 * y
由于y和z是三等分角仪的刻度线所测得的度数,它们是等分的。
因此,我们可以得出结论:角AOC的度数是角A的三分之一。
步骤4:使用三等分角仪
现在我们已经证明了三等分角仪的原理,接下来我们将介绍如何使用三等分角仪来等分角度。
首先,我们需要将需要等分的角度放置在三等分角仪的基线上。
然后,通过刻度线OF和OE来测量角度的度数。
根据之前的证明,我们知道刻度线OF和OE所测得的
度数是等分的。
因此,我们可以通过刻度线的位置来确定角度的等分点。
为了更精确地等分角度,我们可以使用更小的刻度线来增加测量的准确性。
例如,我们可以在刻度线OF和OE之间再添加一些刻度线,使得刻度更加细密。
结论
通过上述证明过程,我们可以得出结论:三等分角仪可以将一个角度等分为三等份。
这个工具的原理是基于等边三角形的性质和三等分角仪的设计。
使用三等分角仪可以帮助我们在各种领域中进行精确的角度划分,如建筑、制图、天文学等。
希望本文的介绍能够帮助读者更好地理解三等分角仪的原理和使用方法。
通过掌握这个工具,我们可以更准确地测量和划分角度,提高工作和学习的效率。
