三等分角的小工具

合集下载

磬折形尺如何三等分一个角

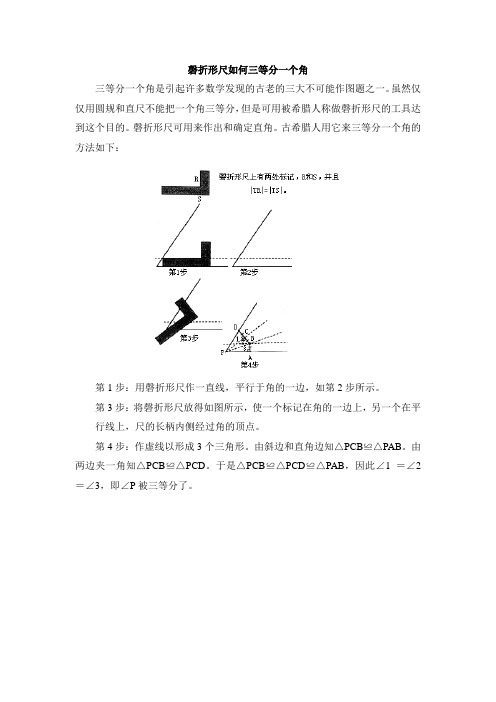
磬折形尺如何三等分一个角
三等分一个角是引起许多数学发现的古老的三大不可能作图题之一。

虽然仅仅用圆规和直尺不能把一个角三等分，但是可用被希腊人称做磬折形尺的工具达到这个目的。

磬折形尺可用来作出和确定直角。

古希腊人用它来三等分一个角的方法如下：
第1步：用磬折形尺作一直线，平行于角的一边，如第2步所示。

第3步：将磬折形尺放得如图所示，使一个标记在角的一边上，另一个在平行线上，尺的长柄内侧经过角的顶点。

第4步：作虚线以形成3个三角形。

由斜边和直角边知△PCB≌△PAB。

由两边夹一角知△PCB≌△PCD。

于是△PCB≌△PCD≌△PAB，因此∠1 ＝∠2＝∠3，即∠P被三等分了。

阿基米德三等分角方法(一)

阿基米德三等分角方法(一)阿基米德三等分角一、背景介绍阿基米德三等分角，是指将一个给定的角分为三等分，是古希腊数学家阿基米德在几何学领域的一项重要成果。

在数学中，人们常常通过多种方法来实现这一任务。

本文将详细介绍其中一些方法。

二、准备工作要进行阿基米德三等分角的操作，我们首先需要准备以下工具：1.直尺：用于测量和绘制直线。

2.路径指示器：用于绘制弧线和角度。

3.钢笔：用于绘制精细直线和弧线。

4.良好的纸张：以确保绘制的角度准确无误。

三、阿基米德方法阿基米德本人提出了一种简单的方法来实现三等分角，以下是具体步骤：1.给定一个角A，用直尺绘制出角的两条边AB和AC。

2.在边AB上取一点D，使得AD = AC。

3.连接点D和C，并延长线段CD与边AC相交于点E。

4.绘制圆心为D，半径为AD的圆，并标记圆心为F，圆与边AC的交点为G。

5.连接点F和G，并延长线段FG与边AB相交于点H。

6.以点H为圆心，半径为HA的圆与边AB和射线AC相交于点I和J。

7.连接点I和D，点J和D，即可得到所求的三等分角。

四、割三法除了阿基米德方法，还存在一种称为割三法的传统方法，以下是具体步骤：1.给定一个角A，用直尺绘制出角的两条边AB和AC。

2.在边AB上取一点D，使得AD = AC。

3.以点D为圆心，半径为AD的圆与角ACB的边AC和射线AB相交于点E和F。

4.连接点E和A，点F和A，并延长线段EF与边AC相交于点G。

5.连接点G和D，并延长线段GD与边AB相交于点H。

6.连接点C和H，并延长线段CH与边AC相交于点I。

7.连接点I和A，即可得到所求的三等分角。

五、三等分角的应用三等分角在几何学和工程学中有着广泛的应用。

以下是一些常见应用场景：1.设计建筑结构中的三等分角，以确保各个构件的位置和角度准确无误。

2.绘制平面图时，通过三等分角来绘制不同位置和角度的线段。

3.制作艺术品和工艺品时，通过三等分角来实现精确的图案和比例。

圆三等分最简单的方法

圆三等分最简单的方法
圆三等分是一项相对困难的几何问题，它要求将一个圆分成三个角度相等的部分。

在几何学中，圆三等分被称为三等分圆周角问题，它的解法有很多种，其中最简单的方法如下：
1.将圆心O作为三个等分角的公共点，画出圆心角AOB(120度)。

2.以O为圆心，OA为半径，画出一个圆弧，将圆心角AOB分成两个相等的角BOC(60度)、AOC(60度)。

3.以O为圆心，OB为半径，画出第二个圆弧，将角BOC(60度)再等分成两个角COD(30度)和EOB(30度)。

4.以O为圆心，OC为半径，画出第三个圆弧，它将原来的角AOC(60度)等分成DEO(20度)和EOC(40度)两个角。

5.经过以上步骤，圆周角AOB已经被等分为三个相等的角所组成的三个角度相等的部分。

通过以上的步骤，我们成功地将圆周角AOB平分成了三个角度相等的部分。

这种方法的关键在于利用三个圆弧分别作为圆心角和第一等分角和第二等分角以及第三等分角的分割工具。

这样，我们就能够有效地分割圆周角，并得到三个角度相等的部分。

总之，通过本文所介绍的方法和步骤，相信大家也能够学会圆三等分
的解法，同时也能够更好地理解相关几何概念，提升自己的数学水平。

尺规角三等分与垂足弧弦切分角

尺规角三等分与垂足弧弦切分角发布时间：2021-06-16T11:43:31.590Z 来源：《现代中小学教育》2021年6月作者：冯国义[导读] 我发明的用无刻度直尺和圆规，可以对任意角进行任意等份的平分方法。

破解了2500年前由古希腊人提出来的，用尺规作图三等分角无解的世界难题。

创作者：冯国义我发明的用无刻度直尺和圆规，可以对任意角进行任意等份的平分方法。

破解了2500年前由古希腊人提出来的，用尺规作图三等分角无解的世界难题。

两千五百年来，无数先人对尺规作图三等分角不断的研究，或画图或演算都没能给予答案，被公认为无解题。

十九世纪法国数学家皮埃尔·旺策尔就曾宣布尺规作图三等分角无解。

我国著名数学家华罗庚曾说过：“用圆规直尺三等分任意角就如同步行上月球一样，是不可能的”。

然而，我经数年攻关研究，终于在1995年11月13日为这个世界难题划上了句号。

非但对任意角三等份，可以五等份，七等份及任意等份的平分。

用我发明的垂足弧弦切分任意角方法，就可以做出任何一个度数的角。

而不用解析几何，函数计算，免除用弧长公式计算查表画图的麻烦。

这一方法定会给工业生产、科研、教学的角平分方面带来方便利好。

第一部分垂足弧弦切分分角方法的做法1、用一个无刻度直尺和圆规和画图用纸，首先在纸面上画两条交叉的直线，相交于一点0。

2、用圆规设一任意长，以0点为圆心在任意角上划弧相交于任意角的两条边线上A点和B点，形成任意角上的弧叫单位弧，所设半径叫单位半径。

3、用直线连接AB两点，形成AB弧上的弦叫单位弦。

4、用圆规以单位半径为单位，在任意角B侧边线上，向0到B从B点向远方再截切二段单位半径长。

交于0B一侧任意角边线上一点B1。

5、用圆规以0点为圆心，以0B1为半径，从B1向0A一侧边线划弧交于0A一侧边线上一点A1，形成A1B1弧叫任意角分角原始弧。

6、从B1点起，以AB弦长为单位用圆规在A1B1弧上截切三段，形成1.2.3点，有余弧没有分完，把余弧分为平分的两份。

论用圆规和直尺能将一个角三等分(续文)

论用圆规和直尺能将一个角三等分（续文）对于此题的证明，是在通过具体解题过程得出解题结果之后，对于这一具体解题结果的正确与否所进行的证明。

通过本人的不懈努力，在三十多年的证明研究过程中，经过了数百次的反复纠改，终使这一结果得到了严谨的理论证实。

解题步骤：参见图1，以任意角的顶点O为原点，以任意长为单位，分别在角的两个边上连续截取三个相等的单位，令第一个单位上的点分别为E、F，令第三个单位上的点分别为P、Q。

以P点为圆心，以E、F两点距离为半径在角内划弧，再从E、F两点引出切线与该弧相切，两条切线相交于点B，以同样的方法以Q点为圆心，可得另一交点C。

B、C两点就是角的三等分线所经过的点。

以O点为圆心，以OB或OC的长度为半径在角内划弧，分别交角的两边于A、D两点。

连接AB、BC和CD，若能证明出AB=BC，或BC=CD，则说明B、C两点，就是角的三等分线所经过的点。

因为OE=OF，OA=OD，OP=OQ，AB=CD，所以，EF、AD、PQ、BC都是关于角平分线对称的点。

证明过程：参见图2，首先连接P、Q，交EB于点H，交FC于点R。

因为OP=3OE，OQ=3OF，所以，PQ=3EF，所以PH=HR=RQ。

连接AD，便得AD∥BC，且AD ∥EF。

连接ER，交AD于N，再连接FH交AD于M。

因此M、N两点也是关于角平分线对称的点，所以MB=NC，同时便得出一个等腰梯形NMBC，则有BN=MC。

因为EF∥=RQ，所以ND∥=RQ，所以ND∥=BC，所以四边形NBCD是一个平行四边形，若证明出四边形NBCD为菱形，就可以说明BC两点就是角的三等分线所经过的点。

参见图3，以N点为圆心，以BC长为半径画弧，交AM于W点；连接WB 并延长到等于一倍WB长的一点Z，则有WB∥=NC，BZ∥=NC，所以，WB=MB （等量代换）。

过M点作NC的平行线，交BN于K，交BC于G，则有BZ∥=MG，再以B点为圆心，以WB长为半径划弧，交由M点所作的与NC相平行的线于T点，连接BT则有WB=MB=BZ=BT，连接ZT和TC以后，若能证明Z、T、C三点是在同一直线上的点，整个问题就可以应刃而解。

苏科版-数学-九年级上册-知识拓展 “三等分角仪”的制作原理是什么？

初中-数学-打印版
初中-数学-打印版
“三等分任意角”属于几何作图三大名题（也是难题）之一．
数学上已经证明，仅用圆规、直尺三等分任意角是不可能的．使用量角器三等分任意角的方法简便易行，但准确性太差．
在工程作图中，为了提高工作效率，适应施工的需要，制图的工具不受圆规、直尺的限制．利用圆的切线的有关性质，可以制作一个三等分任意角的工具——三等分角仪，能把任意一个角分成三等分．
把板材（纸板、木板、金属板、塑料板等）制成图中阴影部分的形状，使AB 与半圆的半径CB 、CD
相等，PB 垂直于AD （即PB 与半圆相切，切点为B ）．这便做成了一个“三等分角仪”．
如果要把∠MPN 三等分时，可将三等分角仪放在∠MPN 上，适当调整它的位置，使PB 通过角的顶点P ，使A 点落在角的PM 边上，使角的另一边与半圆相切于E 点．最后通过B 、C 两点分别作两条射线PB 、PC ，则∠MPB ＝∠BPC ＝∠CPN ．
证明：连结CE ，则CE ⊥PN ．
∵Rt △PAB ≌Rt △PCB ≌Rt △PCE ，
∴∠APB ＝∠BPC ＝∠CPE ＝13
∠MPN ．注：在“三等分角仪”的制作和应用过程中，涉及了圆的切线的下列性质：（1）切线和圆只有一个公共点；（2）切线和圆心的距离等于圆的半径；（3）切线垂直于过切点的半径；
（4）经过圆心垂直于切线的直线必经过切点；（5）经过切点垂直于切线的直线必经过圆心；
（6）从圆外一点引圆的两条切线，它们的切线长相等，圆心和这一点的连线平分两条切线的夹角．。

三等分任意角的作法探讨

㊀㊀㊀㊀㊀１４０数学学习与研究㊀２０２０１０三等分任意角的作法探讨三等分任意角的作法探讨Һ蔡长青㊀（咸丰县中等职业技术学校，湖北㊀咸丰㊀４４５６００）㊀㊀ʌ摘要ɔ 三等分角是古希腊几何中尺规作图的名题，和化圆为方㊁倍立方问题并列为古代数学的三大难题，２４００多年以来，不少学者进行了无数次尝试，都未能找到好的解决方法，笔者经过４０余载的不断探索，吸取前人的数学智慧，突破传统思维，找到简单易行的求作三等分角的方法，该方法可以广泛应用到几何教学或工程技术领域．ʌ关键词ɔ三等分；任意角；作法；证明１９７９年的九月，进入咸丰一中学习的第一堂数学课上，满头银发的数学老师文渊不但满怀激情地介绍了高中三年数学学习的目标和学习方法，还向大家抛出了古代数学的三大难题，即用尺规作图法求作三等分任意角㊁化圆为方以及倍立方问题，从此笔者与三等分角问题结下了不解之缘．三等分角是号称古希腊三大几何问题之一，该问题的完整叙述为：只用圆规及一把没有刻度的直尺将一个给定角三等分．该问题自公元前４８０年以来，不少学者进行了长期的探索，甚至不少著名数学家从不同角度论证了用尺规作图法不可能解决三等分角问题，本着吸取前人数学智慧㊁传承文明㊁尊重科学的治学态度，本人就解决使用尺规作图法三等分任意角问题进行了长期的探索，现将偶有所得分享给大家，希望起到抛砖引玉的作用．一㊁关于三等分任意角的历史溯源１．三等分任意角问题产生的历史背景根据历史记载，公元前４８０年，古希腊和当时的波斯国在当时的雅典郊外萨尼克湾展开了一场惨烈的海战，古希腊大获全胜，从此雅典作为古希腊的政治㊁文化㊁经济中心逐渐走向繁荣．社会分工逐渐细化，一部分人从繁重的体力劳动中解放出来，出现了专门传授学问㊁研究学问的辩论师或称智者，也就是现代的职业教师．这些人为古希腊文明做出了巨大的贡献，其中在几何学上亦留下了三大难题供后人进行研究和探讨：给你一把圆规和直尺（无刻度），经过有限次的步骤，能否：①对任意角作三等分？②作已知立方体的二倍体积的立方体图形？③作与已给的圆面积相等的正方形？以上三个问题分别称为三等分角问题㊁倍立方问题和化圆为方问题，也称古希腊三大几何难题，这些问题看起来很简单，但是，２４００多年来，不少数学家或数学爱好者为了解决这三个问题，耗费了许多心血，都没有取得成功．２．三等分任意角可能无法用尺规作图法求解１６３７年笛卡儿（ＲｅｎｅＤｅｓｃａｒｔｅｓ，１５９６１６５０）创立了解析几何学后，有数学家依据解析几何，认为找到了通过尺规作图法不能解决三等分任意角问题的依据．１８３７年法国数学家旺策尔（ＰｉｅｒｒｅＬａｕｒｅｎｔＷａｎｔｚｅｌ，１８１４１８４８）首先证明了倍立方和三等分任意角不可能用尺规作图解决．１８７３年埃尔米特（ＣｈａｒｌｅｓＨｅｒｍｉｔｅ，１８２２１９０１）证明了ｅ是超越数；１８８２年德国数学家林德曼（Ｌｉｎｄｅｍａｎｎ，１８５２１９３９）证明了π也是超越数，从而变圆为方的不可能性也得以确立．１９６５年以前，数学家华罗庚曾写文章告诫青少年用直尺和圆规三等分任意角是不可能的，不要为这道难题花费精力．２００１年华中师范大学数学系的王中华亦在‘数学通讯“上发文并证明使用尺规作图三等分任意角是不可能的．二㊁三等分任意角仍有研究的价值１．高中数学教学的需要为了加强普通高中的数学教学，在新版的‘普通高中数学课程标准“中增加了三等分角与数域扩充问题，让三等分角问题真正进入我国高中数学教学领域，有利于扩展学生的数学视野，激发学生的学习兴趣，提高学生解决问题㊁分析问题的能力．２．可以促进人的数学思维的发展古希腊的三大几何难题，几千年来尽管耗费了历代数学家不少的心血，但是在解决这类问题的过程中，不仅促进了数学思想的发展，而且在人类其他思想史上亦具有重大意义．三㊁预备知识１．尺规作图法关于尺规作图法，以科学出版社出版的‘数学大辞典“中的规定为主要参考依据：尺规作图法又称初等几何作图法或欧几里得作图法．仅用直尺（无刻度）和圆规（两脚足够长）两种工具按照下述步骤进行有限次的组合来完成的几何作图方法．（１）过两点可画一条直线（或一条射线），连接两点成一线段．（２）延长线段成一条直线或射线．（３）以定点为圆心定长为半径可画圆或圆弧．２．初等几何知识本文涉及的初等几何知识，我们还是沿用科学出版社出版的‘数学大辞典“中的相关论述：（１）关于角的分类平角：两边组成一条直线的角，或一条射线在平面内绕㊀㊀㊀１４１㊀数学学习与研究㊀２０２０１０着它的端点旋转，转到和原来位置构成一条直线时所形成的角．１平角＝１８０ʎ．直角：平角的一半，一直角＝９０ʎ．锐角：大于０ʎ小于直角的角．钝角：大于直角小于平角的角．（２）关于三角形和圆的几个基本知识等腰三角形的定义及性质：两边相等的三角形是等腰三角形，等腰三角形的两个底角相等．三角形外角定理：三角形的外角等于和它不相邻的两个内角之和．圆心角定理：圆心角的度数等于它所对的弧的度数．圆周角定理：圆周角的度数等于它所对的弧的度数的一半．显然，同弧所对的圆心角等于圆周角的２倍．３．关于图学的几点相关知识的说明（１）图学是几何学与行为科学有机结合的综合性学科．图学一开始就是由理论几何学与行为科学有机构成的．从平面几何开始，发展到画法几何㊁工程图㊁地形图等，人们在制图过程中总要依据几何原理，经过人的科学行为（制图）表达完成各类制图工作．（２）图学是理论与实践相结合的科学，图学允许可逆．无论同时行为还是第三度行为，都是在允许行为可逆基础上进行的，行为本身就是四维的运动（时间维㊁空间维），允许可逆自然是在四维时空中进行的．四㊁三等分任意角的作图方法以锐角为例，使用尺规作图法三等分任意角的作图步骤如下：第１步：给定任意角øＡＯＢ．第２步：作边ＯＡ的反向延长线ＯＣ．第３步：以Ｏ点为圆心，Ｒ为半径长画☉Ｏ，圆弧与边ＯＢ交于Ｆ点．第４步：在☉Ｏ上，以Ｅ点为圆心，Ｒ为半径长画☉Ｅ，☉Ｅ与ＯＡ的反向延长线交于Ｄ点，配合使用圆规和直尺，确保圆心Ｅ与Ｄ，Ｆ三点在同一直线上．第５步：连接ＯＥ，最终形成如图所示的几何图形．需要特别说明的是在作图过程中，第４步圆心的确认很关键，有可能需要多次逼近才能确定．五㊁三等分任意角的证明通过以下两种方法分别证明前面的作图方法可以三等分任意角．方法一：在☉Ｅ中，因为øＯＤＦ为圆周角，øＯＥＦ为圆心角所以øＯＥＦ＝２øＯＤＦ．因为ＯＥ＝ＯＦ，所以әＥＯＦ为等腰三角形，øＥＦＯ＝øＯＥＦ＝２øＯＤＦ，øＡＯＢ＝øＯＤＦ＋øＥＦＯ＝３øＯＤＦ，故有øＯＤＦ＝１３øＡＯＢ．方法二：在әＤＥＯ中，因为ＤＥ＝ＯＥ，所以әＤＥＯ为等腰三角形，所以øＯＤＥ＝øＥＯＤ，øＯＥＦ＝２øＯＤＥ，因为ＯＥ＝ＯＦ，所以әＥＯＦ为等腰三角形，所以øＥＦＯ＝øＯＥＦ＝２øＯＤＦ，øＡＯＢ＝øＯＤＦ＋øＥＦＯ＝３øＯＤＦ，故有øＯＤＦ＝１３øＡＯＢ．六㊁结㊀论通过以上的作图和证明，我们有理由认为对三等分任意角的作法有革命性的突破．１．作图过程中严格遵守尺规作图法的要求，且在有限的步骤内准确三等分角．２．通过初等几何理论对所作图形进行了严密的证明，结果正确．３．整个作图过程符合图学是理论与实践相结合的科学观点：图学允许可逆，无论同时行为还是第三度行为，都是在允许行为可逆基础上进行的．路曼曼其修远兮，吾将上下而求索．ʌ参考文献ɔ［１］娄桐城．中学数学词典［Ｍ］．北京：知识出版社，１９８４．［２］王元．数学大辞典［Ｍ］．北京：科学出版社，２０１０．［３］熙国维．运动论［Ｍ］．北京：海洋出版社，１９９３．［４］Ｒ．柯良（ＲｉｃｈａｒｄＣｏｕｒａｎｔ），Ｈ．罗宾（ＨｅｒｔｂｅｒｔＲｏｂｂｉｎｓ）．什么是数学［Ｍ］．左平，张饴慈译．上海：复旦大学出版社，２００８．［５］欧几里得．几何原本［Ｍ］．邹忌译．重庆：重庆出版社，２０１８．［６］（日）远山启著．吕砚山㊁李诵雪㊁马杰㊁莫德举译著．数学与生活［Ｍ］．北京：人民邮电出版社，２０１４．［７］王中华．用尺规作图不可能三等分任意角［Ｊ］．数学通讯，２００１（１９）．４８．。

把角三等分

另有一机械作图的方法可以三等分角，简介如下：
如右图：ABCD为一正方形，设AB均匀向CD平行移动，AD以D为中心依顺时针方向转到DC，若AB抵达DC时DA也恰好抵达DC，则他们交点的轨迹AO即曲线称为三分线。
令A是AC弧上的任一点，我们要三等分 ADC，设DA与三分线AO交于R，过R作AB之并行线交AD、BC于A、B，令T、U是AD之三等分点，过T、U作AB之并行线交三分线AO于V、W，则DV、DW必将 ADC三等分。
回答者：暗夜男爵星 - 高级魔法师七级 3-4 21:05
古希腊三个著名问题之一的三等分角，现在美国就连许多没学过数学的人也都知道．美国的数学杂志社和以教书为职业的数学会员，每年总要收到许多“角的三等分者”的来信；并且，在报纸上常见到：某人已经最终地“解决了”这个不可捉摸的问题．这个问题确实是三个著名的问题中最容易理解的一个，因为二等分角是那么容易，这就自然会使人们想到三等分角为什么不同样的容易呢？
为了解三等分角归结成的斜向问题，有许多高次平面曲线已被发现．这些高次平面曲线中最古老的一个是尼科梅德斯(约公元前240年)发现的蚌线．设c为一条直线，而O为c外任何一点，P为c上任何一点，在PO的延长线上截PQ等于给定的固定长度k．于是，当P沿着c移动时，Q的轨迹是c对于极点O和常数k的蚌线(conchoid)(实际上，只是该蚌线的一支)．设计个画蚌线的工具并不难①，用这样一个工具，就可以很容易地三等分角．这样，令∠AOB为任何给定的锐角，作直线MN垂直于OA，截OA于D，截OB于L(如图32所示)．然后，对极点O和常数2(OL)，作MN的蚌线．在L点作OA的平行线，交蚌线于C．则OC三等分∠AOB．
在研究「三等分角」的过程中发现了如蚌线、心脏线、圆锥曲线等特殊曲线。人们还发现，只要放弃「尺规作图」的戒律，三等分角并不是一个很难的问题。古希腊数学家阿基米得（前287－前212）发现只要在直尺上固定一点，问题就可解决了。现简介其法如下：在直尺边缘上添加一点P，命尺端为O。设所要三等分的角是∠ACB，以C为圆心，OP为半径作半圆交角边于A，B；使O点在CA延在线移动，P点在圆周上移动，当尺通过B时，连OPB（见图）。由于OP＝PC＝CB，所以∠COB＝∠AC B／3。这里使用的工具已不限于标尺，而且作图方法也与公设不合。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

下面介绍一种三等分角的小工具。

（一）工具的制作
1．材料：透明直尺五根、透明圆一个、空心铆钉六只。

2．制作方法：将五根透明直尺用铆钉钉成如图所示的并列的两个全等的菱
形，透明的直径d等于DF，圆心钉
在E点上。

如图（一）
图一
（二）操作方法
把任意∠POQ三等分，将此工具
的点B与∠POQ的顶点O重合，BC
与OP重合，然后根据四边形的不稳定
形，扭动小工具，使边OQ与透明圆在
AD上交于同一点M，射线OE，OF
就将∠POQ三等分。

（三）证明
连结FM交BE于点N，连BF，
图二
∵以DF为直径的圆及OQ边交于AD于M。

∴FM⊥AD
∵AD∥OE，DE=EF，
∴ON是FM的垂直平分线，
∴∠QOP=∠EOF。

又∵四边形OEFC是菱形
∴∠EOF=∠FOP
∴∠QOE=∠EOF=∠FOP
∴OE，OF三等分∠QOP
P。