速度瞬心法作机构速度分析
机械原理-简单机构速度分析的速度瞬心法

三心定理
作平面运动的三个构件共有三个瞬ቤተ መጻሕፍቲ ባይዱ,
它们位于同一直线上.
Vk1 K 2 1 Vk2
瞬心的应用
瞬心的应用
1 与3 的关系 已知四杆机构的尺寸及 1求全部瞬心、
P24 1 2 2
v p13 1 p14 p13 l
p23
3
p12 1 P13 p14
4
3
v p13 3 p34 p13 l
∞
v2 v p1 2 1 p13 p12 l
p13
1
p12
已知下列机构的尺寸及
求全部瞬心、 与
的关系
3
∞ P23
2
p13
p12
1
v2 v p1 2 1 p13 p12 l
速度瞬心
VA A B VB
v p1 v p2 0
绝对瞬心
P12
VA1 A2
2 A B
v p1 v p2 0
VB1B 2
相对瞬心
1
P12
P12
瞬心的数目
n ( n 1) N 2
•N-瞬心数
•n-构件数
瞬心的求法
观察法
P12
P12在无穷远
P12 P12在公法线上
三心定理
4 p34
p34 p13 1 3 p14 p13
已知下列机构的尺寸及
求全部瞬心、 与
的关系
p13 P12 1
v p12 1 p13 p12 l 2 p23 p12 l
p23 p12 1 2 p13 p12
2
p23
3
已知下列机构的尺寸及
求全部瞬心、 与
的关系
3.2 平面机构运动分析的图解法

第三章平面机构的运动分析3.2平面机构运动分析的图解法3.2.1速度瞬心法化1) 速度瞬心与位置图3.2F01所示的两构件1、2均作平面运动,在任一瞬时的相对运动都可以看作是绕平面上某一点的相对转动,而该点则称为它们的速度瞬心,简称为瞬心,以P12表示。
瞬心是两构件上相对速度为零的点,或者说是两构件上速度相等的点。
若在该瞬心的绝对速度为零,则称为绝对瞬心。
若不为零,则称为相对瞬心。
由于每两个构件具有一个瞬心,所以对于由N个构件组成的机构,根据排列组合的知识可知,其瞬心总数K 为K =N(N-1)/2 (3.1)【点击链接转摆变换的平面六杆机构的二维动画】对于例图,瞬心数目K为K =6(6-1)/2=15 (3.1')(1) 通过运动副直接相连的两构件的瞬心位置(a) 以转动副相连的两构件,如图3.1(a)所示,其瞬心在转动副的中心上。
(b) 以移动副相连的两构件,如图3.1b 所示,由于在平面任一点处两构件相对运动的速度方向均平行于移动副导路,所以,P12一定位于无穷远。
(c) 以平面高副相连的两构件,如图3.1c 所示,若高副两元素之间为纯滚动(ω12为相对滚动的角速度),则两元素的接触点M即为瞬心P12。
(d) 若高副两元素间既有相对滚动,又有相对滑动(V12为相对滑动速度),则瞬心P12必定位于高副过接触点的公法线n-n上,如图3.1d 所示,具体位置需要根据其他条件来确定。
(2) 不直接通过运动副相连的两构件的瞬心位置不直接通过运动副相连接的两构件的瞬心位置由三心定理予以确定。
所谓三心定理是指三个彼此作平面相对运动的构件的三个瞬心必定位于同一直线上。
只有K在P12、P13的连线上,V K2与V K3才能方向相同,当位置合适, V K2与V K3大小一样,为此。
平面相对运动的构件的三个瞬心必定位于同一直线上。
2) 用速度瞬心作机构的速度分析(1) 铰链四杆机构如图 3.3 所示,比例尺为μL (单位为m/mm)的铰链四杆机构,若已知原动件1以角速度ω1顺时针方向回转,求从动件2、3的角速度ω2、ω3。
械原理第二章平面结构的运动分析(朱理)

1) 作机构运动简图 取μl,作机构运动简图,确定位置。 2) 速度分析 选取研究对象,写速度矢量方程, 取μv,作速度图; 3) 加速度分析 写加速度矢量方程; 取μa,作加速度图。
用图解法作机构的速度及加速度分析
例:已知摇块机构各构件尺寸,lAB=100mm,lAC=200mm,lBS2=86mm,
目的
了解已有机械的运动性能、设计新的机械和研究 机械的动力性能。
方法
主要有图解法和解析法。
用速度瞬心法作机构的速度分析
1.瞬心及其位置确定
(1)速度瞬心:
速度瞬心: 即两构件上的瞬时等速重合点,用Pij表示。 绝对瞬心:Vp=0 相对瞬心:Vp≠0 机构瞬心的数目为: K N(N 1) / 2
(2)瞬心的位置确定 ■由瞬心定义确定瞬心的位置 P30图2-2
C3
D
2
4
B
1 w1
A
p (b3)
b2(b1)
vB3B2方向线 vB3方向线
p'
atB3
b2'
b3'
arB3B2方向线
例2.3 在图示机构中,设已知各构件的尺寸,原动件角速度
w1为常数。试求机构在图示位置时滑块5的速度、加 速度,构件3和构件4的角速度及角加速度。 解: 1) 作机构运动简图 取μl,作机构运动简图,确定位置。 2) 速度分析
如构件2上C、B点间的相对速度为:
vCB v bc m/s
vCB 的方向为 bc。
E
2. 同一构件上两点间的加速度分析
2
C
由已a知B得B点a的Bn加速a度Bt为:
方向:? BA ⊥AB
α1 B
ω2
ω1 A1
第二讲 机构的运动分析
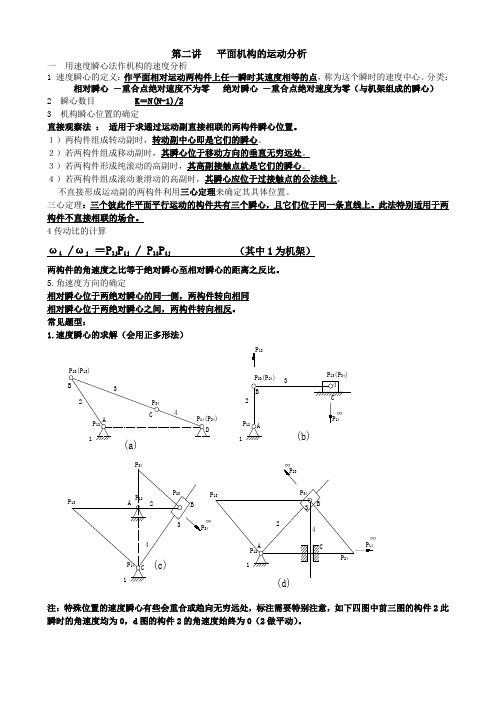
第二讲平面机构的运动分析一用速度瞬心法作机构的速度分析1 速度瞬心的定义:作平面相对运动两构件上任一瞬时其速度相等的点,称为这个瞬时的速度中心。
分类:相对瞬心-重合点绝对速度不为零绝对瞬心-重合点绝对速度为零(与机架组成的瞬心)2 瞬心数目 K=N(N-1)/23 机构瞬心位置的确定直接观察法:适用于求通过运动副直接相联的两构件瞬心位置。
1)两构件组成转动副时,转动副中心即是它们的瞬心。
2)若两构件组成移动副时,其瞬心位于移动方向的垂直无穷远处。
3)若两构件形成纯滚动的高副时,其高副接触点就是它们的瞬心。
4)若两构件组成滚动兼滑动的高副时,其瞬心应位于过接触点的公法线上。
不直接形成运动副的两构件利用三心定理来确定其具体位置。
三心定理:三个彼此作平面平行运动的构件共有三个瞬心,且它们位于同一条直线上。
此法特别适用于两构件不直接相联的场合。
4传动比的计算ωi /ωj=P1j P ij / P1i P ij(其中1为机架)两构件的角速度之比等于绝对瞬心至相对瞬心的距离之反比。
5.角速度方向的确定相对瞬心位于两绝对瞬心的同一侧,两构件转向相同相对瞬心位于两绝对瞬心之间,两构件转向相反。
注:特殊位置的速度瞬心有些会重合或趋向无穷远处,标注需要特别注意,如下四图中前三图的构件2此瞬时的角速度均为0,d图的构件2的角速度始终为0(2做平动)。
2利用速度瞬心求解速度。
ωi /ωj=P1j P ij / P1i P ij 四杆机构题型:(江苏大学2014)哈工大东华2014 四杆以上机构题型:二、用矢量方程图解法作机构的速度和加速度分析 1.同一构件上两点之间速度,加速度的关系。
①由各速度矢量构成的图形称为速度多边形(或速度图);由各加速度矢量构成的图形称为加速度多边形(或加速度图)。
p ,'p 称为极点。
②在速度多边形中,由极点p 向外放射的矢量,代表构件上相应点的绝对速度。
而连接两绝对速度矢端的矢量,则代表构件上相应两点间的相对速度,方向与角标相反,如bc 代表CB v (C 点相对B 点的速度)。
平面复杂机构速度分析的速度瞬心法

平面复杂机构速度分析的速度瞬心法李晋山( 开封大学机械系, 河南开封475004)摘要:利用速度瞬心法,通过有目的地找出相关瞬心和目标瞬心,解决了多自由度的平面复杂机构速度分析问题。
关键词:瞬心;相关瞬心;目标瞬心;构件关系图;相关构件关系图分类号: T H112文献标识码:A问题的提出1机构运动分析的方法很多,一般认为,对简单的平面机构来说,应用速度瞬心法进行速度分析,特别是对平面高副机构比较简便。
但是,如果是多杆机构,则由于瞬心数目很多,因而将速度分析问题复杂化,这是瞬心法的缺点。
因此,对于复杂机构多采用矢量方程图解法和解析法。
笔者通过研究,认为对于复杂机构的速度分析,只需要找出少数相关瞬心,利用本文中的方法,找出目标瞬心,就可以把问题简单化。
该方法为我们在解决平面复杂机构速度分析的问题时提供了一个既方便又简洁的好方法。
平面复杂机构速度分析的速度瞬心法2对于一个复杂机构,按比例绘出其机构运动简图,对构件进行编号( 包括机架) ,由复杂机构的运动输入端到运动输出端将复杂机构分解成若干个简单的子机构,由机构学知识知道,一般来说,上一个子机构的输出机构即是下一个子机构的输入机构。
从第一个子机构开始,分别作各简单机构的构件关系图。
构件关系图的作法:按环形布置几个点,点的个数与简单机构的构件个数相同,点的编号应与机构中构件号的顺序一致,则任意两点的连线即表示该两构件的瞬心,为了方便解题,用实线表示成副构件的瞬心,用虚线表示不成副构件的瞬心。
这样,成副构件的瞬心直接可以求得,不成副构件的瞬心可利用三心定理求得。
要最终找出目标瞬心(即复杂机构的原动构件与待求构件的瞬心) 还应画一个复杂机构的相关构件关系图,在该图上只需要描述四个点即可。
这四个点分别是原动件、待求构件、机架和最后一个简单机构的输入构件,其结构如图1 。
图中实线相连两构件的瞬心, 我们称之为相关瞬心,虚线相连两构件的瞬心即目标瞬心。
收稿日期:1999 - 11 - 08作者简介:李晋山(1969 - ) ,男,河南开封人,开封大学机械系教师。
考研机械原理第二讲 机构的运动分析

第二讲平面机构的运动分析一用速度瞬心法作机构的速度分析1 速度瞬心的定义:作平面相对运动两构件上任一瞬时其速度相等的点,称为这个瞬时的速度中心。
分类:相对瞬心-重合点绝对速度不为零绝对瞬心-重合点绝对速度为零2 瞬心数目 K=N(N-1)/23 机构瞬心位置的确定直接观察法:适用于求通过运动副直接相联的两构件瞬心位置。
1)两构件组成转动副时,转动副中心即是它们的瞬心。
2)若两构件组成移动副时,其瞬心位于移动方向的垂直无穷远处。
3)若两构件形成纯滚动的高副时,其高副接触点就是它们的瞬心。
4)若两构件组成滚动兼滑动的高副时,其瞬心应位于过接触点的公法线上。
不直接形成运动副的两构件利用三心定理来确定其具体位置。
三心定理:三个彼此作平面平行运动的构件共有三个瞬心,且它们位于同一条直线上。
此法特别适用于两构件不直接相联的场合。
4传动比的计算ωi /ωj=P1j P ij / P1i P ij两构件的角速度之比等于绝对瞬心至相对瞬心的距离之反比5.角速度方向的确定相对瞬心位于两绝对瞬心的同一侧,两构件转向相同相对瞬心位于两绝对瞬心之间,两构件转向相反。
常见题型:1.速度瞬心的求解(会用正多形法)2利用速度瞬心求解速度。
ωi /ωj =P 1j P ij / P 1i P ij例题:在图示四杆机构中,AB l =60mm ,CD l =90mm ,AD l =BC l =120mm ,2ω=10rad/s ,试用瞬心法求: (1)当ϕ=45°时,点C 的速度C v;(2)当ϕ=165°时,构件3的BC 线上(或其延长线上)速度最小的一点E 的位置及其速度大小;(3)当C v =0时,ϕ角之值(有两个解)。
P 13C(a)解:以选定的比例尺0.005/l m mm μ=作机构运动简图如图3-2所示。
(1)定瞬心P 13的位置,求v c 。
131331 6.07rad /AP DP l l s ωω==30.547/c l v CD m s μω==(2)如图(b )所示,定出构件2的BC 线上速度最小的一点E 位置及速度的大小。
第3章机构的运动分析-1
an EB
C 3 4
ω3
aE e'
b'
ω2
A
2
aB
1
w4
D
a
t EB
a
n EB
(P12 )
以曲柄滑块机构为例,进一步说明用矢量方程图 解法作机构的速度分析和加速度分析的具体步骤。
例 : 已知曲柄滑块机构原动件 AB 的运动规律和各构件尺寸。求: (1)图示位置连杆BC的角速度和 其上各点速度。 (2)连杆BC的角加速度和其上C点 加速度。 ω2 2
极点
C
vEC
vCB vEB
b
bc 代表 vCB 。
e
3)在速度多边形中,极点p 代表机构中速 度为零的点。 4)已知某构件上两点的速度 ,可用速度影 像法求该构件上第三点的速度。
速度多边形
E B
A
C
vC x
p
极点
C
vEC e
vCB
vB
vEB
b
△bce ~ △BCE
已知连杆上两点的速度vB 、vC 用速度影像法可以确定vE 。
④确定点的轨迹(连杆曲线)。
V型发动机运动简图
D
E
C B
A
3-1
机构运动分析的任务、目的及方法
1.机构运动分析的任务与目的
(2)速度分析
5 4
①掌握从动件的度变化规律 是否满足工作要求。如牛 头刨床; ②为加速度分析作准备。
2
1 3
6
3-1 机构运动分析的任务、目的及方法
1.机构运动分析的任务与目的
用三心定理可以确定ω3、ω4 的大小。
平面铰链四杆机构
例2:用三心定理分析凸轮机构速度 (v3)。 1
机械原理教案04速度瞬心法在机构运动分析中的应用
内 容2. 解析法:计算精度高,随着数学软件和计算机辅助设计软件的不断完善和发展,采用解析法解决机构的分析、综合过程中的相关问题越来越普及。
利用计算机求解,相当方便。
例如:杆组法——将机构拆成若干基本杆组,在对机构进行运动分析时调用相应的杆组运动分析的通用子程序,进行计算,非常方便。
3. 实验法:在现有设备上测运动参数,能反映机构在工作环境下的真实运动,但需要设备。
3-2 速度瞬心及其在平面机构速度分析中的应用 一、 速度瞬心1.瞬心的定义、分类:彼此作平面相对运动的两刚体,在任一瞬时,其相对运动都可以看做是绕某一重合点的转动,此重合点称为瞬时速度中心,简称瞬心。
显然,速度瞬心是相对运动的两构件上绝对速度相等(相对速度为零)的瞬时重合点。
若两构件之一是静止的,则该瞬心处的绝对速度为零,称为绝对瞬心;若两构件都是运动的,则其瞬心处的绝对速度不为零,称为相对瞬心。
通常用ijP 或jiP 表示构件i 、j 的速度瞬心。
2. 瞬心的数目由于任意两个构件形成一个瞬心,若机构由N 个构件(含机架)组成,则瞬心的数目为:2)1(2-=N N C N 。
如:四杆机构有6个瞬心。
其中3个绝对瞬心,3个相对瞬心。
3、瞬心的求法A )、直接接触的两构件间的瞬心(如图3-2所示) ● 转动副相连的两构件,转动副的中心为12P ,图a● 移动副联接的两构件,其瞬心在垂直于导路的无穷远处,图b ● 两构件组成高副时,若为纯滚动,则接触点为瞬心,图c ;● 若为滚动兼滑动:瞬心在过接触点的公法线上,具体位置另需条件确定。
图3-4 内 容B )、不直接接触的两构件间的瞬心不直接接触的两构件其瞬心常借助于“三心定理”来确定。
“三心定理”——三个彼此作平面运动的3个构件,共有3个瞬心,它们必位于同一条直线上。
例【3-1】:求铰链四杆机构的瞬心(如图3-4所示) 其中哪些是绝对瞬心,哪些是相对瞬心? 思考:构件3上速度为零的点是哪一点?二、速度瞬心法在机构速度分析上的应用用速度瞬心法对机构进行速度分析的一般方法是:找到已知构件与待求构件的相对瞬心,它是这两个构件上绝对速度大小相等、方向相同的点,建立待求运动构件与已知运动构件的速度关系即可求解。
机械原理 瞬心法求速度.
2.确定瞬心的位置
34
P
P24
P 13
A B
P12
C
P 14
P23
3.利用瞬心,由“图”求v3。 因P13是构件1、3的同速重合点,
v3 vP13 1lP
13P 14
VP13 1lP
1P P 13 14 l
P 13 14
3.利用瞬心,由“图”求v3。
得: 从机构位置图中量出图长: P13P14=12.3mm,
(1)两构件组成运动副
根据瞬心的定义,通过观察直接确定两构件的瞬心 位置
两构件组成纯滚动高副
接触点就是其瞬心。 两构件组成滚动兼滑动高副 瞬心在接触点处两高副元素的 公法线n-n上。
1
2
(2)两构件不组成运动副
不直接接触的两构 件,用三心定理确定 其瞬心的位置.
三心定理:
作平面运动的三个构件的三个瞬心位于同一直线上。
v3 vP
注意:
13
1P 13P 14l
m/s
=10×0.0123×2=0.246
图解法的特点体现在直接从“机构位置 图”中量出两点之间的距离。
瞬心法小结
直接利用待求构件和已知构件的相对瞬心,来建立两 者的运动关系。 图解法的特点体现在从“机构位置图”中直接量出两 点之间的距离。 瞬心法适于对构件数较少的机构进行速度分析,不受 机构类型的限制。
下课
1机械原理用速度瞬心法对机构进行速度分析用速度瞬心法对机构进行速度分析瞬心的概念瞬心数目位置例题定义瞬心就是两构件上瞬时绝对速度相同的重合点即等速重合点
机械原理
用速度瞬心法对机构进行速度分析
用速度瞬心法对机构进行速度分析 瞬心 瞬 心 的 概 念
瞬心法求速度
VB2B1
P
1
2
瞬心 绝对速度相等的重合点
VP1 = VP2 相对速度为零的重合点
VP1P2 = 0
2、平面机构瞬心的数目
每两个构件之间有一个瞬心,机构中含有个k个
构件,则全部瞬心的数目 N为:
N
Ck 2
k(k 1) 2
3、瞬心位置的确定
1)两个构件之间用运动副连接时,可直接 判断出的瞬心位置
2)两个构件之间没有用运动副连接时,可 用三心定理求出的瞬心位置
1)两个构件之间用运动副连接的瞬心位置 (1)两个构件用转动副连接时的瞬心位置
1
P12
2
1 2
P12
1 瞬心在转动中心
P12 2
(2)两个构件用移动副连接时的瞬心位置
P12 ∞
1
2
瞬心在垂直导路方向 V12 无穷远处
1)两个构件之间用运动副连接的瞬心位置
2 3
1 4
1、瞬心N=k(k-1)/2=43/2=6 2、找出直接观察出的瞬心 3、利用瞬心多边形判断其余瞬心
P24
1 P12
2
1 P12
2
2 P23
P14
P12
3
P13
ቤተ መጻሕፍቲ ባይዱ
P23 P14
P23 p24
1
4
3
4
3
P13
P43
P43
4
P43
P14
例题二:求出曲柄滑块机构的全部瞬心
1、瞬心N=k(k-1)/2=43/2=6 2、找出直接观察出的瞬心 3、利用瞬心多边形判断其余瞬心
LP13 P14
3 LP13 P 34
1
已知凸轮角速度1,求推杆速度V2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
⊥CP36 ⊥AC
3-19 图示齿轮连杆机构中,MM为固定齿条,齿轮3的直径是 齿轮4的2倍,设已知原动件1以角速度ω1顺时针方向回转, 试以图解法求机构在图示位置时E点的速度VE以及齿轮3、4 的速度影像。
h
p
e H b
c
vC vB vCB
大小 √ √
k B 2 B3
b2’ p’ n’(c3’)
?
⊥ BD
?
∥BC
230vB2B3
n t aC3 aC3 aC3
方向
B→A
B→D
t ' aB 3 a n ' b3 3 lBD l BD
3-13 图示机构的B点是否存在哥氏加速度?又在何位置哥氏 加速度为零? 作出相应的机构位置图。并思考下列问题: 1)在什么条件下存在哥氏加速度? 组成移动副的两构件作 平面运动或定轴转动 2) 哥氏加速度为零的位置
ω3=ω2=0
vB 2 vB3 vB 2 B3
大小 方向
VC3=0 p’
⊥AB
0 ? ⊥BD
?
//CD
aB2 aB 3 a aB 2 B 3 a
n t B3 r
大小 方向 √ B→A 0
k B 2 B3
b2’ (c3’)
b3’
?
⊥ BD
?
∥CD
230 B2B3 v
t aB 3 a p ' b3' 3 2 lBD l BD
用瞬心法求1/ 3
找出构件1和构件3的相对瞬心P13, 应用三心定理
通过P16 、 P36及P23、P12求P13
P23
P12
P13
P36
P16
2 3
1 P36 P13 3 P16 P13
1 6 5
4
3-6 已知各杆长度,ω2=10rad/s,用瞬心法求:
1)当φ=165°时,C点的速度vc 2)当φ=165°时,构件3的BC线上(或延长线)速度最 小的点E的位置及其速度大小 3)当vC=0时,φ角之值 解: 1)根据 P24的含义
aB 2 aB3
3
t B2
n p aC 3 aB3 aC 3 B 3 atC 3 B 3
0?
?
√
B→A
0
b3 α3 lBC
b3’
pb a 方向 a 2 lBC l BC
(c3)
t
⊥BC
aC 3B3 aB3
b
(c3) p
b2 VB3=0, VB2B3=VB2
VF=0
3-11 标出各速度方向
VB
VBC
VAB
V B= VC + V BC V C = VA + V CA
VC VCA VA
V A = VB + V AB
3-12 求构件3上C点的速度和加速度
a
大小 方向
vB3 vB 2 vB3B 2
ω1 lAB
⊥AB
?
⊥BC
?
//BC
VB2=0, VB3B2=VB3
大小 方向
c
f
? ?
⊥AC
a
d VF /VC =VF /V1 = 3
⊥BC
请同学们思考,若加一组菱形如图,θ3不变,VI /V1 = ?
3-8 作速度多边形
V C = VB + V CB
VCB = 0,
V C = VB + V CB V D = VB + V DB V E= VC + V EC =VD+VED 构件BCE瞬时平动
P23
vc
2 P24 P L 4 P24 P L 12 14
P34
4
P24 P 12 2 4.5(rad / s) P24 P 14
VC 4 lCD 4.5 90 405(mm / s)
或利用P13, 此时3构件绕 P13定轴转动
vB
P24
第3章作业 速度瞬心法作机构速度分析
3-3 求图示机构的全部瞬心
P13 P24 P23 P13
∞
∞
P34 P24
P12 P14
(a) ∞
P12 P23
∞
P14
∞
P24
(b)
P13
P23
P13
P12 P23
∞
P14
P34
∞
P24
P34
∞
P12
(c)
P14
P24
∞
(d)
3-4
2 aB3 aB1 1 l AB
ω2=ω3=0
aB3 aB 2 aB 2 a
n t
大小 方向 √ B→A
t
r B3 B 2
0
a
k B3 B 2
vC 3 vB3 vC 3B3
大小 方向
0
?
⊥ BC
?
0 22 vB3B2
?
√
⊥AB
0 ⊥ BC
∥BC
大小
' 3 ' 3
(c3’ ) p’
P12
ω3
P14 P13 B
V / P P VC / P P 23 13 34 13
2)当φ=165°时,构件3的BC线上(或延长线) 速度最小的点E的位置及其速度大小
3 VC / lP
34 P 13
2.65(rad / s)
VE 3 EP L 365.7(mm / s) 13
3)a
K B2B3
=2ω2*vB2B3对吗?为什么? 就计算结果来说是对的, 因为此题的ω2=ω3
3-17自卸货车翻转机构。已知v21,求车厢转至30°时ω5。
vC 2 vC1 vC 2C1 vD vC 3 vDC 3
大小 方向
d c3 ω5 = VD / LDG p
?
?
//AC c1
3)当vc=0时,φ角之值
量得:
Φ1=26°
Φ2=226°
3-7 图示机构中,已知各杆长度,滑块1、2的速度V1=V2,
求机构在θ3=45°位置时速度之比VF/V1 vF vD vFD vE vFE
大小 方向 b
? ?
⊥DF e
⊥EF
p
vC vA vCA vB vCB
aC3 3lCD atB3 lCD / lBD aB2
c
p c
b2(b3)
vB 2 vB3 vB 2 B3
大小 方向
3
⊥AB
?
⊥BD
0 ? //BC
vB 3 v pb3 lBD l BD
aB2 aB 3 a aB 2 B 3 a
n t B3 r
