材料力学习题答案 刘文鸿 第四版
材料力学第四版课后习题答案

材料力学第四版课后习题答案1. 引言。
材料力学是材料科学与工程中的重要基础课程,通过学习材料力学,可以帮助我们更好地理解材料的性能和行为。
本文档将针对材料力学第四版的课后习题进行答案解析,帮助学习者更好地掌握课程内容。
2. 第一章。
2.1 课后习题1。
答,根据受力分析,可以得到杆件的受力情况。
然后利用杆件的受力平衡条件,可以得到杆件的应力状态。
最后,根据应力状态计算应变和变形。
2.2 课后习题2。
答,利用受力分析,可以得到杆件的受力情况。
然后利用杆件的受力平衡条件,可以得到杆件的应力状态。
最后,根据应力状态计算应变和变形。
3. 第二章。
3.1 课后习题1。
答,利用受力分析,可以得到梁的受力情况。
然后利用梁的受力平衡条件,可以得到梁的应力状态。
最后,根据应力状态计算应变和变形。
3.2 课后习题2。
答,利用受力分析,可以得到梁的受力情况。
然后利用梁的受力平衡条件,可以得到梁的应力状态。
最后,根据应力状态计算应变和变形。
4. 第三章。
4.1 课后习题1。
答,利用受力分析,可以得到薄壁压力容器的受力情况。
然后利用薄壁压力容器的受力平衡条件,可以得到薄壁压力容器的应力状态。
最后,根据应力状态计算应变和变形。
4.2 课后习题2。
答,利用受力分析,可以得到薄壁压力容器的受力情况。
然后利用薄壁压力容器的受力平衡条件,可以得到薄壁压力容器的应力状态。
最后,根据应力状态计算应变和变形。
5. 结论。
通过对材料力学第四版课后习题的答案解析,我们可以更好地掌握材料力学的基本原理和方法。
希望本文档能够对学习者有所帮助,促进大家对材料力学的深入理解和应用。
刘鸿文《材料力学》复习笔记和课后习题(含考研真题)详解(应力和应变分析强度理论)【圣才出品】

平面的外法线方向。
7 / 135
圣才电子书 十万种考研考证电子书、题库视频学习平台
三、三向应力状态分析 1.三向应力圆 如图 7-1-4 所示,以三个主应力表示的单元体,由三个相互垂直的平面分别作应力圆, 将三个平面的应力圆绘在同一平面上得到三向应力状态下的应力圆,如图 7-1-5 所示。与 每一主应力所对应的应力圆可由与该主平面相正交的其余面上的应力作出。 注意:作三向应力圆应至少知道一个主应力的大小和方向。
1 / 135
圣才电子书 十万种考研考证电子书、题库视频学习平台
实例:在滚珠轴承中,滚珠与外圈接触点处的应力状态,可以作为三向应力状态的实例。 二、二向应力状态分析 1.解析法 如图 7-1-1(a)所示,一单元体 abcd 处于平面应力状态,采用截面法取左边部分单 元体 eaf 为研究对象,如图 7-1-1(b)所示。
5 / 135
圣才电子书 十万种考研考证电子书、题库视频学习平台
图 7-1-3(a)
图 7-1-3(b) ③求主应力数值和主平面位置 a.求主应力数值的方法 如图 7-1-3(b)所示,点 A1 和点 B1 分别为代表最大主应力和最小主应力,其大小为
6 / 135
圣才电子书 十万种考研考证电子书、题库视频学习平台
圣才电子书 十万种考研考证电子书、题库视频学习平台
第 7 章 应力和应变分析强度理论
7.1 复习笔记
一、应力状态 一点的应力状态:过一点不同方向面上应力的集合。 应力状态的研究对象是单元体,其特征为:①单元体的尺寸无限小,每个面上应力均匀 分布;②任意一对平行平面上的应力相等。 主单元体是指各侧面上切应力均为零的单元体。其中,单元体上切应力为零的面称为主 平面,主平面上的正应力称为主应力。 说明:一点处必定存在一个单元体,使得三个相互垂直的面均为主平面,三个互相垂直 的主应力分别记为 σ1、σ2、σ3,且规定按代数值大小的顺序来排列,即 σ1≥σ2≥σ3。 应力状态分类及实例 (1)单向应力状态:也称为简单应力状态,三个主应力 σ1、σ2、σ3 中只有一个不等 于零。 实例:简单的拉伸或压缩。 (2)平面(二向)应力状态:三个主应力 σ1、σ2、σ3 中有两个不等于零。 实例:薄壁圆筒横截面上的点和圆形容器包含直径的任意横截面上的点。 (3)空间(三向)应力状态:和平面应力状态统称为复杂应力状态,三个主应力 σ1、 σ2、σ3,均不等于零。
材料力学ppt(刘鸿文第四版含课后答案)

l1
A' l3
(3) 物理关系
A
l1
N1l
E1A1 cos
l1 l2 A' l3
(1) 静平衡方程
N1 N2
(1)
N3 2N1 cos P 0 (2)
(2) 变形协调方程 l1 l源自 l3 cos (3)(3) 物理关系
l1
N1l
E1A1 cos
0.52 104 (m)
AB杆的变形
lAB lBD lCD lAC 1.05104(m)
例 2 (书例2. 7) 已知: BC杆: d=20mm, BD杆: 8号槽钢。[]= 160 MPa, E=200GPa, P=60kN。 求:校核强度及B点位移。 解:(1) 求轴力
Al
l Nl Pl 胡克定律的
EA EA
另一种形式
EA 抗拉(或抗压)刚度
注意:上式只在应力不超过比例极限时成立。
推广: (1) 阶梯轴
l Nili
Ei Ai
(2) 变截面轴
l
l
N ( x) EA(x)
dx
l1
l2
l3
A1
A2
A3
x
N(x)+dN(x)
N(X)
应力 A2 1024.8106 m2
1
N1 A1
143MPa
[ ] 160MPa
2
N2 A2
73.2 MPa
[ ] 160MPa
(3) 计算杆的变形
BC杆变形
l1
BB1
N1l1 EA1
材料力学ppt(刘鸿文第四版含课后答案)

应力分布均匀 均匀时 应力分布均匀时
N Al N l U = uV = V = = 2 2E 2EA 2EA
Nl 推广到多杆系统 U = ∑ i=1 2E A i i
1 由能量守恒原理 U =W= P∆l 2 2 n 有 1 Ni li P∆l = ∑ 2 i=1 2E A i i
n 2 i i
关于静不定的基本概念
静定问题
静不定问题 —— 静不定次数 —— 多余约束 ——
求解静不定问题的基本方法
力的平衡关系。 静力平衡方程 -力的平衡关系。 变形与约束的协调关系。 变形协调方程 - 变形与约束的协调关系。 力与变形的关系。 物理关系 - 力与变形的关系。
例 1 (书p.50) 书 已知:1、2杆相同,抗拉 杆相同, 已知: 、 杆相同 刚度为E 刚度为 1A1 , 3杆的抗拉 杆的抗拉 长为l 角 刚度为E 刚度为 3A3 , 长为 , α角。 各杆的内力。 求:各杆的内力。 解: 静不定的次数? 静不定的次数?
(2) 变形协调方程 (3) 物理关系
∆l1 = ∆l2 = ∆l3 cosα (3) N1l N3l ∆l1 = ∆l3 = E1A cosα E3 A 1 3
(4)
物理关系代入变形协调方程
N1l N3l = cosα E A cosα E3 A 1 1 3
与平衡方程联立,可解出 与平衡方程联立,可解出:
D
C
B
2 l N2
3
1
αα
A P y N3
αα
∑X = 0 N1 sin α − N2 sinα = 0 N1 = N2 ∑Y = 0 N3 +2N1 cosα − P = 0
N1
x
P
7.刘鸿文版材料力学-弯曲变形解析

§6-3 用积分法求弯曲变形
3)列挠曲线近似微分方程并积分 AC 段: 0 x1 a
d 2 y1 Fb EI M ( x ) x1 1 2 dx1 l dy Fb 2 EI 1 EI ( x1 ) x 1 C1 dx1 2l
a x2 l
y
A
A
F
D
C
B
B x
y
A
A
F
D
C
B
B x
FBy
FAy x1
ymax
x2
CB 段: a x2 l
EI 2
a
b
Fb 2 F Fb 2 x2 ( x2 a ) 2 (l b 2 ) 2l 2 6l
Fb 3 F Fb 2 3 EIy 2 x2 ( x 2 a ) (l b 2 ) x2 6l 6 6l
目录
§6-4 用叠加法求弯曲变形
yC
2)再将处理后的梁分解为简单 载荷作用的情形,计算各自C截 面的挠度和转角。
ql 4 ql3 yC 1 , C1 8 EI 6 EI l ql 3 yC 2 y B 2 B 2 C 2 2 48EI ql 4 ql 3 l , 128EI 48EI 2
y yi
i 1
n
i ,
i 1
n
重要结论: 梁在若干个载荷共同作用时的挠度或转角, 等于在各个载荷单独作用时的挠度或转角的代数 和。这就是计算弯曲变形的叠加原理。
目录
§6-4 用叠加法求弯曲变形
例3 已知简支梁受力如图示,q、 l、EI均为已知。求C 截面的挠 度yC ;B截面的转角B
§6-4 用叠加法求弯曲变形
材料力学刘德华版课后习题问题详解word版
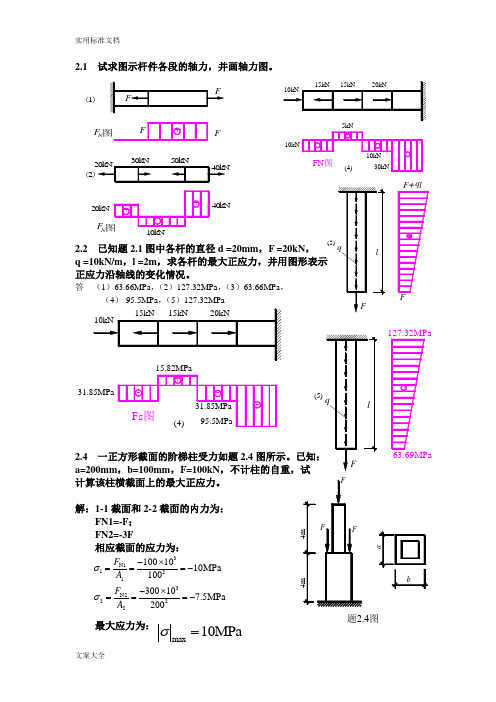
2.1 试求图示杆件各段的轴力,并画轴力图。
2.2 已知题2.1图中各杆的直径d =20mm ,F =20kN ,q =10kN/m ,l =2m ,求各杆的最大正应力,并用图形表示 正应力沿轴线的变化情况。
答 (1)63.66MPa ,(2)127.32MPa ,(3)63.66MPa ,(4)-95.5MPa ,(5)127.32MPa2.4 一正方形截面的阶梯柱受力如题2.4图所示。
已知:a=200mm ,b=100mm ,F=100kN ,不计柱的自重,试 计算该柱横截面上的最大正应力。
解:1-1截面和2-2截面的内力为: FN1=-F ;FN2=-3F相应截面的应力为:最大应力为:15kN15kN20kN10kN(4)10kN5kN10kN 30kN+---FN 图-+++FF FF 20kN 30kN 50kN 40kN40kN10kN 20kN (2)(1)F N 图图N F l(5)q FFF q ll(5)qF+127.32MPa63.69MPa15kN 15kN 20kN 10kN (4)31.85MPa 15.82MPa +---Fs 图31.85MPa95.5MPa 4m4mabF题2.4图FF3N11213N22221001010MPa 100300107.5MPa200F A F A σσ-⨯===--⨯===-max 10MPaσ=2.6 钢杆受轴向外力如图所示,横截面面积为500mm2,试求 ab 斜截面上的应力。
解: FN=20kN2.8 图示钢杆的横截面积 A=1000mm2,材料的弹性模量E=200GPa ,试求:(1)各段的轴向变形;(2)各段的轴向线应变;(3)杆的总伸长。
解:轴力图如图所示2.10 图示结构中,五根杆的抗拉刚度均为EA ,杆AB 长为l ,ABCD 是正方形。
在小变形条件下,试求两种加载情况下,AB 杆的伸长。
解 (a )受力分析如图,由C 点平衡可知:3020kNob aa b a b p αs αατF N o N N 0cos30==F F p A A ααo 2oN 03cos30cos 302010330MPa 5004F p A σ==⨯=⨯=αα3o o o N020103sin30cos30sin3017.32MPa 5004F p A ⨯===⨯=αατ-+20kN20kN 20kN ⅠⅡⅢ20kN20kN1m 1m 2m12320N 0N 20N N N N F k F k F k ===-41119624333962011020010100010020221020010100010N N F l L m EA L m F l L m EA ----⨯∆===⨯⨯⨯∆=⨯∆===-⨯⨯⨯⨯4411122244333101010210102L m l mL l L ml mεεε----∆===∆==∆-⨯===-41243100210L m L m L m--∆=∆=∆=-⨯I II III 0.1mm 00.2mm 0.1mm l l l l ∆=∆+∆+∆=+-=-实用标准文档F ’AC=F ’CB=0;由D 点平衡可知: F ’AD=F ’BD=0; 再由A 点的平衡:因此(b )受力分析如图,由C 点平衡可知:再由A 点的平衡:因此2.12 图示结构中,水平刚杆AB 不变形,杆①为钢杆,直径d1=20mm ,弹性模量E1=200GPa ;杆②为铜杆,直径d2=25mm ,弹性模量E2=100GPa 。
材料力学-刘鸿文-第四版-第五章

σmax
M
y max max Iz
σ
1.弯矩最大的截面上
2.离中性轴最远处
3.变截面梁要综合考虑 M与 Iz
4.脆性材料抗拉和抗压性能不同,二方面都要考虑
s t,max s t
s c,max s c
2019年9月22日2时45分
材料力学 第五章 弯曲应力
根据强度条件可进行:
s t,max
2.5103 88103 7.64106
28.8106 Pa 28.8MPa s t
2019年9月22日2时45分
材料力学 第五章 弯曲应力
例5-3-5:图a所示为横截面如图b所示的槽形截面铸铁梁,该 截面对于中性轴z 的惯性矩Iz=5493×104 mm4。已知图a中, b=2 m。铸铁的许用拉应力[st]=30 MPa,许用压应力[s c]=90 MPa 。试求梁的许可荷载[F]。
4
Iz
显然,B截面上的最大拉应力控制了梁的强度。
2019年9月22日2时45分
材料力学 第五章 弯曲应力 第四章 弯曲应力
于是由B截面上最大拉应力不得超过铸铁的许用拉应
力[st]的条件来求该梁的许可荷载[F]:
F 2 m 86103 m
2
5493108 m4
l /2
F
AaCB Nhomakorabeal
z
NO.16
2019年9月22日2时45分
材料力学 第五章 弯曲应力
解: 1)s C EC 210 103 400 10 6 84MPa
M
C
s C
FB (l a) 0.25F
刘鸿文《材料力学》复习笔记和课后习题及考研真题详解(10-12章)【圣才出品】

第 10 章 动载荷
10.1 复习笔记
本章节的主要研究内容是构件作匀加速运动时,或受到作匀加速运动的物体作用时,以 及构件受到冲击时的应力和变形计算。
静载荷:载荷由零平缓地增加到最终值,且之后载荷值再也不变化。 动载荷:随时间明显变化的载荷,即具有较大加载速率的载荷。 一、动静法的应用 动静法是将动力学问题转化为静力学问题的方法,来自于达朗贝尔原理:假想地在做加 速运动的质点系上的每一个质点上施加惯性力,使原力系与惯性力系组成平衡力系。质点上 的惯性力等于该质点质量 m 与其加速度 a 的乘积,惯性力方向与加速度反向。 对于匀加速平动杆件或者匀角加速转动杆件,使用动静法作动应力分析的一般步骤: (1)求出动荷系数 Kd; (2)按静载荷求解应力 σst、变形 Δst 等; (3)将所得结果乘以动荷系数 Kd 可得动载荷作用下的动应力和变形分别为 σd=Kdσst Δd=KdΔst
= st
1−
Fd P
2.交变应力 在静平衡位置上下作受迫振动的杆件,其上各点应力作周期性交替变化。交变应力下的 强度条件不可用静载的方法建立。
3.动应力、动荷载与放大因子的关系(
曲线)
①ω/ω0→1:即干扰力频率接近系统固有频率,此时 β 最大,引起共振。通过改变 ω/ω0 或增大阻尼 δ 可降低 β 避免共振。
dmax
= st
1+
Fd st
= st
1+
Fd P
=
Kd st
式中,振动的动荷载因数
Kd
=1+
Fd st
=1+
Fd P
4 / 128
Fd 为干扰力 Fd 按静载荷方式作用在弹性系统上的静位移。
