spss曲线拟合与回归分析
spss中的回归分析

7、Plots(图)对话框 单击“Plots”按钮,对话框如下图所示。Plots可帮助分析
资料的正态性、线性和方差齐性,还可帮助检测奇异值或异常值。
(1)散点图:可选择如下任何两个变量为Y(纵轴变量)与X (横轴变量)作图。为 获得更多的图形,可单击“Next”按钮来重 复操作过程。
Variables
Model
Entered
1
INCOMEa
Variables
Removed
Method
. Enter
a. All requested variables entered.
b. Dependent Variable: FOODEXP
输 入 / 移 去 的 变 量b
模型 1
输入的变量 移去的变量
DEPENDENT:因变量。 *ZPRED:标准化预测值。 *ZRESID: 标准化残差。 *DRESID:删除的残差。 *ADJPRED:调整残差。 *SRESID:Student氏残差。 *SDRESID: Student氏删除残差。 (2)Standardized Residual Plots:标准化残差图。 Histogram:标准化残差的直方图,并给出正态曲线。 Normal Probality Plot:标准化残差的正态概率图(P-P图)。 (3)Produce all Partial plots:偏残差图。
Coefficie nts Beta
.923
系 数a
t -.781 12.694
Sig. .441 .000
模型
1
(常量)
非标准化系数
B
标准误
spss曲线拟合与回归分析
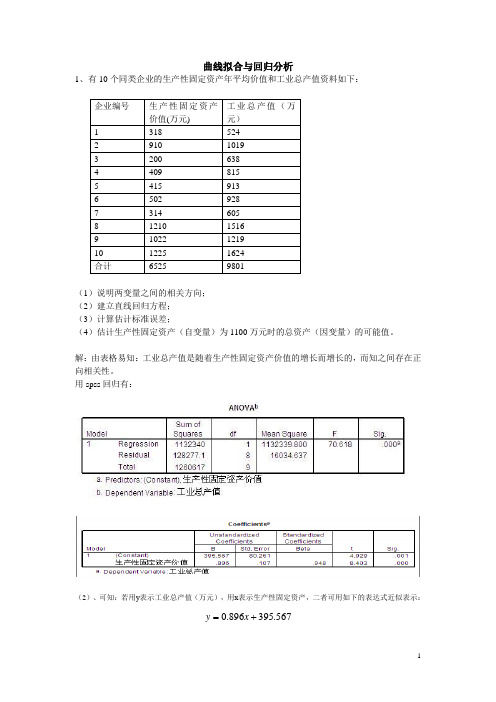
曲线拟合与回归分析1、有10个同类企业的生产性固定资产年平均价值和工业总产值资料如下:(1)说明两变量之间的相关方向;(2)建立直线回归方程;(3)计算估计标准误差;(4)估计生产性固定资产(自变量)为1100万元时的总资产(因变量)的可能值。
解:由表格易知:工业总产值是随着生产性固定资产价值的增长而增长的,而知之间存在正向相关性。
用spss回归有:(2)、可知:若用y表示工业总产值(万元),用x表示生产性固定资产,二者可用如下的表达式近似表示:=x.0+y.567395896(3)、用spss回归知标准误差为80.216(万元)。
(4)、当固定资产为1100时,总产值可能是(0.896*1100+395.567-80.216~0.896*1100+395.567+80.216)即(1301.0~146.4)这个范围内的某个值。
另外,用MATLAP也可以得到相同的结果:程序如下所示:function [b,bint,r,rint,stats] = regression1x = [318 910 200 409 415 502 314 1210 1022 1225];y = [524 1019 638 815 913 928 605 1516 1219 1624];X = [ones(size(x))', x'];[b,bint,r,rint,stats] = regress(y',X,0.05);display(b);display(stats);x1 = [300:10:1250];y1 = b(1) + b(2)*x1;figure;plot(x,y,'ro',x1,y1,'g-');industry = ones(6,1);construction = ones(6,1);industry(1) =1022;construction(1) = 1219;for i = 1:5industry(i+1) =industry(i) * 1.045;construction(i+1) = b(1) + b(2)* construction(i+1);enddisplay(industry);display( construction);end运行结果如下所示:b =395.56700.8958stats =1.0e+004 *0.0001 0.0071 0.0000 1.6035industry =1.0e+003 *1.02201.06801.11601.16631.21881.2736construction =1.0e+003 *1.2190 0.3965 0.3965 0.3965 0.3965 0.3965200400600800100012001400生产性固定资产价值(万元)工业总价值(万元)2、设某公司下属10个门市部有关资料如下:(1)、确定适宜的 回归模型; (2)、计算有关指标,判断这三种经济现象之间的紧密程度。
SPSS 10.0高级教程十二:多元线性回归与曲线拟合

SPSS 10.0高级教程十二:多元线性回归与曲线拟合回归分析是处理两个及两个以上变量间线性依存关系的统计方法。
在医学领域中,此类问题很普遍,如人头发中某种金属元素的含量与血液中该元素的含量有关系,人的体表面积与身高、体重有关系;等等。
回归分析就是用于说明这种依存变化的数学关系。
§10.1Linear过程10.1.1 简单操作入门调用此过程可完成二元或多元的线性回归分析。
在多元线性回归分析中,用户还可根据需要,选用不同筛选自变量的方法(如:逐步法、向前法、向后法,等)。
例10.1:请分析在数据集Fat surfactant.sav中变量fat对变量spovl的大小有无影响?显然,在这里spovl是连续性变量,而fat是分类变量,我们可用用单因素方差分析来解决这个问题。
但此处我们要采用和方差分析等价的分析方法--回归分析来解决它。
回归分析和方差分析都可以被归入广义线性模型中,因此他们在模型的定义、计算方法等许多方面都非常近似,下面大家很快就会看到。
这里spovl是模型中的因变量,根据回归模型的要求,它必须是正态分布的变量才可以,我们可以用直方图来大致看一下,可以看到基本服从正态,因此不再检验其正态性,继续往下做。
10.1.1.1 界面详解在菜单中选择Regression==>liner,系统弹出线性回归对话框如下:除了大家熟悉的内容以外,里面还出现了一些特色菜,让我们来一一品尝。
【Dependent框】用于选入回归分析的应变量。
【Block按钮组】由Previous和Next两个按钮组成,用于将下面Independent框中选入的自变量分组。
由于多元回归分析中自变量的选入方式有前进、后退、逐步等方法,如果对不同的自变量选入的方法不同,则用该按钮组将自变量分组选入即可。
下面的例子会讲解其用法。
【Independent框】用于选入回归分析的自变量。
【Method下拉列表】用于选择对自变量的选入方法,有Enter(强行进入法)、Stepwise(逐步法)、Remove(强制剔除法)、Backward(向后法)、Forward(向前法)五种。
《SPSS统计分析》第11章 回归分析

返回目录
多元逻辑斯谛回归
返回目录
多元逻辑斯谛回归的概念
回归模型
log( P(event) ) 1 P(event)
b0
b1 x1
b2 x2
bp xp
返回目录
多元逻辑斯谛回归过程
主对话框
返回目录
多元逻辑斯谛回归过程
参考类别对话框
保存对话框
返回目录
多元逻辑斯谛回归过程
收敛条件选择对话框
创建和选择模型对话框
返回目录
曲线估计
返回目录
曲线回归概述
1. 一般概念 线性回归不能解决所有的问题。尽管有可能通过一些函数
的转换,在一定范围内将因、自变量之间的关系转换为线性关 系,但这种转换有可能导致更为复杂的计算或失真。 SPSS提供了11种不同的曲线回归模型中。如果线性模型不能确 定哪一种为最佳模型,可以试试选择曲线拟合的方法建立一个 简单而又比较合适的模型。 2. 数据要求
线性回归分析实例1输出结果2
方差分析
返回目录
线性回归分析实例1输出结果3
逐步回归过程中不在方程中的变量
返回目录
线性回归分析实例1输出结果4
各步回归过程中的统计量
返回目录
线性回归分析实例1输出结果5
当前工资变量的异常值表
返回目录
线性回归分析实例1输出结果6
残差统计量
返回目录
线性回归分析实例1输出结果7
返回目录
习题2答案
使用线性回归中的逐步法,可得下面的预测商品流通费用率的回归系数表:
将1999年该商场商品零售额为36.33亿元代入回归方程可得1999年该商场 商品流通费用为:1574.117-7.89*1999+0.2*36.33=4.17亿元。
数据统计分析软件SPSS的应用(五)——相关分析与回归分析

数据统计分析软件SPSS的应用(五)——相关分析与回归分析数据统计分析软件SPSS的应用(五)——相关分析与回归分析数据统计分析软件SPSS是目前应用广泛且非常强大的数据分析工具之一。
在前几篇文章中,我们介绍了SPSS的基本操作和一些常用的统计方法。
本篇文章将继续介绍SPSS中的相关分析与回归分析,这些方法是数据分析中非常重要且常用的。
一、相关分析相关分析是一种用于确定变量之间关系的统计方法。
SPSS提供了多种相关分析方法,如皮尔逊相关、斯皮尔曼相关等。
在进行相关分析之前,我们首先需要收集相应的数据,并确保数据符合正态分布的假设。
下面以皮尔逊相关为例,介绍SPSS 中的相关分析的步骤。
1. 打开SPSS软件并导入数据。
可以通过菜单栏中的“File”选项来导入数据文件,或者使用快捷键“Ctrl + O”。
2. 准备相关分析的变量。
选择菜单栏中的“Analyze”选项,然后选择“Correlate”子菜单中的“Bivariate”。
在弹出的对话框中,选择要进行相关分析的变量,并将它们添加到相应的框中。
3. 进行相关分析。
点击“OK”按钮后,SPSS会自动计算所选变量之间的相关系数,并将结果输出到分析结果窗口。
4. 解读相关分析结果。
SPSS会给出相关系数的值以及显著性水平。
相关系数的取值范围为-1到1,其中-1表示完全负相关,1表示完全正相关,0表示没有相关关系。
显著性水平一般取0.05,如果相关系数的显著性水平低于设定的显著性水平,则可以认为两个变量之间存在相关关系。
二、回归分析回归分析是一种用于探索因果关系的统计方法,广泛应用于预测和解释变量之间的关系。
SPSS提供了多种回归分析方法,如简单线性回归、多元线性回归等。
下面以简单线性回归为例,介绍SPSS中的回归分析的步骤。
1. 打开SPSS软件并导入数据。
同样可以通过菜单栏中的“File”选项来导入数据文件,或者使用快捷键“Ctrl + O”。
2. 准备回归分析的变量。
SPSS-回归分析

SPSS-回归分析回归分析(⼀元线性回归分析、多元线性回归分析、⾮线性回归分析、曲线估计、时间序列的曲线估计、含虚拟⾃变量的回归分析以及逻辑回归分析)回归分析中,⼀般⾸先绘制⾃变量和因变量间的散点图,然后通过数据在散点图中的分布特点选择所要进⾏回归分析的类型,是使⽤线性回归分析还是某种⾮线性的回归分析。
回归分析与相关分析对⽐:在回归分析中,变量y称为因变量,处于被解释的特殊地位;;⽽在相关分析中,变量y与变量x处于平等的地位。
在回归分析中,因变量y是随机变量,⾃变量x可以是随机变量,也可以是⾮随机的确定变量;⽽在相关分析中,变量x和变量y都是随机变量。
相关分析是测定变量之间的关系密切程度,所使⽤的⼯具是相关系数;⽽回归分析则是侧重于考察变量之间的数量变化规律。
统计检验概念:为了确定从样本(sample)统计结果推论⾄总体时所犯错的概率。
F值和t值就是这些统计检定值,与它们相对应的概率分布,就是F分布和t分布。
统计显著性(sig)就是出现⽬前样本这结果的机率。
标准差表⽰数据的离散程度,标准误表⽰抽样误差的⼤⼩。
统计检验的分类:拟合优度检验:检验样本数据聚集在样本回归直线周围的密集程度,从⽽判断回归⽅程对样本数据的代表程度。
回归⽅程的拟合优度检验⼀般⽤判定系数R2实现。
回归⽅程的显著性检验(F检验):是对因变量与所有⾃变量之间的线性关系是否显著的⼀种假设检验。
回归⽅程的显著性检验⼀般采⽤F 检验。
回归系数的显著性检验(t检验): 根据样本估计的结果对总体回归系数的有关假设进⾏检验。
1.⼀元线性回归分析定义:在排除其他影响因素或假定其他影响因素确定的条件下,分析某⼀个因素(⾃变量)是如何影响另⼀事物(因变量)的过程。
SPSS操作2.多元线性回归分析定义:研究在线性相关条件下,两个或两个以上⾃变量对⼀个因变量的数量变化关系。
表现这⼀数量关系的数学公式,称为多元线性回归模型。
SPSS操作3.⾮线性回归分析定义:研究在⾮线性相关条件下,⾃变量对因变量的数量变化关系⾮线性回归问题⼤多数可以化为线性回归问题来求解,也就是通过对⾮线性回归模型进⾏适当的变量变换,使其化为线性模型来求解。
spss曲线拟合与回归分析

曲线拟合与回归分析1、有10个同类企业的生产性固定资产年平均价值和工业总产值资料如下:(1)说明两变量之间的相关方向;(2)建立直线回归方程;(3)计算估计标准误差;(4)估计生产性固定资产(自变量)为1100万元时的总资产(因变量)的可能值。
解:由表格易知:工业总产值是随着生产性固定资产价值的增长而增长的,而知之间存在正向相关性。
用spss回归有:(2)、可知:若用y表示工业总产值(万元),用x表示生产性固定资产,二者可用如下的表达式近似表示:=x.0+y.567395896(3)、用spss回归知标准误差为80.216(万元)。
(4)、当固定资产为1100时,总产值可能是(0.896*1100+395.567-80.216~0.896*1100+395.567+80.216)即(1301.0~146.4)这个范围内的某个值。
另外,用MATLAP也可以得到相同的结果:程序如下所示:function [b,bint,r,rint,stats] = regression1x = [318 910 200 409 415 502 314 1210 1022 1225];y = [524 1019 638 815 913 928 605 1516 1219 1624];X = [ones(size(x))', x'];[b,bint,r,rint,stats] = regress(y',X,0.05);display(b);display(stats);x1 = [300:10:1250];y1 = b(1) + b(2)*x1;figure;plot(x,y,'ro',x1,y1,'g-');industry = ones(6,1);construction = ones(6,1);industry(1) =1022;construction(1) = 1219;for i = 1:5industry(i+1) =industry(i) * 1.045;construction(i+1) = b(1) + b(2)* construction(i+1);enddisplay(industry);display( construction);end运行结果如下所示:b =395.56700.8958stats =1.0e+004 *0.0001 0.0071 0.0000 1.6035industry =1.0e+003 *1.02201.06801.11601.16631.21881.2736construction =1.0e+003 *1.2190 0.3965 0.3965 0.3965 0.3965 0.3965200400600800100012001400生产性固定资产价值(万元)工业总价值(万元)2、设某公司下属10个门市部有关资料如下:(1)、确定适宜的 回归模型; (2)、计算有关指标,判断这三种经济现象之间的紧密程度。
SPSS的线性回归分析

线性回归方程的预测
(一)点估计
y0
(二)区间估计 300
200
领 导(管 理)人 数( y)
x0为xi的均值时,预 测区间最小,精度最
100
高.x0越远离均值,预 测区间越大,精度越
低.
0
200
400
600
800
1000
1200
1400
1600
1800
普通职工数(x)
18
多元线性回归分析
(一)多元线性回归方程 多元回归方程: y= β0 +β1x1+β2x2+...+βkxk
– β1、β2、βk为偏回归系数。 – β1表示在其他自变量保持不变的情况下,自变量x1变动一个
单位所引起的因变量y的平均变动
(二)多元线性回归分析的主要问题
– 回归方程的检验 – 自变量筛选 – 多重共线性问题
19
多元线性回归方程的检验
(一)拟和优度检验:
(1)判定系数R2:
R21n n k11S SS ST ER21因均 变方 量误 的差 样
n
n
(yˆi y)2
(yi yˆ)2
R2
i1 n
1
i1 n
(yi y)2
(yi y)2
i1
i1
– R2体现了回归方程所能解释的因变量变差的比例;1-R2则体 现了因变量总变差中,回归方程所无法解释的比例。
– R2越接近于1,则说明回归平方和占了因变量总变差平方和 的绝大部分比例,因变量的变差主要由自变量的不同取值造 成,回归方程对样本数据点拟合得好
27
线性回归分析中的共线性检测
(一)共线性带来的主要问题
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
曲线拟合与回归分析1、有10个同类企业的生产性固定资产年平均价值和工业总产值资料如下:企业编号生产性固定资产价值(万元) 工业总产值(万元)1 318 5242 910 10193 200 6384 409 8155 415 9136 502 9287 314 6058 1210 15169 1022 121910 1225 1624合计6525 9801(1)说明两变量之间的相关方向;(2)建立直线回归方程;(3)计算估计标准误差;(4)估计生产性固定资产(自变量)为1100万元时的总资产(因变量)的可能值。
解:由表格易知:工业总产值是随着生产性固定资产价值的增长而增长的,而知之间存在正向相关性。
用spss回归有:(2)、可知:若用y表示工业总产值(万元),用x表示生产性固定资产,二者可用如下的表达式近似表示:567.395896.0+=xy(3)、用spss回归知标准误差为80.216(万元)。
(4)、当固定资产为1100时,总产值可能是(0.896*1100+395.567-80.216~0.896*1100+395.567+80.216)即(1301.0~146.4)这个范围内的某个值。
另外,用MATLAP也可以得到相同的结果:程序如下所示:function [b,bint,r,rint,stats] = regression1x = [318 910 200 409 415 502 314 1210 1022 1225];y = [524 1019 638 815 913 928 605 1516 1219 1624];X = [ones(size(x))', x'];[b,bint,r,rint,stats] = regress(y',X,0.05);display(b);display(stats);x1 = [300:10:1250];y1 = b(1) + b(2)*x1;figure;plot(x,y,'ro',x1,y1,'g-');industry = ones(6,1);construction = ones(6,1);industry(1) =1022;construction(1) = 1219;for i = 1:5industry(i+1) =industry(i) * 1.045;construction(i+1) = b(1) + b(2)* construction(i+1);enddisplay(industry);display( construction);end运行结果如下所示:b =395.56700.8958stats =1.0e+004 *0.0001 0.0071 0.0000 1.6035industry =1.0e+003 *1.02201.06801.11601.16631.21881.2736construction =1.0e+003 *1.2190 0.3965 0.3965 0.3965 0.3965 0.3965200400600800100012001400生产性固定资产价值(万元)工业总价值(万元)2、设某公司下属10个门市部有关资料如下:(1)、确定适宜的 回归模型; (2)、计算有关指标,判断这三种经济现象之间的紧密程度。
解:用spss 进行回归分析:若用21,,x x y 分别表示销售利润率、职工平均销售额和流通费用水平,则通过以上的分析结果可知21985.0909.2769.6x x y ++-=;并且由显著性水平可知:流通费用水平对销售利润率影响不大(0.131大于0.05),而职工平均销售额的显著性水平为0,说明它对销售利润率的影响很大。
第五章 方差分析与假设检验1、(P75)为比较5种品牌的合成木板的耐久性,对每个品牌取4个样品作摩擦实验测量磨损量,得以下数据:(1)、它们的耐久性有无明显差异? (2)、有选择的作两品牌的比较,能得出什么结果? 解:(1)、用spss 进行方差分析有:A、B、C、D四种品牌的标准差相近,它们的耐久性没有明显的差异。
用MA TLAP分析有:function anova_1fm1 = [2.2 2.1 2.4 2.5;2.2 2.3 2.4 2.6;2.2 2.0 1.9 2.1;2.4 2.7 2.6 2.7;2.3 2.5 2.3 2.4;];p=anova1(fm1);display(p);得到:p= 0.5737>0.05,也能得到相同的结论。
(2)、从五种品牌的平均值可以判断这种品牌的总体耐久性的好坏,其方差和标准差可以说明它的各个样本之间耐久性的差异。
例如A、B两种品牌,B的总体水平要稍高,而且它的各个样品间差异较小。
2、将土质基本相同的一块耕地分成5块,每块又均等分成4小块。
在每块地内把4个品种的小麦分种在4小块内,每小块的播种量相等,册的收获量如下:A1 A2 A3 A4 A5B1 32.3 34.0 34.7 36.0 35.5B2 33.2 33.6 36.8 34.3 36.1B3 30.8 34.4 32.3 35.8 32.8B4 29.5 26.2 28.1 28.5 29.4考察地块和品种对小麦的收获量有无显著影响?并在必要时做进一步比较。
解:利用MATLAP进行分析:function anova_2fm1 = [32.3 34.0 34.7 36.0 35.5;33.2 33.6 36.8 34.3 36.1;30.8 34.4 32.3 35.8 32.8;29.5 26.2 28.1 28.5 29.4;];p=anova2(fm1,2);display(p);得到:p =0.7770 0.0121 0.9393由于05.07770.01>=p ,所以地块对小麦的收获量没有影响; 由于05.00121.001.02<=<p ,所以品种对其收获量有显著影响; 由于05.09393.03>=p ,所以地块和品种的交互作用对收获量也没有影响。
进一步比较:把种在B2中的小麦品种放在A3这块地中种植可得到最高产量。
第六章 计算机模拟1、你到海边度假,听到当地气象台的天气预报每天下雨的机会是40%,用蒙特卡罗方法模拟你的假期中有4天连续下雨的概率。
解:可以假设该地方的天气情况为一个半径为5的大圆,然后下雨这种情况是它内部半径是10的同心圆,利用蒲丰投针的方法,就可以知道“连续四次投到小圆”这种情况发生的概率就是连续4天下雨的概率。
其MA TLAP 程序如下所示: function rain_value l = 5;d = sqrt(10); m = 0;b=0; n = 10000; for i = 1:(n-4)a = unifrnd(0,d,n,1); y = unifrnd(0,l,n,1); for j= 1:4if pi*a(i+j)*a(i+j) <= pi*y(i+j)*y(i+j) b = b + 1 ; end endif b == 10 m = m+1; elseif n<10 b = 0; end endp = 4*m/n; display(p)运行结果: p =4.0000e-003由此可知:连续4天都下雨的概率为:0.4*0.4*0.4*0.4=0.02562、一个带有船只卸货的岗楼,任何时间仅能为一艘船只卸货。
船只进港是为了卸货,相邻两艘船只到达的时间间隔在15分钟到145分钟之间变化。
一艘船只卸货的时间由所卸货物类型决定,在45分钟到90分钟之间变化,请回答以下问题:(1)、每艘船只在港口的平均时间和最长时间是多少?(2)、若一艘船只的等待时间是从到达到开始卸货的时间,每艘船只的平均等待时间和最长等待时间是多少?(3)、卸货设备空闲时间的百分比是多少?(4)、船只排队最长的长度是多少?解:这个问题可以看做是一个排队的例子,用MATLAP求解程序如下所示:function timeWaiting = simu3_ship(n)n = input('n=');m=0;x = zeros(1,n);y = zeros(1,n);D = zeros(1,n);leng = zeros(1,n);t = unifrnd(65,130,1,n)+15; %两艘船到达的时间间隔s = unifrnd(22.5,45,1,n)+45; %一艘船只的卸货时间x(1) = t(1); %第一艘船到达的时间for i = 2:ny(i) = x(i-1) + t(i); %第2~n搜船到达的时间j = i - 1;c(j) = x(j) + s(j)+ D(j); %计算第一艘船离开的时间if c(j) < y(i) %比较相邻两艘船离开、到达时刻的大小D(i) = 0;D3(i) = y(i)-c(j); %D3用来计算空闲的时间elseD(i) = c(j) - y(i);D3(i) = 0;endx(i) = y(i);D1(i) = D(i)+s(i);D2(i) = D(i);for k = 2:nif c(j) > y(k)m = m+1;endleng(j) = m; %计算每艘船在卸货的时候,等待的船只个数endm = 0;endaverageWaiting1 = mean(D1);maxWaiting1 = max(D1);averageWaiting2 = mean(D2);maxWaiting2 = max(D2);maxLength = max(leng);freerate3 = sum(D3(i))/(sum(D3(i))+sum(s(i-1)));display(averageWaiting1);display(maxWaiting1);display(averageWaiting2);display(maxWaiting2);display(freerate3);display(maxLength);在命令窗口输入:n=10运行结果:averageWaiting1 =72.5714maxWaiting1 =72.5714averageWaiting2 =0.7345maxWaiting2 =7.3453freerate3 =0.2007maxLength =8可知:(1)、每艘船只在港口的平均时间和最长时间是72.5714和72.5714分种。
(2)、若一艘船只的等待时间是从到达到开始卸货的时间,每艘船只的平均等待时间和最长等待时间是0.7345和7.3453分种。
