钢结构基本原理第七章压弯构件习题
钢结构计算例题(轴压、受弯、拉弯与压弯)

4 轴压构件例题例1:下图所示为一轴心受压柱的工字形截面,该柱承受轴心压力设计值N=4500kN,计算长度为,5.3,7m l m l oy ox ==钢材为Q235BF ,2/205mm N f =,验算该柱的刚度和整体稳定性。
227500mm A =,49105089.1mm I x ⨯=,48101667.4mm I y ⨯=,150][=λ。
λ 15 20 25 30 35 40 45 ϕ0.983 0.970 0.953 0.936 0.918 0.899 0.878解:mm AI i xx 2.234==,mm AI i y y 1.123==(1)刚度验算:4.281.12335009.292.2347000======yoy y x ox x i l i l λλ 150][9.29max =<=λλ(2)整体稳定算:当9.29=λ时,936.0=ϕ223/205/3.19227500936.0104500mm N f mm N A N =<=⨯⨯=ϕ例2:右图示轴心受压构件,44cm 1054.2⨯=x I ,43cm 1025.1⨯=y I ,2cm 8760=A ,m 2.5=l ,Q235钢,截面无削弱,翼缘为轧制边。
问:(1)此柱的最大承载力设计值N ?(2)此柱绕y 轴失稳的形式?(3)局部稳定是否满足要求?解:(1)整体稳定承载力计算 对x 轴:m2.50==l l x ,cm 176.871054.24=⨯==A I i x x 150][6.30175200=≤===λλx x x i l 翼缘轧制边,对x 轴为b 类截面,查表有:934.0=x ϕkN 1759102158760934.03=⨯⨯⨯==-Af N x x ϕ 对y 轴: m6.22/0==l l y ,cm 78.36.871025.13=⨯==A I i y y 150][8.6878.35200=≤===λλy y y i l翼缘轧制边,对y 轴为c 类截面,查表有:650.0=y ϕkN 122410215876065.03=⨯⨯⨯==-Af N y y ϕ 由于无截面削弱,强度承载力高于稳定承载力,故构件的最大承载力为:kN 1224max ==y N N (2)绕y 轴为弯扭失稳(3)局部稳定验算8.68},max {max ==y x λλλ,10030max ≤≤λ1) 较大翼缘的局部稳定y f t b 235)1.010(79.614/95/max 1λ+≤==88.16235235)8.681.010(=⨯+=,可2) 腹板的局部稳定y w f t h 235)5.025(4010/400/max 0λ+≤==4.59235235)8.685.025(=⨯+=,可例3:下图所示轴心受压格构柱承受轴力设计值N=800kN ,计算长度l ox =l oy =10m ,分肢采用2[25a :A=2×34.91=69.82cm 2,i y =9.81cm,I 1=175.9cm 4,i 1=2.24cm ,y 1=2.07cm ,钢材为Q235BF ,缀条用L45×4,A d =3.49cm 2。
《钢结构》课程练习题

《钢结构》课程练习题适用层次 所有层次适应专业 土木工程使用学期 2010 秋 自学学时90面授学时32实验学时使用教材 教材名称《钢结构基本原理》编 者同济大学,沈祖炎 陈扬骥陈以一等 出版社中国建工出版社习题:2. 2; 2. 6; 2. 81.如图2-35所示的钢材在单向拉伸状态下的 6 &曲线,试验时分别在 A 、B 、C 卸载 至零,则在三种情况下,卸载前应变 &卸载后残余应变 &及可恢复的弹性应变 &练习题' 2E = 1000 N/mm 。
2 5 2= 270 N/mm , ;F =0.025, E = 2.06 10 N/mm ,2•—两跨连续梁,在外荷载作用下,截面上2A 点正应力为 匚1 =120N/mm ,二2 =-80N/mm 2, B 点正应力-1 =-20N/mm 2,二 ^-120N/mm 2,求该梁 A 点与 B 点的应力和应力幅是多少?3.根据钢材选择原则,请选择下列结构中的钢材牌号:(1) 在北方严寒地区建造厂房露天仓库使用非焊接吊车梁,承受起重量 的中级工作制吊车,应选用何种规格钢材品种? (2)一厂房采用焊接钢结构,室Q >500kN第四章索及轴心受力构件习题:4. 1 ; 4. 41. 如图4-18 (a )所示桁架,承受节点荷载 P=720kN ,验算下弦杆AB 是否安全。
AB练习题杆采用2L 100X63X8,钢材采用 Q235A , f d =215N/mm 2,杆件计算长度l = 12m ,l ox =6m 。
在C 节点处设有安装孔,孔径为 d o = 21.5mm 。
各是多少? f y =235N/mm图2-35理想化的x 图第五章轴心受压构件习题:5. 5; 5. 71•两端铰接的轴心受压柱, 高10m ,截面由三块钢板焊接而成,翼缘为剪切边,材料为Q235,强度设计值f d =205N/mm 2,承受轴心压力设计值 3000kN (包括自重)。
同济大学钢结构基本原理课后习题答案完全版

第二章如图2-34所示钢材在单向拉伸状态下的应力-应变曲线,请写出弹性阶段和非弹性阶段的σε-关系式。
图2-34 σε-图(a )理想弹性-塑性 (b )理想弹性强化解:(1)弹性阶段:tan E σεαε==⋅非弹性阶段:y f σ=(应力不随应变的增大而变化)(2)弹性阶段:tan E σεαε==⋅非弹性阶段:'()tan '()tan yyy y f f f E f E σεαεα=+-=+-如图2-35所示的钢材在单向拉伸状态下的σε-曲线,试验时分别在A 、B 、C 卸载至零,则在三种情况下,卸载前应变ε、卸载后残余应变c ε及可恢复的弹性应变y ε各是多少? 2235/y f N mm = 2270/c N mm σ= 0.025F ε= 522.0610/E N mm =⨯2'1000/E N mm =图2-35 理想化的σε-图解:(1)A 点:卸载前应变:52350.001142.0610yf E ε===⨯卸载后残余应变:0c ε= 可恢复弹性应变:0.00114y c εεε=-=(2)B 点:卸载前应变:0.025F εε== 卸载后残余应变:0.02386y c f E εε=-= 可恢复弹性应变:0.00114y c εεε=-=(3)C 点:卸载前应变:0.0250.0350.06'c y F f E σεε-=-=+= 卸载后残余应变:0.05869c c E σεε=-= 可恢复弹性应变:0.00131y c εεε=-=试述钢材在单轴反复应力作用下,钢材的σε-曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。
答:钢材σε-曲线与反复应力大小和作用时间关系:当构件反复力y f σ≤时,即材料处于弹性阶段时,反复应力作用下钢材材性无变化,不存在残余变形,钢材σε-曲线基本无变化;当y f σ>时,即材料处于弹塑性阶段,反复应力会引起残余变形,但若加载-卸载连续进行,钢材σε-曲线也基本无变化;若加载-卸载具有一定时间间隔,会使钢材屈服点、极限强度提高,而塑性韧性降低(时效现象)。
第7章 拉弯、压弯构件

§7-1 应用和截面形式
钢结构基本原理及设计
单向拉弯和压弯构件的截面形式 对拉弯构件,一般只需计算其强度和长细比,不需计算 其稳定。但在拉弯构件所受弯矩较大而拉力较小时,由于其 作用已接近受弯构件,就需要验算其整体稳定;在拉力和弯 矩作用下出现翼缘板受压时,也需验算翼缘板的局部稳定。 这些当由设计人员根据具体情况加以判断。
钢结构基本原理及设计
因此,根据边缘屈服准则,压弯构件弯矩作用平面内截 面最大应力应满足: mx M x Nv0 N M xmax1 M xmax2 N fy A W1x A W1x (1 N N Ex ) 式中A、W1x ——压弯构件截面面积和最大受压纤维的 毛截面模量
A f =b×t
fy
fy
fy
fy
fy
fy
A w = h w× t w H fy
(a) (b) (c)
hw h
x Mx
x
N
fy
(d)
压弯构件截面应力的发展过程
§7-2 拉弯、压弯构件的强度
ηh (1-2 η)h ηh
H
钢结构基本原理及设计
二.强度计算准则:
①边缘屈服准则,截面边缘纤维屈服的弹性受力阶段 极限状态作为强度计算的承载能力极限状态。 ②全截面屈服准则,截面塑性受力阶段极限状态作为 强度计算的承载能力极限状态,形成塑性铰。 ③部分发展塑性准则,截面部分塑性发展作为强度计 算的承载能力极限状态 1.边缘屈服准则 令截面屈服轴力Np=A· fy,屈服弯矩Mex=Wex fy,则得N 和Mx的线性相关公式: N M x f
1.单向拉弯、压弯构件按下式计算截面强度:
Mx N f An xWnx
2.双向拉弯、压弯构件计算截面强度:
钢结构基本原理(第二版)习题参考解答第七章

7.1 一压弯构件长15m ,两端在截面两主轴方向均为铰接,承受轴心压力1000N kN =,中央截面有集中力150F kN =。
构件三分点处有两个平面外支承点(图7-21)。
钢材强度设计值为2310/N mm 。
按所给荷载,试设计截面尺寸(按工字形截面考虑)。
解:选定截面如下图示:图1 工字形截面尺寸下面进行截面验算:(1)截面特性计算()23002026502021420540A mm =⨯⨯+-⨯⨯=339411300650286610 1.45101212x I mm =⨯⨯-⨯⨯=⨯ 63/325 4.4810x x W I mm ==⨯337411220300610149.01101212y I mm =⨯⨯⨯+⨯⨯=⨯ 53/150 6.0110y y W I mm ==⨯266.2x i mm ==66.2y i m m = (2)截面强度验算36226100010562.510172.3/310/20540 4.4810x M N N mm f N mm A W σ⨯⨯=+=+=<=⨯ 满足。
(3)弯矩作用平面内稳定验算 长细比1500056.3266.2x λ== 按b 类构件查附表4-4,56.368.2,查得0.761x ϕ=。
2257222.061020540' 1.20101.1 1.156.3EX x EA N N ππλ⨯⨯⨯===⨯⋅⨯ 弯矩作用平面内无端弯矩但有一个跨中集中荷载作用:371000101.00.2 1.00.20.981.2010 1.1mx EX N N β⨯=-⨯=-⨯=⨯⨯, 取截面塑性发展系数 1.05x γ= 363611000100.98562.5100.7612054010001010.8 1.05 4.481010.8' 1.2010mx x x x x EX M N A N W N βϕγ⨯⨯⨯+=+⨯⎛⎫⎛⎫⨯-⨯⨯⨯-⨯ ⎪ ⎪ ⎪⨯⎝⎭⎝⎭ 22189.54/310/N mm f N mm =<= ,满足。
钢结构受弯构件_附答案

钢结构受弯构件_附答案时磊忖呎…7.当梁上有固定较大集中荷载作用时,其作用点处应(B )。
A )设置纵向加劲肋B )设置横向加劲肋C )减少腹板宽度D )增加翼缘的厚度X 8焊接组合梁腹板中,布置横向加劲肋对防止(A )引起的局部失稳最有效,布置纵向加劲肋对防止(B )引起的局部失稳最有效。
A )剪应力B )弯曲应力D )复合应力D )局部压应力X 9 .确定梁的经济高度的原则是(B )。
A )制造时间最短 C )最便于施工B )用钢量最省 D )免于变截面的麻烦X 10 .当梁整体稳定系数抵〉0.6时,用$'弋替啟主要是因为(B )A )梁的局部稳定有影响B )梁已进入弹塑性阶段C )梁发生了弯扭变形D )梁的强度降低了XX 11.分析焊接工字形钢梁腹板局部稳定时,腹板与翼缘相接处可简化为(练习五受弯构件、选择题(X 不做要求) 1计算梁的( A )时,应用净截面的几何参数。
A )正应力 B )剪应力 C )整体稳定 M x 2 ?钢结构梁计算公式 -中,Y ( C )。
x W nx A )与材料强度有关 B )是极限弯矩与边缘屈服弯矩之比 C )表示截面部分进人塑性 D )与梁所受荷载有关D )局部稳定XX ?在充分发挥材料强度的前提下, Q235钢梁的最小咼度 h min ( C ) Q345钢梁的h min(其他条件均相同)A )大于B )小于 X 4 .梁的最小高度是由(C A )强度 B )建筑要求 5. 单向受弯梁失去整体稳定时是( A )弯曲 B )扭转 6. 为了提高梁的整体稳定,(B C )等于D )不确定)控制的。
C )刚度 D )整体稳定 C )失稳。
C )弯扭 D )都有可能)是最经济有效的办法。
A )增大截面 B )增加支撑点,减小11C )设置横向加劲肋D )改变荷载作用的位置D )。
1------------------- 布磊5『彳 ----- ----- ---- --------------------A )自由边B )简支边C )固定边D )有转动约束的支承边x %2 .梁的支承加劲肋应设置在( C ) oA )弯曲应力大的区段B )剪应力大的区段C )上翼缘或下翼缘有固定荷载作用的部位D )有吊车轮压的部位13?双轴对称工字形截面梁,经验算,其强度和刚度正好满足要求,而腹板在弯曲应力作用下有发生局部失稳的可能。
同济大学钢结构基本原理课后习题答案完全

第二章如图2-34所示钢材在单向拉伸状态下的应力-应变曲线,请写出弹性阶段和非弹性阶段的σε-关系式。
图2-34 σε-图(a )理想弹性-塑性 (b )理想弹性强化解:(1)弹性阶段:tan E σεαε==⋅非弹性阶段:y f σ=(应力不随应变的增大而变化)(2)弹性阶段:tan E σεαε==⋅非弹性阶段:'()tan '()tan yyy y f f f E f E σεαεα=+-=+-如图2-35所示的钢材在单向拉伸状态下的σε-曲线,试验时分别在A 、B 、C 卸载至零,则在三种情况下,卸载前应变ε、卸载后残余应变c ε及可恢复的弹性应变y ε各是多少? 2235/y f N mm = 2270/c N mm σ= 0.025F ε= 522.0610/E N mm =⨯2'1000/E N mm =图2-35 理想化的σε-图解:(1)A 点:卸载前应变:52350.001142.0610yf E ε===⨯卸载后残余应变:0c ε= 可恢复弹性应变:0.00114y c εεε=-=(2)B 点:卸载前应变:0.025F εε== 卸载后残余应变:0.02386y c f E εε=-= 可恢复弹性应变:0.00114y c εεε=-=(3)C 点:卸载前应变:0.0250.0350.06'c y F f E σεε-=-=+= 卸载后残余应变:0.05869c c E σεε=-= 可恢复弹性应变:0.00131y c εεε=-=试述钢材在单轴反复应力作用下,钢材的σε-曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。
答:钢材σε-曲线与反复应力大小和作用时间关系:当构件反复力y f σ≤时,即材料处于弹性阶段时,反复应力作用下钢材材性无变化,不存在残余变形,钢材σε-曲线基本无变化;当y f σ>时,即材料处于弹塑性阶段,反复应力会引起残余变形,但若加载-卸载连续进行,钢材σε-曲线也基本无变化;若加载-卸载具有一定时间间隔,会使钢材屈服点、极限强度提高,而塑性韧性降低(时效现象)。
钢结构基本原理课后习题答案完全版
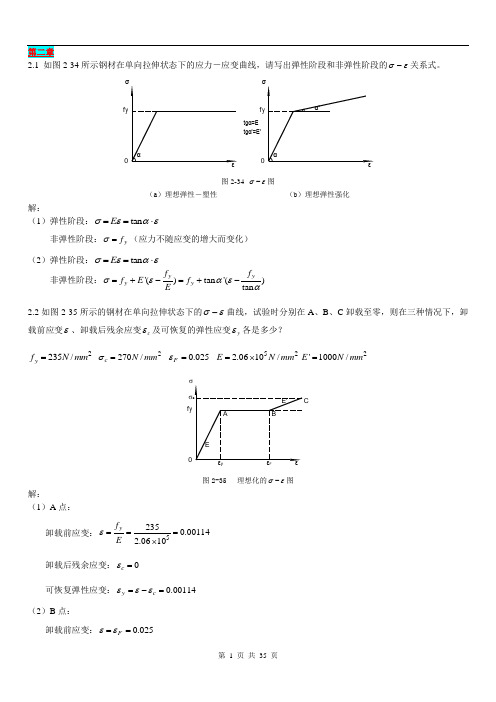
2.1 如图2-34所示钢材在单向拉伸状态下的应力-应变曲线,请写出弹性阶段和非弹性阶段的-关系式。
tgα'=E'f 0f 0tgα=E 图2-34 σε-图(a )理想弹性-塑性(b )理想弹性强化解:(1)弹性阶段:tan E σεαε==⋅非弹性阶段:y f σ=(应力不随应变的增大而变化) (2)弹性阶段:tan E σεαε==⋅ 非弹性阶段:'()tan '()tan y y y y f f f E f Eσεαεα=+-=+-2.2如图2-35所示的钢材在单向拉伸状态下的σε-曲线,试验时分别在A 、B 、C 卸载至零,则在三种情况下,卸载前应变ε、卸载后残余应变c ε及可恢复的弹性应变y ε各是多少?2235/y f N mm = 2270/c N mm σ= 0.025F ε= 522.0610/E N mm =⨯2'1000/E N mm =f 0σF图2-35 理想化的σε-图解:(1)A 点:卸载前应变:52350.001142.0610y f Eε===⨯卸载后残余应变:0c ε=可恢复弹性应变:0.00114y c εεε=-=(2)B 点:卸载前应变:0.025F εε==卸载后残余应变:0.02386y c f Eεε=-=可恢复弹性应变:0.00114y c εεε=-=(3)C 点: 卸载前应变:0.0250.0350.06'c yF f E σεε-=-=+=卸载后残余应变:0.05869cc Eσεε=-=可恢复弹性应变:0.00131y c εεε=-=2.3试述钢材在单轴反复应力作用下,钢材的σε-曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。
答:钢材σε-曲线与反复应力大小和作用时间关系:当构件反复力y f σ≤时,即材料处于弹性阶段时,反复应力作用下钢材材性无变化,不存在残余变形,钢材σε-曲线基本无变化;当y f σ>时,即材料处于弹塑性阶段,反复应力会引起残余变形,但若加载-卸载连续进行,钢材σε-曲线也基本无变化;若加载-卸载具有一定时间间隔,会使钢材屈服点、极限强度提高,而塑性韧性降低(时效现象)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
7.3一压弯构件的受力支承及截面如图7-23所示(平面内为两端铰支支承)。
设材料为Q235(2235/y f N mm =),计算其截面强度和弯矩作用平面内、平面外的
稳定性,其中 1.07b ϕ=
B =
—300×12—376×10
—300×12
图7-23习题7.3
解:(1)截面特性计算:
截面面积:2
2300123761010960A mm =××+×=绕截面主轴x 轴的惯性矩:3384
1(300400290376) 3.151012
x I mm =
×−×=×绕截面主轴y 轴的截面模量:374
1(3761000212300) 5.401012y I mm =×+××=×绕截面主轴x 轴的截面模量:631.5810200x x I W mm ==×绕截面主轴x 轴的截面塑性模量:
2634001240012223001210 1.7510222px
W mm ⎛⎞⎛⎞−⎜⎟⎜⎟⎛⎞⎝
⎠⎜⎟=×××−+×=×⎜⎟⎜⎟⎝⎠⎜⎟⎝⎠(2)截面强度计算(验算右端):
A 按边缘屈服准则计算:
36226
8001012010149.10/215/10960 1.5810x x M N N mm f N mm A W σ××=+=+=<=×
B 按部分发展塑性准则计算(取 1.05x γ=):
36226
8001012010145.47/215/10960 1.05 1.5810x x x M N N mm f N mm A W σγ××=+=+=<=××C 按全截面屈服准则计算:
36226
8001012010141.55/215/10960 1.7510x px M N N mm f N mm A W σ××=+=+=<=×故截面强度满足要求。
(3)平面内稳定计算(验算右端):
回转半径:169.6x i mm ==平面内为两端铰支,故计算长度为:012000x l mm
=长细比:01200070.74169.6
x x x l i λ===
相对长细比为:70.74x λλ==折减后的欧拉临界力为:225'
22
2.0610109604047.81.1 1.170.74Ex x EA N kN ππλ×××===×由于弯矩作用平面内构件段没有横向荷载作用,有端弯矩作用且端弯矩产生反向曲率,故取:800.650.350.417120
mx β=−×=采用B 类截面,查附表4-4得:0.746
x φ=采用稳定极限承载力准则(取截面塑性发展系数 1.05x γ=):
36
61'2
800100.417120100.88000.74610960 1.05 1.5810(1)10.84047.8133.72215/mx x x x x Ex M N A N W N f N mm βϕγ×××+=+××⎛⎞×××−−⎜⎟⎝
⎠=<=故平面内稳定满足要求。
(4)平面外稳定计算(验算右端):回转半径:mm
A I i y
y 2.70==平面外计算长度为:06000y l mm
=长细比:0600085.4770.2
y
y y l i λ===
相对长细比为:85.47
y λλ==
整体稳定系数: 1.070.904
b ϕ=−=右段两端弯矩分别为:()
112080202B M kN m +−==⋅2120B M kN m =⋅,由
于弯矩作用平面外右端构件段没有横向荷载作用,有端弯矩作用且端弯矩产生同向曲率,故取:200.650.350.708120
tx β=+×=采用B 类截面,查附表4-4得:0.652
y φ=3626
80010 1.00.8212010171.58215/0.652109600.904 1.5810tx x y b x M N f N mm A W βηϕϕ××××+=+=<=×××故平面外稳定满足要求。
