钢结构之拉弯和压弯构件
《金属结构设计》第五章 拉弯和压弯构件

mx ——等效弯矩系数。
5. 拉弯和压弯构件
§5.3.1弯矩作用平面内的稳定计算(续6) 上式中的等效弯矩系数应按下列规定采用。 ① 框架柱和两端支承的构件:
a.无横向荷载作用:
mx
0.65 0.35
率(无反弯点)时取同号,使构件产生反向曲率(有反弯点)时取异号, M1 M 2 ;
5. 拉弯和压弯构件
§5.1拉弯和压弯构件的特点(续2)
进行拉弯和压弯构件设计时,应同时满足: 承载能力极限状态和正常使用极限状态的要求。 拉弯构件:需要计算强度和刚度(限制长细比); 压弯构件:需要计算强度、整体稳定(弯矩作用平面内稳定和弯矩作用平面外稳 定)、局部稳定和刚度(限制长细比)。 拉弯构件的容许长细比和轴心拉杆相同,压弯构件的容许长细比和轴心压杆相同。
N A
mx M x
N xW2 x 1 1.25 / N Ex
f
(5-12)
式中:W1x——受拉侧最外纤维的毛截面模量。 式中的系数1.25是经过与理论计算结果比较后引进的修正系数。
5. 拉弯和压弯构件
§5.3.2弯矩作用平面外的稳定计算 开口薄壁截面压弯构件的抗扭刚度及弯矩作用平面外的抗弯刚度通常较小,当构件 在弯矩作用平面外没有足够的支撑以阻止其产生侧向位移和扭转时,构件可能因弯扭屈 曲而破坏。 《钢结构设汁规范》采用的实腹式压弯构件弯矩作用平面外稳定计算的相关公式 M N tx x f (5-13) y A bW1x 式中:Mx——所计算构件段范围内(构件侧向支承点间)的最大弯矩; βtx——等效弯矩系数,应根据两相邻支承点间构件段内的荷载和内力情况确定, 取值方法与弯矩作用平面内的等效弯矩系数βmx相同; η——截面影响系数,闭合截面η=0.7,其他截面η=1.0; fy——弯矩作用平面外的轴心受压构件稳定系数; fb——均匀弯曲受弯构件的整体稳定系数,采用近似计算公式计算,这些公式 已考虑了构件的弹塑性失稳问题,因此当fb大于0.6时不必再换算。 对闭口截面 fb=1.0;
钢结构——拉弯构件和压弯构件

钢结构——拉弯构件和压弯构件钢结构是指采用钢材作为主要构造材料的建筑结构。
在钢结构中,常见的构件有拉弯构件和压弯构件。
拉弯构件主要承受拉力,而压弯构件则主要承受压力。
本文将分别介绍拉弯构件和压弯构件的特点、设计和应用。
拉弯构件是指同时承受拉力和弯矩的构件。
它们常常用于桥梁、塔架等需要抵抗拉力的结构中。
拉弯构件受力时,在受拉面上会产生拉应变,而在另一侧会产生压应变。
拉弯构件的设计目标是在满足强度和刚度的要求下,最大程度地减小构件重量。
为了实现这一目标,拉弯构件通常采用I型、H型或者箱型截面,这些截面具有较大的截面面积和惯性矩,能够提供足够的强度和刚度。
拉弯构件的设计需要考虑以下几个因素:首先是受力情况。
拉弯构件在受力时,应根据实际情况确定构件的截面形状和尺寸,以满足承受拉力和弯矩的要求。
其次是构件的材料选择。
常见的拉弯构件材料有普通碳素钢和高强度钢。
高强度钢具有较高的强度和刚度,能够减小构件的截面尺寸和重量。
最后是构件的连接方式。
拉弯构件的连接方式有焊接、螺栓连接和铆接等,设计时需要选择适合的连接方式以满足受力要求。
压弯构件是指同时受到压力和弯矩作用的构件。
它们通常用于承担压力的柱子和梁等结构中。
压弯构件在受力时,产生的主要应力是压应力和弯曲应力。
与拉弯构件相比,压弯构件的设计更加复杂,需要考虑稳定性问题。
在设计过程中,需要根据实际情况确定构件的截面形状和尺寸,以满足承受压力和弯矩的要求,并保证构件的稳定性。
常见的压弯构件截面有角钢、工字钢和管材等。
与拉弯构件相比,压弯构件的设计更注重稳定性。
在设计压弯构件时,需要考虑构件的临界压弯强度,即其能够承受的最大弯矩和压力。
为了提高构件的稳定性,常见的设计方法有增大截面尺寸、采用合适的截面形状、设置剪力加强构件等。
此外,还需要考虑构件的支撑条件和边界约束等因素,以保证压弯构件在受力过程中不发生屈曲或失稳。
拉弯构件和压弯构件在钢结构设计和应用中都起着重要的作用。
me 钢结构第六章(拉弯、压弯构件)

压弯构件弯矩作用平面外失稳——当构件 在弯矩作用平面外没有足够的支撑以阻止 其产生侧向位移和扭转时,构件可能发生 弯扭屈曲(弯扭失稳)而破坏,这种弯扭 N 屈曲又称为压弯构件弯矩作用平面外的整 体失稳。 a) 弯曲失稳
N
b) 弯扭失稳
15
§6.3 压弯构件的稳定
6.3.1 弯矩作用平面内的稳定
N
mx M
x
xA
x W x 1 1 0 .8 N / N E x
f
(6.13)
19
§6.3 压弯构件的稳定
N
xA
mx M
x
x W x 1 1 0 .8 N / N E x
f
(6.13)
x — 平面内轴心受压构件的稳定系数;
M x — 压弯构件的最大弯距设计值;
1.边缘纤维屈服准则
对于沿全长均匀弯矩作用下的压弯构件,考虑二阶效应后, 最大弯矩为:
M
x m ax N Ex
考虑初始缺陷的影响,同时考虑二阶效应后,由初弯曲产 生最大弯矩为: N0
M
x m ax 2
1 N / N Ex
根据边缘屈曲准则,压弯构件弯矩作用平面内截面最大应 力应满足: M x N 0 N M x m ax 1 M x m ax 2 N fy (6.8) A W x1 A W x1 1 N / N E x
以 强截 度面 计边 算缘 的屈 依服 据作 为
2、刚度
拉弯和压弯构件的允许长细比[λ]同轴心受力构件(P77表4.1、4.2)
14
§6.3 压弯构件的稳定
压弯构件弯矩作用平面内失稳 ——在N和 M同时作用下,一开始构件就在弯矩作用 平面内发生变形,呈弯曲状态,当N 和M 同时增加到一定大小时则到达极限,超过 此极限,要维持内外力平衡,只能减 小N 和M。在弯矩作用平面内只产生弯曲变形 (弯曲失稳),属于极值失稳。
钢结构之拉弯和压弯构件

拉弯和压弯构件对于压弯构件,当承受的弯矩较小时其截面形式与一般的轴心受压构件相同。
当弯矩较大时,宜采用弯矩平面内截面高度较大的双轴或单轴对称截面(图1)。
图1 弯矩较大的实腹式压弯构件截面设计拉弯构件时,需计算强度和刚度(限制长细比);设计压弯构件时,需计算强度、整体稳定(弯矩作用平面内稳定和弯矩作用平面外稳定)、局部稳定和刚度(限制长细比)。
拉弯和压弯构件的容许长细比分别与轴心受拉构件和轴心受压构件相同。
一、拉弯和压弯构件的强度计算拉弯和压弯构件的强度计算式f W M A Nnxx x n ≤+γ (1) 承受双向弯矩的拉弯或压弯构件,采用的计算公式f W M W M A Nnyy y nx x x n ≤++γγ (2) 式中 n A ——净截面面积;nx W 、ny W ——对x 轴和y 轴的净截面模量;x γ、y γ——截面塑性发展系数。
当压弯构件受压翼缘的外伸宽度与其厚度之比t b />y f /23513,但不超过y f /23515时,应取x γ=1.0。
对需要计算疲劳的拉弯和压弯构件,宜取x γ=y γ=1.0,即按弹性应力状态计算。
二、实腹式压弯构件在弯矩作用平面内的稳定计算确定压弯构件弯矩作用平面内极限承载力的方法很多,可分为两大类,一类是边缘屈服准则的计算方法,一类是精度较高的数值计算方法。
1. 边缘屈服准则边缘纤维屈服准认为当构件截面最大纤维刚刚屈服时构件即失去承载能力而发生破坏,较适用于格构式构件。
按边缘屈服准则导出的相关公式y Ex x x xx f N N W M AN=⎪⎪⎭⎫⎝⎛-+ϕϕ11 (3)式中x ϕ——在弯矩作用平面内的轴心受压构件整体稳定系数。
2.最大强度准则实腹式压弯构件当受压最大边缘刚开始屈服时尚有较大的强度储备,即容许截面塑性深入。
因此若要反映构件的实际受力情况,宜采用最大强度准则,即以具有各种初始缺陷的构件为计算模型,求解其极限承载力。
规范修订时,采用数值计算方法,考虑构件存在l/1000的初弯曲和实测的残余应力分布,借用了弹性压弯构件边缘纤维屈服时计算公式的形式,经过数值运算,得出比较符合实际又能满足工程精度要求的实用相关公式y Ex px xx f N N W M AN=⎪⎪⎭⎫⎝⎛-+8.01ϕ (4)式中 px W ——截面塑性模量。
钢结构工程施工单元5 拉弯和压弯构件计算

5.2 拉弯、压弯构件的强度和刚度
• 《钢结构设计规范》(GB50017—2003)中的计算公式:
•
N M f
An Wn
(5-1)
• (2)对于直接承受动力荷载的实腹式拉弯、压弯构件,截面塑性发
展后的性能研究还不够成熟,因此《钢结构设计规范》(GB500
17—2003)规定以截面边缘屈服状态作为强度极限状态。对于
上一页 返回
5.2 拉弯、压弯构件的强度和刚度
• 5.2.1 拉弯、压弯构件的强度
• 拉弯构件和不致整体及局部失稳的压弯构件,其最不利截面(最大弯 矩截面或有严重削弱的截面)最终将形成塑性铰而达到承载能力极限。
• 以简单的矩形截面构件来讨论这一问题。图5-5所示为一受轴力N和
弯矩M共同作用的矩形截面构件。设N为定值而逐渐增加M。当截面边
下一页 返回
5.3 实腹式压弯构件的整体稳定性
• 5.3.1 压弯构件在弯矩作用平面内的稳定 性
• 实腹式压弯构件在弯矩作用平面外的抗弯刚度较大,或截面抗扭刚度 较大,或有足够的侧向支承可以阻止弯矩作用平面外的弯扭变形时, 将发生弯矩作用平面内的失稳破坏。确定压弯构件弯矩作用平面内稳 定承载能力的方法很多,可分为两类:一类是边缘屈服准则的计算方 法,一类是极限承载能力准则的计算方法。
缘纤维最大应力
N M An Wn
f y时,截面达到边缘屈服状态。当M继续增加,
最大应力一侧的塑性区将向截面内部发展,随后另一侧边缘达到屈服
并向截面内部发展,最终以整个截面屈服形成塑性铰而达到强度承载
能力极限。
下一页 返回
5.2 拉弯、压弯构件的强度和刚度
• 由于拉弯、压弯构件的截面形式和工作条件不同,故其强度计算方法 所依据的应力状态亦分为如下两种:
钢结构设计原理---拉弯压弯构件
max maxx,y []
[]取值同 轴压构件。
第六章 拉弯、压弯构件
§6.2 拉弯、压弯构件的强度
对拉弯构件、截面有削弱或构件端部弯矩大于跨间 弯矩的压弯构件,需要进行强度计算。
hw h
h (1-2)h h
Af=bt y
x Mx x Aw=hwtw
y
fy
fy
fy
fy H
N
H
fy
fy
(a) (b) (c
第六章 拉弯、压弯构件
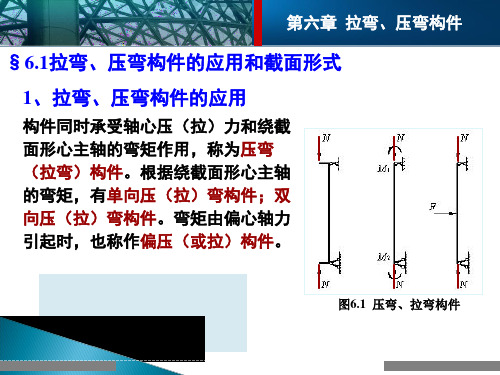
§6.1拉弯、压弯构件的应用和截面形式 1、拉弯、压弯构件的应用
构件同时承受轴心压(拉)力和绕截 面形心主轴的弯矩作用,称为压弯 (拉弯)构件。根据绕截面形心主轴 的弯矩,有单向压(拉)弯构件;双 向压(拉)弯构件。弯矩由偏心轴力 引起时,也称作偏压(或拉)构件。
图6.1 压弯、拉弯构件
2. 箱形截面的腹板
考虑到两块腹板可能受力不均,因而箱形截面高厚比值取为共字
型截面腹板的0.8倍。但不应小于
40 235/ fy
第六章 拉弯、压弯构件
3.T形截面的腹板
当弯矩作用在T形截面对称轴内并使腹板自由边受压时:
当0≤1.0时
h0 15 tw
235/ fy
(6.26a)
当0>1.0时
h0 18 tw
(6.4)
第六章 拉弯、压弯构件
1.单向拉弯、压弯构件强度计算公式
N Mx f
An xWnx
(6.5a)
第六章 拉弯、压弯构件
2.双向拉弯、压弯构件强度计算公式
N Mx My f
An xWnx yWny
(6.5b)
N——轴心压力设计值
An——验算截面净截面面积
第七章拉弯和压弯构件
例7.1 如下图所示拉弯构件,承受的荷载的设计 值为:轴向拉力800kN,横向均布荷载7kN/m。 试选择其截面,设截面无削弱,材料为Q235钢。
解:
试采用普通工字钢I28a,截面面积A=55.37cm2, 自重0.43kN/m,Wx=508cm3,ix=11.34cm,iy=2.49cm。 构件截面最大弯距Mx=(7+0.43×1.2)×62/8=
Af=aAW a=Af/AW
(7.4)
工字形截面绕强轴受弯的压弯构件轴力弯距相 关曲线:式(7.3)、式(7.4)曲线
规范采用直线式相关公式代替曲线公式:
(7.5)
曲线与直线相差不大 直线考虑附加挠度的 不利影响 直线代替曲线偏安全
式(7.3)和 (7.4)曲线
式(7.5)直线
考虑截面塑性部分发展
➢ W1x-按受压最大纤维确定的毛截面的模量
较适用于格构式构件,
对短粗实腹杆偏于安全,对细长实腹杆偏于不安全
❖ 7.3.1.2 最大强度准则
容许截面塑性深入,以具有各种初始缺陷的 构件为计算模型,求解其极限承载能力
考虑一定初弯曲和实测残 余应力数值计算得到200 条相关曲线
考虑截面的塑性发展,借用边缘纤维屈 服准则公式(7.10)根据极限承载力曲 线,得出近似相关公式:
压弯构件
拉弯构件
拉弯和压弯构件也可按其截面形式分为 实腹式构件和格构式构件两种
➢ 当受力较小时,可选用热轧型钢或冷弯薄壁 型钢截面
➢ 当受力较大时,可选用钢板焊接组合截面或 型钢与型钢、型钢与钢板的组合截面
➢ 当构件计算长度较大且受力较大时,为提高 截面的抗弯刚度,采用格构式截面
➢ 对称截面一般适用于所受弯矩值不大或正负 弯矩值相差不大的情况
钢结构压弯+拉弯构件
04
CATALOGUE
压弯、拉弯构件的维护与保养
日常维护
01
02
03
保持清洁
定期清除钢结构压弯、拉 弯构件表面的灰尘和污垢 ,避免积累造成腐蚀。
防止撞击
避免钢结构压弯、拉弯构 件受到硬物撞击,以免造 成损坏或变形。
定期涂装
为防止腐蚀,应定期对钢 结构压弯、拉弯构件进行 涂装,保持其防腐性能。
定期检查
验收交付
完成检查调整后,进行验收并交付使用。
安装注意事项
注意安全
在安装过程中,应采取必要的安 全措施,如佩戴安全带、使用安 全帽等,确保施工人员的安全。
控制误差
在安装过程中,应尽量减小误差 ,确保各部件的位置和尺寸符合 设计要求。
防腐防锈
对于暴露在外的压弯、拉弯构件 ,应采取防腐防锈措施,如涂刷 防锈漆等,以提高其耐久性。
详细描述
某大型桥梁的压弯构件采用高强度钢材,通过精确的力学分析和设计,实现了大跨度跨越和承载能力。该构件在 制造过程中采用了先进的焊接技术,保证了结构的安全性和稳定性。同时,为了应对地震等自然灾害,该构件还 进行了抗震设计,提高了桥梁的抗震性能。
案例二:某高层建筑的拉弯构件
总结词
高层建筑的拉弯构件主要承受拉力,其设计需要充分考虑风载、地震等外部载荷的影响 。
实现多样化结构需求
通过压弯、拉弯构件的应用,可以实 现多样化的结构需求,满足各种建筑 和工程设计的要求。
压弯、拉弯构件的应用场景
建筑结构
在建筑结构中,压弯、拉弯构件 广泛应用于梁、柱、板等部位, 能够提高建筑结构的稳定性和承
载能力。
桥梁结构
在桥梁结构中,压弯、拉弯构件常 用于主梁、斜拉索等部位,能够提 高桥梁的承载能力和稳定性。
钢结构设计原理第六章拉弯和压弯构件
钢结构设计原理第六章拉弯和压弯构件首先介绍拉弯构件。
拉弯构件主要受到正弯矩和拉力的作用。
在设计拉弯构件时,需要考虑结构的受力特点,根据结构所受到的相应受力,选择合适的杆件截面形状。
在选择截面形状时,需要综合考虑截面的承载能力、弹性变形能力和抗扭刚度等因素。
根据拉弯构件的受力特点,可以选择T形截面、双角截面、工字型截面等形式,以提高结构的强度和刚度。
接下来是压弯构件的设计原理。
压弯构件主要受到负弯矩和压力的作用。
在设计压弯构件时,同样需要综合考虑结构的受力特点,并选择合适的杆件截面形状。
在选择截面形状时,需要考虑截面的承载能力、塑性变形能力和抗扭刚度等因素。
压弯构件的常用截面形状包括工字型截面、双角截面、矩形截面等形式。
除了截面形状的选择原则外,还需要对拉弯和压弯构件进行强度计算。
计算时需要考虑截面的承载能力和结构所受到的荷载。
拉弯构件的强度计算一般通过确定杆件的等效长度来进行,根据拉弯构件的长度和截面形状,选择合适的等效长度,然后根据相应的拉弯构件等效长度和所受到的荷载,计算出截面的承载能力。
压弯构件的强度计算一般需要采用压杆稳定性原理进行,根据杆件的截面形状、弹性模量和地面特性等因素,计算出截面的临界压力。
若所受压力小于临界压力,则认为结构是稳定的。
总结来说,设计拉弯和压弯构件时,需要综合考虑结构的受力特点,并选择合适的杆件截面形状。
在选择截面形状时,需要综合考虑截面的承载能力、弹性变形能力和抗扭刚度等因素。
此外,还需要进行强度计算,以确保构件的稳定性和安全性。
钢结构基本原理 4-3 拉弯、压弯构件
钢结构基本原理 Primary Principles of Steel Structure
4-3 拉弯、压弯构件
b. 拉弯、压弯构件强度与刚度计算
1.单向拉弯、压弯构件强度计算公式
小时则到达极限状态,超过此极限状态,要维
持内外力平衡,只能减 小N和M。在弯矩作用平
面内只产生弯曲屈曲。 压弯构件弯矩作用平面外失稳——当构件在弯 矩作用平面外没有足够的支撑以阻止其产生侧
向位移和扭转时,构件可能发生弯扭屈曲而破
坏,这种弯扭屈曲又称为压弯构件弯矩作用平
面外的整体失稳。 双向压弯构件的失稳——同时产生双向弯曲变 形并伴随有扭转变形属弯扭失稳。
§4.3.2 拉弯、压弯构件的强度
a. 拉弯、压弯构件的强度计算准则
对拉弯构件、截面有削弱或构件端部弯矩大于跨间弯矩的压弯构件, 需要进行强度计算。
hw h
h (1-2)h h
Af=bt y
x Mx x Aw=hwtw
y
fy
fy
fy
fy H
N
H
fy
fy
(a) (b) (c)
(d)
图4.3.3 压弯构件截面应力的发展过程
钢结构基本原理 Primary Principles of Steel Structure
4-3 拉弯、压弯构件
N A
xW2 x
§4-3 拉弯、压弯构件
1、拉弯、压弯构件的应用和截面形式 2、拉弯、压弯构件的强度 3、实腹式压弯构件在弯矩作用平面内的稳定计算 4、实腹式压弯构件在弯矩作用平面外的稳定计算 5、实腹式压弯构件的局部稳定 6、实腹式压弯构件的截面设计
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
拉弯和压弯构件对于压弯构件,当承受的弯矩较小时其截面形式与一般的轴心受压构件相同。
当弯矩较大时,宜采用弯矩平面内截面高度较大的双轴或单轴对称截面(图1)。
图1 弯矩较大的实腹式压弯构件截面设计拉弯构件时,需计算强度和刚度(限制长细比);设计压弯构件时,需计算强度、整体稳定(弯矩作用平面内稳定和弯矩作用平面外稳定)、局部稳定和刚度(限制长细比)。
拉弯和压弯构件的容许长细比分别与轴心受拉构件和轴心受压构件相同。
一、拉弯和压弯构件的强度计算拉弯和压弯构件的强度计算式f W M A Nnxx x n ≤+γ (1) 承受双向弯矩的拉弯或压弯构件,采用的计算公式f W M W M A Nnyy y nx x x n ≤++γγ (2) 式中 n A ——净截面面积;nx W 、ny W ——对x 轴和y 轴的净截面模量;x γ、y γ——截面塑性发展系数。
当压弯构件受压翼缘的外伸宽度与其厚度之比t b />y f /23513,但不超过y f /23515时,应取x γ=1.0。
对需要计算疲劳的拉弯和压弯构件,宜取x γ=y γ=1.0,即按弹性应力状态计算。
二、实腹式压弯构件在弯矩作用平面内的稳定计算确定压弯构件弯矩作用平面内极限承载力的方法很多,可分为两大类,一类是边缘屈服准则的计算方法,一类是精度较高的数值计算方法。
1. 边缘屈服准则边缘纤维屈服准认为当构件截面最大纤维刚刚屈服时构件即失去承载能力而发生破坏,较适用于格构式构件。
按边缘屈服准则导出的相关公式y Ex x x xx f N N W M AN=⎪⎪⎭⎫⎝⎛-+ϕϕ11 (3)式中 x ϕ——在弯矩作用平面内的轴心受压构件整体稳定系数。
2.最大强度准则实腹式压弯构件当受压最大边缘刚开始屈服时尚有较大的强度储备,即容许截面塑性深入。
因此若要反映构件的实际受力情况,宜采用最大强度准则,即以具有各种初始缺陷的构件为计算模型,求解其极限承载力。
规范修订时,采用数值计算方法,考虑构件存在l/1000的初弯曲和实测的残余应力分布,借用了弹性压弯构件边缘纤维屈服时计算公式的形式,经过数值运算,得出比较符合实际又能满足工程精度要求的实用相关公式y Ex px xx f N N W M AN=⎪⎪⎭⎫⎝⎛-+8.01ϕ (4)式中 px W ——截面塑性模量。
3. 实腹式压弯构件整体稳定计算式(4)仅适用于弯矩沿杆长均匀分布的两端铰支压弯构件,为了把式(4)推广应用于其他荷载作用时的压弯构件,可用等效弯矩x mx M β (x M 为最大弯矩)代替公式中的x M 。
另外,考虑部分塑性深入截面,采用x x px W W 1γ=,并引入抗力分项系数,即得到规范所采用的实腹式压弯构件弯矩作用平面内的稳定计算式f N N W M ANEx x x xmx x ≤⎪⎭⎫ ⎝⎛-+'18.01γβϕ (5)式中 N ——轴向压力设计值;x M ——所计算构件段范围内的最大弯矩;x ϕ——轴心受压构件的稳定系数;x W 1——受压最大纤维的毛截面模量;'Ex N ——参数,'EX N =)1.1/(22x EA λπ; mx β——等效弯矩系数,按下列情况取值:(1)框架柱和两端支承的构件:①无横向荷载作用时:mx β=0.65+0.351M /2M ,1M 和2M 为端弯矩,使构件产生同向曲率(无反弯点)时取同号,使构件产生反向曲率(有反弯点时)取异号,1M >2M ;②有端弯矩和横向荷载同时作用时:使构件产生同向曲率时,mx β=1.0;使构件产生反向曲率时,mx β=0.85;③无端弯矩但有横向荷载作用时:mx β=1.0。
(2)悬臂构件和分析内力未考虑二阶效应的无支撑纯框架和弱支撑框架柱,mx β=1.0。
对于T 形截面等单轴对称压弯构件,当弯矩作用于对称轴平面且使较大翼缘受压时,构件失稳时除存在受压区屈服和受压、受拉区同时屈服两种情况外,还可能在受拉区首先出现屈服而导致构件失去承载能力,故除了按式(5)计算外,还应按下式计算f N N W M ANEx x x xmx ≤⎪⎪⎭⎫⎝⎛--'225.11γβ (6)式中 x W 2——受拉侧最外纤维的毛截面模量。
三、实腹式压弯构件在弯矩作用平面外的稳定计算压弯构件在弯矩作用平面外稳定计算的相关公式为f W M A Nxb x tx y ≤+1ϕβηϕ (7) 式中 x M ——所计算构件段范围内(构件侧向支承点间)的最大弯矩;η——截面影响系数,闭合截面η=0.7,其他截面η=1.0;y ϕ——弯矩作用平面外的轴心受压构件稳定系数;b ϕ——均匀弯曲梁的整体稳定系数,可采用近似计算公式,对闭合截面0.1=b ϕ;tx β——等效弯矩系数(1)在弯矩作用平面外有支承的构件,应根据两相邻支承点间构件段的荷载和内力情况确定。
①无横向荷载作用时:mx β=0.65+0.351M /2M ,1M 和2M 为端弯矩,使构件产生同向曲率(无反弯点)时取同号,使构件产生反向曲率(有反弯点时)取异号,1M >2M ;②有端弯矩和横向荷载同时作用时:使构件产生同向曲率时,mx β=1.0;使构件产生反向曲率时,mx β=0.85;③无端弯矩但有横向荷载作用时:mx β=1.0。
(2)弯矩作用平面外为悬臂构件,mx β=1.0。
四、压弯构件的局部稳定为保证压弯构件中板件的局部稳定,应限制翼缘和腹板的宽厚比及高厚比。
1.翼缘的宽厚比压弯构件的受压翼缘板,其应力情况与梁受压翼缘基本相同,因此其自由外伸宽度与厚度之比以及箱形截面翼缘在腹板之间的宽厚比均与梁受压翼缘的宽厚比限值相同。
2.腹板的宽厚比 (1)工字形截面的腹板 当0≤0α≤1.6时,y w f t h 235)255.016(00++≤λα (8a ) 当1.6<0α≤2.0时,yw f t h 235)2.265.048(00-+≤λα (8b ) maxminmax 0σσσα-=(9)式中 0α——应力梯度;max σ——腹板计算高度边缘的最大压应力;min σ——腹板计算高度另一边缘相应的应力,压应力为正,拉应力为负;λ——为构件两方向长细比的较大值。
当30<λ时,取30=λ;当100>λ时,取100=λ 。
(2)T 形截面的腹板当0α<1.0(弯矩较小)时,T 形截面腹板中压应力分布不均的有利影响不大,其宽厚比限值采用与翼缘板相同;当0α>1.0(弯矩较大)时,此有利影响较大,故提高20%。
弯矩使腹板自由边受压 当0.10≤α时,y w f t h 235150≤ (10a ) 当0.10>α时,yw f t h 235180≤ (10b ) 弯矩使腹板自由边受拉 热轧剖分T 形钢y w f t h 235)2.015(0λ+≤ (11) 焊接T 形钢 yw f t h 235)17.013(0λ+≤ (12) (3)箱形截面的腹板考虑两腹板受力可能不一致,而且翼缘对腹板的约束因常为单侧角焊缝也不如工字形截面,因而箱形截面的宽厚比限值取为工字形截面腹板的0.8倍。
当0≤0α≤1.6时,y w f t h 235)255.016(8.000++≤λα (13a ) 当1.6<0α≤2.0时, yw f t h 235)2.265.048(8.000-+≤λα (13b ) (4)圆管截面一般圆管截面构件的弯矩不大,故其直径与厚度之比的限值与轴心受压构件的规定相同。
)235(100yf t D ≤ (14)五、框架柱的计算长度1. 单层等截面框架柱在框架平面内的计算长度框架分为无支撑的纯框架和有支撑框架,其中有支撑框架根据抗侧移刚度的大小,分为强支撑框架和弱支撑框架。
当支撑结构(支撑桁架、剪力墙、电梯井等)的侧移刚度(产生单位侧倾角的水平力)S b 满足下式的要求时,为强支撑框架。
S b ≥3(1.2∑N bi -∑N 0i ) (15)式中 ∑N bi ,∑N 0i ——第i 层层间所有框架柱用无侧移框架和和有侧移框架柱计算长度系数算得的轴压杆稳定承载力之和。
强支撑框架,其失稳形式一般为无侧移的。
当支撑结构的侧移刚S b 不满足上式的要求时,为弱支撑框架。
弱无支撑的框架,其失稳形式为有侧移的。
有侧移失稳的框架,其临界力比无侧移失稳的框架低得多。
(1)无支撑纯框架 1)一阶弹性分析方法框架柱的上端与横梁刚性连接。
横梁对柱的约束作用取决于横梁的线刚度l I /1与柱的线刚度H I /的比值1K ,即H I lI K //11=(16)对于单层多跨框架,1K 值为与柱相邻的两根横梁的线刚度之和1I /1l +2I /2l 与柱线刚度I /H 之比H I l I l I K ///22111+=(17)框架柱在框架平面内的计算长度0H 可用下式表达HH μ=0 (18)式中 H ——柱的几何长度;μ——计算长度系数。
μ值与框架柱柱脚与基础的连接形式及1K 值有关。
有侧移的框架失稳时,框架柱的计算长度系数都大于1.0。
柱脚刚接的有侧移框架柱,μ值约在1.0~2.0之间。
柱脚铰接的有侧移框架柱,μ值总是大于2.0。
对于无侧移的框架柱,柱子的计算长度系数μ将小于1.0。
2)二阶弹性分析方法当采用二阶弹性分析方法计算内力且在每层柱顶施加按式(19)计算的假想水平力H ni时,框架柱的计算长度系数μ=1.0。
siy ni n Q H 12.0250+=α (19) 式中 Q i ——第i 楼层的总重力荷载设计值;n s ——框架总层数,当112.0>+sn 时,取此根号值为1.0; αy ——钢材强度影响系数,其值为 Q235钢1.0;Q345钢1.1;Q390钢1.2;Q420钢1.25。
(2)有支撑框架 1)强支撑框架对于强支撑的无侧移框架柱,柱子的计算长度系数μ可按查表确定。
2)弱支撑框架弱支撑框架柱的轴压稳定系数ϕ直接按下式计算∑∑--+=)2.1(3)(0010i bi bN N S ϕϕϕϕ (20)式中 ϕ1,ϕ0——分别按无侧移框架柱和有侧移框架柱计算长度系数算得得轴心压杆稳定系数。
2. 多层等截面框架柱在框架平面内的计算长度多层多跨框架的失稳形式也分为有侧移失稳和无侧移失稳两种情况。
在确定柱的计算长度时,假设柱子开始失稳时相交于上下两端节点的横梁对于柱子提供的约束弯矩,按其与上下两端节点柱的线刚度之和的比值1K 和2K 分配给柱子。
1K 为相交于柱上端节点的横梁线刚度之和与柱线刚度之和的比值;2K 为相交于柱下端节点的横梁线刚度之和与柱线刚度之和的比值。
柱与基础刚接时,从理论上来说2K =∞,但考虑到实际工程情况,取2K ≥10时的μ值。
3. 框架柱在框架平面外的计算长度框架柱在框架平面外的计算长度取支撑点间的距离。
