高中数学零点存在定理中取点问题
高中数学考点12 零点定理(讲解)(解析版)知识点解析
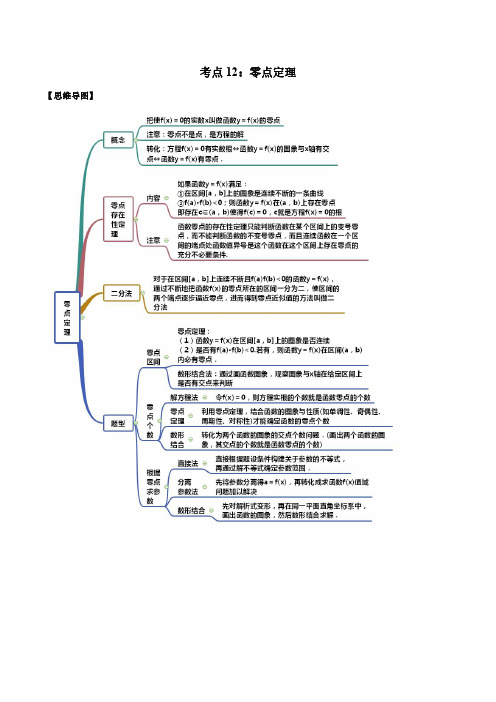
考点12:零点定理【思维导图】【常见考法】考点一:求零点1.若幂函数()f x x α=的图象过点(,则函数()()3g x f x =-的零点是。
【答案】9【解析】∵幂函数()f x x α=的图象过点,∴2α=,解得1=2α,∴()12f x x =∴()123g x x =-由()1230g x x =-=,得9x =.2.函数()234f x x x =+-的零点是____________.【答案】1,4-【解析】令f (x )=0,即x 2+3x-4=0,解得:x=-4,x=1.3.若函数()2,01,0x e x f x x x ⎧≤=⎨->⎩,则函数()1y f x =-的零点是___________.【答案】0【解析】要求函数()1y f x =-的零点,则令()10y f x =-=,即()1f x =,又因为:()2,01,0x e x f x x x ⎧≤=⎨->⎩,①当0x ≤时,()xf x e =,1x e =,解得0x =.②当0x >时,()21f x x =-,211x -=,解得x =,所以x =.综上所以,函数()1y f x =-的零点是0.故答案为:04.函数y =11x-的图象与函数y =2sinπx(-2≤x≤4)的图象所有交点的横坐标之和等于.【答案】8【解析】函数y 1=11x-与y 2=2sinπx 的图象有公共的对称中心(1,0),作出两个函数的图象,由图象可知,两个函数在[-2,4上共有8个交点,两两关于点(1,0)对称设对称的两个点的横坐标分别为m 、n 则m+n=2×1=2,故所求的横坐标之和为8,故答案为8.考点二:零点区间1.函数()42xxf x -=-的零点所在区间是()A .(1,0)-B .1(0,4C .11(,42D .1(,1)2【答案】D【解析】易知函数()f x 为减函数,又121111(402424f -=-=->,11(1)042f =-<,根据零点存在性原理,可知函数()42xx f x -=-的零点所在的区间是1(,1)2,故选D.2.函数()2312x f x x -⎛⎫=- ⎪⎝⎭的零点所在的区间为()A .()0,1B .()1,2C .()2,3D .()3,4【答案】B【解析】∵函数()2312x f x x -⎛⎫=- ⎪⎝⎭单调递增,∴f (0)=-4,f (1)=-1,f (2)=7>0,根据零点的存在性定理可得出零点所在的区间是()1,2,故选B .3.函数()ln 3f x x x =+-的零点所在的区间为()A .()0,1B .()1,2C .()2,3D .()3,4【答案】C【解析】∵f (x )=ln x +x -3在(0,+∞)上是增函数f (1)=-2<0,f (2)=ln2-1<0,f (3)=ln3>0∴f (2)•f (3)<0,根据零点存在性定理,可得函数f (x )=ln x +x -3的零点所在区间为(2,3)故选:C .4.已知()f x 是定义在()0,∞+上的单调函数,满足()()2ln 21xf f x ex e --+=-,则函数()f x 的零点所在区间为()A .210,e ⎛⎫ ⎪⎝⎭B .211,e e ⎛⎫⎪⎝⎭C .1,1e ⎛⎫ ⎪⎝⎭D .()1,e 【答案】C【解析】设()2ln 2xf x e x t --+=,即()2ln 2xf x e x t =+-+,()1f t e =-,因为()f x 是定义在()0,∞+上的单调函数,所以由解析式可知,()f x 在()0,∞+上单调递增.而()12f e t =-+,()1f t e =-,故1t =,即()2ln 1xf x e x =+-.因为()110f e =->,11112ln 13ee f e e e e ⎛⎫=+-=- ⎪⎝⎭,由于11ln ln 3ln 30ee e-=-<,即有13e e <,所以1130e f e e ⎛⎫=-< ⎪⎝⎭.故()110f f e ⎛⎫< ⎪⎝⎭,即()f x 的零点所在区间为1,1e ⎛⎫ ⎪⎝⎭.故选:C .考点三:零点个数1.函数f(x)=|x-2|-lnx 在定义域内零点的个数为。
高中数学常见题型解法归纳 函数的零点个数问题的求解方法

高中数学常见题型解法归纳 函数的零点个数问题的求解方法【知识要点】一、方程的根与函数的零点(1)定义:对于函数()y f x =(x D ∈),把使f(x)=0成立的实数x 叫做函数()y f x =(x D ∈)的零点.函数的零点不是一个点的坐标,而是一个数,类似的有截距和极值点等.(2)函数零点的意义:函数()y f x =的零点就是方程f(x)=0的实数根,亦即函数()y f x =的图像与x 轴的交点的横坐标,即:方程f(x)=0有实数根⇔函数()y f x =的图像与x 轴有交点⇔函数()y f x =有零点.(3)零点存在性定理:如果函数()y f x =在区间[,]a b 上的图像是一条连续不断的曲线,并且有0)()(<⋅b f a f ,那么函数()y f x =在区间(,)a b 内至少有一个零点,即存在(,c a b ∈)使得()0f c =,这个c 也就是方程的根.函数()y f x =在区间[,]a b 上的图像是一条连续不断的曲线,并且有0)()(<⋅b f a f 是函数()y f x =在区间(,)a b 内至少有一个零点的一个充分不必要条件.零点存在性定理只能判断是否存在零点,但是零点的个数则不能通过零点存在性定理确定,一般通过数形结合解决. 二、二分法(1)二分法及步骤对于在区间[,]a b 上连续不断,且满足0)()(<⋅b f a f 的函数()y f x =,通过不断地把函数的零点所在的区间一分为二,使区间的两个端点逐步逼近零点,进而得到函数零点近似值的方法叫做二分法. (2)给定精确度ε,用二分法求函数的零点近似值的步骤如下: 第一步:确定区间[,]a b ,验证0)()(<⋅b f a f ,给定精确度ε. 第二步:求区间(,)a b 的中点1x .第三步:计算1()f x :①若1()f x =0,则1x 就是函数的零点;②若1()()0f a f x <,则令1b x = (此时零点01(,)x a x ∈)③若1()()0f x f b <,则令1a x =(此时零点01(,)x x b ∈)第四步:判断是否达到精确度ε即若a b ε-<,则得到零点值a 或b ,否则重复第二至第四步.三、一元二次方程2()0(0)f x ax bx c a =++=≠的根的分布讨论一元二次方程2()0(0)f x ax bx c a =++=≠的根的分布一般从以下个方面考虑列不等式组: (1)a 的符号; (2)对称轴2bx a=-的位置; (3)判别式的符号; (4)根分布的区间端点的函数值的符号.四、精确度为0.1指的是零点所在区间的长度小于0.1,其中的任意一个值都可以取;精确到0.1指的是零点保留小数点后一位数字,要看小数点后两位,四舍五入. 五、方法总结函数零点问题的处理常用的方法有:(1) 方程法;(2)图像法;(3)方程+图像法. 【方法点评】方法一 方程法使用情景 方程可以直接解出来. 解题步骤 先解方程,再求解.【例1 】已知函数2()32(1)(2)f x x a x a a 区间(1,1)-内有零点,求实数a 的取值范围.【点评】(1)本题如果用其它方法比较复杂,用这种方法就比较简洁.关键是能发现方程能直接解出来.(2)对于含有参数的函数要尝试因式分解,如果不好因式分解,再考虑其它方法.【反馈检测1】函数2()(1)cos f x x x =-在区间[0,4]上的零点个数是( ) A .4 B .5 C .6 D . 7方法二 图像法使用情景 一些简单的初等函数或单调性容易求出,比较容易画出函数的图像.解题步骤先求函数的单调性,再画图分析.【例2】(2017全国高考新课标I 理科数学)已知函数2()(2)xx f x ae a e x =+--.(1)讨论()f x 的单调性;(2)若()f x 有两个零点,求a 的取值范围.(2) ①若0,a ≤由(1)知()f x 至多有一个零点.②若0a >,由(1)知当ln x a =-时,()f x 取得最小值,1(ln )1ln f a a a-=-+. (i )当1a =时,(ln )f a -=0,故()f x 只有一个零点. (ii )当(1,)a ∈+∞时,由于11ln a a-+>0,即(ln )0f a ->,故()f x 没有零点. (iii )当0,1a ∈()时,11ln 0a a-+<,即(ln )0f a -<. 422(2)(2)2220,f ae a e e ----=+-+>-+>故()f x 在(,ln )a -∞-只有一个零点.00000000003ln(1),()(2)203ln(1)ln ,()n n n n n n f n e ae a n e n n aa f x a>-=+-->->->->-∞设正整数满足则由于因此在(-lna,+)有一个零点.综上所述,a 的取值范围为(0,1).【点评】(1)本题第2问根据函数的零点个数求参数的范围,用的就是图像法. 由于第1问已经求出了函数的单调性,所以第2问可以直接利用第1问的单调性作图分析. (2) 当0,1a ∈()时,要先判断(,ln )a -∞的零点的个数,此时考查了函数的零点定理,(ln )0f a -<,还必须在该区间找一个函数值为正的值,它就是422(2)(2)2220,f aea e e ----=+-+>-+>要说明(2)0f ->,这里利用了放缩法,丢掉了42ae ae --+.(3) 当0,1a ∈()时,要判断(ln ,)a -+∞上的零点个数,也是在考查函数的零点定理,还要在该区间找一个函数值为正的值,它就是03ln(1)n a>-,再放缩证明0()f n >0. (4)由此题可以看出零点定理在高考中的重要性.【例3】已知3x =是函数()()2ln 110f x a x x x =++-的一个极值点. (Ⅰ)求a ;(Ⅱ)求函数()f x 的单调区间;(Ⅲ)若直线y b =与函数()y f x =的图象有3个交点,求b 的取值范围.(Ⅲ)由(Ⅱ)知,()f x 在()1,1-内单调增加,在()1,3内单调减少,在()3,+∞上单调增加,且当1x =或3x =时,()'0f x =所以()f x 的极大值为()116ln 29f =-,极小值为()332ln 221f =- 因此()()21616101616ln 291f f =-⨯>-=()()213211213f e f --<-+=-<所以在()f x 的三个单调区间()()()1,1,1,3,3,-+∞直线y b =有()y f x =的图象各有一个交点,当且仅当()()31f b f <<,因此,b 的取值范围为()32ln 221,16ln 29--【点评】本题第(3)问,由于函数()f x 中没有参数,所以可以直接画图数形结合分析解答.【反馈检测2】已知函数2()1x e f x ax=+,其中a 为实数,常数 2.718e =.(1) 若1 3x=是函数()f x的一个极值点,求a的值;(2) 当4a=-时,求函数()f x的单调区间;(3) 当a取正实数时,若存在实数m,使得关于x的方程()f x m=有三个实数根,求a的取值范围.方法三方程+图像法使用情景函数比较复杂,不容易求函数的单调性.解题步骤先令()0f x=,重新构造方程()()g x h x=,再画函数(),()y g x y h x==的图像分析解答.【例4】函数()lg cosf x x x=-的零点有()A.4 个 B.3 个 C.2个 D.1个【点评】调性不是很方便,所以先令()lg cos0f x x x=-=,可化为lg cosx x=,再在同一直角坐标系下画出lgy x=和cosy x=的图像分析解答.(2)方程+图像是零点问题中最难的一种,大家注意理解掌握和灵活应用.【反馈检测3】设函数()()()221ln,1,02f x x m xg x x m x m=-=-+>.(1)求函数()f x的单调区间;(2)当1m≥时,讨论函数()f x与()g x图象的交点个数.422510152025oy=cosxy=lgxyx参考答案【反馈检测1答案】C【反馈检测2答案】(1)95a =;(2)()f x 的单调增区间是51(1)2-,15(,12+; ()f x 的单调减区间是1(,)2-∞-,15(,12-,5(1)++∞;(3)a 的取值范围是(1,)+∞. 【反馈检测2详细解析】(1)222(21)()(1)xax ax e f x ax -+'=+ 因为13x =是函数()f x 的一个极值点,所以1()03f '=,即12910,935a a a -+==. 而当95a =时,229591521(2)()()59533ax ax x x x x -+=-+=--,可验证:13x =是函数()f x 的一个极值点.因此95a =.(2) 当4a =-时,222(481)()(14)xx x e f x x -++'=-令()0f x '=得24810x x -++=,解得51x =,而12x ≠±.所以当x 变化时,()f x '、()f x 的变化是x1(,)2-∞-15(,1)22-- 512-51(1,)22-15(,1)22+ 512+5(1,)2++∞ ()f x '--++-()f x极小值极大值因此()f x 的单调增区间是51(1,)22-,15(,1)22+;()f x 的单调减区间是1(,)2-∞-,15(,1)2--,5(1,)++∞; 【反馈检测3答案】(1)单调递增区间是),m +∞, 单调递减区间是(m ;(2)1.【反馈检测3详细解析】(1)函数()f x 的定义域为()()(0,,'x m x m f x x+∞=.当0x m <<()'0f x <,函数()f x 单调递减,当x m >时,()'0f x >函数()f x 单调递增,综上,函数()f x 的单调递增区间是),m +∞, 单调递减区间是(m .(2)令()()()()211ln ,02F x f x g x x m x m x x =-=-++->,问题等价于求函数()F x 的零点个数,()()()1'x x m F x x--=-,当1m =时,()'0F x ≤,函数()F x 为减函数,F x有唯一零点,即两函数图象总有一个交点.综上,函数()。
高中数学取点问题与极值点偏移30例

例 1. 已知函数 f x axe x a 1x 12,a R
(1)若 f x 只有一个极值点,求a 的取值范围;
(2)证明:当 0 a
1 时,f x 2
有两个零点,记为x 与x ,且 3 x x
1
2
1
2
2
分析与解答:分离参数法,放缩取点
f x
1 x
2
1 2x x
f x
在
0,1 2
,在
1 2
,
f x
f
1 2
ln2
0
fx
在 0,
(2) f x 1 lnx 2ax ,令 f x 0 在 0, 有两个不同的实数根
方法一:分离参数法,导数法研究函数的大致图像
分离参数 2a 1 ln x , x 0 导数法研究函数的大致图象问题(略) x
要有两个不等根的充要条件
htln3ln3,0,h t 0 0 m s ,ln3,h s 0
3 ln3 2 ,( ln3 约 1.10 )
因为y f x 有两个零点,x ' 0 ,x ' x ,即e x0 3x 1
1
2
0
0
由(1)知,h x f x
在x ' 0 处的切线为y 2x x m
2a 2a
2a
2
又 g 1 2a 0 ,放缩取点,导数法可证: ln x 2 x 1, x 0 e e
g
1 a2
ln
1 a2
2a.
1 a2
1
2
1 a2
1
2 a
1 0
综上所述, 0 a 1 2
高中数学-函数零点问题及例题解析

高中数学-函数零点问题及例题解析一、函数与方程基本知识点1、函数零点:(变号零点与不变号零点)(1)对于函数)(x f y =,我们把方程0)(=x f 的实数根叫函数)(x f y =的零点。
(2)方程0)(=x f 有实根⇔函数()y f x =的图像与x 轴有交点⇔函数()y f x =有零点。
若函数()f x 在区间[],a b 上的图像是连续的曲线,则0)()(<b f a f 是()f x 在区间(),a b 内有零点的充分不必要条件。
2、二分法:对于在区间[,]a b 上连续不断且()()0f a f b ⋅<的函数()y f x =,通过不断地把函数()y f x =的零点所在的区间一分为二,使区间的两个端点逐步逼近零点,进而得到零点的近似值的方法叫做二分法; 二、函数与方程解题技巧零点是经常考察的重点,对此部分的做题方法总结如下:(一)函数零点的存在性定理指出:“如果函数)(x f y =在区间[a,b]上的图象是连续不断的一条曲线,并且0)()(<b f a f ,那么,函数)(x f y =在区间(a,b )内有零点,即存在),(b a c ∈,使得0)(=c f ,这个c 也是方程0)(=x f 的根”。
根据函数零点的存在性定理判断函数在某个区间上是否有零点(或方程在某个区间上是否有根)时,一定要注意该定理是函数存在零点的充分不必要条件:如例、函数xx x f 2)1ln()(-+=的零点所在的大致区间是( ) (A )(0,1); (B )(1,2); (C ) (2,e ); (D )(3,4)。
分析:显然函数xx x f 2)1ln()(-+=在区间[1,2]上是连续函数,且0)1(<f ,0)2(>f ,所以由根的存在性定理可知,函数xx x f 2)1ln()(-+=的零点所在的大致区间是(1,2),选B(二)求解有关函数零点的个数(或方程根的个数)问题。
高中数学函数零点问题及解题策略探究

高中数学函数零点问题及解题策略探究郭文峰(福建省宁德市民族中学ꎬ福建宁德355000)摘㊀要:函数是高中数学学习的重难点ꎬ函数零点问题则是函数的重点所在.本论文结合具体的例题ꎬ对不同类型的函数零点问题的解题方式进行了探究.关键词:高中数学ꎻ零点问题ꎻ策略探究中图分类号:G632㊀㊀㊀文献标识码:A㊀㊀㊀文章编号:1008-0333(2023)10-0036-03收稿日期:2023-01-05作者简介:郭文峰(1983.2-)ꎬ男ꎬ福建省福安人ꎬ本科ꎬ中学一级教师ꎬ从事高中数学教学研究.㊀㊀函数零点是沟通函数㊁方程和图象的重要媒介ꎬ充分体现了函数和方程之间的内在联系ꎬ也蕴含了丰富的数学思想.在函数零点问题解答中ꎬ由于题目类型不同ꎬ解题思路也就有所不同ꎬ学生不仅要理清这一类型题目的特点ꎬ还应掌握多种零点问题的解答方法ꎬ才能灵活应对各种函数零点问题的解答ꎬ真正提升学生的解题效率.1高中函数零点问题常考类型分析1.1求函数零点的值求函数零点值问题只要掌握了函数零点的定义ꎬ将函数问题转化成为方程ꎬ即可通过方程的根得出函数的零点值.例1㊀已知f(x)=x3-3x2-4xꎬ求该函数的零点.㊀解析㊀令f(x)=0ꎬ即x3-3x2-4x=0ꎬ解方程得出x1=0ꎬx2=4ꎬx3=-1.因此ꎬ函数f(x)的零点就是x3-3x2-4x=0的三个根ꎬ即0ꎬ4ꎬ-1.例2㊀已知f(x)=2x3-ax2+bꎬ求该函数的极值点.解析㊀由题可知fᶄ(x)=2x(3x-a)ꎬ令fᶄ(x)=0ꎬ得出x=0或x=a3.当a=0时ꎬ在(-¥ꎬ+¥)上ꎬfᶄ(x)ȡ0.因此ꎬf(x)=2x3-ax2+b在该区间内单调递增ꎬ不存在极值点.当a>0时ꎬ在(-¥ꎬ0)ꎬ(a3ꎬ+¥)上ꎬfᶄ(x)>0ꎬ因此ꎬf(x)=2x3-ax2+b在该区间内单调递增ꎻ在(0ꎬa3)上ꎬfᶄ(x)<0ꎬ则f(x)=2x3-ax2+b单调递减.此时ꎬ该函数具备极大值点0ꎬ极小值点a3.当a<0时ꎬ在(-¥ꎬa3)ꎬ(0ꎬ+¥)上ꎬfᶄ(x)>0ꎬ则f(x)=2x3-ax2+b单调递增ꎻ在(a3ꎬ0)上ꎬfᶄ(x)<0ꎬ则f(x)=2x3-ax2+b单调递减.因此ꎬ该函数具备极大值点a3ꎬ极小值点为0[1].1.2求函数零点个数此类题目可以先将函数的零点求出来ꎬ然后看零点一共有多少个ꎻ还可以利用零点存在性定理ꎬ并结合函数的单调性ꎬ对函数零点的个数进行确定ꎻ也可以通过构造函数的方式ꎬ将函数的零点问题进行转化ꎬ使其成为求函数图象的交点个数问题.例3㊀求函数f(x)=log0.5x-(12)x的零点63个数.解析㊀令log0.5x-(12)x=0ꎬ得出log0.5x=(12)xꎬ令y1=log0.5xꎬy2=(12)xꎬ绘制出函数图象(如图1所示).图1结合图象分析得出ꎬy1=log0.5xꎬy2=(12)x之间存在两个交点.因此ꎬ原函数f(x)=log0.5x-(12)x存在2个零点.例4㊀已知a>1eꎬ判断f(x)=ax2+(a+1)x-(a+1)xlnx-1的零点个数.解析㊀在函数定义域(0ꎬ+¥)内ꎬfᶄ(x)=2ax-(a+1) lnxꎬ令2ax-(a+1) lnx=h(x)ꎬ则hᶄ(x)=2a-a+1x=2ax-(a+1)x.令hᶄ(x)=0ꎬ则x=a+12a.当0<x<a+12a时ꎬ则hᶄ(x)<0ꎻ当x>a+12a时ꎬ则hᶄ(x)>0ꎬ所以fᶄ(x)在区间(0ꎬa+12a)内单调递减ꎬ在区间(a+12aꎬ+¥)内单调递增ꎬ因此ꎬfᶄ(x)的最小值为fᶄ(a+12a)=(a+1)(1-lna+12a).因为a>1eꎬ所以a+12a=12+12a<12+e2<eꎬ即fᶄ(x)最小值为fᶄ(a+12a)=(a+1)(1-lna+12a)>0.因此ꎬf(x)在(0ꎬ+¥)单调递增ꎬ至多存在一个零点.因为f(1)=2a>0ꎬ所以f(x)在区间(1ꎬ+¥)内没有零点.又因为a为常数ꎬ当xң0时ꎬ在原函数中ꎬax2ң0ꎬ(a+1)xң0ꎬlnxң-¥ꎬ所以f(x)ң-1<0.综上ꎬ函数f(x)在区间(0ꎬ1)内有一个零点ꎬ在(0ꎬ+¥)内有一个零点[2].1.3求函数零点的范围例5㊀已知函数f(x)=1x-2x在(n-1nꎬnn+1)上存在零点ꎬ则正整数n的值为多少?解析㊀易知函数f(x)为减函数ꎬ因为f(12)=2-2>0ꎬf(1)=1-2<0ꎬ因此该函数在(12ꎬ1)中存在零点.同时ꎬ由已知条件得出f(x)在(n-1nꎬnn+1)上存在零点ꎬ因此ꎬ0<n-1n<nn+1<1ꎬ得出nɤ2ꎻ将n=2代入nn+1ꎬ得出nn+1=23ꎬ所以f(23)<0ꎬ因此n=2符合题意.1.4根据函数零点个数求解参数范围1.4.1基于转化思想解决零点问题例6㊀已知函数f(x)=-x2+2ex+m-1ꎬg(x)=x+e2x(x>0).(1)若g(x)=m存在零点ꎬ求m的取值范围ꎻ(2)确定m的取值范围ꎬ使得函数h(x)=g(x)-f(x)存在两个零点.解析㊀(1)因为g(x)=x+e2xȡ2e2=2e(x>0)ꎬ当且仅当x=e2x时ꎬ取等号.因此ꎬ该函数存在最小值ꎬ即2e.所以ꎬ当mɪ[2eꎬ+¥)时ꎬ函数存在零点.(2)要使得h(x)=g(x)-f(x)存在两个零点ꎬ即g(x)-f(x)=0存在两个不同的实数根(如图2所示)ꎬ即两个函数的图象有两个不同的交点.因为f(x)=-x2+2ex+m-1=-(x-e)2+m-1+e2ꎬ其对称轴为x=e.所以当m>-e2+2e+173图2时ꎬ函数h(x)=g(x)-f(x)存在两个零点.1.4.2基于数形结合思想解决零点问题在高中函数零点问题中ꎬ数形结合思想是一种非常有效的方法ꎬ主要是借助函数零点的概念ꎬ引导学生对函数图象进行观察ꎬ明确函数图象与坐标轴的交点ꎬ在图象的辅助下ꎬ顺利解决函数零点问题.例7㊀已知函数f(x)=2-x-1ꎬxɤ0ꎬf(x-1)ꎬx>0ꎬ{若方程f(x)=x+a有且只有两个不相等的实数根ꎬ求实数a的取值范围.解析㊀将f(x)=x+a有且只有两个不相等的实数根ꎬ看做成为g(x)=f(x)-x-a存在两个不相同的零点.在平面直角坐标系中分别作出函数f(x)=2-x-1ꎬxɤ0ꎬf(x-1)ꎬx>0ꎬ{以及h(x)=x的图象(如图3)ꎬ接着对h(x)=x进行平移.当a<1时ꎬ两个函数存在两个交点ꎻ此时ꎬf(x)=x+a有且只有两个不相等的实数根.图41.4.3基于分类与整合思想解决零点问题分类讨论与整合ꎬ就是化整为零㊁各个击破ꎬ是一种非常有效的函数零点问题解决手段.通常ꎬ这一种方法常常被用于综合性的函数零点问题中ꎬ需要在解题的过程中ꎬ通过分类讨论ꎬ最终在各个击破的基础上ꎬ整合到一起.例8㊀已知函数f(x)是定义在R上的偶函数ꎬ当xȡ0时ꎬf(x)=x2-2mx+mꎬ如果函数存在两个不同的零点ꎬ求m的取值范围.解析㊀因为f(x)=x2-2mx+m的图象开口向上ꎬ且图象必须经过(0ꎬm)点㊁图象对称轴为x=m.(1)当m>0时ꎬ由于函数必然经过(0ꎬm)点ꎬ且y轴为图象的对称轴ꎬ根据判别式值等于0ꎬ得出m=1ꎻ(2)当m=0时ꎬ因为函数只有一个零点ꎬ所以m=0与题意不相符ꎻ(3)当m<0时ꎬ通过函数图象即可得知ꎬ该函数存在两个不同的零点ꎬ其符合题意.2基于函数零点问题解答的日常教学启示结合上述例题研究显示ꎬ学生对函数零点的概念㊁零点存在性定理的掌握情况以及对函数和方程㊁图象之间的关系熟悉程度ꎬ直接决定了学生的解题能力.鉴于此ꎬ为了真正提升学生的数学解题能力ꎬ高中数学教师在日常教学中ꎬ唯有坚持以生为本的理念ꎬ引导学生积极主动参与到相关数学概念和定理的探究学习中.为了全面提升学生的解题能力ꎬ唯有彻底转变传统的教学模式ꎬ指向数学新课程的要求ꎬ灵活借助多种方式优化课堂教学ꎬ包括:探究式学习㊁多媒体信息技术教学等ꎬ使得学生在多样化学习中ꎬ高效完成课堂学习目标.在最新的课程标准中明确提出了数学六大核心素养ꎬ并且已经成为当前考查的方向.在常见的函数零点问题中就蕴含了数形结合思想㊁转化化归思想㊁分类讨论思想等ꎬ学生唯有熟练掌握这些数学思想ꎬ才能促使其形成正确的解题思路.鉴于此ꎬ高中数学教师在日常教学时ꎬ应结合不同的例题内容ꎬ针对性地融入数学思想ꎬ使得学生在日常学习中ꎬ逐渐完成数学思想的内化和应用ꎬ进而提升自身的数学解题能力.参考文献:[1]孟彩彩ꎬ巩铠玮.基于波利亚 怎样解题表 的习题教学案例研究 以 函数的零点 为例[J].数学教学通讯ꎬ2022(09):6-8.[2]寿啸天.高中数学函数零点解决方法探究[J].试题与研究ꎬ2020(28):31-32.[责任编辑:李㊀璟]83。
高中数学讲义:零点存在的判定与证明

零点存在的判定与证明一、基础知识:1、函数的零点:一般的,对于函数()y f x =,我们把方程()0f x =的实数根0x 叫作函数()y f x =的零点。
2、零点存在性定理:如果函数()y f x =在区间[],a b 上的图像是连续不断的一条曲线,并且有()()0f a f b ×<,那么函数()y f x =在区间(),a b 内必有零点,即()0,x a b $Î,使得()00f x =注:零点存在性定理使用的前提是()f x 在区间[],a b 连续,如果()f x 是分段的,那么零点不一定存在3、函数单调性对零点个数的影响:如果一个连续函数是单调函数,那么它的零点至多有一个。
因此分析一个函数零点的个数前,可尝试判断函数是否单调4、几个“不一定”与“一定”(假设()f x 在区间(),a b 连续)(1)若()()0f a f b ×<,则()f x “一定”存在零点,但“不一定”只有一个零点。
要分析()f x 的性质与图像,如果()f x 单调,则“一定”只有一个零点(2)若()()0f a f b ×>,则()f x “不一定”存在零点,也“不一定”没有零点。
如果()f x 单调,那么“一定”没有零点(3)如果()f x 在区间(),a b 中存在零点,则()()f a f b ×的符号是“不确定”的,受函数性质与图像影响。
如果()f x 单调,则()()f a f b ×一定小于05、零点与单调性配合可确定函数的符号:()f x 是一个在(),a b 单增连续函数,0x x =是()f x 的零点,且()0,x a b Î,则()0,x a x Î时,()0f x <;()0,x x b Î时,()0f x >6、判断函数单调性的方法:(1)可直接判断的几个结论:① 若()(),f x g x 为增(减)函数,则()()f x g x +也为增(减)函数② 若()f x 为增函数,则()f x -为减函数;同样,若()f x 为减函数,则()f x -为增函数③ 若()(),f x g x 为增函数,且()(),0f x g x >,则()()f x g x ×为增函数(2)复合函数单调性:判断()()y f g x =的单调性可分别判断()t g x =与()y f t =的单调性(注意要利用x 的范围求出t 的范围),若()t g x =,()y f t =均为增函数或均为减函数,则()()y f g x =单调递增;若()t g x =,()y f t =一增一减,则()()y f g x =单调递减(此规律可简记为“同增异减”)(3)利用导数进行判断——求出单调区间从而也可作出图像7、证明零点存在的步骤:(1)将所证等式中的所有项移至等号一侧,以便于构造函数(2)判断是否要对表达式进行合理变形,然后将表达式设为函数()f x (3)分析函数()f x 的性质,并考虑在已知范围内寻找端点函数值异号的区间(4)利用零点存在性定理证明零点存在例1:函数()23x f x e x =+-的零点所在的一个区间是( )A.1,02æö-ç÷èø B.10,2æöç÷èø C.1,12æöç÷èø D.31,2æöç÷èø思路:函数()f x 为增函数,所以只需代入每个选项区间的端点,判断函数值是否异号即可解:1211234022f e -æöæö-=+×--=-<ç÷ç÷èøèø,()020f =-<11232022f æö=+×-=-<ç÷èø()12310f e e =+-=->()1102f f æö\×<ç÷èø01,12x æö\Îç÷èø,使得()00f x =答案:C例2:函数()()ln 1f x x x =-+的零点所在的大致区间是( )A.31,2æöç÷èø B.3,22æöç÷èøC.()2,eD.(),e +¥思路:先能判断出()f x 为增函数,然后利用零点存在性判定定理,只需验证选项中区间端点函数值的符号即可。
高中数学例题:函数零点的存在性定理

高中数学例题:函数零点的存在性定理 例.函数2()ln f x x x =-的零点所在的大致区间是( )A .(1,2)B .(2,3)C .1(1,)e和(3,4) D .(e ,+∞)【答案】 B【解析】 从已知的区间(a ,b )中,求()f a 和()f b ,判断是否有()()0f a f b ⋅<. ∵(1)20f =-<,(2)ln 210f =-<,∴在(1,2)内()f x 无零点,A 错; 又2(3)ln 303f =->,∴(2)(3)0f f ⋅<,∴()f x 在(2,3)内有一个零点.【总结升华】这是最基本的题型,所用的方法也是基本方法:只要判断区间[a ,b]的端点值的乘积是否满足()()0f a f b ⋅<,还要看函数()f x 的图象在[a ,b]上是否是连续曲线即可. 解答这类判断函数零点的大致区间的选择题,只需用函数零点的存在性定理依次检验所提供的区间,即可得到答案.利用函数零点的存在性定理判定函数的零点(或方程的实根)所在的大致区间,有时比用数形结合(即作出两函数y=ln x 与2y x=的图象,再确定两图象交点的横坐标所在的大致区间)更简捷,因此要善于灵活运用函数零点的存在性定理来分析解决问题.举一反三:【变式1】若函数3()31,[1,1]f x x x x =+-∈-,则下列判断正确的是( )A .方程f (x )=0在区间[0,1]内一定有解B .方程f (x )=0在区间[0,1]内一定无解C .函数f (x )是奇函数D .函数f (x )是偶函数【答案】A【变式2】 根据表格中的数据,可以判定方程20x e x --=的一个根所在的最小区间为 .【答案】()1,2【解析】令()2x f x e x =--,由表格中数据知(1)f -=0.37-1=-0.63<0,f(0)=1-2=-1<0,f(1)=2.72-3=-0.28<0,f(2)=7,39-4=3.39>0,f(3)=20.09-5=15.09>0,由于(1)(2)0f f ⋅<,所以根所在的最小区间为(1,2).【变式3】若方程2210ax x --=在(0,1)恰好有一解,求a 的取值范围.【答案】()1,+∞【解析】(1)当0a =时,方程为()10,1x =-∈,不满足题意舍去.(2)当0a ≠时,令2()21f x ax x =--,分情况讨论:①0180,(0,1)a x ∆=+=⎧⎨∈⎩,0182(0,1)a x ⎧=-⎪∴⎨⎪=-∉⎩ 18a ∴=-不满足题意舍去. ②180a ∆=+>,18a ∴>- 若(0)1f =-且(1)0f >即2110a -->,1a ∴>满足题意. 若(0)1f =-且(1)0f =即1a =时,()0f x =的另一解是12-. 综上所述,满足条件的a 的取值范围是()1,a ∈+∞.。
高中新教材数学必修件第章函数的零点

05
思想
对称性在函数零点中体现
函数零点的对称性
对于某些函数,其零点在坐标系上呈现出对称性,如二次函数的两个零点关于对 称轴对称。
对称性的美学价值
对称性在数学中是一种重要的美学特征,它体现了数学中的平衡和和谐,使得函 数图像更加美观。
简洁性在函数零点中体现
函数零点的简洁性
函数零点作为函数与x轴交点的横坐标,具有简洁明了的数学 表达形式,如一次函数的零点即为其斜率和截距的比值。
对于函数$y = f(x)$,若存在$x_0 in D$(D为函数定义域),使得 $f(x_0) = 0$,则称$x_0$为函数 $y = f(x)$的零点。
零点与图像的关系
函数$y = f(x)$的零点即为函数图 像与x轴交点的横坐标。
函数零点存在性定理
零点存在性定理
若函数$y = f(x)$在闭区间[a, b]上连 续,且$f(a) cdot f(b) < 0$,则函数 $y = f(x)$在区间(a, b)内至少存在一 个零点。
分段函数和复合函数零点问题
分段函数零点求解
针对每一段分别求解,注意端点处的取值情况,以及各段之间的 连续性。
复合函数零点分析
将复合函数分解为若干个基本函数,分别研究各基本函数的零点, 再综合得出复合函数的零点。
零点存在性定理的应用
在求解分段函数和复合函数零点时,可以运用零点存在性定理来判 断零点的存在性。
零点存在性定理的推论
若函数$y = f(x)$在区间(a, b)内单调 ,且$f(a) cdot f(b) < 0$,则函数$y = f(x)$在区间(a, b)内有且仅有一个零 点。
函数零点与方程根关系
01
函数零点与方程根的关系
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
当 x 0, 时,
h1 e 1 0 ,
h
1 2
e 2 0 ,又 h x 在 0, 上单调递增的,所以有唯
一的零点。
(II)若 a 0 ,则
当 x , 0 时, h x ex 1 a 0 恒成立,则没有零点;
(3)如果关于 x 的方程 f x 2 有且只有一个解,求实数 b 的取值范围.
【答案】(1) b 1, f x 的最小值为 2(2)见解析(3) b 1,或 b 1
e
e
【解析】
(1)由 f 1 f 1 得: e b 1 1 ,解得 b e (舍),或 b 1 ,
x
x
则 x2 ax 1 0, 取 x0 a
a2 2
4
0
,则
h x0
0
,又
h a
ea
1 a
a
0
,所以
hx
在
, 0 有唯一的零点,
当 x 0, 时, h 1 a e1a 1 a 1 a 1 a 1 1 0 ,
f
x
min
f
1 ,
f
1 min
f
1
2e,
所以, f x 在1,1 上的值域为2 e,1 .
(2)令
f
x
0 ,得
x ex
ax
1
0,
x 0 显然不是方程的根,
那么原方程等价于 ex 1 a 0 实根的个数,令 h x ex 1 a , x , 0) (0,
令 b 2 得: y0 ex0 2x0 ;令 b 3 得: y0 ex0 3x0 ,
∴ 2x0 2x0 ,
3 x0 2
1,解得唯一解 x0 0
∴ y0 2
经检验当 x 0 时, f 0 2
∴函数 y f x 的图像经过唯一定点 0, 2 .
零点存在定理中取点问题
如果函数 y f x 在区间[a, b] 上的图象是连续不断的一条曲线,并且有 f a f (b) 0 ,那么,函数 y f x 在区间 (a,b) 内有零点,即存在 c (a,b) ,使得 f c 0 ,这个 c 也就是方程 f x 0 的根.
eb
e
经检验
f
x
ex
1 ex
为偶函数
∴b 1 . e
又
f
x
ex
1 ex
2 ,当且仅当 x 0 时取等号,
∴ f x 的最小值为 2.
(2)假设 y f x 过定 点 x0, y0 ,则 y0 ex0 bx0 对任意 b 0 ,且 b 1恒成立.
【解析】
(1)当 a 1时,
f
x
x ex
ax
1 ,则
f
x
1 x ex
1
g
x
,
而
gx
x2 ex
0 在1,1 上恒成立,所以
g x
f
x 在1,1 上递减,
f
x
max
f 1
2e 1 0 ,
f
x
min
x
当 x 0, 时,
h
1 a
1
e a
0,
h
2
1
a
1
e 2a
2
1
e2
2
0
,又
hx
在 0, 上单调递
增的,所以有唯一的零点
(III)若 a 0 ,则
当 x , 0 时,由 ex x x R ,则 ex 1 a x 1 a 0, (x 0) ,
1 a
1 a
1 a
h
1 2
a
1
e 2a
2
a
a
2Fra biblioteka2
a
a
a
0 ,又
hx
在 0, 上单调递增的,所以有
唯一的零点
综上所述,当 a 0 时, f x 只有一个零点;当 a 0 时, f x 有两个零点.
【名师指点】涉及函数的零点问题、方程解的个数问题、函数图像交点个数问题,一般先通过导数研究函 数的单调性、最大值、最小值、变化趋势等,再借助函数的大致图象判断零点、方程根、交点的情况,归 根到底还是研究函数的性质,如单调性、极值,然后通过数形结合的思想找到解题的思路. 类型二 利用放缩法取点
f
1
1
0,
所以 f x 在1,1 上存在唯一的 x0 0 ,使得 f 0 0 ,而且
当 x 1,0 时, f x 0 , f x 递增;当 x 0,1 时 f x 0 , f x 递减;
所以,当 x 0 时, f x 取极大值,也是最大值,即 f x f 0 1, max
x
x
原命题也等价于 h x ex 1 a 在 x , 0) (0, 上的零点个数;
x
又因为 h x
ex
1 x2
0 ,所以 h x 在 , 0 和 0, 上都是单调递增的;
(I)若 a 0 ,则
当 x , 0 时, h x ex 1 0 恒成立,则没有零点;
在实际应用中,如何取 a, b ,是解决问题的难点.
类型一 利用方程的根或部分代数式的根取点
典例 1
已知函数
f
x
x ex
ax 1.
(1)当 a 1时,求 y f x 在 x 1,1 上的值域;
(2)试求 f x 的零点个数,并证明你的结论.
【答案】(1) 2 e,1(2)当 a 0 时, f x 只有一个零点;当 a 0 时, f x 有两个零点.
典例 2 已知 b 0 ,且 b 1,函数 f x ex bx ,其中 e 为自然对数的底数:
(1)如果函数 f x 为偶函数,求实数 b 的值,并求此时函数的最小值;
(2)对满足 b 0 ,且 b 1的任意实数 b ,证明函数 y f x 的图像经过唯一的定点;
