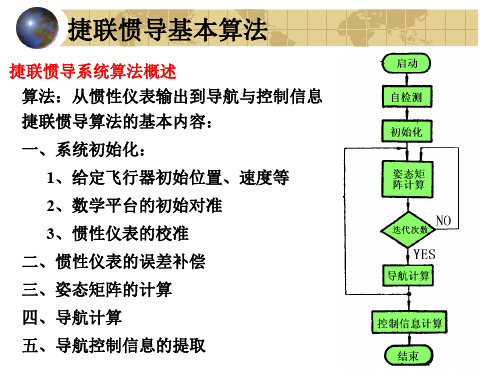
捷联惯导系统
捷联惯性导航系统的解算方法

捷联惯性导航系统的解算方法捷联惯性导航系统(Inertial Navigation System,简称INS)是一种利用陀螺仪和加速度计等惯性测量单元测量物体的加速度和角速度,然后通过对这些测量值的积分计算出物体的速度和位置的导航系统。
INS广泛应用于航空航天、无人驾驶车辆和船舶等领域,具有高精度和自主性等特点。
INS的解算方法一般分为初始对准、运动状态估计和航位推算三个主要过程。
初始对准是指在启动导航系统时,通过利用外部辅助传感器(如GPS)或静态校准等方法将惯性传感器的输出与真实姿态和位置进行初次校准。
在初始对准过程中,需要获取传感器的初始偏差和初始姿态,一般采用标定或矩阵运算等方法进行。
运动状态估计是指根据惯性传感器的测量值,使用滤波算法对物体的加速度和角速度进行实时估计。
常用的滤波算法包括卡尔曼滤波、扩展卡尔曼滤波和粒子滤波等。
其中,卡尔曼滤波是一种最优估计算法,通过对观测值和状态进行线性组合,得到对真实状态的最佳估计。
扩展卡尔曼滤波则是基于卡尔曼滤波的非线性扩展,可以应用于非线性INS系统。
粒子滤波是一种利用蒙特卡洛采样技术进行状态估计的方法,适用于非高斯分布的状态估计问题。
航位推算是指根据运动状态估计的结果,对物体的速度和位置进行推算。
INS最基本的航位推算方法是利用加速度值对速度进行积分,然后再对速度进行积分得到位置。
但是,在实际应用中,由于传感器本身存在噪声和漂移等误差,导致航位推算过程会出现积分漂移现象。
为了解决这个问题,通常采用辅助传感器(如GPS)和地图等数据对INS的输出进行校正和修正。
当前,还有一些先进的INS解算方法被提出,如基于深度学习的INS 解算方法。
这些方法利用神经网络等深度学习模型,结合原始传感器数据进行端到端的学习和预测,以实现更高精度的位置和姿态估计。
综上所述,捷联惯性导航系统的解算方法主要包括初始对准、运动状态估计和航位推算三个过程。
其中,运动状态估计过程利用滤波算法对传感器的测量值进行处理,得到物体的加速度和角速度的估计。
§3.9捷联式惯导系统介绍

G G dωie G dr 对上式求导,假定地球旋转角速度是常矢量, = 0且 = ve ,可得 dt dt e G K dv e G G d 2r K K G = + ωie × ve + ωie × [ωie × r ] 2 dt i dt i
而
K G G d 2r = f +G dt 2 i
G G G G G dv e K K G = f − ωie × ve − ωie × [ωie × r ] + G dt i
b 标系 Oe X iYi Z i 的角速度 ωib ,上角标 b 表示该角速度在 b 坐标系上的投 b 进行姿态矩阵 Cbi 计算。由于姿态矩阵 Cbi 中的元素是 影。利用 ωib
OX bYb Z b 相对 OX iYi Z i 的航向角、横滚角、俯仰角的三角函数构成,
所以当求得了姿态矩阵 Cbi 的即时值,便可进行加速度计信息的坐标 变换和提取姿态角的大小。 这三项功能实际上就代替了平台式惯性导 航系统中的稳定平台的功能, 这样计算机中的这三项功能也就是所谓
哥氏校正
fb
比力测量值 的分解
fi
∑
∑
速度v e和 位置的估 计值
i
导航计算
Cbi
固连于载体 的陀螺
ω
b ib
速度和位置的初始估计值 姿态计算
姿态的初始估值
图 捷联式惯导系统——惯性坐标系机械编排
3、当地地理坐标系的机械编排
在这种机械编排中,地理坐标系表示的地速是 vet ,它相对于地理 坐标系的变化率可通过其在惯性坐标系下的变化率表示 G G dv e dv e G G G = − [ wie + wet ] × ve dt t dt i G G G G G G dv e dve 用 ,得 = f − ωie × ve + g1 替代 dt t dt i G G dv e G G G K = f − [2 wie + wet ] × ve + g1 dt t 表示在选定的导航坐标系(地理坐标系)中,有
捷联惯导系统算法.ppt
cos
b Ebz
注意事项:当 θ= 90 度时,方程出现奇点
姿态计算 矩阵方程精确解1
二、方向余弦矩阵微分方程及其解 C C
其中
C bE
CbE
b Eb
0
b Eb
z
z
0
y
x
y x
0
由于陀螺仪直接测得的是载体 相对惯性空间的角速度,所以:
CbE
b ib
E iE
C
E b
或四元数微分方程:
q(t)
(
b ib
b iE
)q(t)
注意事项: 1、上述两个方程中的角速度表达式不一样 2、方程第二项较小,计算时速度可以低一些
增量算法 矩阵方程精确解
一、角增量算法
角增量:陀螺仪数字脉冲输出,每个脉冲代表一个角增量
一个采样周期内,陀螺输出脉冲数对应的角增量为:
C
0
0
c os
0 0 0 sin
sin
sin
c os
cos cos
求解欧拉角速率得
1 0
0
cos
0 sin
惯性器件的误差补偿
姿态计算 欧拉角微分方程1
姿态矩阵的计算 假设数学坐标系模拟地理坐标系 飞行器姿态的描述:
航向角ψ、俯仰角θ、滚动角γ 一、欧拉微分方程
从地理坐标系到载体坐标系 的旋转顺序:
Ψ →θ →γ
捷联惯导系统原理框图

t t
t t
θ t dt Φ t ( )dt
表征旋转的另一种形式: Φ u
q cos Φ Φ sin Φ 2Φ 2
Φ&
b nb
(t
)
1 2
Φ
ωbnb
(t
)
1 12
Φ
(Φ
ωbnb
(t
))
捷联惯导系统
泰勒级数展开、曲线拟合的方法(几个采样角就为几子样算法)
0 h
常数拟合:ωnbb (tk ) a
考系则 、 和 即为一组欧拉角。
& sin cos
&
sin
& cos cos
cos
0
sin
0 1
1
nnbbbbyx
sin cos cos
0 0
cos cos sin
nnbbbbxy
0 nbbz
sin tan
1
cos
tan
nbbz
当 90o时,方程退化,故不能全姿态工作。
q q q q n b(m)
n(m) n(m1)
n b(m1)
b(m) b(m1)
毕卡求解法(角增量) 1)定时采样增量法:采样时间间隔相同; 2)定量采样增量法:角增量达到一固定值时才更新;
Θ
Q(tk1) (I 2 )Q(tk )
捷联惯导系统 2.3.3 四元数初值的确定与归一化
q1
q2
T13 T23 T33
真值表判断
sin1(T32 )
主
tan 1 (
T31 T33
)
主
tan 1 ( T12 T22
)
捷联惯导系统
车载捷联惯导系统基本原理
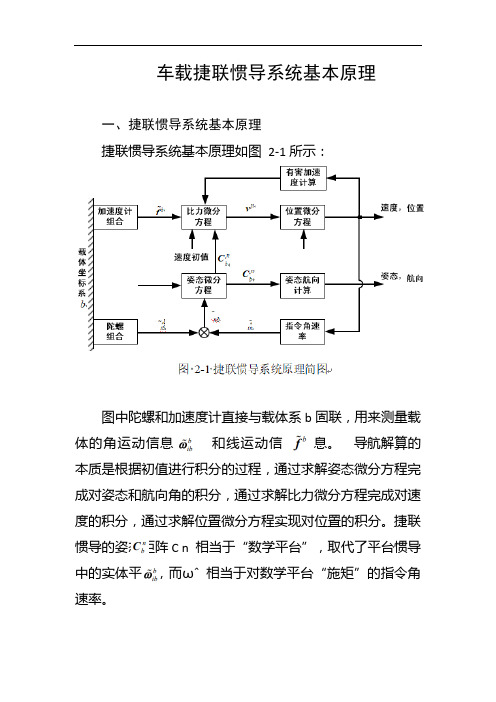
车载捷联惯导系统基本原理一、捷联惯导系统基本原理捷联惯导系统基本原理如图2-1所示:图中陀螺和加速度计直接与载体系b固联,用来测量载体的角运动信息和线运动信息。
导航解算的本质是根据初值进行积分的过程,通过求解姿态微分方程完成对姿态和航向角的积分,通过求解比力微分方程完成对速度的积分,通过求解位置微分方程实现对位置的积分。
捷联惯导的姿态矩阵C n 相当于“数学平台”,取代了平台惯导中的实体平台,而ωˆ相当于对数学平台“施矩”的指令角速率。
二、捷联惯导微分方程(一)姿态微分方程在捷联惯导系统中,导航坐标系n 和载体坐标系b 之间的角位置关系通常用姿态矩阵、四元数和欧拉角表示,相应也存在姿态矩阵微分方程、四元数微分方程和欧拉角微分方程三种形式。
姿态矩阵微分方程的表达式为:在欧拉角微分方程式(2.2-7)中,当俯仰角θ趋于90º时,cosθ趋于0,tanθ趋于无穷,方程存在奇异性,所以这种方法不能在全姿态范围内正常工作;姿态矩阵微分方程式(2.2-1)可全姿态工作,但姿态矩阵更新相当于求解包含9个未知量的线性微分方程组,计算量大;四元数微分方程式(2.2-6)同样可以全姿态工作,且更新算法只需求解4个未知量的线性微分方程组,计算量小,算法简单,是较实用的工程算法。
(二)速度微分方程速度微分方程即比力方程,是惯性导航解算的基本关系式:三、捷联惯性导航算法捷联惯导解算的目的是根据惯性器件输出求解载体姿态、速度和位置等导航信息,实际上就是求解三个微分方程的过程,相应存在姿态更新算法、速度更新算法和位置更新算法。
(一)姿态更新算法求解微分方程式(2.2-6)可得四元数姿态更新算法为:在车辆行驶过程中,一般不存在高频大机动环境,并且车载导航系统往往不工作在纯惯性导航方式,而是利用里程仪或零速条件进行组合导航,所以算法误差的影响有限,常用的5ms采样周期和二子样优化算法即可满足要求。
四、捷联惯导误差模型传感器误差、初值误差和算法误差是SINS的主要误差源,其中器件误差和初值误差又是影响导航结果的主要因素。
捷联惯性导航原理

捷联惯性导航原理捷联惯性导航(Inertial Navigation System,简称INS)是一种基于捷联惯性测量单元(Inertial Measurement Unit,IMU)的导航系统。
该系统通过测量物体在空间中的加速度和角速度,进而推导出它的位置、速度和航向等导航信息。
捷联惯性导航系统由三个主要组件组成:加速度计、陀螺仪和计算机。
加速度计用于测量物体的加速度,陀螺仪用于测量物体的角速度,而计算机则用于整合和处理这些测量数据。
加速度计和陀螺仪通常被组合在一起形成IMU,IMU被安装在导航系统的载体上。
加速度计是用来测量物体的线性加速度的设备。
它的作用类似于测力仪,通过测量物体所受的力,可以计算出物体的加速度。
加速度计一般使用压电传感器或气泡级感应器来测量物体的加速度。
陀螺仪则是用来测量物体的角速度的设备。
它的原理基于陀螺效应,通过测量物体围绕轴线旋转的角速度来推导物体的旋转状态。
陀螺仪分为一体式陀螺仪和光纤陀螺仪两种类型,一体式陀螺仪主要使用电子仪器的原理,而光纤陀螺仪则使用光学原理。
在捷联惯性导航系统中,加速度计和陀螺仪的输出数据会被输入到计算机中进行处理。
计算机通过积分和滤波等算法,对加速度和角速度进行处理,推导出物体的位置和速度等导航信息。
计算机还会结合其他传感器如GPS等,以提高导航系统的精度和稳定性。
然而,捷联惯性导航也存在一些局限性。
首先,由于加速度计和陀螺仪的精度和稳定性有限,导致导航系统随着时间的推移会产生累积误差。
其次,在长时间的运动过程中,加速度计和陀螺仪可能受到震动、振动和温度变化等外界因素的影响,进而导致导航系统的精度下降。
为了解决这些问题,通常将捷联惯性导航系统与其他导航系统如GPS进行组合导航。
通过将两种导航系统的输出数据进行融合,可以克服各自的缺点,提高导航系统的精度和鲁棒性。
总结起来,捷联惯性导航是一种基于物体惯性特性的导航系统,通过测量物体的加速度和角速度,推导出物体的位置、速度和航向等导航信息。
激光陀螺捷联惯导系统多位置标定方法

激光陀螺捷联惯导系统多位置标定方法我折腾了好久这个激光陀螺捷联惯导系统多位置标定方法,总算找到点门道。
说实话,一开始我对这玩意儿完全是瞎摸索。
我就知道这是个挺复杂的事儿,要想标定准确,肯定得从不同位置下手,但具体怎么做,那真是一头雾水。
我最开始的尝试啊,就是很笨的方法。
我简单地把系统放在几个不同的、自认为是有代表性的位置,然后就按照常规的标定流程去弄。
就好比你要给一个形状奇怪的东西量尺寸,你随便从几个地方开始量,以为能量准,结果发现根本不是那么回事。
这个时候得到的数据那叫一个混乱,偏差大得很,这就是失败的教训啊。
后来我就仔细研究这个激光陀螺和捷联惯导系统的原理。
我发现啊,对于激光陀螺,不同位置的磁场、温度这些外部因素影响很大。
我要是想标定准确,就得把这些外部因素考虑进去。
比如说,在一些靠近大型金属设备的位置,磁场干扰严重,那这个位置的数据可能就不准确。
这就像是你测量东西的时候,旁边有人一直捣乱,你肯定测量不好。
我又开始了新的尝试。
我把位置选择得更加科学了。
我先找那些环境比较稳定的地方,比如远离大型设备、温度比较恒定的角落。
然后慢慢地增加一些不同影响因素的位置,就像给孩子吃辅食,一点点加种类。
每次在新位置标定的时候,我都特别注意记录环境数据,看看是不是和之前的假设有出入。
我也犯过这样的错,就是在改变位置之后,没有等待足够的时间让系统稳定。
就像你从一个很冷的地方突然到一个很热的地方,得让自己适应适应吧,系统也一样。
结果那次得到的数据就不太对啊。
再比如说,多位置标定,也不是位置越多越好。
我曾经试过把能想到的所有位置都来一遍,结果数据多得我自己都看懵了,而且由于操作过程太长,还引入了很多其他不可控的误差,就像是你做菜放了太多调料,最后味道全乱了。
我的心得就是,在进行激光陀螺捷联惯导系统多位置标定的时候,位置选择要精心,要考虑外部因素,操作过程得细致,给系统稳定的时间,同时也不要过度追求位置数量。
目前我这个方法虽然不能说是完美的,但相比最开始已经成功了许多。
捷联式惯导系统初始对准方法研究

捷联式惯导系统初始对准方法研究一、本文概述随着导航技术的不断发展,捷联式惯导系统(StrapdownInertial Navigation System, SINS)已成为现代导航领域的重要分支。
由于其具有自主性强、隐蔽性好、不受外界电磁干扰等优点,被广泛应用于军事、航空、航天、航海等领域。
然而,捷联式惯导系统的初始对准问题是其实际应用中的一大难题。
初始对准精度的高低直接影响到系统的导航精度和稳定性。
因此,研究捷联式惯导系统的初始对准方法具有重要意义。
本文旨在深入研究和探讨捷联式惯导系统的初始对准方法。
对捷联式惯导系统的基本原理和组成进行简要介绍,为后续研究奠定基础。
对初始对准的定义、目的和重要性进行阐述,明确研究的重要性和方向。
接着,重点分析现有初始对准方法的优缺点,包括传统的静基座对准、动基座对准以及近年来兴起的智能对准方法等。
在此基础上,提出一种新型的初始对准方法,并对其进行详细的理论分析和仿真验证。
通过实验验证所提方法的有效性和优越性,为捷联式惯导系统的实际应用提供有力支持。
本文的研究内容对于提高捷联式惯导系统的初始对准精度、增强其导航性能和稳定性具有重要意义。
所提出的新型初始对准方法有望为相关领域的研究提供新的思路和方向。
二、捷联式惯导系统初始对准理论基础捷联式惯导系统(Strapdown Inertial Navigation System,SINS)的初始对准是其正常工作的前提,对于提高导航精度和长期稳定性具有重要意义。
初始对准的主要目的是确定惯导系统载体在导航坐标系中的初始姿态,以便为后续的导航计算提供准确的基准。
捷联式惯导系统的初始对准过程涉及多个理论基础知识,包括载体运动学、动力学模型、误差分析以及滤波算法等。
载体运动学模型描述了载体在三维空间中的姿态、速度和位置变化,是初始对准过程中姿态解算的基础。
动力学模型则用于描述载体在受到外力作用下的动态行为,为误差分析提供了依据。
在初始对准过程中,误差分析是至关重要的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
作业思考题
1、简要说明捷联惯导系统的基本组成和原理。 2、什么是数学平台?它有什么作用?
惯性导航系统
第四十四讲 捷联惯导系统 力学编排方程(一)
捷联式惯导系统(SINS)
加速度计
fb
数学平台
姿态矩阵 Cbp
f p 导航 速度、位置
计算机 姿态、航向
姿态矩阵计算
陀螺
ibb
pbb
b ip
姿态航向
-
C11 C21 C31
Cep 1 Cep T
C12 C13 1 C11 C21
C22
C23
C12
C22
C32 C33 C13 C23
C11 C22C33 C23C32 C21 C13C32 C12C33 C31 C12C23 C22C13
C31
C32
C33
位置矩阵微分方程组
Cep 0 f 0,0,0
1
p p epx epy
g g egx egy
R VeggxVeggy
VeppxVeppy
三、位置速率方程
11
p p epx epy
g g egx egy
RN RE
捷联惯导的发展
1、1950年起,德雷珀实验室捷联系统得到成熟的探索; 2、1969年,在“阿波罗-13”宇宙飞船,备份捷联惯导系统; 3、20世纪80~90年代,波音757/767、A310民机以及F-20战 斗机上使用激光陀螺惯导系统,精度达到1.85km/h的量级; 4、20世纪90年代,美国军用捷联式惯导系统已占有90% 。光 纤陀螺的捷联航姿系统已用于战斗机的机载武器系统中及波 音777飞机上。 5、国内由90年代挠性捷联惯导到现在激光捷联惯导、光纤陀 螺捷联航姿系统。
姿态计算
飞行器
方向余弦元素
教学内容
一、位置矩阵 二、位置矩阵微分方程 三、位置速率方程 四、速度方程
捷联惯导系统分类
按使用的陀螺仪分为:
速率捷联惯导系统:液浮、动调、激光、光纤 位置捷联惯导系统:静电
按选择的导航坐标系分为:
指北方位惯导系统:地理系 游移方位惯导系统:游移方位坐标系 自由方位惯导系统:自由方位坐标系
eppy
p epx
0 C31 C32 C33
坐标变换矩阵微分方程
速度向量的坐标变换形式:
PRs =CsvPR v +PCsvR v
哥氏定理矢量形式:
PsR=PvR+ωsv R
哥氏定理矩阵形式:
PR
s
=Csv
PR
v
+Csvω
vk svv
=Csvω
vk sv
或: Csv =-ωvsvkCsv
CC1123
eppyC32 eppyC33
CC2223
C p epx 32
C p epx 33
C32 C33
C p epy 12
C p epy 13
C p epx 22
p epx
C23
C11 C22C33 C23C32 C21 C13C32 C12C33 C31 C12C23 C22C13
C31 C32 C33
m
arcsin C33, m
arctan
C32 C31
,m
arctan
C13 C23
导航位置真值计算
m
m , C31 0
m m
180 180
,C31
0 mm
0 0
m
m
360
,C23
m 180 ,
0
m m
C23 0
0 0
注:
CC3312
cos cos
yg
xp
zgzp
xg
ze zt yg
zzgp
O
yt
xt
yt
xe
ye
位置矩阵
C C C C p
pgt
e
cos sin
0
gt
sin
cos
0
100e100
0
cos90 sin 90
0
cos 90
sin 90 sin 90
cos90 0
sin 90 cos 90
导航位置方程
目的: 、、
Veppx、
Veppx、
Vp epx
方法: Cep
Cep
一、位置矩阵 Cep
ωepp
Vp ep
fb
坐标变换矩阵
xe yeze 90 xt yt zt 90 x g y g z g x p y pz p
(e系)
(t)
(g)
(p)
zz22
γ zb
θ zR z1
xR
ψ x1
缺点: 陀螺动态范围要求大 惯性器件误差补偿要求高 算法复杂,计算量大
捷联惯导系统分类
按使用的陀螺仪分为:
速率捷联惯导系统:液浮、动调、激光、光纤 位置捷联惯导系统:静电
按选择的导航坐标系分为:
指北方位惯导系统:地理系 游移方位惯导系统:游移方位坐标系 自由方位惯导系统:自由方位坐标系
惯性导航系统
第四十三讲 捷联式惯导系统 概述
教学内容
一、捷联惯导基本原理 二、捷联惯导系统的特点 三、捷联惯导系统的分类 四、捷联惯导系统的发展
平台式惯导系统(GINS)
加速度计
比力 f p
指令角速度
p ip
速度、位置 导航 计算机 姿态、航向
陀螺 惯性平台 飞行器
陀螺输出 平台施矩 修正回路
环架姿态
0
0
0 1
cos sin sin sin cos cos cos sin sin sin sin cos
sin
sin
cos
sin
cos
sin cos cos sin sin
cos
cos
cos cos
cos sin
sin
C11 C12 C13
C21
C22
C23
捷联式惯导系统(SINS)
加速度计
fb
数学平台
? 姿态矩阵 Cbp
姿态矩阵计算
fp
导航 计算机
速度、位置 姿态、航向
陀螺
ibb
pbb
b ip
姿态航向
-
姿态计算
飞行器
方向余弦元素
激光捷联惯导系统
捷联惯导系统特点
优点: 便于维护、更换 体积小、重量轻、成本低 便于采用余度技术,进一步提高可靠性
x2
γ
xb
坐标变换矩阵
yy22yb θ
ψ y1 yR
C C C C b
b 21
R
21 R
cos sin 0
C1R sin cos 0
0
0 1
1 0
0
C12 0
cos
sin
0 sin cos
cos 0 sin
Cb2
0
1
0
sin 0 cos
地球系与导航系
ztze yp
sin cos
CC2133
sin cos
cos cos
二、位置矩阵微分方程
Cep ωeppkCep or Cep Cepωeppk
CC1211
C12 C22
C13 C23
0
p epz
eppz
0
p epy
eppx
C11 C21
C12 C22
C13
C23
C31 C32 C33
