汽车比火车跑的快。
离散数学课后答案

离散数学课后答案习题一6.将下列命题符号化。
(1)小丽只能从框里那一个苹果或一个梨.(2)这学期,刘晓月只能选学英语或日语中的一门外语课.答:(1)(p Λ¬q )ν(¬pΛq)其中p:小丽拿一个苹果,q:小丽拿一个梨(2)(p Λ¬q )ν(¬pΛq)其中p:刘晓月选学英语,q:刘晓月选学日语14.将下列命题符号化.(1) 刘晓月跑得快, 跳得高.(2)老王是山东人或河北人.(3)因为天气冷, 所以我穿了羽绒服.(4)王欢与李乐组成一个小组.(5)李辛与李末是兄弟.(6)王强与刘威都学过法语.(7)他一面吃饭, 一面听音乐.(8)如果天下大雨, 他就乘班车上班.(9)只有天下大雨, 他才乘班车上班.(10)除非天下大雨, 他才乘班车上班.(11)下雪路滑, 他迟到了.(12)2与4都是素数, 这是不对的.(13)“2或4是素数, 这是不对的”是不对的.答:(1)p∧q, 其中, p: 刘晓月跑得快, q: 刘晓月跳得高.(2)p∨q, 其中, p: 老王是山东人, q: 老王是河北人.(3)p→q, 其中, p: 天气冷, q: 我穿了羽绒服.(4)p, 其中, p: 王欢与李乐组成一个小组, 是简单命题.(5)p, 其中, p: 李辛与李末是兄弟.(6)p∧q, 其中, p: 王强学过法语, q: 刘威学过法语.(7)p∧q, 其中, p: 他吃饭, q: 他听音乐.(8)p→q, 其中, p: 天下大雨, q: 他乘班车上班.(9)p→q, 其中, p: 他乘班车上班, q: 天下大雨.(10)p→q, 其中, p: 他乘班车上班, q: 天下大雨.(11)p→q, 其中, p: 下雪路滑, q: 他迟到了.(12) ¬ (p∧q)或¬p∨¬q, 其中, p: 2是素数, q: 4是素数.(13) ¬ ¬ (p∨q)或p∨q, 其中, p: 2是素数, q: 4是素数.16.19.用真值表判断下列公式的类型:(1)p→ (p∨q∨r) (2)(p→¬q) →¬q(3) ¬ (q→r) ∧r(4)(p→q) →(¬q→¬p)(5)(p∧r) ↔( ¬p∧¬q)(6)((p→q) ∧ (q→r)) → (p→r)(7)(p→q) ↔ (r↔s)答:(1), (4), (6)为重言式.(3)为矛盾式.(2), (5), (7)为可满足式习题二9.用真值表求下面公式的主析取范式.(1) (pνq)ν(¬pΛr)(2) (p→q) →(¬p↔q)答:(1)(2)p q (p → q) →(¬p ↔ q)0 0 1 0 0 10 1 1 1 1 01 0 0 1 1 11 1 1 0 0 0从真值表可见成真赋值为01, 10.于是(p → q) →(¬p ↔ q) ⇔ m1 ∨ m211.用真值表求下面公式的主析取范式和主合取范式;(1) (pνq)Λr(2) p→(pνqνr)(3) ¬(q→¬p)Λ¬p15.用主析取范式判断下列公式是否等值:(1) (p→q) →r与q→ (p→r)(2) ¬(pΛq)与(¬pνq)答:(1)(p→q) →r ⇔¬(¬p∨q) ∨ r ⇔¬(¬p∨q) ∨ r ⇔ p¬∧q ∨ r ⇔p¬∧q∧(r¬∨r) ∨(p¬∨p) ∧(q¬∨q)∧r ⇔p¬∧q∧r ∨p¬∧q∧¬r ∨ p ∧q∧r ∨ p∧¬q∧r ∨¬p∧q∧r ∨¬p∧¬q∧r = m101 ∨ m100 ∨ m111 ∨m101 ∨ m011 ∨ m001 ⇔m1 ∨ m3 ∨ m4 ∨ m5 ∨ m7 = ∑(1, 3, 4, 5, 7).而 q→(p→r) ⇔¬q ∨(¬p∨r) ⇔¬q ∨¬p ∨r ⇔(¬p∨p)¬∧q∧(¬r∨r) ∨¬p∧(¬q∨q)∧(¬r∨r) ∨(¬p∨p)∧(¬q∨q)∧r ⇔(¬p¬∧q∧¬r)∨(¬p¬∧q∧r)∨(p¬∧q∧¬r)∨(p¬∧q∧r) ∨(¬p∧¬q∧¬r)∨(¬p∧¬q∧r)∨(¬p ∧q∧¬r)∨(¬p∧q∧r) ∨(¬p∧¬q∧r)∨(¬p∧q∧r)∨(p∧¬q∧r)∨(p∧q∧r) = m0 ∨ m1 ∨ m4 ∨ m5 ∨ m0 ∨ m1 ∨ m2 ∨ m3 ∨ m1 ∨ m3 ∨ m5 ∨m7 ⇔ m0 ∨ m1 ∨ m2 ∨ m3 ∨ m4 ∨ m5 ∨ m7 ⇔∑(0, 1, 2, 3, 4, 5, 7). 两个公式的主吸取范式不同, 所以(p→q) →rk q→ (p→r).16. 用主析取范式判断下列公式是否等值:(1)(p→q) →r与q→ (p→r)(2) ¬ (p∧q)与¬ (p∨q)答:(1)(p→q) →r) ⇔m1∨m3∨m4∨m5∨m7q→ (p→r) ⇔m0∨m1∨m2∨m3∨m4∨m5∨m7所以(p→q) →r) k q→ (p→r)(2)¬ (p∧q) ⇔m0∨m1∨m2¬ (p∨q) ⇔m0所以¬ (p∧q) k ¬ (p∨q)习题三15.在自然推理系统P中用附加前提法证明下面各推理:(1)前提: p→ (q→r), s→p, q 结论: s→r(2)前提: (p∨q) → (r∧s), (s∨t) →u 结论: p→u答:(1)证明: ① s 附加前提引入② s→p 前提引入③ p ①②假言推理④ p→(q→r) 前提引入⑤ q→r ③④假言推理⑥ q 前提引入⑦ r ⑤⑥假言推理(2)证明: ① P 附加前提引入② p∨q ①附加③ (p∨q) → (r∧s) 前提引入④ r∧s ②③假言推理⑤④化简⑥ s∨t ⑤附加⑦ (s∨t) →u 前提引入⑧ u ⑥⑦假言推理16.在自然推理系统P中用归谬法证明下面推理:(1)前提: p→¬q, ¬r∨q, r∧¬s 结论: ¬p(2)前提: p∨q, p→r, q→s 结论: r∨s答:(1)证明: ① P 结论否定引入② p→¬q 前提引入③¬q ①②假言推理④¬r∨q 前提引入⑤¬r ③④析取三段论⑥ r∧¬s 前提引入⑦ r ⑥化简⑧¬r∧r ⑤⑦合取⑧ 为矛盾式, 由归谬法可知, 推理正确.(2)证明: ①¬ (r∨s) 结论否定引入② p∨q 前提引入③ p→r 前提引入④ q→s 前提引入⑤ r∨s ②③④构造性二难⑥¬ (r∨s) ∧ (r∨s) ①⑤合取⑥为矛盾式, 所以推理正确.18.在自然推理系统P中构造下面推理的证明.(1)如果今天是星期六, 我们就要到颐和园或圆明园去玩. 如果颐和园游人太多, 我们就不去颐和园玩. 今天是星期六. 颐和园游人太多. 所以我们去圆明园玩.(2)如果小王是理科学生, 他的数学成绩一定很好. 如果小王不是文科生, 他必是理科生. 小王的数学成绩不好. 所以小王是文科学生.(1)令 p: 今天是星期六;q: 我们要到颐和园玩;r: 我们要到圆明园玩;s:颐和园游人太多.前提: p→ (q∨r), s →¬q, p, s. 结论: r.证明① p 前提引入② p→q∨r前提引入③q∨r①②假言推理④s前提引入⑤ s →¬q前提引入⑥¬q ④⑤假言推理⑦ r ③⑥析取三段论r ¬q s →¬q sq∨r p→q∨r p(2)令p: 小王是理科生,q: 小王是文科生,r: 小王的数学成绩很好.前提: p→r, ¬q→p, ¬r 结论: q证明:① p→r 前提引入②¬r 前提引入③¬p ①②拒取式④¬q→p 前提引入⑤ q ③④拒取式习题四在一阶逻辑中将下列命题符号化:(1)没有不能表示成分数的有理数.(2)在北京卖菜的人不全是外地人.(3)乌鸦都是黑色的.(4)有的人天天锻炼身体. 没指定个体域, 因而使用全总个体域.答:(1) ¬∃x(F(x) ∧¬G(x))或∀x(F(x) →G(x)), 其中, F(x): x为有理数, G(x): x能表示成分数.(2) ¬∀x(F(x) →G(x))或∃x(F(x) ∧¬G(x)), 其中, F(x): x在北京卖菜,G(x): x是外地人.(3) ∀x(F(x) →G(x)), 其中, F(x): x是乌鸦, G(x): x是黑色的.(4) ∃x(F(x) ∧G(x)), 其中, F(x): x是人, G(x): x天天锻炼身体.5. 在一阶逻辑中将下列命题符号化:(1)火车都比轮船快.(2)有的火车比有的汽车快.(3)不存在比所有火车都快的汽车.(4)“凡是汽车就比火车慢”是不对的.答:因为没指明个体域, 因而使用全总个体域(1) ∀x∀y(F(x) ∧G(y) →H(x,y)), 其中, F(x): x是火车, G(y): y是轮船, H(x,y):x比y快.(2) ∃x∃y(F(x) ∧G(y) ∧H(x,y)), 其中, F(x): x是火车, G(y): y是汽车, H(x,y):x比y快.(3) ¬∃x(F(x) ∧∀y(G(y) →H(x,y))) 或∀x(F(x) →∃y(G(y) ∧¬H(x,y))), 其中, F(x): x是汽车, G(y): y是火车, H(x,y):x比y快.(4) ¬∀x∀y(F(x) ∧G(y) →H(x,y)) 或∃x∃y(F(x) ∧G(y) ∧¬H(x,y) ), 其中, F(x): x是汽车, G(y): y是火车, H(x,y):x比y慢.9.给定解释I如下:(a)个体域DI为实数集合\.(b)DI中特定元素⎯a =0.(c)特定函数⎯f (x,y)=x−y, x,y∈DI.(d)特定谓词⎯F(x,y): x=y,⎯G(x,y): x<y, x,y∈DI.说明下列公式在I下的含义, 并指出各公式的真值:(1) ∀x∀y(G(x,y) →¬F(x,y))(2) ∀x∀y(F(f(x,y),a) →G(x,y))(3) ∀x∀y(G(x,y) →¬F(f(x,y),a))(4) ∀x∀y(G(f(x,y),a) →F(x,y))答:(1) ∀x∀y(x<y→x≠y), 真值为1.(2) ∀x∀y((x−y=0) →x<y), 真值为0.(3) ∀x∀y((x<y) → (x−y≠0)), 真值为1.(4) ∀x∀y((x−y<0) → (x=y)), 真值为0.习题五5.给定解释I如下:(a) 个体域D={3,4}.(b)⎯f (x)为⎯f (3)=4,⎯f (4)=3.(c)⎯F(x,y)为⎯F(3,3)=⎯F(4,4)=0,⎯F(3,4)=⎯F(4,3)=1.试求下列公式在I下的真值:(1) ∀x∃yF(x,y)(2) ∃x∀yF(x,y)(3) ∀x∀y(F(x,y) →F(f(x),f(y)))答:(1) ∀x∃yF(x,y)⇔(F(3,3)∨F(3,4))∧(F(4,3)∨F(4,4))⇔(0∨1)∧(1∨0) ⇔1(2)∃x∀yF(x,y)⇔(F(3,3)∧F(3,4))∨(F(4,3)∧F(4,4))⇔(0∧1)∨(1∧0)⇔0(3)∀x∀y(F(x,y)→F(f(x),f(y)))⇔(F(3,3)→F(f(3),f(3)))∧(F(4,3)→F(f(4),f(3)))∧(F(3,4)→F(f(3),f(4)))∧(F(4,4)→F(f(4),f(4))) ⇔ (0→0)∧(1→1)∧(1→1)∧(0→0)⇔112.求下列各式的前束范式.(1) ∀xF(x) →∀yG(x, y);(3) ∀xF(x, y) ↔∃xG(x, y);答:前束范式不是唯一的.(1) ∀xF(x) →∀yG(x, y) ⇔∃x(F(x) →∀yG(x, y))⇔∃x∀y(F(x) → G(x, y)).(3) ∀xF(x, y) ↔∃xG(x, y) ⇔ (∀xF(x, y) →∃xG(x, y)) ∧ (∃xG(x, y) →∀xF(x, y)) ⇔ (∀x1F(x1, y) →∃x2G(x2, y)) ∧ (∃x3G(x3, y) →∀x4F(x4, y)) ⇔∃x1∃x2(F(x1, y) → G(x2, y)) ∧∀x3∀x4(G(x3, y) → F(x4, y)) ⇔∃x1∃x2∀x3∀x4((F(x1, y) → G(x2, y)) ∧ (G(x3, y) → F(x4, y))).13.将下列命题符号化, 要求符号化的公式全为前束范式:(1) 有的汽车比有的火车跑得快.(2) 有的火车比所有的汽车跑得快.(3) 说所有的火车比所有的汽车跑得快是不对的.(4) 说有的飞机比有的汽车慢是不对的.答:(1)令F(x):x是汽车,G(y):y是火车,H(x,y):x比y跑得快.∃x(F(x)∧∃y(G(y)∧H(x,y))⇔∃x∃y(F(x)∧G(y)∧H(x, y)).(2)令F(x):x是火车, G( y): y 是汽车,H(x,y):x比y跑得快.∃x(F(x)∧∀y(G(y)→ H(x,y)))⇔∃x∀y(F(x)∧(G y)→H(x,y))).;错误的答案:∃x∀y(F(x)∧G(y)→H(x,y)).(3)令F(x):x是火车,G(y):y是汽车,H(x,y):x比y跑得快.¬∀x(F(x)→∀y(G(y)→H(x,y)))⇔¬∀x∀y(F(x)→(G(y)→H(x,y)))⇔¬∀x∀y(F(x)∧G(y)→H(x,y))(不是前束范式)⇔∃x∃y(F(x)∧G(y)∧H(x,y)).(4)令F(x):x是飞机,G(y):y是汽车,H(x,y):x比y跑得慢.¬∃x(F(x)∧∃y(G(y)∧H(x,y)))⇔¬∃x∃y(F(x)∧G(y)∧H(x,y))(不是前束范式)⇔∀x∀y¬(F(x)∧G(y)∧H(x,y))⇔∀x∀y(F(x)∧G(y)→¬H(x,y)).21.24.在自然推理系统F中, 构造下面推理的证明:每个喜欢步行的人都不喜欢骑自行车. 每个人或者喜欢骑自行车或者喜欢乘汽车. 有的人不喜欢乘汽车, 所以有的人不喜欢步行. (个体域为人类集合) 答:令 F(x): x 喜欢步行, G( x): x喜欢骑自行车, H(x): x 喜欢乘汽车.前提:∀x(F(x)→¬G(x)), ∀x(G(x)∨H(y)),∃x¬H(x).结论:∃x¬F(x).② ∀x(G(x) ∨ H(y)) 前提引入② G(c) ∨ H(c) ①UI③∃x¬H(x) 前提引入④¬H(c) ③UI⑤ G(c) ②④析取三段⑥∀x(F(x) →¬G(x)) 前提引入⑦ F(c) →¬G(c) ⑥UI⑧¬F(c) ⑤⑦拒取⑨∃x¬F(x) ⑧EG习题七12.设A={0, 1, 2, 3}, R是A上的关系, 且R={〈0, 0〉, 〈0, 3〉, 〈2, 0〉, 〈2,1〉, 〈2, 3〉, 〈3, 2〉} 给出R的关系矩阵和关系图.16.设A={a,b,c,d}, R1,R2为A上的关系, 其中R1={〈a,a〉,〈a,b〉,〈b,d〉}R2={〈a,d〉,〈b,c〉,〈b,d〉,〈c,b〉} 求R1·R2, R2·R1,R1²,R2³. R1·R2={〈a,a〉,〈a,c〉,〈a,d〉},R2·R1={〈c,d〉}, R1²={〈a,a〉,〈a,b〉,〈a,d〉},R2³={〈b,c〉,〈b,d〉,〈c,b〉}20.设R1和R2为A上的关系,证明: (1)(R1∪R2) −1=R1−1∪R2−1(2)(R1∩R2) −1=R1−1∩R2−1答:(1)(R1∪R2)−1=R1−1∪R2−1任取〈x,y〉〈x,y〉(∈R1∪R2)−1⇔〈y,x〉(∈R1∪R2)⇔〈y,x〉∈R1∨ (y,x)∈R2)⇔〈x,y〉∈R1−1∨〈x,y〉∈R2−1⇔〈x,y〉∈R1−1∨R2−1所以(R1∪R2) −1=R1−1∪R2−1(2)(R1∩R2) −1=R1−1∩R2−1 任取〈x,y〉〈x,y〉(∈R1∩R2) −1⇔〈y,x〉(∈R1∩R2)⇔〈y,x〉∈R1∧ (y,x)∈R2)⇔〈x,y〉∈R1−1∧〈x,y〉∈R2−1⇔〈x,y〉∈R1−1∧R2−1所以(R1∪R2) −1=R1−1∩R2−126.33.43.16.47.。
人教版小学数学五年级下册7单元测试卷(含答案及周测培优)
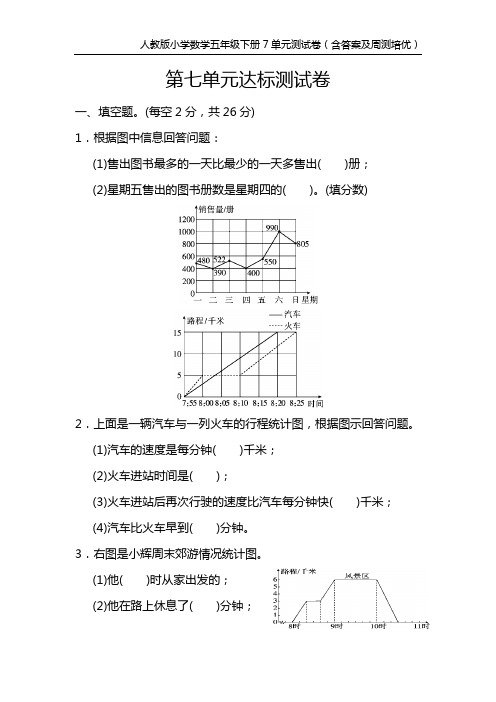
第七单元达标测试卷一、填空题。
(每空2分,共26分)1.根据图中信息回答问题:(1)售出图书最多的一天比最少的一天多售出( )册;(2)星期五售出的图书册数是星期四的( )。
(填分数)2.上面是一辆汽车与一列火车的行程统计图,根据图示回答问题。
(1)汽车的速度是每分钟( )千米;(2)火车进站时间是( );(3)火车进站后再次行驶的速度比汽车每分钟快( )千米;(4)汽车比火车早到( )分钟。
3.右图是小辉周末郊游情况统计图。
(1)他( )时从家出发的;(2)他在路上休息了( )分钟;(3)他家距离风景区( )千米;(4)他在风景区玩了( )小时;(5)他回家用了( )分钟。
4.如果要反映小东6~12岁的身高变化情况,应选用( )统计图;要反映实验小学一至六年级的人数情况,选用( )统计图比较合适。
二、判断题。
(每题1分,共5分)1.工厂需要反映各车间的产量的多少,应选用折线统计图。
( ) 2.在一幅折线统计图中,用1厘米的长度表示30吨,那么120吨应画10厘米长。
( ) 3.医生需要监测病人的体温情况,应选用折线统计图。
( ) 4.反映一个地区一段时间内的气温变化情况,应选用折线统计图。
( ) 5.复式折线统计图不但能反映数量的增减变化,还便于两个数量进行比较。
( ) 三、选择题。
(每空2分,共10分)1.对比两只股票某日的走势情况,应绘制( )。
A.复式条形统计图B.复式折线统计图C.两种都可以2.小林和小明分别骑自行车从学校沿着一条路线到20千米外的公园,已知小林比小明先出发,他们俩所行的路程和时间的关系如图所示,下面说法正确的是( )。
A.他们都骑行了20千米B.两个人同时到达公园C.小林在中途停留了1小时 D.相遇后,小林的速度比小明慢3.如图是某商店2016年下半年毛衣和衬衫销售情况统计图,毛衣的销售量在( )最大,衬衫的销售量在( )最大。
A.9月B.7月C.11月D.12月4.右图是北京某一天的气温,下列说法中错误的是( ) A.这一天的最高气温是24 ℃B.这一天最高气温与最低气温的差是16 ℃C.这一天中只有14时至24时之间的气温在逐渐降低D.这一天中8时至24时之间的气温在逐渐升高四、下面是小林8~12岁的体重与标准体重统计表。
云南十八怪详解

云南十八怪【云南第○一怪】鸡蛋用草串着卖:老乡们为了便于买主携带所购买的鸡蛋,又不被碰坏,便以竹蔑或麦草贴着蛋壳编,每个都隔开,十个为一串,可以挂在墙上,想吃的时候便吃几个拿几个。
【云南第○二怪】摘下斗笠当锅盖:云南竹林较多,因此许多用具都以竹子为原料,而锅盖就形似于内地的斗笠,只是顶略小一点,便于抓拿,而且用此做锅盖,透气保温,做出来的饭更加清香。
【云南第○三怪】三只蚊子一盘菜:云南的许多地区,天气较为炎热,终年蚊蝇不绝,特别是野地与牲畜圈里的蚊子个头都比较大大,故夸张说3个蚊子一盘菜。
【云南第○四怪】火筒能当水烟袋:当地人抽烟所用的烟袋很像内地的吹火筒,只不过吹火筒是往外吹,而它是往里吸,烟气经过水过滤,可以减低焦油的浓度,味道更加清凉香醇。
【云南第○五怪】糌粑被叫做饵块:云南产大稻米,特香糯,把大米蒸熟舂打后,揉制成长条形的半成品,可炒吃、煮吃、蒸着吃,颜色白如雪,象内地做的白米粑,当地称饵块。
【云南第○六怪】背着娃娃谈恋爱:少数民族期盼人丁,盛婚后数日媳妇便回门了,等有了娃娃再回婆家与丈夫相聚,开始真正的谈恋爱。
【云南第○七怪】四季服装同穿戴:云南地区气候多变,夏天不热冬天不寒,白天和晚上的温差较大,可以说是冷热瞬变,在街上四季服饰随处可见,长的、短的、厚的、薄的,颜色艳丽,绚丽多彩。
【云南第○八怪】蚂蚱能做下酒菜:云南许多地区的人都有吃虫的爱好,变害虫为佳肴,化昆虫为美味,所以蚂蚱、蝗虫等,都因为油煎之后,焦脆鲜香,而成为了美味的下酒菜。
【云南第○九怪】姑娘被叫做老太:云南有些地区口音孃娘不分,喊姑娘其实就是指姑与孃,而把姑姑与孃孃喊为老太,所以你问姑娘他说老太,喊老太也就是内地人所称的小姨。
【云南第○十怪】和尚可以谈恋爱:云南与几个信奉佛教的国家接壤,而佛教国家的男子上寺庙当和尚就像内地上学读书或服兵役一样,到时还可以还俗结婚生子,受其影响,边民也穿和尚服谈恋爱。
【云南第十一怪】老太爬山比猴快:云南多高山深谷,当地的妇女们从小到老都勤劳无比,爬山越岭、种地砍柴都习以为常,因此练就了一身矫健的身板与脚劲,七八十岁的老人登山往往如履平地。
各种交通工具的速度

各种交通工具的速度行人:5-6公里/小时自行车:15公里/小时左右电瓶车:25-35公里/小时摩托车:30-100公里/小时(70-80km)汽车:50-200公里/小时(<200公里/小时)(出租车:60km/h、公交车:40km/h)火车:80km/h(<350公里/小时)磁悬浮:400-550km飞机(600-1500公里/小时):固定翼:500km/h ——3600km/h直升机:100km/h ——200km/h客机:500-600km战机:800-5000km火箭:>28440公里/小时核潜艇:20-30节航空母舰:20-40节现在国际上通用的是1节=1海里/小时,1海里=1.852公里。
1节也就是1.852公里/小时。
现代化的超级集装箱船最高速度可以达到30节/小时=55公里/小时常规货轮的速度在15-20节之间=28公里-37公里/小时之间磁悬浮列车:400—500千米每小时火车:200千米每小时汽车:80—150千米每小时摩托车20- -一50千米每小时电动车15—-—30千米每小时自行车10- -—15千米每小时蚂蚁:0。
000001千米每小时自行车平均速度15km/t,最快速度一般我们平时开到30-40km/t很就不错了。
这个速度也骑的不久。
要是职业车手的话,60km/t。
摩托车平均速度40km/t,最快速度一般我们平时开到60-80km/t.飞机客机平均速度现在500km/t,最快是的是美国的战机,最咼时速达到每小时1. 15万公里。
磁悬浮最快达350km/t。
导弹现在最快是超音速2到3倍。
核潜艇最慢有每小时25节。
最快的都超过了每小时30节。
航空母舰最快速度每小时四十节。
步行:5km/h普通自行车:l0-l5km/h一般路况的公交车:25km/h 公路自行车(自行车比赛):40-60km/h 长途汽车(走高速公路):100km/h 高速运行的火车(特快):140km/h飞机飞行时速:8O0-120Okm/h摩托车:70-80km客机:500-600km 战机:800-5000km 核潜艇:20-30节航空母舰:20-40节磁悬浮列车:400—500千米每小时火车:200千米每小时汽车:80 —— 150千米每小时电动车:15—— 30千米每小时自行车:10——15千米每小时蚂蚁:0。
第二章谓词逻辑

主语一般是客体,可以独立存在,可以是具体的
事物也可以是抽象的概念 用以刻划客体性质或关系的是谓词。 原子命题组成:客体、谓词。
第二章
谓词逻辑
谓词:用来刻划个体词的性质或个体词之间相互关系的词。 例如: ① 在命题“ 2 是无理数”中,“…是无理数”是 谓词。 ② 在命题“x 是有理数”中,“…是有理数”是谓词。 ③ 在命题“小王与小李同岁”中,“…与…同岁”是 谓词。 ④ 在命题“x与y具有关系L”中,“…与…具有关系L” 是谓词。
第二章 2.2
谓词逻辑
命题函数与量词
使用量词时应注意以下几点: 1、不同的个体域中,命题符号化的形式可能不一样; 2、若事先没有给出个体域,都应以全总个体域为个体域; 3、引入特性谓词后,使用全称量词与存在量词形式不同; 4、个体域为有限集时如D={a1、…、an},对任意谓词 A(x)有: A(a1)、A(a2)、…、A(an) 5、多个量词同时出现时,不能随意颠倒它们的顺序。
第二章
谓词逻辑
苏格拉底三段论:
2.1 谓词的概念与表示
所有人都是要死的,苏格拉底是人,所以苏格拉底 是要死的。 用P,Q,R分别表示以上三个命题。 则得到推理的形式结构为: (P∧Q)→R
第二章
谓词逻辑
2.1 谓词的概念与表示
谓词逻辑命题符号化的三个基本要素:客体词、 谓词、量词。 反映判断的句子由主语和谓语组成。
第二章 2.2
谓词逻辑
命题函数与量词
量词: 表示个体常项或变项之间数量关系的词。
量词只有两个:全称量词、存在量词。
(1) 全称量词:表示“全部”含义的词。全称量词统 一符号化为“”。
注:a. 常用语中“全部”、“所有的”、“一 切”、“每一个”、“任何”、“任意的”、“凡”、 “都”等词都是全称量词。
2015离散数学谓词量词、变元的约束、翻译

(1)
2 是无理数 .
(2) x是有理数. (3) 小王与小李同岁. (4) x 与y具有同学关系.
(1) 凡人都呼吸 . (2) 所有的人都长着黑头发. (3) 兔子比乌龟跑得快. (4) ቤተ መጻሕፍቲ ባይዱ美国留学的学生未必都是亚洲人.
Universal Quantifier
The universal quantification of P(x) is the statement
定义1:约束变元 谓词公式中 , ,后面所跟的 x ,称为相应 量词的指导变元或作用变元或约束变元。 定义2:量词作用域(量词辖域)
给 定 谓 词 公 式 中 , 形 式 为 (x)P(x) , (x) P(x)中的P(x)称为相应量词的作用域(辖域)。
定义3:自由变元 在谓词公式中,除去约束变元以外所出现的 变元,称作自由变元。
with a certain property. Such statements are expressed using existential quantification. With existential quantification, we form a proposition that is true if and only if P(x) is true for at least one value of x in the domain.
Truth value?
We read ∀xP(x) as “for all xP(x)” or “for every xP(x).”An
element for which P(x) is false is called a counterexample of ∀xP(x).
教科版-物理-八年级物理上册教案 2.3测量物体运动的速度

活动场地:学校操场.
数据记录表:
次数
路程/m
时间/s
平均速度/(m·s-1)
平均值/(m·s-1)
1
50
2
50
3
50
应用:利用这节课所测的自己行走时的平均速度值,要估测自己家到学校的实际路程,还需要什么器材?测量时要注意哪些事项?
学生回答:还需要秒表(或手表);注意行走快慢要和测自己速度时行走快慢程度尽量保持一致,在行走过程中最好不停歇(如果有停歇,要除去所停时间),行走路线尽量不弯曲,拐弯时走直角等.
备课教师
使用教师
授课时间
2018年月日
课时
2
课题
2.3测量物体运动的速度( )
课型
新授
教学目标
一、知识与能力
1.能比较物体运动的快慢.
2.知道匀速直线运动的特征,理解匀速直线运动的速度概念,初步体会用比值定义物理量的方法.
3.知道变速直线运动中的平均速度的概念和计算公式.
二、过程与方法
通过观察图片、阅读教材,根据教材安排的学生自由活动,学会比较快慢和计算速度的方法.
次数
路程/m
时间/s
平均速度
/(m·s-1)
平均值
/(m·s-1)
1
50
2
50
3
50
(5)应用:
课后反思
教学中,教师应向学生说明,实际的运动多是变速的,引入平均速度是把变速运动这一比较复杂的问题当作简单的问题——匀速直线运动来处理.平均速度只能近似地反映变速运动的情况,是对变速运动快慢的粗略描述,但这在实际中却是很有用的.通过平均速度以及今后许多问题的教学,应使学生逐渐体会到,使复杂问题简单化,是一种常用的研究问题的方法.如果教学时间允许,还可以在例2后面设计一道对应的练习来巩固学生对平均速度概念的理解程度,也有利于教师及时得到反馈信息.对于学生活动“我走得有多快”的教学,要组织学生到操场上去完成,应注意以下几点:①有物理兴趣小组在课前最好画出了所要走的50m的起点和终点;②多分几个小组,最好每个同学都能走3趟;(3)提前画好数据记录表,把活动的数据及时填写到对应的表格内.
八年级物理探究比较物体运动的快慢

即学即练
一列长200m的火车通过隧道用了90s。已知火车做匀 速直线运动,速度为36km/h,求这个隧道的长度。
S道
S
S车
t=90s 解:v=36km/h=10m/s S=vt=10m/s×90s=900米 S道=S-S车=900m-200m=700m 答:这个隧道的长度为700m。
例题7:
汽车经过某一车站时,旅客手表的指针恰好 指09:30:00整,经过下一站时,已是09: 32:18。已知两站之间的路程为2.07km,求 汽车的速度。 已知: S=2.07km=2070m t=2分18秒=138秒 求:v=?
精选例题六
一列长150m的火车用5min时间匀速通过一座长度为 7350m的大桥,求火车通过大桥时速度为多少千米/时?
S桥 S车
S
已知:S=S桥+S车 =7350m+150m=7500m
t=5min=300s S 7500m =25m/s =90km/h 解:V= = t 300s 答:火车通过大桥时速度为90km/h
问题:火车的速度是72km/h,汽车的速度是 30m/s,是火车跑得快还是汽车跑得快?
方法一:
方法二:
问题:火车的速度是72km/h,汽车的速度是 30m/s,是火车跑得快还是汽车跑得快?
方法一:
1km 72km/h= 72× 1h
方法二:
1000 m = 72× 3600 s (30m/s>20m/s,汽车快)
s t v
s vt
速度的定义与物理意义的区别
1、定义:物体在单位时间里通过的路程 2、物理意义: 描述物体运动的快慢
(4)速度单位: 国际单位:米/秒 常用单位:千米/小时
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、 汽车比火车跑的快。
)),()()((y x R y Q x P y x →∧∀∀
2、 有的汽车比所有的火车跑的快 ))),()(()((y x R y Q y x P x →∀∧∃
3、 并不是所有的汽车都比火车跑的快 )),()()((y x R y Q x P y x →∧∀⌝∀
4、 特性谓词:当使用全总个体域时,对客体变元的变化范围限制的词,称作特性谓词。
5、
6、指出下列公式的指导变元、作用域、约束变元和自由变元。
(1))),()((y x yR x P x ∃→∀
(2)∃)()),(),((x R z x Q y x P x ∨→
(3)),()),(),()((y x Q y x yR z x xQ x P x ∨∃→∃∧∀ 解 (1)x 是指导变元,x ∀的作用域为),()(y x yR x P ∃→;y 也是指导变元,作用域为),(y x R 。
在指导变元y 的作用域),(y x R 中, y 是约束出现。
在指导变元x 的作用域),()(y x yR x P ∃→中,x ,y 都是约束出现。
(2)x 是指导变元,相应的作用域为),(),(z x Q y x P →,从左向右算起,变量x 的第
一、二次出现是约束出现,x 的第三次出现是自由出现。
变量y ,z 的出现都是自由出现。
(3)x ,y 是指导变元,x ∀的作用域是),(),()(y x yR z x xQ x P ∃→∃∧,x ∃的作用域是),(z x Q ,y ∃的作用域是),(y x R 。
x 的最后一次出现为自由出现,其余为约束出现,y 的第一次出现为约束出现,第二次出现为自由出现。
变元z 为自由出现。
7、将),()),()((y x R y x Q x P x ∧→∀中的约束变元进行换名。
解 可换名为),()),()((y x R y z Q z P z ∧→∀,但不能换名为
),()),()((y x R y y Q y P y ∧→∀
或
),()),()((y x R y x Q z P z ∧→∀,
因为后两种更改都将使公式中的量词的约束范围有所变动。
例2.3.3 将),()),(),()((y x Q y x yR z x xQ x P x ∨∃→∃∧∀中的约束变元进行换名。
解 可换名为),()),(),()((y x Q w u wR z v vQ u P u ∨∃→∃∧∀,但不能换名为
),()),(),()((y x Q y z yR z x xQ z P z ∨∃→∃∧∀
或
),()),(),()((y x Q y x yR z z zQ x P x ∨∃→∃∧∀,
因为后两种更改都将使公式中的量词的约束范围有所变动
例2.3.4 将公式)),()()((y x R y P x ∧∃中的自由变元进行代入。
解 y 为自由变元,代入后公式为)),()()((z x R z P x ∧∃,但是)),()()((x x R x P x ∧∃与)),()()((y x R z P x ∧∃这两种代入都与规则不符。
例2.3.5 将公式),()),()((y x R y x Q x P x ∧→∀中的自由变元进行代入。
解 对自由变元x 进行代入后公式为),()),()((y z R y x Q x P x ∧→∀。
公式中y 也是自由变元,但是变元y 只以一种身份出现,因此,可以不对y 进行代入。
例2.4.3 判断下列公式的类型。
(1))()(x xF x xF ∃→∀
(2)))(),(()(x xF y x yG x x xF ∀→∃∀→∀
(3)),()),(),((y x R y x R y x F ∧→⌝
(4)),(),(y x yF x y x yF x ∀∃→∃∀
解 (1)设I 为任意解释。
如果)(x xF ∀在I 下为真,则对于任意一个个体a 都有)(a F 为真,于是)(x xF ∃为真;如果)(x xF ∀在I 下为假,由条件的前件为假可知)()(x xF x xF ∃→∀为真。
故)()(x xF x xF ∃→∀为永真式。
(2)因为T Q P P P Q P P Q P ⇔⌝∨∨⌝⇔∨⌝∨⌝⇔→→)()()(,而))(),(()(x xF y x yG x x xF ∀→∃∀→∀是)(P Q P →→的代换实例,所以))(),(()(x xF y x yG x x xF ∀→∃∀→∀为永真式。
(3)因为F Q Q P Q Q P Q Q P ⇔∧⌝∧⇔∧∨⌝⌝⇔∧→⌝)()(,而
),()),(),((y x R y x R y x F ∧→⌝是Q Q P ∧→⌝)(的代换实例,,所以),()),(),((y x R y x R y x F ∧→⌝为永假式。
(4)取解释1I 为:个体域为自然数集N ;),(y x F :y x =。
则:),(),(y x yF x y x yF x ∀∃→∃∀F y x y x y x y x ⇔=∀∃→=∃∀⇔)()(。
取解释2I 为:个体域为自然数集N ;),(y x F :x ≤y 。
则),(),(y x yF x y x yF x ∀∃→∃∀x y x (∃∀⇔≤y )x y x (∀∃→≤y )T ⇔。
综上,),(),(y x yF x y x yF x ∀∃→∃∀为可满足式。
1.量词的消去
例2.4.4 设个体域为{a ,b ,c } ,试消去表达式)()(x xQ x P x ∀∧⌝∀中的量词,写成与之等价的命题公式。
解 )(x P x ⌝∀消去量词后的等价的命题公式为:
))()()(()()()(b P b P a P c P b P a P ∨∨⌝⇔⌝∧⌝∧⌝
)(x xQ ∀消去量词后的等价的命题公式为:
)()()(c Q b Q a Q ∧∧
于是,)()(x xQ x P x ∀∧⌝∀消去量词后的等价的命题公式为:
))()()(())()()((c Q b Q a Q b P b P a P ∧∧∧∨∨⌝。
