高二抛物线基础测试题(可编辑修改word版)

合集下载

(完整word版)高二数学抛物线单元测试题1

抛物线一、选择题1. 已知抛物线22y px =上一点M （1，m ）到其焦点的距离为5，则该抛物线的准线方程为（）A ．x=8B ．x=-8C ．x=4D ．x=-42. 将抛物线x y 42=沿向量a 平移得到抛物线x y y 442=-，则向量a 为A ．(－1,2)B ．(1,－2)C ．(－4,2)D ．(4,－2)3. 抛物线2y ax =的焦点坐标为( )A ．1(0,)a B ．(0,)4a C ．1(0,)4a D ．1(,0)4a4. 正三角形的一个顶点位于原点，另外两个顶点在抛物线24y x =上，则这个正三角形的边长为（）A ．B ．C ．8D ．165. 在22y x = 上有一点P ，它到(1,3)A 的距离与它到焦点的距离之和最小，则点P 的坐标是( )A ．（－2，1）B ．（1，2）C ．(2，1）D ．（－1，2）6. 设斜率为2的直线l 过抛物线2(0)y ax a =≠的焦点F,且和y 轴交于点A,若△OAF(O 为坐标原点)的面积为4,则抛物线方程为 ( ).A.24y x =±B.28y x =±C. 24y x =D. 28y x =7. 抛物线y ＝x 2上的点到直线2x －y －10＝0的最小距离为（）A ．955B ．0C ．95D ．55 8. 两个正数,a b 的等差中项是92，一个等比中项是a b >，则抛物线2b y x a =-的焦点坐标是（）A ．5(,0)16-B ．2(,0)5- C ．1(,0)5- D ．1(,0)59. 直线l 过抛物线x y =2的焦点F ，交抛物线于A ，B 两点，且点A 在x 轴上方，若直线l 的倾斜角4πθ≥，则|FA |的取值范围是（）A ．)23,41[ B ．13(,44+ C ．]23,41( D ．]221,41(+ 10. 已知点(1,0),(1,0)A B -及抛物线22y x =，若抛物线上点P 满足PA m PB=，则m 的最大值为（）（A ）3 （B ）2 （C （D二、填空题11. 设点F 为24y x =的焦点，A 、B 、C 为该抛物线上三点，若0FA FB FC ++=，则||||||FA FB FC ++= .12. 已知点P 在抛物线24y x =上，那么点P 到点(21)Q -，的距离与点P 到抛物线焦点距离之和取得最小值时，点P 的坐标为__ 。

高二抛物线基础测试题.docx

1. 已知抛物线y 2 = 2px （p > 0）的焦点弦4B 的两端点为人（召，儿）』（兀2，力），则关系式-的值一定等于（）/ X l X2A. 4B. 一4C ・ p 2D ・-p2. 顶点在原点，坐标轴为对称轴的抛物线过点（-2, 3）,则它的方程是（）A. x 2= - — y y 2= —x B. y 2=x 2= — yC. x 2= — y D. y 2=%2 '3 23 ”3 •2高二抛物线基础测试题一、选择题：本大题共12小题，每小题5分，共60分 1.顶点在原点，焦点是F （0,5）的抛物线方程是（）A ・ y 2=20x B. x 2=20y C ・y-看D ・x -^y抛物线y=—x?的焦点坐标为（ jo,》c.£ oj 3.抛物线y = »2的准线方程是y = 2,则实数a 的值为（）C ・8D ・一84. （2010年高考陕西卷）已知抛物线y 2=2px （p>0）的准线与圆x 2+y 2-6x-7=0相切，则p 的值为（）C. 2D ・ 45. （2010年高考湖南卷）设抛物线y 2=8x 上一点P 到y 轴的距离是4,则点P 到该抛物线焦点的距离是（）A. 4 C. 8 6.若点P 到定点F （4, 0）的距离比它到直线x+5=0的距离小1,则（）B. y 2=-32xD. y 2=16x 或 y=0（x 〈0）7. 以x 轴为对称轴的抛物线的通径（过焦点且与x 轴垂直的弦）长为8,若抛物线的顶点在坐标原点，则其方程为（）A. y 2=8xB. y 2=—8xC ・ y 2=8x 或,=—8xD. x 2=8y 或/=—8y8. 已知抛物线 y 2=2px （p>0）的焦点 F,点 Pi （x 〔，yj 、P 2（x 2, y 2） > P 3（x 3, y3）在抛物线上，且2X 2=XI +X 3, 则有（）A. |FPi| + |FP 2| = |FP 3| B . iFPii 2+iFP 2r=iFP 3r C ・ |FPi| + |FP3|=2|FP 2| D. |FPi| - |FP3| = |FP 2r9. 抛物线y 2=12x 截直线y=2x+1所得弦长等于（）A.伍B. 2^152. B. 6 D. 12A. y 2= —16x C. y 2=16x点P 的轨迹方程是C. 乎 D . 15•10.以抛物线y 2=2px （p>0）的焦半径| PF|为直径的圆与y 轴的位置关系为（）A.相交B.相离C.相切D.不确定11・过抛物线的焦点且垂直于其对称轴的弦是AB,抛物线的准线交x 轴于点M,则）A.锐角B.直角C. 钝角D. 锐角或钝角12. （2010年高考山东卷）已知抛物线y2=2px （p>0）,过其焦点且斜率为1的直线交抛物线于A 、B 两点，若线段AB 的中点的纵坐标为2,则该抛物线的准线方程为（）A. x = 1B. x= —1C. x=2D. x=—213. 设过抛物线的焦点F 的弦为PQ,则以PQ 为直径的圆与抛物线的准线的位置关系是（）A.相交B.相切C.相离D.以上答案均有可能14. 过抛物线）卩=4r 的焦点作直线交抛物线于冬川）恐，“）两点，如果內+丕=6,则|AB |的值为（）A. 10B. 8C. 6D ・ 415. 抛物线的顶点在原点，对称轴为坐标轴，焦点在直线3x-4y-12 = 0上，则抛物线的方程为（）A. y 2= 16xB. x 2= -12yC.=16兀或兀2 =一12）, D .以上均不对16.抛物线y = x 2上一点到直线2x-y-4 = 0的距离最短的点的坐标是（）A. (1, 1) B- GV c-黑)D. (2, 4)17.已知抛物线二2兀的焦点为F,定点A （3, 2）,在此抛物线上求一点P,使|PA| + |PF|最小，则P 点坐标为( )A. (-2, 2)B. (1, V2 )C. (2, 2)D. (1-V2)线的焦点，则直线AB 的方程是二. 填空题（共4题，每题4分）19-顶点在原点，焦点在"轴上且通径长为6的抛物线方程是1& 已知A 、B 抛物线= 2px （p > 0） ±两点,0为坐标原点,若|0A| = |0B|,且AAOB 的垂心恰是此抛物A. x = pC. D.20.过（-1, 2）作直线与抛物线y2=4x只有一个公共点，则该直线的斜率为________________ ,21・已知直线x-y-1= 0与抛物线丫 =玄/相切，贝lja= __________ .22. 抛物线y2=4x上的点P到焦点F的距离是5,则P点的坐标是_________ •23. 抛物线y2=4x与直线2x+y-4=0交于两点A与B, F是抛物线的焦点，则|FA| + |FB|= _______________ .24. 边长为1的等边三角形A0B, 0为原点，AB丄x轴，则以0为顶点，且过A、B的抛物线方程是_____ .三、解答题（本大题共6小题，共74分，解答应写出文字说明，证明过程或演算步骤.）25. （本题满分12分）若抛物线y2=-2px（p>0）上有一点M,其横坐标为一9.它到焦点的距离为10,求抛物线方程和M点的坐标.26. 求与椭圆4x2+5y2 =20有相同的焦点，且顶点在原点的抛物线方程.（12分）27. 已知抛物线的顶点在原点，对称轴是x轴，抛物线上的点M （-3, m）到焦点的距离等于5,求抛物线的方程和m的值.（12分）28 （本题满分12分）.抛物线的焦点F在x轴上，直线y=—3与抛物线相交于点A, |AF|=5,求抛物线的标准方程.29.（本题满分12分）已知抛物线的顶点在坐标原点，焦点在x轴上，其准线I与圆（x-2）2+y2=25相切, 求抛物线的方程.30.(本题满分12分)过点Q(4,1)的抛物线y2=8x的弦AB恰被点Q平分，求AB所在直线方程.31・(本题满分12分)已知抛物线y2=-x与直线I： y = k(x + 1)相交于A, B两点.(1) 求证：0A丄0B；(2) 当AOAB的面积等于帧时，求k的值.32. (2009江苏卷)(本题满分14分)在平面直角坐标系xoy中，抛物线C的顶点在原点，经过点A (2, 2),其焦点F在x轴上。

(完整版)高二抛物线基础测试题

高二抛物线基础测试题一、选择题：1．顶点在原点，焦点是F (0,5)的抛物线方程是( )A ．y 2＝20xB ．x 2＝20yC ．y 2＝120xD ．x 2＝120y2．抛物线y ＝－x 2的焦点坐标为( )A.⎝ ⎛⎭⎪⎫0，14B.⎝⎛⎭⎪⎫0，－14 C.⎝ ⎛⎭⎪⎫14，0 D.⎝ ⎛⎭⎪⎫－14，03．抛物线y ＝ax 2的准线方程是y ＝2，则实数a 的值为( )A.18 B ．－18 C ．8 D ．－84．(2010年高考陕西卷)已知抛物线y 2＝2px (p >0)的准线与圆x 2＋y 2－6x －7＝0相切，则p 的值为( )A.12 B ．1 C ．2 D ．45．(2010年高考湖南卷)设抛物线y 2＝8x 上一点P 到y 轴的距离是4，则点P 到该抛物线焦点的距离是( )A ．4B ．6C ．8D ．126．若点P 到定点F (4,0)的距离比它到直线x ＋5＝0的距离小1，则点P 的轨迹方程是( )A ．y 2＝－16xB ．y 2＝－32xC ．y 2＝16xD ．y 2＝16x 或y ＝0(x <0)7．以x 轴为对称轴的抛物线的通径(过焦点且与x 轴垂直的弦)长为8，若抛物线的顶点在坐标原点，则其方程为( )A ．y 2＝8xB ．y 2＝－8xC ．y 2＝8x 或y 2＝－8xD ．x 2＝8y 或x 2＝－8y8．已知抛物线y 2＝2px (p >0)的焦点F ，点P 1(x 1，y 1)、P 2(x 2，y 2)、P 3(x 3，y 3)在抛物线上，且2x 2＝x 1＋x 3，则有( )A ．|FP 1|＋|FP 2|＝|FP 3|B ．|FP 1|2＋|FP 2|2＝|FP 3|2C ．|FP 1|＋|FP 3|＝2|FP 2|D ．|FP 1|·|FP 3|＝|FP 2|29．抛物线y 2＝12x 截直线y ＝2x ＋1所得弦长等于( )A.15 B ．215C.152D ．15.10．以抛物线y 2＝2px (p >0)的焦半径|PF |为直径的圆与y 轴的位置关系为( )A ．相交B ．相离C ．相切D ．不确定11．过抛物线的焦点且垂直于其对称轴的弦是AB ，抛物线的准线交x 轴于点M ，则∠AMB 是( )A ．锐角B ．直角C．钝角D．锐角或钝角12．(2010年高考山东卷)已知抛物线y2＝2px(p>0)，过其焦点且斜率为1的直线交抛物线于A、B两点，若线段AB的中点的纵坐标为2，则该抛物线的准线方程为( )A．x＝1 B．x＝－1C．x＝2 D．x＝－2二．填空题13．已知直线x－y－1＝0与抛物线y＝ax2相切，则a＝________.14．抛物线y2＝4x上的点P到焦点F的距离是5，则P点的坐标是________．15．抛物线y2＝4x与直线2x＋y－4＝0交于两点A与B，F是抛物线的焦点，则|FA|＋|FB|＝________. 16．边长为1的等边三角形AOB，O为原点，AB⊥x轴，则以O为顶点，且过A、B的抛物线方程是________．三、解答题(解答应写出文字说明，证明过程或演算步骤.)17．若抛物线y2＝－2px(p>0)上有一点M，其横坐标为－9.它到焦点的距离为10，求抛物线方程和M点的坐标．18．抛物线的焦点F在x轴上，直线y＝－3与抛物线相交于点A，|AF|＝5，求抛物线的标准方程．19．已知抛物线y2＝－x与直线l：y＝k(x＋1)相交于A，B两点．(1)求证：OA⊥OB；(2)当△OAB的面积等于10时，求k的值．高二抛物线基础测试题参考答案一.选择题：题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 BBBCBCCCACBB1．解析：选B.由p2＝5得p ＝10，且焦点在y 轴正半轴上，故x 2＝20y .2．解析：选B.x 2＝－y ，∴2p ＝1，p ＝12，∴焦点坐标为⎝ ⎛⎭⎪⎫0，－14.3．解析：选B.由y ＝ax 2，得x 2＝1a y ，14a ＝－2，a ＝－18.4．解析：选C.由抛物线的标准方程得准线方程为x ＝－p2.由x 2＋y 2－6x －7＝0得(x －3)2＋y 2＝16.∵准线与圆相切，∴3＋p2＝4，∴p ＝2.5解析：选B.如图所示，抛物线的焦点为F (2,0)，准线方程为x ＝－2，由抛物线的定义知：|PF |＝|PE |＝4＋2＝6.6．解析：选C.∵点F (4,0)在直线x ＋5＝0的右侧，且P 点到点F (4,0)的距离比它到直线x ＋5＝0的距离小1，∴点P 到F (4,0)的距离与它到直线x ＋4＝0的距离相等．故点P 的轨迹为抛物线，且顶点在原点，开口向右，p ＝8，故P 点的轨迹方程为y 2＝16x . 7．解析：选C.通径2p ＝8且焦点在x 轴上，故选C. 8．解析：选C.由抛物线定义知|FP 1|＝x 1＋p2，|FP 2|＝x 2＋p 2，|FP 3|＝x 3＋p2，∴|FP 1|＋|FP 3|＝2|FP 2|，故选C.9．解析：选A.令直线与抛物线交于点A (x 1，y 1)，B (x 2，y 2)由⎩⎪⎨⎪⎧y ＝2x ＋1y 2＝12x 得4x 2－8x ＋1＝0，∴x 1＋x 2＝2，x 1x 2＝14，∴|AB |＝1＋22x 1－x 22＝5[x 1＋x 22－4x 1x 2]＝15.10．解析：选C.|PF |＝x P ＋p 2，∴|PF |2＝x P 2＋p4，即为PF 的中点到y 轴的距离．故该圆与y 轴相切．11．解析：选B.由题意可得|AB |＝2p .又焦点到准线距离|FM |＝p ，F 为AB 中点，∴|FM |＝12|AB |，∴△AMB 为直角三角形且∠AMB ＝90°.12．解析：选B.∵y 2＝2px (p >0)的焦点坐标为⎝ ⎛⎭⎪⎫p2，0，∴过焦点且斜率为1的直线方程为y ＝x －p 2，即x ＝y ＋p2，将其代入y 2＝2px 得y 2＝2py ＋p 2，即y 2－2py－p 2＝0.设A (x 1，y 1)，B (x 2，y 2)，则y 1＋y 2＝2p ，∴y 1＋y 22＝p ＝2，∴抛物线的方程为y 2＝4x ，其准线方程为x ＝－1. 二．填空题13解析：由⎩⎪⎨⎪⎧x －y －1＝0y ＝ax2，得ax 2－x ＋1＝0，由Δ＝1－4a ＝0，得a ＝14. 答案：1414．解析：设P (x 0，y 0)，则|PF |＝x 0＋1＝5，∴x 0＝4， ∴y 20＝16，∴y 0＝±4. 答案：(4，±4) 15．解析：设A (x 1，y 1)，B (x 2，y 2)，则|FA |＋|FB |＝x 1＋x 2＋2.又⎩⎪⎨⎪⎧y 2＝4x 2x ＋y －4＝0⇒x 2－5x ＋4＝0， ∴x 1＋x 2＝5，x 1＋x 2＋2＝7. 答案：7 16．解析：焦点在x 轴正半轴上时，设方程为y 2＝2px (p >0)代入点(32，12)得p ＝312，焦点在x 轴负半轴上时，设方程为y 2＝－2px (p >0)，∴p ＝－312.综上，所求方程为y 2＝±36x . 答案：y 2＝±36x 三、解答题17．若抛物线y 2＝－2px (p >0)上有一点M ，其横坐标为－9.它到焦点的距离为10，求抛物线方程和M 点的坐标．解：由抛物线定义知焦点为F (－p 2，0)，准线为x ＝p2，由题意设M 到准线的距离为|MN |，则|MN |＝|MF |＝10，即p2－(－9)＝10， ∴p ＝2.故抛物线方程为y 2＝－4x ，将M (－9，y )代入y 2＝－4x ，解得y ＝±6， ∴M (－9,6)或M (－9，－6)．18．抛物线的焦点F 在x 轴上，直线y ＝－3与抛物线相交于点A ，|AF |＝5，求抛物线的标准方程．解：设所求抛物线的标准方程为： y 2＝ax (a ≠0)，A (m ，－3)．则由抛物线的定义得5＝|AF |＝|m ＋a4|，又(－3)2＝am .所以，a ＝±2或a ＝±18.故所求抛物线的方程为y 2＝±2x 或y 2＝±18x .19．已知抛物线y 2＝－x 与直线l ：y ＝k (x ＋1)相交于A ，B 两点．(1)求证：OA ⊥OB ；(2)当△OAB 的面积等于10时，求k 的值．解：(1)证明：联立⎩⎪⎨⎪⎧y 2＝－xy ＝k x ＋1，消去x ，得ky 2＋y －k ＝0.设A (x 1，y 1)，B (x 2，y 2)，则y 1＋y 2＝－1k，y 1·y 2＝－1.因为y 21＝－x 1，y 22＝－x 2，所以(y 1·y 2)2＝x 1·x 2，所以x 1·x 2＝1，所以x 1x 2＋y 1y 2＝0，即OA →·OB →＝0，所以OA ⊥OB .(2)设直线l 与x 轴的交点为N ，则N 的坐标为(－1,0)，所以S △AOB ＝12|ON |·|y 1－y 2|＝12×|ON |×y 1＋y 22－4y 1·y 2 ＝12×1× 1k 2＋4＝10，解得k 2＝136，所以k ＝±16.。

13级高二数学抛物线练习题(2021年整理)

13级高二数学抛物线练习题(word版可编辑修改)
编辑整理：
尊敬的读者朋友们：
这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（13级高二数学抛物线练习题(word版可编辑修改)）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为13级高二数学抛物线练习题(word版可编辑修改)的全部内容。

(完整word版)高中抛物线知识点归纳总结与练习题及答案,推荐文档

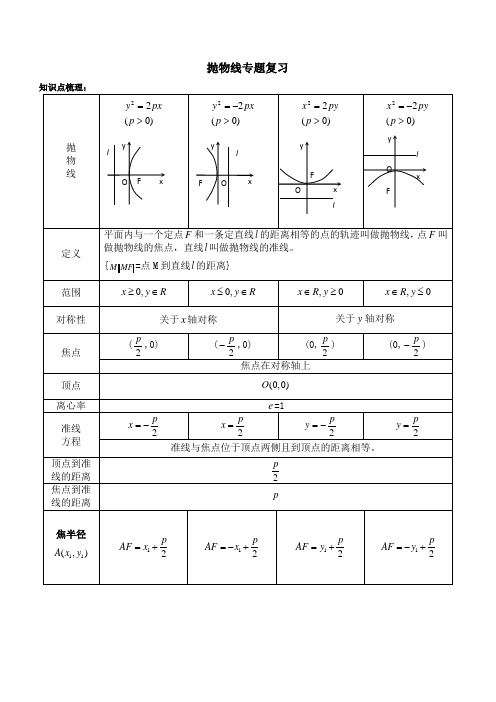
抛物线专题复习焦点弦长 AB12()x x p ++12()x x p -++ 12()y y p ++ 12()y y p -++焦点弦AB 的几条性质11(,)A x y 22(,)B x y以AB 为直径的圆必与准线l 相切若AB 的倾斜角为α，则22sin p AB α=若AB 的倾斜角为α，则22cos pAB α= 2124p x x = 212y y p =-112AF BF AB AF BF AF BF AF BF p++===•• 切线方程00()y y p x x =+ 00()y y p x x =-+ 00()x x p y y =+ 00()x x p y y =-+直线，抛物线，，消y 得：（1）当k=0时，直线l 与抛物线的对称轴平行，有一个交点；（2）当k ≠0时，Δ＞0，直线l 与抛物线相交，两个不同交点； Δ=0，直线l 与抛物线相切，一个切点； Δ＜0，直线l 与抛物线相离，无公共点。

（3）若直线与抛物线只有一个公共点,则直线与抛物线必相切吗?（不一定）二．关于直线与抛物线的位置关系问题常用处理方法直线l ：b kx y += 抛物线，)0(φp联立方程法：⎩⎨⎧=+=pxy bkx y 22⇒0)(2222=+-+b x p kb x k ox ()22,B x yFy ()11,A x y设交点坐标为),(11y x A ,),(22y x B ，则有0φ∆,以及2121,x x x x +，还可进一步求出b x x k b kx b kx y y 2)(212121++=+++=+，2212122121)())((b x x kb x x k b kx b kx y y +++=++= 在涉及弦长，中点，对称，面积等问题时，常用此法，比如相交弦AB 的弦长2122122124)(11x x x x k x x k AB -++=-+=ak ∆+=21 或 2122122124)(1111y y y y k y y k AB -++=-+=ak ∆+=21 抛物线练习1、已知点P 在抛物线y 2 = 4x 上，那么点P 到点Q （2，－1）的距离与点P 到抛物线焦点距离之和取得最小值时，点P 的坐标为 2、已知点P 是抛物线22y x =上的一个动点，则点P 到点（0，2）的距离与P 到该抛物线准线的距离之和的最小值为3、直线3y x =-与抛物线24y x =交于,A B 两点，过,A B 两点向抛物线的准线作垂线，垂足分别为,P Q ，则梯形APQB 的面积为4、设O 是坐标原点，F 是抛物线22(0)y px p =>的焦点，A 是抛物线上的一点，FA u u u r与x 轴正向的夹角为60o，则OA u u u r 为5、抛物线24y x =的焦点为F ，准线为l ，经过F x 轴上方的部分相交于点A ，AK l ⊥，垂足为K ，则AKF △的面积是6、已知抛物线2:8C y x =的焦点为F ，准线与x 轴的交点为K ，点A 在C 上且AK =，则AFK∆的面积为7、已知双曲线22145x y -=，则以双曲线中心为焦点，以双曲线左焦点为顶点的抛物线方程为 8、在平面直角坐标系xoy 中，有一定点(2,1)A ,若线段OA 的垂直平分线过抛物线22(0)y px p =>则该抛物线的方程是。

(完整版)抛物线基础练习题

完整版)抛物线基础练习题抛物线基础练习题1.抛物线方程及性质1.1 抛物线的标准方程为 $y = ax^2 + bx + c$，其中 $a$、$b$、$c$ 是实数常数。

a 的值决定了抛物线的开口方向。

当 $a。

0$ 时，抛物线开口向上。

当 $a < 0$ 时，抛物线开口向下。

1.2 抛物线的对称轴是垂直于 x-轴的直线，可以通过以下公式求得：x = -\frac{b}{2a}$$2.抛物线图像绘制2.1 绘制抛物线图像的步骤：确定抛物线的方程。

找出对称轴的 x 坐标。

绘制对称轴，并确定对称轴上的一点。

根据对称轴上的点，绘制抛物线的图像。

2.2 使用上述步骤绘制以下抛物线的图像：2.2.1 $y = x^2$，开口向上的抛物线。

首先，我们可以得知对称轴的 x 坐标为 $x = 0$。

确定对称轴上的一点 P(0,0)，然后根据 P 点的坐标起始绘制抛物线图像。

绘制结果如下图所示：抛物线图像](image.png)3.练习题请计算并回答下列问题：1.当抛物线方程为 $y = -2x^2 + 3x + 1$ 时，求其对称轴的 x 坐标。

2.给定抛物线方程 $y = 4x^2 + 2x + 1$，求其开口方向。

4.答案解析解答上述练习题：1.根据公式 $x = -\frac{b}{2a}$，代入 $a=-2$ 和 $b=3$，我们可以计算得到对称轴的 x 坐标为 $x = -\frac{3}{2}$。

2.根据抛物线方程 $y = 4x^2 + 2x + 1$，我们可以得知 $a = 4.0$，所以抛物线的开口方向是向上。

希望以上内容能够帮助你理解抛物线的基本概念和绘制方法。

如果还有其他问题，请随时提问。

抛物线的试题及答案高中

抛物线的试题及答案高中一、选择题1. 已知抛物线方程为 $ y^2 = 4px $，其中 $ p > 0 $，该抛物线的焦点坐标是（）。

A. $ (0, 0) $B. $ (p, 0) $C. $ (0, p) $D. $ (2p, 0) $答案：B2. 若抛物线 $ y = ax^2 + bx + c $ 经过点 $ (1, 0) $，则下列哪个条件一定成立？（）A. $ a + b + c = 0 $B. $ a + b + c = 1 $C. $ a - b + c = 0 $D. $ a - b + c = 1 $答案：A二、填空题3. 抛物线 $ x^2 = 4y $ 的准线方程是 ________。

答案：$ y = -1 $4. 抛物线 $ y = -2x^2 + 4x + 5 $ 的顶点坐标是 ________。

答案：$ (1, 6) $三、解答题5. 已知抛物线 $ y = 2x^2 - 4x + 5 $，求其焦点坐标和准线方程。

解：首先，将抛物线方程 $ y = 2x^2 - 4x + 5 $ 转化为标准形式$ x^2 = \frac{1}{2}(y - 5) $。

由此可知，$ p = \frac{1}{4} $，焦点坐标为 $ (0, \frac{5}{4}) $，准线方程为 $ y = -\frac{3}{4} $。

6. 抛物线 $ x^2 = 6y $ 与直线 $ y = mx + 2 $ 相交于两点 A 和 B。

求直线 AB 的斜率。

解：将直线方程 $ y = mx + 2 $ 代入抛物线方程 $ x^2 = 6y $ 得 $ x^2 = 6(mx + 2) $。

整理得 $ x^2 - 6mx - 12 = 0 $。

设A 点坐标为 $ (x_1, y_1) $，B 点坐标为 $ (x_2, y_2) $，由韦达定理得 $ x_1 + x_2 = 6m $，$ x_1x_2 = -12 $。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

A. 0，4 B. 0，－4 ，0 D. －，044一、选择题：高二抛物线基础测试题1. 顶点在原点，焦点是 F (0,5)的抛物线方程是()A ．y 2＝20xB ．x 2＝20y11C ．y 2＝ xD ．x 2＝ y2020 2. 抛物线 y ＝－x 2 的焦点坐标为()( 1) ( 1) (1 ) ( 1 )3. 抛物线 y ＝ax 2 的准线方程是 y ＝2，则实数 a 的值为()1 1A. B ．－ 8 8 C ．8 D ．－8 4．(2010 年高考陕西卷)已知抛物线 y 2＝2px (p >0)的准线与圆 x 2＋y 2－6x －7＝0 相切，则 p 的值为()1 A. B ．12 C ．2 D ．45．(2010 年高考湖南卷)设抛物线 y 2＝8x 上一点 P 到 y 轴的距离是 4，则点 P 到该抛物线焦点的距离是()A ．4B ．6C ．8D ．126. 若点 P 到定点 F (4,0)的距离比它到直线 x ＋5＝0 的距离小 1，则点 P 的轨迹方程是()A ．y 2＝－16xB ．y 2＝－32xC ．y 2＝16xD ．y 2＝16x 或 y ＝0(x <0) 7. 以 x 轴为对称轴的抛物线的通径(过焦点且与 x 轴垂直的弦)长为 8，若抛物线的顶点在坐标原点，则其方程为( )A ．y 2＝8xB ．y 2＝－8xC ．y 2＝8x 或 y 2＝－8xD ．x 2＝8y 或 x 2＝－8y8. 已知抛物线 y 2＝2px (p >0)的焦点 F ，点 P 1(x 1，y 1)、P 2(x 2，y 2)、P 3(x 3，y 3)在抛物线上，且 2x 2＝x 1＋x 3，则有( )A ．|FP 1|＋|FP 2|＝|FP 3|B ．|FP 1|2＋|FP 2|2＝|FP 3|2C ．|FP 1|＋|FP 3|＝2|FP 2|D ．|FP 1|·|FP 3|＝|FP 2|29. 抛物线 y 2＝12x 截直线 y ＝2x ＋1 所得弦长等于( )A. 15 15 B ．2 C. D ．15. 210. 以抛物线 y 2＝2px (p >0)的焦半径|PF |为直径的圆与 y 轴的位置关系为( )A ．相交B ．相离C ．相切D ．不确定 11. 过抛物线的焦点且垂直于其对称轴的弦是 A B ，抛物线的准线交 x 轴于点 M ，则∠AMB 是( )A ．锐角B ．直角C ．钝角D ．锐角或钝角15 C.12．(2010 年高考ft东卷)已知抛物线y2＝2px(p>0)，过其焦点且斜率为1 的直线交抛物线于A、B 两点，若线段AB 的中点的纵坐标为2，则该抛物线的准线方程为( )A．x＝1 B．x＝－1C．x＝2 D．x＝－2二．填空题13.已知直线x－y－1＝0 与抛物线y＝ax2 相切，则a＝.14.抛物线y2＝4x 上的点P 到焦点F 的距离是5，则P 点的坐标是．15.抛物线y2＝4x 与直线2x＋y－4＝0 交于两点A 与B，F 是抛物线的焦点，则|FA|＋|FB|＝.16.边长为1 的等边三角形AOB，O 为原点，AB⊥x 轴，则以O 为顶点，且过A、B 的抛物线方程是．三、解答题(解答应写出文字说明，证明过程或演算步骤.)17.若抛物线y2＝－2px(p>0)上有一点M，其横坐标为－9.它到焦点的距离为 10，求抛物线方程和M 点的坐标．18.抛物线的焦点F 在x 轴上，直线y＝－3 与抛物线相交于点A，|AF|＝5，求抛物线的标准方程．19.已知抛物线y2＝－x 与直线l：y＝k(x＋1)相交于A，B 两点．(1)求证：OA⊥OB；(2)当△OAB 的面积等于10时，求k 的值．高二抛物线基础测试题参考答案一.选择题：p 2．解析：选 B.x 2＝－y ，∴2p ＝1，p ＝，∴焦点坐标为 0，－题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 BBBCBCCCACBBp1．解析：选 B.由＝5 得 p ＝10，且焦点在 y 轴正半轴上，故 x 2＝20y .21 ( 1)1 1 13．解析：选 B.由 y ＝ax 2，得 x 2＝ y ，＝－2，a ＝－ .a 4a 8p4．解析：选 C.由抛物线的标准方程得准线方程为 x ＝－ .2由 x 2＋y 2－6x －7＝0 得(x －3)2＋y 2＝16.p∵准线与圆相切，∴3＋＝4，∴p ＝2.25 解析：选 B.如图所示，抛物线的焦点为 F (2,0)，准线方程为 x ＝－2，由抛物线的定义知：|PF |＝|PE |＝4＋2 ＝6.6. 解析：选 C.∵点 F (4,0)在直线 x ＋5＝0 的右侧，且 P 点到点 F (4,0)的距离比它到直线 x ＋5＝0 的距离小 1，∴点 P 到 F (4,0)的距离与它到直线 x ＋4＝0 的距离相等．故点 P 的轨迹为抛物线，且顶点在原点，开口向右，p ＝8，故 P 点的轨迹方程为 y 2＝16x . 7. 解析：选 C.通径 2p ＝8 且焦点在 x 轴上，故选 C.p8. 解析：选 C.由抛物线定义知|FP 1|＝x 1＋，2p p|FP 2|＝x 2＋，|FP 3|＝x 3＋，2 2∴|FP 1|＋|FP 3|＝2|FP 2|，故选 C.9. 解析：选 A.令直线与抛物线交于点 A (x 1，y 1)，B (x 2，y 2)由Error!得 4x 2－8x ＋1＝0，1∴x 1＋x 2＝2，x 1x 2＝，4p |PF | x P p10. 解析：选 C.|PF |＝x P ＋，∴ ＝＋，即为 PF 的中点到 y 轴的距离．故该圆与 y 轴相切．2 2 2 411. 解析：选 B.由题意可得|AB |＝2p .又焦点到准线距离|FM |＝p ，F 为 AB 中点，1∴|FM |＝ |AB |，2∴△AMB 为直角三角形且∠AMB ＝90°.12．解析：选 B.∵y 2＝2px (p >0)的焦点坐标为( ，0)， 2 p p∴过焦点且斜率为 1 的直线方程为 y ＝x －，即 x ＝y ＋，将其代入 y 2＝2px 得 y 2＝2py ＋p 2，即 y 2－2py －2 2y 1＋y 2p 2＝0.设 A (x 1，y 1)，B (x 2，y 2)，则 y 1＋y 2＝2p ，∴ ＝p ＝2，∴抛物线的方程为 y 2＝4x ，其准线方程2为 x ＝－1.4 2 ∴|AB |＝ 1＋22 x 1－x 2 2 ＝ 5[ x 1＋x 2 2－4x 1x 2]＝ 15. .3 二．填空题13 解析：由Error!，得 ax 2－x ＋1＝0，1 1由 Δ＝1－4a ＝0，得 a ＝ . 答案：4 414．解析：设 P (x 0，y 0)，则|PF |＝x 0＋1＝5，∴x 0＝4， ∴y 20＝16，∴y 0＝±4. 答案：(4，±4) 15．解析：设 A (x 1，y 1)，B (x 2，y 2)，则|FA |＋|FB |＝x 1＋x 2＋2. 又Error!⇒x 2－5x ＋4＝0， ∴x 1＋x 2＝5，x 1＋x 2＋2＝7. 答案：7 16．3 1解析：焦点在 x 轴正半轴上时，设方程为 y 2＝2px (p >0)代入点( ， )得 p ＝，2 2 12焦点在 x 轴负半轴上时，设方程为 y 2＝－2px (p >0)，∴p ＝－ .123 综上，所求方程为 y 2＝± x .63答案：y 2＝± x6三、解答题17. 若抛物线 y 2＝－2px (p >0)上有一点 M ，其横坐标为－9.它到焦点的距离为 10，求抛物线方程和 M 点的坐标．p p解：由抛物线定义知焦点为 F (－，0)，准线为 x ＝，2 2由题意设 M 到准线的距离为|MN |，则|MN |＝|MF |＝10， p即－(－9)＝10， 2∴p ＝2.故抛物线方程为 y 2＝－4x ，将 M (－9，y )代入 y 2＝－4x ，解得 y ＝±6， ∴M (－9,6)或 M (－9，－6)．18. 抛物线的焦点 F 在 x 轴上，直线 y ＝－3 与抛物线相交于点 A ，|AF |＝5，求抛物线的标准方程．解：设所求抛物线的标准方程为： y 2＝ax (a ≠0)，A (m ，－3)．a则由抛物线的定义得 5＝|AF |＝|m ＋ |，4又(－3)2＝am .所以，a ＝±2 或 a ＝±18.故所求抛物线的方程为 y 2＝±2x 或 y 2＝±18x .19. 已知抛物线 y 2＝－x 与直线 l ：y ＝k (x ＋1)相交于 A ，B 两点．(1) 求证：OA ⊥OB ；(2) 当△OAB 的面积等于 10时，求 k 的值．解：(1)证明：联立Error!，31消去x，得ky2＋y－k＝0.设A(x1，y1)，B(x2，y2)，则y1＋y2＝－，y1·y2＝－1.k→→因为y12＝－x ，y2＝－x ，所以(y ·y )2＝x ·x ，所以x ·x ＝1，所以x x ＋y y1所以OA⊥OB.2 1 2 1 2 1 2 1 2 12＝0，即OA·OB＝0，(2)设直线l 与x 轴的交点为N，则N 的坐标为(－1,0)，1所以S△AOB＝ |ON|·|y1－y2|21＝×|ON|×21＝×1×1＋4＝10，2 k21 1解得k2＝，所以k＝± .36 6y1＋y2 2－4y1·y2。