多重共线性案例
多重共线性示例

解决多重共线性实例天津市1974-1987年与粮食销售量有关的影响因素如下表。
建立粮食销售量模型。
年份 Y2X 3X 4X 5X 6X 1974 98.45 560.20 153.20 6.53 1.23 1.89 1975 100.70 603.11 190.00 9.12 1.30 2.03 … … … … … … … 1987 178.69 828.73 1094.67 23.53 11.68 23.37天津统计年鉴(1988)其中:Y 是粮食销售量(万吨);2X 常住人口(万人); 3X 人均收入(元); 4X 肉类销售量(万吨); 5X 蛋类销售量(万吨); 6X 鱼虾销售量(万吨); 一、初步模型及存在的问题多元线性回归模型估计结果如下:65432491445336782073670125305003X X X X X Y......ˆ-++++-=(2.119)(1.945)(2.130)(1.409)(-2.028) 970402.=R 5352.=F7205.ˆ=σ9731.=DW 方程中可决系数2R 和F 统计量很大,但t 统计量较小。
临界值30626140250.)(t .=-,所有参数估计值都不能通过显著性检验。
这是存在多重共线性的典型特征。
如果利用相关系数检验法,可以得到各解释变量之间的相关系数分别为8666023.=r 8823024.=r 8524025.=r 8213026.=r 9459034.=r 9648035.=r 9825036.=r 9405045.=r 9484046.=r 9820056.=r 可见任何两个解释变量之间都有很强的正线性相关关系。
因此样本存在严重的多重共线性。
二、模型的修正由以上结果表明,任何一个解释变量与被解释变量之间的关系都是显著的。
从经济意义角度来看,人口数和人均收入应该构成影响粮食销售量的主要因素,因此建模时常住人口数X和人均收入3X应作为基本解释2变量予以保留。
实验五多重共线性检验参考案例

实验五 多重共线性检验实验时间: 姓名:学号: 成绩:【实验目的】1、掌握多元线性回归模型的估计、检验和预测;2、掌握多重共线性问题的检验方法3、掌握多重共线性问题的修正方法 【实验内容】1、数据的读取和编辑;2、多元回归模型的估计、检验、预测;3、多重共线性问题的检验4、多重共线性问题的修正 【实验背景】为了评价报账最低工资(负收入税)政策的可行性,兰德公司进行了一项研究,以评价劳动供给(平均工作小时数)对小时工资提高的反应,词研究中的数据取自6000户男户主收入低于15000美元的一个国民样本,这些数据分成39个人口组,并放在表1中,由于4个人口组中的某些变量确实,所以只给出了35个组的数据,用于分析的各个变量的定义如下:Y 表示该年度平均工作小时数;X1表示平均小时工资(美元);X2表示配偶平均收入(美元);X3表示其他家庭成员的平均收入(美元);X4表示年均非劳动收入(美元);X5表示平均家庭资产拥有量;X6表示被调查者的平均年龄;X7表示平均赡养人数;X 8表示平均受教育年限。
μ为随机干扰项,考虑一下回归模型:μβββββββββ+++++++++=87654321876543210X X X X X X X X Y (1) 将该年度平均工作小时数Y 对X 进行回归,并对模型进行简单分析; (2) 计算各变量之间的相关系数矩阵,利用相关系数法分析变量间是否具有多重共线性;(3) 利用逐步回归方法检验并修正回归模型,最后再对模型进行经济意义检验、统计检验。
表5观测组Y X1 X2 X3 X4 X5 X6 X7 X81 2157 2.905 1121 291 380 7250 38.5 2.34 10.52 2174 2.97 1128 301 398 7744 39.3 2.335 10.53 2062 2.35 1214 326 185 3068 40.1 2.851 8.94 2111 2.511 1203 49 117 1632 22.4 1.159 11.55 2134 2.791 1013 594 730 1271057.7 1.229 8.86 2185 3.04 1135 287 382 776 38.6 2.602 10.77 2210 3.222 1100 295 474 9338 39 2.187 1128 2105 2.495 1180 310 255 4730 39.9 2.616 9.39 2267 2.838 1298 252 431 8317 38.9 2.024 11.110 2205 2.356 885 264 373 6489 38.8 2.662 9.511 2121 2.922 1251 328 312 5907 39.8 2.287 10.312 2109 2.499 1207 347 271 5069 39.7 3.193 8.913 2108 2.796 1036 300 259 4614 38.2 2.4 9.214 2047 2.453 1213 397 139 1987 40.3 2.545 9.115 2174 3.582 1141 414 498 1023940 2.064 11.716 2067 2.909 1805 290 239 4439 39.1 2.301 10.517 2159 2.511 1075 289 308 5621 39.3 2.486 9.518 2257 2.516 1093 176 392 7293 37.9 2.042 10.119 1985 1.423 553 381 146 1866 40.6 3.833 6.620 2184 3.636 1091 291 560 1124039.1 2.328 11.621 2084 2.983 1327 331 296 5653 39.8 2.208 10.222 2051 2.573 1197 279 172 2806 40 2.362 9.123 2127 3.263 1226 314 408 8042 39.5 2.259 10.824 2102 3.234 1188 414 352 7557 39.8 2.019 10.725 2098 2.28 973 364 272 4400 40.6 2.661 8.426 2042 2.304 1085 328 140 1739 41.8 2.444 8.227 2181 2.912 1072 304 383 9340 39 2.337 10.228 2186 3.015 1122 30 352 7292 37.2 2.046 10.929 2188 3.01 990 366 374 7325 38.4 2.847 10.630 2077 1.901 350 209 95 1370 37.4 4.158 8.231 2196 3.009 947 294 342 6888 37.5 3.047 10.632 2093 1.899 342 311 120 1425 37.5 4.512 8.133 2173 2.959 1116 296 387 7625 39.2 2.342 10.534 2179 2.959 1116 296 387 7625 39.2 2.342 10.535 2200 2.98 1126 204 393 7885 39.2 2.341 10.6 【实验过程】一、利用Evie ws软件建立年度平均工作小时数y的回归模型。
多重共线性案例分析实验报告

《多重共线性案例分析》实验报告表2由此可见,该模型,可决系数很高,F 检验值173.3525,明显显著。
但是当时,不仅、系数的t 检验不显著,而且系数的符号与预期的相反,这表明很可能存在严重的多重共线性。
9954.02=R 9897.02=R 05.0=α776.2)610()(025.02=-=-t k n t α2X 6X 6X②.计算各解释变量的相关系数,选择X2、X3、X4、X5、X6数据,点”view/correlations ”得相关系数矩阵表3由关系数矩阵可以看出:各解释变量相互之间的相关系数较高,证实确实存在严重多重共线性相。
4.消除多重共线性①采用逐步回归的办法,去检验和解决多重共线性问题。
分别作Y 对X2、X3、X4、X5、X6的一元回归 如下图所示变量 X2 X3 X4 X5 X6 参数估计值0.08429.0523 11.6673 34.3324 2014.146 t 统计量8.665913.1598 5.1967 6.4675 8.74870.90370.95580.77150.83940.9054表4 按的大小排序为:X3、X6、X2、X5、X4。
以X3为基础,顺次加入其他变量逐步回归。
首先加入X6回归结果为:t=(2.9086) (0.46214)2R 2R 631784.285850632.7639.4109ˆX X Y t ++-=957152.02=R1995 1375.7 62900 464.0 61.5 115.70 5.97 1996 1638.4 63900 534.1 70.5 118.58 6.49 1997 2112.7 64400 599.8 145.7 122.64 6.60 1998 2391.2 69450 607.0 197.0 127.85 6.64 1999 2831.9 71900 614.8 249.5 135.17 6.74 2000 3175.5 74400 678.6 226.6 140.27 6.87 2001 3522.4 78400 708.3 212.7 169.80 7.01 2002 3878.4 87800 739.7 209.1 176.52 7.19 2003 3442.3 87000 684.9 200.0 180.98 7.30表1:1994年—2003年中国游旅收入及相关数据表2:OLS 回归表3:关系数矩阵变量 X2 X3 X4 X5 X6 参数估计值0.08429.0523 11.6673 34.3324 2014.146 t 统计量8.665913.1598 5.1967 6.4675 8.74870.90370.95580.77150.83940.9054表4:Y 对X2、X3、X4、X5、X6的一元回归六、实验结果及分析1. 在参数估计模型和关系数矩阵中, ,可决系数很高,F 检验值173.3525,明显显著。
多重共线性-例题

2.多重共线性的经济解释(1)经济变量在时间上有共同变化的趋势。
如在经济上升时期,收入、消费、就业率等都增长,当经济收缩期,收入、消费、就业率等又都下降。
当这些变量同时进入模型后就会带来多重共线性问题。
0.E+001.E+112.E+113.E+114.E+11808284868890929496980002GDPCONS0.E+001.E+112.E+113.E+114.E+110.0E+005.0E+101.0E+111.5E+112.0E+112.5E+11CONSGDP of HongKong(2)解释变量与其滞后变量同作解释变量。
0.E+001.E+112.E+113.E+114.E+11808284868890929496980002GDP0.E+001.E+112.E+113.E+114.E+110.E+001.E+112.E+113.E+114.E+11GDP(-1)GDP3.多重共线性的后果(1)当 | r x i x j | = 1,X 为降秩矩阵,则 (X 'X ) -1不存在,βˆ= (X 'X )-1 X 'Y 不可计算。
(2)若 | r x i x j | ≠1,即使 | r x i x j | →1,βˆ仍具有无偏性。
E(βˆ) = E[(X 'X )-1 X 'Y ] = E[(X 'X ) -1X '(X β + u )] = β + (X 'X )-1X ' E(u ) = β. (3)当 | r x i x j | →1时,X 'X 接近降秩矩阵,即 | X 'X | →0,V ar(βˆ) = σ 2 (X 'X )-1变得很大。
所以βˆ丧失有效性。
以二解释变量线性模型为例,当r x i x j = 0.8时,Var(βˆ)为r x i x j = 0时的Var(βˆ)的2.78倍。
第6章(多重共线性)-案例

3.基础解系及其求法 基础解系及其求法
3.1. 基础解系 3.1.2. 基础解系的求法
x1 = − b1, r +1k1 L − b 1 n k n− r x = −b k L − b k 2 ,r +1 1 2n n− r 2 L L L L L L L xr = − br ,r +1k1 L − br n k n− r x r +1 = k 1 k2 xr + 2 = L LLLLL x = k n− r n
在进行经济计量分析时,如果模型地设定出现失误, 在进行经济计量分析时,如果模型地设定出现失误,则容易导 致完全共线性 例如:设定居民消费对工资收入 工资收入S和非劳动收入N及总收入T 例如:设定居民消费对工资收入 和非劳动收入 及总收入 的回 归模型为
C = β 0 + β 1 S + β 2 N + β 3T + ε
§6.1 多重共线性的定义
从数学意义上解释变量之间存在共线性, 从数学意义上解释变量之间存在共线性,就是对于变 量x1,x2,…,xk,如果存在不全为零的数λ1,λ2,…, , 如果存在不全为零的数λ , 使得下式成立: λk,使得下式成立: λ1x1+λ2x2+…+λkxk=0 +λ (*) 则称变量x 则称变量x1,x2,…,xk之间存在一种完全的共线性。 , 在计量经济学中, 在计量经济学中,一个具有两个以上解释变量的线性 回归模型里,如果解释变量之间存在式( 那样的关系, 回归模型里,如果解释变量之间存在式(*)那样的关系, 则称这些解释变量之间存在完全的多重共线性。
设解释变量矩阵为: 设解释变量矩阵为:
1 x 11 1 x 21 X= M M 1 x n1 x 12 x 22 M x n2 L x 1k L x 2k M L x nk
第四章多重共线性实例

表 4.3.3 中国粮食生产与相关投入资料
农业化肥施 粮食播种面 受灾面积 农业机械总
用量 X 1
(万公斤)
积X 2
(千公顷)
X3
(公顷)
动力X 4
(万千瓦)
1659.8
114047 16209.3
18022
1739.8
112884 15264.0
19497
1775.8
108845 22705.3
20913
Yˆ 28259.19 2.240X5
(-1.04) (2.66) R2=0.3064 F=7.07 DW=0.36
• 可见,应选第1个式子为初始的回归模型。
4、逐步回归
将其他解释变量分别导入上述初始回归模型,寻 找最佳回归方程。
C
X1 X2 X3
X4
X5
R2
DW
Y=f(X1)
30868 4.23
0.8852 1.56
t值
25.58 11.49
Y=f(X1,X2)
-43871 4.65 0.67
0.9558 2.01
t值
-3.02 18.47 5.16
Y=f(X1,X2,X3)
-11978 5.26 0.41 -0.19
0.9752 1.53
t值
0.85
19.6 3.35 -3.57
Y=f(X1,X2,X3,X4) -13056 6.17 0.42 -0.17 -0.09
1930.6
110933 23656.0
22950
1999.3
111268 20392.7
24836
2141.5
110123 23944.7
多重共线性处理经典例题
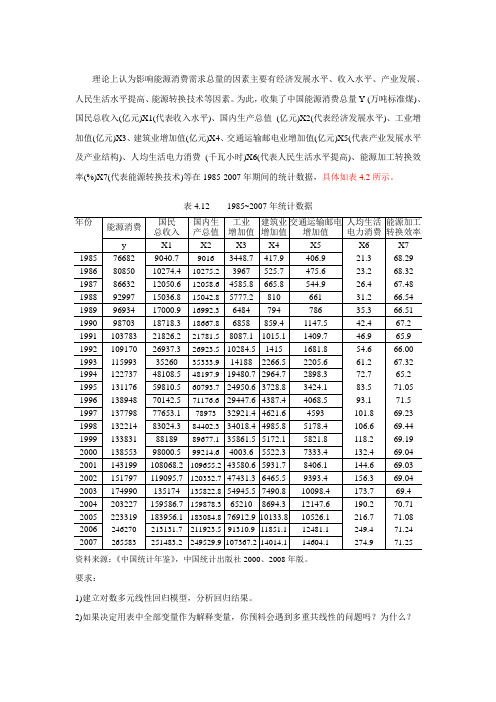
理论上认为影响能源消费需求总量的因素主要有经济发展水平、收入水平、产业发展、人民生活水平提高、能源转换技术等因素。
为此,收集了中国能源消费总量Y (万吨标准煤)、国民总收入(亿元)X1(代表收入水平)、国内生产总值(亿元)X2(代表经济发展水平)、工业增加值(亿元)X3、建筑业增加值(亿元)X4、交通运输邮电业增加值(亿元)X5(代表产业发展水平及产业结构)、人均生活电力消费(千瓦小时)X6(代表人民生活水平提高)、能源加工转换效率(%)X7(代表能源转换技术)等在1985-2007年期间的统计数据,具体如表4.2所示。
表4.12 1985~2007年统计数据资料来源:《中国统计年鉴》,中国统计出版社2000、2008年版。
要求:1)建立对数多元线性回归模型,分析回归结果。
2)如果决定用表中全部变量作为解释变量,你预料会遇到多重共线性的问题吗?为什么?3)如果有多重共线性,你准备怎样解决这个问题?明确你的假设并说明全部计算。
参考解答:(1)建立对数线性多元回归模型,引入全部变量建立对数线性多元回归模型如下:生成: lny=log(y), 同样方法生成: lnx1,lnx2,lnx3,lnx4,lnx5,lnx6,lnx7.作全部变量对数线性多元回归,结果为:从修正的可决系数和F统计量可以看出,全部变量对数线性多元回归整体对样本拟合很好,,各变量联合起来对能源消费影响显著。
可是其中的lnX3、lnX4、lnX6对lnY影响不显著,而且lnX2、lnX5的参数为负值,在经济意义上不合理。
所以这样的回归结果并不理想。
(2) 预料此回归模型会遇到多重共线性问题, 因为国民总收入与GDP本来就是一对关联指标;而工业增加值、建筑业增加值、交通运输邮电业增加值则是GDP的组成部分。
这两组指标必定存在高度相关。
解释变量国民总收入(亿元)X1(代表收入水平)、国内生产总值(亿元)X2(代表经济发展水平)、工业增加值(亿元)X3、建筑业增加值(亿元)X4、交通运输邮电业增加值(亿元)X5(代表产业发展水平及产业结构)、人均生活电力消费(千瓦小时)X6(代表人民生活水平提高)、能源加工转换效率(%)X7(代表能源转换技术)等很可能线性相关,计算相关系数如下:可以看出lnx1与lnx2、lnx3、lnx4、lnx5、lnx6之间高度相关,许多相关系数高于0.900以上。
多重共线性

MultiCollinearity
教学内容
一、多重共线性的概念
二、实际经济问题中的多重共线性
三、多重共线性的后果
四、多重共线性的检验
五、克服多重共线性的方法
六、案例
一、多重共线性的概念 对于模型 Yi=0+1X1i+2X2i++kXki+i i=1,2,…,n 其基本假设之一是解释变量是互相独立的。
因此,给定显著性水平,计算F值,并与相应的 临界值比较,来判定是否存在相关性。
(2)逐步回归法
以Y为被解释变量,逐个引入解释变量,构 成回归模型,进行模型估计。 根据拟合优度的变化决定新引入的变量是否 独立。
如果拟合优度变化显著,则说明新引入的变 量是一个独立解释变量;
如果拟合优度变化很不显著,则说明新引入 的变量与其它变量之间存在共线性关系。
四、
多重共线性的检验
另一等价的检验是: 在模型中排除某一个解释变量Xj,估 计模型; 如果拟合优度与包含Xj时十分接近, 则说明Xj与其它解释变量之间存在共线性。
四、多重共线性的检验
2、逐步回归法
以Y为被解释变量,分别引入解释变量,构成各解释 变量的一元回归模型,进行模型估计。 根据拟合优度选择最好的一个模型作为基础模型,然 后逐个引入其他解释变量,再根据拟合优度的变化和 t 统计量决定新引入的变量是否独立。 如果拟合优度变化显著,则说明新引入的变量是一个 独立解释变量; 如果拟合优度变化很不显著,则说明新引入的变量与 其它变量之间存在共线性关系。
•
高 R2 值伴随着解释变量t值并不都显著!
2. 统计判断法:
•
解释变量之间两两高度相关
• 检查偏相关系数
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
能源消耗量多重共线性
数据来源:《2001年一2015年中国统计年鉴》
最小二乘法:
Dep endent Sample: 20Q1 2015
In eluded observatio ns: 15
Vanable CoefUaent Std Error t-Statistic Prob C 132334.0 103956.8 1.272849 0.2437 GDP -0.344084 0.212689 -1.6177S4 0 1497 QC -2096395 2060207 -1.017566 0.3428 FDL 7.647163 2.353612 3.249118 0.0141 HXXW 3559803 23.04932 1.269123 0.2450 TU 1337.533 729.2753 1.834058 0.1093 HF -3.055542 8.653656 -0.353208 0.7343 LSCL
-1.669657 2.724030
-0.612936
0.5593 R-squared
0.996149 Mean dependentvar 290620 1 Adjusted R-squared 0.992297 S.D dependent var 90737 42 S.E. of regression 7963.604 Akaike info criterion 21.10768 Sum squared resid 4 44E+0S Schwarz critenon 21.48530 Log liKelifiood -1503076 Hannan-Quinn criter. 21.10366 F-statistic
258 6471 Durbin-Watson stat
2.66U01
Prob(F-statistic)
0.000000
得到的回归模型为
Y = 132333.984713 - 0.344084350491*GDP - 20.9639535518*QC + 7.64716297259*FDL +
35.5980328128*HXXW + 1337.53288876*TLJ - 3.0565********HF - 1.66965708916*LSCL
258.6471,明显显著。
但是当 G =0.05时,口2
(n - k-1)=鮎.02
5(15 — 8) = 1.7531 不仅 HF 、HXXW 的系数t 检验不显著,而且 GDP 、QC 、LSCL 系数的符号与预期相反,这样表明可能存在严重的多重共线 性。
计算各解释变量的相关系数,选择 GDP 、QC 、FDL 、HXXW 、TLJ 、HF 、LSCL 的数据
¥
GDP
QC FDL HXXW TLJ HF
LSCL Y
1.D000G0 0 978962 0.9715M 0.993906 0.392043 0 982450 0.95517B OJ70274 GDP
097G962
1 000000
0.933772 0 992184
0993639 098S076 0906618
0936553
t= ( 1.273) (-1.617) (1.269)
(1.834)
R2=0.996,F =258.647 : ,DW=2.661
由以上结果可见,该模型
(-0.353 )
(-1.018 ) (-0.613 )
(3.249 )
2
R =0.996149,修正的可决系数为
0.992297,可决系数非常高, F 检验值为
全部解释变量的相关系数矩阵
由相关系数矩阵可以看岀,各解释变量相互之间的相关系数较高吗,证实确实存在严重的多重共线性。
多重共线性的修正
为消除共线性的影响,首先分别拟合Y对GDP QC FDL HXXW TLJ HF LSCL 的一元回归,得到七个回归模型的参数估计结果。
7个解释变量分别进行一元回归模型的参数估计结果
可以发现,变量FDL拟合效果最佳,且整体拟合效果最好。
即发电量对能源消耗量起主要作用。
按照各个
解释变量一元回归模型的拟合优度大小进行排序:FDL,HXXW,TLJ,GDP,LSCL,QC,HF ,以FDL 为基础依次加入其他解释变量进行逐步回归。
加入HXXW
Y = 79506.7054599 + 4.7901720539*FDL + 15.018962978*HXXW
t = ( 5.08510) ( 2.011848) ( 0.550224)
R =0.988,F=500.22,RSS=1.37*10A9
系数为正
加入TLJ
Y = 83502.3622712 + 4.7662124355*FDL + 10.3033091555*HXXW + 296.631527853*TLJ
t= (4.1385 ) ( 1.925450) (0.325176) (0.334023)
R2
=0.988266 , F=308.8278 , RSS=1.35*10A9
系数为正
加入TLJ
Y = 57002.1055085 + 5.90241783797*FDL + 49.5728951535*HXXW - 0.311419040916*GDP t= (4.088001 ) ( 3.191238 ) ( 2.101646 ) (-3.107994 )
R =0.993689 , F=577.3510 , RSS=7.27*10A8
系数为负,剔除GDP
加入LSCL
Y = 165163.157653 + 5.61116988855*FDL + 16.2680580598*HXXW - 2.25051469861*LSCL
t= ( 1.420467 ) ( 2.104788 ) ( 0.583718 ) (-0.743696 )
R2=0.988715 , F=321.2445 , RSS=1.3*10A9
系数为负,剔除LSCL
加入QC
Y = 56459.2268715 + 6.33133390691*FDL + 21.8258849727*HXXW - 40.2663627237*QC
t= ( 3.160903 ) ( 2.821108 ) ( 0.891906 ) (-2.051861)
R =0.991428 , F=424.0930 , RSS=9.88*10A8
系数为负,剔除QC
加入HF
Y = 49317.0081576 + 3.58414062424*FDL + 18.0157355404*HXXW + 11.3550355173*HF
t=(2.315445) (1.593152 ) ( 0.726667 ) ( 1.898782 )
R? =0.991073 , F=407.0851 RSS=1.03*10A9
最后,从此模型中可以看出,发电量、化学纤维、和化肥对能源消耗量有显著影响。
