浙江省金华市金东区浙江金华第一中学2023-2024学年高三上学期10月月考地理试题
浙江省精诚联盟2023-2024学年高一上学期10月月考数学试题含解析

高一年级数学学科试题(答案在最后)考生须知:1.本卷共4页满分120分,考试时间100分钟.2.答题前,在答题卷指定区域填写班级、姓名、考场号、座位号及准考证号并填涂相应数字.3.所有答案必须写在答题纸上,写在试卷上无效.4.考试结束后,只需上交答题纸.选择题部分一、单选题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.若集合1N 02M x x ⎧⎫=∈≤⎨⎬-⎩⎭∣,则正确的是()A.0M ∉ B.2M ∈C.{}1M⊆ D.1M⊆【答案】C 【解析】【分析】根据元素与集合,集合与集合的关系逐项判断,即可得到结果.【详解】因2{0,N11}0M x x ⎧⎫=∈≤=⎨⎬-⎩⎭∣,所以0M ∈,A 错误;2M ∉,B 错误;{}1M ⊆,C 正确;1M ∈,D 错误.故选:C .2.集合{{}2,A xy B y y x ====∣∣,则A B ⋂等于()A.∅B.{}1xx ≥∣ C.{1xx ≥∣或1}x ≤- D.{}0xx ≥∣【答案】B 【解析】【分析】由210x -≥求出集合A ,由二次函数的性质求出集合B ,再由交集运算求解即可.【详解】由210x -≥,得1x ≤-或1x ≥,则{|1A x x =≤-或1}x ≥,由20y x =≥,得{}0B y y =≥∣,{|1}A B x x ∴=≥ .故选:B .3.下列各组函数表示同一个函数的是()A.()()2,x f x x g x x==B.()()2,f x x g x ==C.()()1,11,1,1x x f x x g x x x +≥-⎧=+=⎨--<-⎩D.()()22(1),f x x g x x=+=【答案】C 【解析】【分析】根据同一函数的概念判断.【详解】对于A ,()()R f x x x =∈与2()(0)x g x x x x==≠的定义域不同,∴不是同一函数,对于B ,()()R f x x x =∈与()2)0(g x x x =≥=的定义域及对应关系均不同,∴不是同一函数,对于C ,()1,111,1x x f x x x x +≥-⎧=+=⎨--<-⎩与()g x 的定义域及对应关系均相同,∴是同一函数,对于D ,()()22(1),f x x g x x =+=的定义域均为R ,但对应关系不同,∴不是同一函数.故选:C .4.已知函数()()3,0,3,0,x x f x f x x ≥⎧=⎨+<⎩则()4f -等于()A.6B.2C.4D.8【答案】A 【解析】【分析】由分段函数概念,代入对应解析式求解即可.【详解】∵()()3,0,3,0,x x f x f x x ≥⎧=⎨+<⎩∴()()()()()4431132326f f f f f -=-+=-=-+==⨯=.故选:A .5.已知函数()f x 的定义域为()0,1,则函数()21f x -的定义域为()A.()0,1 B.()1,1- C.()1,0- D.1,12⎛⎫ ⎪⎝⎭【答案】D 【解析】【分析】直接由()210,1x -∈求解x 的取值集合得答案.【详解】∵函数()f x 的定义域为()0,1,则由0211x <-<,解得11.2x <<∴函数()21f x -的定义域为1(,1).2故选:D .6.若集合223341x x y x x -+=-+的值域为()A.13,3∞⎛⎤- ⎥⎝⎦B.133,3⎛⎤⎥⎝⎦C.130,3⎛⎤⎥⎝⎦D.133,3⎡⎤⎢⎥⎣⎦【答案】B 【解析】【分析】分离参数后,利用二次函数的性质求解最值,即可结合不等式的性质求解.【详解】由223341x x y x x -+=-+可得2131y x x =+-+,由于函数()221331244f x x x x ⎛⎫=-+=-+≥ ⎪⎝⎭,所以213104x x <≤-+,故211333,13y x x ⎛⎤=+∈ ⎥-+⎝⎦,故选:B7.已知命题[]2:0,1,220p x x x a ∃∈--+>;命题2:R,20q x x x a ∀∈--≠,若命题,p q 均为假命题,则实数a 的取值范围为()A.[]1,3- B.[]1,2- C.[]0,2 D.(],1-∞-【答案】B 【解析】【分析】求出,p q 为真命题时a 的范围,进一步可得答案.【详解】由[]20,1,220x x x a ∃∈--+>,得[]20,1,22x a x x ∃+∈>-+,2222(1)3x x x -++=--+,[]0,1x ∈,则当0x =时,222x x -++取最小值2,所以2a >,命题2:R,20q x x x a ∀∈--≠,则2(2)40a ∆=-+<,即1a <-,若命题,p q 均为假命题,则2a ≤且1a ≥-,即12a -≤≤,∴实数a 的取值范围为[]1,2-.故选:B.8.设函数()f x 满足:对任意非零实数x ,均有()()()212f f x f x x=⋅+-,则()f x 在()0,∞+上的最小值为()A.2B.1- C.2- D.1-【答案】A 【解析】【分析】条件式中代入1,2x x ==,可解出()()1,2f f ,从而写出()f x 的解析式,结合基本不等式可求出最值.【详解】对任意非零实数x ,均有()()()212f f x f x x=⋅+-,令1x =,得()()()21121f f f =+-,解得()22f =,令2x =,得()()()212222f f f =⨯+-,解得()312f =,则()322222f x x x =+-≥=,当且仅当322x x =,即233x =时,等号成立,故()f x 在()0,∞+上的最小值为2-.故选:A .二、多选题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符号题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.9.已知,R a b ∈,集合{},,1a b 与集合{}2,,0a a b +相等,下列说法正确的是()A.1b =-B.0b =C.1a =- D.202320231a b +=-【答案】BCD 【解析】【分析】根据题意,利用集合相等的概念,结合集合中元素的互异性可解.【详解】根据题意,0a =,或0b =,当0a =时,20a =,不合题意;当0b =时,{}{},,1,0,1a b a =,{}{}22,,0,,0a a b a a +=,则21a =,解得1a =(舍)或1a =-,所以1,0a b =-=,202320231a b +=-,故选:BCD .10.下列说法正确的是()A.不等式2121x x +>+的解集112xx ⎧⎫-<<⎨⎬⎩⎭∣B.“1ab >”是“1,1a b >>”成立的充分不必要条件C.命题2:R,0p x x ∀∈>,则200:R,0p x x ⌝∃∈≤D.“2a <”是“6a <”的必要不充分条件【答案】AC 【解析】【分析】根据分式不等式的解法可判断A ,根据充分性和必要性的判断可判断AD ,根据命题的否定可判断C.【详解】对于A ,由2121x x +>+得()()22110012102121x x xx x x x +--->⇒>⇒-+<++,解得112x -<<,所以不等式2121x x +>+的解集112xx ⎧⎫-<<⎨⎬⎩⎭∣,故A 正确,对于B,由“1ab >”不能得到“1,1a b >>”,比如2,3a b =-=-,故充分性不成立,故B 错误,对于C ,命题2:R,0p x x ∀∈>,则200:R,0p x x ⌝∃∈≤,故C 正确,对于D ,“2a <”是“6a <”的充分不必要条件,所以D 错误,故选:AC11.已知0,0a b >>,且a b ab +=则()A.()()111a b --=B.ab 的最大值为4C.4a b +的最小值为9D.2212a b +的最小值为23【答案】ACD 【解析】【分析】由条件变形后分解因式可判断A ;利用基本不等式结合解不等式可判断B ;由条件变形可得111a b +=,结合1的妙用可判断C ;由条件可得1b a b =-,代入2212a b+结合二次函数的性质可判断D .【详解】由a b ab +=,得()111a b b --+=,即()()111a b --=,故A 正确;ab a b =+≥(当且仅当2a b ==时取等号),解得4ab ≥,故B 错误;由a b ab +=变形可得111a b+=,所以1144(4)()559b a a b a b a b a b +=++=++≥+=,当且仅当2a b =且a b ab +=,即33,2a b ==时取等号,故C 正确;由a b ab +=,得1ba b =-,01b <<,所以222222212(1)1213332321b a b b b b bb -⎛⎫+=+=-+=-+ ⎪⎝⎭,因为11b >,则113b =,即33,2b a ==时,2212a b +取最小值23,故D 正确.故选:ACD .12.已知函数()2244f x x x k =-++,若对任意的[],,0,3a b c ∈都存在以()()(),,f a f b f c 为边的三角形,则实数k 的可能取值为()A.1k =B.2k = C.3k = D.4k =【答案】CD 【解析】【分析】根据题意,将问题转化为满足min max 2()()f x f x >,利用二次函数的性质求出()f x 的最值,求得k 的取值范围即可.【详解】不妨设()()()f a f b f c ≤≤,则对任意[],,0,3a b c ∈都存在以()()(),,f a f b f c 为边的三角形,等价于对任意的[],,0,3a b c ∈,都有()()()f a f b f c +>等价于min max 2()()f x f x >,()()[]22224,420,3f x x x k x k x ==-++-+∈,当2x =时,2min ()(2)f x f k ==,当0x =时,2max ()(0)4f x f k ==+,所以,由min max 2()()f x f x >得2224k k >+,解得2k <-或2k >,则CD 符合题意.故选:CD .非选择题部分三、填空题:本题共4小题,每小题5分,共20分.13.已知12,01x y -≤≤≤≤,设2z x y =-,则z 的取值范围是__________.【答案】[]3,4-【解析】【分析】根据不等式的性质即可求解.【详解】由12,01x y -≤≤≤≤可得224,10x y -≤≤-≤-≤,所以324x y -≤-≤,因此[]3,4z ∈-,故答案为:[]3,4-14.已知集合{},,,A a b c d =,集合B 中有且仅有2个元素,且B A ⊆,满足下列三个条件:①若a B ∈,则c B ∈;②若d B ∉,则c B ∉;③若d B ∈,则b B ∉.则集合B =__________.(用列举法表示).【答案】{},c d 【解析】【分析】将集合A 的恰有两个元素的子集全部列出,再检验是否满足①②③即可求解.【详解】因为集合{},,,A a b c d =,集合B 中有且仅有2个元素,且B A ⊆,则集合B 可能为{},a b ,{},a c ,{},a d ,{},b c ,{},b d ,{},c d ,若{},B a b =,则不满足①,若{},B a c =,则不满足②,若{},B a d =,则不满足①,若{},B b c =,则不满足②,若{},B b d =,则不满足③,若{},B c d =,则满足①②③.所以{},B c d =.故答案为:{},c d .15.有“中欧骏泰”,“永赢货币”两种理财产品,投资这两种理财产品所能获得的年利润分别是S 和T (万元),它们与投入资金x (万元)的关系有经验方程式:2,55x S T ==,今有5万元资金投资到这两种理财产品,可获得的最大年利润是__________万元.【答案】1.2##65【解析】【分析】根据已知条件,结合换元法,以及二次函数的性质,即可求解.【详解】设“中欧骏泰”,“永赢货币”两种理财产品的投入资金分别为5x -万元,x 万元,利润为y 万元,则5,(05)55x y x -=+≤≤,2161)55y =-+,当1x =时,最大年利润是65万元故答案为:1.2.16.已知R,0,2a b a b ∈>+=,则12a a b+的最小值是__________.【答案】34##0.75【解析】【分析】变形后利用基本不等式可求得答案.【详解】1||||||()2||4||4||4||a a b a a b a a b a b a a b ++=+=++3441≥-+=,当且仅当2,4a b =-=时取到等号,故答案为:34.四、解答题:本题共3小题,17题12分,18题14分,19题14分,共40分.解答应写出文字说明、证明过程或演算步骤.17.已知集合A 为{}2560xx x +-<∣,集合B 为{221}x m x m -<<+∣.(1)当1m =时,求()R A B ð:(2)若A B A ⋃=,求m 的取值范围.【答案】(1){61}xx -<≤-∣(2)0m ≤【解析】【分析】(1)解不等式求得集合A ,然后利用集合的运算求解;(2)若A B A ⋃=,则B A ⊆,分为B =∅,B ≠∅两种情况讨论,列出不等式求解.【小问1详解】{}2560{61}A x x x x x =+-<=-<<∣∣,当1m =时,{13}B xx =-<<∣,R {|3B x x =≥ð或1}x ≤-,∴()R {61}A B xx =-<≤- ∣ð.【小问2详解】若A B A ⋃=,则B A ⊆,当B =∅时,则221m m -≥+,3m ∴≤-,当B ≠∅时,则22126211m m m m -<+⎧⎪-≥-⎨⎪+≤⎩,解得30m -<≤,综上:0m ≤.18.已知函数()21f x ax bx =++.(1)若()12f =,且0,0a b >>,求14a b+的最小值:(2)若1b a =--,解关于x 的不等式()0f x ≤.【答案】(1)9(2)答案见解析【解析】【分析】(1)由条件得1a b +=,利用1的代换结合基本不等式求解最值;(2)根据a 的范围分类讨论求解不等式的解集.【小问1详解】∵()12f =,即1a b +=,且0,0a b >>,∴144()5b a a b a b a b ⎛⎫++=++⎪⎝⎭5≥+9.=当且仅当4b a a b =即12,33a b ==时,等号成立,所以14a b+的最小值为9.【小问2详解】若1b a =--,则由()0f x ≤,得()()2110f x ax a x =-++≤,即()()110x ax --≤,当0a =时,10x -+≤,解得1x ≥,当0a >时,()110a x x a ⎛⎫--≤ ⎪⎝⎭,当11a =,即1a =时,解得1x =,当11a>,即01a <<时,解得11x a ≤≤,当11a <,即1a >时,解得11x a≤≤,当a<0时,解得1x ≥或1x a≤.综上:0a =时,不等式()0f x ≤的解集为{}1xx ≥∣;1a =时,不等式()0f x ≤的解集为{}1xx =∣;01a <<时,不等式()0f x ≤的解集为11xx a ⎧⎫≤≤⎨⎬⎩⎭∣;1a >时,不等式()0f x ≤的解集为11x x a ⎧⎫≤≤⎨⎬⎩⎭∣;a<0时,不等式()0f x ≤的解集为{1xx ≥∣或1}x a≤.19.已知对任意两个实数,m n ,定义{},max ,,m m n m n n m n≥⎧=⎨<⎩,设函数()2f x ax =-,()25g x x bx =+-.(1)若2,4a b ==时,设()()(){}max ,h x f x g x =,求()h x 的最小值:(2)0,R a b >∈,若0x >时,()()0f x g x ≥恒成立,求4b a +的最小值.【答案】(1)8-(2)【解析】【分析】(1)根据x 的范围,确定()h x 的解析式,结合一次函数及二次函数的性质求解最小值;(2)根据不等式分类讨论分析可知20g a ⎛⎫=⎪⎝⎭,然后结合基本不等式求解可得答案.【小问1详解】若2,4a b ==时,()22f x x =-,()245g x x x =+-.()()22245(1)(3)f x g x x x x x x -=--+--+-=,当31x -≤≤时,()()f x g x ≥,当1x >或3x <-时,()()f x g x <,∴()222,3145,13x x h x x x x x --≤≤⎧=⎨+-><-⎩或,当31x -≤≤时,()22h x x =-,则()min ()38h x h =-=-,当1x ≥或3x ≤-时,()2245(2)9h x x x x =+-=+-,则()()38h x h >-=-,综上,()min ()38h x h =-=-.【小问2详解】0,R a b >∈ ,0x >时,()()0f x g x ≥恒成立,由()0f x =解得2x a =,当2x a >时,()0f x >;当20x a <<时,()0f x <,∴当2x a >时,()0g x ≥,当20x a<<时,()0g x ≤,∴202425b g a aa ⎛⎫=+-= ⎪⎝⎭,∴225ab a =-,4522a b a a ∴+=+≥,05a b ==时,取等号,所以4b a +的最小值是.。
2023-2024学年浙江金华第一中学高一上学期10月月考化学试题
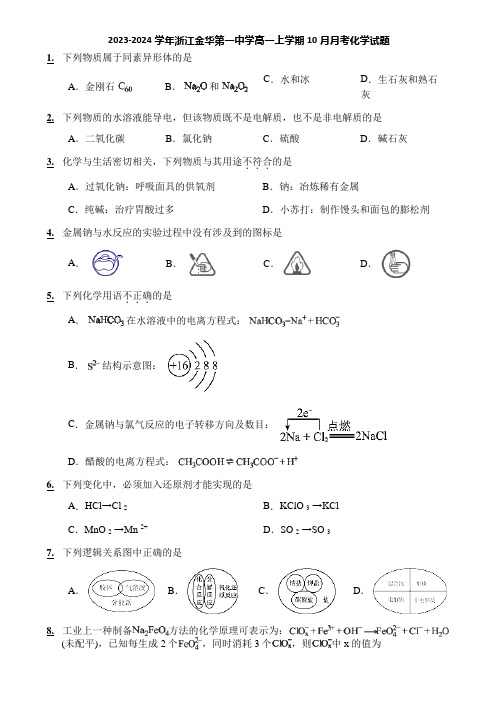
2023-2024学年浙江金华第一中学高一上学期10月月考化学试题1.下列物质属于同素异形体的是A.金刚石B.和C.水和冰D.生石灰和熟石灰2.下列物质的水溶液能导电,但该物质既不是电解质,也不是非电解质的是A.二氧化碳B.氯化钠C.硫酸D.碱石灰3.化学与生活密切相关,下列物质与其用途不符合...的是A.过氧化钠:呼吸面具的供氧剂B.钠:冶炼稀有金属C.纯碱:治疗胃酸过多D.小苏打:制作馒头和面包的膨松剂4.金属钠与水反应的实验过程中没有涉及到的图标是A.B.C.D.5.下列化学用语不正确...的是A.在水溶液中的电离方程式:B.结构示意图:C.金属钠与氯气反应的电子转移方向及数目:D.醋酸的电离方程式:6.下列变化中,必须加入还原剂才能实现的是A.HCl→Cl 2B.KClO 3→KClC.MnO 2→Mn 2+D.SO 2→SO 37.下列逻辑关系图中正确的是A.B.C.D.8.工业上一种制备方法的化学原理可表示为:(未配平),已知每生成2个,同时消耗3个,则中x的值为A.1 B.2 C.3 D.49.下列关于结构、性质与用途具有对应关系且可行的是A.钠有还原性,可用于制造高压钠灯B.、溶液显碱性,可用作食用碱或工业用碱C.胶体有吸附性,可以用于杀菌消毒D.钠比铁活泼,可以利用钠将溶液中的铁置换出来10.下列说法不正确...的是A.对于化学反应:,若A、B为两种化合物,则C、D也一定为化合物B.已知①;②,则氧化性强弱顺序为:C.非金属单质在反应中即可作氧化剂又可作还原剂D.用“人工肾”进行血液透析救治危重新冠肺炎患者,利用了渗析原理11.“类比”是研究物质变化规律的重要方法。
下列有关“类比”对物质性质的推测正确的是A.溶液显酸性,溶液也显酸性B.是酸性氧化物,也是酸性氧化物C.溶于水生成NaOH,MgO溶于水生成D.溶解度大于,的溶解度也大于12.下列各组在溶液中的反应,不管反应物的用量多少,都只能用同一个离子方程式来表示的是A. NaOH与CO 2B. Ca(OH) 2与Ca(HCO 3 ) 2C. FeBr 2与Cl 2 (氧化性:Cl 2>Br 2>Fe 3+ )D. Ca(HCO 3 ) 2与NaOH13.120℃将10g下列物质在足量氧气中完全燃烧,将燃烧产物通过足量后,固体质量增加大于10g,该物质可能是A.B.C.D.14.下列各组离子在给定条件下一定能大量共存的是A.无色溶液:Na +、Cu 2+、Cl −、B.加入锌生成氢气的溶液:、Fe 3+、、C.遇酚酞变红的溶液:Na +、K +、、D.加酚酞显红色的溶液:K +、H +、、15.下列反应的离子方程式书写正确的是A.钠与水反应:B.在溶液中滴入溶液至溶液呈中性:C.向溶液中通入:D.向碳酸钠溶液中逐滴加入少量稀盐酸:16.下列说法正确的是A.当光束通过纳米级金刚石粉末时,可以产生丁达尔效应B.NaCl溶于水,在通电的情况下才能发生电离C.江河入海口三角洲的形成与胶体的性质无关D.火灾现场有大量活泼金属时应使用干燥的沙土来灭火17.为除去括号内的杂质,所选用的试剂或方法错误的是A.气体(HCl),饱和溶液B.固体( ),加热至不再产生气体C.粉末( ),将混合物在氧气中加热D.溶液( ),导入足量的气体18.化学是一门以实验为基础的学科。
2024届浙江省金华市金华十校高三上学期一模英语试题

2024届浙江省金华市金华十校高三上学期一模英语试题一、听力选择题1.A.The man will have black coffee.B.The man has quitted coffee.C.The man is on a diet.D.The man only drinks milk.2. Who is the man?A.A studio designer.B.An oil painter.C.An exhibition host.3. What does the woman advise the man to do?A.Have a rest.B.See a doctor.C.Take exercise.4.A.She is keen on abstract paintings.B.She isn’t able to appreciate the paintings.C.She doesn’t like art history class.D.She has a better taste of art than the man.5. When will the man attend his class?A.On Friday.B.On Saturday.C.On Sunday.二、听力选择题6. 听下面一段较长对话,回答以下小题。
1. What is the man doing in Sydney?A.Traveling.B.Teaching.C.Studying.2. What kind of children is the woman trying to help?A.Who can’t see clearly.B.Who don’t know how to read.C.Who can’t understand what they read.3. What do we know about the course in Sydney?A.It costs less.B.It's well-organized.C.It finishes more quickly.7. 听下面一段较长对话,回答以下小题。
浙江省金华市金华第一中学2023-2024学年英语高三上期末学业水平测试模拟试题含解析

浙江省金华市金华第一中学2023-2024学年英语高三上期末学业水平测试模拟试题注意事项:1.答卷前,考生务必将自己的姓名、准考证号、考场号和座位号填写在试题卷和答题卡上。
用2B铅笔将试卷类型(B)填涂在答题卡相应位置上。
将条形码粘贴在答题卡右上角"条形码粘贴处"。
2.作答选择题时,选出每小题答案后,用2B铅笔把答题卡上对应题目选项的答案信息点涂黑;如需改动,用橡皮擦干净后,再选涂其他答案。
答案不能答在试题卷上。
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新答案;不准使用铅笔和涂改液。
不按以上要求作答无效。
4.考生必须保证答题卡的整洁。
考试结束后,请将本试卷和答题卡一并交回。
第一部分(共20小题,每小题1.5分,满分30分)1.I _____up my mind what I was going to say in the seminar, but it was cancelled. A.have made B.had madeC.was making D.would make2.—Could you check my list to see I have forgotten anything?—No problem.A.whether B.whichC.that D.what3.I really don’t know _________ she gets by on such a modest salary.A.what B.whyC.how D.that4.Adding to their happiness, he says,______ some similarities between the two test papers.A.is B.are C.has D.have5.The national park has a large collection of wildlife, ________ from butterflies to elephants.A.to range B.rangeC.ranging D.ranged6.________ has greater potential than flammable ice being mined from underneath the South China Sea when it comes to a global energy revolution.A.nothing B.neitherC.no one D.none7.--Mum, I don’t think I am qualified enough to do this.--Honey, be confident! You should know it is ____ a man thinks of himself ___ reallydetermines his fate.A.that; that B.how; that C.what; that D.how; that8.Why are some brands more popular than others ______ the products are of similar quality?A.as though B.even if C.so that D.in case9.Either side seems to have a(n) _________ position; there are still many uncertainties on this issue.A.ambiguous B.delicate C.explicit D.confidential10.Anna was in Inner Mongolia for two years, ____ as a volunteer teacher. A.having worked B.working C.worked D.to work 11.There are lots of examples of English idioms ________ animals are used. A.which B.whenC.whose D.where12.—Did you meet Mr. Smith?—Yes. When I arrived, he ________ for New York to attend a press conference. A.was just leaving B.just leftC.just leaves D.had just left13.— David is a green hand at such things.— But I believe he is quite ________ to the task.A.relevant B.accessibleC.equal D.unique14.His sister left home in 1998, and_________________ since.A.had not been heard of B.has not been heard ofC.had not heard of D.has not heard of15.________ children believe they can succeed, they will never become totally independent.A.If B.Since C.Unless D.Though16.At the meeting they discussed three different ________ to the study of mathematics. A.approaches B.meansC.methods D.ways17.—Do you know what EU stands for, Tommy?—Sure.It stands for the European Union,______ European political and economic organization that encourages trade and friendship between ______ countries that are members.A.an; the B.a; the C.the; / D.an; /18.The popularity of government posts has dropped in recent years, though the civilservice jobs are still favored by the Chinese as they offer a _______ stable career. A.relatively B.regularlyC.roughly D.rigidly19._______ many Chinese holidays are directed towards services remembering ancestors, the Ching Ming Festival is beyond doubt the largest.A.Unless B.SinceC.Once D.While20._______child will find his own personal road to success.A.Each B.The otherC.Either D.Another第二部分阅读理解(满分40分)阅读下列短文,从每题所给的A、B、C、D四个选项中,选出最佳选项。
浙江省金华市第一中学高三上学期10月月考语文试题(含解析)

浙江省金华市第一中学高三上学期10月月考语文试题(含解析)金华一中2024届高三10月月考语文试卷本试卷满分150分,考试时间150分钟。
一、现代文阅读(35分)(一)现代文阅读Ⅰ(本题共5小题,19分)阅读下面的文字,完成下面小题。
材料一:①老龄化,在当代具有全球性趋势;关爱老年人生活,是一个具有普遍意义的话题。
第四次中国城乡老年人生活状况抽样调查结果显示:我国老年人目前生活状况整体较好。
但本次调查对老年生活核心内容的语言生活仍缺少必要的关注。
语言生活,简而言之就是以语言文字为桥梁而展开的各种社会活动和个人活动。
语言生活的质量高低和优劣对于老年人的生存状况、生活品质、精神状态、心理健康、身心愉悦等都具有重要影响。
②为了解老年人的真实语言生活状况,笔者课题组于2022年8月在江西、广东、江苏、重庆等省市的30余个城市和农村展开调查,共收到有效问卷455份。
调查对象整体上是80岁以下、文化程度较低的老人。
③调查发现,部分老年人的语言生活存在一些较为明显的不足。
在语言能力方面,多数老年人在社交中不存在语言障碍,但仍有37%的老年人在家庭之外的人际交往中经常存在因方言差异等带来的语言不通问题。
在交际对象方面,老年人日常生活中的交流对象主要是中老年人,与中青年特别是青少年交流明显不够,83%的老年人很少与青少年交流,60%的老年人甚至与子女和孙辈的交流都比较少;70%的老年人表示与中年人交流有代沟,88%的老年人表示与青少年交流有代沟。
在说话时长和交流意愿方面,46%的老年人表示每天说话的时间比之前减少了,43%的老年人表示主动交流的意愿比之前降低了。
在网络交际方面,很多老年人会使用手机购物、查询信息、社交聊天、娱乐等,也有41%的受访老年人表示用手机只打电话,基本不会做别的事;会使用微信的老年人占47%,但会使用微博、邮箱等其他网络应用的老年人只占5%,88%的老年人还是习惯于使用电话进行联系和交际。
浙江省金华市2024-2025学年高三上学期一模考试数学试题

浙江省金华市2024-2025学年高三上学期一模考试数学试题一、单选题1.已知集合{}22M x x =-<<,{}1,0,1,2,3N =-,则M N = ()A .{}1,0,1-B .{}1,0,1,2-C .{}1,0-D .{}0,12.在复平面中,若复数z 满足1i 1z =-,则z =()A .2B .1CD 3.若,a b ∈R ,则a b =是22a b =的()A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件4.已知点F 为抛物线C :()220y px p =>的焦点,点()3,M m 在抛物线C 上,且4MF =,则抛物线C 的方程为()A .2y x=B .22y x=C .24y x=D .26y x=5.已知πtan 6α⎛⎫+= ⎪⎝⎭sin cos αα⋅=()A .14B C .12-D 6.已知函数()32f x x ax bx c =+++的部分图像如图所示,则以下可能成立的是()A .2a =,1b =B .1a =-,2b =C .2a =-,1b =D .2a =,1b =-7.某高中高三(15)班打算下周开展辩论赛活动,现有辩题A 、B 可供选择,每位学生都需根据自己的兴趣选取其中一个作为自己的辩题进行资料准备,已知该班的女生人数多于男生人数,经过统计,选辩题A 的人数多于选辩题B 的人数,则()A .选辩题A 的女生人数多于选辩题B 的男生人数B .选辩题A 的男生人数多于选辩题B 的男生人数C .选辩题A 的女生人数多于选辩题A 的男生人数D .选辩题A 的男生人数多于选辩题B 的女生人数8.已知正方体1111ABCD A B C D -的棱长为P 为正方体内部一动点,球O 为正方体内切球,过点P 作直线与球O 交于M ,N 两点,若OMN 的面积最大值为4,则满足条件的P 点形成的几何体体积为()A .32π3BC.16π3D.32π3二、多选题9.已知向量()3,4a = ,()4,b m =,则()A .5a = B .min 1ab -= C .若a b ∥,则3m =D .若a b ⊥,则3m =10.设函数()sin5sin cos xf x x x=⋅,则()A .()f x 的图象有对称轴B .()f x 是周期函数C .()f x 在区间π0,2⎛⎫⎪⎝⎭上单调递增D .()f x 的图象关于点π,02⎛⎫⎪⎝⎭中心对称三、单选题11.从棱长为1个单位长度的正四面体的一顶点A 出发,每次均随机沿一条棱行走1个单位长度,设行走n 次时恰好为第一次回到A 点的概率为()n P n +∈N ,恰好为第二次回到A 点的概率为()n Q n +∈N ,则()A .329P =B .4127Q =C .2n ≥时,1n nP P +为定值D .数列{}n Q 的最大项为427四、填空题12.已知数列{}n a 为等差数列,11a =,238a a +=,则6a =.13.从1,2,3,4,5,6这六个数中任选三个数,至少有两个数为相邻整数的选法有种14.已知双曲线C :221x y -=,Fl 与C 交于M ,N 两点,设点()11,M x y ,()22,N x y ,其中120x x >>,过M 且斜率为1-的直线与过N 且斜率为1的直线交于点T ,直线TF 交C 于A ,B 两点,且点T 为线段AB 的中点,则点T 的坐标为.五、解答题15.记ABC V 内角A ,B ,C 的对边分别为a ,b ,c ,已知()2cos cos c B A =.(1)求B ;(2)若ABC V 为等腰三角形且腰长为2,求ABC V 的底边长.16.如图,三棱锥A BCD -中,AD ⊥平面BCD ,AD DB DC BC ===,E 为AB 中点,M 为DE 中点,N 为DC 中点.(1)求证://MN 平面ABC ;(2)求直线DE 与平面ABC 所成角的正弦值.17.已知函数()()21ln 12f x x a x a x =-+-,()0a >.(1)若1a =,求()f x 的单调区间;(2)若()22e f x ≥-,求a 的取值范围.18.已知()2,0A 和B ⎛ ⎝⎭为椭圆C :()222210+=>>x y a b a b 上两点.(1)求椭圆C 的离心率;(2)过点()1,0-的直线l 与椭圆C 交于D ,E 两点(D ,E 不在x 轴上).(i )若ADE V,求直线l 的方程;(ii )直线AD 和AE 分别与y 轴交于M ,N 两点,求证:以MN 为直径的圆被x 轴截得的弦长为定值.19.已知正n 边形的每个顶点上有一个数.定义一个变换T ,其将正n 边形每个顶点上的数变换成相邻两个顶点上的数的平均数,比如:记n 个顶点上的n 个数顺时针排列依次为12,,,n a a a ⋅⋅⋅,则()112i i i a a T a -++=,i 为整数,21i n ≤≤-,()212n a a T a +=,()112n n a a T a -+=.设()()()()ni i T a T T T a =⋅⋅⋅(共n 个T ,表示n 次变换)(1)若4n =,i a i =,14i ≤≤,求()21T a ,()22T a ,()23T a ,()24T a ;(2)对于正n 边形,若()i i T a a =,1i n ≤≤,证明:121n n a a a a -==⋅⋅⋅==;(3)设42n k =+,k *∈N ,{}{}12,,,1,2,,n a a a n ⋅⋅⋅=⋅⋅⋅,证明:存在m *∈N ,使得()()1,2,,m i T a i n =⋅⋅⋅不全为整数.。
浙江省金华第一中学2023-2024学年高三上学期10月月考物理试题含答案

2023学年第一学期金华一中10月月考试题高三年级物理学科考生须知:1、本卷共8页,满分100分,考试时间90分钟;2、答题前,在答题卡指定区域填写学校、班级、姓名、考场号、座位号及准考证号;3、所有答案必须写在答题卡上,写在试卷上无效;4、考试结束后,只需上交答题卡。
第Ⅰ卷(选择题共45分)一、选择题Ⅰ(本题共13小题,每小题3分,共39分。
在每小题给出的四个选项中,只有一项是符合题目要求的,选对的得3分,选错的得0分)1. 日本政府拟向太平洋排放核废水引发国际社会的广泛关注与谴责。
辐射的危害程度常用“当量剂量”这一物理量衡量,其国际单位是希沃特,记作Sv。
每千克(kg)人体组织吸收1焦耳(J)为1希沃特。
下列选项中用国际单位制的基本单位表达希沃特,正确的是()A. m2/s2B. kg2·m2/s2C. J/kgD. m2/s2. 下列四幅图中包含的物理思想方法叙述错误的是()A. 图甲:库仑利用扭秤实验探究影响电荷间相互作用的因素时,运用了类比的思想B. 图乙:推导匀变速直线运动的位移公式时,运用了微元法C. 图丙:探究两个互成角度的力的合成规律时,运用了等效替代的方法D. 图丁:伽利略研究力和运动的关系时,运用了理想实验方法3. 关于下列四幅图中的仪器所涉及的物理学原理说法中正确的是( )A. 图甲,火灾报警器利用了烟雾颗粒对光的散射B. 图乙,雷达利用超声波来定位物体是C. 图丙,空间站上的机械臂处于完全失重状态,对载荷要求无限制D. 图丁,红外线体温计利用了物体温度越高,辐射波长越长的特点4. 如图所示,某同学正推着“擦窗神器”在竖直玻璃窗上匀速向上运动,推力的大小为F 、方向与竖直方向的夹角为()090αα︒<<︒,若“擦窗神器”受到的阻力与“擦窗神器”对窗的压力成正比,则下列说法正确的是( )A. “擦窗神器”受到8个力的作用B. “擦窗神器”对窗的压力与窗对“擦窗神器”的支持力是一对平衡力C. 窗对“擦窗神器”的摩擦力大小等于cos F αD. 若α角增大,则推力F 一定增大5. 图甲是学校提醒师生上下课的直流电铃。
2024-2025学年浙江省金华市高三上学期10月联考数学检测试卷(含解析)

2024-2025学年浙江省金华市高三上学期10月联考数学检测试卷考生注意:1.本试卷满分150分,考试时间120分钟.2.考生作答时,请将答案答在答题卡上.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑;非选择题请用直径0.5毫米黑色.墨水签字笔在答题卡上各题的答题区域内作答,超出答题区域书写的答案无效,在试题卷、草稿纸上作答无效.一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 已知集合,集合,则(){}2450A x x x =--<∣{}2,0,2,4,10B =-A B = A .B.{}2,0,2,4-{}2,10-C.D.{}0,2,4{}2,42. 已知,则()1i z =--()1i z -=A .B. 1D. 22-3. 已知非零向量,,则“”是“向量”的()a b a b a b +=- a b ⊥ A. 充分不必要条件 B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件4. 若过点与圆相切的两条直线的夹角为,则( )()224xy +=αcos α=A. B. D. 35455. 二项式的展开式中的常数项为( )622x x ⎛⎫+ ⎪⎝⎭A. 480B. 240C. 120D. 156. 已知底面半径为2的圆锥,其轴截面是正三角形,它的一个内接圆柱的底面半径为SO 1,则此圆柱侧面积与圆锥侧面积的比值为()SO A. 1D. 127. 函数在区间上的所有零点之和为( )()5πsin cos cos 24x f x x x ⎛⎫=-+ ⎪⎝⎭()π,2π-A .B. C. D. 4π2π3π8. 已知函数的定义域为,当或或是无理数时,;当()f x []0,10x =1x =x ()0f x =(,,是互质的正整数)时,.那么当,,,都n x m =n m <m n ()1f x m =a b a b +ab 属于时,下列选项恒成立的是()[]0,1A. B. ()()()f a b f a f b +≤+()()()f a b f a f b +≥⋅C.D.()()()f ab f a f b ≥+()()()f ab f a f b ≥⋅二、多项选择题:本大题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.9. 随机变量,分别服从正态分布和二项分布,且,,则(X Y ()2,1X N ()4,0.5Y B ~)A. B. ()()04P X P X ≤=≥()()04P Y P Y ≤=≥C.D.()()E X E Y =()()22P X P Y ≤=≤10. 在正四棱柱中,,点是棱上的动点(不含端点),1111ABCD A B C D -12AB AA =M 1DD 则()A. 过点有且仅有一条直线与直线,都垂直M AC 11B DB. 过点有且仅有一条直线与直线,都相交M AC 11B DC. 有且仅有一个点满足和的面积相等M MAC △11MB D D. 有且仅有一个点满足平面平面M MAC ⊥11MB D 11. 已知是曲线上的一点,则下列选项中正确的是( )()00,P x y 33:C x y y x +=-A. 曲线的图象关于原点对称C B. 对任意,直线与曲线有唯一交点0x ∈R 0x x =C PC. 对任意,恒有[]01,1y ∈-012x <D. 曲线在的部分与轴围成图形的面积小于C 11y -≤≤y π4三、填空题:本大题共3小题,每小题5分,共15分.12. 已知椭圆的左、右焦点分别为,,椭圆上一点满足,则22143x y +=1F 2F P 212PF F F ⊥线段__________.2PF =13. 已知曲线在处的切线恰好与曲线相切,则实数的值为e xy =1x =l ln y a x =+a ______.14. 数学老师在黑板上写上一个实数,然后老师抛掷一枚质地均匀的硬币,如果正面向上,0x 就将黑板上的数乘以再加上3得到,并将擦掉后将写在黑板上;如果反面向上,0x 2-1x 0x 1x 就将黑板上的数除以再减去3得到,也将擦掉后将写在黑板上.然后老师再抛0x 2-1x 0x 1x 掷一次硬币重复刚才的操作得到黑板上的数为.现已知的概率为0.5,则实数的2x 20x x >0x 取值范围是__________.四、解答题:本大题共5小题,共77分.解答应写出必要的文字说明、证明过程及演算步骤.15. 在中,角的对边分别为,,,已知,ABC V ,,A B C a b c 222c a b ab =++.()sin cos C B A-=(1)求角和角.C B (2)若边的面积.BC ABC V 16. 已知双曲线与过点,的直线有且只2222:1(0,0)x y C a b ab -=>>A⎫⎪⎭(0,B有一个公共点,且双曲线的离心率.T C e =(1)求直线和双曲线的方程;AB C (2)设,为双曲线的左、右焦点,为线段的中点,求证:1F 2F C M 2AF .21MTF TF A ∠=∠17. 如图,在四棱锥中,底面是菱形,,侧面是正三P ABCD -ABCD 60BAD ∠=PAD 角形,是棱的中点.M PC(1)证明:;AD DM ⊥(2)若二面角为,求直线与平面所成角的正弦值.P AD B --60oDM PAB 18. 已知函数.()()e xf x x a =-(1)若,求函数的单调区间和最值;2a =()f x (2)若,且一次函数的图象和曲线相切于处,求函数0a ≤()y g x =()y f x =1x =-的解析式并证明:恒成立.()g x ()()g x f x ≤(3)若,且函数在上有两个极值点,求实数的1a =()()()2h x f x t x x =--1,22x ⎛⎫∈ ⎪⎝⎭t 取值范围.19. 已知整数,数列是递增的整数数列,即4n …{}n a 且.数列满足,.若对于12,,,n a a a ∈Z12n a a a <<<{}n b 11b a =n n b a =,恒有等于同一个常数,则称数列为的“左型间隔数{}2,3,,1i n ∈- 1i i b a --k {}n b {}n a k 列”;若对于,恒有等于同一个常数,则称数列为的{}2,3,,1i n ∈- 1i i a b +-k {}n b {}n a “右型间隔数列”;若对于,恒有或者,则称数k {}2,3,,1i n ∈- 1i i a b k +-=1i i b a k --=列为的“左右型间隔数列”.{}n b {}n a k (1)写出数列的所有递增的“左右1型间隔数列”;{}:1,3,5,7,9n a (2)已知数列满足,数列是的“左型间隔数列”,数列{}n a ()81n a n n =-{}n b {}n a k 是的“右型间隔数列”,若,且有,求{}n c {}n a k 10n =1212n n b b b c c c +++=+++ 的值;k(3)数列是递增的整数数列,且,.若存在的一个递增的“右4型{}n a 10a =27a ={}n a 间隔数列”,使得对于任意的,都有,求的关于{}n b {},2,3,,1i j n ∈- i j i j a b b a +≠+n a 的最小值(即关于的最小值函数).n n ()f n 2024-2025学年浙江省金华市高三上学期10月联考数学检测试卷考生注意:1.本试卷满分150分,考试时间120分钟.2.考生作答时,请将答案答在答题卡上.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑;非选择题请用直径0.5毫米黑色.墨水签字笔在答题卡上各题的答题区域内作答,超出答题区域书写的答案无效,在试题卷、草稿纸上作答无效.一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 已知集合,集合,则(){}2450A x x x =--<∣{}2,0,2,4,10B =-A B = A. B. {}2,0,2,4-{}2,10-C.D.{}0,2,4{}2,4【正确答案】C【分析】先求出集合A ,后根据交集概念计算即可.【详解】因为,{15}A x x =-<<∣{}2,0,2,4,10B =-所以.{}0,2,4A B ⋂=故选:C .2. 已知,则()1i z =--()1i z -=A. B. 1D. 22-【正确答案】A【分析】根据复数的乘法运算即可求解.【详解】因为.()()()21i 1i 1i (i)12z -=---=--=-故选:A .3. 已知非零向量,,则“”是“向量”的()a b a b a b +=- a b ⊥ A. 充分不必要条件 B. 必要不充分条件C. 充要条件 D. 既不充分也不必要条件【正确答案】C【分析】根据充分条件、必要条件的定义及数量积的运算律判断即可.【详解】因为,为非零向量,ab 若,则,则,a b a b+=-()()22a ba b+=- 222222aa b b a a b b +⋅+=-⋅+ 所以,所以,故充分性成立;40a b ⋅= a b ⊥若,则,所以,a b ⊥ 0a b ⋅= 222222a a b b a a b b +⋅+=-⋅+ 所以,则,故必要性成立;()()22a ba b+=- a b a b+=- 所以“”是“向量”的充要条件.a b a b+=-a b ⊥故选:C .4. 若过点与圆相切的两条直线的夹角为,则( )()224xy+=αcos α=A. B.D. 3545【正确答案】A【分析】由题意求出点到圆心的距离为,进而可得,结合二倍角的余()d sin=2rd α弦公式计算即可求解.【详解】点到圆心的距离为,圆的半径为,()()0,0d =2r =所以,于是.sin 2r d α===223cos 12sin 1225αα=-=-=故选:A .5. 二项式的展开式中的常数项为( )622x x ⎛⎫+ ⎪⎝⎭A. 480 B. 240C. 120D. 15【正确答案】B【分析】运用通项公式计算即可.【详解】因为得到常数项,则.()621231662C C 2,rrrr r rr T xxx --+⎛⎫== ⎪⎝⎭4r =.246C 21516240=⨯=故选:B.6. 已知底面半径为2的圆锥,其轴截面是正三角形,它的一个内接圆柱的底面半径为SO 1,则此圆柱侧面积与圆锥侧面积的比值为()SO A. 1D.12【正确答案】C.【详解】作出轴截面,如图所示,由题意可得:,可知分别为的中点,4,2AB DE ==,D E ,SA SB 则分别为的中点,则,,M N ,OAOB 12DM SO ==可得;2πS ==圆柱侧面积π248πS =⨯⨯=圆锥侧面积故选:C .7. 函数在区间上的所有零点之和为( )()5πsin cos cos 24x f x x x ⎛⎫=-+ ⎪⎝⎭()π,2π-A. B. C. D. 4π2π3π【正确答案】B【分析】根据函数零点个数与其对应方程的根、函数图象的交点个数之间的关系,作出函数和的图象,利用数形结合的思想即可求解.5πcos 24x y ⎛⎫=+ ⎪⎝⎭tan y x =【详解】由得,即,()0f x =sin 5πcos cos 24x x x⎛⎫=+ ⎪⎝⎭5πtan cos 24x x ⎛⎫=+ ⎪⎝⎭函数的零点即方程的根,()f x 5πtan cos 24x x ⎛⎫=+ ⎪⎝⎭作出函数和的图象,如图,5πcos 24x y ⎛⎫=+ ⎪⎝⎭tan y x =由图可知两个图均关于中心对称且在上有两个交点,π,02⎛⎫ ⎪⎝⎭π,2π2⎛⎫⎪⎝⎭故函数在区间上有4个零点,所以4个零点的和为.()f x ()π,2π-2π故选:B .8. 已知函数的定义域为,当或或是无理数时,;当()f x []0,10x =1x =x ()0f x =(,,是互质的正整数)时,.那么当,,,都n x m =n m <m n ()1f x m =a b a b +ab 属于时,下列选项恒成立的是()[]0,1A. B. ()()()f a b f a f b +≤+()()()f a b f a f b +≥⋅C.D.()()()f ab f a f b ≥+()()()f ab f a f b ≥⋅【正确答案】D【分析】使用特值法可排除A,B,C,据,的取值可分类讨论证明D 正确.a b 【详解】当时,,,12a b ==()()=1=0f a b f +()11==44f ab f⎛⎫ ⎪⎝⎭,()()11==()22f a f b f =所以,,故排除B 、C ;()()()f a b f a f b +<⋅()()()f ab f a f b <⋅当,时,,,,18a =38b =()11==22f a b f ⎛⎫+ ⎪⎝⎭()11==88f a f ⎛⎫ ⎪⎝⎭()31==88f b f ⎛⎫ ⎪⎝⎭所以,故排除A .()()()f a b f a f b +>+下面证明D 的正确性:当,之一为无理数或者0或者1时,不等式右边为0,显然成立.a b 当,都是真分数时,不妨设,,a b n a m =q b p =则不等式右边为,显然有左边大于或等于.1mp 1mp 所以不等式成立.故选:D .二、多项选择题:本大题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.9. 随机变量,分别服从正态分布和二项分布,且,,则(X Y ()2,1X N ()4,0.5Y B ~)A .B. ()()04P X P X ≤=≥()()04P Y P Y ≤=≥C.D.()()E X E Y =()()22P X P Y ≤=≤【正确答案】ABC【分析】根据正态分布的性质和二项分布的性质计算即可.【详解】对A ,因为,根据对称性,知道,故A 正确;()2E X =对B ,因为,故B 正确;()()()()440411100C (()441622P Y P Y P Y P Y ≤=======≥对C ,因为,故C 正确;()()2,40.52E X E Y ==⨯=对D ,因为,,()122P X ≤=()004113222444111111112C (()C ()()C (()22222216P Y ≤=++=故D 错误.故选:ABC .10. 在正四棱柱中,,点是棱上的动点(不含端点),1111ABCD A B C D -12AB AA =M 1DD 则()A. 过点有且仅有一条直线与直线,都垂直M AC 11B DB. 过点有且仅有一条直线与直线,都相交M AC 11B DC. 有且仅有一个点满足和的面积相等M MAC △11MB D D. 有且仅有一个点满足平面平面M MAC ⊥11MB D 【正确答案】AB【分析】由空间线线、线面、面面的位置关系逐项判断即可.【详解】由图可知直线和直线异面,AC 11B D 则过空间中一点都是有且仅有一条直线与它们垂直,故A 正确;又易知与,都相交,且点在上,1DD AC 11B D M 1DD 所以过点有且仅有一条直线与直线,都相交,故B 正确;M AC 11B D 连接交于,易知,所以,BD AC O MA MC =MO AC ⊥可知到的距离大于,且,M AC DO 1AB A DO ==又到的距离小于,结合所以三角形面积不可能相等,故C 错误;M 11B D 1AA 11AC B D =由正四棱柱易得:平面,又平面,AC ⊥11MB D AC ⊂MAC 所以对任意恒有平面平面,故D 错误.M MAC ⊥11MB D 故选:AB.11. 已知是曲线上的一点,则下列选项中正确的是( )()00,P x y 33:C x y y x +=-A. 曲线的图象关于原点对称C B. 对任意,直线与曲线有唯一交点0x ∈R 0x x =C PC. 对任意,恒有[]01,1y ∈-012x <D. 曲线在的部分与轴围成图形的面积小于C 11y -≤≤y π4【正确答案】ACD【分析】将,替换为,计算即可判断A ;取,可判断有三个交点即可判断x y x -y -0x =B ;利用函数的单调性来得出的取值范围,再结合的单调性3y x x =-300y y -()3f x x x =+进行求解即可判断C ;利用图象的对称性和半圆的面积进行比较即可判断D .【详解】A .对于,将,替换为,,所得等式与原来等价,故A 33x y y x +=-x y x -y -正确;B .取,可以求得,,均可,故B 错误;0x =0y =1y =1y =-C .由,,函数,故,330000x x y y +=-[]01,1y ∈-3y x x =-213y x '=-令,解得:,在,时,,函数单调2130y x '=-=1x =1,x ⎡∈-⎢⎣⎤⎥⎦0'<y 递减,在时,,函数单调递增,所以,x ⎛∈ ⎝0'>y 300y y ⎡-∈⎢⎣又因为是增函数,,所以有,故C 正确;()3f x x x =+1528f ⎛⎫=> ⎪⎝⎭012x <D .当时,,又,[]00,1y ∈3300000x x y y +=-≥320002x x x +≥,所以.32000022y y y y -≤-22000x y y ≤-曲线与轴围成半圆,又曲线的图象关于原点对称,22x y y =-y C 则曲线与轴围成图形的面积小于,故D 正确.C y π4故选:ACD .三、填空题:本大题共3小题,每小题5分,共15分.12. 已知椭圆的左、右焦点分别为,,椭圆上一点满足,则22143x y +=1F 2F P 212PF F F ⊥线段__________.2PF =【正确答案】##32 1.5【分析】由已知可得点的横坐标为,代入椭圆方程即可求得点坐标,得出结果.P 1x =P 【详解】因为椭圆,则,所以,,22143xy +=2,1a b c ===()11,0F -()21,0F 因为,212PF F F ⊥所以点的横坐标为,代入求得纵坐标为,即.P 1x =32±232PF =故3213. 已知曲线在处的切线恰好与曲线相切,则实数的值为e xy =1x =l ln y a x =+a ______.【正确答案】2【分析】根据是曲线在处的切线求出的方程,再求出与曲线相l e xy =1x =l l ln y a x =+切的切点即可求解.【详解】由得,又切点为,故,切线为,e x y =e xy '=(1,e)e =k l e y x =设与曲线的切点为,,所以,解得切点为,l ln y a x =+()00,e x x 1y x '=01e x =1,1e ⎛⎫ ⎪⎝⎭所以,解得.1ln 11e a a +=-=2a =故2.14. 数学老师在黑板上写上一个实数,然后老师抛掷一枚质地均匀的硬币,如果正面向上,0x就将黑板上的数乘以再加上3得到,并将擦掉后将写在黑板上;如果反面向上,0x 2-1x 0x 1x 就将黑板上的数除以再减去3得到,也将擦掉后将写在黑板上.然后老师再抛0x 2-1x 0x 1x 掷一次硬币重复刚才的操作得到黑板上的数为.现已知的概率为0.5,则实数的2x 20x x >0x 取值范围是__________.【正确答案】()(),21,-∞-+∞ 【分析】构造函数,,由两次复合列出不等式求解即可.()23f x x =-+()32xg x =--【详解】由题意构造,,()23f x x =-+()32x g x =--则有,,,.()()43f f x x =-()()9f g x x =+()()92g f x x =-()()342x g g x =-因为,恒成立,()()f g x x>()()g f x x<又的概率为0.5,20x x >所以必有或者解得.43,3,42x x x x ->⎧⎪⎨-≤⎪⎩43,3,42x x x x -≤⎧⎪⎨->⎪⎩()(),21,x ∈-∞-⋃+∞故()(),21,-∞-+∞ 四、解答题:本大题共5小题,共77分.解答应写出必要的文字说明、证明过程及演算步骤.15. 在中,角的对边分别为,,,已知,ABC V ,,A B C a b c 222c a b ab =++.()sin cos C B A-=(1)求角和角.C B (2)若边的面积.BC ABC V 【正确答案】(1),2π3C =π4B =(2【分析】(1)根据余弦定理求出,再将化简为2π3C =()sin cos C B A -=,从而求出即可;2ππsin sin 36B B ⎛⎫⎛⎫-=+ ⎪ ⎪⎝⎭⎝⎭π4B =(2)根据边求出,,利用求解即可.BC 2b =c =1sin 2S bc A =【小问1详解】由余弦定理知,故.2221cos 22a b c C ab +-==-2π3C =因为,所以,()sin cos C B A -=2πππsin cos sin 336B B B ⎛⎫⎛⎫⎛⎫-=-=+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭又,所以,故.π03B <<2ππ36B B -=+π4B =【小问2详解】因为边上的高,解得,,BC sin sin h b C c B ===2b=c =又,()sin sin sin cos sin cos A B C BC C B =+=+=所以的面积.ABC V 1sin 2S bc A ==16. 已知双曲线与过点,的直线有且只2222:1(0,0)x y C a b a b -=>>A ⎫⎪⎭(0,B 有一个公共点,且双曲线的离心率.T C e =(1)求直线和双曲线的方程;AB C (2)设,为双曲线的左、右焦点,为线段的中点,求证:1F 2F C M 2AF .21MTF TF A ∠=∠【正确答案】(1),;:AB y =-2215y x -=(2)证明见解析【分析】(1)由离心率求出关系,并化简双曲线方程,再求出直线方程代入双曲线方程,a b 中,利用求解即可;Δ0=(2)求出点坐标,可进一步证明,进而证明.T 122F F T TF M ∽△△21MTF TF A ∠=∠【小问1详解】因为双曲线的离心率,e =所以,解得,2226a b a +=b =设双曲线方程.222215x y a a -=直线过点,,AB A ⎫⎪⎪⎭(0,B 所以直线,即,AB 1=:AB y =代入双曲线方程,得,22255x y a -=22220x a -+--=由题意,,解得()2Δ24820a =-+=21a =所以双曲线的方程:.C 2215y x -=【小问2详解】因为,于是即,21a =22220xa -+--=2230x -+=所以,代入x=y=y =则,又,所以,T 2F 224TF =因为为线段的中点,所以,M 2AF M ⎫⎪⎪⎭所以.222124F M F F F T ⋅===又,所以,故.122F F T TF M ∠=∠122F F T TF M ∽△△21MTF TF A∠=∠17. 如图,在四棱锥中,底面是菱形,,侧面是正三P ABCD -ABCD 60BAD ∠=PAD 角形,是棱的中点.M PC (1)证明:;AD DM ⊥(2)若二面角为,求直线与平面所成角的正弦值.P AD B --60oDM PAB 【正确答案】(1)证明见解析(2【分析】(1)取与中点,.连接,,,,证明四边形AD PB O N PO OB ON MN 是平行四边形.得到线面垂直,再用性质即可.ODMN (2)建立空间直角坐标系,求出平面的一个法向量为,再用向量夹角计算公式计算PAB n即可.【小问1详解】证明:分别取与中点,.连接,,,,AD PB O N PO OB ON MN 则运用中位线性质知且,则11//,22NM BC NM BC =11//,22OD BC OD BC =,//,OD MN OD MN =则四边形是平行四边形.ODMN 侧面是正三角形,易知,.PAD AD OP ⊥底面是菱形,,则底面是正三角形,则.ABCD 60BAD ∠=BAD AD OB ⊥平面, 平面,,,OP OB O OP OB =⊂ POB AD ∴⊥POB 平面,.ON ⊂ POB AD ON ∴⊥由于四边形是平行四边形.,.ODMN DM ON ∥AD DM ∴⊥【小问2详解】由(1)知为二面角的平面角,即,前面知道,POB ∠P AD B --60POB ∠=AD OB ⊥则过O 做AD 的垂线Oz ,以为坐标原点,为坐标轴,建立空间直角坐标系O ,,OA OB Oz 如图,O xyz -设,则,,,,,2AB =A (1,0,0)()1,0,0D-()C-()B 32P ⎛⎫⎪ ⎪⎝⎭,,,,34M ⎛⎫- ⎪ ⎪⎝⎭34DM ⎛⎫∴= ⎪ ⎪⎝⎭()AB =-32PB ⎛⎫=- ⎪ ⎪⎝⎭ 设平面的一个法向量为,PAB n =(x,y,z )则,进而求得一个法向量为.030x z ⎧-+=⎪-=()n = 设直线与平面所成角为,DM PAB α则.sin DM n DM n α⋅=== 18. 已知函数.()()e xf x x a =-(1)若,求函数的单调区间和最值;2a =()f x (2)若,且一次函数的图象和曲线相切于处,求函数0a ≤()y g x =()y f x =1x =-的解析式并证明:恒成立.()g x ()()g x f x ≤(3)若,且函数在上有两个极值点,求实数的1a =()()()2h x f x t x x =--1,22x ⎛⎫∈ ⎪⎝⎭t 取值范围.【正确答案】(1)单调递减区间为,单调递增区间为,最小值为,(),1-∞()1,+∞()1e f =-无最大值.(2),证明见解析()12e e a ag x x +=--(3).22e e,3⎛⎫⎪⎝⎭【分析】(1)利用导数与单调性的关系求解单调区间,再结合单调性求解最值即可;(2)根据导数的几何意义求出;令12()e e a ag x x +=--,利用导数求出最小值为即()()()()12e e e x a a u x f x g x x a x +=-=-++()u x ()10u -=可;(3)因为函数在上有两个极值点,所以()()()21e xh x x t x x =---1,22⎛⎫⎪⎝⎭在上有两个变号零点,分离参数得,求解直线()()e 21x h x x t x -'=-1,22⎛⎫ ⎪⎝⎭121e x x t x -=与函数在上的图象有两个交点即可.1y t =()21e x x H x x -=1,22⎛⎫⎪⎝⎭【小问1详解】因为,所以,定义域为,求导得,2a =()()2e x f x x =-R ()()1e xf x x -'=故当时,;当时,,(),1x ∞∈-f '(x )<0x ∈(1,+∞)f '(x )>0所以函数的单调递减区间为,单调递增区间为,()f x (),1∞-(1,+∞)所以最小值为,无最大值.()1ef =-【小问2详解】,所以,又,()()1exf x x a =-+'()1e a f '-=-()11e af +-=-所以,即;()()11e e a ag x x +=-+-12()e e a a g x x +=--令,()()()()12e e e x a a u x f x g x x a x +=-=-++则,,这里表示的导函数.()()1e e x au x x a =-++'()()2e xu x x a =-+''()u x ''()u x '令,则,()0u x ''=2=-x a 当变化时,与的变化情况如下表:x ()u x ''()u x 'x(),2a ∞--2a -()2,a ∞-+()u x ''-+()u x '单调递减2e ea a --+单调递增所以当时,函数有极小值,极小值为,也是最小值,2=-x a ()u x '2e e a a--+因为当时,无限趋向于,所以当时,,x →-∞()u x '0e a ≤2x a <-()0u x '<又,此时,在上单调递减,在上单调递增,()10u '-=()u x (),1∞--()1,∞-+所以,即不等式恒成立.()()10u x u ≥-=g (x )≤f (x )【小问3详解】因为函数在上有两个极值点,()()()21e xh x x t x x =---1,22⎛⎫ ⎪⎝⎭所以在上有两个变号零点,()h x '1,22⎛⎫⎪⎝⎭因为,令,即,()()e 21x h x x t x -'=-()0h x '=()e 210x x t x --=因为不是的根,所以,0x =()e 210xx t x --=121e x x t x -=令,则,()2112e 2x x H x x x -⎛⎫=<< ⎪⎝⎭()()()()()()222e 121e 121e e x xxxx x x x x H x x x -+--+==-'当时,;当时,,112x <<()0H x '>12x <<()0H x '<所以函数在上单调递增,在上单调递减,()H x (12,1)()1,2又,,,作出函数在上的图象,102H ⎛⎫= ⎪⎝⎭()11e H =()2322e H =()H x 1,22⎛⎫ ⎪⎝⎭当,即时,直线与函数在上的图象有两个交点,23112e e t <<22e e 3t <<1y t =()H x 1,22⎛⎫ ⎪⎝⎭设两个交点的横坐标分别为,且,12,x x 12x x <由图可知,当或时,,此时,112x x <<22x x <<121e x x t x ->()121e 0e x x x h x tx t x -⎛⎫- ⎝'=>⎪⎭当时,,此时,12x x x <<121e x x t x -<()121e 0e x x x h x tx t x -⎛⎫- ⎝'=<⎪⎭所以函数在上单调递增,在上单调递减,在上单调递增,ℎ(x )11,2x ⎛⎫ ⎪⎝⎭()12,x x ()2,2x 此时,函数有两个极值点,合乎题意.()f x 因此,实数的取值范围为.t 22e e,3⎛⎫⎪⎝⎭19. 已知整数,数列是递增的整数数列,即4n …{}n a 且.数列满足,.若对于12,,,n a a a ∈Z12n a a a <<<{}n b 11b a =n n b a =,恒有等于同一个常数,则称数列为的“左型间隔数{}2,3,,1i n ∈- 1i i b a --k {}n b {}n a k 列”;若对于,恒有等于同一个常数,则称数列为的{}2,3,,1i n ∈- 1i i a b +-k {}n b {}n a “右型间隔数列”;若对于,恒有或者,则称数k {}2,3,,1i n ∈- 1i i a b k +-=1i i b a k --=列为的“左右型间隔数列”.{}n b {}n a k (1)写出数列的所有递增的“左右1型间隔数列”;{}:1,3,5,7,9n a (2)已知数列满足,数列是的“左型间隔数列”,数列{}n a ()81n a n n =-{}n b {}n a k 是的“右型间隔数列”,若,且有,求{}n c {}n a k 10n =1212n n b b b c c c +++=+++ 的值;k (3)数列是递增的整数数列,且,.若存在的一个递增的“右4型{}n a 10a =27a ={}n a 间隔数列”,使得对于任意的,都有,求的关于{}n b {},2,3,,1i j n ∈- i j i j a b b a +≠+n a 的最小值(即关于的最小值函数).n n ()f n 【正确答案】(1)1,2,4,6,9或1,2,4,8,9或1,2,6,8,9或1,4,6,8,9. (2)80k =(3)()()382n n f n -=+【分析】(1)由“左右型间隔数列”的定义,求数列的所有递增的“左右1型k {}:1,3,5,7,9n a 间隔数列”;(2)根据“左型间隔数列”和“右型间隔数列”的定义,由k k,则有,代入通项计算即可;1212n n b b b c c c +++=+++ 1291016a a k a a ++=+(3)由“右4型间隔数列”的定义,有,可知,则144i i i b a a +=->-{}3i i b a n n -∈≥-∣有()()()232431n n n a a a a a a a a -=+-+-++- ,化简即可.()()()()413216n n ≥-+-+-+-++- 【小问1详解】数列的“左右1型间隔数列”为1,2,4,6,9或1,2,4,8,9或{}:1,3,5,7,9n a 1,2,6,8,9或1,4,6,8,9.【小问2详解】由,可得,12101210b b b c c c +++=+++ 239239b b b c c c +++=+++ 即,即,128341088a a a k a a a k ++++=+++- 1291016a a k a a ++=+即,所以.16168988109k +=⨯⨯+⨯⨯80k =【小问3详解】当时,由,可知.{}2,3,,1i n ∈- 144i i i b a a +=->-{}3i i b a n n -∈≥-∣又因为对任意,都有,{},2,3,,1i j n ∈- i j i ja b b a +≠+即当时,两两不相等.{}2,3,,1i n ∈- i i b a -因为()()()232431n n n a a a a a a a a -=+-+-++- ()()()2233117444n n b a b a b a --=++-++-+++- ()()()()223311742n n n b a b a b a --=+-+-+-++- ()()()()413216n n ≥-+-+-+-++- .()382n n -=+所以的最小值函数.n a ()()382n n f n -=+另外,当数列的通项{a n }()0,1,38,2,2i i a i i i n =⎧⎪=⎨-+≤≤⎪⎩间隔数列的通项时也符合题意.{b n }(),1,13,21,2i i a i i n b i i i n ==⎧⎪=⎨-+≤≤-⎪⎩或方法点睛:在实际解决“新定义”问题时,关键是正确提取新定义中的新概念、新公式、新性质、新模式等信息,确定新定义的名称或符号、概念、法则等,并进行信息再加工,寻求相近知识点,明确它们的共同点和不同点,探求解决方法,在此基础上进行知识转换,有效输出,合理归纳,结合相关的数学技巧与方法来分析与解决!。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
浙江省金华市金华第一中学2023-2024学年高三上学期10月月考地理试题本试卷分为第I 卷(选择题)和第Ⅱ卷(非选择题)两部分,共100分,考试时间90分钟。
考生须知:1. 本卷满分100分,考试时间90分钟;2. 答题前,在答题卷指定区域填写学校、班级、姓名、试场号、座位号及准考证号。
3. 所有答案必须写在答题纸上,写在试卷上无效;4. 考试结束后,只需上交答题卷。
第I卷一、选择题I(本大题共20小题,每小题2分,共40分。
每小题列出的四个备选项中只有一个是符合题目要求的,不选、多选、错选均不得分)下表是“我国四省谷物播种面积(单位:千公顷)统计数据(2019年)”,回答1-2题。
1.表中①②③④所示省的简称依次是A. 鄂、黑、鲁、皖B. 鄂、皖、鲁、黑C. 黑、皖、鄂、鲁D. 黑、鄂、皖、鲁2. 有关四省农业生产的叙述,正确的是A.①省谷物种植商品率高B.②省南部分布肥沃的红壤C.③省热量制约耕作条件D.④省主要油料作物为油菜我国某公路长500多千米,南北贯穿了多冰川的山脉,并跨越了多条河流。
公路南端海拔约1070米,为山前洪积平原上的绿洲。
该公路山区段每年9月底至次年5月底封路禁行。
据此3-4题。
3. 该公路山区段定期封路禁行主要是因为A. 洪水频发B. 路面积雪严重C. 泥石流多发D. 路面冻融沉降4. 该公路北端海拔约750米,其所处的自然带是A. 针叶林带B. 山地草原带C. 高寒草甸带D. 灌丛荒漠带南水北调东线工程是把长江的水调往北方的调水工程,调水线路主要为大运河。
读南水北调东线工程调水线路图,完成5-6题。
5.对南水北调东线工程及其可能带来的影响,叙述正确的是①可以解决华北平原的盐碱化问题②有利于改善丙地大运河航运条件③丙至戊段可以自流引水④可缓解戊地的用水紧张A.①②B.③④C.①③D.②④6.南水北调东线工程对长江可能带来的影响,叙述正确的是A.可提高社会对长江水质的关注B.可促使长江的泥沙向海洋输送C.可降低甲地咸水入侵发生的可能D.可改变长江口外海洋潮汐的规律下图为大西洋表层海水密度、大西洋表层海水盐度、全球海洋表层海水温度和全球海洋表层海水盐度随纬度的分布示意图。
完成7-8题。
7. 图中曲线表示全球海洋表层海水盐度的是A.①B.②C.③D.④8. 造成北纬60 °N 附近大西洋不同于全球海洋表层海水盐度的主要因素是A. 海域封闭B. 暖流流经C. 降水量大D. 河流补给澳大利亚地势低平地区,地下水位较高,盐分容易随地下水蒸发而上升到地表,造成盐碱危害。
科学家发现在南部小麦带(下图中阴影区)盐渍化农田上种植一种根系发达、吸水性强的盐生灌木滨藜,3~4年后,土壤盐分明显降低,并可在盐生灌木行间种植大麦、燕麦等作物,发展畜牧业。
完成9-10题。
9. 图中M 地土壤盐分含量最高时为A.1 月B.3 月C.7 月D.9 月10.种植滨藜能使土壤盐分明显降低的主要原因是A. 枝叶茂盛,减少土壤水分蒸发B. 降低地下水位,吸收土壤盐分C. 增加大气降水,稀释土壤盐分D. 根系较发达,增加土壤地下水若尔盖湿地位于青藏高原东北边缘,河曲发育,素有中国最美高寒湿地草原之称。
甲处为若尔盖湿地的位置,右图为该处地层剖面物质组成的示意图。
完成11-12题。
11.从水循环角度,若尔盖湿地形成的原因是①降水均匀,来水丰富②海拔较高,蒸发较弱③河道弯曲,排水不畅④冻土发育,不易下渗A ①②③ B.①②④ C.②③④ D.①②④12.下列说法正确的是A.古深湖相沉积层颜色有可能为红色B.该地层所反映的整体环境变化可能为湿-干-干C.风成沙层取小样研磨溶解于水后溶液可能成酸性D.古河床河漫滩相沉积层沉积物粒径最大,流速最快读“锋面气旋示意图”。
完成13-14题。
13. 下列关于图中锋面的说法,正确的是A. 北半球冷锋B. 南半球冷锋C. 北半球暖锋D. 南半球暖锋14. 图中四地天气状况,最可能的是A. 丁地气压高于丙地B. 甲地风力大于乙地C. 甲、丁正值晴朗天气D. 乙、丙正值阴雨天气2019年以来,江苏省各城市逐步放宽落户政策。
下图为江苏省2016-2021年常住人口自然增长率与人口机械增长率变化图。
据此完成15-16题。
15. 图示年份人口增长率最低的是A.2016 年B.2018 年C.2020 年D.2021 年16、针对图中反映的江苏省人口问题,可采取的措施是①减轻养育负担②消除性别歧视③延迟退休年龄④提高房价水平A.①②B.①③C.②④D.③④交通站点的净客流量为下车流量与上车流量之差。
某中学地理社团对某小城市(甲市) 高铁站的净客流量进行统计,该市与区域中心城市高铁车程约20分钟。
下图为同学们绘制的甲市高铁站部分时段月平均净客流量统计图。
完成17-18题。
17. 中心城市职能被分散到甲市的是A. 居住生活B. 工业生产C. 交通物流D. 商贸会展18. 导致图示人口流动的主要因素是A. 地形与交通B. 教育与文化C. 文化与环境D. 地价与交通我国某中学生发现,在房间的固定观测点上通过窗户可观察到每年二至日的日出,下图甲乙为该地二至日日出位置示意图。
完成19-20 题。
19. 该窗正对朝向A. 正南B. 正东C. 正北D. 正西20.该地甲乙两日日落地方时、正午太阳高度的大小为A. 日落地方时:甲<乙正午太阳高度:甲>乙B. 日落地方时;甲>乙正午太阳高度:甲<乙C. 日落地方时:甲<乙正午太阳高度:甲<乙D. 日落地方时:甲>乙正午太阳高度:甲>乙二、选择题Ⅱ(本大题共5题,每小题3分,共15分。
每小题列出的四个备选项中只有一个是符合题目要求的,不选、多选、错选均不得分。
)【错题】读某区域地质剖面示意图,完成21题。
21. 有关图中岩石叙述正确的是A. 岩石形成时间顺序是②①④⑤B.②主要由石英、云母、和长石组成C.⑤常含有化石且有层理构造D.④受高温高压变质形成片麻岩传统海洋牧场利用人工鱼礁营造特定鱼群的鱼类索饵场、育肥场,聚集渔业资源,无法满足鱼群产卵、育幼、越冬等完整生命周期的生境需求,不能实现渔业资源的再繁殖。
新型海洋牧场营造“三场一通道”生境体系,关注各种鱼类索饵场、产卵场、越冬场及其之间洄游通道等功能性生境场所的系统营造。
下图示意我国某新型海洋牧场黄姑鱼功能群及其“三场一通道”生境体系。
据此完成22-23题。
22. 建设新型海洋牧场的有利影响有①提升鱼类品质②修复鱼类环境③集约利用空间④保障渔业安全A.①②④B.①②③C.②③④D.①③④23. 对新型海洋牧场“三场一通道”生境体系建设影响最大的活动是A. 滨海旅游B. 海洋运输C. 制取海盐D. 潮汐发电伊拉克年平均降水量由南至北为100—500mm, 北部山区达700mm。
2018 年11月22 日至23日,一场特别强大的风暴在伊拉克北部和中部降下暴雨,由此引发的山洪造成重大人员伤亡。
下图为伊拉克地区示意图。
据此完成24-25题。
24.影响伊拉克降水量北多南少的主要因素是A.纬度位置B.大气环流C.地形因素D.海陆分布25.形成伊拉克此次洪水的主要原因是A.西风异常强劲B.准静止锋控制C.积雪大量融化D.气温急剧上升三、非选择题(本大题共3小题,共45分)26. 阅读材料,完成下列问题。
(13分)材料一:哈得孙湾是北冰洋伸入加拿大东北部内陆的大海湾,沿岸的丘吉尔港是加拿大重要的港口之一。
哈得孙湾南部是加拿大的南安大略省,该区人口集中,工农业发达。
材料二:北美局部地区示意图及南安大略地区气候资料表(降水:mm; 气温:℃)。
(1)简述南安大略地区的气候特征。
( 4 分)(2)A 地种植的主要粮食是,简析丘吉尔港形成的有利条件。
(4分)(3)巴芬岛是全球观测极光的绝佳地点。
简述极光的形成过程,并简析巴芬岛观测极的有利条件。
( 5 分)27.阅读图文材料,回答下列问题。
(12分)材料一;丰年虾广泛分布于陆地上的盐田或盐湖中,以藻类为食,营养价值极高。
丰年虾对温度、盐度及溶氧的要求极强,最佳生长温度为25℃~30℃,最佳生长盐度为30% -50%,溶氧则以接近饱和溶氧为佳。
主要栖于浅水区,喜砂泥底。
材料二:乌尔米耶湖位于亚洲西部的伊朗西北部阿塞拜疆地区巨大的中央低地的底部,海拔1275米,含盐分约为海水六倍,不适合鱼类生存,只有一种浮游生物——丰年虾资源丰富。
20世纪80年代后随着水产养殖业的快速发展,丰年虾产业规模不断缩小。
该湖水深春季为4-6米,夏季仅1-2米。
材料三:下图为乌尔米耶湖示意图。
(1)与夏季相比,乌尔米耶湖春季湖水更深,试分析原因(3分)。
(2)推测乌尔米耶湖丰年虾集中分布的区域并分析原因(3分)。
(3)说明20世纪80年代后乌尔米耶湖丰年虾产业规模不断缩小的原因(6分)。
28. 阅读材料,完成下列问题。
(20分)2023年是共建“一带一路”倡议提出10周年。
10年间,中国和中亚国家之间的水利合作项目为当地产业升级、民生改善提供了有力支撑。
如:西北农林科技大学与乌兹别克斯坦共建的中乌节水农业海外示范园于2022年建成,该示范园采用太阳能喷灌和智能水肥一体滴灌。
从信息采集、传输、决策到远程控制,实现灌溉和施肥的信息化、精准化和自动化。
通过智能水肥一体化灌溉设备,可使当地棉花产量提高50%,节水50%,投资减少40%。
图为乌兹别克斯坦位置图。
(1)分析中国选择在乌兹别克斯坦建节水农业海外示范园的地理背景(4分)。
(2)说明示范园采用太阳能喷灌机进行灌溉的原因(6分)。
(3)简析示范园采用智能水肥一体化滴灌后对棉花生产成本的影响(4分)。
(4)简述中乌在节水农业领域的合作对乌兹别克斯坦农业发展的促进作用(6分)。
