反比例函数(初三一轮复习)
2024年中考数学一轮复习-反比例函数K值与几何面积综合(解析版)
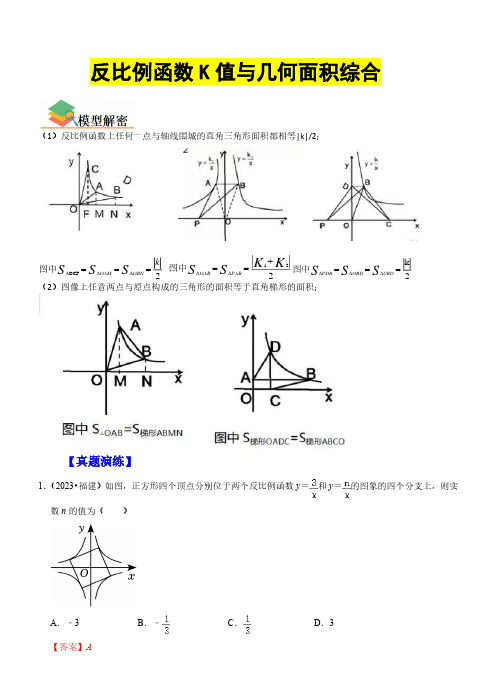
反比例函数K 值与几何面积综合(1)反比例函数上任何一点与轴线围城的直角三角形面积都相等|k|/2;2OCF k S S S OBN OAM ===∆∆∆图中 221K K S S PAB OAB +==∆∆图中2k ===∆∆∆S S S CBD OBD PDB 图中(2)图像上任意两点与原点构成的三角形的面积等于直角梯形的面积;【真题演练】 1.(2023•福建)如图,正方形四个顶点分别位于两个反比例函数y =和y =的图象的四个分支上,则实数n 的值为( )A .﹣3B .﹣C .D .3【答案】A【解答】解:连接正方形的对角线,由正方形的性质知对角线交于原点O,过点A,B分别作x轴的垂线.垂足分别为C、D,点B在函数y=上,如图:∵四边形是正方形,∴AO=BO,∠AOB=∠BDO=∠ACO=90°,∴∠CAO=90°﹣∠AOC=∠BOD,∴△AOC≌△BOD(AAS),∴S△AOC=S△OBD==,∵点A在第二象限,∴n=﹣3,故选:A.2.(2023•张家界)如图,矩形OABC的顶点A,C分别在y轴、x轴的正半轴上,点D在AB上,且AD=AB,反比例函数y=(k>0)的图象经过点D及矩形OABC的对称中心M,连接OD,OM,DM.若△ODM的面积为3,则k的值为()A.2B.3C.4D.5【答案】C【解答】解:解法一:∵四边形OCBA是矩形,∴AB=OC,OA=BC,设B点的坐标为(a,b),∵矩形OABC的对称中心M,∴延长OM恰好经过点B,M(,),∵点D在AB上,且AD=AB,∴D(,b),∴BD=a,∴S△BDM=BD•h=×a×(b﹣)=ab,∵D在反比例函数的图象上,∴ab=k,∵S△ODM=S△AOB﹣S△AOD﹣S△BDM=ab﹣k﹣ab=3,∴ab=16,∴k=ab=4,解法二:连接BM,因为点M是矩形的对称中心,∴三角形DMO的面积=三角形DMB的面积,则三角形DBO的面积为6,∵AD=1/4AB,∴AD:DB=1:3,∴三角形ADO的面积:三角形DBO的面积为1:3,即三角形ADO的面积为2,∴K=4.故选:C.3.(2023•黑龙江)如图,△ABC是等腰三角形,AB过原点O,底边BC∥x轴,双曲线y=过A,B两点,过点C作CD∥y轴交双曲线于点D.若S△BCD=12,则k的值是()A.﹣6B.﹣12C.﹣D.﹣9【答案】C【解答】解:设BC与y轴的交点为F,B(b,),则A(﹣b,﹣),b>0,由题意知,AO=BO,即O是线段AB的中点,过A作AE⊥BC于点E,∵AC=AB,AE⊥BC,∴BE=CE,AE∥y轴,∴CF=3BF=3b,∴C(﹣3b,),∴D(﹣3b,),∴CD=,BC=4b,∴S△BCD=,∴k=﹣.故选:C.4.(2023•宜宾)如图,在平面直角坐标系xOy中,点A、B分别在y、x轴上,BC⊥x轴,点M、N分别在线段BC、AC上,BM=CM,NC=2AN,反比例函数y=(x>0)的图象经过M、N两点,P为x轴正半轴上一点,且OP:BP=1:4,△APN的面积为3,则k的值为()A.B.C.D.【答案】B【解答】解:如图,过点N作NQ⊥x轴于点Q,过C作CT⊥y轴交y轴于T,交NQ于K,设OA=a,OP=b,BM=c,N(m,n),∵OP:BP=1:4,BM=CM,∴A(0,a),B(5b,0),M(5b,c),C(5b,2c),∵∠NCK=∠ACT,∠NKC=90°=∠ATC,∴△NKC∽△ATC,∴==,∵NC=2AN,∴CK=2TK,NK=AT,∴,解得,∴,∴,,∴,∵△APN的面积为3,∴S梯形OANQ﹣S△AOP﹣S△NPQ=3,∴,∴2ab+bc=9,将点M(5b,c),代入得:,整理得:2a=7c,将2a=7c代入2ab+bc=9得:7bc+bc=9,∴,∴,故选:B.5.(2022•日照)如图,矩形OABC与反比例函数y1=(k1是非零常数,x>0)的图象交于点M,N,与反比例函数y2=(k2是非零常数,x>0)的图象交于点B,连接OM,ON.若四边形OMBN的面积为3,则k1﹣k2=()A.3B.﹣3C.D.【答案】B【解答】解:∵y1、y2的图象均在第一象限,∴k1>0,k2>0,∵点M、N均在反比例函数y1=(k1是非零常数,x>0)的图象上,∴S△OAM=S△OCN=k1,∵矩形OABC的顶点B在反比例函数y2=(k2是非零常数,x>0)的图象上,∴S矩形OABC=k2,∴S四边形OMBN=S矩形OABC﹣S△OAM﹣S△OCN=3,∴k2﹣k1=3,∴k1﹣k2=﹣3,故选:B.6.(2022•郴州)如图,在函数y=(x>0)的图象上任取一点A,过点A作y轴的垂线交函数y=﹣(x <0)的图象于点B,连接OA,OB,则△AOB的面积是()A.3B.5C.6D.10【答案】B【解答】解:∵点A在函数y=(x>0)的图象上,∴S△AOC=×2=1,又∵点B在反比例函数y=﹣(x<0)的图象上,∴S△BOC=×8=4,∴S△AOB=S△AOC+S△BOC=1+4=5,故选:B.7.(2022•十堰)如图,正方形ABCD的顶点分别在反比例函数y=(k1>0)和y=(k2>0)的图象上.若BD∥y轴,点D的横坐标为3,则k1+k2=()A.36B.18C.12D.9【答案】B【解答】解:连接AC交BD于E,延长BD交x轴于F,连接OD、OB,如图:∵四边形ABCD是正方形,∴AE=BE=CE=DE,设AE=BE=CE=DE=m,D(3,a),∵BD∥y轴,∴B(3,a+2m),A(3+m,a+m),∵A,B都在反比例函数y=(k1>0)的图象上,∴k1=3(a+2m)=(3+m)(a+m),∵m≠0,∴m=3﹣a,∴B(3,6﹣a),∵B(3,6﹣a)在反比例函数y=(k1>0)的图象上,D(3,a)在y=(k2>0)的图象上,∴k1=3(6﹣a)=18﹣3a,k2=3a,∴k1+k2=18﹣3a+3a=18;故选:B.8.(2022•黑龙江)如图,在平面直角坐标系中,点O为坐标原点,平行四边形OBAD的顶点B在反比例函数y=的图象上,顶点A在反比例函数y=的图象上,顶点D在x轴的负半轴上.若平行四边形OBAD的面积是5,则k的值是()A.2B.1C.﹣1D.﹣2【答案】D【解答】解:设B(a,),∵四边形OBAD是平行四边形,∴AB∥DO,∴A(,),∴AB=a﹣,∵平行四边形OBAD的面积是5,∴(a﹣)=5,解得k=﹣2,故选:D.9.(2023•连云港)如图,矩形OABC的顶点A在反比例函数y=(x<0)的图象上,顶点B、C在第一象限,对角线AC∥x轴,交y轴于点D.若矩形OABC的面积是6,cos∠OAC=,则k=﹣.【答案】﹣.【解答】解:作AE⊥x轴于E,∵矩形OABC的面积是6,∴△AOC的面积是3,∵∠AOC=90°,cos∠OAC=,∴,∵对角线AC∥x轴,∴∠AOE=∠OAC,∵∠OEA=∠AOC=90°,∴△OEA∽△AOC,∴,∴,∴S△OEA=,∵S△OEA=|k|,k<0,∴k=﹣.故答案为:﹣.10.(2023•枣庄)如图,在反比例函数(x>0)的图象上有P1,P2,P3,…P2024等点,它们的横坐标依次为1,2,3,…,2024,分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为S1,S2,S3,…,S2023,则S1+S2+S3+…+S2023=.【答案】.【解答】解:∵P1,P2,P3,...P2024的横坐标依次为1,2,3, (2024)∴阴影矩形的一边长都为1,将除第一个矩形外的所有矩形向左平移至y轴,∴S 1+S2+S3+…+S2023=,把x=2024代入关系式得,y=,即OA=,∴S矩形OABC=OA•OC=,由几何意义得,=8,∴=8﹣=.故答案为:.11.(2023•朝阳)如图,点A是反比例函数y=(k≠0,x>0)的图象上一点,过点A作AB⊥x轴于点B,点P是y轴上任意一点,连接P A,PB.若△ABP的面积等于3,则k的值为.【答案】6.【解答】解:设反比例函数的解析式为y=,∵△AOB的面积=△ABP的面积=3,△AOB的面积=|k|,∴|k|=3,∴k=±6;又∵反比例函数的图象的一支位于第一象限,∴k>0.∴k=6.故答案为:6.12.(2023•衢州)如图,点A,B在x轴上,分别以OA,AB为边,在x轴上方作正方形OACD,ABEF,反比例函数y=(k>0)的图象分别交边CD,BE于点P,Q.作PM⊥x轴于点M,QN⊥y轴于点N.若OA=2AB,Q为BE的中点,且阴影部分面积等于6,则k的值为.【答案】见试题解答内容【解答】解:设OA=4a,∵AO=2AB,∴AB=2a,∴OB=AB+OA=6a,则B(6a,0),由于在正方形ABEF中,AB=BE=2a,∵Q为BE中点,∴BQ=AB=a,∴Q(6a,a),∵Q在反比例函数y=(k>0))上,∴k=6a×a=6a2,∵四边形OACD是正方形,∴C(4a,4a),∵P在CD上,∴P点纵坐标为4a,∵P在反比例函数y=(k>0)上,∴P点横坐标为:x=,∴P(,4a),∵作PM⊥x轴于点M,QN⊥y轴于点N,∴四边形OMNH是矩形,∴NH=,MH=a,∴S矩形OMHN=NH×MH=×a=6,则k=24,故答案为:24.13.(2023•锦州)如图,在平面直角坐标系中,△AOC的边OA在y轴上,点C在第一象限内,点B为AC 的中点,反比例函数y=(x>0)的图象经过B,C两点.若△AOC的面积是6,则k的值为.【答案】4.【解答】解:过点C作CD⊥y轴于点D,如图:设点C的坐标为(a,b),点A的坐标为(0,c),∴CD=a,OA=c,∵△AOC的面积是6,∴,∴ac=12,∵点C(a,b)在反比例函数(x>0)的图象上,∴k=ab,∵点B为AC的中点,∴点,∵点B在反比例函数(x>0)的图象上,∴,即:4k=a(b+c),∴4k=ab+ac,将ab=k,ac=12代入上式得:k=4.故答案为:4.14.(2023•黄石)如图,点A(a,)和B(b,)在反比例函数y=(k>0)的图象上,其中a>b>0.过点A作AC⊥x轴于点C,则△AOC的面积为;若△AOB的面积为,则=.【答案】,2.【解答】解:因为点A(a,)在反比例函数y=的图象上,则,又a>0,解得k=5.根据k的几何意义可知,.过点B作x轴的垂线,垂足为D,则S△OBD+S梯形ACDB=S△AOC+S△AOB,又根据k的几何意义可知,S△OBD=S△AOC,则S梯形ACDB=S△AOB.又△AOB的面积为,且A(a,),B(b,),所以,即.解得.又a>b>0,所以.故答案为:,2.15.(2023•辽宁)如图,矩形ABCD的边AB平行于x轴,反比例函数y=(x>0)的图象经过点B,D,对角线CA的延长线经过原点O,且AC=2AO,若矩形ABCD的面积是8,则k的值为6.【答案】6.【解答】解:如图,延长CD交y轴于E,连接OD,∵矩形ABCD的面积是8,∴S△ADC=4,∵AC=2AO,∴S△ADO=2,∵AD∥OE,∴△ACD∽△OCE,∴AD:OE=AC:OC=2:3,∴S△ODE=3,由几何意义得,=3,∵k>0,∴k=6,故答案为:6.16.(2023•绍兴)如图,在平面直角坐标系xOy中,函数(k为大于0的常数,x>0)图象上的两点A (x1,y1),B(x2,y2),满足x2=2x1,△ABC的边AC∥x轴,边BC∥y轴,若△OAB的面积为6,则△ABC的面积是.【答案】2.【解答】解:如图,延长CA交y轴于E,延长CB交x轴于点F,∴CE⊥y轴,CF⊥x轴,∴四边形OECF为矩形,∵x2=2x1,∴点A为CE的中点,由几何意义得,S△OAE=S△OBF,∴点B为CF的中点,∴S△OAB=S矩形OECF=6,∴S矩形OECF=16,∴S△ABC=×16=2.故答案为:2.217.(2022•烟台)如图,A,B是双曲线y=(x>0)上的两点,连接OA,OB.过点A作AC⊥x轴于点C,交OB于点D.若D为AC的中点,△AOD的面积为3,点B的坐标为(m,2),则m的值为.【答案】见试题解答内容【解答】解:因为D为AC的中点,△AOD的面积为3,所以△AOC的面积为6,所以k=12=2m.解得:m=6.故答案为:6.18.(2022•黄石)如图,反比例函数y=的图象经过矩形ABCD对角线的交点E和点A,点B、C在x轴上,△OCE的面积为6,则k=.【答案】8.【解答】解:如图,过点E作EH⊥BC于H,设点A(a,),C(c,0),∵点E是矩形ABCD的对角线的交点,∴E(,),∵点E在反比例函数y=的图象上,∴=k,∴c=3a,∵△OCE的面积为6,∴OC•EH=c•=×3a•=6,∴k=8,故答案为:8.19.(2022•衢州)如图,在△ABC中,边AB在x轴上,边AC交y轴于点E.反比例函数y=(x>0)的图象恰好经过点C,与边BC交于点D.若AE=CE,CD=2BD,S△ABC=6,则k=.【答案】.【解答】解:如图,作CM⊥AB于点M,DN⊥AB于点N,设C(m,),则OM=m,CM=,∵OE∥CM,AE=CE,∴==1,∴AO=m,∵DN∥CM,CD=2BD,∴===,∴DN=,∴D的纵坐标为,∴=,∴x=3m,即ON=3m,∴MN=2m,∴BN=m,∴AB=5m,∵S△ABC=6,∴5m•=6,∴k=.故答案为:.20.(2022•宜宾)如图,△OMN是边长为10的等边三角形,反比例函数y=(x>0)的图象与边MN、OM分别交于点A、B(点B不与点M重合).若AB⊥OM于点B,则k的值为.【答案】9.【解答】解:过点B作BC⊥x轴于点C,过点A作AD⊥x轴于点D,如图,∵△OMN是边长为10的等边三角形,∴OM=ON=MN=10,∠MON=∠M=∠MNO=60°设OC=b,则BC=,OB=2b,∴BM=OM﹣OB=10﹣2b,B(b,b),∵∠M=60°,AB⊥OM,∴AM=2BM=20﹣4b,∴AN=MN﹣AM=10﹣(20﹣4b)=4b﹣10,∵∠AND=60°,∴DN==2b﹣5,AD=AN=2b﹣5,∴OD=ON﹣DN=15﹣2b,∴A(15﹣2b,2b﹣5),∵A、B两点都在反比例函数y=(x>0)的图象上,∴k=(15﹣2b)(2b﹣5)=b•b,解得b=3或5,当b=5时,OB=2b=10,此时B与M重合,不符题意,舍去,∴b=3,∴k=b•b=9,故答案为:9.21.(2022•鄂尔多斯)如图,正方形OABC的顶点A、C分别在x轴和y轴上,E、F分别是边AB、OA上的点,且∠ECF=45°,将△ECF沿着CF翻折,点E落在x轴上的点D处.已知反比例函数y1=和y2=分别经过点B、点E,若S△COD=5,则k1﹣k2=.【答案】见试题解答内容【解答】解:作EH⊥y轴于点H,则四边形BCHE、AEHO都为矩形,∵∠ECF=45°,∴∠OCD+∠OCF=45°,∵∠DOC+∠OCF=45°,∴∠BCE=∠OCD,∵BC=OC,∠B=∠COD,∴△BCE≌△OCD(ASA),∴S△BCE=S△COD=5,∴S△CEH=5,S矩形BCHE=10,∴根据反比例函数系数k的几何意义得:k1﹣k2=S矩形BCHE=10,故答案为:10.22.(2022•东营)如图,△OAB是等腰直角三角形,直角顶点与坐标原点重合,若点B在反比例函数y=(x>0)的图象上,则经过点A的函数图象表达式为.【答案】y=﹣.【解答】解:如图,作AD⊥x轴于D,BC⊥x轴于C,∴∠ADO=∠BCO=90°,∵∠AOB=90°,∴∠AOD+∠BOC=90°,∴∠AOD+∠DAO=90°,∴∠BOC=∠DAO,∵OB=OA,∴△BOC≌△OAD(AAS),∵点B在反比例函数y=(x>0)的图象上,∴S△OBC=,∴S△OAD=,∴k=﹣1,∴经过点A的反比例函数解析式为y=﹣.故答案为:y=﹣.23.(2022•绍兴)如图,在平面直角坐标系xOy中,点A(0,4),B(3,4),将△ABO向右平移到△CDE 位置,A的对应点是C,O的对应点是E,函数y=(k≠0)的图象经过点C和DE的中点F,则k的值是.【答案】6.【解答】解:过点F作FG⊥x轴于点G,FH⊥y轴于点H,过点D作DQ⊥x轴于点Q,如图所示,根据题意可知,AC=OE=BD,设AC=OE=BD=a,∴四边形ACEO的面积为4a,∵F为DE的中点,FG⊥x轴,DQ⊥x轴,∴FG为△EDQ的中位线,∴FG=DQ=2,EG=EQ=,∴四边形HFGO的面积为2(a+),∴k=4a=2(a+),解得:a=,∴k=6.故答案为:6.24.(2022•内蒙古)如图,在平面直角坐标系中,Rt△OAB的直角顶点B在x轴的正半轴上,点O与原点重合,点A在第一象限,反比例函数y=(x>0)的图象经过OA的中点C,交AB于点D,连接CD.若△ACD的面积是1,则k的值是.【答案】.【解答】解:连接OD,过C作CE∥AB,交x轴于E,∵∠ABO=90°,反比例函数y=(x>0)的图象经过OA的中点C,∴S△COE=S△BOD=k,S△ACD=S△OCD=1,∵CE∥AB,∴△OCE∽△OAB,∴△OCE与△OAB得到面积比为1:4,∴4S△OCE=S△OAB,∴4×k=1+1+k,∴k=.故答案为:.。
2023年中考苏科版数学一轮复习专题练习-反比例函数

2023年中考数学一轮复习专题练习反比例函数一、选择题1. 已知反比例函数y =1x,下列结论不正确...的是( ) A .图象经过点(1,1) B .图象在第一. 三象限C. 当x >1时,0<y <1 D .当x <0时,y 随着x 的增大而增大2. 反比例函数)0(1>-=x xy 的图象如图所示,随着x 值的增大,y 值( ) A .增大 B .减小 C .不变 D .先增大后减小3. 在同一平面直角坐标系中,函数y =mx +m 与y =xm (m ≠0)的图象可能是( )A B C D4. 如图,A . B 两点在双曲线3yx上,分别经过A . B 两点向轴作垂线段,已知S 阴影=1,则S 1+S 2=( )A .3B .4C .5D .65. 如图,O 是坐标原点,菱形OABC 的顶点A 的坐标为(﹣3,4),顶点C 在x 轴的负半轴上,函数y=(x <0)的图象经过顶点B ,则k 的值为( )A .﹣12B .﹣27C .﹣32D .﹣36 6. 若点A (﹣5,y 1),B (﹣3,y 2),C (2,y 3)在反比例函数y=的图象上,则y 1,y 2,y 3的大小关系是( )A .y 1<y 2<y 3B .y 1<y 3<y 2C .y 2<y 1<y 3D .y 3<y 2<y 1二、填空题 第2题 第4题 第5题 第13题7. 已知函数y=(k+2)x是反比例函数,则k=.8. 如果反比例函数y=(k为常数)的图象在二. 四象限,那么k的取值范围是.9. 我们知道,一次函数y=x+1的图象可以由正比例函数y=x的图象向上平移1个长度单位得到.将函数y=的图象向平移个长度单位得到函数y=的图象.10. 三个完全相同的小球上分别标有数字﹣1. 2. 3,从这三个球中任意取出一个球,不放回,再取出一个,两次数据依次记为a. b,那么函数过二. 四象限的概率是.11. 已知正比例函数y=-4x与反比例函数的图象交于A. B两点,若点A的坐标为(x,4),则点B的坐标为______12. 直线y=kx(k>0)与双曲线y=交于A(x1,y1)和B(x2,y2)两点,则3x1y2﹣9x2y1的值为_____________.13. 如图,已知点P(6,3),过点P作PM⊥x轴于点M,PN⊥y轴于点N,反比例函数y=的图象交PM于点A,交PN于点B.若四边形OAPB的面积为12,则k=______________.三、解答题14. 将直线y=3x+1向下平移1个单位长度,得到直线y=3x+m,若反比例函数y=的图象与直线y=3x+m相交于点A,且点A的纵坐标是3.(1)求m和k的值;(2)结合图象求不等式3x+m>的解集.15. 如图,在平面直角坐标系中,OA⊥OB,AB⊥x轴于点C,点A(3,1)在反比例函数y=的图象上.(1)求反比例函数y=的表达式;(2)在x轴的负半轴上存在一点P,使得S△AOP=S△AOB,求点P的坐标;(3)若将△BOA绕点B按逆时针方向旋转60°得到△BDE.直接写出点E的坐标,并判断点E是否在该反比例函数的图象上,说明理由.16. 如图,在平面直角坐标系中A 点的坐标为(8,y ) ,AB ⊥x 轴于点B , sin ∠OAB =54,反比例函数xk y 的图象的一支经过AO 的中点C ,且与AB 交于点D. (1)求反比例函数解析式;(2)若函数y = 3x 与y = k x的图象的另一支交于点M ,求三角形OMB 与四边形OCDB 的面积的比.17. 如图,在直角坐标系中,Rt △ABC 的直角边AC 在x 轴上,∠ACB=90°,AC=1,反比例函数y=(k >0)的图象经过BC 边的中点D (3,1).(1)求这个反比例函数的表达式;(2)若△ABC 与△EFG 成中心对称,且△EFG 的边FG 在y 轴的正半轴上,点E 在这个函数的图象上.①求OF 的长;②连接AF ,BE ,证明四边形ABEF 是正方形.18. 如图,在平面直角坐标系中,▱ABCO的顶点A在x轴正半轴上,两条对角线相交于点D,双曲线y=(x>0)经过C,D两点.(1)求▱ABCO的面积.(2)若▱ABCO是菱形,请直接写出:①tan∠AOC=.②将菱形ABCO沿x轴向左平移,当点A与O点重合时停止,则平移距离t与y轴所扫过菱形的面积S之间的函数关系式:.。
2023年中考九年级数学一轮复习提升练习 综合题 :反比例函数

2023年中考九年级数学一轮复习提升练习(综合题):反比例函数一、综合题1.已知:如图1,函数y1=k x和y2=xk(k>1)的图象相交于点A和点B.(1)求点A和点B的坐标(用含k的式子表示);(2)如图2,点C的坐标为(1,k),点D是第一象限内函数y1的图象上的动点,且在点A的右侧,直线AC、BC、AD、BD分别与x轴相交于点E、F、G、H.①判定△CEF的形状,并说明理由;②点D在运动的过程中,∠CAD和∠CBD的度数和是否变化?如果变化,说明理由;如果不变,求出∠CAD和∠CBD的度数和.2.在平面直角坐标系中,我们把横坐标和纵坐标相等的点叫“梦之点”,例如点(1,1),(-2,-2),(√2,√2),…都是“梦之点”,显然“梦之点”有无数个.(1)若点P(2,m)是反比例函数y=nx(n为常数,n≠0)的图象上的“梦之点”,求这个反比例函数的解析式;(2)函数y=3kx+s-1(k,s为常数)的图象上存在“梦之点”吗?若存在,请求出“梦之点”的坐标,若不存在,说明理由.3.如图,点A是坐标原点,点D是反比例函数y=6x(x>0)图象上一点,点B在x轴上,AD=BD,四边形ABCD是平行四边形,BC交反比例函数y=6x(x>0)图象于点E.(1)平行四边形BCD 的面积等于 ;(2)设D 点横坐标为m ,试用m 表示点E 的坐标;(要有推理和计算过程) (3)求 CE:EB 的值; (4)求 EB 的最小值.4.如图,一次函数y=kx+b 的图象与反比例函数y= mx 的图象交于点A (﹣3,m+8),B (n ,﹣6)两点.(1)求一次函数与反比例函数的解析式; (2)求△AOB 的面积.5.已知双曲线y=1x(x >0),直线l 1:y ﹣√2=k (x ﹣√2)(k <0)过定点F 且与双曲线交于A ,B 两点,设A (x 1,y 1),B (x 2,y 2)(x 1<x 2),直线l 2:y=﹣x+√2. (1)若k=﹣1,求△OAB 的面积S ; (2)若AB=52√2,求k 的值;(3)设N (0,2√2),P 在双曲线上,M 在直线l 2上且PM△x 轴,求PM+PN 最小值,并求PM+PN 取得最小值时P 的坐标.(参考公式:在平面直角坐标系中,若A (x 1,y 1),B (x 2,y 2)则A ,B 两点间的距离为AB=√(x 1−x 2)2+(y 1−y 2)2)6.已知反比例函数y=1−2mx( m为常数)的图象在一、三象限.(1)求m的取值范围.(2)如图,若该反比例函数的图象经过▱ABCD的顶点D,点A,B的坐标分别为(0,3),(-2,0).①求出反比例函数表达式;②设点P是该反比例函数图象上的一点,若OD=OP,则P点的坐标为▲ .若以D,O,P为顶点的三角形是等腰三角形,则满足条件的点P的个数为▲ .7.绘制函数y=x+1x的图象,我们经历了如下过程:确定自变量x的取值范围是x≠0;列表﹣﹣描点﹣﹣连线,得到该函数的图象如图所示.x…-4-3-2-1−12−13−141413121234…y…−414−313−212−2−212−313−4144143132122212313414…观察函数图象,回答下列问题:(1)函数图象在第象限;(2)函数图象的对称性是A.既是轴对称图形,又是中心对称图形B.只是轴对称图形,不是中心对称图形C.不是轴对称图形,而是中心对称图形D.既不是轴对称图形,也不是中心对称图形(3)在x>0时,当x=时,函数y有最(大,小)值,且这个最值等于;在x<0时,当x=时,函数y有最(大,小)值,且这个最值等于;(4)方程x+1x=−2x+1是否有实数解?说明理由.8.菱形ABCD在平面直角坐标系中的位置如图所示,对角线AC与BD的交点E恰好在y轴上,过点D和BC的中点H的直线交AC于点F,线段DE,CD的长是方程x2﹣9x+18=0的两根,请解答下列问题:(1)求点D的坐标;(2)若反比例函数y= kx(k≠0)的图象经过点H,则k=;(3)点Q在直线BD上,在直线DH上是否存在点P,使以点F,C,P,Q为顶点的四边形是平行四边形?若存在,请直接写出点P的坐标;若不存在,请说明理由.9.设P(x,0)是x轴上的一个动点,它与原点的距离为y1.(1)求y1关于x的函数解析式,并画出这个函数的图象;(2)若反比例函数y2=k x的图象与函数y1的图象相交于点A,且点A的纵坐标为2.①求k的值;②结合图象,当y1>y2时,写出x的取值范围.10.受新冠肺炎疫情的影响,运城市某化工厂从2020年1月开始产量下降.借此机会,为了贯彻“发展循环经济,提高工厂效益”的绿色发展理念;管理人员对生产线进行为期5个月的升级改造,改造期间的月利润与时间成反比例函数;到5月底开始恢复全面生产后,工厂每月的利润都比前一个月增加10万元.设2020年1月为第1个月,第x个月的利润为y万元,其图象如图所示,试解决下列问题:(1)分别写出该化工厂对生产线进行升级改造前后,y与x的函数表达式.(2)到第几个月时,该化工厂月利润才能再次达到100万元?(3)当月利润少于50万元时,为该化工厂的资金紧张期,问该化工厂资金紧张期共有几个月?11.(如图,四边形ABCD在平面直角坐标系的第一象限内,其四个顶点分别在反比例函数y1=n x与y2=4n x的图象上,对角线AC△BD于点P,AC△x轴于点N(2,0)(1)若CN=12,试求n的值;(2)当n=2,点P是线段AC的中点时,试判断四边形ABCD的形状,并说明理由;(3)直线AB与y轴相交于E点.当四边形ABCD为正方形时,请求出OE的长度.12.如图点A、B分别在x,y轴上,点D在第一象限内,DC△x轴于点C,AO=CD=2,AB=DA= √5,反比例函数y= k x(k>0)的图象过CD的中点E.(1)求证:△AOB△△DCA;(2)求k的值;(3)△BFG和△DCA关于某点成中心对称,其中点F在y轴上,试判断点G是否在反比例函数的图象上,并说明理由.13.如图所示,一次函数y=kx+b的图象与x轴、y轴分别交于点A、B,且与反比例函数y=m x的图象在第二象限交于点C,CD⊥x轴,垂足为点D.若OB=2OA=3OD=12.(1)求一次函数与反比例函数的解析式;(2)若两函数图象的另一个交点为E,连结DE,求△CDE的面积;(3)直接写出不等式kx+b≤ mx的解集.14.某校九年级数学小组在课外活动中,研究了同一坐标系中两个反比例函数y1=k1x与y2=k2x(k2>k1>0)在第一象限图象的性质,经历了如下探究过程:操作猜想:(1)如图①,当k1=2,k2=6时,在y轴的正方向上取一点A作x轴的平行线交y1于点B,交y2于点C.当OA=1时,AB=,BC=,BCAB=;当OA=3时,AB=,BC=,BCAB=;当OA=a时,猜想BCAB=(2)在y轴的正方向上任意取点A作x轴的平行线,交y1于点B、交y2于点C,请用含k1、k2的式子表示BCAB的值,并利用图②加以证明.(3)如图③,若k2=12,BCAB=12,在y轴的正方向上分别取点A、D(OD>OA)作x轴的平行线,交y1于点B、E,交y2于点C、F,是否存在四边形ADFB是正方形?如果存在,求OA的长和点B的坐标;如果不存在,请说明理由.15.如图,直线y=2x+2与y轴交于A点,与反比例函数y=k x(x>0)的图象交于点M,过M 作MH△x轴于点H,且tan△AHO=2.(1)求H点的坐标及k的值;(2)点P在y轴上,使△AMP是以AM为腰的等腰三角形,请直接写出所有满足条件的P点坐标;(3)点N(a,1)是反比例函数y=kx(x>0)图象上的点,点Q(m,0)是x轴上的动点,当△MNQ的面积为3时,请求出所有满足条件的m的值.16.如图,双曲线y1=k1x与直线y2=xk2的图象交于A、B两点.已知点A的坐标为(4,1),点P(a,b)是双曲线y1=k1x上的任意一点,且0<a<4.(1)分别求出y1、y2的函数表达式;(2)连接PA、PB,得到△PAB,若4a=b,求三角形ABP的面积;(3)当点P在双曲线y1=k1x上运动时,设PB交x轴于点E,延长PA交x轴于点F,判断PE与PF的大小关系,并说明理由.答案解析部分1.【答案】(1)解:由题意,联立 {y =k x y =x k,解得 {x =k y =1 或 {x =−ky =−1 , ∵ 点 A 在第一象限,点 B 在第二象限,且 k >1 ,∴A(k ,1),B(−k ,−1)(2)解:①△CEF 是等腰直角三角形,理由如下: 设直线 BC 的解析式为 y =k 0x +b 0 ,将点 B(−k ,−1),C(1,k) 代入得: {−kk 0+b 0=−1k 0+b 0=k ,解得 {k 0=1b 0=k −1 , 则直线 BC 的解析式为 y =x +k −1 ,当 y =0 时, x +k −1=0 ,解得 x =1−k ,即 F(1−k ,0) , 同理可得:点 E 的坐标为 E(1+k ,0) , ∴CF =√(1−k −1)2+(0−k)2=√2k , CE =√(1+k −1)2+(0−k)2=√2k , EF =1+k −(1−k)=2k ,∴CE =CF ,CE 2+CF 2=4k 2=EF 2 , ∴△CEF 是等腰直角三角形;②由题意,设点 D 的坐标为 D(m ,k m ) ,则 m >k >1 , ∵△CEF 是等腰直角三角形, ∴∠CFE =∠CEF =45° , ∴∠BFH =∠AEG =135° ,设直线 BD 的解析式为 y =k 1x +b 1 ,将点 B(−k ,−1),D(m ,k m ) 代入得: {−kk 1+b 1=−1mk 1+b 1=k m ,解得 {k 1=1m b 1=k−m m, 则直线 BD 的解析式为 y =1m x +k−m m,当 y =0 时, 1m x +k−m m =0 ,解得 x =m −k ,即 H(m −k ,0) ,同理可得:点 G 的坐标为 G(k +m ,0) ,∴DH=√(m−k−m)2+(0−k m)2=k m√1+m2,DG=√(k+m−m)2+(0−k m)2=k m√1+m2,∴DH=DG,∴∠DHG=∠DGH,∵∠DHG=∠BHF,∴∠DGH=∠BHF,∴∠CAD+∠CBD=∠AEG+∠DGH+∠CBD,=∠BFH+∠BHF+∠CBD,=180°,即∠CAD与∠CBD的度数和不变,度数和为180°2.【答案】(1)解:根据题意,“梦之点”就是有关函数图象与直线y=x的交点,其坐标就是对应的方程组的解.由题意可得:m=2由点P(2, 2)在反比例函数y=nx图象上,可得n=2×2=4故所求的反比例函数的解析式为y=4 x(2)解:由题意可得:(△)当k=0时,y=s−1,此时“梦之点”的坐标为(s−1, s−1 ).(△)当k≠0 时, (3k−1)x=1−s显然,此方程的解的情况决定函数y=3kx+s−1的图象上“梦之点”的存在情况,当k=13, s≠1时,方程无解,不存在“梦之点”;当k=13, s=1时,方程有无数个解,此时存在无数个“梦之点”,“梦之点”的坐标可表示为(ℎ,ℎ)(ℎ为任意实数);当k≠13时,得{x=1−s3k−1y=1−s3k−1,即“梦之点”的坐标为(1−s3k−1, 1−s 3k−1)3.【答案】(1)12(2)解:由题意D(m,6 m),由(1)可知AB=2m,∵四边形ABCD是平行四边形,∴CD=AB=2m,∴C(3m,6 m).∵B(2m,0),C(3m,6 m),∴直线BC的解析式为y=6m2x−12m,由{y=6xy=6m2x−12m,解得{x=(√2+1)my=6√2−6m或{x=(1−√2)my=6(1+√2)m(舍弃),∴E((√2+1)m,6√2−6m);(3)解:作EF⊥x轴于F,CG⊥x轴于G. ∵EF//CG,∴CEBE=FGBF=√2+1)m(√2+1)m−2m=√2√2−1=√2;(4)解:∵CEBE=√2∴BE=√2+1,要使得BE最小,只要AD最小,∵AD=√m2+36m2=√(m−6m)2+12,∴AD的最小值为2√3,∴BE的最小值为2√3√2+1=2√6−2√3.4.【答案】(1)解:将A(﹣3,m+8)代入反比例函数y= mx得,m−3=m+8,解得m=﹣6,m+8=﹣6+8=2,所以,点A的坐标为(﹣3,2),反比例函数解析式为y=﹣6 x,将点B(n,﹣6)代入y=﹣6x得,﹣6n=﹣6,解得n=1,所以,点B 的坐标为(1,﹣6),将点A (﹣3,2),B (1,﹣6)代入y=kx+b 得, {−3k +b =2k +b =−6 , 解得 {k =−2b =−4,所以,一次函数解析式为y=﹣2x ﹣4; (2)解:设AB 与x 轴相交于点C , 令﹣2x ﹣4=0解得x=﹣2, 所以,点C 的坐标为(﹣2,0), 所以,OC=2, S △AOB =S △AOC +S △BOC , = 12 ×2×3+ 12 ×2×1, =3+1, =4.5.【答案】(1)解:当k=-1时,l 1:y=﹣x+2√2,联立得,{y =−x +2√2y =1x ,化简得x 2﹣2√2x+1=0, 解得:x 1=√2﹣1,x 2=√2+1,设直线l 1与y 轴交于点C ,则C (0,2√2). S △OAB =S △AOC ﹣S △BOC =12•2√2•(x 2﹣x 1)=2√2;(2)解:根据题意得:{y −√2=k(x −√2)y =1x 整理得:kx 2+√2(1﹣k )x ﹣1=0(k <0), ∵△=[√2(1﹣k )]2﹣4×k×(﹣1)=2(1+k 2)>0,∴x 1、x 2 是方程的两根,∴{x 1+x 2=√2(k−1)k x 1·x 2=−1k①, ∴AB=√(x 1−x 2)2+(y 1−y 2)2=√(x 1−x 2)2+(1x 1−1x 2)2=√(x 1−x 2)2(1+1x 12·x 22)=√[(x 1+x 2)2−4x 1x 2](1+1x 12·x 22),将①代入得,AB=√2(k 2+1)2k 2=√2(k 2+1)−k (k <0),∴√2(k 2+1)−k=5√22,整理得:2k 2+5k+2=0, 解得:k=﹣2,或 k=12;(3)解:∵直线l 1:y ﹣√2=k (x ﹣√2)(k <0)过定点F, ∴ F (√2,√2). 如图:设P (x ,1x ),则M (﹣1x +√2,1x),则PM=x+1x ﹣√2=√(x +1x −√2)2=√x 2+1x 2−2√2(x +1x )+4, ∵PF=√(x −√2)2+(1x −√2)2=√x 2+1x2−2√2(x +1x )+4, ∴PM=PF .∴PM+PN=PF+PN≥NF=2,当点P 在NF 上时等号成立,此时NF 的方程为y=﹣x+2√2,由(1)知P(√2﹣1,√2+1),∴当P(√2﹣1,√2+1)时,PM+PN最小值是2.6.【答案】(1)解:根据题意,得1−2m>0,解得m<12,∴m的取值范围是m<12.(2)解:①∵四边形ABCD是平行四边形,A(0,3),B(−2,0),∴D(2,3).把D(2,3)代入y=1−2mx,得3=1−2m2,∴1−2m=6 .∴反比例函数表达式为y=6x;②(3,2)或(-2,-3)或(-3,-2);4 7.【答案】(1)一、三(2)C(3)1;小;2;−1;大;−2(4)解:方程x+1x=﹣2x+1没有实数解,理由为:y=x+1x与y=﹣2x+1在同一直角坐标系中无交点.8.【答案】(1)解:x2﹣9x+18=0,(x﹣3)(x﹣6)=0,x=3或6,∵CD>DE,∴CD=6,DE=3,∵四边形ABCD是菱形,∴AC△BD,AE=EC= √62−32=3 √3,∴△DCA=30°,△EDC=60°,Rt△DEM中,△DEM=30°,∴DM= 12DE= 32,∵OM△AB,∴S菱形ABCD= 12AC•BD=CD•OM,∴12×6√3×6=6OM,OM=3 √3,∴D(﹣32,3 √3)(2)解:(3)解:如图1,①∵DC=BC,△DCB=60°,∴△DCB是等边三角形,∵H是BC的中点,∴DH△BC,∴当Q与B重合时,如图1,四边形CFQP是平行四边形,∵FC=FB,∴△FCB=△FBC=30°,∴△ABF=△ABC﹣△CBF=120°﹣30°=90°,∴AB△BF,CP△AB,Rt△ABF中,△FAB=30°,AB=6,∴FB=2 √3=CP,∴P(92,√3);②如图2,∵四边形QPFC是平行四边形,∴CQ△PH,由①知:PH△BC,∴CQ△BC,Rt△QBC中,BC=6,△QBC=60°,∴△BQC=30°,∴CQ=6 √3,连接QA,∵AE=EC,QE△AC,∴QA=QC=6 √3,∴△QAC=△QCA=60°,△CAB=30°,∴△QAB=90°,∴Q(﹣92,6 √3),由①知:F(32,2 √3),由F到C的平移规律可得P到Q的平移规律,则P(﹣92﹣3,6 √3﹣√3),即P(﹣152,5√3);③如图3,四边形CQFP是平行四边形,同理知:Q(﹣92,6 √3),F(32,2 √3),C(92,3 √3),∴P(212,﹣√3);综上所述,点P的坐标为:(92,√3)或(﹣152,5 √3)或(212,﹣√3).9.【答案】(1)解:由题意y1=|x|.函数图象如图所示:(2)解:①当点A在第一象限时,由题意A(2,2),∴2=k2,∴k=4.同法当点A在第二象限时,k=−4,②观察图象可知:当k>0时,x>2时,y1>y2或x<0时,y1>y2.当k<0时,x<−2时,y1>y2或x>0时,y1>y2.10.【答案】(1)解:由题意得,设前5个月中y= k x,把x=1,y=100代入得,k=100,∴y与x之间的函数关系式为y= 100x(0<x<5,且x为整数),把x=5代入,得y=20,由题意设5月份以后y与x的函数关系式为y=10x+b,把x=5,y=20代入得,20=10×5+b,解得:b=-30,∴y与x之间的函数关系式为y=10x-30(x>5且x为整数);(2)解:在函数y=10x−30中,令y=100,得10x−30=100解得:x=13答:到第13个月时,该化工厂月利润再次达到100万元.(3)解:在函数y=100x中,当y=50时,x=2,∵100>0,y随x的增大而减小,∴当y<50时,x>2在函数y=10x−30中,当y<50时,得10x−30<50解得:x<8∴2<x<8且x为整数;∴x可取3,4,5,6,7;共5个月.答:该化工厂资金紧张期共有5个月.11.【答案】(1)解:∵点N的坐标为(2,0),CN△x轴,且CN=12,∴点C的坐标为(2,1 2).∵点C在反比例函数y1=nx的图象上,∴n=2× 12=1.(2)解:四边形ABCD为菱形,理由如下:当n=2时,y1=nx=2x,y2=4nx=8x.当x=2时,y1=2x=1,y2=8x=4,∴点C的坐标为(2,1),点A的坐标为(2,4).∵点P是线段AC的中点,∴点P的坐标为(2,5 2).当y=52时,2x=52,8x=52,解得:x=45,x=165,∴点B的坐标为(45,52),点D的坐标为(165,52),∴BP=2﹣45=65,DP=165﹣2=65,∴BP=DP.又∵AP=CP,AC△BD,∴四边形ABCD为菱形.(3)解:∵四边形ABCD为正方形,∴AC=BD,且点P为线段AC及BD的中点.当x=2时,y1=12n,y2=2n,∴点A的坐标为(2,2n),点C的坐标为(2,12n),AC=32n,∴点P的坐标为(2,54 n).同理,点B的坐标为(45,54n),点D的坐标为(165,54n),BD=125.∵AC=BD,∴32n=125,∴n=8 5,∴点A的坐标为(2,165),点B的坐标为(45,2).设直线AB的解析式为y=kx+b(k≠0),将A(2,165),B(45,2)代入y=kx+b,得:{2k+b=16545k+b=2,解得:{b=65k=1,∴直线AB的解析式为y=x+ 6 5.当x=0时,y=x+ 65=65,∴点E的坐标为(0,6 5),∴当四边形ABCD为正方形时,OE的长度为6 5.12.【答案】(1)证明:∵点A、B分别在x,y轴上,点D在第一象限内,DC△x轴,∴△AOB=△DCA=90°,在Rt△AOB和Rt△DCA中,AO=CD,AB=DA∴Rt△AOB△Rt△DCA(HL)(2)解:在Rt△ACD中,CD=2,AD= √5,∴AC= =1,∴OC=OA+AC=2+1=3,∴D点坐标为(3,2),∵点E为CD的中点,∴点E的坐标为(3,1),k=3×1=3(3)解:点G在反比例函数的图象上.理由如下:∵△BFG和△DCA关于某点成中心对称,∴△BFG△△DCA,∴FG=CA=1,BF=DC=2,△BFG=△DCA=90°,而OB=AC=1,∴OF=OB+BF=1+2=3,∴G点坐标为(1,3),∵1×3=3,∴G(1,3)在反比例函数y= 的图象上13.【答案】(1)解:∵OB=2OA=3OD=12∴OA=6,OD=4∴A(6,0),B(0,12)把A(6,0),B(0,12)分别代入y=kx+b得:{6k+b=0b=12,解之得:m=−4×20=−80∴一次函数的解析式为y=−2x+12令x=−4,则y=20∴C(−4,20)把C(−4,20)代入y=mx得:m=−4×20=−80∴反比例函数的解析式为y=−80 x;(2)解:解方程组{y=−2x+12y=−80x得:{x1=−4y1=20,{x2=10y2=−8∴E(10,−8)∴SΔCDE=SΔADC+SΔADE=12AD⋅(CD+|y E|)=12×(4+6)×(20+8)=140(3)解:如图:当x<-4时,y=mx的图象在y=kx+b的下方,即kx+b>mx;当−4≤ x<0时,y=mx的图象在y=kx+b的上方,即kx+b≤mx;当0<x<10时,y=mx的图象在y=kx+b的下方,即kx+b>mx;当x≥10时,y=mx的图象在y=kx+b的上方,即kx+b≤mx;综上可得,不等式kx+b≤ mx的解集为−4≤ x<0或x≥10.14.【答案】(1)2;4;2;23;43;2;2 数学思考:(2)BCAB=k2−k1 k1证明:∵AB·OA=k1,AC·OA=k2,∴AC·OA−AB·OA=BC·OA=k2−k1,∴BCAB=BC·OAAB·OA=k2−k1k1.推广应用:(3)解:若四边形ADFB是正方形,设点B的坐标为(a,b)(a>0,b>0),则有DF=DA=AB=a,OA=b,OD=a+b,∴点F的坐标为(a,a+b).∵k2=12,BCAB=k2−k1k1=12,∴12−k1k1=12,解得:k1=8.∵点B在y=8x图象上,点F在y=12x图象上,∴ab=8,a (a+b)=12,∴a2=12−8=4,∴a=2,∴b=4,∴OA=4,点B的坐标为(2,4).15.【答案】(1)解:由y=2x+2可知A(0,2),即OA=2,∵tan△AHO=2,∴OH=1,∴H (1,0),∵MH△x轴,∴点M的横坐标为1,∵点M在直线y=2x+2上,∴点M的纵坐标为4,即M(1,4),∵点M在y=kx上,∴k=1×4=4;(2)解:①当AM=AP时,∵A(0,2),M(1,4),∴AM=√5,则AP=AM=√5,∴此时点P的坐标为(0,2﹣√5)或(0,2+ √5);②若AM=PM时,设P(0,y),则PM=√(1−0)2+(4−y)2,∴√(1−0)2+(4−y)2=√5,解得y=2(舍)或y=6,此时点P的坐标为(0,6),综上所述,点P的坐标为(0,6)或(0,2+ √5),或(0,2﹣√5);(3)解:∵点N(a,1)在反比例函数y=4x(x>0)图象上,∴a=4,∴点N(4,1),延长MN交x轴于点C,设直线MN的解析式为y=mx+n,则有{m+n=44m+n=1,,解得{m=−1n=5,∴直线MN的解析式为y=﹣x+5.∵点C是直线y=﹣x+5与x轴的交点,∴点C的坐标为(5,0),OC=5,∵S△MNQ=3,∴S△MNQ=S△MQC﹣S△NQC=12×QC×4﹣12×QC×1=32QC=3,∴QC=2,∵C(5,0),Q(m,0),∴|m﹣5|=2,∴m=7或3,故答案为7或3.16.【答案】(1)解:把点A(4,1)代入双曲线y1=k1x得k1=4,∴双曲线的解析式为y1=4x;把点A(4,1)代入直线y2=xk2得k2=4,∴直线的解析式为y2=14x(2)解:∵点P(a,b)在y1=4x的图象上,∴ab=4,∵4a=b,∴4a2=4,则a=±1,∵0<a<4,∴a=1,∴点P的坐标为(1,4),又∵双曲线y1=4x与直线y2=14x的图象交于A、B两点,且点A的坐标为(4,1),∴点B的坐标为(−4,−1),过点P作PG△y轴交AB于点G,如图所示,把x=1代入y2=14x,得到y=14,∴点G的坐标为(1,1 4),∴PG =4−14=154,∴S△ABP=12PG(x A−x B)=12×154×8=15(3)解:PE=PF.理由如下:∵点P(a,b)在y1=4x的图象上,∴b=4 a,∵点B的坐标为(−4,−1),设直线PB的表达式为y=mx+n,∴{am+n=4a−4m+n=−1,∴{m=1an=4a−1,∴直线PB的表达式为y=1a x+4a−1,当y=0时,x=a−4,∴E点的坐标为(a−4,0),同理:直线PA的表达式为y=−1a x+4a+1,当y=0时,x=a+4,∴F点的坐标为(a+4,0),过点P作PH△x轴于H,如图所示,∵P点坐标为(,∴H点的坐标为(a,0),∴EH =x H−x E=a−(a−4)=4,FH =x F−x H=a+4−a=4,∴EH=FH,∴PE=PF.。
九年级中考数学一轮复习教案:反比例函数复习精选全文

精选全文完整版(可编辑修改)《反比例函数》复习课简案【教学目标】1.熟练掌握反比例函数的定义,能应用其图像与性质解决相关问题,会用待定系数法求一次函数的表达式;2. 通过反比例函数知识的整理、归纳,感受数学思考过程的条理性,发展学生的收集、整理、小结、概括、运用的能力;3. 通过学生自主设计问题、教师引导的方式,提高学生自主分析问题、解决问题的能力,培养学生独立思考、合作交流的意识,提升学生学习数学的基本素养.【教学重难点】教学重点:能用反比例函数的图像与性质解决问题,会用待定系数法求反比例函数的表达式; 教学难点:能用反比例函数的知识解决综合问题,提高学生分析问题、解决问题的能力.【教学过程】一、 自主建构,梳理知识1、 反比例函数的定义:2、 反比例函数的图像:3、 反比例函数的图像特征:二、 自主设计,合作交流问题一:已知反比例函数的图像经过3(,4)2Q --(1)写出这个函数表达式;(2)若点Q (-1,m )在这个图像上,写出m 的值;(3)若P (-2,y 1) ,Q (3,y 2) 在这个图像上,你能比较y 1 ,y 2 的大小吗?(4)若P (x 1,y 1) , Q (x 2,y 2) 在这个图像上,且120x x <<,你还能比较y 1、y 2的大小吗?(5)如图,点P 是这个图像上任意一点,PA ⊥x 轴于点A ,PB ⊥y 轴于点B ,你能求出矩形OAPB 的面积吗?在第(5)问的基础上你还能提出哪些问题?一轮复习研讨课三、 变题研究,提高能力 变式1:如图,A 、B 两点在双曲线6y x =上,分别经过A 、B 两点向坐标轴作垂线段,已知S 阴影=1,则S 1+S 2= .变式2:如图,过点P (4,5)分别作PC ⊥x 轴于点C ,PD ⊥y 轴 于点D ,PC 、PD 分别交反比例函数6y x =(x >0)的图象于点 A 、B ,则四边形BOAP 的面积为 .变式3:如图,A 、B 是双曲线6y x=上的两点,过A 点作 AC⊥x 轴,交OB 于D 点,垂足为C.若D 为OB 的中点,则△ADO 的面积为 .四、总结反思,提升素养问题二:1、如图,直线y kx =与反比例函数6y x =的图像交于P 、Q 两点. (1)若P(1,6),你能说出点Q 的坐标吗?(2)在(1)的条件下,结合图像,你能写出方程6kx x =的解吗? 你能写出不等式6kx x >中x 的取值范围吗?2、已知A (3,2)、B (-2,﹣3)两点是一次函数y kx b =+ 和反比例函数m y x =图象的两个交点.(1)求一次函数和反比例函数的解析式;(2)求△AOB 的面积;(3)观察图象,直接写出不等式0m kx b x+->的解集.在这一学年中,不仅在业务能力上,还是在教育教学上都有了一定的提高。
中考一轮复习--第11讲 反比例函数及其应用

1
∴a=2,∴直线 OB 的函数表达式为 y=2x.
(2)如图,作 CD⊥OA 于点 D,∵C(1,2),
∴OC= 12 + 22 = 5.
在平行四边形 OABC 中,
CB=OA=3,AB=OC= 5,
∴四边形 OABC 的周长为 3+3+ 5 + 5
=6+2 5,
即四边形 OABC 的周长为 6+2 5.
动程序.若在水温为30 ℃时接通电源,水温y(℃)与时间x(min)的关
系如图所示.
(1)分别写出水温上升和下降阶段y与x之间的函数关系式;
(2)怡萱同学想喝高于50 ℃的水,请问她最多需要等待多长时间?
考法1
考法2
考法3
考法4
分析:(1)根据函数图象和题意可以求得y关于x的函数关系式,注意
函数图象是循环出现的;(2)根据(1)中的函数解析式可以解答本题.
(1)求k的值及直线OB的函数表达式;
(2)求四边形OABC的周长.
考法1
考法2
考法3
考法4
解:(1)依题意有:点 C(1,2)在反比例函数 y= (k≠0)的图象上,
∴k=xy=2.
∵A(3,0),∴CB=OA=3.又 CB∥x 轴,∴B(4,2).设直线 OB 的函数表达
式为 y=ax,∴2=4a,
考法1
考法2
考法3
考法4
反比例函数的图象和性质
例2(2019·江苏镇江)已知点A(-2,y1),B(-1,y2)都在反比例函数y=- 2
的图象上,则y1
y2.(填“>”或“<”)
答案:<
2
备战九年级中考数学一轮复习第12课 反比例函数(全国通用)

y y
3x 2 12
3
,
解得
x1 y1
4 3
,
x2 2
y2
6
x
∴B点坐标为(-4,-3),
对于一次函数y= 3 x+3, 2
当x=0时,y=3,即OC=3,
∴S△AOB=S△ACO+S△BCO
= 1 ×3×2+ 1 ×3×4
2
2
=9.
(3)两个函数的图象交于点A(2,6),B(-4,-3),
x 5 2m
,
令y=0,则x=5m,故点F(5m,0),
故FG=8m-5m=3m,而BD=4m-m=3m=FG,
又FG∥BD,故四边形BDFG为平行四边形.
19.(202X·怀化)如图,△OB1A1,△A1B2A2,△A2B3A3,…,
△An-1BnAn,都是一边在x轴上的等边三角形,点B1,B2, B3,…,Bn都在反比例函数y= 3 (x>0)的图象上,点A1,
A2,A3,…,An都在x轴上,则An的x 坐标为____2__n_,__0___.
20.(202X·温州)点P,Q,R在反比例函数y= k (常数k>0, x
x>0)图象上的位置如图所示,分别过这三个点作x轴、y轴的 平行线.图中所构成的阴影部分面积从左到右依次27为S1,S2, S3.若OE=ED=DC,S1+S3=27,则S2的值为____5____.
B.y2>y3>y1
C.y1>y3>y2
D.y3>
8.【例2】(202X·内江)如图,等边△OAB的边OA在x 轴上,反比例函数y= 6 的图象经过点B,则
x △OAB的面积为____6____.
9.(202X·抚顺)如图,在△ABC中,AB=AC,点A在反比例
2023年九年级中考数学一轮复习:反比例函数(含答案)

第三部分 一次函数与反比例函数模块二 反比例函数基础知识梳理考点1 反比例函数的图象 考点4 设参数来帮忙 考点2 比大小(增减性) 考点5 反比例与几何综合考点3面积不变性原理1.如果点A (-2,y 1),B (-1,y 2),C (2,y 3)都在反比例函数y =xk(k >0)的图象上,那么y 1,y 2,y 3的大小关系是( )A. y 1<y 3<y 2B. y 2< y 1 <y 3C. y 1<y 2<y 3D. y 3 <y 2 <y 12如图,已知一次函数y =kx - 4的图象与x 轴,y 轴分别交于A ,B 两点,与反比例函数y =x8在第一象限内的图象交于点C ,且A 为BC 的中点,则k =____________。
3.已知双曲线y =x 3和y =xk的部分图象如图所示,点C 是y 轴正半轴上一点,过点C 作AB ∥x 轴分别交两个图象于点A ,B ,若CB =2CA ,则k =____________。
4.如图,一次函数y = k x - 1的图象与x 轴交于点A ,与反比例函数y =x3(x >0)的图象交于B ,BC 垂直x 轴于点C ,若△ABC 的面积为1,则k 的值是___________。
5.如图,点B (3,3)在双曲线y =x k (x >0)上点D 在双曲线y =x4(x <0)上,点A 和点C 分别在x 轴,y 轴的正半轴上,且点A ,B ,C ,D 构成的四边形为正方形。
(1)求k 的值; (2)求点A 的坐标。
6.在同一平面直角坐标系中,函数y =x - 1与函数y =x1的图象可能是( )7.函数y 1=x 和y 2=x1的图象如图所示,则y 1>y 2的x 的取值范围是( ) A. x < - 1或 x >1 B. x < - 1或0 < x < 1 C. - 1 < x < 0 或 x > 1 D. - 1 < x < 0 或 0 < x < 18.如图,四边形ABCD 为菱形,已知A (0,4),B ( - 3,0) (1)求点D 的坐标;(2)求经过点C 的反比例函数解析式。
2024年中考数学一轮复习考点精讲课件—反比例函数的图象、性质及应用

其中,两个变量之间的函数关系可以用如图所示的图象表示的是( )
A.①②
B.①③
C.②③
D.①②③
【详解】解:由函数图象可知,这两个变量之间成反比例函数关系,
①矩形的面积= ⋅ ,因此矩形的面积一定时,一边长y与它的邻边x可以用形如 = ≠ 0 的式子表
示,即满足所给的函数图象;
②耕地面积= ⋅ ,因此耕地面积一定时,该村人均耕地面积S与全村总人口n可以用形如 =
这个函数图象上的点是(
)A. 1,6
1
B. − 2 , 12 ,
C. −2, −3
2
D.
3
,4
2
6
【对点训练1】(2019·吉林长春·中考模拟)如图,函数y=(x>0)、y=(x>0)的图象将第一象限分成了A、
B、C三个部分.下列各点中,在B部分的是( )
即:反比例函数的图象关于直线y=±x成轴对称,关于原点成中心对称.
反比例 待定系数法求反比例函数解析式的一般步骤:
函数解
析式的
确定方
法
k
1)设反比例函数的解析式为y = (k为常数,k≠0);
x
2)把已知的一对x,y的值带入解析式,得到一个关于待定系数k的方程;
3)解方程求出待定系数k;
4)将所求的k值代入所设解析式中.
【例3】(2022上·山东枣庄·九年级校考期末)已知函数 = ( + 1)
是
【详解】∵函数 = ( + 1)
.
2 −5
2 −5
是关于的反比例函数,则的值
是关于的反比例函数,
∴ + 1 ≠ 0,2 − 5 = −1,
∴ = ±2,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
反比例函数一、同步知识梳理知识点1:反比例函数的概念一般的,形如y=x k(k 不等于零的常数)的函数叫反比例函数。
反比例函数的解析式又可以写成:1,kxy k y kx x-===( k 是不等于零的常数), 知识点2:反比例函数的图象及性质(1)反比例函数的图象是两支曲线,且这两支曲线关于原点对称,这种图象通常称为双曲线。
它与x 轴和y 轴没有交点,它的两个分支无限接近坐标轴,但永远不能到达坐标轴. (2)反比例函数y=xk 图象的两个分支位居的象限与k 的正负有关, ① 当k>0时,函数的图象分布在第 一、三象限; (如下图) 函数的图象在每个象限内,曲线从左向右下降,也就是在每个象限内y 的值随x 的增加而 减小;②当k<0时,函数的图象分布在第 二、四 象限、函数的图象在每个象限内,曲线从左向右上升,也就是在每个象限内y 的值随x 的增大而增大。
(3)双曲线既是中心对称图形. 也是轴对称图形,它有两条对称轴,分别是一、三象限和二、四象限的角平分线知识点3:反比例函数中的比例系数k 的几何意义(1)反比例函数x k y =(0≠k )中比例系数k 的几何意义是:过双曲线xky = (0≠k )上任意引x 轴y 轴的垂线,所得矩形面积为k 。
(2)过反比例函数图象上的任意一点作 x 轴的垂线,那么这点与垂足、坐标系原点构成的三角形的面积是一个定值,即22xy k S ==。
知识点4: 反比例函数解析式的确定反比例函数解析式的确定只需确定k 值,需要一个点即可列出方程知识点5:反比例函数在实际问题中的应用在利用反比例函数解决实际问题中,一定要注意y=xk 中的k 不等于零这一条件,结合图像说出性质,根据性质画出图像,以及求函数表达式是必须牢牢记住的知识点二、同步题型分析题型1:反比例函数的概念、图像与性质例1:下列函数关系中,哪些是反比例函数?如果是,比例系数是多少?(1)x y 4=;(2)x y 21-=;(3)2x y =;(4)x y -=1(5)1=xy解:(1)是反比例函数,比例系数是4 (2)是反比例函数,比例系数是21-(3)不是(4)不是(5)是反比例函数,比例系数是1例2:已知函数xk k y )3(+=是反比例函数,则k 应满足的条件是( )A .3≠kB .3-≠kC .0≠k 或3≠kD .0≠k 且3-≠k解析:反比例函数xky =(0≠k ),所以(3)0k k +≠,即D .0≠k 且3-≠k 答案:D 变式:函数32-=x y 的自变量x 的取值范围是 . 总结:反比例函数的取值范围 一般地,函数y=kx(k 是常数,k ≠0)叫做反比例函数,x 的取值范围是x≠0,y 的取值范围是y≠0.例3:已知函数23)2(m xm y --=为反比例函数.(1)求m 的值;(2)它的图象在第几象限内?在各象限内,y 随x 的增大如何变化? (3)当-3≤x ≤21-时,求此函数的最大值和最小值.解:(1)(2)它的图象在第二,三象限内,在各象限内y 随x 的增大而增大(3)当-3≤x ≤21-时,由于在第二象限内y 随x 的增大而增大,所以y 大=8 y 小=34变式: 1.反比例函数1m y x-=的图象在第一、三象限,则m 的取值范围是 .答案:1m ≥ 2.函数y =1x-图象的大致形状是( )A B C D总结:反比例函数ky x=的图象是由两个分支组成的双曲线,图象的位置与比例系数k 的关系有如下两种情况:(1)0k >⇔双曲线的两个分支在第一、三象限 (2)0k <⇔双曲线的两个分支在第二、四象限 答案:D例4:已知函数24213m y m x-⎛⎫=+ ⎪⎝⎭是反比例函数,且在每一象限内,y 随x 增大而减小,求这个反比例函数答案:56y x=解析:因为函数是反比例函数,所以2421m -=-,解得12m =±,又因为函数y 随x增大而减小,所以103m +>,所以12m =,所以反比例函数为56y x =变式:1.关于反比例函数4y x=的图象,下列说法正确的是( )A .必经过点(1,1)B .两个分支分布在第二、四象限 答案:DC .两个分支关于x 轴成轴对称D .两个分支关于原点成中心对称2.反比例函数xk y 3-=的图象,当0>x 时,y 随x 的增大而增大,则k 的范围是( ).答案:B(A )k <3 (B )k ≤3 (C )k >3 (D )k ≥3 总结:反比例函数增减性、对称性1、当k >0时⇔在每一象限内,y 随x 的增大而减小; 当k <0时⇔在每一象限内,y 随x 的增大而增大.2、反比例函数关于原点对称,且关于直线y =x 和y =-x 对称。
题型2:反比例函数解析式的确定 例1:函数1k y x-=的图象经过点(1,3)A -,则k 的值为( ) A .4B .4-C .2D .2-答案:D例2:已知反比例函数xk y =的图象过点(1,-2). (1)求这个函数的解析式,并画出图象;(2)若点A (-5,m )在图象上,则点A 关于两坐标轴和原点的对称点是否还在图象上? 分析:(1) 反比例函数的图象过点(1,-2),即当x =1时,y =-2. 由待定系数法可求出反比例函数解析式;再根据解析式,通过列表、描点、连线可画出反比例函数的图象;(2)由点A 在反比例函数的图象上,易求出m 的值,再验证点A 关于两坐标轴和原点的对称点是否在图象上.解:(1)∵-2=1k∴k=-2 ∴xy 2-= 图略(2)点A (-5,m )在图象上 ∴-5m=-2 ∴m=52 点A 关于x ,y 两坐标轴和原点的对称点分别是 A 1(-5, -52);A 2(5, 52);A 3(5, -52) 由k=-2得,A 1 ;A 2不在图像上。
A 3在图像上变式:若反比例函数ky x=的图象经过点(-1,2),则这个反比例函数的图象一定经过点( ) A 、(2,-1) B 、(12-,2) C 、(-2,-1) D 、(12,2)分析:由反比例函数解析式判断点是否在图像上. 答案:A例3:已知y 与 2x 成反比例,且当x =3时,y =61,那么当x =2时,y =_________,当y =2时,x =_________.答案:14y =, 14x = 题型3:反比例函数K 的几何意义 例1:如图,过反比例函数图象上任意两点A 、B 分别作x 轴的垂线,垂足分别为C 、D ,连结OA 、OB ,设AC 与OB 的交点为E , 与梯形ECDB 的面积分别为,比较它们的大小,可得( ) A.B. C. D. 大小关系不能确定分析:由反比例的几何性质可得,S AOC S BOD =,又1S S AOC S EOC =-,2S S BOD S EOC =-所以,答案:B例2: 如图:点A 在双曲线ky x=上,AB ⊥x 轴于B ,且△AOB 的面积S △AOB=2,则k =______.分析:由反比例的几何性质可得22xy kS ==,即4k =,4k =±,又反比例函数图象过二、四象限,所以4k =-。
例3:如图,A 、B 是函数2y x=的图象上关于原点对称的任意两点,BC ∥x 轴,AC ∥y 轴,△ABC 的面积记为S ,则( )A . 2S =B . 4S= C .24S << D .4S >分析:由反比例的中心对称性质,运用图形割补法,可把△ABC 转化为一个矩形,再由几何性质即可求解。
答案:A题型4:反比例函数的简单应用 例1:如图,点A 、B 在反比例函数k y x=的图象上,且点A 、B 的横坐标分别为,2a a (0)a >,AC ⊥x 轴,垂足为C ,且2AOC S ∆=,(1)求该反比例函数的解析式;(2)若点1(,)a y -、2(2,)a y -在该反比例函数的图象上,试比较1y 、2y 的大小;(3)求△AOB 的面积答案:(1)4yx=;(2)12y y<;(3)3解析:(1)因为2AOCS∆=,所以4k=,所以反比例函数的解析式为4yx=;(2)若点1(,)a y-、2(2,)a y-在该反比例函数的图象上,而且0a>,所以2a a->-,又因为0k>,所以y随x的增大而减小,所以12y y<;(3)把A、B两点横坐标代入到反比例函数的解析式中可以得到442yaya⎧=⎪⎪⎨⎪=⎪⎩,所以得到A、B两点坐标分别为4(,)aa、2(2,)aa,所以CD a=,于是△AOB的面积等于△AOC的面积加上四边形ABCD 的面积减去△OBD的面积,所以△AOB的面积1423()332aa a++⋅-=例2:如图,Rt△AOB的顶点A是直线(1)y x m=+-与双曲线myx=在第一象限内的一个交点,且3AOBS∆=,直线(1)y x m=+-与x轴的交点为C,(1)求m的值;(2)求△ACB的面积答案:(1)6m=;(2)18解析:(1)因为3AOBS∆=,所以6AB OB⋅=,所以6m=;(2)因为6m=,所以直线解析式为5y x=+,所以直线与x轴的交点为C为(5,0)-并且联立直线双曲线解析式可以得到交点A 的坐标为(1,6),所以△ACB 的面积等于11661822AB BC ⋅=⨯⨯= 例3:(2008广州中考22题)如图8,一次函数y kx b =+的图象与反比例函数my x=的图象相交于A 、B 两点(1)根据图象,分别写出A 、B 的坐标; (2)求出两函数解析式;(3)根据图象回答:当x 为何值时,一次函数的函数值大于反比例函数的函数值答案:(1)y =0.5x +1,y =x12(2)-6<x <0或x >4 变式:如图,一次函数y kx b =+的图象与反比例函数m y x=的图象交于A 、B 两点,(1)利用图中条件,求反比例函数和一次函数的解析式;(2)根据图象写出使一次函数的值大于反比例函数值的x 的取值范围答案:(1)2y x =-;1y x =--;(2)2x <-或01x <<解析:(1)因为A 、B 两点的坐标分别为(2,1)-和(1,)n ,所以先把(2,1)-代入到反比例函数的解析式中得到2m =-,于是反比例函数的解析式为2y x=-,再把(1,)n 代入到反比例函数解析式中,可以得到2n =-,所以B 点坐标为(1,2)-,再把A 、B 两点坐标代入到一次函数的解析式中,得到212k b k b -+=⎧⎨+=-⎩,所以解得11k b =-⎧⎨=-⎩,所以一次函数解析式为1y x =--; (2)根据图象,一次函数的值大于反比例函数的值的图象为第三象限A 点左侧和第四象限B 点左侧部分,所以2x <-或01x <<三、课堂达标检测1.(1)已知反比例函数21m y x-=的图象在一,三象限,那么m的取值范围是______________。
