齿轮啮合原理-第四章
机械设计基础 第4章齿轮机构(4-56)讲解
刀具刀号的选择——按被加工齿轮的m、α、z 。
这种切齿方法简单,不需要专用机床,但生产率低、精度差, 故仅适用于单件生产及精度要求不高的场合。
2、拉刀(broaching tool)拉齿
拉刀拉齿主要用来拉削内齿轮,拉刀的形状与齿轮齿 槽形状相同。因拉刀的制造成本高,故它适用于批量生产 的情况。
2、切削过程中的运动(以插齿为例) 1)范成运动
齿条插刀:刀具的节线与被加工齿轮齿坯的分度圆相 切并作纯滚动的运动——刀具移动v =ωr = ωm z / 2。
齿轮插刀:刀具的节圆与齿坯节圆相切并作纯滚动的 运动—— i =ω0 /ω= z /z0)
2)切削运动(↑↓):刀具沿齿轮毛坯轴向的切齿运动。 3)让刀运动(←→):插齿刀具返回时,为避免擦伤已
∵ 分度圆与中线作纯滚动,且刀具分度线上s=e=πm/2;
∴ 切出的齿轮: s=e=πm/2;
ቤተ መጻሕፍቲ ባይዱ
1
ω1
∴ 被切的齿轮
是标准齿轮。 ra1r1'==r1
rb1
h a* m
N1
α '=α
P V2
N 2∞
2 )切制非标准齿轮时,刀具的加工节线与被加工齿轮的 分度圆相切,刀具的加工节线与中线不重合。
∵ 刀具的加工节线上s≠e; ∴ 被切的齿轮是非标准齿轮。
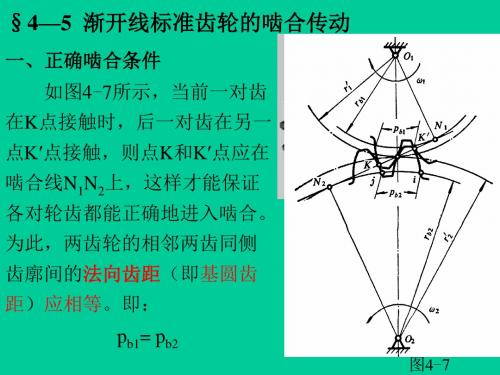
§4—5 渐开线标准齿轮的啮合传动
一、正确啮合条件 如图4-7所示,当前一对齿
在K点接触时,后一对齿在另一 点K′点接触,则点K和K′点应在 啮合线N1N2上,这样才能保证 各对轮齿都能正确地进入啮合。 为此,两齿轮的相邻两齿同侧 齿廓间的法向齿距(即基圆齿 距)应相等。即:
机械基础实验4 齿轮啮合及加工原理

3 4
5
加工Z<Zmin的齿轮而不产生根切的最小移距(变位系数)为 Xmin=(17-Z)/17
(1) 计算被加工标准齿轮的d、db、xmin、da、df,被加 工变位齿轮的da、df。 (2)将“轮坯”安装到仪器的圆盘上,注意必须要对准中 心。 (3)加工标准齿轮: 调节刀具位置:使刀具中线与被加工标准齿轮分度园相切。 “切削”齿廓:先将齿条刀具移向一端,使刀具的齿廓退 出轮坯齿顶圆,刀具每次向另一端移动2~3mm时,用笔将刀 刃在轮坯上的位置记录下来,直到形成完整的齿形,同时应 注意轮坯上齿廓形成的过程。 (4)加工变位齿轮: 调节刀具位置:使刀具中线远离轮坯中心,移动mxmin距离。 “切制”齿廓:同上。 (5)观察根切现象、比较标准齿轮和变位齿轮的异同点。
1. 范成运动:刀具节圆/中线与被加工轮坯节圆作纯滚动。 2. 切削运动:刀具沿轮坯轴线方向作往复运动。 3. 进给运动:为切出齿全高,刀具沿轮坯径向方向运动。 4. 让刀运动:插刀回程时,轮坯沿径向作微让运动,以免刀刃擦伤已形 成的齿面。
齿轮插刀
齿条插刀
● 蜗杆滚刀加工齿轮
滚刀象具有梯形螺纹的螺杆,其纵向开有斜槽而形成 刀刃。加工时,滚刀轴线与轮坯端面间应有一个安装角。 加工直齿圆柱齿轮时,其安装角为,加工斜齿圆柱齿轮 时,根据斜齿轮螺旋角作相应调整。滚刀加工齿轮无须 让刀运动,将范成运动、切削运动、进给运动溶为一体, 具有高的效率。在现代齿轮加工中,是应用最为广泛的齿 轮加工方法。
仿形法加工齿轮
仿形法加工齿轮的三个运动: 1. 切削运动(刀具饶自身轴线回转) 2. 进给运动(轮坯沿轴线方向运动) 3. 分度运动(加工好一个齿槽后,轮坯转过360°/Z)
切削 运动 分 度 运 动
机械原理齿轮啮合

机械原理齿轮啮合齿轮是一种常见的机械传动元件,通过齿与齿之间的啮合运动来传递动力和扭矩。
在机械原理中,齿轮的啮合原理是一个重要的研究领域。
本文将详细介绍齿轮的啮合原理及其相关的机械原理。
1. 齿轮的类型齿轮可以分为直齿轮、斜齿轮、园柱齿轮、锥齿轮和蜗杆齿轮等几种类型。
不同类型的齿轮具有不同的使用场景和特点。
2. 啮合传动原理齿轮的啮合传动原理是通过齿与齿之间的啮合来传递旋转运动和扭矩。
在啮合过程中,齿轮的齿数、模数、压力角和齿轮啮合面的接触性能等因素会影响传动效果和传动特性。
3. 齿轮啮合的计算齿轮啮合的计算是为了确定齿轮的尺寸和传动特性。
计算包括齿轮的模数、齿宽、齿数比、节圆直径等参数的确定,以及齿轮啮合传动的效率和扭矩的计算等内容。
4. 齿轮的设计齿轮的设计是根据具体的传动需求和工作环境来确定齿轮的型号、材料和加工工艺等。
设计需要考虑齿轮的载荷、传动比、传动效率、噪音和寿命等因素。
5. 齿轮的制造和加工齿轮的制造和加工是将设计好的齿轮图纸转化为实际的零件和组装件的过程。
加工齿轮需要考虑齿轮材料、齿轮加工工艺和齿轮精度等因素。
6. 齿轮的润滑和维护齿轮的润滑和维护是保证齿轮传动正常运行和延长使用寿命的重要手段。
润滑可以采用油润滑和脂润滑两种方式,维护则包括定期检查、清洗和更换润滑剂等工作。
7. 齿轮的故障分析与排除在使用过程中,齿轮可能会出现故障,如齿面磨损、断齿、齿面剥落等。
通过故障分析和排除,可以找出故障原因,并采取相应的修复措施。
总结:机械原理中的齿轮啮合是一门复杂的学科,涉及到齿轮设计、制造、加工、润滑和维护等多个方面。
了解齿轮的啮合原理及相关的机械原理可以帮助我们更好地理解机械传动的原理和工作方式,为机械设计和应用提供基础知识和理论支持。
在实际的工程应用中,合理设计和使用齿轮可以提高机械传动的效率和可靠性,减少故障和损坏的发生。
齿轮的啮合原理是机械工程师必备的基础知识,也是机械原理学习的重点内容之一。
第四章齿轮机构

(5)、在任意圆上dk 齿槽宽ek 齿厚SK 齿距PK= ek+SK
基节 Pb
基节—基圆上的齿距
周节 P
周节—分度圆上的齿距
P=s+e=2s=2e
总之,齿轮与齿条啮合时,不论是否标准安装,齿轮分度圆与节 圆总是重合的,啮合角 恒等于分度圆压力角 。只是在非标准安装 时,齿条的节线与其分度线不再重合。
§4-6 渐开线齿轮的加工方法及根切现象
齿轮加 工方法
铸造法 热轧法
冲压法 粉末冶金法 模锻法 成形法
铣削 拉削
切制法 (最常用)
插齿
范成法 滚齿 (展成法 共轭法 剃齿 包络法)
轮齿廓上由齿顶 向齿根移动;
终止啮合点:主动轮的齿顶点与从动轮的齿根处某点
接触,在啮合线N1N2上为主动轮的齿顶 圆与啮合线N1N2的交点B1。
——实际啮合线 齿廓工作段,齿廓非工作段
——理论啮合线
2、连续传动条件
要求:前一对轮齿脱离啮合时,后一对轮齿必须已经进入啮合 或刚刚进入啮合
B1B2 Pb 或
磨齿
一、齿轮轮齿的加工方法 1.成形法(仿形法)
成形法是在普通铣床上用轴向剖面形状与被切齿轮齿 槽形状完全相同的铣刀切制齿轮的方法,如图所示。铣完 一个齿槽后,分度头将齿坯转过3600/z,再铣下一个齿槽 ,直到铣出所有的齿槽。
成形法加工方便易行,但精度难以保证。由于渐开线齿廓形状取 决于基圆的大小,而基圆半径rb=(mzcosα)/2,故齿廓形状与m、z 、α有关。欲加工精确齿廓,对模数和压力角相同的、齿数不同的 齿轮,应采用不同的刀具,而这在实际中是不可能的。生产中通常 用同一号铣刀切制同模数、不同齿数的齿轮,故齿形通常是近似的 。表中列出了1-8号圆盘铣刀加工齿轮的齿数范围。
齿轮齿条介绍

第四章齿轮机构§4-1 齿轮机构的类型一、类型二、特点1、可以用来传递空间任意两轴之间的运动和动力;2、传动准确、平稳、机械效率高;3、使用寿命长,工作安全可靠。
三、功用齿轮机构是现代机械中应用最为广泛的一种传动机构。
如:机械手、汽车变速箱、摄象机、游乐设施等中的传动机构。
§4-2 齿廓啮合基本定律一、齿廓啮合基本定律:过接触点所作两齿廓公法线C:公法线与连心线的交点由三心定理,C点是这对齿廓的相对速度瞬心,则即得齿廓啮合基本定律:两齿廓在任一位置啮合接触时,过接触点所作两齿廓的公法线必通过定点C。
C点:节点节圆:分别以O1、O2为圆心,、为半径所作的圆。
两齿廓的啮合传动相当与一对节圆作纯滚动。
定传动比条件:无论两齿廓在何处啮合,节点C必须为连心线上的一个定点。
变传动比条件:若要求两齿廓作变传动比传动,则节点C不是一个定点,而是按相应的规律在连心线上移动。
二、共轭齿廓共轭齿廓:凡满足齿廓啮合基本定理的一对齿廓称为共轭齿廓共轭曲线:共轭齿廓的齿廓曲线称为共轭曲线共轭:按一定的规律相配的一对三、齿廓曲线的选择1)在给定工作要求的传动比的情况下,只要给出一条齿廓曲线,就可以根据齿廓啮合基本定理求出与其共轭的另一条齿廓曲线。
因此,理论上满足一定传动比规律的共轭曲线有很多。
2)在生产实践中,选择齿廓曲线时还必须综合考虑设计、制造、安装、使用等方面的因素。
3)常用的齿廓曲线有:渐开线、摆线、变态摆线、圆弧曲线、抛物线等,本章主要研究渐开线齿廓的齿轮。
§4-3 渐开线齿廓一、渐开线的形成直线BK沿半径为的圆作纯滚动时,直线上任一点K的轨迹称为该圆的渐开线。
基圆:半径为的圆基圆半径:渐开线的发生线:直线BKK点的展角:二、渐开线的性质1、发生线在基圆上滚过的长度等于基圆上被滚过的圆弧长度。
即=2、渐开线上离基圆越远的部分,其曲率半径越大,渐开线越平直。
发生线BK与基圆的切点B是渐开线在K的曲率中心,是相应的曲率半径,渐开线上离基圆越远的部分,其曲率半径越大,渐开线越平直;渐开线上离基圆越近的部分,其曲率半径越小,渐开线越弯曲;渐开线在基圆上起始点处的曲率半径为零。
第四章 齿轮机构工作原理

o1
rb1 k1
N1
k2
N2
P
rb2 o2
r'2
2
3、渐开线齿轮传动具 有可分性
当两齿轮制成后,基
1
o1 rb1
N1
圆半径便已确定,以不同
的中心距(a或a‘)安装这对 齿轮,其传动比不会改变。 N2
' N1
P
p' rb2
1 o 2 P rb 2 i12 2 o1P rb1
1 o2 p' rb 2 i12 2 o1p' rb1
ω2 P23
的两段成反比。
结论:
1、要使两齿轮的 瞬时传动比为一常数, 则不论两齿廓在任何 位置接触,过接触点 所作的两齿廓公法线 都必须与连心线交于 一定点p。 n o2 (P12)
3
P13 o1
ω1
1 k1k
n
p
2
ω2 P23
3 2、定点p称为节 点,以o1和o2为圆心,
P13 o1
过节点p作的两相切
曲率半径
发生线
K
ρk
rk
N
K0
k
O
基圆
发生线
(3)渐开线齿廓上 各点的压力角不同。
Vk
ρk 曲率半径
k
K
点K离基圆中心O
愈远,压力角愈大。
P k rk K0
N
NOK= k
rb k k
O
基圆
rb cos k rk
(4) 渐开线的形状取决 于基圆的大小,基圆越 大,渐开线越平直,当 基圆半径趋于无穷大时,
pb m1 cos1 m2 cos 2
m1 m2 m
齿轮齿条介绍

(3)结论 * 与模数无关,而随齿数的增加而加大; * 当两轮齿数趋于无穷大时, 将趋于理论上的极限值
当
、 时,
由于两轮均变为齿条,将吻合成一体而无法啮合传动,所以这个理论上的极限值是不可 能达到的。
(4)重合度的含义
* 重合度的大小表明两轮啮合过程中同时参与啮合的轮齿对数, 越大,表明同时参与啮合 的齿轮对数越多,传动越平稳,每对轮齿承受的载荷越小。
三、齿廓曲线的选择
1)在给定工作要求的传动比的情况下,只要给出一条齿廓曲线,就可以根据齿廓啮 合基本定理求出与其共轭的另一条齿廓曲线。因此,理论上满足一定传动比规律的共 轭曲线有很多。
2)在生产实践中,选择齿廓曲线时还必须综合考虑设计、制造、安装、使用等方面 的因素。
3)常用的齿廓曲线有:渐开线、摆线、变态摆线、圆弧曲线、抛物线等,本章主要 研究渐开线齿廓的齿轮。
当其作无侧隙啮合传动时,
中心距
顶隙 (2)非标准安装
实际中心距 (理论中心距),节圆和分度圆分离, 3、齿轮齿条啮合传动 (1)标准安装
,齿侧产生间隙。
由于齿轮分度圆齿厚等于槽宽,齿条中线上的齿厚也等于槽宽,即 故当齿轮齿条作无侧隙啮合传动时,齿轮分度圆与节圆重合,齿条中线与节圆重合,
(2)非标准安装
齿轮插刀向着轮坯方向移动,切出轮齿的高度。 (4)让刀运动
切削完成后,轮坯沿径向微量移动,以免返回时插刀刀刃擦伤已成形的齿面,下一次切 削前又恢复到原来的位置。 *当用齿条插刀(梳齿刀)时:
4、基圆内无渐开线
5、渐开线的形状取决于基圆的大小
基圆越小,渐开线越弯曲;基圆越大,渐开线越平直;当基圆半径为无穷大时,渐开线 将成为一条直线。
三、渐开线方程
1、压力角:当用渐开线作齿轮的齿廓时,齿廓上点 K 速度方向 与 K 点法线 BK 之间所夹的 锐角称为渐开线在 K 点的压力角 。
第四章 齿轮机构

rb ra
2)齿根圆: 过各轮齿的齿槽底 部所作的圆。直径、半 径分别用df、rf表示。
O
图4-6
21/48
3)齿厚:
沿任意圆周所量得的
轮齿的弧线厚度,称为该
sk
ek
圆周的齿厚sk 。
4)齿槽宽: 沿任意圆周所量得的 相邻两齿之间的齿槽的弧 长,称为该圆周的齿槽宽
rf
rb
ra
ek 。
O
22/48
32/48
三、标准直齿轮各部分尺寸的计算公式(应熟记)
d=mz
ha= ha*m p =πm s = e = p / 2=πm /2
hf =(ha*+ c*)m
h = ha+ hf da= d +2 ha=(z+2ha*)m
pb=πdb/z=πm cosα= p cosα
a = m ( z1+z2 ) /2—标准中心距 d′=d—当中心距为标准中心距时
∴πm1 cosα1=πm2 cosα2 ∴m1 cosα1= m2 cosα2 (式中m1 、m2 和α1、α2分别为两轮的模数和压力角)
34/48
m1 cosα1= m2 cosα2 ∵ 模数和压力角都是标准值 ∴必须使: m1 = m2 = m,α1=α2=α
∴ 渐开线齿轮正确啮合的条件是: 两轮的模数和压力角应分别相等 传动比: i12=ω1 /ω2= r2′/r1′= rb2/ rb1 = r2 cosα2 / r1 cosα1 = r2 / r1= m2z2 / m1z1 = z2/z1
b
A
θk
rk
O 基圆
渐开线的切线,故BK为法线。
图4-3
15/48
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
齿轮啮合原理 —平面曲线
小组成员:
谭 张王 罗
惠
成彩
文 军非 煌
平面曲线
齿轮啮合原理
平面曲线
齿轮啮合原理
目录
1 平面曲线的基本要素 2 几种特别的平面曲线 3 平面曲线的相关应用
4
平面曲线
齿轮啮合原理
1 平面曲线的基本要素
1.1 平面曲线的三种表示形式 1.2 平面曲线的切线 1.3 平面曲线的法线 1.4 平面曲线的曲率
线C1、C2、C3分别是渐开线、延伸渐
开线和缩短渐开线。广义渐开线是 这三种曲线的总称。
平面曲线
广义摆线
齿轮啮合原理
在平面上,一个动圆(发生圆) 沿一条固定的直线(基线)作 纯滚动时,与动圆固连的一 点的轨迹称为摆线(该点在发 生圆上),或长幅摆线(该点 在发生圆外),或短幅摆线 (该点在发生圆内)。图中曲
方程式: x2 y2
2
2ax
x2 y2
a2 y2
极值点:C,
D
3 4
a,
3
3 4
a
二重切线的切点:E,
F
3 4
,
3 4
a
曲线长: L = 8a
平面曲线
齿轮啮合原理
2.3 圆内摆线
曲线是一圆周沿另一圆周的内部滚动而无滑动时,圆周 上一点M所描成的轨迹。
平面曲线
齿轮啮合原理
1.1 平面曲线的三种表示形式
1)函数方程: y f (x) (显函数曲线) 2)二元方程: F(x, y) 0 (隐函数曲线) 3)参数方程: x x(t), y y(t) (参数曲线)
平面曲线
齿轮啮合原理
1.2 平面曲线的切线
曲线的切线指的是一条刚好触碰到曲线上某一点的直 线,更准确地说,当切线经过曲线上的某点(即切点)时, 切线的方向与曲线上该点的运动方向是相同的。
平面曲线
齿轮啮合原理
渐开线齿廓自从二百多年前出现后,就一直在工程实践中 居于绝对的统治地位,目前渐开线仍是各种齿轮中最主要 的齿廓曲线形式。利用数学微分几何原理对渐开线曲线进 行曲率分析,求得渐开线各点处曲率中心的分布,可以简 化齿轮传动啮合运动机构分析。另外对渐开线曲线进行曲 率分析,是对渐开线齿轮进行齿廓啮合分析、齿形创新设 计及齿廓修形加工新工艺开发的基础和前提,对齿轮传动 的创新研究和发展具有重要意义。
3.5 齿轮啮合中常见的平面曲线
齿轮啮合原理
在啮合理论中常用到的平面曲线,除了直线和圆外还有 以下几种常用曲线:
广义渐开线 广义摆线 广义外摆线 广义内摆线
平面曲线
广义渐开线
齿轮啮合原理
在平面上,一条动直线(发生线)沿 一个固定的圆(基圆)作纯滚动时, 与动直线固连的一点的轨迹称为渐 开线(该点在发生线上),或延伸渐 开线(该点与基圆圆心位于发生线的 同侧),或缩短渐开线(该点与基圆 圆心位于发生线的异侧)。在图中曲
已知:平面曲线的方程式 F(x, y) 0
和P点的坐标 x0, y0
切线
则:平面曲线的切线为:
y
y0
Fx Fy
x0, x0,
y0 y0
x
x0
切点P
曲线C
平面曲线
齿轮啮合原理
1.3 平面曲线的法线
曲线的法线是垂直于曲线上一点的切线的直线,曲面 上某一点的法线指的是经过这一点并且与该点切平面垂直 的那条直线(即向量)。
平面曲线
齿轮啮合原理
如图所示,为一通用凸轮 曲线的各项运动规律曲线, 通过对推杆位移规律曲线 S的分析处理,可以得到 速度V、加速度a、跃度J 等的参数变化规律从,从 而获取凸轮的运动情况。
平面曲线
齿轮啮合原理
3.3 机械零件检测应用
机械零件自动检测是制造业中生产系统的一个重要环节, 它从一定程度上决定了实现企业柔性制造自动化的进程, 是制造业信息化的关键环节。
已知:平面曲线的方程式 F(x, y) 0
和P点的坐标 x0, y0
切线
则:平面曲线的法线为:
y y0
Fy x0, y0
x x0 Fx x0, y0
切点P
曲线C
法线
平面曲线
齿轮啮合原理
1.4 平面曲线的曲率
r
用矢量函数 r sC2 ,s E 表示的曲线,式中s是曲线的弧长。
平面曲线
齿轮啮合原理
道路设计通常在同一线路坐标系中进行,道路平面曲线元 在线路坐标系中的快速定位、中桩测设坐标和道路中桩、 附属结构物施工放样坐标的准确计算是广大道路工程线路 设计人员、勘测人员以及道路施工放样人员十分关心的问 题,计算工具和测量仪器的改进使这些问题正朝着积极的 方向发展。
平面曲线
曲线上分别与s和(s+ )对s应的两个相邻的点M和N。 而
是点M和N处的两条切线之间的夹角。当点N趋近于点M时,
比值
的极限s 称为曲线在点M处的曲率。
平面曲线
2 几种特殊的平面曲线
2.1 笛卡尔叶形线 2.2 心脏线 2.3 圆内摆线 2.4 阿基米德螺旋线
齿轮啮合原理
平面曲线
2.1 笛卡尔叶形线
平面曲线
齿轮啮合原理
图中所示,对于特定的渐开线,其基圆半径为固定值,渐开 线上各点处的压力角 及曲率半径 可由对应位置的极径 根据理 论公式计算求得。例如对于齿数为30、模数为2.0mm、分度圆 压力角为20°的渐开线标准齿轮,其基圆半径为28.19mm,求 得压力角及曲率半径值沿渐开线齿廓的分布。
平面曲线
齿轮啮合原理
3.2 凸轮轮廓的应用
凸轮机构应用广泛。其最大优点是只要适当设计出凸轮的 轮廓曲线,就可以使推杆实现各种预期的复杂运动规律, 而且响应快速,机构简单紧凑。
平面曲线
齿轮啮合原理
设计方法有图解法、解析法。由于图解法难以满足对凸轮机 构精度的要求,现多采用解析法。用解析法设计凸轮轮廓曲 线时需对该机构进行运动分析,列矢量方程表达式,建立方 程,进行数值求解,得到推杆的运动学、动力学等规律。
侧)。图中曲线C1、C2和C3分别是外
摆线、长幅外摆线和短幅外摆线。 广义外摆线是这三种曲线的总称。
平面曲线
广义内摆线
齿轮啮合原理
在平面上,一个动圆(发生元)沿一 个固定的圆(基圆)的内侧作纯滚动 时,与动圆固连的一点的轨迹称为 内摆线(该点在发生圆上)或长幅内 摆线(该点与基团圆心位于发生因的 同侧),或短幅内摆线(该点与基圆 圆心位于发生圆的异侧)。图中,曲
线C1、C2和C3分别是内摆线、长幅内
摆线和短幅内摆线。广义内摆线是 这三种曲线的总称。
平面曲线
齿轮啮合原理
总之,平面曲线与我们的生活处处相关,平面曲线的应 用无处不在,不一而足。人类对平面曲线问题的深入探 讨与应用必能促进人类的更好发展。
LOGO
线C1、C2和C3分别是摆线、长
幅摆线和短幅摆线。广义摆 线是这三种曲线的总称。
平面曲线
广义外摆线
齿轮啮合原理
在平面上,一个动圆(发生圆)沿一 个固定的圆(基圆)的外侧,作外切 或内切纯滚动时,与动圆固连的一 点的轨迹称为外摆线(该点在发生圆 上),或长幅外摆线(该点与基圆圆 心位于发生圆的同侧),或短幅外摆 线(该点与基圆圆心位于发生圆的异
平面曲线
齿轮啮合原理
3.1齿轮传动中的应用
齿轮是各种机械设备中应用最为广泛的一种机械传动元件。 齿轮传动水平的高低是衡量一个国家机械工业水平高低的 重要标志。
平面曲线
齿轮啮合原理
目前齿轮创新研究和发展的重点、难点集中在轮齿横截面 齿廓曲线形状上,齿轮齿廓形状是影响齿轮承载能力和使 用寿命的主要因素之一。
方程式: a
a v
2 1 Arsh
3
曲率半径:R a 3 12
2 2
扇形M1OM2的面积:
S a2 6
23 13
平面曲线
3、平面曲线相关应用
齿轮啮合原理
平面曲线本身是没有具体实物存在的,它只不过是我们为 了理解事物,解决问题而抽象出来而又能代表问题,通过 对曲线性质的理解和应用,从而解决问题。下面介绍几种 常见的应用。
一般认为,构成机械零件的基本元素是点、直线、圆、 椭圆和曲线。当前运用计算机视觉技术对机械零件的检测 和识别,绝大部分只是对零件的点、直线、圆和椭圆的研 究,而其他形式的曲线的检测和识别研究却比较少。
平面曲线
齿轮啮合原理
3.4 在道路设计中的应用
公路平面设计主线通常采用导线法,即先用导线标定线路走 廊带,然后采用直线、圆曲线和缓和曲线组合,将整个线路 串连起来。匝道平面设计则先定出起点坐标和方位,然后根 据地形特点选择线形和设置线形参数分段向前推进。
方程式: x3 y3 3axy
齿轮啮合原理
渐近线: x y a 0
圈套的面积:
S1
3a2 2
曲线与渐近线之间的面积:
S2
3a2 2
平面曲线
齿轮啮合原理
2.2 心脏线
它是使OM = OP ± a的点M的轨迹(a为圆的直径,P 为圆周上的一点)。它是圆外旋轮线的特例(动圆与定圆 的直径相等)
x a b cos t b cos a b t
方程式:
b
y a bsin t b sin a b t
b
全曲线长:L = 6a
曲线所围成的面积: S 3 a3
8
平面曲线
齿轮啮合原理
2.4 阿基米德螺旋线
曲线为一动点以常速沿一射线运动,而这一射线又以 定角速度绕极点转动时,该动点所描成的轨迹.曲线由两 支曲线组成,它们关于x轴对称。
