4第四章习题解答
高等代数-第4章习题及解答

第四章 多项式4.1习题,()(),..(-)-(-)()()-(-)()--(-)(-)Z a c ad bc q Z s t ad bc q a c a c b d ab cd ad bc a c b d ab cd a c q a c b d q ab cd ∈-+∴∃∈+==++=++=+1. 设a,b,c,d 已知(a-c)(ad+bc),求证(a-c)(ab+cd)证明:又由 () 得 ()() 即 ,,-()()b d q Zb d q Z ac ab cd ∈∴+∈-+即有 121212,65(-3)13,65(-2)5,65-,65(-3)13(-2)571865-(6528)65(-65)-2828m m m m r c c m c m c c c m m r ⨯⨯∃⨯+⨯==-+∴=2. 一个整数被5除余3,被13除余2,求它被65除的余数解:设所求数为由题知 即 有 令 ,, 则有 故有 1723582957,581-143,-143202,0231414a b a b a b a b b a b a b a ==-=-==-=-=-=-=+=⋅+=⋅+3. 对于下列的整数,分别求出以除所得的商和余数: (1), (2), (3), (4)解:)由带余除法,可表示为 故商为,余数为;)同理得 故商为,余数为; )由 知商为,余数为; 49595b a =+ )由 知商为,余数为。
.()001a b a b b aq q Z b q b a q q a b≠≤=∈≠∴≠∴=≥∴≤4. 证明:若a b,b 0,则证明:由 可得 又 又1,) 1.b ∈=1 1 1115. 设a,b 是不全为零的整数,且a=da ,b=db ,d,a ,b Z.证明d 是a 与b 的一个最大公因数的充分必要条件是(a1111111111[] 4.1.3,,..01(,)1[](,)1''1''1,''u v Z s t ua vb d uda vdb d d ua vb a b a b u a v b a bu v u a v b d d d⇒∃∈+=+=≠∴+=∴=⇐=+=+=+=证明:根据定理得 即 又故有 即 则有 综上所述,结论得证6.(,)1,(,) 1.,(1),,..()()(1),,1,1a b a b ab a b ab d d Z d u v Z s t u a b vab d ua u va b d u v a Z u va Za b =+=+=∈≠∴∃∈++=∴++=∈∴+∈= 证明:若则 证明:反证 假设() 且 故 ()与 () 矛盾 ,17.1..,()(),,.a b ab a b p ab p a p b p p mn a b k k Z p abp b b k p a p b p k m b m k m k n b n k n k p ∴+===+∈∴+ () 设是一个大于的整数且具有以下性质:对于任意整数,,若,则或 证明是一个素数 证明:令 又当 不整除,有,不整除 又有,不整除或; 不整除或 若为合数,那,m k n k p p k p b p 么由可知必为素数,否则 同理可证当不整除时,也必为素数4.2习题224324321.,,(21)(1)251\2(2)(21)()12521-2,1,31k h m x hx x kx x x mx x x k h x hk x h k x h k hk m k h m h k +--+=++--=--+--++--=⎧⎪--====⎨⎪+=-⎩求使 解:对于左边 即有 解之得432322.()242,()25 4.()(),()(),()().f x x x x xg x x x x f x g x f x g x f x g x =+---=--++- 设 计算432443270765432()()4292()()6()0254()()()23913131868kki k i k i f x g x x x x x f x g x x x g x x x x x f x g x a b x x x x x x x x -==+=+--+-=+-=⋅+--+∴==+--++--∑∑解:由题得 令323122223.()59-73,()(53),()().-15-50[()()]3691()()04.()0().()0()()()f x x x xg x x x f x g x f x g x x f x g x s f x f x f x f x f x f x ︒=-++=++⨯=±∂===≠≠=⋅∴ 设求乘积 的次数及其系数和解:根据 得 令 则有 的系数和 证明:当时,是偶次多项式证明:又有 根据定理2 4.2.12()()()()(),()()2f x f x f x f x f x n n N f x n ︒︒︒︒︒∂⋅=∂+∂∂=∈∴∂=的()知 ()()() 再令 () 结论得证2225.(),(),()..()()(),()()()0.(),(),()1221222132212f x g x h x f x xg x xh x f x g x h x g x g f x f h x hg h f g g h f h g h f g f ︒︒︒︒︒︒=+===∂=∂=∂=>=+<=+==+= 设是实数域上的多项式证明如下 若是 则 证明:令 () () () 当 时,有 当 时,有 当 时,有 或 2222214()(),(),()(),(),()()()()06.(),(),()()0(),()1()0(),()h f x f x g x h x f x g x h x f x g x h x f x g x h x f x g x i h x f x xg x x xh x x +========-= 又由题可知 是偶次多项式,又由于是实数域上的多项式 故 的次数不存在 即 求一组满足上题结论的不全为零的复系数多项式解:令 , 即 , 222()()0()()0(),()1xg x xh x f x f x g x i h x ∴+===== 满足条件即 ,4.3 习题3221.()321,()321,()()()().f x x x xg x x x g x f x q x r x =-+-=-+设求用除所得的商式和余数232322217393213212133751337147399299172(),()3999()()()()x x x x x x x x x x x x x x x q x x r x f x g x q x r x --+-+--+-+--+--=-=-=+解: 故 即[]2432322412*********.,,(1)()?012,1(1)()3.()(()()),()(()()),:()(()()()()),(),()m p q x mx x px q p m m m r q m p m m q m x mx x px q g x f x f x g x f x f x g x u x f x u x f x u x u x F x ++++⎧+=-=⎨=-⎩=-=-+++++-+在适合什么条件时,解:由题知当余式时有 即当 时 有 设证明其中为中任意两个12121212121211()(()()),()(()())()(()()()())()(()()()())()(),()()3()()(i g x f x f x g x f x f x g x f x f x f x f x g x f x f x f x f x g x f x g x f x u x F x i +-∴++-+-+∃∀∈=多项式 证明:即 根据多项式整除性质)可知 1122112221,2)..()()(),()()()2()()(1,2)..()(()()()())4.(1)(),(1)(),(1)().11(1)(),(1)(i o s t g x u x f x g x u x f x u x F x i s t g x u x f x u x f x x f x x f x x f x x x f x x f ∃∀∈=+-+-≠±-+ 再根据性质)得 若则证明:1212)(),()[]()()(1)(1)()()(1)(2)x u x u x F x f x u x x f x u x x ∴∃∈=+⎧⎨=-⎩221()()(1)(-1)-(2)(1)()(-1)()2u x u x x x f x x -⨯⨯+= 得212()()()[]2(-1)()21-1()0o u x u x u x F x x f x x x f x -∃=∈=== 故 即 或时,可得出 同样结论成立1212121221212125.(1)()(()()),()()()()(2)()()(),()()()()1(),()1,()1()(()())()()()g x f x f x g x f x g x f x g x f x f x g x f x g x f x g x x f x x f x x g x f x f x g x f x f x +==+=-+ 若则且对吗? 若则或对吗?解:()不对 如 :令 可见 而 不整除 和 (21212122()-1,()1,()1()()()()()()g x x f x x f x x g x f x f x g x f x f x ==+=-)不对如 :令 可见 而 不整除 和(1)(2)6.(1)(1),.,1()1(1)(1),(1)(1).(1)(1)(0),1(1)1,(1)(1)(1)(d n n d q d q d q d d n d n n qd r d q r r d n d x x d n d n d n n qd x x x x x x x x x n qd r r d x x x x x x x x --+--⇐=-=-=-+++--⇒--=+≤<-==-+---- 证明:的充分必要条件是(这里是正整数)证明 设 ,即 则 即 设,令则且212121)(1)(1)0,0.7.()110220()32.(),()[]..(1)()10()(1)(2)()2d q d r x x x r d r d n f x x x f x x x u x u x F x s t x u x f x x u x -∴--≤<=++++∃∈++=++ ,又 故 ,即 设被除的余式为,被除的余式为, 求被 除的余式解:设 , 23120()(2)()[]..()32(3)(1)(2)-(2)(1)()32--10(1)434-10(1)f x u x F x s t f x x x u r x x f x x x u u x r x =∃∈=+++⨯+⨯+=+++=+ 又 , () 有 ()() () 由(),()可得习题4.4432424322432312(1)43243221(-1)1.1)()242,()322;2)()441,() 1.()24221)()()2222f x x x x x g x x x x x f x x x x x g x x x f x x x x x x x A x g x x x x x x x x x +-+=+---=+---=--++=--⎛⎫⎛⎫+----⎛⎫==−−−→ ⎪ ⎪ ⎪+---+---⎝⎭⎝⎭⎝⎭−计算以下各式多项式的最大公因式:解:由 11333221()1()21()42222222200x x xx x x x x x x x x x -++-⎛⎫⎛⎫⎛⎫⎛⎫----−−→−−−→−−−→−−−→ ⎪ ⎪ ⎪ ⎪---⎝⎭⎝⎭⎝⎭⎝⎭224324312(4)222212(-)2(1)12()221(1)()2()44132)()()112333212x x d x x f x x x x x x x A x g x x x x x x x x x x x x +++-++∴=-⎛⎫⎛⎫--++--⎛⎫==−−−→ ⎪ ⎪ ⎪----⎝⎭⎝⎭⎝⎭-⎛⎫⎛⎫--⎛⎫−−−−→−−−→−−−→ ⎪ ⎪ ⎪-+---+⎝⎭⎝⎭⎝⎭−−−→ 由 2311110()1x x x d x -⎛⎫⎛⎫⎛⎫→→ ⎪ ⎪ ⎪--⎝⎭⎝⎭⎝⎭∴=2.(),()(),,0,(()(),()())((),()).((),())()()(),()()()()()),()()())(),()(f x g x F x a b c d F ad bc af x bg x cf x dg x f x g x f x g x d x d x f x d x g x d x af x bg x d x cf x dg x h x h x af ∈∈-≠++==∴++∃∀另而,,,并且证明证明:令 即有 ( ( 又设 ()()),()()())-0()()())-()())---()()())()())--()(),()(),()x bg x h x cf x dg x ad bc d bf x af x bg x cf x dg x ad bc ad bc c ag x af x bg x cf x dg x ad bc ad bch x f x h x g x h x d ++≠∴=++=+++∴ (有 (( (( 从而有 ()()()()())()(()(),()())((),())x af x bg x cf x dg x d x af x bg x cf x dg x f x g x ++=++= 即 (, 即 :3.()0,()((),())(()()(),()).()0(),..()()()()()()-()()1((),())(()())((),())(()()(g x h x f x g x f x h x g x g x g x h x s t f x g x h x r x r x f x g x h x f x g x g x r x f x g x f x h x g x ≠=-≠∃=+===-设为任意多项式,证明: 证明: 故 即 由引理可知 , 即 ),())g x1122121212124.1)(,)2)(,)(,)(,,,),,,().1(,),,,,(,),[],..f g hf gh f g f g f f f g g f g g f g h F x f g d d f d g dh fh dh gh dh hf hg f g d u v F x s t uf vg d ===∃∈+=∴证明:是与的最大公因式;此处都是的多项式证明:)设 即 从而有 即 是与的公因式又由 得 112211211212211211221214.4.42)(,),(,),(,[]),;,,,,(,),(,),,,ufh vgh dhdh fh gh f g m f g n m n F x m f m g m f m g mn f f mn f g mn f g mn g g f g m f g n k k l +===∈==∃ 由定理知 是与的最大公因式 设 即 从而有 又由 知 211112222121211221221121212122112112212122112[],..,(,,,)(,)(,)(,,,)l F x s t k f l g m k f l g nk k f f k f l g l k f g l l g g mn mn f f f g f g g g f g f g f f f g f g g g ∈+=+=+++=== 即有 由此可知 从而有4323243232324323235.(),()()()()()((),()):1)()343,()310232)()421659,()25453431033113333102301310u x v x u x f x v x g x f x g x f x x x x x g x x x x f x x x x x g x x x x x x x x x x x x x x x x +==+---=++-=--++=--+⎛⎫+--------→ ⎪++-⎝⎭+2求使解:)(A(x),I )=222322222232230159935993913310230156553296331393555591393132563555555x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x ⎛⎫⎪⎪ ⎪+-⎝⎭⎛⎫----⎛⎫---- ⎪→→ ⎪- ⎪++---- ⎪⎝⎭⎝⎭⎛-+⎛⎫-+------ ⎪ ⎪→→--+ ⎪------+- ⎪⎝⎭⎝33-x -x 22243232323231550**321,()55122342165910332540125401x x x x x x x v x x x x x x x x x x x x x x ⎫ ⎪ ⎪ ⎪ ⎪⎭⎛⎫-+- ⎪→ ⎪ ⎪⎝⎭-∴-=⎛⎫⎛⎫--+---++ ⎪→ ⎪ ⎪--+ ⎪⎝⎭--+⎝⎭2 u(x)= 2)(A(x),I )=22222222121223231333332222412(2)1333312231330**1223(),()33x xx x x x x x x x xx x x x x x x x x x x u x v x ⎛⎫-++⎛⎫--+--- ⎪⎪ ⎪⎪→→ ⎪ ⎪--++--+-+- ⎪ ⎪⎝⎭⎝⎭⎛⎫--+- ⎪→ ⎪ ⎪⎝⎭--+∴==4322432436.()1,()(1),,,()().(),()2,()()()()(,,)()(2)(2)(2)1of x Ax Bxg x x A B f x g x f x g x g x f x g x ax bx c a b c F f x ax b a x c b a x b c x c Ax Bx a A =++=-∂==++∈∴=+-+-++-+=++=设试决定使与 的最大公因式为二次多项式解:由于() 即 为最大公因式故不妨设 即有 -23,2,13,-4202013,-4b a B a bc A B c b a b c c A B ⎧⎪=⎪⎪=====-+=⎨⎪-=⎪=⎪⎩∴== 解得 即7.(),()((),())()()()(),((),())1((),())()()()()*()()()()()()()()()()*(),()[].f x g x f x g x u x f x v x g x u x v x f x g x u x f x v x g x u x f x v x g x f x u x f x v x g x g x m x n x F x s =+==+++∃∈设 不全为零,且证明:证明:()有 , 再由 () .()()[()()()()]()()[()()()()]1-()()()()()()11-()())()()()()221()t f x m x u x f x v x g x g x n x u x f x v x g x m x u x f x m x v x g x n x v x g x n x u x f x f x =+=+== 即() () ( () 将()代入(),消去得1-()()1-()()()()()()()()(),(),()01-()()()()()()()()()()()()1()()()()4.4.5((),())1m x u x n x v x g x m x v x g x n x u x f x g x g x n x v x m x u x m x n x u x v x m x n x u x v x m x n x u x v x u x v x =≠∴-+=∴==()()不全为零 即令 由定理 得8.((),()) 1.((),()) 1.,,((),()) 1.1()()()[]()()()()()()((),())1n m n o n n n f x g x n f x g x m n f x g x g x g x k x F x g x k x g x g x g x k x f x g x ===∃∈=∴==设令是任意正整数,证明:由此进一步证明: 对于任意正整数都有证明: 易见 , 即 s.t. (1)又 ()()1()()1()((),())1()(),()[]()()()()()()nn m m m f x g x f x g x k x f x g x x f x l x F x f x l x f x f x f x l x ∴∃∈+=+==∃∈=∴=o u(x),v(x)F[x] s.t. u(x)v(x) (2)v(x) 将(1)代入(2)得 u(x) 由定理4.4.5 知 2易见 f 即 s.t. ((),())1'''()()'()()11'()()'()()1()((),())1n n mn m n f x g x u x f x v x g x u x f x v x g x l x f x g x =∴∃∈+=+== (3)又u (x),v (x)F[x] s.t. (4) 将(3)代入(4)得 由定理4.4.5知 [][]1111119.((),()) 1.((),()())((),()())(()(),()()) 1.((),()())()()(),()()()()[()()]()()()]f x g x f x f x g x g x f x g x f x g x f x g x f x f x g x d x d x F x u x v x F x u x f x v x f x g x d x u x v x =+=+=+=+=∈∴∃∈++=+设 证明: 证明:令 ()s.t. 即 [1()()()()((),())1()1((),()())1((),()())1(()(),()())1f x v xg x d x f x g x d x f x f x g x g x f x g x f x g x f x g x +===+=+=+=故 即 同理可证得 再根据互素性质可知10.()0,()0,:1(),()()()()(),((),())12(),()(),()()()()(),((),())11((),())()1,()()f x g x h x f x g x h x f x h x f x g x h x f x h x g x h x f x g x h x f x g x f x g x d x f x d x m ≠≠===≠=设证明 )若对于任意多项式由可得到则必有 )若对于任意多项式由可得到则必有 证明:) 假设 则有(),()()()()()()()()()()()()()()x g x d x n x m x f x f x g x h x h x f x g x m x f x m x ︒︒=∂<∂∴ 其中 () ()又 (为任意多项式)即有()()((),())12((),())()1()()()()()()()()(),()()()()()()()1((f x m x f x g x f x g x d x f x d x m x h x m x g x f x g x m x g x g x m x f x g x g x m x f x ==≠==∴ 但 不整除,从而矛盾, 故 )假设 ,且 令 即有 () 又),())()()()()()()()1((),())1g x d x f x m x f x g x g x m x f x g x ︒︒︒︒=∴∂>∂∂>∂∴= () ()故 () () 与()矛盾1212111212112211.(),(),,()().1)((),(),,())(((),,()),((),,())),112(),(),,()(),(),,()()()()()()()n n k k n n n n f x f x f x F x f x f x f x f x f x f x f x k n f x f x f x u x u x u x F x u x f x u x f x u x +∈=≤≤-∈+++设证明: )互素的充分且必要条件是存在多项式 ,使得1211121()11((),(),,())(),((),,()(),((),,()()()(),1,2,,()(),1,2,,;()(),1,2,,()(),n n k k n i s t f x f x f x f x d x f x f x d x f x f x d x d x f x i nd x f x s k d x f x t k k nd x d x +=====∴==++∴证明:)设21212()()()(),1,2()(),1,2,,;()(),1,2,,()(),1,2,,()(),2((),(),,())1i s t i n d x d x c x d x i d x f x s k d x f x t k k nc x f x i nc xd x f x f x f x ===++∴=∴= 设结论得证。
第四章 习题答案

第四章的习题及答案4-1 设有一台锅炉,水流入锅炉是之焓为62.7kJ ·kg -1,蒸汽流出时的焓为2717 kJ ·kg -1,锅炉的效率为70%,每千克煤可发生29260kJ 的热量,锅炉蒸发量为4.5t ·h -1,试计算每小时的煤消耗量。
解:锅炉中的水处于稳态流动过程,可由稳态流动体系能量衡算方程:Q W Z g u H s +=∆+∆+∆221体系与环境间没有功的交换:0=s W ,并忽 动能和位能的变化, 所以: Q H =∆设需要煤mkg ,则有:%7029260)7.622717(105.43⨯=-⨯m解得:kg m 2.583=4-2 一发明者称他设计了一台热机,热机消耗热值为42000kJ ·kg -1的油料0.5kg ·min -1,其产生的输出功率为170kW ,规定这热机的高温与低温分别为670K 与330K ,试判断此设计是否合理?解:可逆热机效率最大,可逆热机效率:507.06703301112max =-=-=T T η 热机吸收的热量:1m in210005.042000-⋅=⨯=kJ Q热机所做功为:1m in 102000m in)/(60)/(170-⋅-=⨯-=kJ s s kJ W该热机效率为:486.02100010200==-=Q W η 该热机效率小于可逆热机效率,所以有一定合理性。
4-3 1 kg 的水在1×105 Pa 的恒压下可逆加热到沸点,并在沸点下完全蒸发。
试问加给水的热量有多少可能转变为功?环境温度为293 K 。
解:查水蒸气表可得始态1对应的焓和熵为:H 1=83.93kJ/kg, S 1=0.2962kJ/kg.K 末态2对应的焓和熵为:H 2=2675.9kJ/kg, S 2=7.3609kJ/kg.K)/(0.259293.839.267512kg kJ H H Q =-=-=)/(0.522)2962.03609.7(15.2930.25920kg kJ S T H W sys id =-⨯-=∆-∆=4-4如果上题中所需热量来自温度为533 K 的炉子,此加热过程的总熵变为多少?由于过程的不可逆性损失了多少功? 解:此时系统的熵变不变)./(0647.7K kg kJ S sys =∆炉子的熵变为)./(86.45330.2592K kg kJ T H T Q S sur -=-=∆-==∆ )./(205.286.40647.7K kg kJ S t =-=∆ )/(0.646205.215.2930kg kJ S T W t l =⨯=∆=4-5 1mol 理想气体,400K 下在气缸内进行恒温不可逆压缩,由0.1013MPa 压缩到1.013MPa 。
第四章 交流绕组理论 _ 习题与解答 _

为
;在电枢绕组中所感应的电势频率为
;如 3 次谐波相电势有效值为 E3,
则线电势有效值为
;同步电机三相电枢绕组中一相单独流过电流时,所产
生的 3 次谐波磁势表达式为
。三相绕组流过对称三相电流
时 3 次谐波磁势幅值为
。
答:
τ 3
,3f,0,
Fφ
3
cos
3
π τ
x cosωt ,0
10. ★某三相两极电机中,有一个表达式为δ=F COS(5ωt+ 7θS)的气隙磁势波,这表明:
;
由数学知:相量和总是小于(或等于)其代数和,即 Et( y<τ ) < Et( y=τ ) 及 Eq(q>1) < Eq(q=1) , 故
其比值 即 K y 及 K q 总是小于 1.
4. ★在交流发电机定子槽的导体中感应电动势的频率、波形、大小与哪些因素有关?这些因
素中哪些是由构造决定的,哪些是由运行条件决定的?
绕组串联匝数有关,由构造决定;与频率、每极下磁通量有关,由运行条件决定。
6. ★★试从物理和数学意义上分析,为什么短距和分布绕组能削弱或消除高次谐波电动势?
答: 因谐波电动势 Eφν = 4.44 fν Nk pν kdν Φν ,欲要消除或削弱某次谐波电动势,只需使某次
谐波的短距系数 k pν 或分布系数 kdν 为零(或很小)即可。
τ。
答:ν −1 ν
5. ★三相对称绕组通过三相对称电流,顺时针相序(a-b-c-a),其中 ia = 10 sin ωt ,当 Ia=10A
时,三相基波合成磁势的幅值应位于
;当 Ia =-5A 时,其幅值位于
。
答:A 相绕组轴线处,B 相绕组轴线处。
第四章-混合物化学位-习题-解答

第四章 流体混合物的热力学性质思考题1) 在化工热力学中引入偏摩尔性质的意义何在?在进行化工计算时,什么情况下不能使用偏摩尔量?2) 简述Gibbs-Duhem 方程的用途,说明进行热力学一致性检验的重要性。
3) 简述求混合性质变化的实际用途。
4) 讨论理想气体的混合物和气态理想溶液的区别和联系。
5) 真实气体混合物的非理想性表现在哪几个方面? 6) 说明在化工热力学中引入逸度计算的理由。
7) 解释活度定义中的标准态,为什么要引入不同的标准态?8) 混合物的逸度和逸度系数与它的组元逸度和逸度系数有什么关系?由这种关系我们可以得出什么结论?9) 讨论偏摩尔性质、混合性质变化和超额性质这三个概念在化工热力学中各起的作用。
10) 试总结和比较各种活度系数方程,并说明其应用情况。
计算题1. 某酒厂用96%(wt )的食用酒精配酒,酒中的乙醇含量为56%(wt )。
现决定用1吨食用酒精进行配制,问需加多少水才能配成所需的产品?所得酒有多少m 3?已知在25℃和解:1吨食用酒精中乙醇质量:1*0.96=0.96吨 可配成酒的质量:0.96/0.56=1.714(吨) 所需水的质量:1.714-1=0.714(吨)酒中水的质量:1-0.96+0.714=0.754(吨) 配成的酒的体积22H O EtOH H O EtOH30.9530.754 1.2430.960.718562 1.193281.911842(m )Vt V m V m =⋅+⋅=⨯+⨯=+=2. 298.15K 下,有若干NaCl(B)溶解于1kg 水(A)中形成的溶液,其总体积为2B2/3B B t n 119.0n 773.1n 625.1638.1001V +++= (3cm )。
求B n =0.5mol 时,水和NaCl 的偏摩尔B A V ,V 。
123(),,316.625 1.7730.1192218.625(cm )B AB B B nV V T P n n n n ⎡⎤∂=⎢⎥∂⎣⎦=+⨯⨯+⨯⨯=3322223()31001.3816.625 1.7730.11916.625 1.77320.11921001.12655.5518.022(cm )t B B A AB B B B B B AV n V V n n n n n n n n -=⎡⎤+++--⨯-⨯⎢⎥⎣⎦===3. 在30℃和10.133kPa 下,苯(1)和环几烷(2)的液体混合物的容积数据可用2611(109.416.8 2.64)10V x x -=--⨯表示。
第四章习题解答

第四章习题解4-3 已知调制信号()cos(2000)cos(4000)m t t t ππ=+,载波为4cos10t π,进行单边带调制,试确定该单边带信号的表示式,并画出频谱图。
[解]首先计算()m t 的希尔伯特变换,ˆ()sin(2000)sin(4000)mt t t ππ=+, 然后分别计算上边带与下边带的单边带调制信号。
上边带信号:44444411ˆ()()cos(10)()sin(10)221{[cos(2000)cos(10)sin(2000)sin(10)]2[cos(4000)cos(10)sin(4000)sin(10)]}1[cos(12000)cos(14000)]2U s t m t t mt t t t t t t t t t t t ππππππππππππ=−=−+−=+ 类似地,下边带信号为:1()[cos(8000)cos(6000)]2D s t t t ππ=+。
频谱图:实线为上边带信号,虚线为下边带信号。
4-6 某调制系统如图P4-6所示,为了在输出端同时得到f 1(t )和f 2(t ),试确定接收端的c 1(t)和c (t)f 1(t f 2(t f 1(t )f 2(t )[解] 1020()()cos 2()sin 2s t f t f t f t f t ππ=⋅+如果 10()cos 2c t f t π=,20()sin 2c t f t π= 则11020111()()cos4()sin 4222g t f t f t f t f t ππ⎡⎤=++⋅⎢⎥⎣⎦21020111()()sin 4()cos 4222g t f t f t f t f t ππ⎡⎤=⋅+−⎢⎥⎣⎦通过低通滤波器则输出正好是)(211t f 和)(212t f 。
(相干解调)4-7 设某信道具有均匀的双边噪声功率谱密度()n P f =0.5×10−3W/Hz ,在该信道中传输抑制载波的双边带信号,并设调制信号()m t 的频带限制在5kHz ,而载波为100kHz ,已调信号的功率为10kW 。
第四章 习题解答

1 第四章 习题解答3/150、试用实验方法鉴别晶体SiO 2、SiO 2 玻璃、硅胶和SiO 2 熔体。
它们的结构有什么不同?解答:利用X-射线粉末衍射检测。
晶体SiO 2——质点在三维空间做有规律的排列,各向异性。
SiO 2 熔体——内部结构为架状,近程有序,远程无序。
SiO 2 玻璃——各向同性。
硅胶——疏松多孔。
7/151、SiO 2 熔体的粘度在1000℃时为1014 Pa·s ,在1400℃时为107 Pa·s 。
SiO 2 玻璃粘滞流动的活化能是多少?上述数据为恒压下取得,若在恒容下获得,你认为活化能会改变吗?为什么?解答:(1)根据公式:)exp(0RTE ∆=ηη 1000℃时,η=1014 Pa·s ,T=1000+273=1273K , )1273314.8exp(10014⨯∆=E η (1) 1400℃时,η=107 Pa·s ,T =1400+273=1673K ,)1673314.8exp(1007⨯∆=E η (2) 联立(1)和(2)式解得:η0 = 5.27×10-16 Pa·s ,△E = 713.5 kJ/mol(2)若在在恒容下获得,活化能不会改变。
因为活化能是液体质点作直线运动所必需的能量。
它与熔体组成和熔体[SiO 4]聚合程度有关。
212/151、一种用于密封照明灯的硼硅酸盐玻璃,它的退火点是544℃,软化点是780℃。
求:(1)这种玻璃粘性流动的活化能;(2)它的工作范围;(3)它的熔融范围。
解答:(1)根据公式:)exp(0RTE ∆=ηη 退火点544℃, η=1012Pa·s ,T=544+273=817K , )817314.8exp(10012⨯∆=E η (1) 软化点为780℃,η=4.5×106 Pa·s ,T=780+273=1053K ,)1053314.8exp(104.506⨯∆=⨯E η (2)联立(1)和(2)式解得:η0 = 1.39×10-12 Pa·s ,△E = 373.13 kJ/mol 。
04化工原理第四章习题答案

4-1、燃烧炉的平壁由下列三种材料构成:耐火砖的热导率为,K m W 05.111−−⋅⋅=λ厚度mm 230=b ;绝热砖的热导率为11K mW 151.0−−⋅⋅=λ;普通砖的热导率为11K m W 93.0−−⋅⋅=λ。
若耐火砖内侧温度为C 10000,耐火砖与绝热砖接触面最高温度为C 9400,绝热砖与普通砖间的最高温度不超过C 1300(假设每两种砖之间接触良好界面上的温度相等)。
试求:(1)绝热砖的厚度。
绝热砖的尺寸为:mm 230mm 113mm 65××;(2)普通砖外测的温度。
普通砖的尺寸为:mm 240mm 1200mm 5××。
(答:⑴m 460.02=b ;⑵C 6.344°=t )解:⑴第一层:1121λb t t AQ −=第二层:2232λb t t AQ −=⇒()()32222111t t b t t b −=−λλ⇒()()130940151.0940100023.005.12−=−b ⇒m446.02=b 因为绝热砖尺寸厚度为mm 230,故绝热砖层厚度2b 取m 460.0,校核:()()3940460.0151.0940100023.005.1t −=−⇒C 3.1053°=t ;⑵()()43332111t t b t t b −=−λλ⇒C 6.344°=t 。
4-2、某工厂用mm 5mm 170×φ的无缝钢管输送水蒸气。
为了减少沿途的热损失,在管外包两层绝热材料:第一层为厚mm 30的矿渣棉,其热导率为11K m 0.065W −−⋅⋅;第二层为厚mm 30的石棉灰,其热导率为11K m 0.21W −−⋅⋅。
管内壁温度为C 3000,保温层外表面温度为C 400。
管道长m 50。
试求该管道的散热量。
(答:kW 2.14=Q )解:已知:11 K m 0.065W −−⋅⋅=λ,11 K m 0.21W −−⋅⋅=λ查表得:11K m W 54−−⋅⋅=钢λ()34323212141ln 1ln 1ln 12d d d d d d t t lQλλλπ++−=其中:0606.016.017.0ln ln 12==d d ,302.017.023.0ln ln 23==d d ,231.023.029.0ln ln 34==d d()1m W 28421.0231.0065.0302.0450606.0403002−⋅=++−=πlQ ,kW 2.14W 1042.1502844=×=×=Q 。
第四章 习题答案
习题4.1选择填空1、选用差分放大电路的原因是 A 。
A 、克服温漂B 、 提高输入电阻C 、稳定放入倍数2、用恒流源取代长尾式差分放大电路中的发射极电阻Re ,将使电路的 B 。
A 、差模放大倍数数值增大B 、抑制共模信号能力增强C 、差模输入电阻增大 3、差动放大器中的差模输入是指两输入端各加大小___相等_____、相位___相反____的信号。
4、设差放电路的两个输入端对地的电压分别为v i1和v i2,差模输入电压为v id ,共模输入电压为v ic ,则当v i1=50mV ,v i2=50mV 时,v id =_0mV __,v ic =_50mV __;当v i1=50mV ,v i2=-50mV 时,v id =_100mA __,v ic =_0mA__;当v i1=50mV ,v i2=0V 时,v id =_50mV __,v ic =_25mA __。
5、电流源常用于放大电路,作为_A ___(A.有源负载,B.电源,C.信号源),使得放大倍数__A __(A.提高,B.稳定)。
6、电压放大电路主要研究的指标是 a 、 b 、 c ;功率放大电路主要研究的指标是 d 、 e 、 f 、 g 、(a 电压放大倍数 b 输入电阻 c 输出电阻 d 输出功率 e 电源提供的功率 f 效率 g 管耗)7、功率放大电路中,___甲类____功率放大电路导通角最大;_____乙类___功率放大电路效率较高。
(甲类、乙类、甲乙类) 8、甲类功放效率低是因为 B 。
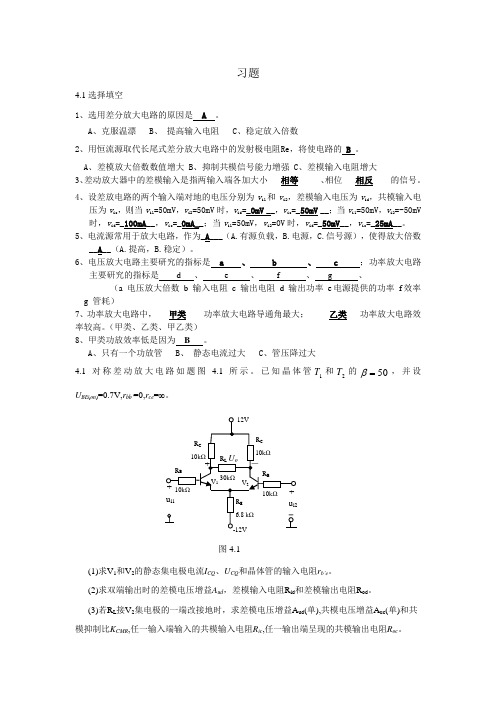
A 、只有一个功放管B 、 静态电流过大C 、管压降过大4.1对称差动放大电路如题图 4.1所示。
已知晶体管1T 和2T 的50=β,并设U BE (on )=0.7V,r bb ’=0,r ce =∞。
(1)求V 1和V 2的静态集电极电流I CQ 、U CQ 和晶体管的输入电阻r b’e 。
(2)求双端输出时的差模电压增益A ud ,差模输入电阻R id 和差模输出电阻R od 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1,2-加成生成的中间体正碳离子为P-л共轭和有三个C-H键与其超共轭,而1,4-加成的中间体比其少三个C-H键超共轭。
2.为什么1,4-加成产物比1,2-加成产物稳定?
解:1,2-加成产物有一个C-H键与双键超共扼,而1,4-加成产物有五个C-H键与双键超共扼。与双键超共扼的C-H键越多,产物越稳定。
十四、1,3-丁二烯和氯化氢在醋酸中室温下加成,可以得到78%的CH3CH(Cl)CH=CH2和22%的CH3CH=CHCH2Cl的混合物,此混合物再经过长时间加热或和三氯化铁一起加热,则混合物的组成改变为前者仅占25%,后者占75%,解释原因。
解:低温反应,为动力学控制反应,由中间体的稳定性决定反应主要产物,为1,2-加成为主。
第四章第四章炔烃、二烯烃
第五章
二、用系统命名法或衍生物命名法命名下列化合物。
三、写出下列化合物的构造式。
四、写出1-丁炔与下列试剂作用的反应式。
五、完成下列反应式。
六、以反应式表示以丙炔为原料,并选用必要的无机试剂,合成
下列化合物。
七、完成下列反应式。
八、指出下列化合物可由那些原料通过双烯合成而得。
CH2=CHCH=CHCH=CH2
分子式:C6H8为1,3,5-己三烯。
(完)
作业:94页,2,4,5,6,7,8,9,10,11,14
高温时反应为热力学控制反应,由产物的稳定性决定主要产物,1,4-加成产物比1,2-加成稳定。
十五、一个碳氢化合物,测得其相对分子质量为80,催化加氢时,10mg样品可吸收8.40mL氢气。原样品经臭氧化反应后分解,只得甲醛和乙醛。问这个烃是什么化合物?
解:10mg样品为0.125mmole
8.40mL氢气为0.375mmole。可见化合物分子中有三个双键或一个双键,一个叁键。但是根据臭氧化反应产物,确定化合物分子式为:
十二、试用适当的化学方法将下列混合物中的少量杂志除去。
1,1,除去粗乙烷中少量的乙炔。
解:将混合物通入硝酸银的氨溶液,乙炔生成乙炔银而沉淀除去。
2,2,除去粗乙烯中的少量乙炔。
解:将混合物进行Lindlar催化加氢,则乙炔变为乙烯。
十三、
1.1,3-丁二烯和溴化氢的1,2-加成和14-加成,那种速度快?为什么?
九、以反应式表示以乙炔为原料,并可选用必要无机试剂合成下列化合物。
十、以四个碳原子以下烃为原料合成下列化合物。
十一、用化学方法区别下列各组化合物。
1.乙烷、乙烯、乙炔
解:
乙烷
乙烯
乙炔
Br2/CCl4
不变褪色ຫໍສະໝຸດ 褪色硝酸银氨溶液不变
2.CH3CH2CH2C三CH和CH3C三CCH3
解:分别加入硝酸银氨溶液,有炔银沉淀的位1-丁炔。
