第5章-圆管流动
流体力学第5章不可压缩流体的一维层流流动

微元体上z方向的各力之和为:
p
rz
dz
r β g
p
u
p z
dz
u
40
① 切应力方程
将上述各式代入(5-1)并整理得关于切 应力的微分方程
( rz r ) p p r ( g cos ) r r z z
*
其中,p*=p-ρgzcosβ,әp*/әz可用-Δp*/L代替, 说明流动过程为压降过程 其中
ω
kR R
33
解:此题为狭缝剪切流。由于间隙远 小于筒体半径,可近似认为水平狭缝中的 剪切流。由狭缝流动的剪切应力分布公式:
yx
1 p U (b 2 y ) 2 x b
*
其中外筒壁面的速度U=R ω,狭缝宽度 b=(1-k)R,对于水平剪切流,әp*/әx=0,于是 可得切应力分布为:
y x
β g
25
5.2.3 水平狭缝压差流动的流动阻力
对于水平狭缝,由于β=π/2,故有әp*/әx= әp/әx=const 。则可用-△p/L代替,其中△p是 流动方向上长度为L的流道的进出口压力之差, △p=p0-pL,称为压力降。由于是压差流,则两 平壁固定,则有U=0,得水平狭缝压差流的平 均速度为:
5
若切应力所在平面的外法线与y轴正向相反, 规定指向x轴负方向的切应力为正,反之为负。
y x z z y
x
yx 0
yx 0
第三步.将式(5-2)代入式(5-1),则 得关于流体速度的微分方程——流体微分方 程。
6
5.1.2
常见边界条件
常见工程问题的流场边界条件可分为三类: (1)固壁—流体边界:由于流体具有粘滞性,
* 2
流体力学D课件 第五章

hf
Vd
对数形式为
lg 1.806 lg Re
在尼古拉兹图中为一条斜直线。
(2) 过渡区 (2300 Re 4000) (3) 湍流完全光滑管区
情况复杂,无单一计算公式。
布拉修斯公式 (4000 Re 105 )
0.3164 Re0.25 基于湍流速度分布导出。
水头损失的两种形式
2 p1 v12 p2 v2 z1 1 z2 2 hw g 2g g 2g
hf hj
沿程损失
局部损失
流体克服粘性阻力 而损失的能量,流 程越长,损失越大
流体克服边界形状改变 所产生的阻力而损失的 能量,发生在局部范围
直圆管流动的沿程损失 1 达西公式 不可压缩粘性流体在内壁粗糙的直圆管中作定常流动时,压 强降低(损失)的表达式(可用量纲分析方法确定)
V12 V2 2 1 1 1 2 2 hm ( p1 p2 ) (V1 V2 ) V2 (V2 V1 ) 1 ( ) g 2g g 2g V1
V12 d12 2 V12 (1 2 ) K e1 2g 2g d2
d K e1 1 d
2. 等效粗糙度 穆迪引入等效粗糙度概念 。对实际商用管,粗糙度呈随机分 布,可通过与尼古拉兹实验曲线作对比,确定其等效粗糙度。 材料(新) 铆钉钢 ε(mm) 0.9~9.0
常用商用管的 等效粗糙度列于 右表中。
水泥 木板
铸铁 镀锌铁 镀锌钢 无缝钢
0.3~3.0 0.18~0.9
0.26 0.15 0.25 ~0.50 0.012 ~0.2
1 2
1
(
Re1=4.22×104,查Mooddy图得λ2=0.027 ,重新计算速度
流体力学第五章 管中流动-1

Re vd 1.0 0.1 76453 Rec 2300 6 1.308 10
管中流动为湍流。 (2) Rec vc d
vc
Rec
d
1.308 106 2300 0.03 0.1
2012年12月15日 20
5.2 圆管中的层流
本章所讨论的流体 1. 流体是不可压缩的; 2. 运动是定常的;
主要内容: • 速度分布 • 流量计算 • 切应力分布 • 沿程能量损失
2012年12月15日 21
过流截面上流速分布的两种方法
vd
我们知道当
较小,即速度和管子直径较小而粘度较大时出现层流
哈根-伯肃叶(Hagen-Poiseuille)定律, 它与精密实验的测定结果完全一致。
2012年12月15日 26
粘 度 的 测 定 方 法
利用哈根-伯肃叶(Hagen-Poiseuille)定律可以测定粘度,它是测 定粘度的依据。因为,根据公式可以导出:
pd 4
128qvl
pd 4t
4 A 4 Bh 2h 4cm S 2B vd 要使 Re H 2320 v 0.017 m / s dH
2012年12月15日 18
例题三:某段自来水管,d=100mm,v=1.0m/s,
水温10℃, (1)试判断管中水流流态? (2)若要保持层流,最大流速是多少?
(2)速度分布具有轴对称性,速度分布呈抛物线形。 (3)等径管路中,压强变化均匀。 (4)管中的质量力不影响流动性。
2012年12月15日 22
• 1.第一种方法 • 根据圆管中层流的流动特点,对N-S方程式
流体力学 第5章 圆管流动..

第5章圆管流动一.学习目的和任务1.本章学习目的(1)掌握流体流动的两种状态与雷诺数之间的关系;(2)切实掌握计算阻力损失的知识,为管路计算打基础。
2.本章学习任务了解雷诺实验过程及层流、紊流的流态特点,熟练掌握流态判别标准;掌握圆管层流基本规律,了解紊流的机理和脉动、时均化以及混合长度理论;了解尼古拉兹实验和莫迪图的使用,掌握阻力系数的确定方法;理解流动阻力的两种形式,掌握管路沿程损失和局部损失的计算;了解边界层概念、边界层分离和绕流阻力。
二.重点、难点重点:雷诺数及流态判别,圆管层流运动规律,沿程阻力系数的确定,沿程损失和局部损失计算。
难点:紊流流速分布和紊流阻力分析。
由于实际流体存在黏性,流体在圆管中流动会受到阻力的作用,从而引起流体能量的损失。
本章将主要讨论实际流体在圆管内流动的情况和能量损失的计算。
5.1 雷诺(Osborne Reynolds)实验和流态判据5.1.1 雷诺实验1883年,英国科学家雷诺通过实验发现,流体在流动时存在两种不同的状态,对应的流体微团运动呈现完全不同的规律。
这就是著名的雷诺实验,它是流体力学中最重要实验之一。
105如图5-1所示为雷诺实验的装置。
其中的阀门T1保持水箱A 内的水位不变,使流动处在恒定流状态;水管B 上相距为l 处分别装有一根测压管,用来测量两处的沿程损失f h ,管末端装有一个调节流量的阀门T3,容器C 用来计量流量;容器D 盛有颜色液体,T2控制其流量。
进行实验时,先微开阀门T3,使水管中保持小速度稳定水流,然后打开颜色液体阀门T2放出连续的细流,可以观察到水管内颜色液体成一条直的流线,如图5-2(a )所示;从这一现象可以看出,在管中流速较小时,它与水流不相混和,管中的液体质点均保持直线运动,水流层与层间互不干扰,这种流动称为层流(Laminar flow )。
比如,实际中黏性较大的液体在极缓慢流动时,属层流运动。
随后,逐渐开大阀门T3,增大管中液体流速,流速达到一定速度时,管内颜色液体开始抖动,具有波形轮廓,如图5-2(b )所示。
流体力学第5章管内不可压缩流体运动

64 Re
层流沿程水力摩阻系数
5.1.5 层流流动入口段长度
le 0.058Re d 湍流流动圆管入
le 25 ~ 40 d
口段长度
层流流动时管道 入口段长度
例题
原油沿管长为50m,直径为0.1m的管道 流动,已知动力粘度为0.285N.s/m3,密 度为950kg/m3,试确定(1)为保证层流 状态允许最大的流量;(2)相应的进 出口压力差(3)管路中流速的最大值 (4)壁面处的最大切应力。
5.1.0概述(阻力产生的原因)
1、阻力产生的原因 (1)外因 ③管壁粗糙度:一般而言,管路越粗糙, 水流阻力越大。 绝对粗糙度——壁面上粗糙突起的高度。 平均粗糙度——壁面上粗糙颗粒的平均 高度或突起高度的平均值。以e表示。 相对粗糙度——e/d ,管路绝对粗糙度 相对于管径的无量纲比值。
第5章 管内不可压缩流体运动
5.1 管内层流流动及粘性摩擦损失
【内容提要】 本节主要讨论流动阻力产生的原因 及分类 ,同时讨论两种流态及转化标准 并且在此基础上讨论圆管层流状态下流 速分布、流量计算、切应力分布、沿程 水头损失计算等规律。
5.1.0概述(阻力产生的原因)
1、阻力产生的原因 (1)外因 ①断面面积及几何形状 ② 管路长度 L:水流阻力与管长成正比。 ③管壁粗糙度:一般而言,管路越粗糙, 水流阻力越大。
5.1.1 层流与湍流流动
2、流态的判别: (1)临界流速
5.1.1 层流与湍流流动
2、流态的判别: (1)临界流速 缺点:临界流速的值随着管径以及工作 液粘度的变化而变化,并不是一个常数, 作为判别标准并不实用。
5.1.1 层流与湍流流动
2、流态的判别: (2)临界雷诺数 dv dv Re 对于圆管而言,雷诺数: 。 同临界流速类似,Re有上临界雷诺数Rec’和下 临界雷诺数 Rec之分。大量实验表明:不同流 体通过不同管径流动时,临界流速vc值不同, 但下临界雷诺数 Rec却大致相同,约在 2000~ 2300 范围之内。(上临界雷诺数 Rec’ 不稳定, 且Rec’ >Rec,约在4000~12000之间)。
流体力学课件 第五章 流动阻力

斜直线分布
r hf 1 g grJ 2 l 2
du grh f dr 2l
抛物线分布
2.流速分布 3.流量
Q
r0 0
gh f 2 2 u (r0 r ) 4l
gh f 2 2 gh f 4 (r0 r ) 2 rdr d 4l 128l
(3)粗糙区
莫迪
§5-7 局部损失计算
一、边界层理论
1.边界层:贴近平板存在 较大切应力、粘性影响不能 忽略的这一层液体 。
2.边界层的厚度:当流速达到 边界层的厚度顺流增大,即δ是x的函数。
处时,它
3.转捩点,临界雷诺数 转捩点:在x=xcr处边界层由层流转变为紊流的过渡点。
临界雷诺数: Recr
三、总水头损失
hw h f h j
i 1 i 1 n n
§5-2 流体流动的两种型态
一、雷诺实验
1883年英国物理学家雷诺按图示试验装置对粘性流体进行 实验,提出了流体运动存在两种型态:层流和紊流。
1 4
(a)
hf 5
(b)
2
3
(c)
1.层流 :管中水流呈层状流动,各层的流体质点互不掺混的 流动状态。
四、湍流切应力分布和流速分布
1.切应力分布
du 2 du 2 1 2 L ( ) dy dy
摩擦切应力 普朗特混合长度 : 附加切应力
y L ky 1 r0
k 称为卡门常数
k 0.36 ~ 0.435
2.流速分布 (1)近壁层流层: 管壁切应力
du u 0 dy y
§5-6 湍流的沿程损失
一、湍流沿程损失计算
第五章 管中流动

一、时均流动与脉动
根据图所示的一点上的速度变化曲线,用一 定时间间隔T内的统计平均值,称为时均流 速 v 来代替瞬时速度,即
1 v T
T
0
vt dt
瞬时速度v与时均速度 v 之间的差值称为脉动 速度,用v’表示,即
v v v
想一想:湍流的瞬时流速、 时均流速、脉动流速、断面 平均流速有何联系和区别?
流体粘性切应力与附加切应力的产生有着本质的区别,前者是流体分子无 规则运动碰撞造成的,而后者是流体质点脉动的结果。
2. 混合长度理论
湍流附加切应力 t v vy 中,脉动流速 v , vy 均为随机量,不能直接计 x x 算,无法求解切应力。所以1925年德国力学家普兰特比拟气体分子自由程的概念, 提出了混合长理论。
p P h f gqV gqV pqV Fv g
2 128lqV P pqV d 4
七、层流起始段
流体以均匀的速度流入管道后,由于粘性,近壁处产生边界层,边界 层沿着流动方向逐渐向管轴扩展,因此沿流动方向的各断面上速度分布不 断改变,流经一段距离L后,过流断面上的速度分布曲线才能达到层流或 湍流的典型速度分布曲线,这段距离L称为进口起始段。
二、混合长度理论
1. 湍流流动中的附加切应力
t v vy 0 x
——雷诺切应力 雷诺切应力的时均值
t v vy x
在湍流运动中除了平均运动的粘性切应力 而外,还多了一项由于脉动所引起的附加 切应力,总的切应力为
dv v v x y dy
速度分布按对数规律,特 点是速度梯度小。
一、临界速度与临界雷诺数
上临界流速vc:层流→湍流时的流速。 下临界流速vc:湍流→层流时的流速。 vc < vc Re= vd/ 上临界雷诺数Rec :层流→湍流时的临界雷诺数,它易受外界干扰, 数值不稳定。 下临界雷诺数Rec :湍流→层流时的临界雷诺数,是流态的判别标准。 判别依据:
《流体力学》第五章孔口管嘴管路流动
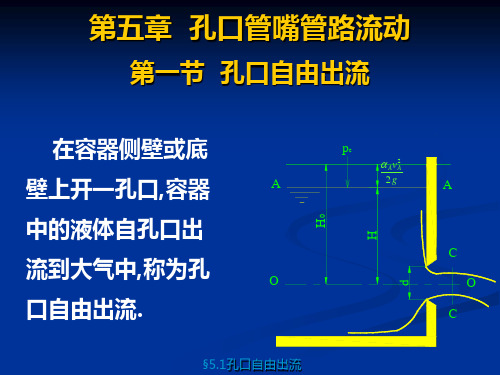
2g
A
C O
C
(C
1)
vc2 2g
(ZA
ZC )
pA
pC
Av
2 A
2g
令
H0
(Z A
ZC )
pA
pC
AvA2
2g
§5.1孔口自由出流
1
则有
vc
c 1
2gH0
H0
(Z A
ZC )
pA
pC
AvA2
2g
H0称为作用水头,是促使
力系数是不变的。
§5.4 简单管路
SH、Sp对已给定的管路是一个定数,它综合 反映了管路上的沿程和局部阻力情况,称为 管路阻抗。
H SHQ2
p SpQ2
简单管路中,总阻力损失与体积流量平方成 正比。
§5.4 简单管路
例5-5:某矿渣混凝土板风道,断面积为1m*1.2m, 长为50m,局部阻力系数Σζ=2.5,流量为14m3/s, 空气温度为20℃,求压强损失。
2v22
2g
1
vc2 2g
2
vc2 2g
令 H0 (H1 ζH12:局)液部体p阻1 经力p孔2系口数处1v的122g1 2v22
1
H1 H
H2
2
2
H0 (1 2 ) 2vcg2突ζ然2:液扩体大在的收局缩部断阻面力之系后数 C
C
§5.2 孔口淹没出流
1
c 1
2gH0
Q A 2gH0 A 2gH0
出流
H0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
e/d
Re
莫迪图λ
结论
0.03 0.1473 0.00102 1.732×106 0.02 用0.02重算
0.02 0.1358 0.0011 1.87×106 0.02
一致
d 0.298 1/5 0.1358m 即设计的最小管径为0.1358m
5.6 圆管湍流的沿程损失
5.6.3 非圆管的湍流沿程损失
——摩擦阻力系数,与
管径d、管中流速u和管 壁的光滑程度有关;
5.4 圆管中流体的湍流运动:
湍流剪应力分布与普朗特混合长度理论
1
2'
du dy
ux'
u
' y
平均值:
脉动值:
Re数较小时,1 占主导地位
Re数很大时, 2 1
牛顿内摩擦力 雷诺应力
y
u(y l')
第五章 圆管流动
内容提纲
5.1 雷诺实验与流态判据 5.2 圆管中流体的层流运动 5.3 椭圆管中流体的层流运动(自学) 5.4 圆管中流体的湍流运动 5.5 流体运动的两种阻力 5.6 圆管湍流的沿程损失 5.7 管路的局部损失 5.8 管路计算(自学)
按流体与固体接触情况来分,流体运动主要有下列四种形式。
1 2 umax
(层流时平均速度为最大速度的1/2)
5.4 圆管中流体的湍流运动:
湍流运动:三维随机运动,脉动性
瞬时速度 = 时均速度 + 脉动速度
u u u'
u 1
T
udt
T0
u' u u, 1 T u'dt 0
T0
湍流研究 时均法
圆管湍流分层:层流边层、过渡层、 核心湍流
5.1 雷诺实验与流态判据 5.1.1 雷诺实验
5.1.2 流体的两种流动状态
黏性流体按其力学参数(如速度、压力等)在时间与空间中是 否发生不规则脉动,分为层流与湍流两种流动状态 。
(1) 层流 黏性流体作层流运动时,流体微团间无宏观的互相掺混,
其参数没有不规则脉动,流线有条不紊,层次分明,摩擦阻力相 对于湍流而言就较小。这种流动称为层流。
镀锌管当量粗糙度δ=0.15mm,δ/d=0.00015/d 速度 v=4q/(πd2) = 0.2546/ d2 Re= ρvd/μ=0.2538 ×106/d
根据水头损失计算公式:
hf
l d
v2 2g
35 (0.2546 / d 2 )2
d
2g
50
d 0.298 1/5
λ
d (m)
m0kg0s0
Re为一无因次量,称为雷诺数。
这就是说,液体流动时的雷诺数若相同,则它的 流动状态也相同。另一方面液流由层流转变为湍流时 的雷诺数和由湍流转变为层流的雷诺数是不同的,前 者称为上临界雷诺数,后者为下临界雷诺数,后者数 值小,所以一般都用后者作为判别液流状态的依据, 简称临界雷诺数。当液流实际流动时的雷诺数小于临 界雷诺数时,液流为层流,反之液流则为湍流。常见 的液流管道的临界雷诺数可由实验求得。
1. 水力半径R
R A
χ——湿周
圆管: R A d 2 4 d d 4
d 2
a b
边长分别为a和b的矩形断面水力半径
L d
v2 2g
确定系数λ即可计算沿程阻力损失
p1
圆管层流
64 water, 75 : 80 oil
Re
Re
多段管路的沿程水头损失采用分段计算方法
hf
hf 1
hf
2
...
1
L1 d1
u12 2g
2
L2 d2
u22 2g
...
2
u
p2 R
多段管路 如何计算?
过渡区 层流边层 湍流核心区
5.4 圆管中流体的湍流运动:
湍流运动:水力光滑管、粗糙管
管壁粗糙度被层流“淹没”,湍流核 心区边界为光滑的层流底层
管壁粗糙度接触湍流核心区,影响核心 区流动,核心区边界具有“粗糙度”
水力光滑:Ⅲ区
δΔ
δΔ
水力粗糙:Ⅴ区 圆管湍流速度分布
30d Re
为什么选择 相对粗糙度?
a
e
c
d b
e f
不同线为 粘附不同 粗糙度砂 砾的圆管
d
f (Re), /d = 0, 1 , 1 , 1 , 1 , 1 , 1 1014 512 252 120 61 30
f
lg(Re)
λ为分段函数,随Re分为5段
5.6 圆管湍流的沿程阻力损失计算 尼古拉兹实验:层流、过渡、湍流
5.6 圆管湍流的沿程损失
如何查阅莫迪图?1.计算Δ/d 2.计算雷诺数 3. 查
Δ/d
5.6 圆管湍流的沿程损失
例:给水管长30m,直径d=75mm,材料为新铸铁管,流
量Q=7.25L/s,水温t=10℃,求该管段的沿程水头损失。
(铸铁管当量粗糙度取0.25mm)
分析:沿程损失计算公式应用,计算Re,相对粗糙度,
R
u
max
1
r R
2
上式即为管内层流时的速度分布表达式,u 随r 按抛物线分布, 在空间的速度分布图形则为一旋转抛物面。
(2) 平均速度
取半径为r,厚度为dr 的环形流体
R
作分析。设环形流体以速度u向
r
前运动,则体积流量dqv为
dr
u
管道材料 新氯乙烯管 铅管、铜管、 玻璃管 钢管 涂沥青铸铁管
常用工业管道的Δ
Δ(mm)
管道材料
0~0.002
镀锌钢管
0.01
新铸铁管
0.046 0.12
钢板制风管 混凝土管
Δ(mm) 0.15
0.15~0.5
0.15 0.3~3.0
5.6 圆管湍流的沿程损失
莫迪图:L.F. Moody,1940, Princeton 工业管实验结果
Re≤2320
层流
流型判据: 2320< Re<13800 过渡状态
(或为层流或为湍流)
Re ≥ 13800
湍流
5.2 圆管中流体的层流运动
流体在管内流动的受力分析
在长度为l的管段内划出半径
为r的圆柱形流体段作分析 〈。1〉压力(取流速方向为正)
P1 r 2 p1,P2 r 2 p 2
dqv ur 2r dr
层流时:ur
umax (1
r2 R2
)
故:dqv
umax 2r(1
r2 R2
)dr
u max
Δ p R2
4l
通过整个截面的体积流量为
qv
2umax
R r(1 r 2
0
R 2 )dr R 2 umax
2
平均速度:
u
qv
R 2
5.6 圆管湍流运动的沿程损失
1 尼古拉兹实验
hf
L
d
v2 2g
沿程水头损失计算公式
层流: 64 water, 75 : 80 oil
Re
Re
湍流:不同工况 λ 取不同数值
沿程阻力系数
尼古拉兹实验图 莫迪图
5.6 圆管湍流的沿程损失
f Re,V d
(1)实验曲线 lg(100λ)
(2) 湍流 当流体微团间互相掺混作无序地流动,其流速、压力等力学 参数在时间和空间中发生不规则脉动的流体运动,称为湍流,又 称为紊流。湍流是在大雷诺数下发生的,其基本特征是流体微团 运动的随机性。湍流中由于这种随机运动而引起的动量、热量和 质量的传递,其传递率比层流高很多。它一方面强化传递和反应 的效果;另一方面剧增了摩擦阻力和能量损耗。
λ=f(Re),实际意义不大
层流→湍流过渡区
a c
b d
Ⅲ区(cd线,lg(Re)>3.6,Re>4000) 湍流光滑区λ=f(Re)
水力光滑管:Δ<δ Re主导,δ对湍流核心无影响
Δ/d大的管子在Re较低时离开此线
Δ
0.3164 Re1/ 4
布拉休斯(Blasius)公式
δ
a
e
c
b
d
f
Ⅳ区(cd、ef之间的曲线族) 湍流过渡区λ=f(Re,δ/d)
p
2l
rdr
ur
p
2l
r2 2
c
因紧贴在管壁上的运动速度为零:即r = R, u= 0,代入上式求c
c Δ p R2
4l
ur
p
4l
(R2
r2)
在管中心,r =0, ur 达到最大值umax
u max
Δ p
4l
R2
ur
pR 2
4l
1
r
2
雷诺应力计算:普朗特混合长度理论 l '
u( y)
A
动量输送理论
u' x
l'
du dy
,
u' y
kl '
du dy
l' u(y l')
B
y l
x
2
u'xu' y
kl'2 ( d u )2
