第二章 第一节 圆曲线半径
圆曲线要素及计算公式
第二章圆曲线要素及计算公式
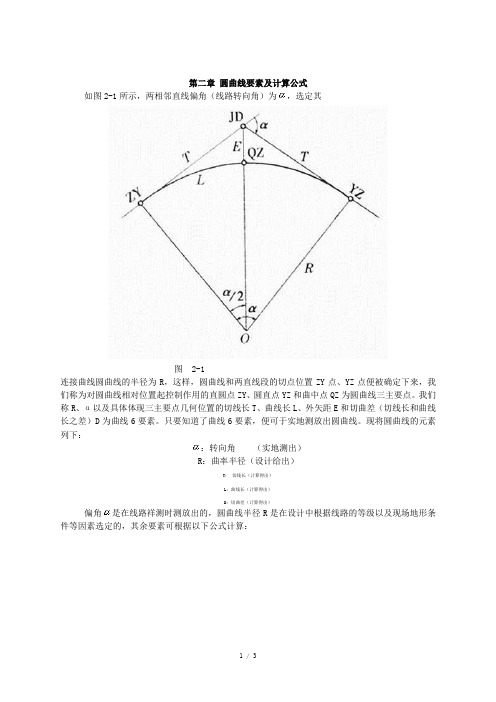
如图2-1所示，两相邻直线偏角（线路转向角）为，选定其
图2-1
连接曲线圆曲线的半径为R，这样，圆曲线和两直线段的切点位置ZY点、YZ点便被确定下来，我们称为对圆曲线相对位置起控制作用的直圆点ZY、圆直点YZ和曲中点QZ为圆曲线三主要点。
我们称R、α以及具体体现三主要点几何位置的切线长T、曲线长L、外矢距E和切曲差（切线长和曲线长之差）D为曲线6要素。
只要知道了曲线6要素，便可于实地测放出圆曲线。
现将圆曲线的元素列下：
：转向角（实地测出）
R：曲率半径（设计给出）
T：切线长（计算得出）
L：曲线长（计算得出）
D：切曲差（计算得出）
偏角是在线路祥测时测放出的，圆曲线半径R是在设计中根据线路的等级以及现场地形条件等因素选定的，其余要素可根据以下公式计算：
温馨提示：最好仔细阅读后才下载使用，万分感谢！。
圆曲线
第十章 曲线测设曲线测设是施工测量中的常用方法，是测量工作的一项重要技术。
它是几何大地测量学中建立国家大地控制网的主要方法之一，也是为地形测图、测量和各种工程测量建立控制点的常用方法第一节 线路平面组成和平面位置的标志铁路与公路线路的平面通常由直线和曲线构成，这是因为在线路的定线中，由于受地形、地物或其他因素限制,需要改变方向。
在改变方向处，相邻两直线间要求用曲线连结起来,以保证行车顺畅安全。
这种曲线称平面曲线。
铁路与公路中线上采用的平面曲线主要有圆曲线和缓和曲线。
如图10-1所示,圆曲线是具有一定曲率半径的圆弧；缓和曲线是连接直线与圆曲线的过渡曲线,其曲率半径由无穷大(直线的半径)逐渐变化为圆曲线半径。
根据铁道部公布的《铁路工程技术规范》规定,在铁路干线线路中都要加设缓和曲线；但在地方专用线、厂内线路及站场内线路中,由于列车速度不高,有时可不设缓和曲线,只设圆曲线。
在地面上标定线路的平面位置时,常用方木桩打入地下,并在桩面上钉一小钉,以表示线路中心的位置,在线路前进方向左侧约0.3 m 处打一标志桩,写明主桩的名称及里程。
所谓里程是指该点离线路起点的距离,通常以线路起点为K 0+000.0。
图10-2中的主桩为直线上的一个转点(ZD )，它的编号为31；里程为K 3+402.31，K 3表示3 km ；402.31 表示公里以下的米数,即注明此桩离开线路起点的距离为3 402.31 m 。
第二节 圆曲线及其测设一、圆曲线概述 （一）圆曲线半径我国《新建铁路测量工程规范》和《铁路技术管理规程》中规定,在正线上采用的圆曲线半径为4000、3000、2500、2000、1800、1500、1200、1000、800、700、600、550、500、450、400和350米。
各级铁路曲线的最大半径为4000米。
Ⅰ、Ⅱ级铁路的最小半径在一般地区分别为1000米和800米，在特殊地段为400米；Ⅲ级铁路的最小半径在一般地区为600米，在特殊困难地区为350米。
道路平面设计之道路平面线形
2 h
l
y
=
l3 6R lh
−
l7 336 ⋅ R 3lh3
l ―回旋线上任一点到 曲线起点的曲线长度
R―主曲线半径 lh ―缓和曲线长度
坐标原点在ZH、HZ
（4）在圆曲线上任意点的坐标公式
ϕm
=
αm
+
β0
=
90
π
⋅ ( 2lm + lh R
)
x = q + R ⋅sin ϕm
y = ΔR + R(1− cosϕm )
三. 缓和曲线
2、缓和曲线的选择
（1）缓和曲线轨迹特点：由直线驶入圆曲线 转弯时，其轨迹上的任一点的曲率半径与其行 程l（自转弯开始点算起）成反比，此轨迹方程 为回旋曲线方程。因此我国《标准》规定缓和 曲线采用回旋曲线。
三. 缓和曲线
（2）缓和曲线的一般方程式：
ρ ⋅l = C
(2-26)
为了设计方便，使量纲一致，故令A2=C，则
一. 直 线
断背曲线：互相通视的同向曲线间若插以短直 线，容易产生把直线和两端的曲线看成为反向曲 线的错觉，当直线过短时甚至把两个曲线看成是 一个曲线，这种线形破坏了线形的连续性，且容 易造成驾驶操作的失误，通常称为断背曲线。
设计中应尽量避免。
一. 直 线
断背曲线
X 直线的计算
一. 直 线
不设超高最小半径（m） 5500 4000 2500 1500 600 350 150
二. 圆曲线
3、平曲线长度（curve radius）
（1）平曲线最小长度规定
① 从驾驶员操纵方便、行车舒适性以及视觉要求来 看，应对平曲线长度加以限制。
高中数学人教B版必修二第二章2.3.1 圆的标准方程课件
奥运五环 日出东方
车行天下
概念形成 问题1：圆的定义是什么？
M
平面内到一定点的距离等于定长的点的轨迹是圆
C·.
圆心C
半径 r 动点M
CM r
概念形成 问题2：根据圆的定义，确定一个圆需要哪些条件？
M r
•C
圆心C 半径r
圆的位置 圆的大小
概念形成
反之，适合这个方程的解为坐标的点 M (x, y) ，
都在 C 上吗？
CM r
概念形成 问题5：两个方程之间有什么关系？
(x a)2 (y b)2 r2
x2 y2 r2
圆心 C(a,b) ，半径 r
圆心 C(0, 0) ，半径 r
概念形成 问题6：圆的标准方程由哪些量决定？方程在结构形式上具有 什么特点？
合作与探究
问题3：类比直线方程的研究方法，如何确定圆的方程？
M
•C
(x a)2 (y b)2 r2 x2 y2 r2
概念形成 问题4：类比直线方程的概念，上述两个方程是圆的方程吗？
y
M r
•C
思
O
x
考
以方程 (x a)2 ( y b)2 r2 推导为例，
我们可以发现
C 上任意一点 M 的坐标 (x, y) 都满足这个方程；
根据两点间的距离公式可得： (x a)2 (y b)2 r
列式
两边平方可得：(x a)2 (y b)2 r2 化简 验证
概念深化（二） 问题8：在平面直角坐标系中，如何判定平面上一个点 M 0 (x0 , y0 ) 与圆 (x a)2 ( y 的b位)2 置 r关2 系呢？
y M2
圆曲线
（3）增加燃料消耗和轮胎磨损
μ 使车辆的燃油消耗和轮胎磨损增加。
横向力系数μ
燃料消耗（%） 轮胎磨损（%）
0
100
100
0.05
105
160
0.10
110
220
0.15
115
300
0.20
120
390
（4）行旅不舒适 μ 值的增大，乘车舒适感恶化。 当μ 〈0.10时，不感到有曲线存在，很平稳； 当μ = 0.15时，稍感到有曲线存在，尚平稳； 当μ = 0.20时，己感到有曲线存在，稍感不稳定； 当μ = O.35时，感到有曲线存在，不稳定； 当μ = 0.40时，非常不稳定，有倾车的危险感。
（4）选用曲线半径时，应注意前后线形的协调，不应 突然采用小半径曲线；
（5）长直线或线形较好路段，不能采用极限最小半径。
（6）从地形条件好的区段进入地形条件较差区段时， 线形技术指标应逐渐过渡，防止突变。
（三）圆曲线最大半径
选用圆曲线半径时，在与地形等条件相适应的前提 下应尽量采用大半径。
圆曲线几何元素为：
α T Rtg
2 L π αR
180 α
E R(sec 1) 2
J 2T L
曲线主点里程桩号计算：
计算基点为交点里程桩号，记为JD，
ZY=JD-T
YZ=ZY+L
QZ=ZY+L/2
JD=QZ+J/2
二、圆曲线半径
（一）计算公式与因素 根据汽车行驶在曲线上力的平衡式计算曲线半径：
μ——横向力系数；
完整高速铁路第二章
结果分析加试验表明
缓和曲线类型 并不是制约行车运行速度的决定性因素， 缓和 曲线的长度 也就是缓和曲线的动力学参数取值，才是影响行 车速度的关键。
考虑到三次抛物线线形简单、设计方便、现场运用经验丰富等特 点，高铁仍以 三次抛物线为首选线型 。困难条件下，缓和曲线不 能保证足够长度时，可采用 三次抛物线圆改善型缓和曲线 。
? 11.8
v2 max
[h ? hq ]
最高速度
（km/h）
200 250 300 350
纯高速线最小圆曲线半径（m）
圆曲线最小半径(课堂PPT)
10
超高横坡度
公路等级 一般地区
汽车专用公路 一般公路
高速 一级 二级 三级 四级 公路 公路 公路 公路 公路
10%
8%
积雪冰
6%
冻地区
11
根据汽车行驶在曲线上力的平衡式计算曲线最小半径：
R V2
127( i)
行车速度
横向力系数
超高横坡度
极限最小半径 最小半径的计算 一般最小半径
不设超高的最小半径
R V2
1202
5569.29m 符合规定
127( i) 127(0.035 0.015)
与《公路工程技术标准》规定相对照。
表5-1
24
考虑了汽车在这种曲线上以设计速度或接近设计速度
行驶时，旅客有充分的舒适感。
推
荐
采
考虑到地形比较复杂的情况下不会过多增加工程量。
用
19
3.不设超高的最小半径 不必设置超高就能满足汽车行驶稳定性的最小半径。
20
三种最小半径的对比
21
例：
22
例：已知某平原区高速公路，其计算行车速度V=120km/h，
一、圆曲线最小半径的重要性
设计合理的圆曲线 设计不良的圆曲线
控制性因素：
实
圆曲线最小半径
例
1
“恐怖的百慕大”——320国道黄花桥路段
设计不合理，最小弯道半
径为250米。
而黄花桥最小弯道半径仅
216米。
The important of circular cu2 rve
二、圆曲线最小半径的计算公式
一般情况，超高
有些情况，路拱
3
F Gv 2 gR
X F cos ih G sin ih
第2讲 圆曲线设计概要
第一节 道路平面设计 第2讲 圆曲线设计
主讲人：于国锋
圆曲线
• 圆曲线半径及其选择
–汽车转弯时的横向稳定性分析
Ga—汽车总重
Y
基 础 工 程 技 术 专 业 课 程
C—离心力
hg—汽车重心高度 α—道路横向坡度角 b —汽车轮距(m) i0—路拱横坡度
道 路 工 程 技 术
脚踏实地 追求卓越
8%
最大超高 6% 4% 不设超高 最小半径（ m） 路拱≤2.0% 路拱>2.0%
650
710 810 5500 7500
400
440 500 4000 5250
250
270 300 2500 3350
125
135 150 1500 1900
60
60 65 600 800
30
35 40 350 450
解：根据公式计算得： T=71.6546 L=140.6735 E=8.4386 D=2.6356 曲线主点桩号计算如下： ZY=JD- T=87369.7754 YZ=ZY+ L=87510.4290 QZ=YZ-L/2=87440.0922 JD=QZ+D/2=87441.4100
脚踏实地 追求卓越
极限最小半径
不设超高最小半径
道 路 工 程 技 术
脚踏实地 追求卓越
圆曲线
• 圆曲线半径及其选择
–圆曲线最小半径
例题：高速公路设计车速为V=120km/h，路拱横坡度为2%，若横向力系数采
用0.040。试计算不设超高园曲线最小半径（取500米的整数倍）。 解：根据汽车行驶在曲线上力的平衡方程式: 可计算如下：
圆曲线
2021-2022年高中数学 第二章综合曲线与方程知识精讲 文 北师大版选修1-1
2021-2022年高中数学第二章综合曲线与方程知识精讲文北师大版选修1－1一、教学内容选修1－1 曲线与方程二、教学目标1、理解曲线与方程的概念及进一步认识坐标法的应用。
2、能用直译法、定义法、相关点法等方法求简单的曲线方程。
3、进一步培养学生对数学思想方法的应用能力、推理能力、计算能力。
三、知识要点分析1、曲线的方程与方程的曲线在平面直角坐标系中，曲线C上的点与二元方程f（x，y）=0的实数解建立如下关系：（1）曲线上的点的坐标x，y都是方程f（x，y）=0的解。
（2）以方程f（x，y）=0的解x，y为坐标的点（x，y）都在曲线C上。
则曲线C叫方程f（x，y）=0的曲线，方程f（x，y）=0叫曲线C的方程。
2、求曲线方程的步骤：（1）建系——建立适当的坐标系。
（2）设点——设轨迹上任意点P（x，y）（3）列式——写出满足某种条件的动点P（x，y）的关系式。
（4）代换——将动点P（x，y）转化为f（x，y）=0并化简。
（5）证明——证明所求的方程为符合条件的动点轨迹方程。
3、求曲线轨迹方程的几种常用的方法：求曲线的轨迹方程常采用的方法有直译法、定义法、代入法、参数法。
（1）直译法：是将动点满足的几何条件或者等量关系，直接坐标化，列出等式化简即得动点轨迹方程。
（2）定义法：若动点轨迹的条件符合某一基本轨迹的定义（如椭圆、双曲线、抛物线、圆等），可用定义直接探求。
（3）相关点法：根据相关点所满足的方程，通过转换而求动点的轨迹方程。
【典型例题】考点一：用直译法求曲线的轨迹方程例1：已知A、B为两定点，动点M到A与到B的距离比为正的常数λ，求点M的轨迹方程。
【思路分析】可设|AB|=2a（a>0），然后建立如图所示的坐标系，此时A（－a，0），B （a，0），设M的坐标为（x，y），表示出|MA|，|MB|，根据已知条件得：，然后再化简。
解：建立坐标系如图所示，设M （x ，y ）是轨迹上任意一点。
《圆曲线的测设》课件
总结与展望
圆曲线测量的总结
圆曲线测量是交通工程中的重要一环，测量精度和质量对工程建设有重要影响。需要重视和 加强相关人员的培训和管理。
未来圆曲线测量的发展方向
随着科技和工程技术的发展，圆曲线测量也将不断创新和完善。发展方向可能是在测量精度、 测量速度、测量范围等方面进行改进和提升。
参考文献
1. 交通运输部. 道路工程设计规范. 北京: 化学工业出版社, 2018. 2. 中国测绘出版社. 实用测量学手册. 北京: 中国测绘出版社, 2019.
测量要点及方法
圆曲线的要素
圆曲线的要素包括圆半径、 曲线长度、切线长度、切 角和曲率半径等。测量圆 曲线需要准确测量这些参 数。
圆曲线的测量方法
圆曲线测量包括弧长方法、 切线方法和坐标法等多种 方法。选择合适的方法可 提高测量效率和准确度。
水准测量及对高差的 影响
水准测量是圆曲线测量中 的重要一步，它能够实现 高度的测量。同时需要注 意高差对圆曲线测量的影 响。
圆曲线的测设
本PPT课件介绍圆曲线的定义、特点、作用、优点、测量方法、测量工具及 仪器、测量示例和实践案例、注意事项和问题解答、总结与展望。
引言
圆曲线的定义和特点
圆曲线是道路或轨道中的曲线，它呈现出一段弧 线与圆弧的形态。圆曲线具有曲率连续、道路平 稳等特点。
圆曲线的作用和优点
圆曲线在交通路线的建设中具有重要的作用，它 能够缓解路线转弯的限制，实现道路的平稳过渡， 提高行车安全性和车速，同时也节省了土地使用。
圆曲线在实践案例中的应用
圆曲线应用广泛，如铁路中的过弯路段、高速公 路的汇入汇出口等等。这些案例显示了圆曲线在 交通建设中的重要作用和价值。
圆曲线要素及计算公式
圆曲线要素及计算公式前言《礼记》有云：大学之道，在明德，在亲民。
在提笔撰写我的毕业设计论文的时候，我也在向我的大学生活做最后的告别仪式。
我不清楚过去的一切留给现在的我一些什么，也无从知晓未来将赋予我什么，但只要流泪流汗，拼过闯过，人生才会少些遗憾！非常幸运能够加入水利工程这个古老而又新兴的行业，即将走向工作岗位的时刻，我仿佛感受到水利行业对我赋予新的历史使命，水利是一项以除害兴利、趋利避害，协调人与水、人与大自然关系的高尚事业。
水利工作，既要防止水对人的侵害，更要防止人对水的侵害；既要化解自然灾害对人类生命财产的威胁，又要善待自然、善待江河、善待水，促进人水和谐，实现人与自然和谐相处。
这种使命，更让我用课堂中的知识用于实际生产中来。
特别是这两个月来的毕业设计，我越发感觉到学会学精测量基础知识对于我贡献水利是多么的重要。
所以，我越发不愿放弃不多的大学时光，努力提高自己的实践动手能力，而本学期的毕业设计，为我提供了绝好的机会，我又怎能放弃？刚刚从老师那里得到毕业设计的题目和任务时，我的心里真的没底。
作为毕业设计的主体工作，我们主要运用电子水准仪对某幢建筑物进行变形观测与计算，布设控制点进行平面控制测量和高程控制测量；用全站仪进行了中心多边行角度和距离的测量，并用条件平差原理进行平差，通过控制点的放样来计算土的挖方量，还有圆曲线的计算与测设。
而我研究的毕业课题是圆曲线测设。
大学的最后一个学期过得特别快，几乎每天扛着仪器，奔走在校园的每个角落，生活亦很有节奏。
今天我提笔写毕业论文，我的毕业设计也接近尾声。
不管成果如何，毕竟心里不再是没底了，挑着两个多月的辛苦换来的数据和成果，并不断的完善他们，心里感觉踏实多了。
在本次毕业设计论文的设计中要感谢水利系为我们的工作提供了测量仪器，还有各指导老师的教导和同学的帮助。
摘要：在公路、铁路的路线圆曲线测设中，一般是在测设出曲线各主点后，随之在直圆点或圆直点进行圆曲线详细测设。
曲线电子教本资料文档
ｖ≥300km/h时，R=25000ｍ。
２．抛物线形竖曲线
《设规》规定改建既有线和增建第二线时， 若既有线为抛物线形竖曲线，且折算竖曲 线半径不小于圆曲线形的规定时，则可保 留既有线的坡段连接标准。
３．连续短坡竖曲线
当相邻两坡段的坡度急剧变化时，可采 用连续短坡竖曲线连接。短坡长度应为钢 轨长度的倍数，一般为25～75ｍ，以利于 线路维修养护；坡度的变坡率由0.5‰～ 0.75‰，一般为0.5‰的倍数。，它的总长 不得小于200m。
2．圆曲线的最小半径Rmin
区间线路最小曲线半径
铁路等级 路段设计行车速度（km/h）
160
I
120
80
120 II
80
100
III 80
最小曲线半径（m）
一般
困难
2000
1600
1200
800
500
450
1000
800
450
400
600
550
400
广深准高速铁路最小曲线半径(m)
行车速度 （km/h）
＝95－53.1＝41.9mm
检算结果： h欠 ＝52.5mm＜75mm h过＝41.9mm＜50mm
符合规定要求。
故该曲线设置95mm的超高值。
第三节 外轨最大超高的允许值
1.稳定系数n
S1 n 2 S1
e 2e
2曲线上容许设置的最大超高
图2－2
保证列车稳定的安全值n=3。我国货车重心到轨 顶的高度H＝2220mm，则
《铁路线路维修规则》规定：实设最大超高，在 单线上不得大于125mm，在双线上不得大于 150mm。
简述圆曲线半径的类型及适用条件
简述圆曲线半径的类型及适用条件在数学和物理学中，圆曲线是一种常见的曲线形式。
圆曲线半径的类型和适用条件是圆曲线研究的重要内容。
本文将对圆曲线半径的类型和适用条件进行简述。
下面是本店铺为大家精心编写的3篇《简述圆曲线半径的类型及适用条件》，供大家借鉴与参考，希望对大家有所帮助。
《简述圆曲线半径的类型及适用条件》篇1一、圆曲线半径的类型圆曲线半径是指圆曲线上某一点的曲率半径。
根据圆曲线的曲率性质，圆曲线半径可以分为以下几种类型:1. 常数半径圆曲线：其半径为一个常数，即在圆曲线上所有点的曲率半径都相等。
2. 变量半径圆曲线：其半径为一个变量，即在圆曲线上不同点的曲率半径不同。
3. 径向变量半径圆曲线：其半径是一个径向变量，即在圆曲线上不同点的曲率半径与该点到圆心的距离有关。
4. 切向变量半径圆曲线：其半径是一个切向变量，即在圆曲线上不同点的曲率半径与该点处的切线方向有关。
二、圆曲线半径的适用条件圆曲线半径的适用条件主要取决于圆曲线的曲线形式和应用场景。
以下是一些常见的适用条件:1. 常数半径圆曲线适用于圆形、椭圆形等曲线，其半径为一个常数，适用于各种曲线形式。
2. 变量半径圆曲线适用于一些复杂的曲线形式，如螺旋线、花瓣曲线等，其半径随着曲线的变化而变化。
3. 径向变量半径圆曲线适用于一些具有径向对称性的曲线形式，如行星轨道、太阳系天体运动等，其半径随着距离圆心的距离的变化而变化。
4. 切向变量半径圆曲线适用于一些具有切向对称性的曲线形式，如涡旋、龙卷风等，其半径随着切线方向的变化而变化。
圆曲线半径的类型和适用条件是圆曲线研究的重要内容。
《简述圆曲线半径的类型及适用条件》篇2圆曲线半径是一种用于描述圆曲线的参数，它通常用于计算机图形学、数学和物理学等领域。
圆曲线半径有多种类型，每种类型都有其适用条件。
1. 常数半径：常数半径是指在圆曲线上，所有点的半径都相等的情况。
常数半径适用于圆曲线上的点是等距离分布的情况，例如圆形、正多边形等。
圆曲线半径与超高值
注：括号值为路拱大于2%时的不设超高最小半径
新的路线设计规范要求超高应该按照运行速度进行选取。
在进行运行速度计算后，根据这个公式反算
R=V2/127（f+i）
式中：V—运行速度(km/h)；
f—路面与轮胎间的横向力系数；
i—路面超高横坡度。
超高过渡段长度按下式计算：
LC = B △i/P
式中：LC —超高过渡段长度(m)；
B —旋转轴至行车道(设路缘带时为路缘带)外侧边缘的宽度(m)；
△i—超高坡度与路拱坡度的代数差(%)；
P —超高渐变率，即旋转轴与行车道(设路缘带时为路缘带) 外侧边缘线之间的相对坡度，其值如表7.5.4。
根据上式求得过渡段长度，应凑整成5m的倍数，并不小于20m的长度。
2第二章道路勘测设计
第六节
平面设计成果
一、直线曲线转角表 通过测角、量中线、配半径后的成果，反映设计者对 平面线形的布置意图，绘制平面图的依据。 内容： 1、交点号： JD12 2、交点桩号： K3+254 3、偏角值：α左=32°34′58″；α右=27°56′13″
4、曲线要素： 曲线半径 R ； 缓和曲线参数A2=R×LS； 缓和曲线长度LS (由计算或查表取得)；
α
hc
iF
Lc
B
ic i hc
（三）超高的构成
1、绕内边缘转（新建路）
2、绕中轴转（改建路）
二、弯道加宽(P36)
因弯道行驶时占路宽比直线宽，因此在弯道部分路基应加宽。 （一）加宽值计算 单车道：e=R- R 2 L2 R—平曲线半径 L—前保险杠到后轴的距离 R2-L2= R2+e2-2Re 由于2Re>> e2，因此略去e2 得e= L2/2R 考虑汽车的摆动幅度，在弯道上加宽。
（二）超高缓和段
1、边轴旋转法 超高缓和段LC=BiC/iF iC=tgα=hC/B ic——超高横坡度 i——路拱坡度 2、中轴旋转法 iF= hC/LC ，LC= hC/iF 因 hC=Bi/2+ BiC/2 得：LC=（B/2）×（iC+i）/iF iF 平区—1%；重区—2% 超高渐变率(P33) 边转与中转相比：LC边>LC中 LC采用5的倍数，不小于10M
（3）错车视距SZ （4）超车视距Sq （5）避让障碍视距S
二、视距标准
1、停车视距：
L1 Ss L0
S停=L1+SS+L0=Vt/3.6+V2K/254(Φ+i)+L0 V—Km/h t—S K—制动器使用系数1.2-1.4 Φ—纵向附着系数 i—纵坡度 上坡“+”下坡“-” V 120 Φ 0.29 计算完取整 平 110 100 0.31 80 60 50 0.31 0.33 0.35 二 重 40 平 75 三 重 30 平 40 40 0.38 30 0.44 四 重 20 20 0.44
第二章 第一节 圆曲线半径
第二节 圆曲线
❖ 不设超高最小半径是判断圆曲线设不设超高
的一个界限，当圆曲线半径大于或等于该公路等级 对应的不设超高的最小半径时，圆曲线横断面采用 与直线相同的双向路拱横断面，不必设计超高；反 之则采用向内倾斜单向超高横断面形式。
第二节 圆曲线
不设超高的圆曲线最小半径
表 2-6
设计速度（Km/h） 120 100 80 60 40 30 20
5. 《规范》规定圆曲线最大半径不宜超过10000m。
考虑汽车行驶的横向稳定性 考虑驾驶员操作 考虑燃料消耗和轮胎磨损 考虑乘车的舒适性
第二节 圆曲线
（1）考虑汽车行驶的横向稳定性 汽车在圆曲线上行驶的稳定性包括横向倾覆稳定性和横
向滑移稳定性。
汽车在设计和制造时，已充分考虑横向倾覆稳定性，在
正常装载和行驶情况下，不会在横向上产生倾覆。
在平曲线设计过程中，主要考虑横向滑移稳定性，即保
V2 127R
ih
（三）汽车转弯时横向稳定性分析
▪ 横向倾覆：汽车在平曲线上行驶时，由于横向力的 作用，使汽车绕外侧车轮触地点产生向外横向倾覆。
▪ 汽车内侧车轮支反力N1为0。 ▪ 倾覆力矩等于或大于稳定力矩。
1、横向倾覆平衡条件分析：
▪ 倾覆力矩：Xhg
稳定力矩：
b
bb
Y2(Fh iG2)G2
横向倾覆平衡条件分析：
▪ 倾覆力矩：Xhg
稳定力矩： Yb 2(Fh iGb 2)Gb 2
稳定、平衡条件：
Xhg
G
b 2
X b G 2hg
汽车在平曲线上行驶时，不产生横向倾覆的最小 平曲线半径R min：
Rmin
V2
127( b
2hg
圆曲线半径与超高值
＜ 360~ 290
＜ 320~ 240
＜ 200~ 135
1
文档来源为 :从网络收集整理 .word 版本可编辑 .欢迎下载支持 .
＜ 7 1070~
910
＜ 980~ 790
＜ 760~ 640
＜ 690~ 530
＜ 500~ 410
＜ 420~ 320
＜
＜
8 910~ 790~
790
650
＜ 640~ 540
＜ 290~ 240
＜ 240~ 170
＜ 240~ 190
＜ 170~ 125
＜ 190~ 150
＜ 150~ 115
20
最大超高
8%
6%
4%
＜ 150 ( ＜ 200) ~ 140 ＜ 140~
90 ＜ 90~
70
＜ 150 ( ＜ 200) ~ 110 ＜110~
70 ＜ 70~
40
＜ 150 ( ＜200) ~ 70
＜ 430~ 320
＜ 800~ 500 ＜ 500~ 320 ＜ 320~ 200
＜ 610~ 270
＜ 270~ 150
＜
＜
6 1280~ 1190~ ＜970~
710
1070 980
＜ 920~ 760
＜ 860~ 690
＜ 630~ 440
＜ 610~ 500
＜ 550~ 420
＜ 400~ 270
6%
4%
2%
超
＜600 ＜ 600 ＜600
＜ 600
＜ 350
＜ 350
＜ 350
＜ 350
高 2 ( ＜800) ( ＜800) ( ＜800) ( ＜800)
圆曲线半径
圆曲线半径
圆曲线半径是数学中最重要的概念之一，它有着深远的意义，影响着许多方面的计算和问题的解决。
为了更有效地利用圆曲线半径，本文将详细阐述它的定义、特性、计算方法以及一些实际应用。
从数学的角度来看，圆曲线半径定义为圆曲线中总长度与上下限（即有限范围）之比。
这意味着，当我们在一个有限的范围内，给定一条圆曲线，我们可以通过以下计算，求出这条圆曲线的圆曲线半径：首先，求出圆曲线上下限之间的总长度，然后将其除以上下限之比，得到的即是此圆曲线的半径。
圆曲线半径具有多种特征，其中最重要的是它可以指示出圆曲线的大小和形状。
换句话说，圆曲线半径可以用来衡量圆曲线的复杂度，例如，若一条圆曲线具有较大的圆曲线半径，则表明此圆曲线更加复杂，反之则简单。
此外，圆曲线半径也可用来比较圆曲线的长度，从而提供有效的圆曲线相似性检测的基础。
此外，圆曲线半径还可以用于计算问题及其答案的解决方案。
例如，如果要解决一个复杂的数学问题，我们可以通过寻找具有较大半径的圆曲线，从而求出问题的解决方案。
此外，圆曲线半径还可用于计算任意轨迹的圆心，而这些轨迹的圆心也可以用于求解更加复杂的问题。
此外，圆曲线半径还有广泛的实际应用，例如在机器视觉领域，它可以用于检测和识别图像特征；在机械设计领域，它可用于求解机械零件的外形形状；在视频服务器端，它可以用于提高视频流质量，
以便更好地进行视频流媒体服务。
综上所述，圆曲线半径是一个重要的数学概念，它在数学领域有着重要的意义，同时也有许多实际应用。
通过本文的介绍，可以更有效地利用圆曲线半径，从而实现一系列理想的结果。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第二节
圆曲线
不设超高的圆曲线最小半径
表 2-120 路拱 ≤2.0% 100 80 60 40 30 20
5500 4000 2500 1500
600
350
150
不设超 高最小 半径(m) 半径(m)
路拱＞ 路拱＞ 2.0%
7500 5250 3350 1900
汽车在平曲线上行驶时， 汽车在平曲线上行驶时，不产生横向倾覆的最小平 曲线半径R 曲线半径 min：
R min V2 ≥ b 127( + ih ) 2h g
V2 µ= − ih 127 R
2.横向滑移条件分析 横向滑移：汽车在平曲线上行驶时，因横向力的存 横向滑移： 汽车在平曲线上行驶时， 可能使汽车沿横向力的方向产生横向滑移。 在，可能使汽车沿横向力的方向产生横向滑移。 横向力大于轮胎和路面之间的横向附着力。 横向力大于轮胎和路面之间的横向附着力。 极限平衡条件： X = Yϕh ≈ Gϕh 极限平衡条件 ：
第二节 圆曲线
2．超高横坡度
（1）最大超高横坡度
ib max
考虑汽车在公路上的各种状况特别是兼顾快、 考虑汽车在公路上的各种状况特别是兼顾快、慢车的行驶安全 等必须满足： 等必须满足： (fw —一年中气候恶劣季节路面的横向摩阻系数 ） 一年中气候恶劣季节路面的横向摩阻系数 《规范》对各级公路最大超横坡度的规定见 表2-3 规范》 （2）最小超高横坡度 公路的超高横坡度不应该小于公路直线段的路拱横坡度， 公路的超高横坡度不应该小于公路直线段的路拱横坡度，否则 不利于公路的排水， 不利于公路的排水，因此有
1、横向倾覆平衡条件分析： 横向倾覆平衡条件分析： 倾覆力矩： 倾覆力矩：Xhg 稳定力矩： 稳定力矩：
b b b Y = (Fih + G) ≈ G 2 2 2
横向倾覆平衡条件分析： 横向倾覆平衡条件分析：
倾覆力矩：Xhg 倾覆力矩：
b b b 稳定力矩： 稳定力矩： Y = (Fih + G) ≈ G 2 2 2 b X b 稳定、平衡条件： 稳定、平衡条件： Xh g ≤ G µ= ≤ 2 G 2h g
（ 式 ２－１）
第二节 圆曲线
在指定车速V 在指定车速V下，最小 横向力系数
Rmin 决定于容许的最大
µmax
和该曲线的最大超高
ib(max) 。
对这些因素讨论如下： 对这些因素讨论如下： 横向力系数 超高横坡度
µ
ib
第二节 圆曲线半径
1．关于横向力系数
横向力系数可近似为单位车重上受到的横向力。 横向力系数可近似为单位车重上受到的横向力。 横向力的存在对行车产生不利影响，而且越大越不利， 横向力的存在对行车产生不利影响，而且越大越不利， 主要表现在以下几方面： 主要表现在以下几方面： 考虑汽车行驶的横向稳定性 考虑驾驶员操作 考虑燃料消耗和轮胎磨损 考虑乘车的舒适性
第二节 圆曲线
δ
无横向力作用 时的轮迹
有横向力作用 时的轮迹
横向力X
横向力X
a)
b)
轮胎横向变形
轮迹的偏移角
图2-3 汽车轮胎的横向偏移角
第二节 圆曲线
（3）考虑燃料消耗和轮胎磨损 由于横向力的影响， 由于横向力的影响，行驶在曲线上的汽车比在直线上的 汽车的燃料消耗和轮胎磨损都要大。 汽车的燃料消耗和轮胎磨损都要大。 （4）考虑乘车的舒适性 汽车行驶在弯道上，随横向力系数值的大小不同， 汽车行驶在弯道上，随横向力系数值的大小不同，乘客 将有不同的感受。 将有不同的感受。 研究表明：的舒适界限，由0.10到0.16随行车速度而变 研究表明：的舒适界限， 0.10到0.16随行车速度而变 设计中对高、低速路可取不同的数值。 化，设计中对高、低速路可取不同的数值。
F= Gv 2 gR
受力分析： 受力分析： 横向力X——失稳 失稳 横向力 竖向力Y——稳定 稳定 竖向力
（二）横向力系数 将离心力F与重力 与重力G分解为平行于汽车路面的横 将离心力 与重力 分解为平行于汽车路面的横 向力X和垂直于路面的竖向力 和垂直于路面的竖向力Y， 向力 和垂直于路面的竖向力 ，
ib,max ≤ fw
ib,m in
ib,m = il in
（il ——路拱横坡度 路拱横坡度） 路拱横坡度
第二节 圆曲线
各级公路圆曲线最大超高值
表2-3
公路等级 一般地区/% 一般地区/% 积雪冰冻 地区/% 地区/%
高速 一级 二级 三级 四级 10 6 8
第一节 圆曲线半径
圆曲线是公路平面设计中最常用的线形之一。 圆曲线是公路平面设计中最常用的线形之一。
第二节
圆曲线
不设超高最小半径是判断圆曲线设不设超高 的一个界限， 的一个界限，当圆曲线半径大于或等于该公路等级 对应的不设超高的最小半径时， 对应的不设超高的最小半径时，圆曲线横断面采用 与直线相同的双向路拱横断面，不必设计超高； 与直线相同的双向路拱横断面，不必设计超高；反 之则采用向内倾斜单向超高横断面形式。 之则采用向内倾斜单向超高横断面形式。
轮胎与路面间的摩阻系数） f 轮胎与路面间的摩阻系数 µ ≤ f （f——轮胎与路面间的摩阻系数
第二节 圆曲线
（2）考虑驾驶员操作 弯道上行驶的汽车，在横向力作用下， 弯道上行驶的汽车，在横向力作用下，轮 胎会产生横向变形， 胎会产生横向变形，使轮胎的中间平面与轮迹 前进方向形成一个横向偏移角， 前进方向形成一个横向偏移角，致使增加了汽 车在方向操纵上的困难，尤其是车速较高时， 车在方向操纵上的困难，尤其是车速较高时， 就更不容易保持驾驶方向上的稳定。 就更不容易保持驾驶方向上的稳定。 汽车轮胎的横向偏移角见图 汽车轮胎的横向偏移角见图2-3
第二章 平 面 设 计
第一节 第二节 第三节 第四节 第五节 第六节 第七节 第八节 第九节 圆曲线半径 圆曲线上的全超高 圆曲线上的全加宽 缓和段 缓和曲线 平曲线最小长度 行车视距 平面线形设计要点 平面设计成果
第一节
圆曲线半径
（一）离心力计算
一、汽车转弯时力的平衡
汽车在平曲线上行驶时会产生离心力， 汽车在平曲线上行驶时会产生离心力，其作用 点在汽车的重心，方向水平背离圆心。 点在汽车的重心，方向水平背离圆心。 离心力
一、圆曲线的几何要素及计算式 圆曲线的几何要素及计算式
切线长：T=R·tanα 切线长 外 距： E=R（secα－1） 式中： 式中： T—切线长 切线长，m； 切线长 E —外距 外距，m； 外距 L—曲线长 曲线长，m； 曲线长 J—切曲差（或校正值），m; 切曲差（或校正值） 切曲差 曲线长：L=Rα 曲线长 切曲差：J=2T－L 切曲差
Gv v X = F − Gih = − Gih = G ( − ih ) gR gR
采用横向力系数来衡量稳定性程度，其意义为单位车 采用横向力系数来衡量稳定性程度， 重的横向力， 重的横向力，即
X v µ= = − ih G gR
2
V2 µ= − ih 127 R
（三）汽车转弯时横向稳定性分析
横向倾覆： 汽车在平曲线上行驶时， 横向倾覆 ： 汽车在平曲线上行驶时 ， 由于横向力的 作用， 使汽车绕外侧车轮触地点产生向外横向倾覆。 作用 ， 使汽车绕外侧车轮触地点产生向外横向倾覆 。 汽车内侧车轮支反力N 汽车内侧车轮支反力N1为0。 倾覆力矩等于或大于稳定力矩。 倾覆力矩等于或大于稳定力矩。
0.15 0.15 0.16
8
8 400
8 250
8 125
8 55
8 30
8 15
圆曲线极限 650 最小半径（ 最小半径（m）
第二节
2.一般最小半径 2.一般最小半径
圆曲线
一般最小半径介于极限最小半径和不设超高最小半径之 间。一方面要考虑汽车以设计速度在这种小半径的曲线上行驶 时的安全性、稳定性和旅客有充分的舒适性， 时的安全性、稳定性和旅客有充分的舒适性，另一方面也要注 意到在地形比较复杂的情况不会过多的增加工程数量。 意到在地形比较复杂的情况不会过多的增加工程数量。 确定一般最小半径时，横向力系数μ和超高横坡度ib没有 确定一般最小半径时，横向力系数μ和超高横坡度i 取到极限最大值，都留有一定的余地。通常在路线设计时， 取到极限最大值，都留有一定的余地。通常在路线设计时，圆 曲线半径应尽量采用大于或等于一般最小半径。 曲线半径应尽量采用大于或等于一般最小半径。 《标准》规定了“一般最小半径”， 表２－５。 标准》规定了“一般最小半径”
R—圆曲线半径 圆曲线半径，m； α —转角 转角，（°） 圆曲线半径 转角
第二节
圆曲线
表 2-4
圆曲线极限最小半径
设计速度 （Km/h） Km/h） 横向力系数 µmax 超高值 ib（max）（%） max） 120 0.10 100 0.12 80 0.13 60 40 30 20 0.17
700
400
200
100
65
30
第二节
3.不设超高的最小半径 3.不设超高的最小半径
圆曲线
在设计速度一定时，当圆曲线半径较大时，离心力就比较小， 在设计速度一定时，当圆曲线半径较大时，离心力就比较小， 此时弯道即使采用与直线相同的双向路拱断面时，离心力对外 此时弯道即使采用与直线相同的双向路拱断面时， 侧车道上行驶的汽车的影响也很小；因此我国《标准》制 侧车道上行驶的汽车的影响也很小；因此我国《标准》 6 所示。 制定了“不设超高的最小半径” 制定了“不设超高的最小半径”，如 表2—6 所示。此时横向 力系数μ=0.035 0.015。 力系数μ=0.035 和横坡度 i = 0.015。
第二节
圆曲线
圆曲线一般最小半径
表 2--5
设计速度 （km/h） km/h） 横向力系数 µ 超高值i 超高值ib （%） 120 0.05 6 100 0.05 6 80 0.06 7 60 0.06 8 40 0.06 7 30 0.05 6 20 0.05 6