钢结构轴心受力构件PPT课件
合集下载
4-钢结构设计原理-轴心受力构件1 钢结构设计原理

第四章 轴心受力构件
4 轴
主要内容:
心
受 力
1、轴心受拉构件的强度和刚度
构
件 设
2、轴心受压构件的强度
计
3、轴心受压实腹式构件的整体稳定
4、轴心受压格构式构件的整体稳定
5、轴心受压实腹式构件的局部稳定
6、轴心受压格构式构件的局部稳定
7、轴心受力构件的刚度
学习目标
1.掌握轴心受拉构件强度的计算方法、净截面的概念;
4
轴
心 受
所谓分支点失稳,是指当荷载逐渐增加到某一数值
力 构
时,结构除了按原有变形形式可能维持平衡之外,还可
件 设
能以其他变形形式维持平衡,这种情况称为出现平衡的
计
分支。出现平衡的分支是此种结构失稳的标志。
对于受偏心压力的细长直杆,当荷载逐渐增大而趋
于某一数值时,其原有变形形式急剧增大,致使结构丧
失承载能力。这种失稳现象称为极值点失稳。
结构或构件在外力增加到某一数值时,稳定的平衡
状态开始丧失,稍有扰动,结构变形迅速增大,使结构 丧失正常工作的能力,称为失稳。
在桥梁结构中,总是要求沿各个方向保持稳定的平
衡,也即沿各个方向都是稳定的,避免不稳定的平衡或 随遇平衡。
结构稳定问题的两种形式:
第一类稳定问题,分支点失稳问题; 第二类稳定问题,极值点失稳问题。
4
轴 心 受 力 构 件 设 计
4.3.3轴压稳定理论的沿革——具有初始缺陷的实际轴心压杆的稳 定问题
有关轴心压杆的整体稳定问题的理论经历了由理想状态杆件的
单曲线函数关系到实际状态杆件多曲线函数关系的沿革。传统的
理想状态压杆的单曲线稳定理论认为轴压杆是理想状态的,它在
4 轴
主要内容:
心
受 力
1、轴心受拉构件的强度和刚度
构
件 设
2、轴心受压构件的强度
计
3、轴心受压实腹式构件的整体稳定
4、轴心受压格构式构件的整体稳定
5、轴心受压实腹式构件的局部稳定
6、轴心受压格构式构件的局部稳定
7、轴心受力构件的刚度
学习目标
1.掌握轴心受拉构件强度的计算方法、净截面的概念;
4
轴
心 受
所谓分支点失稳,是指当荷载逐渐增加到某一数值
力 构
时,结构除了按原有变形形式可能维持平衡之外,还可
件 设
能以其他变形形式维持平衡,这种情况称为出现平衡的
计
分支。出现平衡的分支是此种结构失稳的标志。
对于受偏心压力的细长直杆,当荷载逐渐增大而趋
于某一数值时,其原有变形形式急剧增大,致使结构丧
失承载能力。这种失稳现象称为极值点失稳。
结构或构件在外力增加到某一数值时,稳定的平衡
状态开始丧失,稍有扰动,结构变形迅速增大,使结构 丧失正常工作的能力,称为失稳。
在桥梁结构中,总是要求沿各个方向保持稳定的平
衡,也即沿各个方向都是稳定的,避免不稳定的平衡或 随遇平衡。
结构稳定问题的两种形式:
第一类稳定问题,分支点失稳问题; 第二类稳定问题,极值点失稳问题。
4
轴 心 受 力 构 件 设 计
4.3.3轴压稳定理论的沿革——具有初始缺陷的实际轴心压杆的稳 定问题
有关轴心压杆的整体稳定问题的理论经历了由理想状态杆件的
单曲线函数关系到实际状态杆件多曲线函数关系的沿革。传统的
理想状态压杆的单曲线稳定理论认为轴压杆是理想状态的,它在
钢结构课件 轴心受压构件的整体稳定性

N=1000kN, 柱的长度4.2m。柱截面为焊接工字形,具有轧制边 翼缘,尺寸2-10×220, 腹板1-685
4.2.6 轴心受压构件扭转和弯扭屈曲
1、扭转屈曲
根据弹性稳定理论,两端铰支且翘曲无约束的杆件,其扭 转屈曲临界力,可由下式计算:
《钢结构稳定理论与设计》 陈骥 著
NE
fy
弹塑性阶段
N A
Nv0
W 1 N
NE
fy
相对初弯曲 ε0 = v0 / ρ = v0 / (W/A)
N [1 A 1
0
N
] NE
fy
N A
1
1000
i
1
1 N
N
E
fy
上式的解即为Perry-Robertson公式(柏利公式)
i0—截面关于剪心的极回转半径。i02
e02
ix2
i
2 y
引进扭转屈曲换算长细比z :
1、扭转屈曲
满足
I 0
z =5.07b/t
x (y) ≥ z =5.07b/t
z2
25.7
Ai02 It
25.7
Ix
Iy It
2t 2b3 12
25.7 4bt3 3
选择计算 §4.6 板件的稳定和屈曲后强度的利用
§4.3 实腹式柱和格构式柱的截面选择计算
4.3.1 实腹式柱的截面选择计算
1、实腹式轴心压杆的截面形式 ①考虑原则 ②常用截面
2、实腹式轴心压杆计算步骤
§4.3 实腹式柱和格构式柱的截面选择计算
4.2.6 轴心受压构件扭转和弯扭屈曲
1、扭转屈曲
根据弹性稳定理论,两端铰支且翘曲无约束的杆件,其扭 转屈曲临界力,可由下式计算:
《钢结构稳定理论与设计》 陈骥 著
NE
fy
弹塑性阶段
N A
Nv0
W 1 N
NE
fy
相对初弯曲 ε0 = v0 / ρ = v0 / (W/A)
N [1 A 1
0
N
] NE
fy
N A
1
1000
i
1
1 N
N
E
fy
上式的解即为Perry-Robertson公式(柏利公式)
i0—截面关于剪心的极回转半径。i02
e02
ix2
i
2 y
引进扭转屈曲换算长细比z :
1、扭转屈曲
满足
I 0
z =5.07b/t
x (y) ≥ z =5.07b/t
z2
25.7
Ai02 It
25.7
Ix
Iy It
2t 2b3 12
25.7 4bt3 3
选择计算 §4.6 板件的稳定和屈曲后强度的利用
§4.3 实腹式柱和格构式柱的截面选择计算
4.3.1 实腹式柱的截面选择计算
1、实腹式轴心压杆的截面形式 ①考虑原则 ②常用截面
2、实腹式轴心压杆计算步骤
§4.3 实腹式柱和格构式柱的截面选择计算
钢结构课件:轴心受力构件PPT课件

1)有效比例极限 残余应力的存在,使短柱平均 应力到达A点后,出现一过渡曲线 ABC,然后到达屈服点,亦即残余应 力的存在降低了构件的比例极限,使 构件提前进入弹塑性工作。 A点的应力称为有效比例极限, 记为fp 。
第36页/共171页
§3 受压构件的整体稳定
忽略残余应力
残余应力对轴心受压短柱平均应力~应变曲线的影响
第22页/共171页
§3 受压构件的整体稳定
研究结构极限承载能力,可依屈曲后性能将稳定问题分为如下三类:
P
(1)稳定分岔屈曲
分岔屈曲后,结构还可承受荷载增量。
P
轴心压力作用下的杆以及中面受压的
平板都具有这种特征。
平板具有相当可观的屈曲后强度可工
程设计利用。
第23页/共171页
v v
§3 受压构件的整体稳定
第20页/共171页
§3 受压构件的整体稳定
6) 第一类稳定、第二类稳定
结构丧失稳定时,平衡形式发生改变的,称为丧失了第一类稳定性或称 为平衡分枝失稳。
第二类稳定性的特征是结构丧失稳定时弯曲平衡形式不发生改变,只是
由于结构原来的弯曲变形增大将不能正常工作。也称为极值点失稳。
第21页/共171页
§3 受压构件的整体稳定
§3 受压构件的整体稳定
2) 平衡状态的分枝 3) 临界力、临界应力
随遇(中性)平衡是从稳定平衡过渡到不稳定平衡的临界状态; 中性平衡时的轴心压力,称为临界力; 相应的截面应力,称为临界应力。
无缺陷的轴心受压构件发生弯曲屈曲时,构件的变形发生了性质上的变化 ,即构件由直线形式改变为弯曲形式,且这种变化带有突然性。
图净截面面积的计算
第12页/共171页
§2构件的强度和刚度
第36页/共171页
§3 受压构件的整体稳定
忽略残余应力
残余应力对轴心受压短柱平均应力~应变曲线的影响
第22页/共171页
§3 受压构件的整体稳定
研究结构极限承载能力,可依屈曲后性能将稳定问题分为如下三类:
P
(1)稳定分岔屈曲
分岔屈曲后,结构还可承受荷载增量。
P
轴心压力作用下的杆以及中面受压的
平板都具有这种特征。
平板具有相当可观的屈曲后强度可工
程设计利用。
第23页/共171页
v v
§3 受压构件的整体稳定
第20页/共171页
§3 受压构件的整体稳定
6) 第一类稳定、第二类稳定
结构丧失稳定时,平衡形式发生改变的,称为丧失了第一类稳定性或称 为平衡分枝失稳。
第二类稳定性的特征是结构丧失稳定时弯曲平衡形式不发生改变,只是
由于结构原来的弯曲变形增大将不能正常工作。也称为极值点失稳。
第21页/共171页
§3 受压构件的整体稳定
§3 受压构件的整体稳定
2) 平衡状态的分枝 3) 临界力、临界应力
随遇(中性)平衡是从稳定平衡过渡到不稳定平衡的临界状态; 中性平衡时的轴心压力,称为临界力; 相应的截面应力,称为临界应力。
无缺陷的轴心受压构件发生弯曲屈曲时,构件的变形发生了性质上的变化 ,即构件由直线形式改变为弯曲形式,且这种变化带有突然性。
图净截面面积的计算
第12页/共171页
§2构件的强度和刚度
钢结构课件 轴心受力构件的强度及截面选择
37
对于闭口截面
It 4A2 /
ds t
闭合截面的循环剪力流
截面面积相同的两种截面
It≈1:500 , ≈30:1
38
约束扭转: 翘曲变形受到约束的扭转
悬臂工字梁的约束扭转
39
扭转剪应力分布
上翼缘的内力
MT Ms M
其中 Ms GIt GIt
M Vf h EI
23
F E
(a) 弹性工作阶段OE:疲劳计算、冷弯薄壁型钢 (b) 弹塑性工作阶段EC:一般受弯构件 (c) 塑性工作阶段CF:塑性铰 (d) 应变硬化阶段FD:一般不利用
24
a a
σ
fy
xx
fy
fy
M e Wn f y
M p Wpn f y
Wn — 梁净截面模量 Wpn — 梁塑性净截面模量
Q235,截面无削弱,计算长度为12.2m,承受静力荷载设计值
为900kN,要求验算此拉杆的强度。
y
【解】:
1、截面特性计算:查附表得
x
x
截面面积 :An = 2×28.91 = 57.82cm2
回转半径: ix = 3.83cm, iy = 5.41cm
y
2、强度验算
= N / An = 900/57.82×10 = 155.7 < f = 215 N/mm2, 满足
2
§3.1 轴心受力构件的强度及截面选择
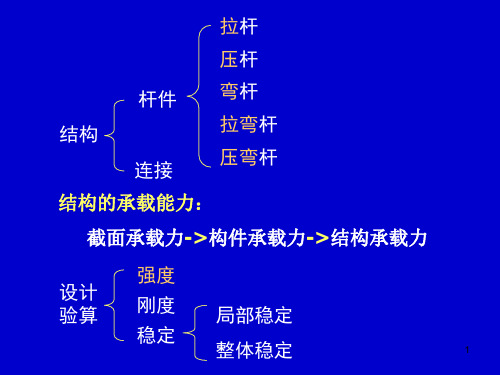
定义:构件只承受轴心力的作用。
承受轴心压力时称为轴心受压构件。 承受轴心拉力时称为轴心受拉构件。
N
N
N
N
3
§3.1 轴心受力构件的强度及截面选择
3.1.1 轴心受力构件的应用和截面形式(了解)
对于闭口截面
It 4A2 /
ds t
闭合截面的循环剪力流
截面面积相同的两种截面
It≈1:500 , ≈30:1
38
约束扭转: 翘曲变形受到约束的扭转
悬臂工字梁的约束扭转
39
扭转剪应力分布
上翼缘的内力
MT Ms M
其中 Ms GIt GIt
M Vf h EI
23
F E
(a) 弹性工作阶段OE:疲劳计算、冷弯薄壁型钢 (b) 弹塑性工作阶段EC:一般受弯构件 (c) 塑性工作阶段CF:塑性铰 (d) 应变硬化阶段FD:一般不利用
24
a a
σ
fy
xx
fy
fy
M e Wn f y
M p Wpn f y
Wn — 梁净截面模量 Wpn — 梁塑性净截面模量
Q235,截面无削弱,计算长度为12.2m,承受静力荷载设计值
为900kN,要求验算此拉杆的强度。
y
【解】:
1、截面特性计算:查附表得
x
x
截面面积 :An = 2×28.91 = 57.82cm2
回转半径: ix = 3.83cm, iy = 5.41cm
y
2、强度验算
= N / An = 900/57.82×10 = 155.7 < f = 215 N/mm2, 满足
2
§3.1 轴心受力构件的强度及截面选择
定义:构件只承受轴心力的作用。
承受轴心压力时称为轴心受压构件。 承受轴心拉力时称为轴心受拉构件。
N
N
N
N
3
§3.1 轴心受力构件的强度及截面选择
3.1.1 轴心受力构件的应用和截面形式(了解)
《钢结构》轴心受力构件图文知识讲解57页文档

END
《钢结构》轴心受力构件图文知识讲 解
41、俯仰终宇宙,不乐复何如。 42、夏日长抱饥,寒夜无被眠。 43、不戚戚于贫贱,不汲汲于富贵。 44、欲言无予和,挥杯劝孤影。 45、盛年不重来,一日难再晨。及时 当勉励 ,岁月 不待人 。
16、业余生活要有意义,不要越轨。——华盛顿 17、一个人即使已登上顶峰,也仍要自强不息。——罗素·贝克 18、最大的挑战和突破在于用人,而用人最大的突破在于信任人。——马云 19、自己活着,就是为了使别人过得更美好。——雷锋 20、要掌握书,莫被书掌握;要为生而读,莫为读而生。——布尔沃
《钢结构设计原理》教学课件—05轴心受力构件

假定: A、达到临界力Ncr时杆件挺直; B、杆微弯时,轴心力增加△N,其产生的平均压应力 与弯曲拉应力相等。
临界力和临界应力:
Ncr
2Et I
l2 0
稳定的影响
如前所述,如果将钢材视为理想的弹塑性材料, 则压杆的临界力与长细比的关系曲线(柱子曲线)应为:
初 始
y
1.截面为双轴对称或极对称构件:
x lox ix
y loy i y
x
x
对于双轴对称十字形截面,为了防止扭 转屈曲(torsional buckling),尚应满足:
y
x或 y 5.07 b t
b t 悬伸板件宽厚比。
y
xt
b
x
2.截面为单轴对称构件:
绕非对称轴x轴: x lox i x
y
绕对称轴y轴屈曲时,一般为弯扭屈曲, y
其临界力低于弯曲屈曲,所以计算时, x
x
以换算长细比λyz代替λy ,计算公式如下:
y
1
yz
1 2
y2
z2
y2 z2
2 4 1 e02
i02
y2z2
2
z2 i02 A It 25.7 I l2
式中:
i02 e02 ix2 iy2
时, 可 采p 用欧E拉f公p 式计算临界应力(critical stress);
当 N A 或f p f y rc 时 , 截p 面出E现f塑p 性区, 由切线模量理论知,用截面弹性区的惯性矩Ie代替全 截面惯性矩I,即得柱的临界应力:
N cr
2 EIe
l2
2 EI
l2
Ie I
cr
2E 2
fp
或长细比:
临界力和临界应力:
Ncr
2Et I
l2 0
稳定的影响
如前所述,如果将钢材视为理想的弹塑性材料, 则压杆的临界力与长细比的关系曲线(柱子曲线)应为:
初 始
y
1.截面为双轴对称或极对称构件:
x lox ix
y loy i y
x
x
对于双轴对称十字形截面,为了防止扭 转屈曲(torsional buckling),尚应满足:
y
x或 y 5.07 b t
b t 悬伸板件宽厚比。
y
xt
b
x
2.截面为单轴对称构件:
绕非对称轴x轴: x lox i x
y
绕对称轴y轴屈曲时,一般为弯扭屈曲, y
其临界力低于弯曲屈曲,所以计算时, x
x
以换算长细比λyz代替λy ,计算公式如下:
y
1
yz
1 2
y2
z2
y2 z2
2 4 1 e02
i02
y2z2
2
z2 i02 A It 25.7 I l2
式中:
i02 e02 ix2 iy2
时, 可 采p 用欧E拉f公p 式计算临界应力(critical stress);
当 N A 或f p f y rc 时 , 截p 面出E现f塑p 性区, 由切线模量理论知,用截面弹性区的惯性矩Ie代替全 截面惯性矩I,即得柱的临界应力:
N cr
2 EIe
l2
2 EI
l2
Ie I
cr
2E 2
fp
或长细比:
中南大学《钢结构原理》课件第五章 轴心受力构件

☆措施(确保长细比不是很小,不扭转失稳)
y (x ) 5.07b / t
☆长细较大时,弯曲失稳起控制作用,作弯曲失稳验算。
中南大学桥梁工程系
第五章 轴心受力构件
5.5 轴心受压构件局部稳定性
1、局部稳定的概念
轴心受压柱局部屈曲变形
轴心受压构件翼缘的凸曲现象
中南大学桥梁工程系
第五章 轴心受力构件
1916年因施工问题又发生一次倒塌事故。
前苏联在1951~1977年间共发生59起重大钢结构事故,有17起 属稳定问题。
(设计、制作、安装或使用不当都可能引发稳定事故)
例如:
1957年前苏联古比雪夫列宁冶金厂锻压车间,7榀1200m2屋盖塌落。 起因是一对尺寸相同的拉压杆装配颠倒。 1974年,苏联一个俱乐部观众厅24×39m钢屋盖倒塌。起因是受力 较大的钢屋架端斜杆失稳。
中南大学桥梁工程系
第五章 轴心受力构件
•荷载初始偏心降低稳定承载力
vm e0 (sec
2
N 1) NE
中南大学桥梁工程系
第五章 轴心受力构件
•残余应力降低稳定承载力
中南大学桥梁工程系
第五章 轴心受力构件
(1)使部分截面提前进入塑性状态,截面的弹性区域减少, 干扰后只有弹性区产生抗力增量,故降低了稳定承载力。
N 1 fy A Ry
N 1 fu An Ru
偏安全简化处理
N 1 fy f An Ry
中南大学桥梁工程系
第五章 轴心受力构件
2、刚度计算
•刚度计算的目的:保证在安装、使用过程中正常使用要求
•实例1:九江桥主拱吊杆涡振现象
中南大学桥梁工程系
第五章 轴心受力构件
y (x ) 5.07b / t
☆长细较大时,弯曲失稳起控制作用,作弯曲失稳验算。
中南大学桥梁工程系
第五章 轴心受力构件
5.5 轴心受压构件局部稳定性
1、局部稳定的概念
轴心受压柱局部屈曲变形
轴心受压构件翼缘的凸曲现象
中南大学桥梁工程系
第五章 轴心受力构件
1916年因施工问题又发生一次倒塌事故。
前苏联在1951~1977年间共发生59起重大钢结构事故,有17起 属稳定问题。
(设计、制作、安装或使用不当都可能引发稳定事故)
例如:
1957年前苏联古比雪夫列宁冶金厂锻压车间,7榀1200m2屋盖塌落。 起因是一对尺寸相同的拉压杆装配颠倒。 1974年,苏联一个俱乐部观众厅24×39m钢屋盖倒塌。起因是受力 较大的钢屋架端斜杆失稳。
中南大学桥梁工程系
第五章 轴心受力构件
•荷载初始偏心降低稳定承载力
vm e0 (sec
2
N 1) NE
中南大学桥梁工程系
第五章 轴心受力构件
•残余应力降低稳定承载力
中南大学桥梁工程系
第五章 轴心受力构件
(1)使部分截面提前进入塑性状态,截面的弹性区域减少, 干扰后只有弹性区产生抗力增量,故降低了稳定承载力。
N 1 fy A Ry
N 1 fu An Ru
偏安全简化处理
N 1 fy f An Ry
中南大学桥梁工程系
第五章 轴心受力构件
2、刚度计算
•刚度计算的目的:保证在安装、使用过程中正常使用要求
•实例1:九江桥主拱吊杆涡振现象
中南大学桥梁工程系
第五章 轴心受力构件
《钢结构轴心受力》课件

03
轴心受力构件的设计
截面设计
01
02
03
截面形式
根据受力特点,选择合适 的截面形式,如实腹式、 格构式等。
截面尺寸
根据承载力要求,计算截 面的尺寸,确保构件的承 载能力。
截面材料
选择合适的材料,如钢材 、混凝土等,以满足承载 力和耐久性要求。
连接设计
连接方式
根据构件的连接要求,选 择合适的连接方式,如焊 接、螺栓连接等。
保持钢结构轴心受力构件的清洁 ,定期清除表面污垢和尘埃,防
止腐蚀。
防腐涂层保护
定期检查并重新涂覆防腐涂层,以 增强钢结构的耐久性和防腐蚀能力 。
紧固件检查
定期检查所有连接螺栓、铆钉等紧 固件,确保其紧固且无松动。
定期检测与评估
外观检查
定期对钢结构轴心受力构件进行 外观检查,观察是否有变形、裂
纹、锈蚀等现象。
《钢结构轴心受力》 PPT课件
目录
• 钢结构轴心受力概述 • 轴心受力构件的特性 • 轴心受力构件的设计 • 轴心受力构件的施工与安装 • 轴心受力构件的维护与检测
01
钢结构轴心受力概述
定义与特点
定义
轴心受力是指钢结构的受力状态 ,其中力的作用线与杆件轴线重 合,使杆件既不发生弯曲也不发 生扭曲。
04
轴心受力构件的施工与安装
施工方法选择
施工方法选择应根据工程实际情况和设计要求进行,综合考虑安全、质量、进度和 成本等因素。
常用的施工方法包括预制施工法、整体吊装法、高空拼装法等,选择时应根据构件 的尺寸、重量、安装高度和场地条件等因素进行选择。
施工方法的确定还应考虑施工机械设备的性能和数量,以及施工人员的技能水平。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
14.2 轴心受力构件强度和刚度
2. 刚度要求
(2) 长细比限值
max
l0 i
max—x和y中 的 较 大 值
1)在承受静力荷载的结构中,可仅计算受拉构 件在竖向平面内的长细比;
2)在直接或间接承受动力荷载的结构中,计算 单角钢受拉构件的长细比时,应采用单角钢 的最小回转半径;计算单角钢交叉杆件平面 外的长细比时,应采用角钢肢边平行轴的回 转半径 。
14.2 轴心受力构件强度和刚度
2. 刚度要求
受拉构件的容许长细比
承受静力荷载和间接承
项 次
构件名称
受动力荷载的结构 直接承受
一般建筑结 构
有重级工 作制吊车
厂房
动力荷载 结构
1
桁架的杆件
350
250
250
2
吊车梁或吊车桁架以下 的柱间支撑
300
200
-
2
其他拉杆、支撑、系杆 (张紧的圆钢除外)
400
最小临界压力
2 EI N cr l 2
cr
N cr A
2E li2
2E 2
3. 弹塑性屈曲
当 cr f p 需要考虑弹塑性屈曲
N
N N
NcrNcra
直线平 衡状态
11
l
l
b
屈曲微
弯状态
cr
非细长压杆
N
11
N N
3. 弹塑性屈曲
根据切线模量理论
fy a
Ncra2E 2 atA,cra2E 2 at
N
N
N
整体失稳类形
➢ 弯曲屈曲
➢ 扭转屈曲 ➢ 弯扭屈曲
u
Φ
uΦ
2. 理想压杆的临界力(弹性弯曲屈曲)
N→Ncr A
cr
Ncr A
f( p 比例极限)
欧拉方程的建立
细长压杆
EI d2 y / dz2 N y 0
l
yN
y
EIy
z
z
y
y
B
B
N
弹性屈曲的临界压力
N cr
n 2 2 EI l2
,当 n 1时,
2)刚度验算
查表(P513) ix=30.5mm A 2 1.2 96 31 .5 8c 22 m 2
I y 2 [ 1.5 7 1 1 9 .2 9 ( 6 0 .5 1 2 .8 ) 2 ] 4 7.7 8 c 5 4 8 m 6
iy
Iy A
78 .7856 4.52 cm 5 4.2 5m 5 m 3.5 822
N
N
孔前传力系数
孔前传 递的力
N
净截面处的传力
N N10.5n1
n
净截面处的强度公式 N An f
同时毛截面处还应满足 N / A f
n1:计算截面(最 外列螺栓处)高强 度螺栓数目;
n:节点或拼接处构 件一端连接的高强 度螺栓总数。
1.强度计算
(3) 单面连接的单角钢按轴心受力计算强度时,钢材 的强度设计值应乘以0.85
网架
14.1 轴心受力构件的工程应用
网壳
14.1 轴心受力构件的工程应用
1. 实腹式构件的截面形式
型钢截面
1. 实腹式构件的截面形式
角钢或双角钢组合截面 型钢或钢板组成的组合截面
冷弯薄壁型钢截面
14.1 轴心受力构件的工程应用
2. 格构式构件的截面形式
x
x1Biblioteka 1yyy
y
y
y
x
x
1
1
x
x
y
yy
y
比如单面连接角钢受压杆件,实际上受力是双向 压弯,为了计算简便还是按轴心受压考虑,只是通过 强度乘以折减系数来反映简化计算的不利影响。
14.2 轴心受力构件强度和刚度
2. 刚度要求
(1)长细比过大产生的不利影响: 1)在运输和安装过程中产生弯曲或过大的变形; 2)使用期间因其自重而屈曲; 3)在动力荷载作用下发生较大的振动; 4)压杆的长细比过大时,还将使构件的承载力 降低过多。
验算长细比
xli0xx
30 090.8 4[]35满 0
3.0 5
足
yli0yy
780 107.42 []35满 0
4.5 25
足
作 业 P462
1.思考题 1 2.计算题 1, 2
14.3 实腹式轴心受压构件的整体稳定
1. 理想轴心压杆的整体失稳
理想轴心压杆 杆件完全挺直、荷载沿杆件形心轴 作用,杆件在受荷之前没有初始应力,也没有初弯 曲和初偏心等缺陷,截面沿杆件是均匀的。
350
-
14.2 轴心受力构件强度和刚度
2. 刚度要求
受压构件的容许长细比
项 次
构件名称
柱、桁架和天窗架中的杆件
1 柱的缀条、吊车梁吊车桁架以下的 柱间支撑
支撑(吊车梁吊车桁架以下的柱间
2
支撑除外)
用以减少受压构件长细比的杆件
容许长细比 150 200
例1 某中级工作制吊车的 厂房屋架的下弦拉杆,有 双角钢组成,型号为 L100×10,布置有交错排 列的普通螺栓连接,螺栓 孔直径d0=20mm。已知 轴心拉力设计值N= 620kN,计算长度l0x= 3000mm,l0y=7800。材料 为Q235钢,试验算该杆 件的强度和刚度。
x
x
格构式构件的 虚轴和实轴
l1
l1
l01
40~70
1x
缀条柱
y
y
1x
1a y
缀板柱
y
h
1b
14.1 轴心受力构件的工程应用
3. 轴向受力构件的设计要求
强度和稳定
轴心受拉:强度 轴心受压:强度和稳定(整体和局部)
刚度要求
保证构件不产生过度的变形,用长细比控制。
14.2 轴心受力构件强度和刚度
1.强度计算(以全截面达到屈服应力为极限状态)
傅昶彬课件系列—结构设计原理
第14章 钢结构轴心受力构件 (1)
主要内容
14.1 轴心受力构件的工程应用 14.2 轴心受力构件的强度和刚度 14.3 实腹式轴心受压构件的整体稳定 14.4 实腹式轴心受压构件的局部稳定
四川大学建环学院 2018.3
14.1 轴心受力构件的工程应用
桁架
塔架
14.1 轴心受力构件的工程应用
a
max 塑性变形发展
fy
应力重分布
N
N
N
N
弹性状态应力
孔洞截面处产 生应力集中
极限状态应力
(1) 除摩擦型高强度螺栓连接处外强度计算式
NAnf An —构件的净截面面积
构件净截面面积An及计算截面的选取
Ⅰ
ⅡⅠ
N
N
并列
Ⅰ
ⅡⅠ ⅡⅠ
错列
N
ⅡⅠ
1.强度计算
(2)摩擦型高强度螺栓连接处
由于摩擦阻 力存在,一部分 荷载已由孔前接 触面传递。
fp
令 Et /E,cra2E 2 a
E E t ,
解:1)强度验算 I-I截面
A n 2 (4 1 5 0 4 0 2 5 ) 0 1 0 34 m 2 0m 0 II-II截面
A n 2 ( 4 5 12 0 4 2 0 0 4 2 5 2 0 ) 1 0 3m 12 5
II-II截面起控制作用
N 6 2 13 0 0 1.6 9 N /6 m2 m f 2N 1/m 52m A n 3154
