层次分析法经典案例
层次分析法经典案例
层次分析法经典案例篇一：层次分析法步骤层次分析法实例与步骤结合一个具体例子，说明层次分析法的基本步骤和要点。
【案例分析】市政工程项目建设决策：层次分析法问题提出市政部门管理人员需要对修建一项市政工程项目进行决策，可选择的方案是修建通往旅游区的高速路（简称建高速路）或修建城区地铁（简称建地铁）。
除了考虑经济效益外，还要考虑社会效益、环境效益等因素，即是多准则决策问题，考虑运用层次分析法解决。
1.建立递阶层次结构应用AHP解决实际问题，首先明确要分析决策的问题，并把它条理化、层次化，理出递阶层次结构。
AHP要求的递阶层次结构一般由以下三个层次组成：? 目标层（最高层）：指问题的预定目标；? 准则层（中间层）：指影响目标实现的准则；? 措施层（最低层）：指促使目标实现的措施；通过对复杂问题的分析，首先明确决策的目标，将该目标作为目标层（最高层）的元素，这个目标要求是唯一的，即目标层只有一个元素。
然后找出影响目标实现的准则，作为目标层下的准则层因素，在复杂问题中，影响目标实现的准则可能有很多，这时要详细分析各准则因素间的相互关系，即有些是主要的准则，有些是隶属于主要准则的次准则，然后根据这些关系将准则元素分成不同的层次和组，不同层次元素间一般存在隶属关系，即上一层元素由下一层元素构成并对下一层元素起支配作用，同一层元素形成若干组，同组元素性质相近，一般隶属于同一个上一层元素（受上一层元素支配），不同组元素性质不同，一般隶属于不同的上一层元素。
在关系复杂的递阶层次结构中，有时组的关系不明显，即上一层的若干元素同时对下一层的若干元素起支配作用，形成相互交叉的层次关系，但无论怎样，上下层的隶属关系应该是明显的。
最后分析为了解决决策问题（实现决策目标）、在上述准则下，有哪些最终解决方案（措施），并将它们作为措施层因素，放在递page1阶层次结构的最下面（最低层）。
明确各个层次的因素及其位置，并将它们之间的关系用连线连接起来，就构成了递阶层次结构。
层次分析例子(1)
正义的、非正义的两类
现代医学还没有真正理解这些疾病
来打网球
求他做事
把书房收拾得干净又整齐
要求他俩准时到报到地点报到
小王爱听音乐剧
缺乏感性的生活经历
不能让黄河的悲剧在长江重演
辽阔的游泳者云集的细沙海滩的景象
在渺无人烟的丛林间披荆斩棘种下果木
禁止携带危险品上车
在美国首都华盛顿的杰弗逊纪念堂屋顶
波澜当代最伟大的诗人和翻译家切斯瓦夫·米沃什
以其震古烁今的哲学伟绩持久地报答母校的培育之恩
一个思想家、艺术家唯一可以做的就是坚持真理和正义
知识分子批判需要清明的理性、知识的底子、专业的水准
在与命运的抗争中彰显人类的向上力量和深邃驳杂的人性魅力的人
对彭德怀元帅一件事情的回忆
把孩子的衣服从箱子里拿出来
生活在持续而严重的饥饿状态中
用大自然赋予人类的乐趣弥补生活中的遗憾往事像潮水一样撞击着我的心扉
建立起充满生机和活力的社会主义经济体制想出了一个好办法
那些关于我们民族历史的教科书
讲演中的一席话说得大家兴奋起来
派人去通知小王马上来报到
写信催妹妹赶快离开杭州回家来
水面上淡淡地笼罩了一层雾气。
层次分析法例题
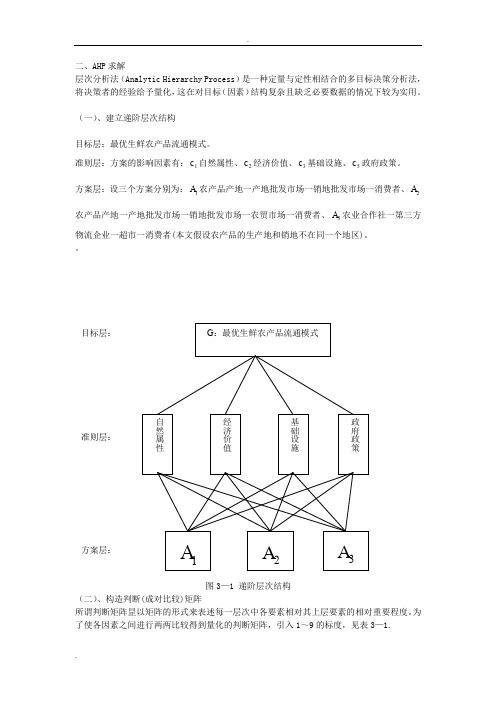
二、AHP 求解 层次分析法（Analytic Hierarchy Process ）是一种定量与定性相结合的多目标决策分析法，将决策者的经验给予量化，这在对目标（因素）结构复杂且缺乏必要数据的情况下较为实用。
（一）、建立递阶层次结构目标层：最优生鲜农产品流通模式。
准则层：方案的影响因素有：1c 自然属性、2c 经济价值、3c 基础设施、5c 政府政策。
方案层：设三个方案分别为：1A 农产品产地一产地批发市场一销地批发市场一消费者、2A 农产品产地一产地批发市场一销地批发市场一农贸市场一消费者、3A 农业合作社一第三方物流企业一超市一消费者(本文假设农产品的生产地和销地不在同一个地区)。
。
图3—1 递阶层次结构（二）、构造判断(成对比较)矩阵所谓判断矩阵昰以矩阵的形式来表述每一层次中各要素相对其上层要素的相对重要程度。
为了使各因素之间进行两两比较得到量化的判断矩阵，引入1～9的标度，见表3—1.目标层：准则层：方案层：表3—1 标度值为了构造判断矩阵，作者对6个专家进行了咨询，根据专家和作者的经验，四个准则下的两两比较矩阵分别为：（三）、层次单排序及其一致性检验层次单排序就是把本层所有要素针对上一层某一要素，排出评比的次序，这种次序以相对的数值大小来表示。
对应于判断矩阵最大特征根λmax的特征向量，经归一化(使向量中各元素之和等于1)后记为W。
W的元素为同一层次因素对于上一层次因素某因素相对重要性的排序权值，这一过程称为层次单排序。
能否确认层次单排序，需要进行一致性检验，所谓一致性检验是指对A确定不一致的允许范围。
a，则λ比n 大的越多，A 的不一致性越严重。
用最大特征值对由于λ连续的依赖于ij应的特征向量作为被比较因素对上层某因素影响程度的权向量，其不一致程度越大，引起的判断误差越大。
因而可以用λ―n数值的大小来衡量 A 的不一致程度。
用一致性指标进行检验：max 1nCI n λ-=-。
层次分析法实例讲解学习
层次分析法实例讲解学习生活实际例题：旅游实例，有三个旅游地点供游客们选择，连云港，常州，徐州。
影响游客们决策的因素主要有以下五项：景色、费用、居住、饮食、旅途。
请根据个人偏好选择最佳旅游地点。
分析 : 旅游点是方案层，将它们分别用B1 , B2, B3表示，影响旅游决策的因素为准则层 A1, A2, A3 , A4 , A5；目标层为选择旅游地，即可以建立以下模型：选择旅游地景色费用居住饮食旅途连云港常州徐州建立判断矩阵：准则层判断矩阵（即各种因素在旅客偏好选择中所占有的不同比重）：1 1/2 43321755A1/ 41/ 711/ 21/ 31/3 1/5 2111/3 1/5 311方案层判断矩阵建立（针对每一个影响因素来对方案层建立）:12511/31/8113B1 1/212B1311/3 B11131/ 51/2 18311/3 1/3 1134111/4B1 1/311B1111/41/411441求准则层判断矩阵 A 的特征值：Matlab 运行程序：[a,b]=eig(A)‘ 矩b ’阵的对角线为准则层判断矩阵 A 的特征值：5.0730 0 0 00.0310 0 b0 0 0.0310 0 0 0 0 0.005 00.005即 1 5.073,20.031,30.031,40.005, 50.005选出最大特征值：max （1, 2, 3, 4,5）1最大特征值的特征向量即为准则层的影响因素所占的权重， 所对应的特征向量为：w 1- 0.4658 - 0.8409 - 0.0951 - 0.1733 - 0.1920归一化（最简 matlab 程序为 w=w1./sum(w1) ）w0.2636 0.4759 0.0538 0.0981 0.1087一致性指标的检验：由 max 是否等于 5 来检验判断矩阵 A 是否为一致矩阵。
由于特征根连续地依赖于矩阵 A 中的值 ，故 max 比 5 大得越多， A 的非一致性程度也就越严重，max 对应的标准化特征向量也就越不能真实地反映出对因素 A i (i 1, ,5) 的影响中所占的比重。
层次分析法经典案例
层次分析法经典案例层次分析法（Analytic Hierarchy Process, AHP）是一种常用的多准则决策方法，被广泛应用于企业管理、工程项目评估、市场调研等领域。
本文将通过一个经典案例，介绍层次分析法的基本原理和应用过程。
一、案例背景某企业计划购买新设备，以提升生产效率和质量。
然而，在众多可选设备中，如何选择最适合企业发展的设备成为了业主面临的难题。
为了解决这一问题，业主决定应用层次分析法进行设备选择。
二、层次分析法基本原理层次分析法基于一个重要思想，即将复杂的决策问题拆解为具有层次结构的多个因素，并通过层次化的比较和综合分析，最终得出决策结果。
1. 构建层次结构首先，我们需要将决策问题划分为不同的层次，并构建层次结构。
在这个案例中，可以将设备选择问题划分为三个层次：目标层、准则层和备选方案层。
目标层代表企业的最终目标，即实现高效生产；准则层包括影响设备选择的各种准则，如设备价格、性能指标、售后服务等；备选方案层包括具体的设备选项。
2. 建立判断矩阵接下来，我们需要对不同层次的因素进行两两比较，建立判断矩阵。
通过专家主观判断，给出两个因素之间的相对重要性，采用1-9的尺度，其中1代表两者具有相同重要性，9代表一个因素相对于另一个因素极端重要。
比如，在准则层中，设备性能指标对设备价格的重要性为6。
3. 计算权重向量利用判断矩阵，我们可以计算出每个层次的权重向量。
通过对判断矩阵进行归一化处理，可获得各因素的权重。
权重向量表示了各因素对当前决策的贡献程度，可作为后续分析的依据。
例如，计算准则层中各因素的权重向量。
4. 一致性检验为了保证判断矩阵的合理性，我们需要进行一致性检验。
通过计算一致性指标和一致性比率，评估判断矩阵是否存在较大的一致性问题。
若一致性比率超过一定阈值，需要检查和修正判断矩阵。
5. 优先级排序最后，结合各层次的权重，我们可以进行优先级排序，得出对不同备选方案的排序结果。
根据排序结果，我们可以选择最合适的备选方案。
经典层次分析法分析及实例教程
当CR 0.1 时，认为层次总排序通过一致性检验。到
此，根据最下层（决策层）的层次总排序做出最后决策。
层次分析法的基本步骤归纳如下
1.建立层次结构模型 该结构图包括目标层，准则层，方案层。
2.构造成对比较矩阵 从第二层开始用成对比较矩阵和1~9尺度。
3.计算单排序权向量并做一致性检验 对每个成对比较矩阵计算最大特征值及其对应的特征向量， 利用一致性指标、随机一致性指标和一致性比率做一致性 检验。若检验通过，特征向量（归一化后）即为权向量； 若不通过，需要重新构造成对比较矩阵。
一般分为三层，最上面为目标层，最下面为方案层，中 间是准则层或指标层。 例1 的层次结构模型
买钢笔
目标层
质颜价外实 量色格形用
准则层
可供选择的笔
方案层
例2 层次结构模型
选择 旅游地
景
费
居
饮
旅
色
用
住
食
途
苏州、杭州、 桂林
目标层Z 准则层A 方案层B
若上层的每个因素都支配着下一层的所有因素，或被下一层所 有因素影响，称为完全层次结构，否则称为不完全层次结构。
A 4 7
2 3
1 3
1 5
2
1
1
1
1
3
1
1
3 5
1 2 5
B1
1 2
1
2
1 5
1 2
1
1
B2
3
1 3 1
1 18 3
8 3 1
1 1 3
B3
1 1
1 1
3
3 3 1
1 3 4
B4
1 3
1
1
ahp层次分析法案例
ahp层次分析法案例AHP层次分析法是一种决策分析方法，适用于解决复杂的决策问题。
以下是一个AHP层次分析法的案例，用于决策一个公司在新市场中选择合适的产品。
某公司考虑进入新市场，希望选择一个适合的产品。
为了做出最佳决策，他们使用AHP层次分析法，按照以下步骤进行分析：1. 首先，确定决策层次结构。
公司将决策分为三个层次：目标层、准则层和备选方案层。
目标层是公司的终极目标，准则层是实现目标所需的因素，备选方案层是可以选择的不同产品。
2. 其次，制定判断矩阵。
为了做出决策，公司需要以对比方式，对准则和备选方案进行比较。
他们使用一个判断矩阵，将每个准则和备选方案两两对比，来确定它们的重要性或优劣。
假设公司选择了三个准则：市场需求、竞争力和技术实施。
他们对每个准则进行两两对比，并使用1-9的标度，表示相对重要性。
例如，市场需求对竞争力的重要性可能被评价为5，而竞争力对技术实施的重要性可能被评价为3。
3. 确定权重向量。
根据判断矩阵，公司计算每个准则的权重。
通过对矩阵的每一列进行平均化，可以计算出每个准则的权重向量。
例如，如果市场需求对竞争力的重要性为5，竞争力对技术实施的重要性为3，则市场需求的权重为5/(5+3)=0.625，竞争力的权重为3/(5+3)=0.375。
4. 计算一致性检查。
公司通过计算一致性指标（CI）和一致性比率（CR）来确定判断矩阵的一致性。
如果CI小于0.10，且CR小于0.10，则认为判断矩阵是一致的。
5. 最后，比较备选方案。
根据判断矩阵和准则的权重，公司可以计算每个备选方案的总权重。
备选方案的总权重越高，表示其相对于其他备选方案的优势越大。
根据AHP层次分析法，公司能够比较不同产品在新市场中的优势，并根据准则的权重，做出最佳选择。
通过AHP层次分析法的应用，公司能够对于复杂的决策问题进行系统化、结构化的分析，以更有根据地做出决策，提高决策的准确性和可靠性。
同时，该方法还能帮助公司更好地理解和分析决策过程中的关键因素和限制条件，以及它们之间的相互关系，从而更好地促进决策的质量和效益。
层次分析法案例
基于层次分析法评选“大学最佳体育运动”一、背景分析如今，大学生课余时间很多，利用课余时间开展一项体育运动很有必要，但许多同学不知道该选择哪一项体育运动。
本文运用层次分析法评选“大学最佳体育运动”，旨在为大学生选择运动方式提供参考。
二、系统分析目标是选择一项开展广泛、关注度高、场地易得、费用低且技术难度低的体育运动。
候选体育运动为：篮球、羽毛球、足球、高尔夫球。
三、影响因素分析影响因素有：参与人数、场地普遍性、关注度、费用、技术难度以及运动量。
优选参与人数多、场地要求小、关注度高、花费低、运动量适中且技术难度较低的运动。
经过分析得出分析图如下：四、制定比例标度比例标度如下，从1至9，数字越大代表强度越大。
五、寻找专家共寻找到了3名专家，分别是：六、第一层分析经过第一层分析可知：关注度所占比重最大，其次是参与人数和运动量六、第二层分析（1）篮球运动分析篮球综合分值为：15×19%+15×13%+18×30%+8×12%+7*10%+14*16%=14.1。
（2）高尔夫球运动分析篮球综合分值为：3×19%+3×13%+12×30%+3×12%+3*10%+3*16%=10.02。
（3）足球运动分析篮球综合分值为：18×19%+7×13%+5×30%+12×12%+8*10%+18*16%=10.95。
（4）羽毛球运动分析篮球综合分值为：5×19%+5×13%+8×30%+8×12%+4*10%+9*16%=6.8。
根据评分情况综合排名为篮球>足球>高尔夫球>羽毛球七、分析这里写分析的原因。
层次分析法经典案例
层次分析法经典案例层次分析法是一种比较常见且实用的决策分析方法，通过对待比较的各种方案的因素逐一分析，将其组织成一种层次结构，然后再运用数学方法对其进行计算，得出最终的结果。
经典案例有很多，比如金融领域、生产制造等许多行业都可以应用到层次分析法，下面我来介绍一下层次分析法在一个工厂的生产制造中的应用案例。
某工厂是一家生产钢管的制造厂，该工厂本着“质量第一、信誉第一”的原则，一直都很重视生产制造中的质量管控。
但是，由于市场竞争日益激烈，不断有新的小厂涌现，压力越来越大，所以该工厂决定对生产制造中的质量问题进行深入分析，并采用层次分析法，制定出更加合理的质量管控方案。
该工厂首先将生产制造中的质量管控分成了几个层次，分别是管理层次、生产层次、产品层次和客户需求层次，当然，每个层次下面还有自己的一些小要素，如管理层次下面就包括质量文化、质量指数等等，生产层次下面包括人员培训、设备状态等等，小要素比较复杂，不做过多介绍。
接下来是层次分析法的重头戏，对每个小要素的影响程度进行量化，以及对不同小要素之间的相关性进行评估，这是做好层次分析法的关键，必须要准确评估，否则得出的结果很可能会偏差较大。
为了保证量化的准确性，该工厂引入了专家协助，共同制定出适合该企业的一套量化标准。
原本需要量化的小要素有50个，经过专家评估和筛选，最终选出了20个，其余30个小要素的影响程度与剩下的20个小要素的相关性贡献较小，因此不被列入对比。
在对20个小要素进行量化之后，该工厂得出了各小要素的权重值，这个权重值表示每个小要素对于决策结果的影响程度，根据这些权重值，可确定各个小要素的重要性，从而制定出更加合理的质量管控方案。
经分析，该工厂管控方案的优先级排序如下：1.产品质量：该项权重值为0.408，被认为是影响质量管理的最重要因素，因为一个工厂的根本目的就是要生产出高质量的产品，切实提高其竞争力。
2.生产管理与控制：该项权重值为0.325，生产管理是确保产品质量的基础，虽然位于产品质量之下，但同样很重要。
层次分析法实例范文
层次分析法实例范文下面我将以一个实例来说明层次分析法的应用。
假设你是一家公司的项目经理，需要在三个设计方案中选择一个最适合的方案。
你希望通过层次分析法来评估并选择最佳方案。
首先，你需要确定准则层。
准则层是评估和比较设计方案的标准。
在本实例中，准则层可以包括三个因素：成本、技术易用性和效果。
其次，你需要对每个准则进行两两比较。
你需要确定哪个准则对你更重要，换句话说，你需要对准则之间的重要性进行评估。
你可以使用一个1到9的尺度来进行评估，其中1表示相对重要性相同，9表示相对重要性非常不同。
在这个例子中，假设你认为成本对你更重要，因此可以给成本的评估为9，而技术易用性和效果的评估都为5接下来，你需要对每个准则的子准则进行两两比较。
对于成本来说，可能的子准则可以包括材料成本、人力成本和设备成本。
你需要评估这些子准则之间的重要性，同样使用1到9的尺度进行评估。
假设你认为人力成本对成本的影响最大，你可以给予人力成本的评估为9、材料成本和设备成本则分别给出评估5和3对于技术易用性和效果这两个准则，你需要进行类似的比较和评估。
比如，你可能认为技术易用性中的用户友好性对你最重要，效果中的创新性最重要。
完成这些比较和评估后，你需要计算总体权重。
通过层次分析法计算权重的方法是对准则之间的比较矩阵进行归一化处理，即计算每列的平均值，然后将每个条目除以其所在列的平均值。
最后，求每行的平均值得到每个准则的权重。
例如，对于成本准则，对应的比较矩阵为：1591/5131/91/31计算每列的平均值为：1/35/95/3然后将每个条目除以其所在列的平均值，得到：15/93/53/511/35/33/11最后，求每行的平均值得到每个准则的权重：0.48780.25920.2529重复这个过程，你可以得到技术易用性和效果的权重。
最后，你可以将每个设计方案在每个准则上进行评估。
同样使用1到9的尺度进行评估，并对每个准则乘以其对应的权重得到总体分数。
句子层次分析法的经典例子
句子层次分析法的经典例子句子层次分析法（Sentence Hierarchy Analysis）是一种文本分析方法，用于确定句子中不同元素之间的层次关系。
这种分析方法可以帮助人们理解句子的结构和语义，并进一步了解文本的内容和意义。
下面将介绍一个经典例子来说明句子层次分析法的应用。
假设有以下一段文字："小明喜欢吃水果，尤其是苹果。
他最喜欢的是红色的苹果，因为他认为红色的苹果最甜。
"首先，我们需要将整段文字分解为单独的句子：1. 小明喜欢吃水果。
2. 尤其是苹果。
3. 他最喜欢的是红色的苹果。
4. 因为他认为红色的苹果最甜。
然后，我们可以按照层次关系对这些句子进行分析。
首先，我们可以确定第一句是主要句子，因为它包含了整个段落的主题和核心信息。
其他句子则是对主句进行支持和补充的。
1. 小明喜欢吃水果。
- 这是主句，表达了主题和核心信息。
2. 尤其是苹果。
- 这是一个对主句的补充信息，说明小明对水果的偏好。
3. 他最喜欢的是红色的苹果。
- 这是对前一句的进一步细化和支持，解释了小明对苹果的偏好。
4. 因为他认为红色的苹果最甜。
- 这是对第三句的原因解释，说明了小明为什么喜欢红色的苹果。
通过这个例子，我们可以看到句子层次分析法帮助我们理清了句子之间的层次关系，从而更好地理解整个段落的内容和意义。
这种分析方法可以应用于各种文本，包括新闻报道、科技文章、小说和散文等。
除了层次关系之外，句子层次分析法还可以揭示句子之间的逻辑关系和语义关系。
例如，在上面的例子中，第四句中的“因为”一词表明了原因和结果之间的因果关系。
这种分析有助于我们更深入地了解文本中的信息和观点。
在实际应用中，句子层次分析法可以用于学术研究、语言教学和自然语言处理等领域。
它可以帮助研究者分析文章结构、探索篇章连贯性，帮助教师教授学生如何进行有效的写作和阅读，帮助计算机程序理解和处理自然语言文本。
总之，句子层次分析法是一种有用的文本分析方法，通过揭示句子之间的层次关系和语义关系，帮助我们更好地理解和分析文本内容。
层次分析法实例分析：以奶茶店的选取为例
层次分析法实例分析：以奶茶店的选取为例一、明确问题南苑市场有三家比较受欢迎的奶茶店，这是我们的分析对象；我们分析的内容是如何在三家奶茶店中选择。
我们通过价格合理、品种丰富。
服务良好三个维度进行测量，在进行一致性检验过后确定三个方案的排序。
二、建立递阶层次分析结构图三、建立要素两两充分对比的判断矩阵目标或上层某指标下一层指标或方案首先作出单层结构图目标层准则层方案层（递阶层次分析结构图）（一）1—9标度表如下（二）按1~9标度赋值建立判断矩阵A 1、 A 2 、A 3，。
1、价格合理（A 1）2、品种丰富（U2）3、服务良好（U3）1 3 1/41/3 1 1/54 5 14、奶茶店选择M的权重向量四、确定矩阵A 1 A 2 A 3 A的最大特征根λmax 对应的特征向量。
1、价格合理A1==w11/3 1 1/54 5 10.2311 0.1036 0.66532、品种齐全（同上计算）3、服务良好（同上计算）4、奶茶店选择五、一致性检验 1、对A 1进行检验：λmax=1/3[0.7082/0.2311+0.3129/0.1036+2.1077/0.6653] =3.084CI=(3.084-3)/(3-1)=0.042 R.I=0.58CR=0.042/0.58=0.0724﹤0.1 A 1通过检验。
2、对A 2进行检验λmax=1/3[1.9478/0.6484+0.3664/0.1223+0.6878/0.2293] =3CI=(3-3)/(3-1)=0 R.I=0.58CR=0/0.58=0﹤0.1 A 2通过检验.3、对A 3进行检验λmax=1/3[1.0188/0.334+0.4262/0.1407+1.6154/0.5253] =3.0515CI=(3.0515-3)/(3-1)=0.0258 R.I=0.58CR=0.0258/0.58=0.04﹤0.1 A 3通过检验。
4、对A 进行检验λmax=1/3[0.7872/0.26+1.944/0.634+0.3186/0.106] =3.033CI=(3.033-3)/(3-1)=0.0165 R.I=0.58CR=0.0165/0.58=0.0284﹤0.1 A 通过检验。
层次分析法实例
层次分析法应用实例问题描述：通讯交流在当今社会显得尤其重要，手机便是一个例子，现在每个人手里都有至少一部手机。
但如今生产手机的厂家越来越多，品种五花八门，如何选购一款适合自己的手机这个问题困扰了许多人。
目标：选购一款合适的手机准则：选择手机的标准大体可以分成四个：实用性，功能性，外观，价格。
方案：由于手机厂家有几十家，我们不妨可以将其归类：○1欧美（iphone）；○2亚洲（索爱）；○3国产（华为）.解决步骤：1.建立递阶层次结构模型图1 选购手机层次结构图2.设置标度人们定性区分事物的能力习惯用5个属性来表示，即同样重要、稍微重要、较强重要、强烈重要、绝对重要，当需要较高精度时，可以取两个相邻属性之间的值，这样就得到9个数值，即9个标度。
为了便于将比较判断定量化，引入1～9比率标度方法，规定用1、3、5、7、9分别表示根据经验判断，要素i与要素j相比：同样重要、稍微重要、较强重要、强烈重要、绝对重要，而2、4、6、8表示上述两判断级之间的折衷值。
注：aij表示要素i与要素j相对重要度之比，且有下述关系：aij=1/aji ；aii=1；i，j=1，2，…，n显然，比值越大，则要素i的重要度就越高。
3.构造判断矩阵A B1 B2 B3 B4B1 1 3 5 1B2 1/3 1 3 1/3B3 1/5 1/3 1 1/5B4 1 3 5 1表1 判断矩阵A—BB1 C1 C2 C3C1 1 1/3 1/5C2 3 1 1/3C3 5 3 1表2 判断矩阵B1—CB2 C1 C2 C3C1 1 3 3C2 1/3 1 1C3 1/3 1 1表3 判断矩阵B2—CB3 C1 C2 C3C1 1 3 6C2 1/3 1 4 C31/61/41表4 判断矩阵B3—CB4 C1 C2 C3C1 1 1/41/6 C2 4 1 1/3 C3631表5 判断矩阵B4—C4.计算各判断矩阵的特征值，特征向量和一致性检验 用求和发计算特征值：○1将判断矩阵A 按列归一化（即列元素之和为1）：bij= ai j /Σaij ； ○2将归一化的矩阵按行求和：ci=Σbij （i=1，2，3….n ）；○3将ci 归一化：得到特征向量W=（w1，w2，…wn ）T ，wi=ci /Σci ， W 即为A 的特征向量的近似值； ○4求特征向量W 对应的最大特征值：1).153111311131311531=A ，按列归一化后为381514522938153831412213833851432235391514522938152).按行求和并归一化后得()T389.0069.0153.0389.0=W3).计算特征根：()TAW 389.0069.0153.0389.015315111513131311531=582.1389.0*1069.0*5153.0*3389.0*11=+++=AW ，同理有 619.02=AW ，275.0AW 3=，582.1AW 4=4).计算最大特征根： 5).进行一致性检验：查同阶平均随机一致性指针（表6所示）知R.I=0.89，（一般认为CI<0.1、 CR<0.1时，判断矩阵的一致性可以接受，否则重新两两进行比较）。
层次分析法实例-PPT
谓动宾 ｜
动宾 定 中
｜
）
定 ）中
状〕中
动｜宾 动｜宾
量短
定） 联＋合
层次分析法实例
9
层次分析法实例
10
层次分析法实例
11
‖
谓
中 动｜ 宾
定 ）中 动｜ 宾 定）中
层次分析法实例
12
层次分析法实例
13
Bye Bye
层次分析法实例
14
定 ）中 定 ） 中
定 ）中
定）中
动｜ 宾 定） 中 联+合
主
‖
谓
定） 中
状〕 中
定） 中
动｜ 宾
定）中
联+合
层次分析法实例
主‖ 谓 兼语
动｜宾
主‖谓
状〕中
6
漫的前沿阵地上 连长马上返回军部开会 历史的书我只看过一本 大伙儿批评了他一顿
（从大到小的层次分析法）
中〈
补 介词短语
方位短语 定） 中 主‖谓 定 ）中
的层次分析原则 来的各个成分都必须有意义。例如： 昨天没有去√
层次分析法实例
昨天没有去 （前一部分没有意义） ※
写来的信
（虚词，如连词、结构助词 语气词要独立出来）
1
2
层次分析法实例
有意义，但
语法上不能搭配）
/蛋※ 咬死了猎人的狗”中，后一种切分就不能成立。
层次分析法实例
3
层次分析法实例
4
质文化生活水平 应该珍惜自己的青春年华 发明针灸的国家 把你的打算向人们讲清楚
主‖
谓
状〕 中
连 ┊谓
动｜宾
主 定） 中
‖谓
层次分析法案例
层次分析法案例层次分析法（Analytic Hierarchy Process，AHP）是一种多目标决策方法，它通过构建层次结构、建立判断矩阵、计算权重和一致性检验等步骤，帮助决策者进行系统化的决策分析。
下面我们通过一个案例来详细介绍层次分析法的具体应用。
案例背景：某公司准备引进一款新的生产设备，但在选择适合的设备时面临多个因素的考量，比如设备的性能、价格、维护成本等。
为了做出最合理的决策，公司决定采用层次分析法来进行决策分析。
步骤一，构建层次结构。
首先，公司将引进新设备的决策问题分解为三个层次，目标层、准则层和方案层。
目标层是引进新设备，准则层包括设备性能、价格和维护成本，方案层则是具体的设备选项。
在这个案例中，我们假设有A、B、C三种设备可供选择。
步骤二，建立判断矩阵。
接下来，公司需要对准则层和方案层进行两两比较，以确定它们之间的相对重要程度。
通过专家意见调查或者问卷调查，公司得到了比较矩阵，比如设备性能对价格的重要程度、设备性能对维护成本的重要程度等。
步骤三，计算权重。
利用AHP的计算方法，公司可以根据比较矩阵计算出每个准则和方案的权重。
这些权重可以帮助公司确定对于引进新设备而言，性能、价格和维护成本的重要程度，以及A、B、C三种设备的优劣。
步骤四，一致性检验。
在计算权重之后，公司需要进行一致性检验，以确保比较矩阵的合理性和可靠性。
如果比较矩阵通过一致性检验，则可以继续进行下一步决策分析。
步骤五，综合分析。
最后，公司可以利用计算出的权重，对三种设备进行综合分析，以确定最佳的选择。
在这个案例中，公司可以根据性能、价格和维护成本的权重，对A、B、C 三种设备进行打分和排名，从而做出最合理的决策。
通过以上案例，我们可以看到层次分析法在多目标决策问题中的应用。
它通过构建层次结构、建立判断矩阵、计算权重和一致性检验等步骤，帮助决策者进行系统化的决策分析，提高决策的科学性和准确性。
总之，层次分析法是一种强大的决策分析工具，它不仅可以用于企业的决策问题，也可以应用于个人生活中的选择问题。
层次分析法具体案例
条理分解法真例取步调之阳早格格创做分离一个简直例子，证明条理分解法的基原步调战重心.【案例分解】合理买买电脑计划：条理分解法问题提出很多的电脑小黑需要对付买买哪个品牌的电脑举止计划，可采用的规划是买买戴我公司死产的条记原（简称买买戴我）或者买买偶像公司死产的条记原（简称买买偶像）.除了思量主板根源中，还要思量CPU本能、隐卡办法等果素，即是多规则计划问题，思量使用条理分解法办理.1. 修坐递阶条理结构【案例分解】合理买买电脑计划：修坐递阶条理结构正在买买哪个品牌的电脑计划问题中，很多电脑小黑期视通过采用分歧的电脑品牌使性价比最下，即计划目标是“合理买买电脑使性价比最下”.为了真止那一目标，需要思量的主要规则有三个，即主板根源，CPU本能，隐卡办法.但是问题绝没有那样简朴.通过深进思索，还认为还必须思量原工厂自产、代工厂提供、主频的大小、核心数、独力式隐卡、集成式隐卡等果素（规则），从相互闭系上分解，那些果素隶属于主要规则，果此搁正在下一条理思量，而且分属于分歧规则.假设原问题只思量那些规则，交下去需要精确为了真止计划目标、正在上述规则下不妨有哪些规划.根据题中所述，原问题有二个办理规划，即买买戴我或者买买偶像，那二个果素动做步伐层元素搁正在递阶条理结构的最下层.很明隐，那二个规划于所有规则皆相闭.将各个条理的果素按其上下闭系晃搁好位子，并将它们之间的闭系用连线连交起去.共时，为了便当后里的定量表示，普遍从上到下用A、B、C、D...代表分歧条理，共一条理从左到左用1、2、3、4...代表分歧果素.那样形成的递阶条理结构如下图. 目标层A规则层B规则层步伐层图1 递阶条理结构示企图2. 构制推断矩阵并赋值【案例分解】合理买买电脑计划：构制推断矩阵并挖写表2 推断矩阵表3. 条理单排序（估计权背量）取考验【案例分解】合理买买电脑计划：估计权背量及考验上例估计所得的权背量及考验截止睹下：表4 条理估计权背量及考验截止表不妨瞅出，所有单排序的C.R.<0.1，认为每个推断矩阵的普遍性皆是不妨交受的.4. 条理总排序取考验【案例分解】合理买买电脑计划：条理总排序及考验上例条理总排序及考验截止睹下：表5 C条理总排序(CR = 0.0000)表表6 D条理总排序(CR = 0.0000)不妨瞅出，总排序的C.R.<0.1，认为推断矩阵的完全普遍性是不妨交受的5. 截止分解通过对付排序截止的分解，得出末尾的计划规划.【案例分解】合理买买电脑计划：截止分解从规划层总排序的截止瞅，买买偶像（D2）的权沉（0.6592）近近大于买买戴我（D1）的权沉（0.3408），果此，最后的计划规划是买买偶像.根据条理排序历程分解计划思路.对付于规则层B的3个果子，主板根源（B1）的权沉最矮（0.1429），cpu（B2）战隐卡（B3）的权沉皆比较下（皆为0.4286），证明正在计划中比较瞅沉cpu战隐卡.对付于没有瞅沉的主板，其做用的二个果子原工厂（C1）、代工厂（C2）单排序权沉皆是买买戴我近近大于买买偶像，对付于比较瞅沉的cpu战隐卡，其做用的四个果子中有三个果子的单排序权沉皆是买买偶像近近大于买买戴我，由此不妨推出，买买偶像规划由于cpu战隐卡较为超过，权沉也会相对付超过.从规则层C总排序截止也不妨瞅出，主频数（C3）、独力隐卡（C5）是权沉值较大的，而如果单独思量那二个果素，规划排序皆是买买偶像近近大于买买戴我.由此咱们不妨分解出计划思路，即计划比较瞅沉的是cpu 战隐卡，没有太瞅沉主板，果此对付于简直果子，主频数战独力隐卡成为主要思量果素，对付于那二个果素，皆是买买偶像规划更好，由此，最后的规划采用买买偶像也便水到渠成了.。
最新-层次分析法经典案例 精品
层次分析法经典案例篇一：层次分析法步骤层次分析法实例与步骤结合一个具体例子，说明层次分析法的基本步骤和要点。
【案例分析】市政工程项目建设决策：层次分析法问题提出市政部门管理人员需要对修建一项市政工程项目进行决策，可选择的方案是修建通往旅游区的高速路（简称建高速路）或修建城区地铁（简称建地铁）。
除了考虑经济效益外，还要考虑社会效益、环境效益等因素，即是多准则决策问题，考虑运用层次分析法解决。
1建立递阶层次结构应用解决实际问题，首先明确要分析决策的问题，并把它条理化、层次化，理出递阶层次结构。
要求的递阶层次结构一般由以下三个层次组成：?目标层（最高层）：指问题的预定目标；?准则层（中间层）：指影响目标实现的准则；?措施层（最低层）：指促使目标实现的措施；通过对复杂问题的分析，首先明确决策的目标，将该目标作为目标层（最高层）的元素，这个目标要求是唯一的，即目标层只有一个元素。
然后找出影响目标实现的准则，作为目标层下的准则层因素，在复杂问题中，影响目标实现的准则可能有很多，这时要详细分析各准则因素间的相互关系，即有些是主要的准则，有些是隶属于主要准则的次准则，然后根据这些关系将准则元素分成不同的层次和组，不同层次元素间一般存在隶属关系，即上一层元素由下一层元素构成并对下一层元素起支配作用，同一层元素形成若干组，同组元素性质相近，一般隶属于同一个上一层元素（受上一层元素支配），不同组元素性质不同，一般隶属于不同的上一层元素。
在关系复杂的递阶层次结构中，有时组的关系不明显，即上一层的若干元素同时对下一层的若干元素起支配作用，形成相互交叉的层次关系，但无论怎样，上下层的隶属关系应该是明显的。
最后分析为了解决决策问题（实现决策目标）、在上述准则下，有哪些最终解决方案（措施），并将它们作为措施层因素，放在递1阶层次结构的最下面（最低层）。
明确各个层次的因素及其位置，并将它们之间的关系用连线连接起来，就构。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
误。如，已判断C1比C2重要，C2比C3较重要，那么，C1应该比C3更重要。 如果又判断C1比C3较重要或同等重要，这就犯了逻辑错误。这就需要进行 一致性检验。 根据层次法原理， 利用A的理论最大特征值λmax与n之差检验一致性。一 致性指标：
CI 3.004 3 0.003 0.1 ，查同阶平均 0.002 <0.1， CR RI n 1 3 1 随机一致性指标（表 5 所示）知 RI 0.58 ， （一般认为 CI<0.1、 CR<0.1 时，
4）求特征向量W对应的最大特征值：
●求根法 1）计算判断矩阵A每行元素乘积的n次方根； wi 2, …, n） 2）将 wi 归一化，得到 wi
wi
n
a
j 1
n
ij
（i =1,
w
i 1
n
；W=（w1，w2，…wn ）T即为A的特
i
征向量的近似值； 3）求特征向量W对应的最大特征值：
表 6 层次总排序 层次 层次
C1 C2 C3 B1 B2 B3
0.230 0.105 0.258 0.637
0.648 0.592 0.333 0.075
.426 0.283 0.291
5、结论 由表 5 可以看出，3 种品牌设备的优劣顺序为： C1 ， C3 ， C 2 ，且品牌 1 明显优于其他两种品牌的设备。
(1)判断矩阵 A B 的特征根、特征向量与一致性检验 ①计算矩阵 A B 的特征向量。 计 算 判 断 矩 阵 A B 各 行 元 素 的 乘 积 Mi ， 并 求 其 n 次 方 根 ， 如
1 2 M 1 1 2 ， W1 3 M 1 0.874 ， 类 似 地 有 ， W2 3 M 2 2.466 ， 3 3 W3 3 M 3 0.464 。对向量 W [W1 , W2 , , Wn ]T 规范化，有 W1 W1
计算 CI
max n
判断矩阵的一致性可以接受，否则重新两两进行比较） 。 表 5 平均随机一致性指标
阶数 3 RI 0.58 4 0.89 5 1.12 6 1.26 7 1.36 8 1.41 9 1.46 10 1.49 11 1.52 12 1.54 13 1.56 14 1.58
按照公式计算判断矩阵最大特征根： n ( AW ) i 0.69 1.948 0.3666 max 3.004 nW 3 0 . 230 3 0 . 648 3 0 . 122 i 1 i ③一致性检验。 实际评价中评价者只能对A进行粗略判断，这样有时会犯不一致的错
W
i 1
n
0.874 0.230 0.874 2.466 0.464
i
类似地有 W2 0.684 ， W3 0.122 。所求得的特征向量即为：
W [0.230, 0.648, 0.122]T
②计算矩阵 A B 的特征根
1 1 / 3 2 T AW 1 5 3 [0.230, 0.648, 0.122] 1 / 2 1 / 5 1 1 AW1 1 0.230 0.648 2 0.122 0.69 3 类似地可以得到 AW 2 1.948 ， AW3 0.3666 。
标度 1 3 5 7 9 2、4、6、8 倒数 定义（比较因素 i 与 j） 因素 i 与 j 同样重要 因素 i 与 j 稍微重要 因素 i 与 j 较强重要 因素 i 与 j 强烈重要 因素 i 与 j 绝对重要 两个相邻判断因素的中间值 因素 i 与 j 比较得判断矩阵 a ij，则因素 j 与 i 相比的判断为 aji=1/aij
(2)判断矩阵 B1 C 的特征根、特征向量与一致性检验 类似于第(1)步的计算过程，可以得到矩阵 B1 C 的特征根、特征向量与 一致性检验如下： W [0.105, 0.258, 0.637]T ， max 3.039 ， CR 0.033 0.1 (3)判断矩阵 B2 C 的特征根、特征向量与一致性检验 类似于第(1)步的计算过程，可以得到矩阵刀：—C 的特征根、特征向量 与一致性检验如下： W [0.592, 0.333, 0.075]T ， max 3.014 ， CR 0.012 0.1 (4)判断矩阵 B C 的特征根、特征向量与一致性检验 类似于第(1)步的计算过程，可以得到矩阵 B C 的特征根、特征向量与一 致性检验如下： W [0.149, 0.066, 0.785]T ， max 3.08 ， CR 0.069 0.1 4、层次总排序
方案C1的重要度（权重）=0.230×0.105+0.648×0.529+0.122×0.149=0.426 方案C2的重要度（权重）=0.230×0.258+0.648×0.333+0.122×0.066=0.283 方案C3的重要度（权重）=0.230×0.637+0.648×0. 075+0.122×0.785=0.291 依据各方案综合重要度的大小，可对方案进行排序、决策。 层次总排 序如表6所示。
3
2 1 1/5
C
7 5 1
B3 C1 C2 C3
C1
C2
C3
1 l/3 7
3 1 9
l/7 1/9 1
3、计算各判断矩阵的特征值、特征向量及一致性检验指标 一般来讲，在AHP法中计算判断矩阵的最大特征值与特征向量，必不需 要较高的精度，用求和法或求根法可以计算特征值的近似值。 ●求和法 1）将判断矩阵A按列归一化（即列元素之和为1）：bij= aij /Σaij； 2）将归一化的矩阵按行求和：ci=Σbij （i=1，2，3….n）； 3）将ci归一化：得到特征向量W=（w1，w2，…wn ）T，wi=ci /Σci ， W即为A的特征向量的近似值；
某物流企业需要采购一台设备，在采购设备时需要从功能、价格与可维护 性三个角度进行评价，考虑应用层次分析法对 3 个不同品牌的设备进行综 合分析评价和排序，从中选出能实现物流规划总目标的最优设备，其层次 结构如下图所示。以 A 表示系统的总目标，判断层中 B1 表示功能， B2 表示 价格， B3 表示可维护性。 C1 ， C 2 ， C3 表示备选的 3 种品牌的设备。
3 3
获得同一层次各要素之间的相对重要度后， 就可以自上而下地计算各级 要素对总体的综合重要度。设二级共有m个要素c1, c2,…,cm，它们对总值的 重要度为w1, w2,…, wm；她的下一层次三级有p1, p2,…,pn共n个要素，令要素 pi对cj的重要度（权重）为vij，则三级要素pi的综合重要度为：
A B1 B2 B3 B1 C1 C2 C3 B2 C1 C2 C3 B1 B2 B3
1 1/3 3 1 1/2 1/5 表 2 判断矩阵 B C
1
2 5 1
C3
C1
C2
1 l/3 3 1 5 3 表 3 判断矩阵 B2-C
C1 C2
1/5 1/3 1
C3
1 1/2 1/7 表 4 判断矩阵 B
注：aij表示要素i与要素j相对重要度之比，且有下述关系： aij=1/aji ；aii=1； i，j=1，2，…，n 显然，比值越大，则要素i的重要度就越高。
2、构建判断矩阵 A 判断矩阵是层次分析法的基本信息，也是进行权重计算的重要依据。 根据结构模型，将图中各因素两两进行判断与比较，构造判断矩阵： ●判断矩阵 A B (即相对于物流系统总目标，判断层各因素相对重要性 比较)如表1所示； ●判断矩阵 B1 C (相对功能，各方案的相对重要性比较)如表 2 所示； ●判断矩阵 B2 C (相对价格，各方案的相对重要性比较)如表 3 所示； ●判断矩阵 B3 C (相对可维护性，各方案的相对重要性比较)如表 4 所 示。 表 1 判断矩阵 A B
目标层 购买设备 A
判断层
功能 B1
价格 B2
维护性 B3
方案层
产品 C1
产品 C2 图 设备采购层次结构图
产品 C3
解题步骤：
1、标度及描述
人们定性区分事物的能力习惯用5个属性来表示，即同样重要、稍微重 要、较强重要、强烈重要、绝对重要，当需要较高精度时，可以取两个相 邻属性之间的值，这样就得到9个数值，即9个标度。 为了便于将比较判断定量化，引入1～9比率标度方法，规定用1、3、5、 7、9分别表示根据经验判断，要素i与要素j相比：同样重要、稍微重要、较 强重要、强烈重要、绝对重要，而2、4、6、8表示上述两判断级之间的折 衷值。