标准极图及吴氏网
《金属学原理》各章习题及解答(晶体的塑性变形)
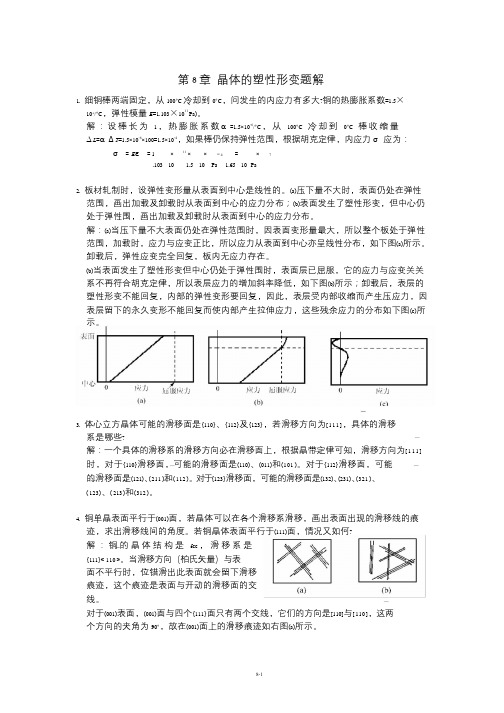
第8 章晶体的塑性形变题解1. 细铜棒两端固定,从100°C 冷却到0°C,问发生的内应力有多大?铜的热膨胀系数=1.5×10-6/°C,弹性模量E=1.103×1011 Pa)。
解:设棒长为 1 ,热膨胀系数α=1.5×10-6/°C ,从100°C 冷却到0°C 棒收缩量∆L=α∆T=1.5×10-6×100=1.5×10-4,如果棒仍保持弹性范围,根据胡克定律,内应力σ应为:σ=Eε=1 ×11 ××−4 =×7.103 10 1.5 10 Pa 1.65 10 Pa2. 板材轧制时,设弹性变形量从表面到中心是线性的。
(a)压下量不大时,表面仍处在弹性范围,画出加载及卸载时从表面到中心的应力分布;(b)表面发生了塑性形变,但中心仍处于弹性围,画出加载及卸载时从表面到中心的应力分布。
解:(a)当压下量不大表面仍处在弹性范围时,因表面变形量最大,所以整个板处于弹性范围,加载时,应力与应变正比,所以应力从表面到中心亦呈线性分布,如下图(a)所示。
卸载后,弹性应变完全回复,板内无应力存在。
(b)当表面发生了塑性形变但中心仍处于弹性围时,表面层已屈服,它的应力与应变关关系不再符合胡克定律,所以表层应力的增加斜率降低,如下图(b)所示;卸载后,表层的塑性形变不能回复,内部的弹性变形要回复,因此,表层受内部收缩而产生压应力,因表层留下的永久变形不能回复而使内部产生拉伸应力,这些残余应力的分布如下图(c)所示。
3. 体心立方晶体可能的滑移面是{110}、{112}及{123},若滑移方向为[111],具体的滑移系是哪些?解:一个具体的滑移系的滑移方向必在滑移面上,根据晶带定律可知,滑移方向为[111] 时,对于{110}滑移面,可能的滑移面是(110)、(011)和(101 )。
晶体取向与多晶体织构

从N极沿子午线大园向赤道方向至某一 纬线间的弧度,叫极距,用ρ标记 极距, 标记。赤 极距 道的极距为90°。 投影点的球面坐标为(ϕ, ρ). ϕ
晶体投影
2、极射赤面投影 、
将球面投影再投影到赤道平面上去的一种投影。 投影方法如图所示。
晶体投影
3、标准投影:选择晶体中对称性高的低指数晶面,如(001)、 、标准投影:选择晶体中对称性高的低指数晶面, )、
晶 体 学 织 构
3、织构的表示方法
择优取向是多晶体在空间聚集的现象,肉眼难于
准确判断其取向。为了直观地表达,必须把这种微观的空间聚集 取向的位置、角度、密度分布与材料的宏观外观坐标系(拉丝及 纤维的轴向,轧板的轧向、横向、板面法向)联系起来。通过材 料宏观的外观坐标系与晶体微观取向的联系,就可直观地了解多 晶体微观的择优取向。 晶体x射线学中织构的表示方法有:晶体学指数 晶体学指数表示; 极图表示 晶体学指数 (正极图 反极图);取向分布函数表示 极图、反极图);取向分布函数表示 极图 反极图);
初始取向
一般取向
晶体取向
2、晶体取向的表达方式 、
用晶体的某晶面、晶向在参考坐标系中的排布方式来表达晶体的 取向。如在立方晶体轧制样品坐标系中用(hkl)[uvw]来表达某一晶 粒的取向,这种晶粒的取向特征为其(hkl)晶面平行于轧面,[uvw] 方向平行于轧向,还可以用[rst]=[hkl]×[uvw]表示平行于轧板横向 的晶向,从而构成一个标准正交矩阵,若用g代表这一取向,则:
不同测试方法所得结果比较: 不同测试方法所得结果比较: X-射线衍射: EBSD: 中子衍射: 样品表层(100µm上下)平均 样品表面(1µm上下)各点 体样平均
晶体取向
1、晶体取向的一般定义方法 、
赤平投影原理经典实用

•赤平投影原理
•4
(二)、投影网:吴尔福网和施密特网
1、吴氏网的结构及成因原理
吴氏网的结构:基圆、径向大圆弧、纬向小圆弧、
东西、南北经纬线,间距2°,误差±0.5°。
(1)、基圆:赤平大圆,代表水平面,0°-
360°方位角刻度。
(2)、两条直径:EW,SN。
(3)、经向大圆弧:由一系列走向SN的,向东
•赤平投影原理
•22
例9: 已知平面产状310°∠50°,如果绕走向SN轴水 平旋转30 °求旋转后的平面产状。
操作步骤: ❖ 投影平面FD; ❖ 将大圆上若干点沿其所在
纬向小圆逆时针旋转30° (箭头所示)到新位置; ❖ 将旋转后得到的新位置点 旋转到同一经向大圆上, 拟合大圆弧即为旋转后的 平面D′F′投影。
•赤平投影原理
•23
例9: 已知一角度不整合上覆地层的产状 240°∠30°,下伏老地层产状为120 ° ∠ 40 °, 求新地层水平时老地层的产状。
❖ 投影新地层DHF 、老地层 ABC 的产状;
❖ 将新地层产状恢复水平,旋 转DHF 大圆弧与SN向经向 大圆重合,将大圆弧上各点 转到基圆上。
❖ 将老地层向相同方向旋转相
同角度,使老地层ABC大圆
达到新位置,将新位置各点
拟合大圆即可。
•赤平投影原理
•24
作业:
P230 9、11、12、16、18
•赤平投影原理
•25
•赤平投影原理
•9
(3) 、法线的投影 关键:法线和平面垂直,倾向相反(90°),倾角互 余。 例3: 产状为90 °∠40 °平面的法线投影。
•赤平投影原理
•10
(4)、已知真倾角求视倾角 例4:某岩层产状300°∠40°,求在
多晶体织构的测定——认识晶体学中的极射赤面投影和吴里夫网2

39
由这三个转动可以确定O-XYZ相对于O-ABC的方位,故多晶体 中每个晶粒都可用一组欧拉角表示其取向Ω(ψ,θ,φ)。 建立直角坐标系O-ψθφ,每种取向对应图中一点,将所有晶 粒的Ω(ψ,θ,φ)均标注在该坐标系内,就得到如图7-19 所示的取向分布图。
40
多晶材料测定各晶粒方位,可用取向密度表示晶粒取向分布 情况
42
ODF已确切表达了晶粒的取向分布,也可计算材料的织构指 数。对板织构可从ODF的取向峰值计算其指数{hkl}〈uvw〉, 晶轴正交的各晶系织构指数计算式如下:
ODF不能直接测定,需由一系列极图数据通过计算机软件来 计算,这些程序往往兼有由ODF获得任何极图和反极图功能。
43
极图和反极图已成为常规的织构表示方法,对丝织构可直接 测算织构指数〈uvw〉。用轴向反极图可进一步描述其织构 的强烈程度,一般不需测定极图;而板织构则需用极图或反 极图或ODF才能全面表达。
4
第一节 极射赤面投影法
实际晶体(空间点阵)均三维空间结构,表达其晶面和晶 向方位及其夹角较为困难,不如在二维平面上容易。 “晶体投影”: 把三维晶体结构中晶向和晶面位向及其夹角关系投影到二 维平面上来,建立三维图形与二维图形间一定对应关系。 极射赤面投影:在各种晶体投影方法中用得最多的一种。
立方晶系标准投影图 a)(001)b)(011)c)(111)
24
晶带轴指数[uvw]与晶带面指数(hkl)间的关系: 即晶带定律:hu+kv+lw=0 立方晶系晶面间夹角公式:
式中,h1k1l1、h2k2l2为二相交晶面的晶面指数; φ为二晶面间夹角。
25
极射投影法与极图的演变过程及其应用

DOI: 10.3969/j.issn.1000-6826.2021.01.0007极射投影法与极图的演变过程及其应用The Evolution and Application of Stereographic Projecting Method and Pole Figure供稿|杨平 / YANG Ping晶体学涉及晶体本身的性质(如对称性和各向异性)及晶体在外部条件变化时的结构变化(如温度、压力、磁场、电场等)。
描述晶体本身及其变化的最常用的工具之一就是极射赤面投影法或极射投影图。
《材料科学基础》课程是材料专业最基本的理论课程,涉及的材料主要是晶体。
如果问刚学过《材料科学基础》课程的学生,哪些概念相对难?苦涩难懂?肯定会有不少同学说,极射投影图难懂,有效使用更难。
如果问及这个工具用于哪些场合?同学们基本能答出用于确定不同晶体学方向夹角的测定,用于多晶织构的表达。
至于熟练应用,就很难达到,或令人望而生畏了。
针对此现象,作者曾编辑出版了《材料科学名人典故与经典文献》[1]一书,收集整理了极射投影图方法的演变历史及在不同领域的应用,并在课程教学中予以展示。
由于作者长期从事的材料学研究中频繁用到极射投影图和极图,因此充分体会到其直观性和便利性;此外,随着科技的不断进步,特别是计算机及软件开发和作者单位:北京科技大学材料科学与工程学院,北京 100083测试技术的进步,晶体学这个既传统又成熟但其应用还远不普及的学科,越来越频繁地被应用,极射投影图也越来越广泛地得以使用。
在此结合作者所收集的资料和自己的科研工作讨论极射投影法和极图的“神奇”、有趣和广泛应用,希望引起读者的兴趣,并在研究工作中注重其应用。
极射赤面投影的基本概念图1给出极射赤面投影原理图。
极射赤面投影方法是由单位球的中心出发的任一晶向,与球面相交(球面投影概念)于A 点,该交点A 向单位球的南极(下半球)投影,投影线AS 与赤道面的交点′A′就是该晶向三维方向的二维坐标或表达。
镁金属织构的标准极图计算

61.9 28.1 , 63.8
18.8, 40.2 , 29.9, 26.2, 13.1, 49.8, 90 50.7, 66.2, 43, 74.9, 80.5, 75.7 56.8 , 87.6 86.1 72.2
102
43.1 46.9 , 70
18.8, 0 , 40 , 53.7 , 11.1, 27.5, 31.9 , 49.8, 72.6, 90 36.9, 67.5, 58.8 , 74.9, 86.3 64.1, 83 61.8 , 87.6 75.2 81.8
镁的基本滑移面和滑移方向
• 根据六方结构金属镁的滑移面主要是 (0001)、{10-10}和{10-11},这是由于它 们的原子密度相差不多, • 滑移方向是<11-20> 。
• 如果对金属镁板进行大塑性轧制变形,在 轧制过程中,孪生变形与滑移变形共同作 用,最终各主要滑移面与轧制面平行或趋 近平行,滑移方向与轧制方向一致。
(c) (102)极图
实测极图的织构分析
• 运用计算极图的逆过程,分析织构。
总结
• 建立了镁的特定织构与特定晶面极图之间的对应关系。 • 绘制了镁 (001)<110> 织构、{110}<001> 织构、{100}<110> 织构、 {101}<110>织构、{001}<110>织构、 (001)∥ND丝织构、 (001)∥RD丝织构和{110}∥ND丝织构等8种织构的标准极图。 • 指出了传统标准晶面极射投影图与织构的标准极图的本质区别 • 提出了实测极图的织构解析方法与传统的分析方法进行对比, 揭示镁的加工方式对织构演变的影响规律。 • 这为镁金属及其合金的织构表征、织构演变和各向异性的研究 提供理论支撑。
实验八多晶材料择优取向的测定
实验八多晶材料择优取向的测定实验八多晶材料择优取向的测定一、实验目的与任务1.了解多晶材料择优取向的特征,注意丝织构与板织构的区别。
2.掌握X射线衍射仪测定丝织构的原理及其测定方法。
3.学会利用反极图描述丝织构的程度。
二、丝织构的基本特征及反极图表示法在材料的制备、合成、加工处理等工艺过程中,经常采用挤压、轧制、加压烧结、拔丝、喷丝、蒸镀、极化等工艺手段,从而引起多晶粉末素坯或多晶材料中晶粒的晶体学取向产生某种择优取向的排列,其中尤以形成丝织构的情况为多。
1.丝织构的特点织构有多种分类法,然而在X射线衍射方法中,与其相关的是织构材料的晶体学特征。
由此出发,通常把织构分成两大类,即丝织构和板织构。
具有丝织构的材料,其晶体学的特征是,在材料内部,各晶粒的某一个或几个晶体学方向倾向于平行试样的某一特定的方向,一般为材料的丝轴、棒轴方向,被挤压方向,晶体生长方向等;其他晶体学方向则以试样的这一特定方向为轴呈对称分布。
图7-1表示了具有丝织构的某种热压烧结柱体中晶体学方向的分布情况,设该材料属四方晶系。
由图看出,材料晶体学[001]方向平行于柱体的轴向,见图7-1(a);而具有特征意义的[100](或[010])方向则绕轴向呈对称分布,见图7-1(b)。
以图7-1表示的情况为理想丝织构状态,这时圆柱体中的晶粒均以[001]方向平行于柱轴方向。
称这种织构为[001]理想织构。
然而,在实际材料中存在的织构,其织构程度往往不是图7-1所示的理想织构状态。
仍以上述具有[001]丝织构的实际材料为图7-1 理想丝织构的示意图图7-2 丝织构材料中的极分布图例,通常存在的织构情况是材料中的各晶粒的[001]方向具有往柱轴方向集中的倾向,即沿柱轴方向的晶粒的[001]方向存在一定的分布函数。
如果[001]方向和柱轴之间的夹角为φ,则[001]极点密度ρ(001)存在如图7-2所示的分布,只是在φ=00处有ρ(001)的极大值。
极射赤平投影原理及使用方法PPT学习教案
二. 赤平投影网的使用方法
(三)法线的赤平投影: 例如: 求一平面产状为90∠40°的法线投影。
1. 透明纸上指北箭头与投影网的0°重合, 从0° 开始, 顺时针数到投影网的90 °处, 用铅笔在该处的基 圆上注记一点。该点为平面的倾向。
第29页/共38页
二. 赤平投影网的使用方法
大圆弧
第6页/共38页
一. 赤平投影的基本原理 (二) 平面的赤平投影解析:
1. 过球心的平面的赤平投影: 直立大圆在赤平面的赤平投影为基圆的一条直
径(即直立大圆PSFN的投影为NS直径);水平大圆的赤 平投影就是基圆(WNES);倾斜大圆的赤平投影是以基 圆直径为弦的大圆弧(ASBN投影成SB’N)
第4页/共38页
一. 赤平投影的基本原理 (二) 平面的赤平投影解析:
1. 过球心的平面的赤平投影: 设想通过球心的平面无限延伸,必定与球面相交
构成一个直径与投影球直径相对的大圆。直立平面与 投影球相交为一直立大圆(SPNF),水平平面与投影球 相交为水平大圆或基圆(WNES),倾斜平面与投影球相 交为一倾斜大圆(SANB) 。
方向数90 °得K点。 4. 将K点转至一经向大圆弧上, 过K点作出大圆弧FG,
FG大圆弧所代表的平面即为产状为70∠40°和290∠30° 两平面的公垂面, 因而在FG大圆弧上两交线之间的夹角为 真二面角, 其中一对为锐角, 另一对为钝角, 二者互为补角。
第33页/共38页
二. 赤平投影网的使用方 法 (四)求两平面的夹角及其等分面:
直径上, 沿着投影网东西直径由投影网圆周向圆心方向数40°, 得一 点A, 该点即为为产状为330∠40°倾斜直线的赤平投影。
第27页/共38页
吴氏网的基本操作
第二组擦痕
70°SE 第一组擦痕
A B
马角坝老鹰嘴一带地质图
中各地层产状如下: C1-2z :320°∠53 ° D3m :310°∠40 ° D3s3 :320°∠53 ° D3s2 :300°∠49 ° D3s1 :310°∠46 ° D1-2g:340°∠40 ° 如果作A-B(10 °)方向
东西、南北经
纬线组成。标 270°
准的吴氏网的
基圆直径为
20cm 经、
240
°
纬度间距2°。
210°
180 °
30° 60°
90
120° 150 °
第二章 吴氏网结构及基本操作(手工)
基圆: 由指北方向N为0°, 顺时针方向刻出0-360°的刻度, 这些刻度起着量度方位角的作用。
经向大圆弧: 由一系列通过球心, 走向南北, 分别向西和向
2.3 面、线投影的手工操作
所需工具:
吴氏网(在实习指导书后面) 透明纸(>20×20cm) [硬纸板(>20×20cm)] 图钉一枚或大头针 橡皮擦 铅笔 透明胶带
2.3 面、线投影的手工操作
(一) 平面的赤平投影:
例1: 一平面的产状为120∠30°
2. 转动透明纸, 使120 °倾向的注记点移动至投影网的东西直径上, 沿着投影网东西直径由投影网圆周向圆心方向数30°, 得一点C, 然 后描绘出过C点的经向大圆弧, 该大圆弧为产状为120∠30°倾斜平 面的赤平投影。
越大,越靠近圆心;反之则远离圆心)
— -
水平面投影 (基圆)
倾 斜 面 投 影 大 圆 弧
平面的投影特征
直立面投影-直线
突 出 方 向 倾 斜 方 向 , 倾 角 愈 大 愈 弯 曲
XRD重要结论
X 光各章重要结论1. 倒空间结论:)(][,)(][**hkl hkl uvw uvw ⊥⊥吴氏网、极网的使用:绕一轴旋转使轴与吴氏网N-S 极重合,绕一点旋转使此点与极点重合。
将二者并用可以获得任意位置的极射投影。
2. X 光谱结论: 最短波长:V4.120≈λ,式中波长之单位为埃,电压单位为千伏。
最大波长为最短波长的1.5倍。
线性吸收系数的Victoreen 经验公式:43λλμD C −=,式中C、D 与物质有关。
3. X 光的衍射公式的由来:晶体中的每一个原子都会在以下几个方面影响最终的衍射线,即:自身的散射因子(与布拉格角有关)、同种类的原子在晶格中的距离(实际为位相差)、自身的位置(确切说为相对位置)。
原子散射因子的计算:假设只有两个几何意义上的点进行衍射,衍射线是增强还是削弱由二者的相对距离、波长和衍射角决定。
在计算原子的衍射因子时,将电子云微分为许多质点,散射的强度与质点的电荷相关,质点的位置决定相位差。
所谓原子散射因子就是整个原子的散射线的振幅与处于原子中心的一个电子散射的振幅之比。
晶体的衍射的一般表达式拥有几个项相乘的形式,但是我们应该知道这个式子并没有明确的物理意义。
这个式子等价于晶体中所有原子的原子散射因子和相位差乘积的和。
当晶体中包含足够多的原子时(其实不需要很多),就只有相位差是π2整数倍的原子种类才有衍射峰了。
点阵消光条件是对于14种布拉维点阵来说的,仅计算点阵中的结点,至于一个结点上有几个原子,属于结构消光条件的事。
对消光条件的一个简单的图解:这种情况下如果是相位差为π2,衍射线加强,那么这样就一定是减弱了。
晶面是不会反射的,事实上光线射到原子上反射的方向是随机的,我们只不过是找了一个刚刚好的晶面,这个晶面的法线与出射线和入射线夹角的平分线重合。
如果出射线和入射线使我们找不到刚好的晶面,那也不用担心,我们已经说过只有相位差是π2整数倍的原子种类才有衍射峰,这样的方向是不会有衍射线的(其实还是有一定强度的,即背底强度)。
