(数学)函数的单调性、极值点、极值、最值
高等数学自考3.3函数的单调性与极值

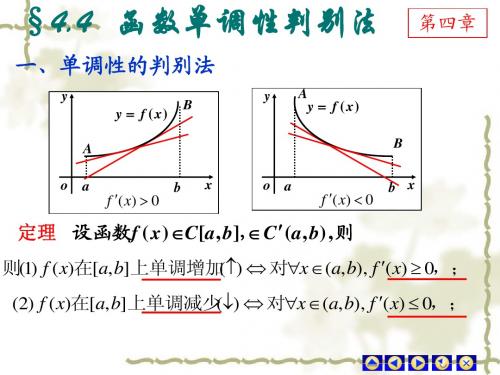
上单调增加; 在 上单调增加 (i)如果在 b)内f ′(x) > 0,则f (x)在[a, b]上单调增加; )如果在(a, 内 , 上单调减少。 (ii)如果在 b)内f ′(x) <0,则f (x)在[a, b]上单调减少。 )如果在(a, 内 , 在 上单调减少
例1 讨论函数 y = e x − x − 1的单调性 . 的单调性 解 Q y′ = e x − 1. 又 Q D : ( −∞ ,+∞ ).
的极值点与极值。 例4 求 f (x) = (x −1) x 的极值点与极值。
3 2
解
定义域( 定义域(−,+)
2 5x − 2 f ′( x) = x + ( x −1) x = 3 , 3 3 x 2 当 x = 时 , f ′( x ) = 0; 5 当 x = 0时 , f ′( x )不存在
4 3
′(x) = 12x3 −12x2 = 12x2 ( x −1), 解 f
令 得驻点: f ′( x) = 0 得驻点 x = 0, 1.
′′( x) = 36x2 − 24x = 12x(3x − 2) f
f ′′(0) = 0, f ′′(1) = 12 > 0.
由极值第二判别法, 由极值第二判别法 ξ=1时, 时 f (ξ)有极小值 f (1)=4. 有极小值: ξ 有极小值 由于 f ′′( 0 ) = 0 所以,需用极值第一判别法判定 所以 需用极值第一判别法判定: 需用极值第一判别法判定
O x
y = x3
定理2 极值存在的一阶充分条件) 定理2(极值存在的一阶充分条件) 在该邻域( 可除外)可导, 在该邻域(x0可除外)可导, 设f (x)在x0的某邻域内连续, 在 的某邻域内连续, 不存在的点。 x0为f (x)的驻点或使 ′(x) 不存在的点。 的驻点或使f 的驻点或使 (i) 若当 < x0 时,f ′(x) > 0;当x > x0 时,f ′(x) < 0, 若当x ; , 则 f (x0) 是f (x)的极大值; 的极大值; 的极大值 (ii) 若当 < x0 时,f ′(x) < 0; 当x > x0 时,f ′(x) >0, 若当x ; , 的极小值; 则 f (x0) 是f (x)的极小值; 的极小值 (iii) 若在 0的两侧,f ′(x)不变号, 若在x 的两侧, 不变号, 不变号 不是极值。 则f (x0)不是极值。 不是极值
函数的单调性与极值 最值

例8
判断函数 y = x − ln x 的单调性
解
函数的定义域为 (0,+∞ ) x −1 1 Q y′ = 1 − = x x 当 0 < x < 1 时数在 ( 0,1) 内单调减少。 单调减少。
内单调增加。 在 (1, +∞ ) 内单调增加。
x >1
时, y′ > 0,
y
f ( x1 )
( 2)
则称函数 f ( x )在区间 I上是单调减少的 ;
f ( x2 )
y = f ( x)
o
x1
x2
x
I
一、函数的单调性
y
2.判别方法 判别方法
y A y = f (x) B
y = f (x)
A
B
o
a
f ′( x ) ≥ 0
b
x
o a
f ′( x ) ≤ 0
b x
在区间(a,b)上单调上升 若 y = f (x)在区间 上单调上升 在区间(a,b)上单调下降 若 y = f (x)在区间 上单调下降
y
间断
∴ 单增区间为 (−∞, −2) , ( 2, +∞ ) 单减区间为 (−2, 0) , (0, 2)
x < ln(1 + x ) < x . 复习 证明当 x > 0 时, 1+ x 课本P124 课本 证法一设 f ( t ) = ln(1 + t ) t ∈ [0, x ]
足拉格朗日中值定理的条件. 则 f ( x ) 在 [0, x ]上满足拉格朗日中值定理的条件. 故
∴ 在(−∞ ,1]上单调增加; −∞ 上单调增加;
f ′( x ) < 0, ∴ 在[1,2]上单调减少; 上单调减少;
大学高等数学上册:4-1单调性与极值

(非严格意义的) 注意
闭区间[a, b]上上述结论不一定成立. o a
bx
y
y
oa
bx o a
bx
1.闭区间上连续函数的最值
闭区间[a, b]上连续函数f (x) 的最大最小值 M,m 的求法. (1) 求出f (x) 在(a, b) 内的所有临界点:x1, x2 , , xn. (2) 求出函数值 f ( x 1), f ( x 2), , f ( x n) 及 f (a),f (b). (3) 比较以上这些函数值的大小即可得:
令 f ( x) 0 得驻点x = -1, 0, 1. f ( x) 6( x2 1)(5 x2 1)
x ( ,1) 1 (1,0) 0 (0, 1) 1
(1, )
f ( x) -
0
-
0
+
0
+
f ( x)
0
+
0
f (x)
非极值
极小值 f (0) = 0
非极值
三、最值
最值是整体概念而极值是局部概念. 结论:若f (x) 在 (a, b) 内有最值点 x0,则 x0 必是极值点.
例如
y x3
y x
x = 0 是驻点但非极值点 x = 0 是极小值点但 y (0) 不存在
结论:极值点必是临界点
极值点的必要条件
问题:如何判别临界点是否为极值点?
3.极值点的充分条件
y x2
y x3
y 3 x2
(1)一阶充分条件:
设 x0 是f ( x )的临界点, f ( x )在某N ( x0 )内连续,在
f ( x )的驻点.
(4) 函数的单调性是一个区间上的性质,不能用一点
函数的单调性与极值

称为“二阶导数非零法” 说明:(1)记忆:几何直观;
o
x0
x
(2) 此法只适用于驻点,不能用于判断不可导点;
(3) 当 f ( x0 ) 0 时,法则失效,如: x 3 , x 4 在 x 0 处 .
24
例8
求函数 f ( x ) x 3 x 9 x 5 的极值.
y
o
(1,0)
x
y ln x 在定义域内单调增加 ,即为增函数.
例2 判断函数 y x cos x 在[0, 2 ]上的单调性. 解
y 1 sin x ,
3 y 0, 且仅在x= 处,y 0. 在[0, 2 ]上, 2
函数y x cos x在[0, 2 ]上单调增加.
7
例3 讨论函数 f ( x) 3 x 2 的单调性.
解
D=(, ) . f ( x )
2 3 x
3
, ( x 0)
当 x 0时, f ( x ) 0, f ( x)在(,0]上单调减少;
当0 x 时,f ( x ) 0, f ( x)在[0, )上单调增加;
15
说明: 1、极值不一定都存在; 2、极值若存在,必在定义区间的内部取到; 而最值既可能在区间内部取到,也可能在端点处取到. 若最值在区间内部取到,则必为极值. 3、极值是局部性的概念,可以有多个,且极大值不一定 比极小值大. 最值是全局概念. 至多有一个最大值,一个最小值.
3 y x 最小值不会大于最大值 . y
第四节
函数的单调性与极值
本节开始, 我们学习导数在实际中的一些应用, 包括 利用导数研究函数的性态(单调性、极值、凹凸性、拐 点)并作图以及最优化问题的求解, 这些应用的理论基
函数单调性和求极值点、最值(知识点及相关练习)

函数单调性和求极值点、最值(知识点及相关练习)本文档将介绍函数的单调性以及如何求函数的极值点和最值。
这些概念是在研究高等数学中非常重要的一部分。
函数的单调性函数的单调性描述了函数图像在定义域内的变化趋势。
一个函数可以是递增的(单调递增),也可以是递减的(单调递减),或者在某个区间内既递增又递减。
判断函数的单调性需要观察函数的导数。
如果函数的导数恒大于零(导函数递增),则函数单调递增;如果导数恒小于零(导函数递减),则函数单调递减。
如果导数在某个区间内既大于零又小于零,则函数在该区间内既递增又递减。
下面是一些相关联系。
练题:1. 设函数 $f(x)=x^3-3x^2+2$,求 $f(x)$ 的单调区间。
- 解答:- 首先求导数:$f'(x)=3x^2-6x$- 然后求解 $f'(x)=0$ 的解,即 $3x^2-6x=0$ ,解得 $x=0, 2$- 将 $x=0$ 和 $x=2$ 代入 $f'(x)$ 的导数符号表,得到如下结果:| $x$ | $(-\infty,0)$ | $(0,2)$ | $(2,+\infty)$ |- 由上表可以看出,函数 $f(x)$ 在区间 $(-\infty, 0)$ 上递减,在区间 $(0,2)$ 上递增,而在区间 $(2,+\infty)$ 上递增,所以函数的单调区间分别为 $(-\infty, 0)$ 和 $(2,+\infty)$。
求函数的极值点和最值函数的极值点是函数某一段上的极大值或极小值点。
函数的最大值和最小值是函数在整个定义域上的最大值和最小值。
为了求函数的极值点和最值,我们需要找到函数的临界点和边界点。
- 临界点:函数定义域内导数为零或不存在的点。
- 边界点:函数定义域的端点。
对于一个函数,如果它有极值点,那么极值点一定在函数的临界点和边界点处。
下面是一些相关练。
练题:1. 设函数 $g(x)=x^3-6x^2+9x+2$,求 $g(x)$ 的极值点和最值。
4.4-5 函数的单调性,极最值,凹凸性,拐点
例4 求下列函数的最值
(1) y 3 ( x 2 2 x ) 2 x 0,3 4( x 1) ( x ) 解 f 33 x 2 2 x 而 令f x) 0,得驻点 x 1, x 0,2是不可导点 ( 由于f (1) 1, f ( 2) 0, f (0) 0, f ( 3) 3 9
内的所有 x 0及f x不存在的点 找出 a, b f (一般有限个) :
x 1 , x 2 , , x k ;在f a , f x 1 , f x 2 , , f x k , f b 中 选取出最大最小 ,
即为f x 在a, b上的M, m.
若 f ( x0 ) f ( x0 ) f ( x0 ) 0,f
( 4)
( x0 ) 0, 则如何?
(1).若 f ( x0 ) f ( x0 ) f ( 2n1) ( x0 ) 0,f
则f ( x)在x0处取极值 .
( 2n)
( x0 ) 0,
x
f (x) f (x)
故
( , 1)
1
0
(1 , 2)
2 0 1
( 2 , )
y
2
(2 , ); 的单调减(单减)区间 为 (1 , 2).
的单调增(单增)区间为 ( , 1) ,
2 1
o
1 2
x
说明:
1) 单调区间的分界点除驻点外,也可是导数不存在的点.
例如,
y y 3 x2
f ( x0 ) f ( x) f ( x0 ) f ( x0 )( x x0 ) ( x x0 ) 2 o ( x x0 ) 2 2!
函数的单调性与极值点

函数的单调性与极值点函数的单调性和极值点是数学中重要的概念,它们用于描述函数在定义域内的增减关系和取得最大值或最小值的点。
本文将详细介绍函数的单调性和极值点的概念,并探讨它们的性质及应用。
一、函数的单调性函数的单调性是指函数在定义域内的增减关系。
具体来说,如果对于定义域内的任意两个不同的自变量值x1和x2,当x1<x2时,函数值f(x1)<f(x2),则称函数为递增函数;当x1<x2时,函数值f(x1)>f(x2),则称函数为递减函数。
为了判断函数的单调性,我们可以计算函数的导数。
对于定义在区间(a, b)上的可导函数,如果在该区间内导函数始终大于零,则函数为递增函数;如果在该区间内导函数始终小于零,则函数为递减函数。
当导函数在某一点处等于零时,该点可能是函数的极值点。
二、函数的极值点函数的极值点是函数取得最大值或最小值的点。
极值点可以分为极大值点和极小值点。
如果在某一点的邻域内,函数在该点处的值大于(或小于)邻域内其他点的函数值,则该点为极大值点(或极小值点)。
为了确定函数的极值点,我们需要计算函数的导数。
首先求得函数的导函数,然后找到导函数为零的解,即导函数的根。
根据极值点的性质,导函数在极大值点或极小值点处的值为零。
因此,将导函数等于零的解代入原函数中,即可求得极值点的值。
需要注意的是,虽然导函数为零的点可能是函数的极值点,但并不是所有导函数为零的点都是极值点。
还需要进一步分析函数的横截点和导函数的符号变化,以确定这些点是否为极值点。
三、函数的单调性与极值点的应用函数的单调性和极值点在各个科学领域中有广泛的应用。
在经济学中,函数的单调性用于分析供需关系以及市场的变化趋势。
在物理学中,函数的单调性和极值点可以用于描述物体的运动规律和力学问题。
在统计学中,函数的单调性和极值点被用于拟合数据和分析数据的趋势。
此外,在优化问题中,函数的单调性和极值点也扮演着重要的角色。
通过研究函数的单调性和极值点,我们可以找到函数取得最大值或最小值的条件,并在实际问题中应用这些条件进行优化。
函数的单调性与极值点例题和知识点总结

函数的单调性与极值点例题和知识点总结在数学的学习中,函数的单调性与极值点是非常重要的概念,它们不仅在数学理论中有着关键地位,还在实际问题的解决中发挥着巨大作用。
下面,我们将通过一些具体的例题来深入理解函数的单调性与极值点,并对相关知识点进行总结。
一、函数单调性的定义函数的单调性指的是函数在其定义域内的增减性质。
如果对于定义域内的某个区间上的任意两个自变量的值$x_1$、$x_2$,当$x_1 <x_2$时,都有$f(x_1) < f(x_2)$(或$f(x_1) > f(x_2)$),那么就称函数在这个区间上是增函数(或减函数)。
例如,函数$f(x) = x^2$在区间$(\infty, 0)$上是减函数,在区间$(0, +\infty)$上是增函数。
二、判断函数单调性的方法1、定义法设$x_1$、$x_2$是给定区间上的任意两个自变量的值,且$x_1 <x_2$,计算$f(x_2) f(x_1)$,若$f(x_2) f(x_1) > 0$,则函数在该区间上是增函数;若$f(x_2) f(x_1) < 0$,则函数在该区间上是减函数。
例 1:判断函数$f(x) = 2x 1$在区间$(\infty, +\infty)$上的单调性。
解:设$x_1$,$x_2$是区间$(\infty, +\infty)$上的任意两个实数,且$x_1 < x_2$。
则$f(x_2) f(x_1) =(2x_2 1) (2x_1 1) = 2(x_2 x_1)$因为$x_1 < x_2$,所以$x_2 x_1 > 0$,$2(x_2 x_1) > 0$,即$f(x_2) f(x_1) > 0$。
所以函数$f(x) = 2x 1$在区间$(\infty, +\infty)$上是增函数。
2、导数法对于可导函数,如果其导数$f'(x) > 0$,则函数在相应区间上是增函数;如果$f'(x) < 0$,则函数在相应区间上是减函数。
