第九章 带限信道的信号设计
高斯信道

信道容量和带宽的关系
1.5
1
C
0.5
0
0
5
10
15 W
20
25
30
中国科学技术大学 刘斌
《信息论基础》
12
带宽有限信道的信道容量
香农公式的物理意义为:当信道容量一定 时,增大信道的带宽,可以降低对信噪功 率比的要求;反之,当信道频带较窄时, 可以通过提高信噪功率比来补偿。香农公 式是在噪声信道中进行可靠通信的信息传 输率的上限值。
定义
6
中国科学技术大学 刘斌
《信息论基础》
高斯信道信道编码定理的证明
中国科学技术大学 刘斌
《信息论基础》
7
高斯信道信道编码定理的证明
1. 码簿的生成:令 为i.i.d. ~ ,形成码 字 2. 编码:码簿生成之后,将其告知发送者和接收者。对消 息下标w,发送器发送 3. 译码:联合典型译码
是联合典型的 不存在其他的下标 满足
1. 下标集 2. 编码函数 a。 生成码字 ,且满足功率限制P,
3. 译码函数 4. 平均误差概率:
中国科学技术大学 刘斌 《信息论基础》 5
高斯信道的信道编码定理
对于一个功率限制为P的高斯信 道,如果存在满足功率限制的一个 码序列,使得最大误差 ,则称码 率R关于该功率限制为P的高斯信道是可 达的。 高斯信道的信道容量即是所有可达码率的 上确界。
转化成离散二元对称信道 离散信道的特点:可纠错,但有量化损失
中国科学技术大学 刘斌 《信息论基础》 3
高斯信道的信道容量
功率限制为P的高斯信道的信道 容量定义为:
定义
高斯信道的信道容量为:
最大值在
中国科学技术大学 刘斌 《信息论基础》
北邮通信原理课件 (9)(全)

a. 在检测的前后窗口的参考音能量大 小,若两窗口能量均大于某个门限时,同 步处于跟踪模糊区内,就自动向固定方向 调一个样点,使同步头脱离跟踪模糊区. b. 在条件①不满足的条件下,检测两 窗口内参考音能量差值,依据前述准则判 别.
(3) Doppler
在通信过程中,由于多种因素的影响 会导致频率漂移,若不对此进行校正,将
在误码率为10 -2 的情况下采用该种校 验方式后,其误码率小于10 -11,可以认为 是无差错传输.另外采用了 S-ARQ技术, 即重发有错的小组,大大地提高了通过率. 另外在ARQ工作方式下,实现了自动 降速的功能,共分为两档:300bit/s以上及 150bit/s以下.在每一挡下,通信速率可以 根据信道的实际情况实现自动的速率升降, 以获得大的通过率.
(1) 电离层的衰耗随时间变化及多 径效应所引起的衰落. (2) 多径效应所引起的波形展宽.
(3) 电离层快速运动和反射层高度 变化所引起的多普勒频移.
一般情况下,短波高速数字通信系统
框图如图9-1所示.
图9-1 短波无线数字通信系统框图
9.2 TCT-301短波高速调制解 调器的基本原理
图9-2和图9-3分别是短波高速 调制解调器的发送端和接收端的 原理框图.
3. 群同步建立,位同步跟踪,
(1)
这里所指的群同步是指译码同步.在 位同步建立之后,抽样的位置确定了.
(2)
在通信过程中,由于时钟等各种因素 的影响,位同步的位置会发生变化,如果 不跟踪其变化,则在通信建立一段时间之 后因同步位置丢失而导致通信中断.
① 上下帧相位突跳点附近有比较好的 线性关系, Diff>0, Diff=0, Diff<0,同步滞后. ② 上,下帧相位突跳点同时位于两窗 口内,则存在一个同步跟踪的模糊区.
《通信原理》各章节重点知识考点

第一章1、通信系统的模型(了解 图1-1 1-4 1-5)2、数字通信的特点(掌握)①抗干扰能力强,且噪声不积累②传输差错可控③便于用现代数字信号处理技术对数字信息进行处理、变换、存储④易于集成,使通信设备微型化,重量轻⑤易于加密处理,且保密性好⑥需要较大的传输带宽 3、平均信息量的简单计算(选、填)221log log ()()()I P x bit P x ==- 21()()log ()(/ni i i H x P x P x bit ==-∑符号)当信息源的每个符号等概率出现时,信息源具有最大熵:2()log n(/H x bit =符号)4、码长、码元速率、信息速率、频带利用率定义、单位、计算码元速率RB :每秒传输码元的数目,单位B 二进制与N 进制码元速率转换关系:RB2=RBNlog2N(B) 信息速率:每秒钟传递的信息量,单位bit/s 在N 进制下Rb=RBNlog2N(bit/s)第二章1、随机过程的概念、分布函数、概率密度函数的定义(理解 P36-37) 均值:1[()](,)()E t xf x t dx a t ∞-∞ξ==⎰方差:2222[()]{()()}[()][()]()D t E t a t E t a t t σξ=ξ-=ξ-=自相关函数:1212(,)[()()]R t t E t t =ξξ 协方差函数:121122(,){[()()][{()()]}B t t E t a t E t a t =ξ-ξ- 2、高斯过程的一维概率密度函数(掌握 P46-47)22()f ())2x a x -=-σ 误差函数:2()2)1xz erf x e dz ϕ-==- 互补误差函数:2()1()22)z xerfc x erf x e dz ϕ∞-=-==-3、高斯白噪声及带限噪声的定义、平均功率的计算(掌握 P57-60) 白噪声:0()()(/z)2n n P f f W H =-∞<<∞ 自相关函数:0()()2nR ξτ=δτ 低通白噪声:020()H n f f n P f ||≤={其他自相关函数:0sin 2()=n 2H HH f R f f ππτττ带通白噪声:0f f 2220()c c n B Bf n P f -≤ ||≤ +={其他自相关函数:0sin ()=n cos 2c B R Bf B πππττττ平均功率:N= 0n B4、噪声的功率谱密度与相关函数的关系 线性系统输出/输入功率谱密度的关系计算(掌握 P42-44 P48-49) 平稳过程的功率谱密度()P f ξ与其自身相关函数()R τ是一对傅里叶变换关系,即()()j P f R e d ∞-ωτξ-∞=ττ⎰()=()j R P f e df ∞ωτξ-∞τ⎰或()()j P R e d ∞-ωτξ-∞ω=ττ⎰ 1()=()2j R P e d π∞ωτξ-∞τωω⎰平稳过程的总功率:(0)=()R P f df ∞ξ-∞⎰输出过程0()t ξ的均值:0()]()(0)t a h d H ∞-∞E[ξ=⋅ττ=α⋅⎰输出过程0()t ξ的自相关函数:0120()()R t t R ,+τ=τ输出过程0()t ξ的功率谱密度:2()()o i P f f P f =⎪H()⎪ 输出过程0()t ξ的概率分布:0()()()i t h t d ∞-∞ξ=τξ-ττ⎰第四章1、恒参、随参信道的定义及特点(填选 P72)2、频率选择性衰落的原因(简答 P75-76)第五章1、调制解调的概念(了解 P86),调制的目的(掌握 P86)①提高天线通信时的天线辐射效率②实现信道的多路复用,提高信道利用率③扩展信号带宽,提高系统抗干扰、抗衰落能力,还可实现传输带宽与信噪比之间的互换2、双/单边带调制系统的带宽、抗噪性能的分析、计算(掌握 P98-101)双边带:()()cos DSB c s t m t t =ω 带宽:2DSB H B f = H f 为调制信号的带宽 o n 为单边功率谱密度经低通后输出信号为:1()()2o m t m t =所以解调器输出的有用信号功率为:221()()4o o S m t m t == 经低通后,解调器最终的输出噪声为:1()()2o c n t n t =所以输出噪声功率为:22111()()444o o i i o N n t n t N n B ====解调器输入信号平均功率:221()()2i m S s t m t == ⇒解调器输入信噪比:21()2i i o m t S N n B = 输出信噪比:221()()414o o o i m t S m t N n B N ==⇒制度增益:/2/o o DSB i i S N G S N ==单边带:11()()cos ()sin 22SSB c c s t m t t m t t ∧=ω+ω 带宽:SSB H B f = H f 为调制信号的带宽经低通后输出信号为:1()()4o m t m t =所以解调器输出的有用信号功率为:221()()16o o S m t m t ==1144o i o N N n B == ⇒输出信噪比: 221()()16144o o o o m t S m t N n B n B ==输入信号平均功率:221()()4i m S s t m t == ⇒ 221()()44i i o o m t S m t N n B n B == ⇒ 制度增益:/1/oo SSB i i S N G S N == 3、卡森公式(P110)、门限的概念(P104)(了解 选填)用相干解调解调各种线性调制信号时不存在门限 AM 包络检波小信噪比时会出现门限效应 FM 小信噪比时也会出现门限效应调频波的有效带宽为:2(1)2()FM f m m B m f f f =+=∆+ m f 时调制信号的最高频率,f m 是最大频偏f ∆与m f 的比值4、FM 优于AM 的原因(P118-119)在大信噪比情况下,AM 包络检波的输出信噪比为:2()o o o S m t N n B=设AM 信号100%调制,且m(t)为单频余弦波,则22()2A m t =因而2/22o o o m S A N n f = FM :2232o f o o mS A m N n f =所以2(/)3(/)o o FM f i i AM S N m S N = 宽带调频(WBFM )信号的传输带宽FM B 与AM 信号的传输带宽AM B 之间关系为:2(1)(1)FM f m f AM B m f m B =+=+ ⇒2(/)3()(/)o o FM FM i i AM AMS N BS N B =在大信噪比情况下,调频系统的抗噪声性能将比调幅系统优越,且其优越程度将随传输带宽的增加而提高5、频分复用的目的(了解 P123)为了充分利用信道的频带或时间资源,提高信道的利用率 6、AM 包络检波的性能222()()22o i mA m t S s t ==+ 2()i i o N n t n B == ⇒ 22()2i o i o S A m t N n B+=大信噪比时:2()o S m t = 2()o i o N n t n B == ⇒2()o o o S m t N n B = ⇒ 222/2()/()o o AM i i o S N m t G S N A m t ==+ 7、FM 非相干解调性能()cos[()]FM c f s t A t K m d =ω+ττ⎰22i A S =i o FMN n B =22i i o FMS A N n B =大信噪比:222()()()o od f S m t K K m t == 223283d o mo K n f N Aπ= ⇒ 23(1)FM f f G m m =+ 第六章1、基带信号的波形及其功率谱(了解 P133-138) s(t)=u(t)+v(t)22u 1212()()()(1))))(1))]()s v s s s s s m P f P f P f f P P f f f mf P mf f mf ∞=-∞=+=-⎪(-(⎪+⎪(+-(⎪δ-∑G G [PG G平均功率:1()()2s s S P d P f df π∞∞-∞-∞=ωω=⎰⎰单极性基带信号功率谱密度为22()(1))(1))]()s s sssm P f f P P f f P mf f mf ∞=-∞=-⎪(⎪+⎪-(⎪δ-∑G G双极性基带信号功率谱密度为22()4(1))(21))]()s s sssm P f f P P f f P mf f mf ∞=-∞=-⎪(⎪+⎪-(⎪δ-∑G G2、码间串扰的概念、传码率与系统带宽(掌握 P146)由于系统传输总特性不理想,导致前后码元的波形畸变、展宽,并使前面波形出现很长的拖尾,蔓延到当前码元的抽样时刻上,从而对当前码元的判决造成干扰。
数字通信第5版

前言很高兴地欢迎Masoud Salehi教授作为《数字通信(第五版)》的合作著者。
这一新版本进行了较大的修订并重新组织了论题,特别是在信道编码和译码方面,同时还增加了一章关于多天线系统的内容。
本书适合作为电子工程系一年级研究生课程的教材,也适合从事数字通信系统设计工程师作为自学课本和参考书。
为了更好地阅读本书,读者应具备基本的微积分、线性系统理论以及概率和随机过程的预备知识等背景知识。
第1章是本书主题的导引,包括回顾与展望、信道特征的描述和信道模型。
第2章是对确定信号和随机信号分析内容的复习,包括带通和低通信号的表示、随机变量尾部概率边界、总和随机变量中心极限定理,以及随机过程。
第3章论述数字调制技术和数字调制信号的功率谱。
第4章重点分析加性高斯白噪声(AWGN)信道的最佳接收机及其差错率性能。
本章还包括格的入门知识和基于格的信号星座图,以及有线和无线通信系统链路预算分析。
第5章专门论述了基于最大似然准则的载波相位估计和定时同步的方法,描述了面向判决和非面向判决的两种方法。
第6章是信息论基础,包括无损信源编码、有损数据压缩、不同信道模型的信道容量以及信道可靠性函数。
第7章论述线性分组码及其特性,包括循环码、BCH码、RS码和级联码。
描述了软判决和硬判决两种译码方法,及其在AWGN信道中的性能评估。
第8章论述基于网格和图形的编码,包括卷积码、Turbo码、低密度校验码、带限信道网格码和基于格的编码,同时也论述了译码算法,包括维特比算法及其在AWGN信道上的性能、Turbo码的迭代译码BCJR算法,以及和积算法。
第9章重点论述带限信道的数字通信。
本章的论题包括带限信道的特征和信号设计,有符号间干扰和AWGN信道的最佳接收机,准最佳均衡方法,亦即,线性均衡、判决反馈均衡和Turbo均衡。
第10章论述自适应信道均衡,描述LMS和递归最小二乘算法及其性能特征,本章还论述盲均衡算法。
第11章论述多信道和多载波调制。
带限信道的信号设计

量高等优点。
调相(PM)调制
02
通过改变信号的相位来传递信息,具有抗干扰能力强、传输质
量高等优点。
调相调频(PM/FM)调制
03
结合调相和调频的优点,具有更高的抗干扰能力和传输质量。
信号编码技术
线性码
将信息序列映射为二进制码序列,具有良好的纠错能 力和较低的误码率。
循环码
一种特殊的线性码,具有循环特性,易于实现且误码 率较低。
硬判决阈值
在解码过程中,确定接收信号质量是否足够好的阈值,低于该阈值 的信号将被判定为错误。
软判决阈值
在解码过程中,根据接收信号的质量进行判决的阈值,允许在阈值 附近有一定的波动范围。
05 带限信道下的信号设计实 例
QAM信号设计实例
总结词
QAM(Quadrature Amplitude Modulation,正交幅度调制)是一种在带限 信道中常用的数字调制方式。
带限信道的信号设计
目录
• 引言 • 带限信道的基本理论 • 带限信道下的信号设计方法 • 带限信道下的信号性能评估 • 带限信道下的信号设计实例 • 结论与展望
01 引言
研究背景
01
信号传输在现代通信中具有重要作用,而带限信道 是信号传输的重要通道。
02
带限信道具有带宽限制和噪声干扰等特点,对信号 传输造成一定影响。
卷积码
将输入的信息序列编码为较长的码序列,具有较好的 纠错能力和抗干扰能力。
信号处理技术
01
滤波处理
通过滤波器对信号进行滤波处理, 以减小噪声和干扰的影响,提高 信号质量。
02
频域处理
将信号从时域转换到频域,进行 频域分析和处理,以实现信号的 优化和增强。
基带传输实验图形

正交信号在AWGN信道下的传输性能代码:clear allnsamp=10;s0=ones(1,nsamp);s1=[ones(1,nsamp/2) -ones(1,nsamp/2)];nsymbol=100000; %每种信噪比下的发送符号数EbN0=0:12; %信噪比,E/N0msg=randint(1,nsymbol); %消息数据s00=zeros(nsymbol,1);s11=zeros(nsymbol,1);indx=find(msg==0); %比特0在发送消息中的位置s00(indx)=1;s00=s00*s0; %比特0影射为发送波形s0 indx1=find(msg==1); %比特1在发送消息中的位置s11(indx1)=1;s11=s11*s1; %比特1映射为发送波形s1 s=s00+s11; %总的发送波形s=s.'; %数据转置,方便接收端处理for indx=1:length(EbN0)decmsg=zeros(1,nsymbol);r=awgn(s,EbN0(indx)-7); %通过AWGN信道r00=s0*r; %与s0相关r11=s1*r; %与s1相关indx1=find(r11>=r00);decmsg(indx1)=1; %判决[err,ber(indx)]=biterr(msg,decmsg);endsemilogy(EbN0,ber,'-ko',EbN0,qfunc(sqrt(10.^(EbN0/10))));title('二进制正交信号在AWGN信道下的误比特率性能')xlabel('Eb/N0');ylabel('误比特率Pe')legend('仿真结果','理论结果')图形改善代码可以不考虑发送信号波形的影响:clear allnsymbol=100000; %发送符号数EbN0=0:12; %信噪比msg=randint(1,nsymbol); %消息数据E=1;r0=zeros(1,nsymbol);r1=zeros(1,nsymbol);indx=find(msg==0);r0(indx)=E;indx1=find(msg==1);r1(indx1)=E;for indx=1:length(EbN0)dec=zeros(1,length(msg));snr=10.^(EbN0(indx)/10); %dB转换为线性值sigma=1/(2*snr); %噪声方差r00=r0+sqrt(sigma)*randn(1,length(msg)); %相关器的输出r11=r1+sqrt(sigma)*randn(1,length(msg));indx1=find(r11>=r00); %判决dec(indx1)=1;[err,ber(indx)]=biterr(msg,dec);endfiguresemilogy(EbN0,ber,'-ko',EbN0,qfunc(sqrt(10.^(EbN0/10))));title('二进制正交信号在AWGN信道下的误比特率性能')xlabel('Eb/N0');ylabel('误比特率Pe')legend('仿真结果','理论结果')图形:这种修改可以使仿真的运行时间变短,效率高用simulink仿真上边的代码:仿真时间设为100000双极性信号在AWGN信道下的传输性能程序代码如下clear allnsamp=10; %每个脉冲信号的抽样点数s0=ones(1,nsamp); %基带脉冲信号s1=-s0;nsymbol=100000; %每种信噪比下的发送符号数EbN0=0:10; %信噪比,E/N0msg=randint(1,nsymbol); %消息数据s00=zeros(nsymbol,1);s11=zeros(nsymbol,1);indx=find(msg==0); %比特0在发送消息中的位置s00(indx)=1;s00=s00*s0; %比特0影射为发送波形s0 indx1=find(msg==1); %比特1在发送消息中的位置s11(indx1)=1;s11=s11*s1; %比特1映射为发送波形s1 s=s00+s11; %总的发送波形s=s.'; %数据转置,方便接收端处理for indx=1:length(EbN0)decmsg=zeros(1,nsymbol);r=awgn(s,EbN0(indx)-7); %通过AWGN信道r00=s0*r; %与s0相关indx1=find(r00<0);decmsg(indx1)=1; %判决[err,ber(indx)]=biterr(msg,decmsg);endsemilogy(EbN0,ber,'-ko',EbN0,qfunc(sqrt(10.^(EbN0/10))),'-k*',EbN0,qfunc(sqrt(2*10.^(EbN0/1 0))));title('双极性信号在AWGN信道下的误比特率性能')xlabel('Eb/N0');ylabel('误比特率Pe')legend('双极性信号仿真结果','正交信号理论误比特率','双极性信号误理论误比特率')运行结果:单极性信号在AWGN信道下的传输性能程序代码:clear allnsamp=10; %每个脉冲信号的抽样点数s0=zeros(1,nsamp); %基带脉冲信号s1=ones(1,nsamp);nsymbol=100000; %每种信噪比下的发送符号数EbN0=0:10; %信噪比,E/N0msg=randint(1,nsymbol); %消息数据s00=zeros(nsymbol,1);s11=zeros(nsymbol,1);indx=find(msg==0); %比特0在发送消息中的位置s00(indx)=1;s00=s00*s0; %比特0影射为发送波形s0indx1=find(msg==1); %比特1在发送消息中的位置s11(indx1)=1;s11=s11*s1; %比特1映射为发送波形s1s=s00+s11; %总的发送波形s=s.'; %数据转置,方便接收端处理for indx=1:length(EbN0)decmsg=zeros(1,nsymbol);r=awgn(s,EbN0(indx)-7); %通过AWGN信道r00=s1*r; %与s1相关indx1=find(r00>5);decmsg(indx1)=1; %判决[err,ber(indx)]=biterr(msg,decmsg);endsemilogy(EbN0,ber,'-ko',EbN0,qfunc(sqrt(10.^(EbN0/10)/2)),EbN0,qfunc(sqrt(10.^(EbN0/10))),'-k*',EbN0,qfunc(sqrt(2*10.^(EbN0/10))),'-kv');title('单极性信号在AWGN信道下的误比特率性能')xlabel('Eb/N0');ylabel('误比特率Pe')legend('单极性信号仿真结果','单极性信号理论误比特率','正交信号理论误比特率','双极性信号理论误比特率')程序运行结果3基带PAM信号传输3.1基带4—PAM的信号波形3.2基带4—PAM信号在AWGN信道下的最佳接收3.3基带4—PAM信号在AWGN信道下的传输性能程序代码:clear allnsymbol=100000; %每种信噪比下的发送符号数nsamp=10; %每个脉冲信号的抽样点数M=4; %4-PAMgraycode=[0 1 3 2]; %Gray编码规则EsN0=0:15; %信噪比,E/N0msg=randint(1,nsymbol,4); %消息数据msg1=graycode(msg+1); %Gray映射msg2=pammod(msg1,M); %4-PAM调制s=rectpulse(msg2,nsamp); %矩形脉冲成形for indx=1:length(EsN0)decmsg=zeros(1,nsymbol);r=awgn(real(s),EsN0(indx)-7,'measured'); %通过AWGN信道r1=intdump(r,nsamp); %相关器输出msg_demod=pamdemod(r1,M); %判决decmsg=graycode(msg_demod+1); %Gray逆映射[err,ber(indx)]=biterr(msg,decmsg,log2(M)); %求误比特率[err,ser(indx)]=symerr(msg,decmsg);endsemilogy(EsN0,ber,'-ko',EsN0,ser,'-k*',EsN0,1.5*qfunc(sqrt(0.4*10.^(EsN0/10)))); title('4-PAM信号在AWGN信道下的性能')xlabel('Es/N0');ylabel('误比特率和误符号率')legend('误比特率','误符号率','理论误符号率')程序运行结果:4带限信道的信号传输4.1带限信道4.2带限信道信号无ISI的条件4.3带线信道信号传输的仿真程序代码:原始数据与脉冲成型后的数据滤波器的冲击响应程序代码clear allnsymbol=100000; %每种信噪比下的发送符号数Fd=1; %符号采样频率Fs=10; %滤波器采样频率rolloff=0.25; %滤波器滚降系数delay=5; %滤波器时延M=4; %4-PAMgraycode=[0 1 3 2]; %Gray编码规则EsN0=0:15; %信噪比,E/N0msg=randint(1,nsymbol,4); %消息数据msg1=graycode(msg+1); %Gray映射msgmod=pammod(msg1,M); %4-PAM调制rrcfilter = rcosine(Fd,Fs,'fir/sqrt',rolloff,delay); %设计根升余弦滤波器s=rcosflt(msgmod,Fd,Fs,'filter',rrcfilter);for indx=1:length(EsN0)decmsg=zeros(1,nsymbol);r=awgn(real(s),EsN0(indx)-7,'measured');rx=rcosflt(r,Fd,Fs,'Fs/filter',rrcfilter);rx1=downsample(rx,Fs);rx2=rx1(2*delay+1:end-2*delay);msg_demod=pamdemod(rx2,M); %%判决decmsg=graycode(msg_demod+1); %Gray逆映射[err,ber(indx)]=biterr(msg,decmsg,log2(M)); %求误比特率[err,ser(indx)]=symerr(msg,decmsg);endsemilogy(EsN0,ber,'-ko',EsN0,ser,'-k*',EsN0,1.5*qfunc(sqrt(0.4*10.^(EsN0/10)))); title('4-PAM信号在AWGN理想带限信道下的性能')xlabel('Es/N0');ylabel('误比特率和误符号率')legend('误比特率','误符号率','理论误符号率')运行结果。
信道的定义及分类ppt课件

其中,Si (t) 为输入的已调信号;So (t) 为信道总输 出波形;n(t) 为加性噪声/干扰,且与 Si (t) 相互 独立。
f si t 表示已调信号通过网络所发生的(时变)
线性变换。
若设 f si t k(t)si (t) ,则有 so t k(t)si (t) nt
7
调制信道对信号的影响
22
Communication Theory
典型音频电话信道的相对衰耗
23
Communication Theory
影响:不均匀衰耗使传输信号的幅度随频率发生畸 变,引起信号波形的失真;传输数字信号,还会引 起相邻码元波形在时间上的相互重叠,造成码间串 扰。 抑制措施:为了减小幅度—频率畸变,在设计总的 电话信道传输特性时,一般都要求把幅度—频率畸 变控制在一个允许的范围内;即通过一个线性补偿 网络,使衰耗特性曲线变得平坦,这一措施通常称 之为“均衡”;在载波电话信道上传输数字信号时, 通常要采取均衡措施。
29
Communication Theory
2.5 随参信道举例
1、短波电离层反射信道 短波的定义:波长为100~10m(相应的频率为3~ 30MHz)的无线电波; 短波信道:既可沿地表面传播,也可由电离层反射 传播; 地波传播:一般是近距离的,限于几十公里范围; 天波传播:借助于电离层的一次反射或多次反射可 传输几千公里,乃至上万公里的距离;
k
k
0
0
理想 的 相位-频率特性及群时延-频率特性 26
Communication Theory
实际的信道特性总是偏离理想的相位—频率特性及群 时延-频率特性,下图给出一个典型的电话信道的群迟 延-频率特性。
27
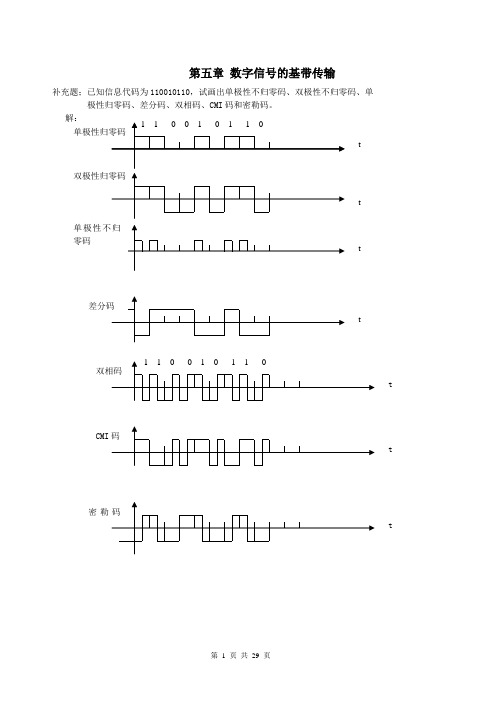
天津大学现代通信原理课后习题答案(5-9章)
解;
(1)∵“0”和“1”分别由g(t)和-g(t)组成 而其对应的频谱分别为G(f)和-G(f)故其双边功率谱为
其功率为
(2)因为矩形脉冲的频谱为
∵τ=TS故ωTs/2=Kπ时为零点
即f=Kfs时均为零点,故该序列不存在离散分量fs。
(3)∵τ=TS/2 故 ωTs/4=Kπ时为零点
即f=2Kfs时为零点,而fS的奇数倍时存在离散分量Fs。
(2) 若保持误码率Pe不变,改用非相干解调需要接收信号幅度A是多少?
解:
B=2RB=2×104HZ
Pe=2.055×10-5
(1)在相干解调时 ASK
(2)在非相干解调时
6-7 传码率为200波特的八进制ASK系统的带宽和信息速率。如果采用二进制ASK系统,其带宽和信息速率又为多少?
解:
(1) N=8时 B=2RB=2×200=400HZ
第六章 数字信号的频带传输
6-1 设数字信息码流为10110111001,画出以下情况的2ASK、2FSK和2PSK的 波形。
(1) 码元宽度与载波周期相同。
(2) 码元宽度是载波周期的两倍。
解:
(1)
(2)
6-2 已知数字信号{an}=1011010,分别以下列两种情况画出2PSK,2DPSK及相对码{bn}的波形(假定起始参考码元为1)。
(2)求匹配传递函数与冲激响应及t0;
(3)该信道噪声谱为n0=10-10W/Hz,信号幅度A=1V,持续时间T=1s,求输出最大信噪比;
(4)求输出信号表达式并画出其波形。
(1)解:
(2)解:
(3)
(4)
6-14若某二进制先验等概率FSK信号的最佳接收机,其输入信号能量与噪声功率密度之比为14分贝,试算其误码率。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
n 0
{I n }离散信息符号序列
g (t )具有带限频率响应信号 G( f ) 的一个脉冲,
而且: | f | W 时,G ( f ) 0 信道的频率响应 C ( f ) ,限制在 | f | W 接收信号表示为 rl (t ) I n h(t nT ) z(t ) n 0 h 式中: (t ) g ( )c(t )d (线性滤波器信道) z (t ) 加性高斯白噪声
1 x(t ) sinc(2W t) sinc[2 (W t )] 2
1 n 1 x(nT ) 1 n 1 0 其它 1 1 f j f (e jf W e jf W ) e jf 2W cos sin X ( f ) 2W W 2W W W 0 (t T ) (t T ) x(t ) sin c sin c T T
例2.
| f | W | f | W
③ 两个以上非零值(过程)
x(t )
n
x(
n n ) sin c 2W (t ) 2W 2W
n
X(f )
1 2W 0
x(
n )e jn f 2W
W
(| f | W ) (| f | W )
m
0
( n 0) ( n 0)
的充要条件是其
X ( f m T) T
时,(图)无法设计一个
证明:(P401) 结论:1) T
2) T
1 1 或 2W 2W T
无ISI的系统;
1 1 或 2W 时,小的空时偏差会产生 2W T
ISI的总和不收敛;
1 3) T 时,实现无ISI → 理想的升余弦谱。 2W
C ( f )表征带限信道的等效低通频率响应
C ( f ) [线性滤波器]
3. 非理想的信道频率响应特性 幅度失真 符号间干扰 线性均衡器 适时失真 (补偿线性失真 )
引起因素: 线性失真 信号传输损伤 —— 非线性失真 频率偏移 相位抖动 脉冲噪声 热噪声
二. 带限信道的信号设计
1. 接收机信号表示 数字调制等效低通发送信号的形式
选择 X f ( f ) X rc ( f ) 的零ISI的情况, X rc ( f ) 是具有 任意滚降因子的升余弦谱。 (2)信道补偿由发送机和接收机滤波器两者平均分 X rc ( f ) 摊。
| GT ( f ) | | C( f ) | | GR ( f ) | | C( f ) |
3. 具有受控ISI的带限信号设计 —— 部分响应信号 放宽ISI的条件: ① 零ISI的条件是:当 n 0时, x(nT ) 0 ② 受控ISI,有限个可控非零值 例1. x(nT ) 1 (n 0,1)
其它
X(f )
0
1 (1 e jf 2W 0
W
)
| f | W f W
I
n k n
x
) vk
I
n k n
x
vk
I k 期望信号符号
n 0 , n k
I
n
xk n 符号间干扰
vk 在第k个抽样时刻加性高斯噪声变量
2. 无符号间干扰的带限信号的设计 ——基于奈奎斯特准则 yk I k I n xk n vk
n 0, n k
第九章 带限信道的信号设计
主要内容:1. 带限信道的特征
2. 带限信道的信号设计
基本概念:1. 带限信道
2. 奈奎斯特准则 3. 部分响应信号 4. 错误概率
一. 带限信道的特征
1. 带限信道 信道带宽为指定的带宽 带宽 W Hz 问题:① 信号设计 —— 在线性调制信号脉冲 g (t ) 的设计 ② 如何避免符号间干扰(ISI) 2. 带限信道理想的信道频率响应特性 | f | W时, C( f ) 0
1 2 6 av PM 2(1 2 )Q[ ( ) ] 2 M 4 M 1 N0
GT ( f )C ( f )GR ( f ) X d ( f )e j 2ft 0 | f | W
X d ( f )是调制器、信道和解调器三者级联的期望
t 频率响应, 0是保证调制和解调滤波器物理可实现
的必要延时。
选择期望频率响应 X d ( f ) 在抽样时刻产生零ISI或 者受控ISI。
无符号间干扰的条件是
1 xk x (t kT ) 0 k 0 k 0
寻求使 x (t )满足上述关系的 X ( f ) 的必要且充分 条件 → 奈奎斯特脉冲成形准则 (零ISI奈奎斯特条件)
定理(奈奎斯特定理) : 1 使 x (t )满足 x(nT )
傅立叶变换 X ( f ) 满足
yk y (kT 0 ) I n x(kT nT 0 ) v(kT 0 ) y k I n xk n vk
n 0 n 0
1 yk x0 ( I k x0 取x0 1, yk I k
n 0,n k
n 0,n k
1
(| f | W )
2
X rc ( f )
1 2
(| f | W )
三. 谱成形调制码
平均发射功率 接收滤波器输出端的噪声方差 检测器的SNR
谱成形码(调制码)→(线性码,数据变换码)
使基带信号中的直流分量消除或减到最小
(磁记录、光记录、电缆系统)的数字通信
四. PAM检测的错误概率
脉冲幅度调制
以速率 1T抽样(符号/s),最佳滤波, 则接收滤波器的输出为:
y (t ) I n x(t nT ) v(t )
n 0
x (t ) 为接收滤波器对输入脉冲 h(t )的响应,
v (t )为接收滤波器对噪声 z (t )的相应。
离散化,抽样 ——(采样滤波器) k 在 t kT 0 时刻, 0,1, y (t ) 抽样, 对 0 是信道的传输延时。
加性高斯白噪声 决方案。 (1)在发送机中对总的信道失真进行预补偿,接收 滤波器匹配于接收信号。
X rc ( f ) | GT ( f ) | | C( f ) | | GR ( f ) | X rc ( f ) (| f | W ) (| f | W )
(nn ( f )
N0 ) 情况下的两种可能解 2
4. 有失真信道的信号设计
带限信道:信道频率响应 C( f ) (| f | W ) C 当 | f | W 时, ( f ) 0
目标:选择滤波器响应 GT ( f ), GR ( f ) (发送和接收滤波器)
GR ( f )
解调器输出的信号分量必须满足条件
加性高斯白噪声情况下解调和检测M元PAM信 号的性能评估。 1. 具有零ISI的PAM检测的错误概率
2 g 2( M 1) PM Q[ ] M N0
g | GT ( f ) |2 df
W
W
2. 部分响应信号检测的错误概率 (1)逐符号检测器(上边界)
av 平均发送符号能量 (2)最大似然检测 欧氏距离度量求错误事件概率。
