2018年北京市初三数学二模分类汇编-第9讲:选择压轴题
北京市门头沟区2018年6月中考综合练习(二模)数学试题及答案
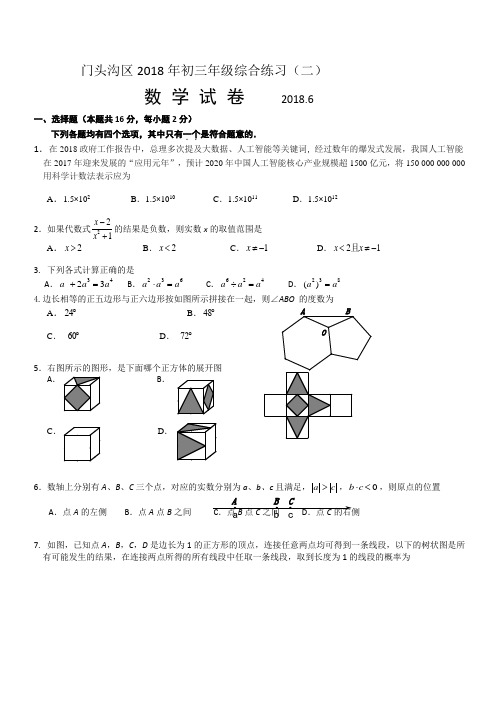
门头沟区2018年初三年级综合练习(二)数 学 试 卷 2018.6一、选择题(本题共16分,每小题2分)下列各题均有四个选项,其中只有一个..是符合题意的. 1.在2018政府工作报告中,总理多次提及大数据、人工智能等关键词, 经过数年的爆发式发展,我国人工智能在2017年迎来发展的“应用元年”,预计2020年中国人工智能核心产业规模超1500亿元,将150 000 000 000用科学计数法表示应为A .1.5×102B .1.5×1010C .1.5×1011D .1.5×1012 2.如果代数式221x x -+的结果是负数,则实数x 的取值范围是 A .2x > B .2x < C .1x ≠- D .21x x <≠-且3. 下列各式计算正确的是A .3423a a a +=B .236a a a ⋅=C .624a a a ÷= D .238()a a =4.边长相等的正五边形与正六边形按如图所示拼接在一起,则∠ABO 的度数为A .24︒B .48︒C . 60︒D . 72︒5.右图所示的图形,是下面哪个正方体的展开图 A . B .C .D .6.数轴上分别有A 、B 、C 三个点,对应的实数分别为a 、b 、c 且满足,a c >,0b c ⋅<,则原点的位置A .点A 的左侧B .点A 点B 之间C .点B 点C 之间D .点C 的右侧7. 如图,已知点A ,B ,C ,D 是边长为1的正方形的顶点,连接任意两点均可得到一条线段,以下的树状图是所有可能发生的结果,在连接两点所得的所有线段中任取一条线段,取到长度为1的线段的概率为B OA cb a A B CC ABE DOA .14 B .13C .12D .23 8.某中学举办运动会,在1500米的项目中,参赛选手在200米的环形跑道上进行,下图记录了跑得最快的一位选手与最慢的一位选手的跑步全过程(两人都跑完了全程),其中x 代表的是最快的选手全程的跑步时间,y 代表的是这两位选手之间的距离,下列说不合理的是 A .出发后最快的选手与最慢的选手相遇了两次;B .出发后最快的选手与最慢的选手第一次相遇比第二次相遇的用时短;C .最快的选手到达终点时,最慢的选手还有415米未跑;D .跑的最慢的选手用时446′″.二、填空题(本题共16分,每小题2分) 9.两个三角形相似,相似比是12,如果小三角形的面积是9,那么大三角形的面积是______. 10. 写出一个不过原点,且y 随x 的增大而增大的函数_________. 11. 如果23410a a +-=,那么2(21)(2)(2)a a a +--+的结果是 .12.某生产商生产了一批节能灯,共计10000个,为了测试节能灯的使用寿命(使用寿命大于等于6000小时为合格产品),从中随机挑选了100个产品进行测试,有5个不合格产品,预计这批节能灯有_________个不合格产品.13. 如图,⊙O 的直径CD 垂直弦AB 于点E , 且CE =2,AB =8,则OB 的长为________.14. 某校为学生购买名著《三国演义》100套、《西游记》80套,共用了12000元,《三国演义》每套比《西游记》每套多16元,求《三国演义》和《西游记》每套各多少元? 设西游记每套x 元,可列方程为_____________________.15. 如图:已知Rt ABC ∆,对应的坐标如下, 请利用学过的变换(平移、旋转、轴对称)知识 经过若干次图形变化,使得点A 与点E 重合、 点B 与点D 重合,写出一种变化的过程_____.16. 以下是通过折叠正方形纸片得到等边三角形的步骤 取一张正方形的纸片进行折叠,具体操作过程如下: 第一步:如图,先把正方形ABCD 对折,折痕为MN ;y xC OAB 446(′″, 15)yxED CBA OE PM AD第二步:点E 在线段MD 上,将△ECD 沿EC 翻折,点D 恰好落在MN 上,记为点P ,连接BP 可得△BCP 是等边三角形问题:在折叠过程中,可以得到PB=PC ; 依据是________________________.三、解答题(本题共68分,第17-24题,每小题5分,第25题6分,第26、27题7分,第28题8分)解答应写出文字说明,演算步骤或证明过程. 17.计算:()0323232cos30π-+-+-+︒.18. 解不等式组:30229+2.xx x ⎧-⎪⎨⎪+⎩≤,≤4()19.已知:如图,在Rt △ABC 中,∠C =90°,点D 在CB 边上,∠DAB =∠B ,点E 在AB 边上且满足∠CAB =∠BDE . 求证: AE =BE .20. 如图,在平面直角坐标系xOy 中,一次函数y x =与反比例函数k y x=(k ≠0)的图象相交于点(2,2)M .(1)求k 的值;(2)点(0,)P a 是y 轴上一点,过点P 且平行于x 轴的直线分别与一次函数y x =、反比例 函数ky x=的图象相交于点1(,)A x b 、2(,)B x b , 当12x x <时,画出示意图并直接写出a 的取值范围.21.如图,以BC 为底边的等腰△ABC ,点D ,E ,G 分别在BC ,AB ,AC 上,且EG ∥ BC ,DE ∥AC ,延长GE 至点F ,使得BF =BE .(1)求证:四边形BDEF 为平行四边形;(2)当∠C =45°,BD =2时,求D ,F 两点间的距离.22.已知:关于x 的一元二次方程22(1)20(0)ax a x a a --+-=>. (1)求证:方程有两个不相等的实数根;(2)设方程的两个实数根分别为1x ,2x (其中1x >2x ).若y 是关于a 的函数,且212y ax x =-,求这个函数的表达式.DECBA F D GCA B E yxM (2,2)O23.如图,BC 为⊙O 的直径,CA 是⊙O 的切线,连接AB 交⊙O 于点D ,连接CD ,∠BAC 的平分线交BC 于点E ,交CD 于点F . (1)求证:CE =CF ; (2)若BD =43DC ,求DF CF的值.24. 在“朗读者”节目的影响下,某中学在暑期开展了“好书伴我成长”读书话动,并要求读书要细读,最少要读完2本书,最多不建议超过5本。
【精品】2018年海淀初三二模数学试题及答案
下面是小明的探究过程,请补充完整:
记一次运营出租车行驶的里程数为 x (单位:公里) ,相应的实付车费为 y (单位:元) .
( 1)下表是 y 随 x 的变化情况
行驶里程数 x
0
0< x< 3.5
3.5 ≤x<4
4≤x< 4.5
4.5≤x< 5
5≤x< 5.5 …
实付车费 y
0
13
14
15
…
( 2)在平面直角坐标系 xOy 中,画出当 0 x 5.5 时 y 随 x 变化的函数图象;
知 5.考试结束,将本试卷、答题卡和草稿纸一并交回。
一、选择题 (本题共 16 分,每小题 2 分)
第 1-8 题均有四个选项,符合题意的选项只有一个 ...
1.若代数式 3 有意义,则实数 x 的取值范围是 x1
A.x 1 C. x 1
B. x 1 D. x 0
2.如图,圆 O 的弦 GH , EF , CD , AB 中最短的是
分关于直线 l 翻折,其余部分保持不变, 得到一个新函数的图象, 如果这个新函数是限减函数, 且限减系数 k 1 , 直接写出 P 点横坐标 n 的取值范围.
海淀区九年级第二学期期末练习
数学参考答案及评分标准
初三年级(数学) 第 10 页(共 18 页)
此函数 y x 2 是限减函数,它的限减系数为
1.
( 1)写出函数 y 2 x 1 的限减系数;
( 2) m
0 ,已知 y
1 (1
x
m, x
0 )是限减函数,且限减系数
x
k 4 ,求 m 的取值范围.
( 3)已知函数 y x2 的图象上一点 P ,过点 P 作直线 l 垂直于 y 轴,将函数 y x2 的图象在点 P 右侧的部
2018年北京市各区初三二模数学分类汇编-新定义问题(28题)压轴题2018.5

2018年北京市各区初三二模数学分类汇编-新定义问题(28题)1.(2018昌平二模)在平面直角坐标系xOy 中,对于任意三点A 、B 、C 我们给出如下定义:“横长”a :三点中横坐标的最大值与最小值的差,“纵长”b :三点中纵坐标的最大值与最小值的差,若三点的横长与纵长相等,我们称这三点为正方点.例如:点A (2-,0) ,点B (1,1) ,点C (1-,2-),则A 、B 、C 三点的 “横长”a =|1(2)--|=3,A 、B 、C 三点的“纵长”b =|1(2)--|=3.因为a =b ,所以A 、B 、C 三点为正方点.(1)在点R (3,5) ,S (3,2-) ,T (4-,3-)中,与点A 、B 为正方点的是; (2)点P (0,t )为y 轴上一动点,若A ,B ,P 三点为正方点,t 的值为; (3)已知点D (1,0).①平面直角坐标系中的点E 满足以下条件:点A ,D ,E 三点为正方点,在图中画出所有符合条件的点E 组成的图形;②若直线l :12y x m =+上存在点N ,使得A ,D ,N 三点为正方点,直接写出m 的取值范围.(备用图)yxyxxy研究发现,抛物线214y x =上的点到点F (0,1)的距离与到直线l :1y =-的距离相等.如图1所示,若点P 是抛物线214y x =上任意一点,PH ⊥l 于点H ,则.基于上述发现,对于平面直角坐标系x O y 中的点M ,记点M 到点P 的距离与点P 到点F 的距离之和的最小值为d ,称d 为点M 关于抛物线214y x =的关联距离;当24d ≤≤时,称点M 为抛物线214y x =的关联点.(1)在点1(20)M ,,2(12)M ,,3(45)M ,,4(04)M -,中,抛物线214y x =的关联点是______ ; (2)如图2,在矩形ABCD 中,点(1)A t ,,点(13)C t +,.①若4t =,点M 在矩形ABCD 上,求点M 关于抛物线214y x =的关联距离d 的取值范围; ②若矩形ABCD 上的所有点都是抛物线214y x =的关联点,则t 的取值范围是__________.PH PF=对于平面直角坐标系xOy 中的点P 和M ,给出如下定义:若M 上存在两个点A ,B ,使AB =2PM ,则称点P 为M 的“美好点”. (1)当M 半径为2,点M 和点O 重合时,○1点()120P -,,()211P ,,()322P ,中,O 的“美好点”是; ○2点P 为直线y=x+b 上一动点,点P 为O 的“美好点”,求b 的取值范围; (2)点M 为直线y=x 上一动点,以2为半径作M ,点P 为直线y =4上一动点,点P 为M 的“美好点”,求点M 的横坐标m 的取值范围.对于平面直角坐标系xOy 中的点(,)Q x y (x ≠0),将它的纵坐标y 与横坐标x 的比yx称为点Q 的“理想值”,记作Q L .如(1,2)Q -的“理想值”221Q L ==--. (1)①若点(1,)Q a 在直线4y x =-上,则点Q 的“理想值”Q L 等于_________;②如图,C ,⊙C 的半径为1. 若点Q 在⊙C 上,则点Q 的“理想值”Q L 的取值范围是.(2)点D 在直线+3y =上,⊙D 的半径为1,点Q 在⊙D 上运动时都有0≤L Q 点D 的横坐标D x 的取值范围;(3)(2,)M m (m >0),Q 是以r 为半径的⊙M 上任意一点,当0≤L Q ≤的最大圆,并直接写出相应的半径r 的值.(要求画图位置准确,但不必尺规作图)5.(2018朝阳二模)对于平面直角坐标系xOy 中的点P 和直线m ,给出如下定义:若存在一点P ,使得点P 到直线m 的距离等于1,则称P 为直线m 的平行点. (1)当直线m 的表达式为y =x 时, ①在点P 1(1,1),P 2(0,2),P 3(22-,22)中,直线m 的平行点是; ②⊙O 的半径为10,点Q 在⊙O 上,若点Q 为直线m 的平行点,求点Q 的坐标. (2)点A 的坐标为(n ,0),⊙A 半径等于1,若⊙A 上存在直线x y 3=的平行点,直接写出n 的取值范围.6.(2018房山二模)已知点P ,Q 为平面直角坐标系xOy 中不重合的两点,以点P 为圆心且经过点Q 作⊙P ,则称点Q 为⊙P 的“关联点”,⊙P 为点Q 的“关联圆”.(1)已知⊙O 的半径为1,在点E (1,1),F (-12,32 ),M (0,-1)中,⊙O 的“关联点”为;(2)若点P (2,0),点Q (3,n ),⊙Q 为点P 的“关联圆”,且⊙Q 的半径为 5 ,求n 的值;(3)已知点D (0,2),点H (m ,2),⊙D 是点H 的“关联圆”,直线443y x =-+与x 轴,y 轴分别交于点A ,B . 若线段AB 上存在⊙D 的“关联点”,求m 的取值范围.7.(2018丰台二模)在平面直角坐标系xOy 中,将任意两点()11,y x P 与()22y x Q ,之间的“直距”定义为:2121y y x x D PQ -+-=.例如:点M (1,2-),点N (3,5-),则132(5)5MN D =-+---=. 已知点A (1,0)、点B (-1,4).(1)则_______=AO D ,_______=BO D ;(2)如果直线AB 上存在点C ,使得CO D 为2,请你求出点C 的坐标; (3)如果⊙B 的半径为3,点E 为⊙B 上一点,请你直接写出EO D 的取值范围.8.(2018海淀二模)对某一个函数给出如下定义:若存在实数k ,对于函数图象上横坐标之差为1的任意两点1(,)a b ,2(1,)a b +,21b b k -≥都成立,则称这个函数是限减函数,在所有满足条件的k 中,其最大值称为这个函数的限减系数.例如,函数2y x =-+,当x 取值a 和1a +时,函数值分别为12b a =-+,21b a =-+,故211b b k -=-≥,因此函数2y x =-+是限减函数,它的限减系数为1-.(1)写出函数21y x =-的限减系数; (2)0m >,已知1y x=(1,0x m x -≤≤≠)是限减函数,且限减系数4k =,求m 的取值范围.(3)已知函数2y x =-的图象上一点P ,过点P 作直线l 垂直于y 轴,将函数2y x =-的图象在点P 右侧的部分关于直线l 翻折,其余部分保持不变,得到一个新函数的图象,如果这个新函数是限减函数,且限减系数1k ≥-,直接写出P 点横坐标n 的取值范围.9.(2018石景山二模)在平面直角坐标系xOy 中,对于任意点P ,给出如下定义:若⊙P 的半径为1,则称⊙P 为点P 的“伴随圆”. (1)已知,点()1,0P ,①点1,2A ⎛ ⎝⎭在点P 的“伴随圆”(填“上”或“内”或“外”); ②点()1,0B -在点P 的“伴随圆”(填“上”或“内”或“外”); (2)若点P 在x 轴上,且点P 的“伴随圆”与直线x y 33=相切,求点P 的坐标; (3)已知直线2+=x y 与x 、y 轴分别交于点A ,B ,直线2-=x y 与x 、y 轴分别 交于点C ,D ,点P 在四边形ABCD 的边上并沿DA CD BC AB →→→的方 向移动,直接写出点P 的“伴随圆”经过的平面区域的面积.。
2018年北京市西城区初三数学二模试题及答案
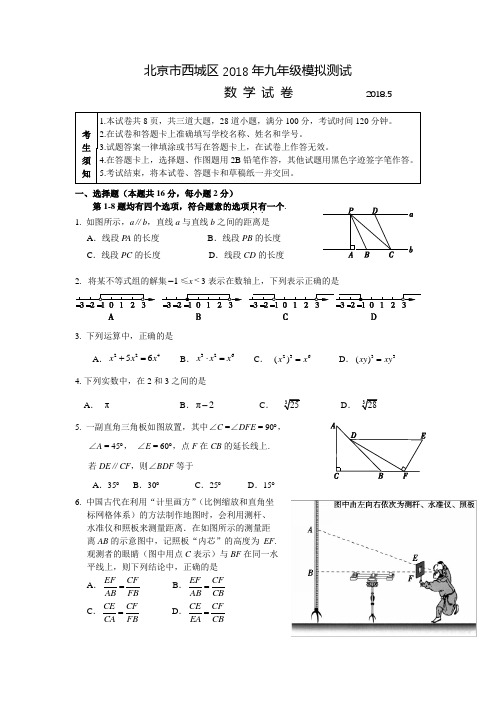
北京市西城区2018年九年级模拟测试数 学 试 卷 2018.5一、选择题(本题共16分,每小题2分)第1-8题均有四个选项,符合题意的选项只有..一个. 1. 如图所示,a ∥b ,直线a 与直线b 之间的距离是 A .线段P A 的长度 B .线段PB 的长度 C .线段PC 的长度 D .线段CD 的长度2. 将某不等式组的解集≤x 3表示在数轴上,下列表示正确的是3. 下列运算中,正确的是A .B .C .D .4.下列实数中,在2和3之间的是A .B .C .D .5. 一副直角三角板如图放置,其中∠C =∠DFE = 90︒, ∠A = 45︒, ∠E = 60︒,点F 在CB 的延长线上. 若DE ∥CF ,则∠BDF 等于A .35︒B .30︒C .25︒D .15︒ 6. 中国古代在利用“计里画方”(比例缩放和直角坐 标网格体系)的方法制作地图时,会利用测杆、水准仪和照板来测量距离.在如图所示的测量距 离AB 的示意图中,记照板“内芯”的高度为 EF . 观测者的眼睛(图中用点C 表示)与BF 在同一水 平线上,则下列结论中,正确的是A .EF CF AB FB = B .EF CFAB CB=C .CE CFCA FB = D .CE CF EA CB=1-<22456x x x +=326x x x ⋅=236()x x =33()xy xy =π π2-7. 在一次男子马拉松长跑比赛中,随机抽取了10名选手,记录他们的成绩(所用的时间)如下:A .这组样本数据的平均数超过130B .这组样本数据的中位数是147C .在这次比赛中,估计成绩为130 min 的选手的成绩会比平均成绩差D .在这次比赛中,估计成绩为142 min 的选手,会比一半以上的选手成绩要好8.如图1所示,甲、乙两车沿直路同向行驶,车速分别为20 m/s 和v (m/s),起初甲车在乙 车前a (m)处,两车同时出发,当乙车追上甲 车时,两车都停止行驶.设x (s)后两车相距y (m),y 与x 的函数关系如图2所示.有以下 结论:①图1中a 的值为500; ②乙车的速度为35 m/s ; ③图1中线段EF 应表示为5005x +;④图2中函数图象与x 轴交点的横坐标为100. 其中所有的正确结论是A .①④B .②③C .①②④D .①③④ 二、填空题(本题共16分,每小题2分)9. 有意义,那么x 的取值范围是 .10.不透明袋子中装有5个红色球和3个蓝色球,这些球除了颜色外没有其他差别.从袋子中随机摸出一个球,摸出蓝色球的概率为 .11. 如图,等边三角形ABC 内接于⊙O ,若⊙O 的半径为2,则图中阴影部分的面积等于 .12.某校“百变魔方”社团为组织同学们参加学校科技节的 “最强大脑”大赛,准备购买A ,B 两款魔方.社长发现 若购买2个A 款魔方和6个B 款魔方共需170元,购买 3个A 款魔方和购买8个B 款魔方所需费用相同. 求每 款魔方的单价.设A款魔方的单价为x 元,B款魔方的单价为y 元,依题意可列方程组为 .13. 如图,在矩形ABCD 中,顺次连接矩形四边的中点得到四边形EFGH . 若AB=8,AD=6,则四边形EFGH 的周长等于 .14.在平面直角坐标系xOy 中,将抛物线23(2)1y x =+-平移后得到抛物线232y x =+.请你写出一种平移方法. 答: .15. 如图,AB 为⊙O 的直径,AC 与⊙O 相切于点A ,弦BD ∥OC .若36C ∠=︒,则∠DOC= ︒.16. 我们知道:四边形具有不稳定性.如图,在平面直角坐标系xOy 中,矩形ABCD 的边AB 在x 轴上,,,边AD 长为5. 现固定边AB ,“推”矩形使点D 落在y 轴的正半轴上(落点记为),相应地,点C 的对应点的坐标为 .三、解答题(本题共68分,第17~21题每小题5分,第22、23题每小题6分,第24题5分,第25、26题每小题6分,第27、28题每小题7分) 17.计算:06cos60(π2)2︒-.18.解方程:1322x x x+=--.19. 如图,在四边形ABCD 中,E 为AB 的中点,DE ⊥AB 于点E ,66A ∠=︒,90ABC ∠=︒,BC= AD ,求∠C 的度数.20.先化简,再求值:2569122x x x x -+⎛⎫-÷⎪++⎝⎭,其中5x =-.21.如图,在Rt △ABC 中,90ACB ∠=︒,CD ⊥AB 于点D ,BE ⊥AB 于点B ,BE=CD ,连接CE ,DE . (1)求证:四边形CDBE 为矩形; (2)若AC =2,1tan 2ACD ∠=,求DE 的长.(3,0)A -(4,0)B D 'C'22.阅读下列材料:材料一:早在2011年9月25日,北京故宫博物院就开始尝试网络预售门票,2011年全年网络售票仅占1.68%.2012年至2014年,全年网络售票占比都在2%左右.2015年全年网络售票占17.33%,2016年全年网络售票占比增长至41.14%.2017年8月实现网络售票占比77%.2017年10月2日,首次实现全部网上售票.与此同时,网络购票也采用了“人性化”的服务方式,为没有线上支付能力的观众提供代客下单服务.实现全网络售票措施后,在北京故宫博物院的精细化管理下,观众可以更自主地安排自己的行程计划,获得更美好的文化空间和参观体验.材料二:以下是某同学根据网上搜集的数据制作的2013-2017年度中国国家博物馆参观人数及年增长率统计表.他还注意到了如下的一则新闻:2018年3月8日,中国国家博物馆官方微博发文,宣布取消纸质门票,观众持身份证预约即可参观. 国博正在建设智慧国家博物馆,同时馆方工作人员担心的是:“虽然有故宫免(纸质)票的经验在前,但对于国博来说这项工作仍有新的挑战.参观故宫需要观众网上付费购买门票,他遵守预约的程度是不一样的.但(国博)免费就有可能约了不来,挤占资源,所以难度其实不一样.”尽管如此,国博仍将积极采取技术和服务升级,希望带给观众一个更完美的体验方式.根据以上信息解决下列问题:(1)补全以下两个统计图;(2)请你预估2018年中国国家博物馆的参观人数,并说明你的预估理由.23.如图,在平面直角坐标系xOy中,函数myx=(0x<)的图象经过点(4,)A n-,AB⊥x轴于点B,点C与点A关于原点O对称,CD⊥x轴于点D,△ABD的面积为8.(1)求m,n的值;(2)若直线y kx b=+(k≠0)经过点C,且与x轴,y轴的交点分别为点E,F,当2CF CE=时,求点F的坐标.24.如图,AB是⊙O的直径,C是圆上一点,弦CD⊥AB于点E,且DC=AD.过点A作⊙O的切线,过点C作DA的平行线,两直线交于点F,FC的延长线交AB的延长线于点G.(1)求证:FG与⊙O相切;(2)连接EF,求tan EFC∠的值.25.阅读下面材料:已知:如图,在正方形ABCD 中,边1AB a .按照以下操作步骤,可以从该正方形开始,构造一系列的正方形,它们之间的边满足一定的关系,并且一个比一个小.请解决以下问题:(1)完成表格中的填空:① ;② ; ③ ;④ ;(2)根据以上第三步、第四步的作法画出第三个正方形CHIJ (不要求尺规作图).26. 抛物线M :241y ax ax a =-+- (a ≠0)与x 轴交于A ,B 两点(点A 在点B 左侧),抛物线的顶点为D .(1)抛物线M 的对称轴是直线____________; (2)当AB =2时,求抛物线M 的函数表达式;(3)在(2)的条件下,直线l :y kx b =+(k ≠0)经过抛物线的顶点D ,直线y n =与抛物线M 有两个公共点,它们的横坐标分别记为1x ,2x ,直线y n =与直线l 的交点的横坐标记为(),若当≤n ≤时,总有13320x x x x ->->,请结合函数的图象,直接写出k 的取值范围.27. 如图1,在等边三角形ABC 中,CD 为中线,点Q 在线段CD 上运动,将线段QA 绕点Q 顺时针旋转,使得点A 的对应点E 落在射线BC 上,连接BQ ,设∠DAQ =α (0°<α<60°且α≠30°). (1)当0°<α<30°时,①在图1中依题意画出图形,并求∠BQE (用含α的式子表示); ②探究线段CE ,AC ,CQ 之间的数量关系,并加以证明; (2)当30°<α<60°时,直接写出线段CE ,AC ,CQ 之间的数量关系.3x 30x >2-1-28. 对于平面直角坐标系xOy 中的点(,)Q x y (x ≠0),将它的纵坐标y 与横坐标x 的比yx称为点Q 的“理想值”,记作Q L .如(1,2)Q -的“理想值”221Q L ==--. (1)①若点(1,)Q a 在直线4y x =-上,则点Q 的“理想值”Q L 等于_________;②如图,C ,⊙C 的半径为1. 若点Q 在⊙C 上,则点Q 的“理想值”QL 的取值范围是 .(2)点D 在直线+3y =上,⊙D 的半径为1,点Q 在⊙D 上运动时都有0≤L Q D 的横坐标D x 的取值范围;(3)(2,)M m (m >0),Q 是以r 为半径的⊙M 上任意一点,当0≤L Q ≤满足条件的最大圆,并直接写出相应的半径r 的值.(要求画图位置准确,但不必尺规作图)北京市西城区2018年九年级模拟测试数学试卷答案及评分标准 2018.5二、 填空题(本题共16分,每小题2分) 9. x ≤2. 10.. 11. .12.13. 20. 14.答案不唯一,例如,将抛物线先向右平移2个单位长度,再向上平移3个单位长度得到抛物线232y x =+. 15. 54. 16. .三、解答题(本题共68分,第17~21题每小题5分,第22、23题每小题6分,第24题5分,第25、26题每小题6分,第27、28题每小题7分) 17.解:161(22=⨯-- ……………………………………………………… 4分313=-+-2=-. ……………………………………………………………………………5分18.解方程:. 解:去分母,得.……………………………………………………… 1分去括号,得.……………………………………………………… 2分 移项,得.合并同类项,得 .………………………………………………………… 3分系数化为1,得.…………………………………………………………… 4分 经检验,原方程的解为.……………………………………………………5分19. 解:如图1,连接BD .∵ E 为AB 的中点,DE ⊥AB 于点E ,∴ AD= BD , ……………… ………… 1分∴ . ∵ ,∴ .………………………… ……2分 ∵ ,384π326170,38.x y x y +=⎧⎨=⎩23(2)1y x =+-(7,4)06cos60(π2)2︒-1322x x x+=--13(2)x x -=-136x x -=-361x x -=-25x =52x =52x =1A ∠=∠66A ∠=︒166∠=︒90ABC ∠=︒∴ . …………………………… 3分 ∵ AD=BC ,∴ BD=BC .…………………………………………………………………………4分 ∴ .∴1802==782C ︒-∠∠︒. …………………………………………………… 5分20.解: ………………………………………………………………… 3分 .……………………………………………………………………………… 4分 当时,原式.……………………………………………………………5分21. (1)证明:如图2.∵ CD ⊥AB 于点D ,BE ⊥AB 于点B , ∴ 90CDA DBE ∠=∠=︒.∴ CD ∥BE .………………………………… 1分 又∵ BE=CD ,∴ 四边形CDBE 为平行四边形.……………2分 又∵90DBE ∠=︒,∴ 四边形CDBE 为矩形. ……………………………………………… 3分(2)解:∵ 四边形CDBE 为矩形,∴ DE=BC .………………………………………………………………… 4分 ∵ 在Rt △ABC 中,,CD ⊥AB , 可得 .∵ , ∴ . ∵ 在Rt △ABC 中,,AC =2,, ∴ . ∴ DE=BC=4.…………………………………………………………… 5分22.解:(1)补全统计图如图3.2124ABC ∠=∠-∠=︒3C ∠=∠2569122x x x x -+⎛⎫-÷⎪++⎝⎭2322(3)x x x x -+=⨯+-13x =-5x =-18=-90ACB ∠=︒1ACD ∠=∠1tan 2ACD ∠=1tan 1tan 2ACD ∠=∠=90ACB ∠=︒1tan 12∠=4tan 1ACBC ==∠图2………………………………………………………………… 4分(2)答案不唯一,预估理由合理,支撑预估数据即可. ……………………… 6分23. 解:(1)如图4.∵ 点A 的坐标为,点C 与点A 关于原点O 对称,∴ 点C 的坐标为.∵ AB ⊥x 轴于点B ,CD ⊥x 轴于点D ,∴ B ,D 两点的坐标分别为,.∵ △ABD 的面积为8,, ∴ .解得 . …………………………………………………………… 2分 ∵ 函数()的图象经过点, ∴ . …………… 3分(2)由(1)得点C 的坐标为. ① 如图4,当时,设直线与x 轴,y 轴的交点分别为点,.由 CD ⊥x 轴于点D 可得CD ∥.∴ △CD ∽△O .∴ . ∵ ,∴.∴ . ∴ 点的坐标为.②如图5,当时,设直线与x 轴,y 轴的交点分别为(4,)A n -(4,)C n -(4,0)B -(4,0)D 11()8422ABD S AB BD n n =⨯=⨯-⨯=- 48n -=2n =-m y x=0x <(4,)A n -48m n =-=(4,2)C 0k <y kx b =+1E 1F 1OF 1E 1E 1F 1111E C DC OF E F =112CF CE =113DC OF =136OF DC ==1F 1(0,6)F 0k >y kx b =+图4点,.同理可得CD ∥,. ∵ ,∴ 为线段的中点,.∴ 22OF DC ==.∴ 点的坐标为.…………6分综上所述,点F 的坐标为,.24. (1)证明:如图6,连接OC ,AC .∵ AB 是⊙O 的直径,弦CD ⊥AB 于点E ,∴ CE=DE ,AD=AC .∵ DC=AD ,∴ DC=AD= AC .∴ △ACD 为等边三角形.∴ ∠D =∠DCA=∠DAC =60︒.∴ . ∵ FG ∥DA ,∴ 180DCF D ∠+∠=︒. ∴ .∴ .∴ FG ⊥OC .∴ FG 与⊙O 相切.……………………………………………………… 3分(2)解:如图6,作EH ⊥FG 于点H .设CE= a ,则DE= a ,AD=2a .∵ AF 与⊙O 相切,∴ AF ⊥AG .又∵ DC ⊥AG ,可得AF ∥DC .又∵ FG ∥DA ,∴ 四边形AFCD 为平行四边形.∵ DC =AD ,AD=2a ,∴ 四边形AFCD 为菱形.∴ AF=FC=AD=2 a ,∠AFC=∠D = 60︒.由(1)得∠DCG= 60︒,sin60EH CE =⋅︒=,1cos602CH CE a =⋅︒=. ∴52FH CH CF a =+=. ∵ 在Rt △EFH 中,∠EHF= 90︒,∴2tan 52EH EFC FH a ∠===. …………………………………… 5分2E 2F 2OF 2222E C DC OF E F =222CF CE =2E 2CF 222E C E F =2F 2(0,2)F -1(0,6)F 2(0,2)F -11302DCA ∠=∠=︒180120DCF D ∠=︒-∠=︒190OCF DCF ∠=∠-∠=︒图6图525.解:(1)①斜边和一条直角边分别相等的两个直角三角形全等 .………………… 1分②11)a .………………… 2分③211)a .…………………3分④111)n a -.……………… 4分(2)所画正方形CHIJ 见图7.……………………………6分26.解:如图8.(1).…………………………… 1分 (2)∵ 抛物线241y ax ax a =-+-的对称轴为直线,抛物线M 与x 轴的 交点为点A ,B (点A 在点B 左侧),AB =2,∴ A ,B 两点的坐标分别为,.……………………………… 2分∵ 点A 在抛物线M 上,∴ 将的坐标代入抛物线的函数表达式,得.解得 . ………………………………………………………………… 3分 ∴ 抛物线M 的函数表达式为213222y x x =-+-. ………………………… 4分 (3)54k >. …………………… 6分27. 解:(1)当0°<α<30°时,①画出的图形如图9所示.…………… 1分∵ △ABC 为等边三角形,∴ ∠ABC=60°.∵ CD 为等边三角形的中线,Q 为线段CD上的点,由等边三角形的对称性得QA=QB .∵ ∠DAQ =α,∴ ∠ABQ =∠DAQ=α,∠QBE =60°-α.2x =2x =(1,0)A (3,0)B (1,0)A 410a a a -+-=12a =-∵ 线段QE 为线段QA 绕点Q 顺时针旋转所得,∴ QE = QA .∴ QB=QE .可得 1802(60)602αα=︒-︒-=︒+.……… 2分②.……………………………………………………… 3分证法一:如图10,延长CA 到点F ,使得AF=CE ,连接QF ,作QH ⊥AC于点H .∵ ∠BQE =60°+2α,点E 在BC 上,∴ ∠QEC =∠BQE+∠QBE =(60°+2α)+( 60°-α)=120°+α.∵ 点F 在CA 的延长线上,∠DAQ =α,∴ ∠QAF =∠BAF +∠DAQ=120°+α.∴ ∠QAF=∠QEC .又∵ AF =CE ,QA=QE ,∴ △QAF ≌△QEC .∴ QF=QC .∵ QH ⊥AC 于点H ,∴ FH=CH ,CF=2CH .∵ 在等边三角形ABC 中,CD 为中线,点Q 在CD 上,∴ ∠ACQ=12ACB ∠=30°,即△QCF 为底角为30°的等腰三角形. ∴cos cos30CH CQ HCQ CQ =⋅∠=⋅︒=.∴ CE AC AF AC CF +=+=2CH =.即. ………………………………………… 6分思路二:如图11,延长CB 到点G ,使得BG=CE ,连接QG ,可得△QBG ≌△QEC ,△QCG 为底角为30°的等腰三角形,与证法一同理可得CE AC BG BC CG +=+=.1802BQE QBE ∠=︒-∠CE AC +=CE AC +=图10(2)如图12,当30°<α<60°时,.………………………… 7分28.解:(1)①. ………………………………………………………………………… 1分② 0≤Q L ……………………………………………………………… 2分(2)设直线+3y =与x 轴,y 轴的交点分别为点A ,点B ,可得A ,(0,3)B .∴OA =,3OB =,30OAB ∠=︒.由0≤Q L ,作直线y .①如图13,当⊙D 与x 轴相切时,相应的圆心1D 满足题意,其横坐标取到最大值.作11D E x ⊥轴于点1E ,可得11D E ∥OB ,111D E AE BO AO =. ∵ ⊙D 的半径为1,∴ 111D E=.∴ 1AE11OE OA AE =-=∴ 1D x =②如图14,当⊙D 与直线y 相切时,相应的圆心2D 满足题意,其横坐标取到最小值.AC CE -=3-图11 图12作22D E x ⊥轴于点2E ,则22D E ⊥OA .设直线y =与直线+3y =的 交点为F .可得60AOF ∠=︒,OF ⊥AB .则9cos 2AF OA OAF =⋅∠==. ∵ ⊙D 的半径为1,∴ 21D F =.∴ 2272AD AF D F =-=.∴ 22cos AE AD OAF =⋅∠72==,22OE OA AE =-=.∴2D x =.由①②可得,D x的取值范围是≤D x≤.………………………………………… 5分(3)画图见图15.7分。
2018北京门头沟区初三(二模)数学

ABO 的度数为()
A.
B.
C.
D.
5. 下图所示的图形,可能是下面哪个正方体的展开图(
)
A.
B.
C.
D.
6. 数轴上分别有 A、 B、 C 三个点,对应的实数分别为 a、b、 c 且满足,
,
,则原点的位置()
A. 点 A 的左侧 B. 点 A 点 B 之间 C. 点 B 点 C 之间 D. 点 C 的右侧
学计数法表示应为() A. 1.5 ×10 2 B. 1.5 ×10 10 C.
1.5 ×10 11 D.
1.5 ×10 12
2. 如果代数式
的结果是负数,则实数 x 的取值范围是()
A.
B.
C.
D.
3. 下列各式计算正确的是()
A.
B.
C.
D.
4. 边长相等的正五边形与正六边形按如图所示拼接在一起,则∠
7. 如图,已知点 A,B, C, D 是边长为 1 的正方形的顶点,连接任意两点均可得到一条线段,以下的树状图是所有
可能发生的结果,在连接两点所得的所有线段中任取一条线段,取到长度为
1 的线段的概率为()
1 / 25
A. B.
C.
D.
8. 某中学举办运动会,在 1500 米的项目中,参赛选手在 200 米的环形跑道上进行,下图记录了跑得最快的一位选 手与最慢的一位选手的跑步全过程 (两人都跑完了全程) ,其中 x 代表的是最快的选手全程的跑步时间, y 代表的是 这两位选手之间的距离,下列说不合理的是()
20. 如图,在平面直角坐标系 xOy 中,一次函数
与反比例函数
(k≠0)的图象相交于点
.
( 1)求 k 的值;
2018年北京市西城区初三二模数学试题及答案

90° ,CD⊥AB 于点 D, 21.如图,在 Rt△ABC 中, ∠ACB =
BE⊥AB 于点 B,BE=CD,连接 CE,DE. (1)求证:四边形 CDBE 为矩形;
1 (2)若 AC=2, tan ∠ACD = ,求 DE 的长. 2
九年级模拟测试 数学试卷
第 3 页 (共 17 页)
22.阅读下列材料: 材料一: 早在 2011 年 9 月 25 日,北京故宫博物院就开始尝试网络预售门票,2011 年全年网络售 票仅占 1.68%.2012 年至 2014 年,全年网络售票占比都在 2%左右.2015 年全年网络售票占 17.33%,2016 年全年网络售票占比增长至 41.14%.2017 年 8 月实现网络售票占比 77%.2017 年 10 月 2 日,首次实现全部网上售票.与此同时,网络购票也采用了“人性化”的服务方式, 为没有线上支付能力的观众提供代客下单服务.实现全网络售票措施后,在北京故宫博物院 的精细化管理下, 观众可以更自主地安排自己的行程计划, 获得更美好的文化空间和参观体 验. 材料二: 以下是某同学根据网上搜集的数据制作的 2013-2017 年度中国国家博物馆参观人数及 年增长率统计表. 年度 参观人数(人次) 年增长率(%) 2013 7 450 000 38.7 2014 7 630 000 2.4 2015 7 290 000 -4.5 2016 7 550 000 3.6 2017 8 060 000 6.8
3 x +3 上,⊙D 的半径为 1,点 Q 在⊙D 上运动时都有 3
0≤LQ≤ 3 ,求点 D 的横坐标 xD 的取值范围; ,Q 是以 r 为半径的⊙M 上任意一点,当 0≤LQ≤ 2 2 时,画出 (3) M (2, m) (m>0) 满足条件的最大圆,并直接写出相应的半径 r 的值.(要求画图位置准确,但不 必尺规作图)
北京市各区2018年初三数学中考二模《代几综合题》汇编.docx

北京市各区2018 年初三下学期数学二模试题分类汇编2018 昌平二模28.在平面直角坐标系xOy 中,对于任意三点A、B、 C我们给出如下定义:“横长” a:三点中横坐标的最大值与最小值的差,“纵长”b:三点中纵坐标的最大值与最小值的差,若三点的横长与纵长相等,我们称这三点为正方点 .例如:点 A ( 2 ,0),点 B (1,1),点 C( 1, 2 ),则A、B、C 三点的“横长”a=|1 (2)|= 3 ,A、B、C三点的“纵长”b = |1 ( 2) |=3. 因为a = b ,所以A、B、C三点为正方点 .(1)在点R (3,5), S (3,2),T (4, 3 )中,与点A、B为正方点的是;(2)点 P (0,t) 为y轴上一动点,若A,B,P三点为正方点,t 的值为y432B1Ax –4–3–2–1O1 2 3 4–1C–2–3–4;(3)已知点D (1 ,0) .①平面直角坐标系中的点 E 满足以下条件:点 A ,D, E 三点为正方点,在图中画出所有符合条件的点 E 组成的图形;1m 上存在点N,使得 A ,D,N三点为正方点,直接写出m 的取②若直线 l :yx2值范围.y y55443322A 1A1DxDx–5–4–3–2–1 O 1 2 3 4 5–5–4–3–2–1 O 1 2 3 4 5–1–1–2–2–3–3–4–4–5–52018 朝阳二模28. 对于平面直角坐标系xOy 中的点 P 和直线 m,给出如下定义:若存在一点P,使得点 P 到直线 m 的距离等于,则称P为直线m的平行点.(1)当直线m 的表达式为y=x 时,①在点 P1(1, 1), P2( 0, 2 ),P3(2,2)中,直线m的平行点是;22②⊙ O 的半径为10 ,点Q在⊙O上,若点Q为直线m的平行点,求点Q 的坐标 .(2)点 A 的坐标为( n, 0),⊙ A 半径等于1,若⊙ A 上存在直线y3x 的平行点,直接写出 n 的取值范围.2018 东城二模28. 研究发现,抛物线 y1x 2 上的点到点 F(0,1)的距离与到直线 l : y1的距离相等 .4如图 1 所示,若点 P 是抛物线 y1 x2 上任意一点, PH ⊥ l 于点 H ,则 PFPH .4基于上述发现, 对于平面直角坐标系 x O y 中的点 M ,记点 M 到点 P 的距离与点 P 到点 F的距离之和的最小值为d 称 d 为点 M 关于抛物线y1 2 ,x 的关联距离; 当 2≤ d ≤4 时,4称点 M 为抛物线 y1x 2 的关联点 .4( 1 )在点 M 1 (2,0) , M 2 (12), , M 3 (4,5) , M 4 (0, 4) 中,抛物线 y1x 2 的关联点是4______ ;(2)如图 2,在矩形 ABCD 中,点 A(t ,1) ,点 C (t 13),①若 t=4,点 M 在矩形 ABCD 上,求点 M 关于抛物线 y1 x2 的关联距离 d 的取值范4围;②若矩形 ABCD 上的所有点都是抛物线y1 x2 的关联点,则 t 的取值范围是4__________.2018 房山二模28. 已知点 P,Q 为平面直角坐标系xOy 中不重合的两点,以点 P 为圆心且经过点Q 作⊙ P,则称点 Q 为⊙ P 的“关联点” ,⊙ P 为点 Q 的“关联圆” .(1)已知⊙O的半径为1,在点E F13( 1, 1),(-2,2),M( 0,- 1)中,⊙ O 的“关联点”为;(2)若点P2, 0),点Q n Q为点P的“关联圆” ,且⊙Q的半径为 5 ,求n (( 3,),⊙的值;3)已知点D0 2H m2),⊙D是点H的“关联圆” ,直线 y4((,),点(,x 4与 x3轴, y 轴分别交于点A, B. 若线段 AB 上存在⊙ D 的“关联点” ,求 m 的取值范围 .2018 丰台二模28.在平面直角坐标系 xOy 中,将任意两点 P x 1 , y 1 与 Q x 2, y 2 之间的“直距” 定义为:D PQ x 1 x 2y 1 y 2 .MN1 32 ( 5) 5例如:点 M ( 1,), 点 N ( 3,5),则2D.已知点 A(1, 0)、点 B(- 1,4).(1)则 D AO_______ , D BO _______;( 2)如果直线 AB 上存在点 C ,使得 D CO 为 2,请你求出点 C 的坐标;( 3)如果⊙ B 的半径为 3,点 E 为⊙ B 上一点,请你直接写出 D EO 的取值范围 .yy6 6 5 5 4 4 3 3 2 2 117 6 5 4 3 2 1 O1 2 3 4 5 6 x 7 6 5 4 3 2 1O 1 2 3 4 5 6 x1 12 23 34 45 56 67 7 882018 海淀二模28.对某一个函数给出如下定义:若存在实数 k ,对于函数图象上横坐标之差为 1 的任意两点 (a,b1) , (a 1,b2 ) ,b2 b1k 都成立,则称这个函数是限减函数,在所有满足条件的 k 中,其最大值称为这个函数的限减系数.例如,函数y x 2 ,当x取值a和 a1时,函数值分别为 b1a 2 , b2a1,故 b2 b11k ,因此函数 y x 2 是限减函数,它的限减系数为 1 .(1)写出函数y2x1的限减系数;(2)m 0,已知y 1x m, x0 )是限减函数,且限减系数k 4 ,求m的取( 1x值范围.(3)已知函数y x2的图象上一点P ,过点 P 作直线l垂直于 y 轴,将函数y x2的图象在点 P 右侧的部分关于直线l 翻折,其余部分保持不变,得到一个新函数的图象,如果这个新函数是限减函数,且限减系数k 1 ,直接写出P点横坐标n的取值范围.y y665544332211 7 6 5 4 3 2 1 O1 2 3 4 5 6 x 7 6 5 4 3 2 1O1 2 3 4 5 6 x11 22 33 44 55 66 77 882018 平谷二模28.对于平面直角坐标系xOy 中的点 P 和⊙M,给出如下定义:若⊙M 上存在两个点A,B,使 AB=2PM,则称点 P 为⊙M的“美好点”.(1)当⊙M半径为 2,点 M 和点 O 重合时,○P 2,0P 11,P 2,2中,⊙ O 的“美好点”是;1点1,2,3○2点 P 为直线 y=x+b 上一动点,点P 为⊙O的“美好点”,求 b 的取值范围;(2)点 M 为直线 y=x 上一动点,以 2 为半径作⊙M,点 P 为直线 y=4 上一动点,点P 为⊙ M 的“美好点”,求点M 的横坐标 m 的取值范围.2018 石景山二模28.在平面直角坐标系 xOy 中,对于任意点 P ,给出如下定义:若⊙ P 的半径为 1,则称⊙ P 为点 P 的“伴随圆” .(1)已知,点 P 1,0 ,①点 A1,3 22在点 P 的“伴随圆” (填“上”或“内”或“外”);②点 B 1,0 在点 P 的“伴随圆”(填“上”或“内”或“外” );(2)若点 P 在 x 轴上,且点 P 的“伴随圆”与直线 y3x 相切,求点 P 的坐标;(3)已知直线 y x 2 与 x 、 y 轴分别交于点3x 2 与 x 、 y 轴分别交于点 A ,B ,直线 yC ,D ,点 P 在四边形 ABCD 的边上并沿 AB BCCDDA 的方向移动,直接写出点 P 的“伴随圆”经过的平面区域的面积.2018 西城二模28. 对于平面直角坐标系xOy 中的点Q( x, y)( x≠0),将它的纵坐标 y 与横坐标 x 的比y称x为点 Q 的“理想值” ,记作L Q .如Q(21,2) 的“理想值” L Q 2 .1(1)①若点Q(1,a)在直线y x 4上,则点 Q 的“理想值”L Q等于_________;②如图, C( 3,1) ,⊙C的半径为 1.若点Q在⊙C上,则点Q的“理想值”L Q的取值范围是.(2)点 D 在直线y 3x+3 上,⊙D的半径为1,点Q在⊙D上运动时都有0≤ LQ≤ 3 ,3求点 D 的横坐标x D的取值范围;(3)M (2, m)( m> 0),Q 是以 r 为半径的⊙ M 上任意一点,当0≤ L Q≤2 2 时,画出满足条件的最大圆,并直接写出相应的半径r 的值 .(要求画图位置准确,但不必尺规作图)2018 怀柔二模1AP28. A 为⊙ C 上一点,过点 A 作弦 AB,取弦 AB 上一点 P,若满足1,则称P3AB为点 A 关于⊙ C 的黄金点.已知⊙ C 的半径为 3,点 A 的坐标为( 1, 0).(1)当点 C 的坐标为( 4,0)时,①在点 D( 3, 0), E(4, 1), F( 7, 0)中,点 A 关于⊙ C 的黄金点是;②直线 y33x上存在点 A 关于⊙ C 的黄金点 P,求点 P 的横坐标的取值范围;33(2) 若 y 轴上存在点 A 关于⊙ C 的黄金点,直接写出点 C 横坐标的取值范围...。
2018年北京数学初三期末压轴题汇总(绝对干货!)

2018数学期末综合题压轴题(24—28题)汇总24.如图,AB 为⊙O 的直径,C 、F 为⊙O 上两点,且点C 为弧BF 的中点,过点C 作AF的垂线,交AF 的延长线于点E ,交AB 的延长线于点D .(1)求证:DE 是⊙O 的切线;(2)如果半径的长为3,tan D=34,求AE 的长.25.小明根据学习函数的经验,对函数4254y x x =-+ 的图象与性质进行了探究.下面是小明的探究过程,请补充完整:(1)自变量x 的取值范围是全体实数,x 与y 的几组对应数值如下表: 其中m = ;(2)如图,在平面直角坐标系xOy 中,描出了以上表中各组对应值为坐标的点,根据描出的点,画出该函数的图象;(3)观察函数图象,写出一条该函数的性质 ; (4)进一步探究函数图象发现:①方程42540x x -+=有 个互不相等的实数根;②有两个点(x 1,y 1)和(x 2,y 2)在此函数图象上,当x 2 >x 1>2时,比较y 1和y 2的大小关系为:y 1 y 2 (填“>”、“<”或“=”) ;③若关于x 的方程4254x x a -+=有4个互不相等的实数根,则a 的取值范围是 .26.在平面直角坐标系xOy 中,抛物线y=mx 2-2mx -3 (m ≠0)与y 轴交于点A ,其对称轴与x 轴交于点B 顶点为C 点. (1)求点A 和点B 的坐标;(2)若∠ACB =45°,求此抛物线的表达式;(3)在(2)的条件下,垂直于轴的直线与抛物线交于点P (x 1,y 1)和Q (x 2,y 2),与直线AB 交于点N (x 3,y 3),若x 3<x 1<x 2,结合函数的图象,直接写出x 1+x 2+x 3的取值范围为 .五、解答题(共2道小题,每小题7分,共14分)27.已知,△ABC 中,∠ACB =90°,AC =BC ,点D 为BC 边上的一点.(1)以点C 为旋转中心,将△ACD 逆时针旋转90°,得到△BCE ,请你画出旋转后的图形;(2)延长AD 交BE 于点F ,求证:AF ⊥BE ;(3)若AC,BF =1,连接CF ,则CF 的长度为 .y l 备用图AACDB BDC28.对于平面直角坐标系xOy 中的点P ,给出如下定义:记点P 到x 轴的距离为1d ,到y 轴的距离为2d ,若12d d ≥,则称1d 为点P 的最大距离;若12d d <,则称2d 为点P 的最大距离.例如:点P (3-,4)到到x 轴的距离为4,到y 轴的距离为3,因为3 < 4,所以点P 的最大距离为4.(1)①点A (2,5-)的最大距离为 ;②若点B (a ,2)的最大距离为5,则a 的值为 ; (2)若点C 在直线2y x =--上,且点C 的最大距离为5,求点C 的坐标;(3)若⊙O 上存在..点M ,使点M 的最大距离为5,直接写出⊙O 的半径r 的取值范围.24. 已知:如图,AB 是半圆O 的直径,D 是半圆上的 一个动点(点D 不与点A ,B 重合), .∠=∠CAD B (1)求证:AC 是半圆O 的切线;(2)过点O 作BD 的平行线,交AC 于点E ,交AD 于点F, 且EF=4, AD=6, 求BD 的长.25.如图,AB = 6cm ,∠C AB = 25°,P 是线段AB 上一动点,过点P 作PM ⊥AB 交射线AC于点M ,连接MB ,过点P 作PN ⊥MB 于点N .设A ,P 两点间的距离为x cm , P ,N 两点间的距离为y cm .(当点P 与点A 或点B 重合时,y 的值均为0) 小海根据学习函数的经验,对函数y 随自变量x 的变化而变化的规律进行了探究.下面是小海的探究过程,请补充完整:(1)通过取点、画图、测量,得到了x 与y 的几组值,如下表:(说明:补全表格时相关数值保留两位小数)(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;(3)结合画出的函数图象,解决问题:当y =0.5时,与之对应的x 值的个数是 . 26. 已知一次函数1112=-y x ,二次函数224=-+y x mx (其中m >4). (1)求二次函数图象的顶点坐标(用含m 的代数式表示);(2)利用函数图象解决下列问题:①若5=m ,求当10y >且2y ≤0时,自变量x 的取值范围; ②如果满足10y >且2y ≤0时自变量x 的取值范围内有 且只有一个整数,直接写出m 的取值范围.27.已知:如图,AB 为半圆O 的直径,C 是半圆O 上一点,过点C 作AB 的平行线交⊙O于点E ,连接AC 、BC 、AE ,EB . 过点C 作CG ⊥AB 于点G ,交EB 于点H.(1)求证:∠BCG=∠E BG ; (2)若55sin =∠CAB ,求GB EC 的值.28. 一般地,我们把半径为1的圆叫做单位圆,在平面直角坐标系xOy 中,设单位圆的圆心与坐标原点O 重合,则单位圆与x 轴的交点分别为(1,0),(-1,0),与y 轴的交点分别为(0,1),(0,-1).在平面直角坐标系xOy 中,设锐角α的顶点与坐标原点O 重合,α的一边与x 轴的正半轴重合,另一边与单位圆交于点P 11(,)x y ,且点P 在第一象限. (1) 1x =_ __ (用含α的式子表示);1y =____ _ (用含α的式子表示) ;(2)将射线OP 绕坐标原点O 按逆时针方向 旋转90︒后与单位圆交于点22(,)Q x y . ①判断1y 2与的数量关系,并证明;x ②12y y +的取值范围是:_ ___.24. 如图,在Rt △ABC 中,∠ACB =90°,点D 是AB 边上一点,以BD 为直径的⊙O 与边AC 相切于点 E ,连接DE 并延长DE 交BC 的延长线于点F . (1)求证:BD =BF ; (2)若CF =2,4tan 3B =,求⊙O 的半径.25. 如图25-1,点C 是⊙O 中直径AB 上的一个动点,过点C 作CD AB ⊥交⊙O 于点D ,点M 是直径AB 上一固定点,作射线DM 交⊙O 于点N .已知6cm AB =, 2cm AM =,设线段AC 的长度为xcm ,线段MN 的长度为ycm .小东根据学习函数的经验,对函数y 随自变量x 的变化而变化的规律进行了探索. 下面是小东的探究过程,请补充完整:(1)通过取点、画图、测量,得到了x 与y 的几组值,如下表:(说明:补全表格时相关数值保留一位小数)(2)在图25-2中建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画 出该函数的图象;(3)结合画出的函数图象,解决问题:当AC MN =时,x 的取值约为__________cm .B图25-1图25-226. 在平面直角坐标系xOy 中,二次函数2y x bx c =++的图象如图所示. (1)求二次函数的表达式;(2)函数图象上有两点1(,)P x y ,2(,)Q x y ,且满足12x x <,结合函数图象回答问题; ①当3y =时,直接写出21x x -的值; ②当213x x -2≤≤,求y 的取值范围.27.如图27-1有两条长度相等的相交线段AB 、CD ,它们相交的锐角中有一个角为60°,为了探究AD 、CB 与CD (或AB )之间的关系,小亮进行了如下尝试:(1)在其他条件不变的情况下使得AD BC ∥,如图27-2,将线段AB 沿AD 方向平移AD 的长度,得到线段DE ,然后联结BE ,进而利用所学知识得到AD 、CB 与CD (或AB )之间的关系:____________________;(直接写出结果)(2)根据小亮的经验,请对图27-1的情况(AD 与CB 不平行)进行尝试,写出AD 、CB 与CD (或AB )之间的关系,并进行证明;(3)综合(1)、(2)的证明结果,请写出完整的结论: __________________________.图27-1图27-228.以点P 为端点竖直向下的一条射线PN ,以它为对称轴向左右对称摆动形成了射线1PN ,2PN ,我们规定:12N PN ∠为点P 的“摇摆角”, 射线PN 摇摆扫过的区域叫作点P 的“摇摆区域”(含1PN ,2PN ). 在平面直角坐标系xOy 中,点(2,3)P .(1)当点P 的摇摆角为60︒时,请判断(0,0)O 、(1,2)A 、(2,1)B、(20)C 属于点P 的摇摆区域内的点是______________________(填写字母即可);(2)如果过点(1,0)D ,点(5,0)E 的线段完全在点P 的摇摆区域内,那么点P 的摇摆角至少为_________°;(3)⊙W 的圆心坐标为(,0)a ,半径为1,如果⊙W 上的所有点都在点P 的摇摆角为60︒ 时的摇摆区域内,求a 的取值范围.备用图24.二次函数m mx x y 522+-=的图象经过点)2,1(-. (1)求二次函数图象的对称轴; (2)当14≤≤-x 时,求y 的取值范围.25.如图,AC 是⊙O 的直径,点D 是⊙O 上一点,⊙O 的切线CB 与AD 的延长线交于点B ,点F 是直径AC 上一点,连接DF 并延长交⊙O 于点E ,连接AE . (1)求证:∠ABC =∠AED ; (2)连接BF ,若AD 532=,AF =6,tan 34=∠AED ,求BF 的长.26.在平面直角坐标系xOy 中,抛物线n mx x y ++-=2经过点)0,1(-A 和)3,0(B . (1)求抛物线的表达式;(2)抛物线与x 轴的正半轴交于点C ,连接BC .设抛物线的顶点P 关于直线t y =的对称点为点Q ,若点Q 落在△OBC 的内部,求t 的取值范围.CA27.在正方形ABCD中,点P在射线AC上,作点P关于直线CD的对称点Q,作射线BQ交射线DC于点E,连接BP.(1)当点P在线段AC上时,如图1.①依题意补全图1;②若EQ=BP,则∠PBE的度数为,并证明;(2)当点P在线段AC的延长线上时,如图2.若EQ=BP,正方形ABCD的边长为1,请写出求BE长的思路.图1图228.在平面直角坐标系xOy 中,点P 的坐标为),(11y x ,点Q 的坐标为),(22y x ,且21x x ≠,21y y ≠,若PQ 为某个等腰三角形的腰,且该等腰三角形的底边与x 轴平行,则称该等腰三角形为点P ,Q 的“相关等腰三角形”.下图为点P ,Q 的“相关等腰三角形”的示意图....(1)已知点A 的坐标为)1,0(,点B 的坐标为)0,3(-,则点A ,B 的“相关等腰三角形”的顶角为_________°;(2)若点C 的坐标为)3,0(,点D 在直线34=y 上,且C ,D 的“相关等腰三角形”为等边三角形,求直线CD 的表达式; (3)⊙O 的半径为2,点N 在双曲线xy 3-=上.若在⊙O 上存在一点M ,使得点M 、N 的“相关等腰三角形”为直角三角形,直接写出点N 的横坐标N x 的取值范围.24.已知:如图, AB 为⊙O 的直径,CE ⊥AB 于E ,BF ∥OC ,连接BC ,CF .求证:∠OCF =∠ECB .25.如图,在平面直角坐标系xOy 中,直线2y x =-与双曲线k y x=(k ≠0)相交于A ,B 两点,且点A 的横坐标是3.(1)求k 的值;(2)过点P (0,n )作直线,使直线与x 轴平行,直线与直线2y x =-交于点M ,与双曲线ky x=(k ≠0)交于点N ,若点M 在N 右边, 求n 的取值范围.26.已知:如图,在△ABC 中,AB =AC ,以AC 为直径作⊙O 交BC 于点D ,过点D 作⊙O 的切线交AB 于点E ,交AC 的延长线于点F .(1)求证:DE ⊥AB ; (2)若tan ∠BDE =12, CF =3,求DF 的长.27.综合实践课上,某小组同学将直角三角形纸片放到横线纸上(所有横线都平行,且相邻两条平行线的距离为1),使直角三角形纸片的顶点恰巧在横线上,发现这样能求出三角形的边长.(1)如图1,已知等腰直角三角形纸片△ABC,∠ACB=90°,AC=BC,同学们通过构造直角三角形的办法求出三角形三边的长,则AB=;(2)如图2,已知直角三角形纸片△DEF,∠DEF=90°,EF=2DE,求出DF的长;(3)在(2)的条件下,若橫格纸上过点E的横线与DF相交于点G,直接写出EG的长.28.在平面直角坐标系xOy 中,抛物线219y x bx =+经过点A (-3,4). (1)求b 的值;(2)过点A 作x 轴的平行线交抛物线于另一点B ,在直线AB 上任取一点P ,作点A 关于直线OP 的对称点C ;①当点C 恰巧落在x 轴时,求直线OP 的表达式; ②连结BC ,求BC 的最小值.24.如图,A ,B ,C 三点在⊙O 上,直径BD 平分∠ABC ,过点D 作DE ∥AB 交弦BC 于点E ,在BC 的延长线上取一点F ,使得EF =DE . (1)求证:DF 是⊙O 的切线;(2)连接AF 交DE 于点M ,若 AD =4,DE =5,求DM 的长.25.如图,在△ABC 中,90ABC ∠=︒,40C ∠=°,点D 是线段BC 上的动点,将线段AD绕点A 顺时针旋转50°至AD ',连接BD '.已知AB =2cm ,设BD 为x cm ,B D '为y cm .小明根据学习函数的经验,对函数y 随自变量x 的变化而变化的规律进行了探究,下面是小明的探究过程,请补充完整.(说明:解答中所填数值均保留一位小数) (1)通过取点、画图、测量,得到了x 与y 的几组值,如下表:(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象.(3)结合画出的函数图象,解决问题:线段BD '的长度的最小值约为__________cm ;若BD '≥BD ,则BD 的长度x 的取值范围是_____________.D'B D CA26.已知二次函数243y ax ax a =-+.(1)该二次函数图象的对称轴是x = ; (2)若该二次函数的图象开口向下,当14x ≤≤时,y 的最大值是2,求当14x ≤≤时,y 的最小值;(3)若对于该抛物线上的两点11() P x y , ,22() Q x y ,,当1+1t x t ≤≤,25x ≥时,均满足12y y ≥,请结合图象,直接写出t 的最大值.27.对于⊙C 与⊙C 上的一点A ,若平面内的点P 满足:射线..AP 与⊙C 交于点Q (点Q 可以与点P 重合),且12PAQA≤≤,则点P 称为点A 关于⊙C 的“生长点”. 已知点O 为坐标原点,⊙O 的半径为1,点A (-1,0).(1)若点P 是点A 关于⊙O 的“生长点”,且点P 在x 轴上,请写出一个符合条件的点P 的坐标________;(2)若点B 是点A 关于⊙O 的“生长点”,且满足1tan 2BAO ∠=,求点B 的纵坐标t的取值范围;(3)直线y b =+与x 轴交于点M ,与y 轴交于点N ,若线段MN 上存在点A 关于⊙O 的“生长点”,直接写出b 的取值范围是_____________________________.28.在△ABC 中,∠A =90°,AB =AC .(1)如图1,△ABC 的角平分线BD ,CE 交于点Q ,请判断“QB =”是否正确:________(填“是”或“否”);(2)点P 是△ABC 所在平面内的一点,连接P A ,PB ,且PB=A .①如图2,点P 在△ABC 内,∠ABP =30°,求∠P AB 的大小;②如图3,点P 在△ABC 外,连接PC ,设∠APC =α,∠BPC =β,用等式表示α,β之间的数量关系,并证明你的结论.图1 图2 图3PPEDQB CAB CAB CA22. 如图,ABC △是等腰三角形,AC AB =,以AC 为直径的⊙O 与BC 交于点D ,DE AB ⊥,垂足为E ,ED 的延长线与AC 的延长线交于点F . (1)求证:DE 是⊙O 的切线;(2)若⊙O 的半径为2,1BE =,求cos A 的值.23. 如图1,在矩形ABCD 中,点E 为AD 边中点,点F 为BC 边中点;点G ,H 为AB边三等分点,I ,J 为CD 边三等分点.小瑞分别用不同的方式连接矩形对边上的点,如图2,图3所示.那么,图2中四边形GKLH 的面积与图3中四边形KPOL 的面积相等吗? (1)小瑞的探究过程如下图1 图2 图3在图2中,小瑞发现, ABCD GKLH S S _______=; 在图3中,小瑞对四边形KPOL 面积的探究如下. 请你将小瑞的思路填写完整: 设a S DEP =△,b S AKG =△ ∵AF EC ∥∴DAK DEP ∽△△,且相似比为2:1,得到a S DAK 4=△∵BI GD ∥∴ABM AGK ∽△△,且相似比为3:1,得到b S ABM 9=△ 又∵ABCD DAG S b a S 614=+=△,ABCD ABF S a b S 419=+=△ ∴a b b a S ABCD 436624+=+=∴b a ____=,b S ABCD _____=,b S KPOL _____=∴ABCD KPO L S S _____=,则G KLH KPO L S S ____(填写“>”,“<”或“=”)(2)小瑞又按照图4的方式连接矩形ABCD 对边上的点.则ABCD ANML S S _____=.图424. 在平面直角坐标系xOy 中,二次函数()0122>+-=a ax ax y 的对称轴为b x =.点()m A ,2-在直线3+-=x y 上.(1)求m ,b 的值;(2)若点()23,D 在二次函数()0122>+-=a ax ax y 上,求a 的值;(3)当二次函数()0122>+-=a ax ax y 与直线3+-=x y 相交于两点时,设左侧的交点为()11,y x P ,若131-<<-x ,求a 的取值范围.25.点P 的“d 值”定义如下:若点Q 为圆上任意一点,线段PQ 长度的最大值与最小值之差即为点P 的“d 值”,记为P d .特别的,当点P ,Q 重合时,线段PQ 的长度为0. 当⊙O 的半径为2时: (1)若点⎪⎭⎫⎝⎛-0,21C ,()4,3D ,则=C d _________,=D d _________; (2)若在直线22+=x y 上存在点P ,使得2=P d ,求出点P 的横坐标; (3)直线()033>+-=b b x y 与x 轴,y 轴分别交于点A ,B .若线段AB 上存在点P ,使得32<≤P d ,请你直接写出b 的取值范围.备用图 备用图24.如图,AB 是半圆的直径,过圆心O 作AB 的垂线,与弦AC的延长线交于点D ,点E 在OD 上,=DCE B ∠∠. (1)求证:CE 是半圆的切线;(2)若CD=10,2tan 3B =,求半圆的半径.25.已知抛物线G :221y x ax a =-+-(a 为常数). (1)当3a =时,用配方法求抛物线G 的顶点坐标; (2)若记抛物线G 的顶点坐标为(,)P p q .①分别用含a 的代数式表示p ,q ;②请在①的基础上继续用含p 的代数式表示q ; ③由①②可得,顶点P 的位置会随着a 的取值变化而变化,但点P 总落在 的图象上.A .一次函数B .反比例函数C .二次函数(3)小明想进一步对(2)中的问题进行如下改编:将(2)中的抛物线G 改为抛物线H :22y x ax N =-+(a 为常数),其中N 为含a 的代数式,从而使这个新抛物线H 满足:无论a 取何值,它的顶点总落在某个一次函数的图象上.请按照小明的改编思路,写出一个符合以上要求的新抛物线H 的函数表达式:(用含a 的代数式表示),它的顶点所在的一次函数图象的表达式y kx b =+(k ,b 为常数,k ≠0)中,k= ,b= .26.在平面直角坐标系xOy 中,抛物线M :2 (0)y ax bx c a =++≠经过(1,0)A -,且顶点坐标为(0,1)B .(1)求抛物线M 的函数表达式;(2)设(,0)F t 为x 轴正半轴...上一点,将抛物线M 绕点F 旋转180°得到抛物线1M . ①抛物线1M 的顶点1B 的坐标为 ;②当抛物线1M 与线段AB 有公共点时,结合函数的图象,求t 的取值范围.27.如图1,在Rt△AOB中,∠AOB=90°,∠OAB=30°,点C在线段OB上,OC=2BC,AO 边上的一点D满足∠OCD=30°.将△OCD绕点O逆时针旋转α度(90°<α<180°)得到△OC D'',C,D两点的对应点分别为点C',D',连接AC',BD',取AC'的中点M,连接OM.(1)如图2,当C D''∥AB时,α= °,此时OM 和BD'之间的位置关系为;(2)画图探究线段OM和BD'之间的位置关系和数量关系,并加以证明.28.在平面直角坐标系xOy 中,A ,B 两点的坐标分别为(2,2)A ,(2,2)B -.对于给定的线段AB 及点P ,Q ,给出如下定义:若点Q 关于AB 所在直线的对称点Q '落在△ABP 的内部(不含边界),则称点Q 是点P 关于线段AB 的内称点. (1)已知点(4,1)P -.①在1(1,1)Q -,2(1,1)Q 两点中,是点P 关于线段AB 的内称点的是____________; ②若点M 在直线1y x =-上,且点M 是点P 关于线段AB 的内称点,求点M 的横坐标M x 的取值范围;(2)已知点(3,3)C ,⊙C 的半径为r ,点(4,0)D ,若点E 是点D 关于线段AB 的内称点,且满足直线DE 与⊙C 相切,求半径r 的取值范围.24.如图,AB 是⊙O 的直径,点C 是»AB 的中点,连接AC 并延长至点D ,使CD AC =,点E 是OB 上一点,且23OE EB =,CE 的延长线交DB 的延长线于点F ,AF 交⊙O 于点H ,连接BH .(1)求证:BD 是⊙O 的切线; (2)当2OB =时,求BH 的长.25.如图,点E 是矩形ABCD 边AB 上一动点(不与点B 重合),过点E 作EF ⊥DE 交BC于点F ,连接DF .已知AB = 4cm ,AD = 2cm ,设A ,E 两点间的距离为x cm ,△DEF 面积为y cm 2.小明根据学习函数的经验,对函数y 随自变量x 的变化而变化的规律进行了探究.下面是小明的探究过程,请补充完整:(1)确定自变量x 的取值范围是 ;(2)通过取点、画图、测量、分析,得到了x 与y 的几组值,如下表:(3)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;(4)结合画出的函数图象,解决问题:当△DEF 面积最大时,AE 的长度为cm .DC BAF26.在平面直角坐标系xOy 中,抛物线2y x bx c =-++经过点(2,3),对称轴为直线x =1.(1)求抛物线的表达式;(2)如果垂直于y 轴的直线l 与抛物线交于两点A (1x ,1y ),B (2x ,2y ),其中01<x ,02>x ,与y 轴交于点C ,求BC -AC 的值;(3)将抛物线向上或向下平移,使新抛物线的顶点落在x 轴上,原抛物线上一点P 平移后对应点为点Q ,如果OP =OQ ,直接写出点Q 的坐标.27.如图,∠BAD=90°,AB=AD ,CB=CD ,一个以点C 为顶点的45°角绕点C 旋转,角的两边与BA ,DA 交于点M ,N ,与BA ,DA 的延长线交于点E ,F ,连接AC . (1)在∠FCE 旋转的过程中,当∠FCA =∠ECA 时,如图1,求证:AE =AF ; (2)在∠FCE 旋转的过程中,当∠FCA ≠∠ECA 时,如图2,如果∠B=30°,CB=2,用等式表示线段AE ,AF 之间的数量关系,并证明.EMNFA CEMN FAC图1图228.对于平面直角坐标系xOy 中的点P 和⊙C ,给出如下定义:如果⊙C 的半径为r ,⊙C外一点P 到⊙C 的切线长小于或等于2r ,那么点P 叫做⊙C 的“离心点”. (1)当⊙O 的半径为1时,①在点P 1(12,P 2(0,-2),P 30)中,⊙O 的“离心点”是 ; ②点P (m ,n )在直线3y x =-+上,且点P 是⊙O 的“离心点”,求点P 横坐标m 的取值范围;(2)⊙C 的圆心C 在y 轴上,半径为2,直线121+-=x y 与x 轴、y 轴分别交于点A ,B . 如果线段AB 上的所有点都是⊙C 的“离心点”,请直接写出圆心C 纵坐标的取值范围.24.在平面直角坐标系xOy 中,直线24y x =+与反比例函数ky x=(k ≠0)的图象交于点()3,A a -和点B .(1)求反比例函数的表达式和点B 的坐标; (2)直接写出不等式24kx x+<的解集.25.如图,在△ABC 中,AB =AC ,以AB 为直径的O 与边BC ,AC 分别交于点D ,E .DF 是O的切线,交AC 于点F . (1)求证:DF ⊥AC ;(2)若AE =4,DF =3,求tan A .26.在平面直角坐标系xOy 中,抛物线y=mx 2﹣2mx+n (m ≠0)与x 轴交于点A, B ,点A 的坐标为(02-,).(1)写出抛物线的对称轴; (2)直线n m x y -4-21=过点B ,且与抛物线的另一个交点为C . ①分别求直线和抛物线所对应的函数表达式;②点P 为抛物线对称轴上的动点,过点P 的两条直线l 1: y=x+a 和l 2 : y=-x+ b 组成图形G .当图形G 与线段BC 有公共点时,直接写出点P 的纵坐标t 的取值范围.27. 如图1,在△ABC 中,∠ACB =90°,AC =2,BC=以点B点P为B 上的动点,连接PC ,作P C PC '⊥,使点P '落在直线BC的上方,且满足:P C PC '=BP ,AP '.(1)求∠BAC 的度数,并证明△AP C '∽△BPC ; (2)若点P 在AB 上时,①在图2中画出△AP’C ; ②连接BP ',求BP '的长;图1 图2(3)点P 在运动过程中,BP '是否有最大值或最小值?若有,请直接写出BP '取得最大值或最小值时∠PBC 的度数;若没有,请说明理由.备用图28.对于平面直角坐标系xOy中的点M和图形G,若在图形G上存在一点N,使M,N两点间的距离等于1,则称M为图形G的和睦点.(1)当⊙O的半径为3时,在点P1(1,0),P21),P3(72,0),P4(5,0)中,⊙O的和睦点是________;(2)若点P(4,3)为⊙O的和睦点,求⊙O 的半径r的取值范围;(3)点A在直线y=﹣1上,将点A向上平移4个单位长度得到点B,以AB为边构造正方形ABCD,且C,D两点都在AB右侧.已知点E,若线段OE上的所有点都是正方形ABCD的和睦点,直接写出点A的横坐标Ax的取值范围.24. 如图,在△ABC 中,∠C =90°,以BC 为直径的⊙O 交AB 于点D ,⊙O 的切线DE 交AC 于点E . (1)求证:E 是AC 中点;(2)若AB =10,BC =6,连接CD ,OE ,交点为F ,求OF 的长.25. △ACB 中,∠C =90°,以点A 为中心,分别将线段AB ,AC 逆时针旋转60°得到线段AD ,AE ,连接DE ,延长DE 交CB 于点F . (1)如图1,若∠B =30°,∠CFE 的度数为 ; (2)如图2,当30°<∠B <60°时,①依题意补全图2;②猜想CF 与AC 的数量关系,并加以证明.图1 图2E C26.如图,直线AM 和AN 相交于点A ,∠MAN =30°,在射线AN 上取一点B ,使AB =6cm ,过点B 作BC ⊥AM 于点C ,D 是线段AB 上的一个动点(不与点B 重合),过点D 作CD 的垂线交射线CA 于点E(1)确定点B 的位置,在线段AB 上任取一点D ,根据题意,补全图形; (2)设AD=x cm ,CE=y cm ,探究函数y 随自变量x 的变化而变化的规律.① 通过取点、画图、测量,得到了x 与y 的几组对应值,如下表:(要求:补全表格,相关数值保留一位小数)② 建立平面直角坐标系xOy ,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;③ 结合画出的函数图象,解决问题:当AD 为Rt △CDE 斜边CE 上的中线时,AD 的长度约为 cm (结果保留一位小数).27. 已知抛物线l 1与l 2形状相同,开口方向不同,其中抛物线l 1:2782--=ax ax y 交x 轴于A ,B 两点(点A 在点B 的左侧),且AB =6,抛物线l 2与l 1交于点A 和点C (5,n ).(1)求抛物线l 1,l 2的表达式; (2)当x 的取值范围是 时,抛物线l 1与l 2上的点的纵坐标同时随横坐标的增大而增大;(3)直线MN ∥y 轴,交x 轴,l 1,l 2分别相交于点P (m ,0),M ,N ,当1≤m ≤7时,求线段MN 的最大值.28. 在平面直角坐标系xOy中,点A (0, 6),点B在x轴的正半轴上. 若点P,Q在线段AB上,且PQ为某个一边与x轴平行的矩形的对角线,则称这个矩形为点P,Q的“X矩形”.下图为点P,Q的“X矩形”的示意图.(1)若点B(4,0),点C的横坐标为2,则点B,C的“X矩形”的面积为.(2)点M,N的“X矩形”是正方形,①当此正方形面积为4,且点M到y轴的距离为3时,写出点B的坐标,点N的坐标及经过点N的反比例函数的表达式;②当此正方形的对角线长度为3,且半径为r的⊙O与它没有交点时,直接写出r的取值范围.2018数学期末选填压轴题(8、16题)汇总(通州)8. 如图,在ABCRt△中,︒=∠90A,4==ACAB.点E为ABCRt△边上一点,以每秒1单位的速度从点C出发,沿着BAC→→的路径运动到点B为止.连接CE,以点C为圆心,CE长为半径作⊙C,⊙C与线段BC交于点D.设扇形DCE面积为S,点E的运动时间为t.则在以下四个函数图象中,最符合扇形面积S关于运动时间t的变化趋势的是()A. B. C. D.16.阅读下面材料:在数学课上,老师提出如下问题:小霞的作法如下:小霞的作图依据是尺规作图:作已知角的角平分线.已知:如图,已知BAC∠.求作:BAC∠的角平分线AP.(1)如图,在平面内任取一点O;(2)以点O为圆心,AO为半径作圆,交射线AB于点D,交射线AC于点E;(3)连接DE,过点O作射线OP垂直线段DE,交⊙O于点P;(4)连接AP.8.两个少年在绿茵场上游戏.小红从点A 出发沿线段AB 运动到点B ,小兰从点C 出发,以相同的速度沿⊙O 逆时针运动一周回到点C ,两人的运动路线如图1所示,其中AC =DB .两人同时开始运动,直到都停止运动时游戏结束,其间他们与点C 的距离y 与时间x (单位:秒)的对应关系如图2所示.则下列说法正确的是图1 图2A .小红的运动路程比小兰的长B .两人分别在1.09秒和7.49秒的时刻相遇C .当小红运动到点D 的时候,小兰已经经过了点D D .在4.84秒时,两人的距离正好等于⊙O 的半径15.在同车道行驶的机动车,后车应当与前车保持足以采取紧急制动措施的安全距离.如图,在一个路口,一辆长为10m 的大巴车遇红灯后停在距交通信号灯20m 的停止线处,小张驾驶一辆小轿车跟随大巴车行驶.设小张距大巴车尾x m ,若大巴车车顶高于小张的水平视线0.8m ,红灯下沿高于小张的水平视线3.2m ,若小张能看到整个红灯,则x 的最小值为 .16.下面是“作一个30°角”的尺规作图过程.请回答:该尺规作图的依据是 .停止线信号灯8.如图,抛物线32++=bx ax y (a ≠0)的对称轴为直线1x =, 如果关于x 的方程082=-+bx ax (a ≠0)的一个根为4,那么 该方程的另一个根为( ).A .4-B .2-C .1D . 315.如图,抛物线2 (0)y ax bx c a =++≠与y 轴交于点C ,与x 轴 交于A ,B 两点,其中点B 的坐标为(4,0)B ,抛物线的对称轴交 x 轴于点D ,CE ∥AB ,并与抛物线的对称轴交于点E .现有下列结论: ①0a >;②0b >;③420a b c ++<;④4AD CE +=.其中所有 正确结论的序号是 .16. 如图,⊙O 的半径为3,A ,P 两点在⊙O 上,点B 在⊙O 内, 4t a n 3APB ∠=,AB AP ⊥.如果OB ⊥OP ,那么OB 的长为 . .已知抛物线2y ax bx c =++上部分点的横坐标x 与纵坐标y 的对应值如下表:①抛物线2y ax bx c =++的开口向下;②抛物线2y ax bx c =++的对称轴为直线1x =-; ③方程20ax bx c ++=的根为0和2;④当y >0时,x 的取值范围是x <0或x >2. 其中正确的是 A .①④B .②④C .②③D .③④15.在北京市治理违建的过程中,某小区拆除了自建房,改建绿地. 如图,自建房占地是边长为8m 的正方形ABCD ,改建的绿地是矩形AEFG ,其中点E 在AB 上,点G 在AD 的延长线上,且DG = 2BE . 如果设BE 的长为x (单位:m ),绿地AEFG 的面积为y (单位:m 2),那么y 与x 的函数的表达式为 ;当BE AEFG 的面积最大.16.E DGFH AC下面有四个推断:①当移植的树数是1 500时,表格记录成活数是1 335,所以这种树苗成活的概率是0.890; ②随着移植棵数的增加,树苗成活的频率总在0.900附近摆动,显示出一定的稳定性,可以估计树苗成活的概率是0.900;③若小张移植10 000棵这种树苗,则可能成活9 000棵; ④若小张移植20 000棵这种树苗,则一定成活18 000棵.其中合理的是 A .①③ B .①④ C. ②③ D .②④15. 已知函数2-2-3y x x =,当-1x a ≤≤时,函数的最小值是-4,则实数a 的取值范围是 .16.如图,在平面直角坐标系xOy 中,已知()8,0A ,()0,6C ,矩形OABC 的对角线交于点P ,点M 在经过点P 的函数()0ky x x=>的图象上运动,k 的值为 ,OM 长的最小值为 .8. 如图,一条抛物线与x 轴相交于M 、N 两点(点M 在点N其顶点P 在线段AB 上移动.若点A 、B 的坐标分别为(﹣2,3(1,3),点N的横坐标的最大值为4,则点M (A) -1 (B) -3 (C) -5 15. “π的估计”有很多方法,下面这个随机模拟实验就是一种,其过程如下:如图,随机撒一把米到画有正方形及其内切圆的白纸上,统计 落在圆内的米粒数m 与正方形内的米粒数n ,并计算频率nm同条件下,大量重复以上试验,当nm估计出π的值为nm4. 请说出其中所蕴含的原理: . 16. 下面是“作顶角为120°的等腰三角形的外接圆”的尺规作图过程. 请回答:该尺规作图的依据是 .8.小苏和小林在如图所示的跑道上进行4×50米折返跑.在整个过程中,跑步者距起跑线的距离y (单位:m )与跑步时间t (单位:s )的对应关系如下图所示.下列叙述正确的是A .两人从起跑线同时出发,同时到达终点.B .小苏跑全程的平均速度大于小林跑全程的平均速度. C. 小苏在跑最后100m 的过程中,与小林相遇2次. D .小苏前15s 跑过的路程小于小林前15s 跑过的路程. 15.如图,在平面直角坐标系xOy 中,△CDE 可以看作是△AOB 经过若干次图形的变化(平移、轴对称、旋转)得到的,写出一种 由△AOB 得到△CDE 的过程: .16.阅读以下作图过程:第一步:在数轴上,点O 表示数0,点A 表示数1,点B 表示数5,以AB 为直径作半圆(如图);第二步:以B 点为圆心,1为半径作弧交半圆于点C (如图); 第三步:以A 点为圆心,AC 为半径作弧交数轴的正半轴于点M .请你在下面的数轴中完成第三步的画图(保留作图痕迹,不写画法),并写出点M 表示的数为________.(第16题图)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第9讲 选择压轴题
【2018·朝阳二模】1.如图,矩形ABCD 中,AB =4,BC =3,F 是AB 中点,以点A 为圆心,AD 为半径作弧交AB 于点E ,以点B 为圆心,BF 为半径作弧交BC 于点G ,则图中阴影部分面积的差S 1-S 2为
(A )41312π
-
(B )4
912π-
(C )4
136π
+ (D )6 【答案】A
【2018·东城二模】2. 有一圆形苗圃如图1所示,中间有两条交叉过道AB ,CD ,它们为苗圃O e 的直径,
且AB ⊥CD . 入口K 位于»
AD 中点,园丁在苗圃圆周或两条交叉过道上匀速行进.设该园丁行进的时间为x ,与入口K 的距离为y ,表示y 与x 的函数关系的图象大致如图2所示,则该园丁行进的路线可能是
图2
A. A →O →D
B. C→A→O → B
C. D →O →C
D. O→D→B→C 【答案】B
【2018·丰台二模】3.某移动通讯公司有两种移动电话计费方式,这两种计费方式中月使用费y (元)
与主叫时间x (分)的对应关系如图所示:(主叫时间不到1分钟,按1分钟收费)下列三个判断中正确的是
① 方式一每月主叫时间为300分钟时,月使用费为88元 ② 每月主叫时间为350分钟和600分钟时,两种方式收费相同 ③ 每月主叫时间超过600分钟,选择方式一更省钱 (A )①② (B )①③ (C )②③ (D )①②③ 【答案】A
【2018·房山二模】4.一列动车从A 地开往B 地,一列普通列车从B 地开往A 地,两车同时出发,设普通列车行驶的时间为x (小时),两车之间的距离为y (千米),如图中的折线表示y 与x 之间的函数关系.下列叙述错误..
的是
A .A
B 两地相距1000千米 B .两车出发后3小时相遇
C .动车的速度为 小时后,动车到达终点B 地,此时普通列车还需行驶
2000
3
千米到达A 地 D .普通列车行驶t 【答案】C
【2018·西城二模】5.如图1所示,甲、乙两车沿直路同向行驶, 车速分别为20 m/s 和v (m/s),起初甲车在乙 车前a (m)处,两车同时出发,当乙车追上甲车时,两车都停止行驶.设x (s)后两车相距y (m),y 与x 的函数关系如图2所示.有以下
方式二
方式一x /分
1000
3
结论:
①图1中a 的值为500; ②乙车的速度为35 m/s ;
③图1中线段EF 应表示为5005x ;
④图2中函数图象与x 轴交点的横坐标为100. 其中所有的正确结论是
A .①④
B .②③
C .①②④
D .①③④ 【答案】A
【2018·昌平二模】6.一辆慢车从甲地匀速行驶至乙地,一辆快车同时从乙地出发匀速行驶至甲地,两车之间的距离y (千米)与行驶时间x (小时)的对应关系如图所示,下列叙述正确的是( ) A .甲乙两地相距1200千米 B .快车的速度是80千米∕小时 C .慢车的速度是60千米∕小时
D .快车到达甲地时,慢车距离乙地100千米
【答案】C
【2018·海淀二模】7.“单词的记忆效率”是指复习一定量的单词,一周后能正确默写出的单词个数与复习的单词个数的比值.右图描述了某次单词复习中,,,M N S T 四位同学的单词记忆效率y 与复习的单词个数x 的情况,则这四位同学在这次单词复习中正确默写出的单词个数最多的是
A .M
B .N
C .S
D .T 【答案】C
【2018·石景山二模】8.甲、乙两位同学进行长跑训练,甲和乙所跑的路程S (单位:米)与所用时间t (单位:秒)之间的函数图象分别为线段OA 和折线OBCD .则下列说法正确的是 (A )两人从起跑线同时出发,同时到达终点 (B )跑步过程中,两人相遇一次
(C )起跑后160秒时,甲、乙两人相距最远 (D )乙在跑前300米时,速度最慢 【答案】C
200
S (米)
t (秒)
O
D
C B
A 160
70
800600
300。
