电磁场理论A第四章
电磁场理论2019第4章-39页文档

(3)c1c2k2 c2为正数, c1 为负数
d2g
d 2
k2g
0
gA kch kB ksh k
该解不合理
例 题:
为ε在的均无匀限电长场均匀E0 介中质,圆放柱置体一,根它半的径轴为线a、与介电垂E常直0 ,数 柱外是自由空间,介电常数为ε0,求圆柱内外的电 位函数和电场强度。
三、唯一性定理
唯一性定理:满足给定边界条件的泊松方程或 拉普拉斯方程的解是唯一的。
4.2 分离变量法
概述
分离变量法是求解偏微分方程的一种数学方法。 直接使用分离变量法的适用条件: 1、偏微分方程为齐次方程; 2、方程各项是仅对一个变量的偏微分。
解题步骤:
1、根据已知导体与介质分界面的形状,选择适当
y
E0
a
x
2
0
1
4.3 镜 像 法
主要内容
静电场中的镜像法 恒定磁场中的镜像法 电轴法
一、静电场中的镜像法
镜像法的根据是唯一性定理 用镜像法求解静电场问题的关键是寻找合适的镜 像电荷 寻找镜像电荷的方法是从边界条件出发
1、平面导体与点电荷
设一个接地的无限大导体平板前方有一个点电荷q, 它到平板的垂直距离是x0,取直角坐标系,x=0的 平面与导体平面重合。求x>0区域的电位函数Φ
反向问题:已知 EHA等,求电荷、电流分布。
2、边值型问题:已知给定区域的边界条件,求该区域中的 场量和位函数。归结为在一定边界条件下求解泊松方程 或拉普拉斯方程。
根据已知边界条件的不同,边值问题分为三种类型:
第一类边值问题(狄里赫利问题):
已知全部边界上各点的 值。
第二类边值问题(牛曼(诺诶曼)问题): 已知全部边界上各点的 值。 n
电磁场理论

2011-9-20
麦克斯韦方程组;电磁场
在真空中 u0 = c =
2
1
ε 0μ0
= c = 3.0 ×108 m s
2 2
1∂E 2 ∇ E− 2 2 =0 u ∂t
1 ∂ E ∂ E = 2 2 2 u ∂t ∂x
2 2
1 ∂B ∇ B− 2 2 =0 u ∂t
对于仅沿 x 方向传播的一维平面电磁波,有
2011-9-20
麦克斯韦方程组;电磁场
一、电磁波的波动方程
无限大均匀介质或真空中,空间内无自由电荷, 也无传导电流。则麦克斯韦方程组
∂B ∇×E = − ∂t
∇• D = 0
∂D ∇×H = ∂t
∇• B = 0
介质性质方程:
D = εE
2011-9-20
B = μH
麦克斯韦方程组;电磁场
∂B ∇×E = − ∂t
通过电场中某截面的位移电流等于电位移通量的时间变化率 在无传导电流的介质中 ID = 回路导线段 传导电流I 一般情况位移电流 I D = dΦD = d D⋅ dS = ∂D ⋅ dS ∫∫S ∂t S dt dt ∫∫
2011-9-20 麦克斯韦方程组;电磁场
变化的电场象传导电流一样能产生磁场,从产生 磁场的角度看,变化的电场可以等效为一种电 ∂D 流。I = dΦD = d D⋅ dS ⋅ dS = ∫∫ D ∫∫S S ∂t dt dt 若把最右端电位移通量的时间变化率看作为一种电流, 那么电路就连续了。麦克斯韦把这种电流称为位移电流。
§4 麦克斯韦方程组;电磁场
§4-1 位移电流 §4-2 全电流安培环路定理 §4-3 麦克斯韦方程组 §4-4 电磁波 §4-5 电磁波能量与电磁波谱
高中物理选择性必修2 第四章 第2、3节 电磁场与电磁波 无线电波的发射和接收

第四章第2、3节电磁场与电磁波、无线电波的发射和接收教学设计一、教材分析电磁场的形成、电磁波的产生以及发射和接收是这两节的知识主干,在物理观念的形成上作为重点落实。
由于LC回路产生电磁振荡不如机械振动直观,要引导学生结合教材图示分析理解,并通过多媒体手段和实验演示等讲这一过程形象化,帮助学生在物理思维的培养上再上一个台阶。
电磁场的概念和麦克斯韦电磁理论是电磁学的核心内容,但是中学对电磁场理论是要求初步了解。
教材突出了理论的核心内容是:变化的电场产生磁场,变化的磁场产生电场,交替产生的电场和磁场传播出去形成电磁波。
能够动手实验的要学生亲自动手培养学生的科学探究能力。
无线电波的发射和接收涉及概念较多,可以结合图表、思维导图、流程图等多种手段,或者利用运送货物的装卸等流程来帮助学生理解调制、调谐、解调等一系列名次含义。
对电磁波的发现以及无线电波的应用,可以介绍赫兹和马可尼等人的不懈努力以及科技成果,落实培养学生的科学态度与责任。
二、学情分析学生在学习电磁场理论时,已经具备:静电场的知识、电流的产生和电流的磁效应知识、电磁感应现象等知识;接触并了解过电磁波的接收(半导体收音机等)或发射的机械设备。
学生对电磁场的知识掌握还不够全面和系统化,要更好的创设情境,精心组织素材,进一步培养学生的抽象思维和创造思维能力。
三、素养目标1.了解电磁场的形成、电磁波的产生。
2.了解电磁波的发射、传播和接收过程,知道无线电通信的基本原理。
3.能正确区分调制、调幅、调频、调谐和解调等概念。
4.结合实际生活,说出无线电通信在生活中的应用。
四、教学重点、难点1.教学重点:电磁场的形成、电磁波的产生、无线电的传播过程。
2.教学难点:无线电波传播的各种概念辨析。
五、教学方法实验演示法、类比分析法.六、教学过程同学们请看,这是电视台发射电视信号的信号塔效果图。
那么,为什么要建高耸入云的发射塔呢?这是为了接受信号,也就是电磁波。
接下来我们就来学习一下关于电磁波以及电磁波的发射和接收的相关知识。
2007-2008《电磁场理论》4-A定

2007-2008《电磁场理论》4-A 定D1.2. ( )两磁介质边界Γ两侧的磁位分别为()1|m rφΓ和()2|m r φΓ,磁导率分别为1μ和2μ,磁位的边界条件为 。
A .()()1122||m m rr μφμφΓΓ= B .1221||m m n n φφμμΓΓ∂∂=∂∂C .()()2112||m m rrμφμφΓΓ=D .1212||m m n n φφμμΓΓ∂∂=∂∂3. ( )磁矢位与磁感应强度的方向的关系互相 。
A .方向相反B .互相平行C .互相垂直D .方向相同4. ( ) 下面式子中, __________表明恒定磁场是非保守场。
A . 0=⋅⎰l d H cB . 0=⋅⎰s d B sC . S d J l d H sc⋅=⋅⎰⎰ D . ⎰⎰⎰⋅∂∂+⋅=⋅SSCS d tD l d BS J d 5. ( )非磁性良导体的复介电常数c jσεεω=-,满足1σωε>>,其中σ、ε、ω分别为电导率、介电常数和角频率,该良导体的电阻SR 为_______。
A.2ωμσB.)012j ωμσ+ C. )012j ωμσ- D. 02ωμσ6. ( )坡印亭定理的复数表示形式为__________。
A. ()()****E H j H B E D E J ω-∇⋅⨯=⋅-⋅+⋅B. ()()****E H j H B E D E J ω-∇⋅⨯=⋅-⋅+⋅ C. ()()****E H j H B E D E J ω-∇⋅⨯=⋅-⋅+⋅D. ()()****E H j H B E D E J ω-∇⋅⨯=⋅-⋅+⋅7. ( )电介质极化后,其内部存在 。
A .自由正电荷B .自由负电荷C .自由正负电荷D .电偶极子8. ( )在理想电介质中_____, (传导电流密度:c J ;自由电荷体密度:ρ)c c c c A. =0, =0 B. 0, =0C. 0, 0 D. =0, 0J J J J ρρρρ≠≠≠≠9. ( )导电媒质中电磁波的传播速度_______光速。
电磁场与电磁波(电磁场理论)第四章ppt课件
解 E r(z,t)Re[erxjExmcos(kzz)ejt] Re[erxExmcos(kzz)ej(tπ 2)]
erxExmcos(kzz)cos(tπ 2)
e r x E x m c o s ( k z z ) s in (t)
例题:已知正弦电磁场的电场瞬时值为 E ( z ,t) E 1 ( z ,t) E 2 ( z ,t)
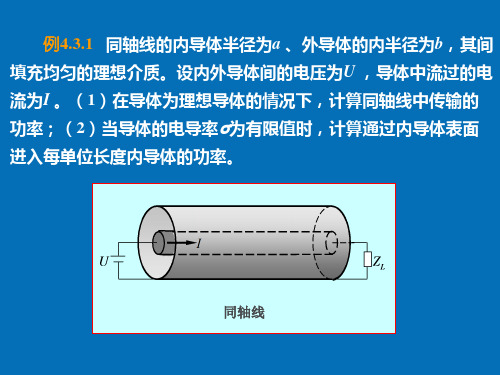
电磁能量在内外导体之间的介质中沿轴方向流动,即由电源流向 负载,如图所示。
同轴线中的电场、磁场和坡印廷矢量 (理想导体情况)
穿过任意横截面的功率为
P SS re rzd Sa b2 π 2 U ln I(ba )2 π d U I
(2)当导体的电导率σ为有限值时,导体内部存在沿电流方
向的电场
r
所以 E r & m ( z ) e r x E x m e j ( k z x ) e r y E y m e j ( k z y π /2 )
(e rxE x m e jx e ryjE y m e jy)e jk z
(2)因为 c o s (k zt) c o s (t k z )
E r ( z ,t ) e r x E x m c o s (t k z x ) e r y E y m c o s (t k z y π 2 ) R e [ e r x E x m e j ( t k z x ) e r y E y m e j ( t k z y π /2 ) ]
erx0.03cos(108πtkzπ2)erx0.04cos(108πtkzπ/3)
Re[erx0.03ej(108πtkzπ/2)]Re[erx0.04ej(108πtkzπ/3)]
《电磁场理论》第4章(辐射)

远区场 r>>λ的区域称为远区(远区常称为辐射区).在远区,各 场量可近似地以下面的公式表示
H
r
= H θ = E r = Eφ = 0 = j I l sin θ j 2λπ r e 2λr
H
φ
Eθ =
0 I l sin θ j j e ε0 2λr
2 πr
λ
}
远区场为辐射场,向空间辐射功率.由以上各式可见, 和 H E 在空间互相垂直,在时间上同相,大小的比值为
( A ) 以上结果虽然可利用 B = × A , E = j ω A = j ω A + j ωε
H 计算,但上述算法更为方便. 和 E 的各个分量分别是
I l Hφ = e 2 4πr
j
2π
λ
r
(1 + j
2πr
λ
) sin θ
Hθ = H r = 0
Er = Eθ =
H
r
= H θ = Eθ = 0 I l sin θ = 4π r 2 p cos θ 4 πε 0 r 3
H
φ
Eθ = 2 Eθ =
p 式中: =
p sin θ 4 πε 0 r 3
I l .以上表达式与静态场类似,近区中电场与磁场的 jω
分布规律与相应的静电场和恒定磁场相似,推迟效应可以忽略.
dq dt
如图2所示,设单元偶极子 中的电流为
z
Aθ
A
Ar
er eφ
i φ )
对应的相量形式是
I = Ie
jφ
~
x
+q
I l
θ
r
eθ
y
q
假设l << r,线电流段产生的矢量位 r
电磁场理论基础第4章PPT课件

1 2
C 1
D2
1 2
C1 b
33
第四章 恒定电流的电场和磁场
所以得
1
C1 r
C2
C
1
1 a
1 r
U
0
1 a
1 c
U0 1
2
1 c
1 b
1 r
1 c
2 1
1 a
U0
1 c
1 c
1 b
1 c
1 b
2 12a11cU01cb11rb1
34
第四章 恒定电流的电场和磁场
导体表面上总的场强为
E Et2En2 0.565 V/m
电场强度与导体表面的夹角为
aarctEgt 19.5 En
V/m
27
第四章 恒定电流的电场和磁场
例 4.2 设有一同心金属球, 内外球体之间均匀充满二层电导 率分别为σ1和σ2的导电媒质, σ1、σ2远小于金属球的电导率。 σ1≈σ2, 为常数。导体球及导电媒质的半径如图4-8所示。内外球间 加有直流电压U0, 极性如图。试求两区域中恒定电场的电流、 电 流密度、电场强度及电位的分布。
tg1 tg2
1 2
11007101
017
22
第四章 恒定电流的电场和磁场 3. 第一种媒质为理想介质, 第二种媒质为导体
图 4-6 理想介质与导体交界面的电场强度
23
第四章 恒定电流的电场和磁场
E1 E12n E12t
由上式可知E1不垂直导体表面, 那么导体表面不是等位面, 导体也不是等位体, 这是由于σ2有限, 导体中沿电流方向存在电 场。 而在静电场中, 导体内电场强度为零, 介质中的场强总是垂 直导体表面, 导体是等位体, 其表面是等位面。这一点, 恒定电场 与静电场有根本的区别。然而σ2越大, E2t和E1t越小, θ1也越小, 直 至σ2=∞时, E1就垂直导体表面, 导体表面为等位面。
电磁场复习纲要

《电磁场理论》知识点第一章矢量分析一、基本概念、规律矢量微分算子在不同坐标系中的表达,标量场的梯度、矢量场的散度和旋度在不同坐标系中的计算公式,常用的矢量恒等式(见附录一1•和2.)、矢量积分定理(高斯散度定理、斯托克斯旋度定理及亥姆霍兹定理)。
二、基本技能练习1、已知位置矢量r x? y@y ze?z,r是它的模。
在直角坐标系中证明r r(1) r (2) ?r 3 (3) x r 0 (4) x( r) 0 (5) ?-y 0r r22、已知矢量A e x x e y xy gy z,求出其散度和旋度。
r3、在直角坐标系证明 A 04、已知矢量A e x 2?y, B e x3e z,分别求出矢量A和B的大小及A B5、证明位置矢量r £x X e『y e z Z的散度,并由此说明矢量场的散度与坐标的选择无关。
6、矢量函数A x2e x y?y x?z,试求(1)A(2)若在xy平面上有一边长为2的正方形,且正方形的中心在坐标原点,试求该矢量A穿过此正方形的通量。
第二章静电场一、基本常数二、基本概念、规律静电场、库仑定律、电场强度、电位及其微分方程、电荷密度、电偶极子模型、高斯定理、环路定理、极化强度矢量、电位移矢量、场方程(真空中和电介质中)、介质性能方程,边界条件,场能及场能密度。
三、基本技能练习2、证明极化介质中,极化电荷体密度b与自由电荷体密度的关系为:bD?(—)。
3、一半径为a内部均匀分布着体密度为0的电荷的球体。
求任意点的电场强度及电位。
媒质2。
已知空气中的电场强度为E14e x e z,求(1)空气中的电位移矢量(2)媒质2中的电场强度。
5、半径为a的均匀带电无限长圆柱导体,单位长度上的电荷量为,求空间电场强度分布。
6、半径为a的导体球外套一层厚为(b a)的电介质(其介电系数为),设导体球带电为q,求任意点的电位。
7、一个半径为a的电介质球内含有均匀分布的自由电荷,电荷体密度为证明其中心点的电位是(2 r 1) a 厶8、一个半径为a,带电量为Q的导体球,球外套有半径为b的同心介质球壳,壳外是空气,壳内介质的介电系数为「求空间任一点的D, E, P及束缚电荷密度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第 四 章
恒定磁场
例 4.1.2 真空中有一载流为 I,半径为R的圆环,
试求其轴线上 P 点的 磁感应强度 B 。 解:元电流 Idl 在 P 点产生的 B 为
0 Idl e r ( Idl dB 2
4 πr
2 4π( R 2 x 2 )
er )
dB
0 Idl sin
图3.1.3 圆形载流回路
0 Idl (r r ) 4π l r r 3
体电流
J (r ) (r r ) B V r r 3 dV 4π
0
面电流
0 K (r ) (r r ) B dS 3 4π S r r
毕奥-沙伐定律 适用于无限大均匀媒质。
安培环路定律
图3.2.10 同轴电缆
B dS I
l 0
2 I π 2 I 2 π12 1
I
B dl 2πB
l
I 2
0
12
故
图3.2.11 安培定律示意图
0 I B e 2 2 π1
返 回 上 页 下 页
第 四 章
恒定磁场
m=IdS dS
图3.2.13 磁偶极子
2)介质的磁化
无外磁场作用时,介质对 n 外不显磁性, m 0
i 1
i
在外磁场作用下,磁偶极 子发生旋转, n
i 1
mi 0
图3.2.14 介质的磁化
返 回 上 页 下 页
第 四 章
恒定磁场
转矩为 Ti=mi×B ,旋转方向 使磁偶极矩方向与外磁场方向一
0 Kdx 0 Kdx y 0 Kydx dBx cos 2π 2π 2π( x 2 y 2 )
根据对称性 ,By = 0
Bx
dx 2π ( x 2 y 2 ) 0 K ex y0 2 0 K ex y0 2
返 回 上 页 下 页
x 2 2 2 2 4 π( R x ) R x
0 IR2
2( R x )
2 2 3/ 2
ex
返 回 上 页 下 页
第 四 章
恒定磁场
例 4.1.3 无限大导体平面通有面电流 K K e z , 试求磁感应强度 B 分布。 解:取宽度 dx 的一条无限长线电流
思考 当电流与安培环路呈右手螺旋关系时,电流取正 值,否则取负;
环路上的 B 仅与环路交链的电流有关吗?
返 回 上 页 下 页
第 四 章
恒定磁场
例4.2.1 试求无限大载流导板产生的磁感应强度 B。 解:定性分析场分布,取安培环
路与电流呈右手螺旋
B dl B L B L KL
得到
0 I B e 2 2π 2
2 3 2 3 2
图3.2.12 同轴电缆的磁 场分布
返 回 上 页 下 页
第 四 章
恒定磁场
4. 介质的磁化(magnetization) 1)磁偶极子 (magnetic dipole) 磁偶极矩 m IdS Am2
( magnetic dipole moment )
B
图3.1.5 无限大电流片及 B 的分布
第 四 章
4.2 磁通连续性原理 • 安培环路定律
恒定磁场
Magnetic Flux Continue Theorem & Ampere’s Circuital Law 4.2.1 磁通连续性原理 ( Magnetic Flux Continue Theorem )
0 L I B dz 2 2 32 4π L ( z )
1 2
0 I L1 L2 [ ] 4π 2 L 2 2 L2 2 1
0 I (sin1 sin 2 ) 4π
图3.1.2 长直导线的磁场
返 回 上 页 下 页
0 I e 当 L1 , L2 时, B 2π
S
u0 I u0 M dl
l
移项后
B l ( 0 M ) dl I B H -M 0
图3.2.16 H 与I 成右螺旋关系
定义:磁场强度 则有
A/m
H dl I
l
安培环路定律
返 回 上 页 下 页
第 四 章
恒定磁场
H dl I
l
安培环路定律
力 = 受力电流 磁感应强度
定义:磁感应强度
0 I 'd l e R B 4π l R 2
0 Idl (r r ) 4π l r r 3
单位 T(Wb/m2)
返 回 上 页 下 页
第 四 章
恒定磁场
线电流
0 I 'd l e R B 4π l R 2
返 回 上 页 下 页
第 四 章
恒定磁场
图3.2.5 一对反向电流传输线
图3.2.6 一对同向电流传输线
图3.2.7 两对反相电流传输线
图3.2.8 两对同向电流传输线
返 回 上 页 下 页
第 四 章
恒定磁场
4.2.2 安培环路定律 (Apere’s Circuital Law) 1. 恒定磁场的旋度
返 回 上 页 下 页
第 四 章
恒定磁场
例4.1.1 试求有限长直载流导线产生的磁感应强度。 解: 采用圆柱坐标系,取电流 I dz,
0 Idl e R 式中 R2 2 z 2 B 4 π L R 2 dl e R dz sin e dz sin e dze R
2) 1 2
得到
0 I B e 2 π
l
B dl 2πB 0 I
3) 2 3,
2 32 2 2 2 I I I 2 I 2 2 2 3 2 3 2
0 I ( 32 2 ) l B dl 2πB 32 22
Bx B y Bz dx dy dz
图3.2.2 B 的通量
返 回 上 页 下 页
第 四 章
恒定磁场
磁感应线的性质:
磁感应线是闭合的曲线; 磁感应线不能相交; 闭合的磁感应线与交链 的电流成右手螺旋关系;
图3.2.3 导线位于铁板上方
磁感应强处 ,磁感应线
稠密,反之,稀疏。
图3.2.4 长直螺线管的磁场
l 1 2 0
图3.2.9 无限大载流导板
根据对称性 B1 B2 B
x0
x0
返 回 上 页 下 页
B
0 K ey 2
0 K ey 2
第 四 章
恒定磁场
例 4.2.2 试求载流无限长同轴电缆产生的磁感应强度。 解: 平行平面磁场, B B( )e
1 ) 0 1
J ( x, y, z) (r r ) B dV ( 毕奥-沙伐定律 ) 3 V 4π r r
0
旋度运算后,得到
0 J (有电流区) B(r ) 恒定磁场是有旋场 0 (无电流区)
在直角坐标系中
ex B x Bx ey y By ez By Bx Bx Bz Bz By ( )e x ( )e y ( )e z z y z z x x y Bz
第 四 章
第四章 恒定磁场
Steady Magnetic Field
恒定磁场
序 磁感应强度 磁通连续性原理∙安培环路定律 恒定磁场基本方程∙分界面上的衔接条件 磁矢位及边值问题 磁位及边值问题 镜像法 电感 磁场能量与力
磁路
返 回 下 页
第 四 章
恒定磁场
4.0 序
Introduction 导体中通有直流电流时,在导体内部和它周围 的媒质中,不仅有电场还有不随时间变化的磁场, 称为恒定磁场。 恒定磁场和静电场是性质完全不同的两种场,
分离变量法
镜像法
电感的计算
磁场能量及力
磁路及其计算
返 回 上 页 下 页
第 四 章
恒定磁场
本章要求
深刻理解磁感应强度、磁通、磁化、磁场强度 的概念。 掌握恒定磁场的基本方程和分界面衔接条件。 了解磁位及其边值问题。 熟练掌握磁场、电感、能量与力的各种计算方 法。了解磁路及其计算方法。
返 回
上 页
下 页
返 回 上 页 下 页
第 四 章
恒定磁场
2. 真空中的安培环路定律
B 的旋度
B 0 J
等式两边取面积分 用斯托克斯定理
( B) dS J dS B dl I
S 0 S
n l 0 k 1 k
B dl I
l 0
真空中的安培环路定律
但在分析方法上却有许多共同之处。学习本章时,
注意类比法的应用。 恒定磁场的知识结构。
返 回 上 页 下 页
第 四 章
恒定磁场
基本实验定律 (安培力定律)
磁感应强度(B)(毕奥—沙伐定律)
H 的旋度
基本方程 分界面衔接条件 边值问题
B 的散度
磁位( m) 数值法
磁矢位(A) 解析法
有限差分法
有限元法
p P en
Jm M
m IdS
K m M en
返 回
上 页
下 页
第 四 章
恒定磁场
4.有磁介质时的环量与旋度
B dl I 0 ( I I m )
l 0
0 I 0 J m dS
s
u0 I u0 ( M ) dS
