四川省渠县崇德实验学校2020年中考第二轮九年级数学三角形、四边形压轴题专题复习(无答案)
2020年九年级数学典型中考压轴题专项训练:四边形(含答案)

四川省渠县崇德实验学校2020年中考九年级数学:四边形综合专题复习题1、如图,四边形ABCD为平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E.(1)求证:BE=CD;(2)连接BF,若BF⊥AE,∠BEA=60°,AB=4,求平行四边形ABCD的面积.2、如图,矩形ABCD中,延长AB至E,延长CD至F,BE=DF,连接EF,与BC、AD分别相交于P、Q两点.(1)求证:CP=AQ;(2)若BP=1,PQ=2,∠AEF=45°,求矩形ABCD的面积.3、如图,在▱ABCD中,点E,F在对角线AC上,且AE=CF.求证:(1)DE=BF;(2)四边形DEBF是平行四边形.4、如图,E是▱ABCD的边CD的中点,延长AE交BC的延长线于点F.(1)求证:△ADE≌△FCE.(2)若∠BAF=90°,BC=5,EF=3,求CD的长.5、如图,AC是矩形ABCD的对角线,过AC的中点O作EF⊥AC,交BC于点E,交AD于点F,连接AE,CF.(1)求证:四边形AECF是菱形;(2)若AB=,∠DCF=30°,求四边形AECF的面积.(结果保留根号)6、如图,▱ABCD中,AB=2,AD=1,∠ADC=60°,将▱ABCD沿过点A的直线l折叠,使点D 落到AB边上的点D′处,折痕交CD边于点E.(1)求证:四边形BCED′是菱形;(2)若点P时直线l上的一个动点,请计算PD′+PB的最小值.7、如图,菱形ABCD的对角线AC与BD交于点O,∠ABC:∠BAD=1:2,BE∥AC,CE∥BD.(1)求tan∠DBC的值;(2)求证:四边形OBEC是矩形.8、在矩形ABCD中,AB=3,AD=4,动点Q从点A出发,以每秒1个单位的速度,沿AB向点B移动;同时点P从点B出发,仍以每秒1个单位的速度,沿BC向点C移动,连接QP,QD,PD.若两个点同时运动的时间为x秒(0<x≤3),解答下列问题:(1)设△QPD的面积为S,用含x的函数关系式表示S;当x为何值时,S有最大值?并求出最小值;(2)是否存在x的值,使得QP⊥DP?试说明理由.9、如图,点P在矩形ABCD的对角线AC上,且不与点A,C重合,过点P分别作边AB,AD 的平行线,交两组对边于点E,F和G,H.(1)求证:△PHC≌△CFP;(2)证明四边形PEDH和四边形PFBG都是矩形,并直接写出它们面积之间的关系.10、如图,在四边形ABCD中,AD∥BC,∠A=∠C,点P在边AB上.(1)判断四边形ABCD的形状并加以证明;(2)若AB=AD,以过点P的直线为轴,将四边形ABCD折叠,使点B、C分别落在点B′、C′上,且B′C′经过点D,折痕与四边形的另一交点为Q.①在图2中作出四边形PB′C′Q(保留作图痕迹,不必说明作法和理由);②如果∠C=60°,那么为何值时,B′P⊥AB.11、某同学要证明命题“平行四边形的对边相等.”是正确的,他画出了图形,并写出了如下已知和不完整的求证.已知:如图,四边形ABCD是平行四边形.求证:AB=CD,BC=DA(1)补全求证部分;(2)请你写出证明过程.证明:∵四边形ABCD是平行四边形,∴AB∥CD,AD∥BC,∴∠BAC=∠DCA,∠BCA=∠DAC,在△ABC和△CDA中,,∴△ABC≌△CDA(ASA),∴AB=CD,BC=DA..12、在矩形ABCD中,E为CD的中点,H为BE上的一点,,连接CH并延长交AB于点G,连接GE并延长交AD的延长线于点F.(1)求证:;(2)若∠CGF=90°,求的值.13、如图,将矩形ABCD沿AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接DG.(1)求证:四边形EFDG是菱形;(2)探究线段EG、GF、AF之间的数量关系,并说明理由;(3)若AG=6,EG=2,求BE的长.14、如图,已知▱ABCD的三个顶点A(n,0)、B(m,0)、D(0,2n)(m>n>0),作▱ABCD 关于直线AD的对称图形AB1C1D(1)若m=3,试求四边形CC1B1B面积S的最大值;(2)若点B1恰好落在y轴上,试求的值.15、已知正方形ABCD,P为射线AB上的一点,以BP为边作正方形BPEF,使点F在线段CB的延长线上,连接EA、EC.(1)如图1,若点P在线段AB的延长线上,求证:EA=EC;(2)若点P在线段AB上.①如图2,连接AC,当P为AB的中点时,判断△ACE的形状,并说明理由;②如图3,设AB=a,BP=b,当EP平分∠AEC时,求a:b及∠AEC的度数.16、如图1,我们把对角线互相垂直的四边形叫做垂美四边形.(1)概念理解:如图2,在四边形ABCD中,AB=AD,CB=CD,问四边形ABCD是垂美四边形吗?请说明理由.(2)性质探究:试探索垂美四边形ABCD两组对边AB,CD与BC,AD之间的数量关系.猜想结论:(要求用文字语言叙述)___________________________写出证明过程(先画出图形,写出已知、求证).(3)问题解决:如图3,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG 和正方形ABDE,连接CE,BG,GE,已知AC=4,AB=5,求GE长.17、如图1,已知点E,F,G,H分别是四边形ABCD各边AB,BC,CD,DA的中点,根据以下思路可以证明四边形EFGH是平行四边形:(1)如图2,将图1中的点C移动至与点E重合的位置,F,G,H仍是BC,CD,DA的中点,求证:四边形CFGH是平行四边形;(2)如图3,在边长为1的小正方形组成的5×5网格中,点A,C,B都在格点上,在格点上画出点D,使点C与BC,CD,DA的中点F,G,H组成正方形CFGH;(3)在(2)条件下求出正方形CFGH的边长.18、如图,面积为6的平行四边形纸片ABCD中,AB=3,∠BAD=45°,按下列步骤进行裁剪和拼图.第一步:如图①,将平行四边形纸片沿对角线BD剪开,得到△ABD和△BCD纸片,再将△ABD纸片沿AE剪开(E为BD上任意一点),得到△ABE和△ADE纸片;第二步:如图②,将△ABE纸片平移至△DCF处,将△ADE纸片平移至△BCG处;第三步:如图③,将△DCF纸片翻转过来使其背面朝上置于△PQM处(边PQ与DC重合,△PQM和△DCF在DC同侧),将△BCG纸片翻转过来使其背面朝上置于△PRN处,(边PR与BC 重合,△PRN和△BCG在BC同侧).则由纸片拼成的五边形PMQRN中,对角线MN长度的最小值为.19、如图,在矩形ABCD中,点O为坐标原点,点B的坐标为(4,3),点A、C在坐标轴上,点P在BC边上,直线l1:y=2x+3,直线l2:y=2x﹣3.(1)分别求直线l1与x轴,直线l2与AB的交点坐标;(2)已知点M在第一象限,且是直线l2上的点,若△APM是等腰直角三角形,求点M的坐标;(3)我们把直线l1和直线l2上的点所组成的图形为图形F.已知矩形ANPQ的顶点N在图形F上,Q是坐标平面内的点,且N点的横坐标为x,请直接写出x的取值范围(不用说明理由).20、如图1,在正方形ABCD内作∠EAF=45°,AE交BC于点E,AF交CD于点F,连接EF,过点A作AH⊥EF,垂足为H.(1)如图2,将△ADF绕点A顺时针旋转90°得到△ABG.①求证:△AGE≌△AFE;②若BE=2,DF=3,求AH的长.(2)如图3,连接BD交AE于点M,交AF于点N.请探究并猜想:线段BM,MN,ND之间有什么数量关系?并说明理由.参考答案:1、【解答】(1)证明:∵四边形ABCD是平行四边形,∴AD∥BC,AB∥CD,AB=CD,∴∠B+∠C=180°,∠AEB=∠DAE,∵AE是∠BAD的平分线,∴∠BAE=∠DAE,∴∠BAE=∠AEB,∴AB=BE,∴BE=CD;(2)解:∵AB=BE,∠BEA=60°,[来源:学#科#网] ∴△ABE是等边三角形,∴AE=AB=4,∵BF⊥AE,∴AF=EF=2,∴BF===2,∵AD∥BC,∴∠D=∠ECF,∠DAF=∠E,在△ADF和△ECF中,,∴△ADF≌△ECF(AAS),∴△ADF的面积=△ECF的面积,∴平行四边形ABCD的面积=△ABE的面积=AE•BF=×4×2=4.2、【解答】(1)证明:∵四边形ABCD是矩形,∴∠A=∠ABC=∠C=∠ADC=90°,AB=CD,AD=BC,AB∥CD,AD∥BC,∴∠E=∠F,∵BE=DF,∴AE=CF,在△CFP和△AEQ中,,∴△CFP≌△AEQ(ASA),∴CP=AQ;(2)解:∵AD∥BC,[来源:学#科#网Z#X#X#K]∴∠PBE=∠A=90°,∵∠AEF=45°,∴△BEP、△AEQ是等腰直角三角形,∴BE=BP=1,AQ=AE,∴PE=BP=,∴EQ=PE+PQ=+2=3,∴AQ=AE=3,∴AB=AE﹣BE=2,∵CP=AQ,AD=BC,∴DQ=BP=1,∴AD=AQ+DQ=3+1=4,∴矩形ABCD的面积=AB•AD=2×4=8.3、【解答】证明:(1)∵四边形ABCD是平行四边形,∴AD∥CB,AD=CB,∴∠DAE=∠BCF,在△ADE和△CBF中,∴△ADE≌△CBF,∴DE=BF.(2)由(1),可得∴△ADE≌△CBF,∴∠ADE=∠CBF,∵∠DEF=∠DAE+∠ADE,∠BFE=∠BCF+∠CBF,∴∠DEF=∠BFE,∴DE∥BF,又∵DE=BF,∴四边形DEBF是平行四边形.4、【解答】(1)证明:∵四边形ABCD是平行四边形,∴AD∥BC,AB∥CD,∴∠DAE=∠F,∠D=∠ECF,∵E是▱ABCD的边CD的中点,∴DE=CE,在△ADE和△FCE中,,∴△ADE≌△FCE(AAS);(2)解:∵ADE≌△FCE,∴AE=EF=3,∵AB∥CD,∴∠AED=∠BAF=90°,在▱ABCD中,AD=BC=5,∴DE===4,∴CD=2DE=8.5、【解答】(1)证明:∵O是AC的中点,且EF⊥AC,∴AF=CF,AE=CE,OA=OC,∵四边形ABCD是矩形,∴AD∥BC,∴∠AFO=∠CEO,在△AOF和△COE中,,∴△AOF≌△COE(AAS),∴AF=CE,∴AF=CF=CE=AE,∴四边形AECF是菱形;(2)解:∵四边形ABCD是矩形,∴CD=AB=,在Rt△CDF中,cos∠DCF=,∠DCF=30°,∴CF==2,∵四边形AECF是菱形,∴CE=CF=2,∴四边形AECF是的面积为:EC•AB=2.6、【解答】证明:(1)∵将▱ABCD沿过点A的直线l折叠,使点D落到AB边上的点D′处,∴∠DAE=∠D′AE,∠DEA=∠D′EA,∠D=∠AD′E,∵DE∥AD′,∴∠DEA=∠EAD′,∴∠DAE=∠EAD′=∠DEA=∠D′EA,∴∠DAD′=∠DED′,∴四边形DAD′E是平行四边形,∴DE=AD′,∵四边形ABCD是平行四边形,∴AB=DC,AB∥DC,∴CE=D′B,CE∥D′B,∴四边形BCED′是平行四边形;∵AD=AD′,∴▱DAD′E是菱形,(2)∵四边形DAD′E是菱形,∴D与D′关于AE对称,连接BD交AE于P,则BD的长即为PD′+PB的最小值,过D作DG⊥BA于G,∵CD∥AB,∴∠DAG=∠CDA=60°,∵AD=1,∴AG=,DG=,∴BG=,∴BD==,∴PD′+PB的最小值为.7、【解答】(1)解:∵四边形ABCD是菱形,∴AD∥BC,∠DBC=∠ABC,∴∠ABC+∠BAD=180°,∵∠ABC:∠BAD=1:2,∴∠ABC=60°,∴∠BDC=∠ABC=30°,则tan∠DBC=tan30°=;(2)证明:∵四边形ABCD是菱形,∴AC⊥BD,即∠BOC=90°,∵BE∥AC,CE∥BD,∴BE∥OC,CE∥OB,∴四边形OBEC是平行四边形,则四边形OBEC是矩形.8、【解答】解:(1)∵四边形ABCD为矩形,∴BC=AD=4,CD=AB=3,当运动x秒时,则AQ=x,BP=x,∴BQ=AB﹣AQ=3﹣x,CP=BC﹣BP=4﹣x,∴S△ADQ=AD•AQ=×4x=2x,S△BPQ=BQ•BP=(3﹣x)x=x﹣x2,S△PCD=PC•CD=•(4﹣x)•3=6﹣x,又S矩形ABCD=AB•BC=3×4=12,∴S=S矩形ABCD﹣S△ADQ﹣S△BPQ﹣S△PCD=12﹣2x﹣(x﹣x2)﹣(6﹣x)=x2﹣2x+6=(x﹣2)2+4,即S=(x﹣2)2+4,∴S为开口向上的二次函数,且对称轴为x=2,∴当0<x<2时,S随x的增大而减小,当2<x≤3时,S随x的增大而增大,又当x=0时,S=5,当S=3时,S=,但x的范围内取不到x=0,∴S不存在最大值,当x=2时,S有最小值,最小值为4;(2)存在,理由如下:由(1)可知BQ=3﹣x,BP=x,CP=4﹣x,当QP⊥DP时,则∠BPQ+∠DPC=∠DPC+∠PDC,∴∠BPQ=∠PDC,且∠B=∠C,∴△BPQ∽△PCD,∴=,即=,解得x=(舍去)或x=,∴当x=时QP⊥DP.9、【解答】证明:(1)∵四边形ABCD为矩形,∴AB∥CD,AD∥BC.∵PF∥AB,∴PF∥CD,∴∠CPF=∠PCH.∵PH∥AD,∴PH∥BC,∴∠PCF=∠CPH.在△PHC和△CFP中,,∴△PHC≌△CFP(ASA).(2)∵四边形ABCD为矩形,∴∠D=∠B=90°.又∵EF∥AB∥CD,GH∥AD∥BC,∴四边形PEDH和四边形PFBG都是矩形.∵EF∥AB,∴∠CPF=∠CAB.在Rt△AGP中,∠AGP=90°,PG=AG•tan∠CAB.在Rt△CFP中,∠CFP=90°,CF=PF•tan∠CPF.S矩形DEPH=DE•EP=CF•EP=PF•EP•tan∠CPF;S矩形PGBF=PG•PF=AG•PF•tan∠CAB=EP•PF•tan∠CAB.∵tan∠CPF=tan∠CAB,∴S矩形DEPH=S矩形PGBF.10、【解答】解:(1)四边形ABCD是平行四边形证明:∵在四边形ABCD中,AD∥BC,∴∠A+∠B=180°,∵∠A=∠C,∴∠C+∠B=180°,∴AB∥CD,∴四边形ABCD是平行四边形;(2)①作图如下:②当AB=AD时,平行四边形ABCD是菱形,由折叠可得,BP=B′P,CQ=C′Q,BC=B′C′,∠C=∠C′=60°=∠A,当B′P⊥AB时,由B′P∥C′Q,可得C′Q⊥CD,∴∠PEA=30°=∠DEB′,∠QDC′=30°=∠B′DE,∴B′D=B′E,设AP=a,BP=b,则直角三角形APE中,PE=a,且B′P=b,BC=B′C′=CD=a+b,∴B′E=b﹣a=B′D,∴C′D=a+b﹣(b﹣a)=a+a,∴直角三角形C′QD中,C′Q=a=CQ,DQ=C′Q=a,∵CD=DQ+CQ=a+b,∴a+a=a+b,整理得(+1)a=b,∴==,即=.11、【解答】(1)已知:如图,四边形ABCD是平行四边形.求证:AB=CD,BC=DA;故答案为:BC=DA;(2)证明:连接AC,如图所示:∵四边形ABCD是平行四边形,∴AB∥CD,AD∥BC,∴∠BAC=∠DCA,∠BCA=∠DAC,在△ABC和△CDA中,,∴△ABC≌△CDA(ASA),∴AB=CD,BC=DA;故答案为:∵四边形ABCD是平行四边形,∴AB∥CD,AD∥BC,∴∠BAC=∠DCA,∠BCA=∠DAC,在△ABC和△CDA中,,∴△ABC≌△CDA(ASA),∴AB=CD,BC=DA.12、【解答】(1)证明:∵四边形ABCD是矩形,∴CD∥AB,AD=BC,AB=CD,AD∥BC,∴△CEH∽△GBH,∴.(2)解:作EM⊥AB于M,如图所示:则EM=BC=AD,AM=DE,∵E为CD的中点,∴DE=CE,设DE=CE=3a,则AB=CD=6a,由(1)得: =3,∴BG=CE=a,∴AG=5a,∵∠EDF=90°=∠CGF,∠DEF=∠GEC,∴△DEF∽△GEC,∴,∴EG•EF=DE•EC,∵CD∥AB,∴=,∴,∴EF=EG,∴EG•EG=3a•3a,解得:EG=a,在Rt△EMG中,GM=2a,∴EM==a,∴BC=a,∴==3.13、【解答】解:(1)证明:∵GE∥DF,∴∠EGF=∠DFG.∵由翻折的性质可知:GD=GE,DF=EF,∠DGF=∠EGF,∴∠DGF=∠DFG.∴GD=DF.∴DG=GE=DF=EF.∴四边形EFDG为菱形.(2)EG2=GF•AF.理由:如图1所示:连接DE,交AF于点O.∵四边形EFDG为菱形,∴GF⊥DE,OG=OF=GF.∵∠DOF=∠ADF=90°,∠OFD=∠DFA,∴△DOF∽△ADF.∴,即DF2=FO•AF.∵FO=GF,DF=EG,∴EG2=GF•AF.(3)如图2所示:过点G作GH⊥DC,垂足为H.∵EG2=GF•AF,AG=6,EG=2,∴20=FG(FG+6),整理得:FG2+6FG﹣40=0.解得:FG=4,FG=﹣10(舍去).∵DF=GE=2,AF=10,∴AD==4.∵GH⊥DC,AD⊥DC,∴GH∥AD.∴△FGH∽△FAD.∴,即=.∴GH=.∴BE=AD﹣GH=4﹣=.14、【解答】解:(1)如图1,∵▱ABCD与四边形AB1C1D关于直线AD对称,∴四边形AB1C1D是平行四边形,CC1⊥EF,BB1⊥EF,∴BC∥AD∥B1C1,CC1∥BB1,∴四边形BCEF、B1C1EF是平行四边形,∴S▱BCEF=S▱BCDA=S▱B1C1DA=S▱B1C1EF,∴S▱BCC1B1=2S▱BCDA.∵A(n,0)、B(m,0)、D(0,2n)、m=3,∴AB=m﹣n=3﹣n,OD=2n,∴S▱BCDA=AB•OD=(3﹣n)•2n=﹣2(n2﹣3n)=﹣2(n﹣)2+,∴S▱BCC1B1=2S▱BCDA=﹣4(n﹣)2+9.∵﹣4<0,∴当n=时,S▱BCC1B1最大值为9;(2)当点B1恰好落在y轴上,如图2,∵DF⊥BB1,DB1⊥OB,∴∠B1DF+∠DB1F=90°,∠B1BO+∠OB1B=90°,∴∠B1DF=∠OBB1.∵∠DOA=∠BOB1=90°,∴△AOD∽△B1OB,∴=,∴=,∴OB1=.由轴对称的性质可得AB1=AB=m﹣n.在Rt△AOB1中,n2+()2=(m﹣n)2,整理得3m2﹣8mn=0.∵m>0,∴3m﹣8n=0,∴=.15、【解答】解:(1)∵四边形ABCD和四边形BPEF是正方形,∴AB=BC,BP=BF,∴AP=CF,在△APE和△CFE中,,∴△APE≌△CFE,∴EA=EC;(2)①∵P为AB的中点,∴PA=PB,又PB=PE,∴PA=PE,∴∠PAE=45°,又∠DAC=45°,∴∠CAE=90°,即△ACE是直角三角形;②∵EP平分∠AEC,EP⊥AG,∴AP=PG=a﹣b,BG=a﹣(2a﹣2b)=2b﹣a∵PE∥CF,∴=,即=,解得,a=b;作G H⊥AC于H,∵∠CAB=45°,∴HG=AG=×(2b﹣2b)=(2﹣)b,又BG=2b﹣a=(2﹣)b,∴GH=GB,GH⊥AC,GB⊥BC,∴∠HCG=∠BCG,∵PE∥CF,∴∠PEG=∠BCG,∴∠AEC=∠ACB=45°.∴a:b=:1;∴∠AEC=45°.16、【解答】解:(1)四边形ABCD是垂美四边形.证明:∵AB=AD,∴点A在线段BD的垂直平分线上,∵CB=CD,∴点C在线段BD的垂直平分线上,∴直线AC是线段BD的垂直平分线,∴AC⊥BD,即四边形ABCD是垂美四边形;(2)猜想结论:垂美四边形的两组对边的平方和相等.如图2,已知四边形ABCD中,AC⊥BD,垂足为E,求证:AD2+BC2=AB2+CD2证明:∵AC⊥BD,∴∠AED=∠AEB=∠BEC=∠CED=90°,由勾股定理得,AD2+BC2=AE2+DE2+BE2+CE2,AB2+CD2=AE2+BE2+CE2+DE2,∴AD2+BC2=AB2+CD2;(3)连接CG、BE,∵∠CAG=∠BAE=90°,∴∠CAG+∠BAC=∠BAE+∠BAC,即∠GAB=∠CAE,在△GAB和△CAE中,,∴△GAB≌△CAE,∴∠ABG=∠AEC,又∠AEC+∠AME=90°,∴∠ABG+∠AME=90°,即CE⊥BG,∴四边形CGEB是垂美四边形,由(2)得,CG2+BE2=CB2+GE2,∵AC=4,AB=5,∴BC=3,CG=4,BE=5,∴GE2=CG2+BE2﹣CB2=73,∴GE=.17、【解答】(1)证明:如图2,连接BD,∵C,H是AB,DA的中点,∴CH是△ABD的中位线,∴CH∥BD,CH=BD,同理FG∥BD,FG=BD,∴CH∥FG,CH=FG,∴四边形CFGH是平行四边形;(2)如图3所示,(3)解:如图3,∵BD=,∴FG=BD=,∴正方形CFGH的边长是.18、【解答】解:∵△ABE≌△CDF≌△PMQ,∴AE=DF=PM,∠EAB=∠FDC=∠MPQ,∵△ADE≌△BCG≌△PNR,∴AE=BG=PN,∠DAE=∠CBG=∠RPN,∴PM=PN,∵四边形ABCD是平行四边形,∴∠DAB=∠DCB=45°,∴∠MPN=90°,∴△MPN是等腰直角三角形,当PM最小时,对角线MN最小,即AE取最小值,∴当AE⊥BD时,AE取最小值,过D作DF⊥AB于F,∵平行四边形ABCD的面积为6,AB=3,∴DF=2,∵∠DAB=45°,∴AF=DF=2,∴BF=1,∴BD==,∴AE===,∴MN=AE=,故答案为:.19、【解答】解:(1)直线l1:当y=0时,2x+3=0,x=﹣则直线l1与x轴坐标为(﹣,0)直线l2:当y=3时,2x﹣3=3,x=3则直线l2与AB的交点坐标为(3,3);(2)①若点A为直角顶点时,点M在第一象限,连结AC,如图1,∠APB>∠ACB>45°,∴△APM不可能是等腰直角三角形,∴点M不存在;②若点P为直角顶点时,点M在第一象限,如图2,过点M作MN⊥CB,交CB的延长线于点N,则Rt△ABP≌Rt△PNM,∴AB=PN=4,MN=BP,设M(x,2x﹣3),则MN=x﹣4,∴2x﹣3=4+3﹣(x﹣4),x=,∴M(,);③若点M为直角顶点时,点M在第一象限,如图3,设M1(x,2x﹣3),过点M1作M1G1⊥OA,交BC于点H1,则Rt△AM1G1≌Rt△PM1H1,∴AG1=M1H1=3﹣(2x﹣3),∴x+3﹣(2x﹣3)=4,x=2∴M1(2,1);设M2(x,2x﹣3),同理可得x+2x﹣3﹣3=4,∴x=,∴M2(,);综上所述,点M的坐标为(,),(2,1),(,);(3)x的取值范围为﹣≤x<0或0<x≤或≤x≤或≤x≤2.20、【解答】解:(1)①由旋转的性质可知:AF=AG,∠DAF=∠BAG.[来源:学。
四川省渠县崇德实验学校2020年九年级数学中考考前练习题(无答案)

(3)如图3,当E,F分别在直线DC,CB上移动时,连接AE和DF交于点P,由于点E,
四川省渠县崇德实验校 2020 年中考九年级数考前练习题
1、先化简,再求值( + )÷ ,其中x满足x2+4x+3=0.
2、先化简,再求值:÷- ,其中x=4.
3、计算:
4、(1)计算:
(2)先化简,再求值:(2x+3y)2﹣(2x+y)(2x﹣y),其中x= ,y=﹣ .
5、如图,已知在四边形ABCD中,点E在AD上,∠BCE=∠ACD=90°,∠BAC=∠D,
10、如图,已知⊙O是以AB为直径的圆,C为⊙O上一点,D为OC延长线上一点,BC的延长线交AD于E,∠DAC=∠DCE.
(1)求证:AD为⊙O的切线;
(2)求证:DC2=ED•DA;
(3)若AB=2,sinD=,求AE的长.
11、如图,四边形ABCD的顶点在⊙O上,BD是⊙O的直径,延长CD、BA交于点E,连接AC、BD交于点F,作AH⊥CE,垂足为点H,已知∠ADE=∠ACB.
推理证明
(1)求证:四边形A′BDC是矩形;实践操作
(2)在图1中将△ABD或△BDC进行平移、旋转或轴对称变换,重新构造一个特殊四边形.
要求:①画出图形,标明字母;②写出构图过程及构造的特殊四边形的名称.(不要求证明)
16、如图1,在矩形ABCD中AD=4,AB=2 ,将矩形ABCD绕点A逆时针旋转α(0
1),以 AB 为边作菱形 ABCD,点 D 恰好在 y 的正半轴上,对角线AC⊥x轴,垂足为
四川省渠县崇德实验学校2020年中考九年级数学几何图形综合题专题复习(包含答案)

四川省渠县崇德实验学校2020 年中考九年级数学几何图形综合题专题复习1、如图,在 ?ABCD中,点 E 在边 BC上,点 F 在边 AD的延长线上,且DF=BE,BE与 CD交于点 G(1)求证: BD∥ EF;( 2)若=,BE=4,求EC的长.2、如图,在Rt △ABC中,∠C= 90°,AC=6,∠BAC= 60°,AD均分∠BAC交BC于点D,过点 D作 DE∥ AC交 AB于点 E.点 M是线段 AD上的动点,连结BM并延长分别交DE,AC于点F, G.EF(1)求 CD的长;(2)若点 M是线段 AD的中点,求DF的值;(3)请问当 DM的长知足什么条件时,在线段DE上恰巧只有一点 P,使得∠ CPG=60°?3、如图,在△ABC中, AD⊥ BC, BE⊥ AC,垂足分别为D,E, AD与 BE订交于点F.(1)求证:△ ACD∽△ BFD;(2)当 tan ∠ ABD=1, AC=3时,求 BF的长.4、如图, ?ABCD的对角线AC、 BD交于点 O, EF过点 O且与 BC、 AD分别交于点E、 F.试猜想线段 AE、 CF 的关系,并说明原因.5、如图,平行四边形 ABCD的对角线 AC、BD订交于点 O,E,F 分别是 OA,OC的中点,连结BE, DF(1)依据题意,补全原形;(2)求证:BE=DF.6、如图,在正方形ABCD中,点E是BC的中点,将△ABE沿AE折叠后获得△AFE,点F在正方形 ABCD的内部,延长 AF交 CD于点 G.(1)猜想并证明线段 FG与 CG的数目关系;(2) 若将图①中的正方形改成矩形,其余条件不变,如图②,那么线段FG与 CG之间的数目关系能否改变?请证明你的结论;(3) 若将图①中的正方形改成平行四边形,其余条件不变,如图③,那么线段FG 与 CG 之间的数目关系能否会改变?请证明你的结论.7、如图,四边形ABCD是菱形, CE⊥ AB交 AB的延长线于点E, CF⊥AD交 AD的延长线于点F,求证: DF=BE.8、如图,□A BCD中, BD是它的一条对角线,过A、C 两点作 AE⊥ BD,CF⊥ BD,垂足分别为E、 F,延长 AE、 CF分别交 CD、 AB于 M、 N。
四川省渠县崇德实验学校中考九年级数学:相似三角形复习测试题(含答案)

四川省渠县崇德实验学校2020年中考九年级数学:相似三角形复习测试题一、选择题(每小题3分,共36分)1.下列说法正确的是( )A.两个直角三角形一定相似B.两个相似图形一定是位似图形C.两个菱形一定相似D.两个正三角形一定相似 2.如图,点C 把线段AB 分成两条线段AC 和BC ,如果AC AB =BCAC,那么称线段AB 被点C 黄金分割,AC 与AB 的比叫做黄金比,其比值是( )A.5-12B.3-52C.5+12D.3+523.下列命题是真命题的是( )A.如果两个三角形相似,相似比为4∶9,那么这两个三角形的周长比为2∶3B.如果两个三角形相似,相似比为4∶9,那么这两个三角形的周长比为4∶9C.如果两个三角形相似,相似比为4∶9,那么这两个三角形的面积比为2∶3D.如果两个三角形相似,相似比为4∶9,那么这两个三角形的面积比为4∶9 4.如图,在△ABC 中,点D ,E ,F 分别在边AB ,AC ,BC 上,且DE∥BC,EF∥AB.若AD =2BD ,则CFBF的值为( )A.12B.13C.14D.235.要制作两个形状相同的三角形框架,其中一个三角形的三边长分别为5 cm ,6 cm 和9 cm ,另一个三角形的最短边长为2.5 cm ,则它的最长边为( ) A.3 cm B.4 cm C.4.5 cm D.5 cm6.如图,在△ABC 中,点D 是边AB 上的一点,∠ADC=∠ACB,AD =2,BD =6,则边AC 的长为( )A.2B.4C.6D.87.学校门口的栏杆如图所示,栏杆从水平位置BD 绕O 点旋转到AC 位置,已知AB⊥BD,CD⊥BD.垂足分别为B ,D ,AO =4 m ,AB =1.6 m ,CO =1 m ,则栏杆C 端应下降的垂直距离CD 为( )A.0.2 mB.0.3 mC.0.4 mD.0.5 m 8.如图,在△ABC 中,点D ,E 分别在AB 和AC 上,DE∥BC,M 为BC 边上一点(不与点B ,C 重合),连接AM 交DE 于点N ,则( )A.AD AN =AN AEB.BD MN =MN CEC.DN BM =NE MCD.DN MC =NE BM9.如图,⊙O 是△ABC 的外接圆,已知AD 平分∠BAC 交⊙O 于点D ,交BC 边于点E ,AD =5,BD =2,则DE 的长为( )A.35B.425C.225D.4510.如图,在△ABC 中,点D ,E 分别在AB ,AC 边上,DE∥BC,∠ACD=∠B.若AD =2BD ,BC =6,则线段CD 的长为( )A.2 3B.3 2C.2 6D.511.如图,在正方形ABCD 中,E ,F 分别在边AD ,CD 上,AF ,BE 相交于点G.若AE =3ED ,DF =CF ,则AGGF的值是( )A.43B.54C.65D.7612.如图所示,若△ABC 内一点P 满足∠PAC=∠PBA=∠PCB,则点P 为△ABC 的布洛卡点.三角形的布洛卡点(Brocard point)是法国数学家和数学教育家克洛尔(A.L.Crelle 1780-1855)于1816年首次发现,但他的发现并未被当时的人们所注意,1875年,布洛卡点被一个数学爱好者法国军官布洛卡(Brocard 1845-1922)重新发现,并用他的名字命名.问题:已知在等腰Rt△DEF 中,∠EDF=90°.若点Q 为Rt△DEF 的布洛卡点,DQ =1,则EQ +FQ =( )A.5B.4C.3+ 2D.2+ 2 二、填空题(每小题3分,共18分) 13.若x y =23,则x -2y y=.14.如图,在▱ABCD 中,点E 是边AD 的中点,EC 交对角线BD 于点F ,则EF∶FC 等于.15.如图,一组平行横格线,其相邻横格线间的距离都相等,已知点A ,B ,C ,D ,O 都在横格线上,且线段AD ,BC 交于点O ,则AB∶CD 等于.16.如图,点E 是▱ABCD 的边BC 延长线上一点,连接AE ,交CD 于点F ,连接BF.写出图中任意一对相似三角形:17.在▱ABCD 中,E 是AD 上一点,且点E 将AD 分为2∶3的两部分,连接BE ,AC 相交于F ,则S △AEF ∶S △CBF 是18.如图,在Rt△ABC中,∠ACB=90°,AB=10,BC=6,CD∥AB,∠ABC的平分线BD交AC于E,DE=三、解答题(共66分)19.如图,在▱ABCD中,连接对角线AC,延长AB至点E,使BE=AB,连接DE,分别交BC,AC交于点F,G.(1)求证:BF=CF;(2)若BC=6,DG=4,求FG的长.20.如图,在正方形ABCD中,点E,F分别在边AB,AD上,EF⊥CE于点E. (1)求证:△AEF∽△BCE;(2)若BEAE=12,求EFCE的值.21.如图,∠ABD=∠BCD=90°,DB平分∠ADC,过点B作BM∥CD交AD于点M,连接CM交DB于点N.(1)求证:BD2=AD·CD;(2)若CD=6,AD=8,求MN的长.22.如图,Rt△ABC中,∠ACB=90°,AC=BC,P为△ABC内部一点,且∠APB=∠BPC=135°.(1)求证:△PAB∽△PBC;(2)求证:PA=2PC;(3)若点P到三角形的边AB,BC,CA的距离分别为h1,h2,h3,求证:h21=h2h3.参考答案:一、选择题1-12 DABACBCCDCCD二、填空题13、-43 14、1∶2 15、2∶3 16、答案不唯一,如△EFC∽△AFD,△EAB∽△AFD,△EFC∽△EAB. 17、4∶25或9∶25. 18、955. 三、解答题19、解:(1)证明:∵四边形ABCD 是平行四边形, ∴AD∥BC,AD =BC. ∴△EBF∽△EAD. ∴BF AD =EB EA =12. ∴BF=12AD =12BC.∴BF=CF.(2)∵四边形ABCD 是平行四边形, ∴AD∥BC.∴△FGC∽△DGA. ∴FG DG =FC AD ,即FG 4=12. 解得FG =2.20、解:(1)∵∠A=∠B=90°,∠FEC=90°, ∴∠AEF+∠AFE=90°,∠AEF+∠BEC=90°. ∴∠AFE=∠BEC. ∴△AEF∽△BCE. (2)由BE AE =12,设BE =x ,则AE =2x ,AB =3x =BC. ∵△AEF∽△BCE,∴EF CE =AE BC =23. 21解:(1)证明:∵BD 平分∠ADC, ∴∠ADB=∠BDC.又∵∠ABD=∠BCD=90°, ∴△DAB∽△DBC.∴BD CD =ADBD,即BD 2=AD·CD. (2)由(1)可知:BD 2=AD·CD. ∵CD=6,AD =8,∴BD 2=6×8=48. ∴BC 2=BD 2-CD 2=48-36=12.∵BM∥CD,∴∠MBD=∠BDC=∠ADB,∠MBC=180°-∠BCD=90°. ∴DM=BM.∵∠ADB+∠A=∠MBD+∠MBA=90°, ∴∠A=∠MBA.∴AM=BM =DM =12AD =4.∴CM=BM 2+BC 2=16+12=27. ∵BM∥CD,∴△BMN∽△DCN.∴MN CN =BMCD.设MN =x ,则CN =27-x. 则x 27-x =46.解得x =475.经检验,x =475是原分式方程的解.∴MN=475. 22、证明:(1)∵∠ACB=90°,AC =BC , ∴∠ABC=∠PBA+∠PBC=45°. 又∵∠APB=135°,∴∠PAB+∠PBA=45°.∴∠PBC=∠PAB. 又∵∠APB=∠BPC=135°,∴△PAB∽△PBC. (2)∵△PAB∽△PBC,∴PA PB =PB PC =ABBC . 在Rt△ABC 中,BC =AC ,∴ABBC= 2. ∴PB=2PC ,PA =2PB.∴PA=2PC.(3)过点P 作PD⊥BC 于点D ,PE⊥A C 于点E ,PF⊥AB 于点F. ∴PF=h 1,PD =h 2,PE =h 3.∵∠CPB+∠APB=135°+135°=270°, ∴∠APC=90°.∴∠EAP+∠ACP=90°. 又∵∠ACB=∠ACP+∠PCD=90°, ∴∠EAP=∠PCD.∴Rt△AEP∽Rt△CDP. ∴PE DP =AP PC =2,即h 3h 2=2.∴h 3=2h 2.∵△PAB∽△PBC,∴h1h2=ABBC=2.∴h1=2h2.∴h21=2h22=2h2·h2=h2h3,即h21=h2h3.。
四川省渠县崇德实验学校2020年中考九年级数学:几何四边形 复习练习题(无答案)

四川省渠县崇德实验学校2020年中考九年级数学:几何四边形复习练习题一.选择题1.矩形具有而平行四边形不一定具有的性质是()A.对边平行且相等B.对角相等C.对角线互相平分D.对角线相等2.在正方形ABCD中,AB=1,则AC的长是()A.1 B C D.23.如图,设M是▱ABCD一边上任意一点,设△AMD的面积为S1,△BMC的面积为S2,△CDM 的面积为S,则()A.S=S1+S2B.S>S1+S2C.S<S1+S2D.不能确定4.四边形ABCD的对角线AC、BD互相平分,要使它成为矩形,需要添加的条件是()A.AB=CD B.AC=BD C.AB=BC D.AC⊥BD5.已知△ABC(如图1),按图2图3所示的尺规作图痕迹,(不需借助三角形全等)就能推出四边形ABCD是平行四边形的依据是()A.两组对边分别平行的四边形是平行四边形 B.对角线互相平分的四边形是平行四边形C.一组对边平行且相等的四边形是平行四边形 D.两组对边分别相等的四边形是平行四边形6.如图,在四边形ABCD中,AC与BD相交于点O,∠OAB=∠OAD,BO=DO,那么下列条件中不能判定四边形ABCD是菱形的为()A.OA=OC B.BC=DC C.AD=BC D.AD=DC7.若四边形的两条对角线相等且互相垂直,则顺次连接该四边形各边中点所得的四边形是()A.平行四边形B.矩形C.菱形D.正方形8.如图,四个菱形①②③④的较小内角均与已知平行四边形ABCD的∠A相等,边长各不相同.将这四个菱形如图所示放入平行四边形中,未被四个菱形覆盖的部分用阴影表示.若已知两个阴影部分的周长的差,则不需测量就能知道周长的菱形为()A.①B.②C.③D.④9.如图,在边长为2的正方形ABCD中,以BC为边作等边△BCM,连接AM并延长交CD于N,则CN的长为()A.B.C D10.如图,在矩形ABCD中,AD AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:①∠AED=∠CED;②OE=OD;③BH=HF;④BC﹣CF=2HE;⑤AB=HF.其中正确的有()A.①②③④⑤B.①②③④C.①③④⑤D.①②③⑤二.填空题11.在平行四边形ABCD中,∠A与∠B的度数之比为2:1,则∠A=°.12.如图,四边形ABCD是矩形,对角线AC、BD相交于点O,如果再添加一个条件,即可推出该四边形是正方形,这个条件可以是.13.如图,四边形ABCD是菱形,对角线AC=8cm,DB=6cm,DH⊥AB于点H,则DH的长为.14.如图,把矩形ABCD沿EF折叠,使点C落在点A处,点D落在点G处,若CD=2,AD=3,则边ED的长为.15.如图,在▱ABCD中,AC与BD交于点M,点F在AD上,AF=6cm,BF=12cm,∠FBM=∠CBM,点E是BC的中点,若点P以1cm/s秒的速度从点A出发,沿AD向点F运动;点Q同时以2cm/秒的速度从点C出发,沿CB向点B运动,点P运动到F点时停止运动,点Q也同时停止运动,当点P运动秒时,以P、Q、E、F为顶点的四边形是平行四边形.三.解答题16.如图,在▱ABCD中,点E,F分别在边BC,AD上,且AF=CE.求证:四边形AECF是平行四边形.17.如图,矩形ABCD的对角线AC、BD相交于点O,DE∥AC,CE∥BD.(1)判断四边形OCED的形状,并进行证明;(2)点E是否在AB的垂直平分线上?若在,请进行证明;若不在,请说明理由.18.如图,在四边形ABCD中,对角线AC、BD交于点O,AB∥DC,AB=BC,BD平分∠ABC,过点C作CE⊥AB交AB的延长线于点E,连接OE.(1)求证:四边形ABCD是菱形;(2)若AB=BD=4,求OE的长.19.如图,在菱形ABCD中,对角线AC,BD相交于点O,过点O作一条直线分别交DA,BC 的延长线于点E,F,连接BE,DF.(1)求证:四边形BFDE是平行四边形;(2)若EF⊥AB,垂足为M,1=2MOMB,AE=2,求菱形ABCD的边长.20.如图1,在正方形ABCD中,点E是CD上一点(不与C,D两点重合),连接BE,过点C 作CH⊥BE于点F,交对角线BD于点G,交AD边于点H,连接GE,(1)求证:△DHC≌△CEB;(2)如图2,若点E是CD的中点,当BE=8时,求线段GH的长;(3)设正方形ABCD的面积为S1,四边形DEGH的面积为S2,当CEDE的值为34时,12SS的值为.。
四川省渠县崇德实验学校中考第二轮九年级数学三角形、四边形压轴题专题复习(无答案)

四川省渠县崇德实验学校 2021年中考第二轮九年级数学三角形、四边形压轴题专题复习一、选择题1、如图,矩形ABCD 中,AB =4,AD =2,E 为AB 的中点,F 为EC 上一动点,P 为DF 中点, 连接PB ,那么PB 的最小值是〔 〕A .2B .4C . 2D .2 22、如图,在Rt△ABO 中,∠OBA=90°,A(4,4),点C 在边AB 上,且AC=1,点D 为BC 3OB 的中点,点P 为边OA 上的动点,当点 P 在OA 上移动时,使四边形 PDBC 周长最小的点 P 的坐标为〔〕A .(2,2)B .(5,5)C .(8,8)D .(3,3)2 23 33、如图,正方形 ABCD ,点F 在边AB 上,且AF :FB =1:2,CE ⊥DF ,垂足为 M ,且交AD 于点E ,AC 与DF 交于点N ,延长CB 至G ,使BG =1BC ,连接GM .有如下结论:①DE =22 AF ;②AN =AB ;③∠ADF =∠GMF ;④S △ANF :S 四边形CNFB =1:8.上述结论中,所有正4确结论的序号是〔 〕A.①②B.①③C.①②③D.②③④二、填空题4、在矩形 ABCD中,M,N,P,Q分别为边AB,BC,CD,DA上的点〔不与端点重合〕.对于任意矩形ABCD,下面四个结论中,①存在无数个四边形MNPQ是平行四边形;②存在无数个四边形MNPQ是矩形;③存在无数个四边形MNPQ是菱形;④至少存在一个四边形MNPQ是正方形.所有正确结论的序号是______5、如图,一个正方体由27个大小相同的小立方块搭成,现从中取走假设干个小立方块,得到一个新的几何体.假设新几何体与原正方体的外表积相等,那么最多可以取走个小立方块.6、如图,?ABCD的对角线AC,BD交于点O,CE平分∠BCD交AB于点E,交BD于点F,且∠ABC=60°,AB=2BC,连接OE.以下结论:①EO⊥AC;②S△AOD=4S△OCF;③AC:BD=:7;④FB2=OF?DF.其中正确的结论有〔填写所有正确结论的序号〕7、如图,在以A为直角顶点的等腰直角三角形纸片ABC中,将B角折起,使点B落在AC边上的点D〔不与点A,C重合〕处,折痕是EF.如图1,当CD=1AC时,tanα1=3;如图2,当CD=1AC时,tanα2=5;24312如图3,当CD=137;依此类推,当CD=14AC时,tanα=24AC〔n为正整数〕时,n+1tanαn=.8、在平面直角坐标系中,直线l:y=x+1与y轴交于点A1,如下图,依次作正方形OA1B1C1,正方形C1A2B2C2,正方形C2A3B3C3,正方形C3A4B4C4,,点A1,A2,A3,A4,在直线l上,点C1,C2,C3,C4,在x轴正半轴上,那么前n个正方形对角线长的和是.三、解答题9、如图1,正方形ABDE和BCFG的边AB,BC在同一条直线上,且AB=2BC,取EF的中点M,连接MD,MG,MB.〔1〕试证明DM⊥MG,并求MB的值.MG〔2〕如图2,将图1中的正方形变为菱形,设∠EAB=2α〔0<α<90°〕,其它条件不变,问〔1〕中MB的值有变化吗?假设有变化,求出该值〔用含α的式子表示〕;假设无变化,说MG明理由.10、【问题探究】〔1〕如图1,△ABC和△DEC均为等腰直角三角形,∠ACB=∠DCE=90°,点B,D,E在同一直线上,连接AD,BD.①请探究AD与BD之间的位置关系:;②假设AC=BC=,DC=CE=,那么线段AD的长为;【拓展延伸】〔2〕如图2,△ABC和△DEC均为直角三角形,∠ACB=∠DCE=90°,AC=,BC=,CD=,CE=1.将△DCE绕点C在平面内顺时针旋转,设旋转角∠BCD为α〔0°≤α<360°〕,作直线BD,连接AD,当点B,D,E在同一直线上时,画出图形,并求线段AD的长.11、如图,在正方形E点ABCD中,AB=10cm,E为对角线BD上一动点,连接AE,CE,过作EF⊥AE,交直线BC于点F.E点从B点出发,沿着BD方向以每秒2cm的速度运动,当点E与点D重合时,运动停止.设△BEF的面积为ycm2,E点的运动时间为x秒.〔1〕求证:CE=EF;〔2〕求y与x之间关系的函数表达式,并写出自变量x的取值范围;〔3〕求△BEF面积的最大值.12、在△ABC中,∠BAC=90°,AB=AC,AD⊥BC于点D.1〕如图1,点M,N分别在AD,AB上,且∠BMN=90°,当∠AMN=30°,AB=2时,求线段AM的长;2〕如图2,点E,F分别在AB,AC上,且∠EDF=90°,求证:BE=AF;3〕如图3,点M在AD的延长线上,点N在AC上,且∠BMN=90°,求证:AB+AN=AM.13、如图,四边形ABCD是正方形,△EFC是等腰直角三角形,点E在AB上,且∠CEF=90°,FG⊥AD,垂足为点C.1〕试判断AG与FG是否相等?并给出证明;(2〕假设点H为CF的中点,GH与DH垂直吗?假设垂直,给出证明;假设不垂直,说明理由.ABCD中,AB∥CD,∠ACB=90°,AB=10cm,BC=8cm,OD14、:如图,在四边形垂直平分 A C.点P从点B出发,沿BA方向匀速运动,速度为1cm/s;同时,点Q从点D出发,沿DC方向匀速运动,速度为1cm/s;当一个点停止运动,另一个点也停止运动.过点P作PE⊥AB,交BC于点E,过点Q作QF∥AC,分别交AD,OD于点F,G.连接OP,EG.设运动时间为t〔s〕〔0<t<5〕,解答以下问题:1〕当t为何值时,点E在∠BAC的平分线上?(2〕设四边形PEGO的面积为S〔cm2〕,求S与t的函数关系式;〔3〕在运动过程中,是否存在某一时刻t,使四边形PEGO的面积最大?假设存在,求t的出值;假设不存在,请说明理由;〔4〕连接OE,OQ,在运动过程中,是否存在某一时刻t,使OE⊥OQ?假设存在,求t的出值;假设不存在,请说明理由.15、如图1,在矩形ABCD中,AB=8,AD=10,E是CD边上一点,连接AE,将矩形ABCD 沿AE折叠,顶点D恰好落在BC边上点F处,延长AE交BC的延长线于点G.〔1〕求线段CE的长;2〕如图2,M,N分别是线段AG,DG上的动点〔与端点不重合〕,且∠DMN=∠DAM,设AM=x,DN=y.①写出y关于x的函数解析式,并求出y的最小值;②是否存在这样的点M,使△DMN是等腰三角形?假设存在,请求出x的值;假设不存在,请说明理由.16、如图,△ABC和△ADE是有公共顶点的等腰直角三角形,∠BAC=∠DAE=90°.〔1〕如图1,连接BE,CD,BE的廷长线交AC于点F,交CD于点P,求证:BP⊥CD;〔2〕如图2,把△ADE绕点A顺时针旋转,当点D落在AB上时,连接BE,CD,CD的延长线交BE于点P,假设BC=6,AD=3,求△PDE的面积.17、如图1,菱形AEGH的顶点E、H在菱形ABCD的边上,且∠BAD=60°,请直接写出HD:GC:EB的结果〔不必写计算过程〕〔2〕将图1中的菱形AEGH绕点A旋转一定角度,如图2,求HD:GC:EB;〔3〕把图2中的菱形都换成矩形,如图3,且AD:AB=AH:AE=1:2,此时HD:GC:EB的结果与〔2〕小题的结果相比有变化吗?如果有变化,直接写出变化后的结果〔不必写计算过程〕;假设无变化,请说明理由.18、问题提出:如图,图①是一张由三个边长为1的小正方形组成的“L〞形纸片,图②是一张a×b的方格纸〔a×b的方格纸指边长分别为a,b的矩形,被分成a×b个边长为1的小正方形,其中a≥2,b≥2,且a,b为正整数〕.把图①放置在图②中,使它恰好盖住图②中的三个小正方形,共有多少种不同的放置方法?问题探究:为探究规律,我们采用一般问题特殊化的策略,先从最简单的情形入手,再逐次递进,最后得出一般性的结论.探究一:把图①放置在2×2的方格纸中,使它恰好盖住其中的三个小正方形,共有多少种不同的放置方法?如图③,对于2×2的方格纸,要用图①盖住其中的三个小正方形,显然有4种不同的放置方法.探究二:把图①放置在3×2的方格纸中,使它恰好盖住其中的三个小正方形,共有多少种不同的放置方法?如图④,在3×2的方格纸中,共可以找到2个位置不同的22×方格,依据探究一的结论可知,把图①放置在3×2的方格纸中,使它恰好盖住其中的三个小正方形,共有2×4=8种不同的放置方法.探究三:把图①放置在a×2的方格纸中,使它恰好盖住其中的三个小正方形,共有多少种不同的放置方法?如图⑤,在a×2的方格纸中,共可以找到个位置不同的2×2方格,依据探究一的结论可知,把图①放置在a×2的方格纸中,使它恰好盖住其中的三个小正方形,共有种不同的放置方法.探究四:把图①放置在a×3的方格纸中,使它恰好盖住其中的三个小正方形,共有多少种不同的放置方法?如图⑥,在a×3的方格纸中,共可以找到个位置不同的2×2方格,依据探究一的结论可知,把图①放置在a×3的方格纸中,使它恰好盖住其中的三个小正方形,共有种不同的放置方法.问题解决:把图①放置在a×b的方格纸中,使它恰好盖住其中的三个小正方形,置共有多少种不同的放方法?〔仿照前面的探究方法,写出解答过程,不需画图.〕问题拓展:如图,图⑦是一个由4个棱长为1的小立方体构成的几何体,图⑧是一个长、宽、高分别为a,b,c〔a≥2,b≥2,c≥2,且a,b,c是正整数〕的长方体,被分成了a×b×c个棱长为1的小立方体.在图⑧的不同位置共可以找到个图⑦这样的几何体.四川省渠县崇德实验学校中考第二轮九年级数学三角形、四边形压轴题专题复习(无答案)11 / 111119、如图1,菱形ABCD 的顶点A ,D 在直线上,∠BAD =60°,以点A 为旋转中心将菱形ABCD 顺时针旋转α〔0°<α<30°〕,得到菱形AB ′C ′D ′,B ′C ′交对角线AC 于点M ,C ′D ′交直线l 于点N ,连接MN .1〕当MN ∥B ′D ′时,求α的大小.2〕如图2,对角线B ′D ′交AC 于点H ,交直线l 与点G ,延长C ′B ′交AB 于点E ,连接EH .当△HEB ′的周长为2时,求菱形ABCD 的周长.20、如图,在正方形DM 边分别与射线ABCDBA 、直线中,边长为 4,∠MDNAC 交于E 、Q 两点,=90°,将∠DN 边与射线MDN 绕点BC 交于点D 旋转,其中F ;连接EF ,且EF 与直线AC交于点P .1〕如图1,点E 在线段AB 上时,①求证:AE =CF ;②求证:DP 垂直平分EF ;2〕当AE =1时,求PQ 的长.。
四川省渠县崇德实验学校2020年九年级中考数学备战:和切线有关压轴题复习(无答案,Word版)
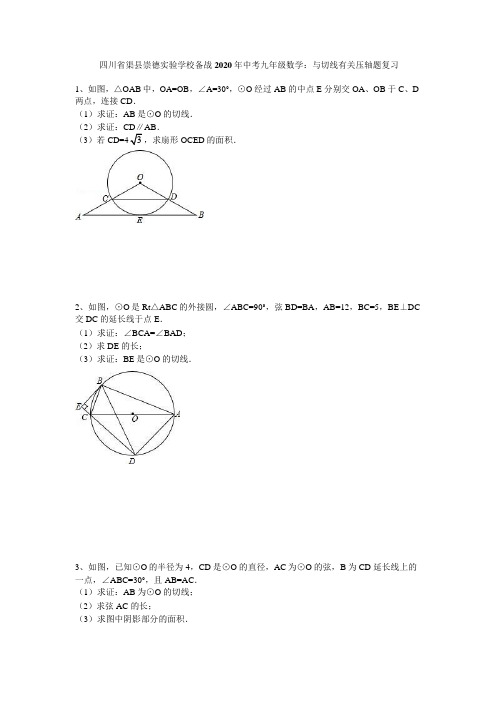
四川省渠县崇德实验学校备战2020 年中考九年级数学:与切线有关压轴题复习1、如图,△OAB 中,OA=OB,∠A=30°,⊙O 经过AB 的中点E 分别交OA、OB 于C、D 两点,连接CD.(1)求证:AB 是⊙O 的切线.(2)求证:CD∥AB.(3)若CD=4,求扇形OCED 的面积.2、如图,⊙O 是Rt△ABC 的外接圆,∠ABC=90°,弦BD=BA,AB=12,BC=5,BE⊥DC 交DC 的延长线于点E.(1)求证:∠BCA=∠BAD;(2)求DE 的长;(3)求证:BE 是⊙O 的切线.3、如图,已知⊙O 的半径为4,CD 是⊙O 的直径,AC 为⊙O 的弦,B 为CD 延长线上的一点,∠ABC=30°,且AB=AC.(1)求证:AB 为⊙O 的切线;(2)求弦AC 的长;(3)求图中阴影部分的面积.4、如图,已知⊙O 是等腰直角三角形ADE 的外接圆,∠ADE=90°,延长ED 到C 使DC=AD,以AD,DC 为邻边作正方形ABCD,连接AC,连接BE 交AC 于点H.求证:(1)AC 是⊙O 的切线.(2)HC=2AH.5、如图,在△ABC 中,AB=AC,以AB 为直径的圆O 交BC 于点D,交AC 于点E,过点D 作DF⊥AC,垂足为F.(1)求证:DF 为⊙O 的切线;(2)若过A 点且与BC 平行的直线交BE 的延长线于G 点,连接CG.当△ABC 是等边三角形时,求∠AGC 的度数.6、如图,⊙O 是△ABC 的外接圆,AC 是直径,过点O 作OD⊥AB 于点D,延长DO 交⊙O 于点P,过点P 作PE⊥AC 于点E,作射线DE 交BC 的延长线于F 点,连接PF.(1)若∠POC=60°,AC=12,求劣弧PC 的长;(结果保留π)(2)求证:OD=OE;(3)求证:PF 是⊙O 的切线.7、如图,AB、AC 分别是⊙O 的直径和弦,点D 为劣弧AC 上一点,弦DE⊥AB 分别交⊙O 于E,交AB 于H,交AC 于F.P 是ED 延长线上一点且PC=PF.(1)求证:PC 是⊙O 的切线;(2)点D 在劣弧AC 什么位置时,才能使AD2=DE•DF,为什么?(3)在(2)的条件下,若OH=1,AH=2,求弦AC 的长.8、如图所示,AB 是⊙O 的直径,AE 是弦,C 是劣弧AE 的中点,过C 作CD⊥AB 于点D,CD 交AE 于点F,过C 作CG∥AE 交BA 的延长线于点G.(1)求证:CG 是⊙O 的切线.(2)求证:AF=CF.(3)若∠EAB=30°,CF=2,求GA 的长.9、如图,⊙O 是△ABC 的外接圆,BD 为圆O 的直径,AB=AC,AD 交BC 于E,ED=2AE.(1)求证:AB2=AD•AE;(2)求∠ADB 的度数;(3)延长DB 到F,使BF=BO,连接FA.求证:直线FA 为⊙O 的切线.10、如图,直线AB 经过⊙O 上的点C,并且OA=OB,CA=CB,⊙O 交直线OB 于E,D,连接EC,CD.(1)求证:直线AB 是⊙O 的切线;(2)试猜想BC,BD,BE 三者之间的等量关系,并加以证明;(3)若tan∠CED=12,⊙O 的半径为3,求OA 的长.11、已知△ABC 内接于⊙O,过点A 作直线EF.(1)如图①所示,若AB 为⊙O 的直径,要使EF 成为⊙O 的切线,还需要添加的一个条件是(至少说出两种):或者.(2)如图②所示,如果AB 是不过圆心O 的弦,且∠CAE=∠B,那么EF 是⊙O 的切线吗?试证明你的判断.12、如图,在△ABC 中,∠BAC=90°,AB=AC,AB 是⊙O 的直径,⊙O 交BC 于点D,DE⊥AC 于点E,BE 交⊙O 于点F,连接AF,AF 的延长线交DE 于点P.(1)求证:DE 是⊙O 的切线;(2)求tan∠ABE 的值;(3)若OA=2,求线段AP 的长.13、如图,在△ABC 中,∠ABC=90°,D 是边AC 上的一点,连接BD,使∠A=2∠1,E 是BC 上的一点,以BE 为直径的⊙O 经过点D.(1)求证:AC 是⊙O 的切线;(2)若∠A=60°,⊙O 的半径为2,求阴影部分的面积.(结果保留根号和π)14、如图,在△ABC 中,∠ABC=90°,以AB 的中点O 为圆心、OA 为半径的圆交AC 于点D,E 是BC 的中点,连接DE,OE.(1)判断DE 与⊙O 的位置关系,并说明理由;(2)求证:BC2=CD•2OE;(3)若cos∠BAD=35,BE=6,求OE 的长.15、如图,在平面直角坐标系,A,B 两点的坐标分别为(0,﹣2),(0,8),以AB 为一边作正方形ABCD,再以CD 为直径的半圆P.设x 轴交半圆P 于点E,交边CD 于点F.(1)求线段EF 的长;(2)连接BE,试判断直线B 与⊙P 的位置关系,并说明你的理由;(3)直线BE 上是否存在着点Q,使得以Q 为圆心、r 为半径的圆,既与y 轴相切又与⊙P 外切?若存在,试求r 的值;若不存在,请说明理由.16、如图,△ABC 内接于半圆,AB 为直径,过点A 作直线MN,若∠MAC=∠ABC.(1)求证:MN 是半圆的切线.(2)设D 是弧AC 的中点,连接BD 交AC 于G,过D 作DE⊥AB 于E,交AC 于F,求证:FD=FG.(3)在(2)的条件下,若△DFG 的面积为4.5,且DG=3,GC=4,试求△BCG 的面积.17、如图,在平面直角坐标系中,直线l:y=﹣2x﹣8 分别与x 轴,y 轴相交于A,B 两点,点P(0,k)是y 轴的负半轴上的一个动点,以P 为圆心,3 为半径作⊙P.(1)连接PA,若PA=PB,试判断⊙P 与x 轴的位置关系,并说明理由;(2)当k 为何值时,以⊙P 与直线l 的两个交点和圆心P 为顶点的三角形是正三角形.18、如图所示,扇形OAB 的半径OA=r,圆心角∠AOB=90°,点C 是上异于A、B 的动点,过点C 作CD⊥OA 于点D,作CE⊥OB 于点E,点M 在DE 上,DM=2EM,过点C 的直线PC 交OA 的延长线于点P,且∠CPD=∠CDE.(1)求证:DM=23r;(2)求证:直线PC 是扇形OAB 所在圆的切线;(3)设y=CD2+3CM2,当∠CPO=60°时,请求出y 关于r 的函数关系式.19、已知四边形ABCD 内接于⊙O,∠ADC=90°,∠DCB<90°,对角线AC 平分∠DCB,延长DA,CB 相交于点E.(1)如图1,EB=AD,求证:△ABE 是等腰直角三角形;(2)如图2,连接OE,过点E 作直线EF,使得∠OEF=30°,当∠ACE≥30°时,判断直线EF 与⊙O 的位置关系,并说明理由.20、如图,在直角坐标系xoy 中,O 是坐标原点,点A 在x 正半轴上,,点B在y 轴的正半轴上,OB=12cm,动点P 从点O 开始沿OA 以cm/s 的速度向点A 移动,动点Q 从点A 开始沿AB 以4cm/s 的速度向点B 移动,动点R 从点B 开始沿BO 以2cm/s 的速度向点O 移动.如果P、Q、R 分别从O、A、B 同时移动,移动时间为t(0<t<6)s.(1)求∠OAB 的度数.(2)以OB 为直径的⊙O′与AB 交于点M,当t 为何值时,PM 与⊙O′相切?(3)写出△PQR 的面积S 随动点移动时间t 的函数关系式,并求s 的最小值及相应的t 值.(4)是否存在△APQ 为等腰三角形?若存在,求出相应的t 值;若不存在请说明理由.。
四川省渠县崇德实验 学校2020年中考九年级数学专题复习:图形和坐标练习题(无答案)

四川省渠县崇德实验 学校2020年中考九年级数学专题复习:图形与坐标练习题一、选择题(本题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的) 1.若点P (m ,2+m )的横坐标与纵坐标互为相反数,则点P 一定在( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限 2.已知点P (-2,5),Q (n ,5)且PQ =4,则n 的值为( ) A .2 B .2或4 C .2或-6 D .-63.在平面直角坐标系中,点A (0,2),B (4,0),点N 为线段AB 的中点,则点N 的坐标为( ) A .(1,2) B .(4,2) C .(2,4) D .(2,1)4.小明和小丽下棋,小明执白子,小丽执黑子,如图是在直角坐标系中棋子摆出的图案,若再摆放一白一黑两枚棋子,使9枚棋子组成的图案既是轴对称图形又是中心对称图形,则这两枚棋子的坐标分别是( ) A .黑子(2,3),白子(1,3) B .黑子(1,3),白子(2,3) C .黑子(2,3),白子(4,0) D .黑子(4,0),白子(2,3)5.若点A 位于x 轴上方,到x 轴的距离为2,到y 轴的距离为5,则 点A 坐标为( )A .(2,5)B .(5,2)或(-5,2)C .(5,2)D .(2,5)或(-2,5)6.已知点A (2m -2,m 5+4)在第一象限角平分线上,则m 的值为( ) A .6 B .-1 C .2或3 D .-1或67.如图,ABO Rt ∆和CBD Rt ∆中,=∠=∠CBD ABO 90°,若=∠CBA 60°,BD BO =,点A 坐标为(32,-2)则点C 的坐标是( )A .(2,32)B .(1,3)C .(3,1)D .(32,2) 8.如图,⊙1O 与x 轴相交于点A (2,0),B (8,0),与y 轴相切于点C ,则圆心1O 的坐标是( )A .(3,5)B .(5,3)C .(4,5)D .(5,4)9.如图,在ABC ∆中,ACB ∠=90°,AC =2,BC =1,点A 和点C 分别在x 轴和y 轴上,当点A 在x 轴正半轴上运动时,点C 随之在y 轴正半轴上运动,在运动过程中,点B 到原点O 的最大距离为( )A .5B .6C .1+2D .310.若A (-2,0),B (1,2),点P 为直线y =4上一动点,且PAB ∆的面积为6,则点P 的坐标为( )A .(-2,4)B .(0,4)或(10,4)C .(9,4)D .(-2,4)或(10,4) 二、填空题(本题共6小题,每小题4分,共24分)11.在电影票上如果将“8排4号”记作(8,4),那么“3排5号”记作_______. 12.直角坐标平面内有两点A (-3,1)和B (3,-1),则A 和B 两点间的距离等于_______. 13.点A (a ,5)和点B (3,b )关于y 轴对称,则b a +=_______.14.线段CD 是由线段AB 平移得到的,点A (-1,-4)的对应点为C (3,0),则点B (-3,1)的对应点D 的坐标是_______.第8题图15.如图,过点A (-3,4)的直线l ∥x 轴,OA =5,点B 在x 轴的正半轴上,OC 平分AOB ∠ 交l 于点C ,则点C 的坐标是_______.16.如图,1A ,2A ,3A ,4A ,…,n A ,1+n A 是直线1l :x y 3=上的点,且===32211A A A A OA …21=+n n A A ,分别过点1A ,2A ,3A ,4A ,…,n A ,1+n A 作1l 的垂线与直线2l :x y 33=相交于点1B ,2B ,3B ,4B …,n B ,1+n B ,连接21B A ,21A B ,32B A ,32A B ,…,1+n n B A ,1+n n A B ,交点依次为1P ,2P ,3P ,4P ,…,n P ,设211A A P ∆,322A A P ∆,433A A P ∆,…,1+∆n n n A A P 的面积分别为1S ,2S ,3S ,…,n S ,则n S =__________. 三、解答题(第17题8分,第18题10分,共18分)17.直线3+=kx y 和x 轴,y 轴的交点分别为B ,C ,点A (3-,0),OBC ∠=30°,另一条直线经过点A ,C .(1)求点B 的坐标及k 的值; (2)求证:BC AC ⊥.18.如图,在平面直角坐标系中,ABC ∆的顶点坐标分别是A (0,1),B (1,3),C (4,3). (1)将ABC ∆平移得到111C B A ∆,且1C 的坐标是(0,-1),画出111C B A ∆; (2)将ABC ∆绕点A 逆时针旋转90°得到222C B A ∆,画出222C B A ∆,写出的2C 坐标.四、解答题(第19题10分,第20题10分,共20分)19.如图,直线4+=kx y 与x 轴和y 轴分别相交于点B 和点C ,且点B (8,0).若点A 的坐标为(6,0),点P (x ,y )是该直线在第一象限上的一个动点.(1)求k的值;(2)在点P运动的过程中,求出POA∆的面积S与x的函数关系式;(3)若POA∆的面积是6,求点P的坐标.y=,经过A(2,4),xAB⊥轴于点B.(1)求该正比例函数的解析式;(2)将ABO∆绕点A逆时针旋转90°,得到ADC∆,求点C的坐标.五、解答题(第21题10分,第22题10分,共20分)21.如图,点A的坐标为(1,0),点B在y轴上,将OAB∆沿x轴负方向平移,平移后的图形为DEC∆,且点C的坐标为(-3,2).(1)直接写出点E的坐标;(2)在四边形ABCD中,点P从点B出发,沿BC→CD移动,若点P的速度为每秒1个单位长度,运动时间为t秒,回答下列问题:①t=_______秒时,点P的横坐标与纵坐标互为相反数;②用含有t的式子表示点P的坐标.22.如图,在平面直角坐标系中,等边OAB ∆的一条边OB 在x 轴的正半轴上,点A 在双曲线xky =(k ≠0)上,其中点B 为(2,0). (1)求k 的值及点A 的坐标;(2)OAB ∆沿直线OA 平移,当点B 恰好在双曲线上时,求平移后点B 的对应点1B 的坐标.六、解答题(满分12分)23.如图,在平面直角坐标系中,四边形OABC 为菱形,点C 的坐标为(4,0),AOC ∠=60°,垂直于x 轴的直线l 从y 轴出发,沿x 轴正方向以每秒1个单位长度的速度运动,设直线l 与菱形OABC 的两边分别交于点M 和点N (点M 在点N 的上方). (1)求A ,B 两点的坐标;(2)设OMN ∆的面积为S ,直线l 运动时间为t (0≤t ≤6)秒,试求S 与t 的函数表达式.七、解答题(满分12分)24.在平面直角坐标系中,A(-2,0),点B在y轴负半轴上,以点A为顶点,AB为腰,在x轴下方作等腰ABCRt∆.(1)如图①,若OB=4且点C在第三象限,求点C的坐标;(2)如图②,若点C在第四象限且xOB-的值;CE⊥轴于点E,求CE(3)如图③,点P(-2,-2),点M(0,m)在y轴负半轴上,点N(n,0)在x轴正半轴上,且PNm+的值.PM⊥,请直接写出n八、解答题(满分14分)25.如图,在平面直角坐标系中,抛物线c=2与x轴交于A,B两点,与y轴交于点C,+xbxy+对称轴为直线x=2,点A的坐标为(1,0).(1)求该抛物线的表达式及顶点坐标;(2)点D为抛物线上一点(不与点A重合),连接CD.当ACB∠时,求点D的坐标;=DCB∠(3)在对称轴上是否存在点P,使以P,B,C三点为顶点的三角形是直角三角形,若存在,请直接写出点P的坐标;若不存在,请说明理由.备用图。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
四川省渠县崇德实验学校2020年中考第二轮九年级数学三角形、四边形压轴题专题复习一、选择题1、如图,矩形ABCD中,AB=4,AD=2,E为AB的中点,F为EC上一动点,P为DF中点,连接PB,则PB的最小值是()A.2B.4C D.2、如图,在Rt△ABO中,∠OBA=90°,A(4,4),点C在边AB上,且ACBC=13,点D为OB的中点,点P为边OA上的动点,当点P在OA上移动时,使四边形PDBC周长最小的点P的坐标为()A.(2,2) B.(52,52) C.(83,83) D.(3,3)3、如图,正方形ABCD,点F在边AB上,且AF:FB=1:2,CE⊥DF,垂足为M,且交AD于点E,AC与DF交于点N,延长CB至G,使BG=12BC,连接GM.有如下结论:①DE=AF;②AN=4AB;③∠ADF=∠GMF;④S△ANF:S四边形CNFB=1:8.上述结论中,所有正确结论的序号是()A.①②B.①③C.①②③D.②③④二、填空题4、在矩形ABCD中,M,N,P,Q分别为边AB,BC,CD,DA上的点(不与端点重合).对于任意矩形ABCD,下面四个结论中,①存在无数个四边形MNPQ是平行四边形;②存在无数个四边形MNPQ是矩形;③存在无数个四边形MNPQ是菱形;④至少存在一个四边形MNPQ是正方形.所有正确结论的序号是______5、如图,一个正方体由27个大小相同的小立方块搭成,现从中取走若干个小立方块,得到一个新的几何体.若新几何体与原正方体的表面积相等,则最多可以取走个小立方块.6、如图,▱ABCD的对角线AC,BD交于点O,CE平分∠BCD交AB于点E,交BD于点F,且∠ABC=60°,AB=2BC,连接OE.下列结论:①EO⊥AC;②S△AOD=4S△OCF;③AC:BD=:7;④FB2=OF•DF.其中正确的结论有(填写所有正确结论的序号)7、如图,在以A为直角顶点的等腰直角三角形纸片ABC中,将B角折起,使点B落在AC 边上的点D(不与点A,C重合)处,折痕是EF.如图1,当CD=12AC时,tanα1=34;如图2,当CD=13AC时,tanα2=512;如图3,当CD=14AC时,tanα3=724;…依此类推,当CD=1n1+AC(n为正整数)时,tanαn=.8、在平面直角坐标系中,直线l:y=x+1与y轴交于点A1,如图所示,依次作正方形OA1B1C1,正方形C1A2B2C2,正方形C2A3B3C3,正方形C3A4B4C4,……,点A1,A2,A3,A4,……在直线l上,点C1,C2,C3,C4,……在x轴正半轴上,则前n个正方形对角线长的和是.三、解答题9、如图1,正方形ABDE和BCFG的边AB,BC在同一条直线上,且AB=2BC,取EF的中点M,连接MD,MG,MB.(1)试证明DM⊥MG,并求MBMG的值.(2)如图2,将图1中的正方形变为菱形,设∠EAB=2α(0<α<90°),其它条件不变,问(1)中MBMG的值有变化吗?若有变化,求出该值(用含α的式子表示);若无变化,说明理由.10、【问题探究】(1)如图1,△ABC和△DEC均为等腰直角三角形,∠ACB=∠DCE=90°,点B,D,E在同一直线上,连接AD,BD.①请探究AD与BD之间的位置关系:;②若AC=BC=,DC=CE=,则线段AD的长为;【拓展延伸】(2)如图2,△ABC和△DEC均为直角三角形,∠ACB=∠DCE=90°,AC=,BC=,CD=,CE=1.将△DCE绕点C在平面内顺时针旋转,设旋转角∠BCD为α(0°≤α<360°),作直线BD,连接AD,当点B,D,E在同一直线上时,画出图形,并求线段AD的长.11、如图,在正方形ABCD中,AB=10cm,E为对角线BD上一动点,连接AE,CE,过E点作EF⊥AE,交直线BC于点F.E点从B点出发,沿着BD方向以每秒2cm的速度运动,当点E与点D重合时,运动停止.设△BEF的面积为ycm2,E点的运动时间为x秒.(1)求证:CE=EF;(2)求y与x之间关系的函数表达式,并写出自变量x的取值范围;(3)求△BEF面积的最大值.12、在△ABC中,∠BAC=90°,AB=AC,AD⊥BC于点D.(1)如图1,点M,N分别在AD,AB上,且∠BMN=90°,当∠AMN=30°,AB=2时,求线段AM的长;(2)如图2,点E,F分别在AB,AC上,且∠EDF=90°,求证:BE=AF;(3)如图3,点M在AD的延长线上,点N在AC上,且∠BMN=90°,求证:AB+AN=AM.13、如图,四边形ABCD是正方形,△EFC是等腰直角三角形,点E在AB上,且∠CEF=90°,FG⊥AD,垂足为点C.(1)试判断AG与FG是否相等?并给出证明;(2)若点H为CF的中点,GH与DH垂直吗?若垂直,给出证明;若不垂直,说明理由.14、已知:如图,在四边形ABCD中,AB∥CD,∠ACB=90°,AB=10cm,BC=8cm,OD 垂直平分A C.点P从点B出发,沿BA方向匀速运动,速度为1cm/s;同时,点Q从点D 出发,沿DC方向匀速运动,速度为1cm/s;当一个点停止运动,另一个点也停止运动.过点P作PE⊥AB,交BC于点E,过点Q作QF∥AC,分别交AD,OD于点F,G.连接OP,EG.设运动时间为t(s)(0<t<5),解答下列问题:(1)当t为何值时,点E在∠BAC的平分线上?(2)设四边形PEGO的面积为S(cm2),求S与t的函数关系式;(3)在运动过程中,是否存在某一时刻t,使四边形PEGO的面积最大?若存在,求出t的值;若不存在,请说明理由;(4)连接OE,OQ,在运动过程中,是否存在某一时刻t,使OE⊥OQ?若存在,求出t的值;若不存在,请说明理由.15、如图1,在矩形ABCD中,AB=8,AD=10,E是CD边上一点,连接AE,将矩形ABCD 沿AE折叠,顶点D恰好落在BC边上点F处,延长AE交BC的延长线于点G.(1)求线段CE的长;(2)如图2,M,N分别是线段AG,DG上的动点(与端点不重合),且∠DMN=∠DAM,设AM=x,DN=y.①写出y关于x的函数解析式,并求出y的最小值;②是否存在这样的点M,使△DMN是等腰三角形?若存在,请求出x的值;若不存在,请说明理由.16、如图,△ABC和△ADE是有公共顶点的等腰直角三角形,∠BAC=∠DAE=90°.(1)如图1,连接BE,CD,BE的廷长线交AC于点F,交CD于点P,求证:BP⊥CD;(2)如图2,把△ADE绕点A顺时针旋转,当点D落在AB上时,连接BE,CD,CD的延长线交BE于点P,若BC=6,AD=3,求△PDE的面积.17、如图1,菱形AEGH的顶点E、H在菱形ABCD的边上,且∠BAD=60°,请直接写出HD:GC:EB的结果(不必写计算过程)(2)将图1中的菱形AEGH绕点A旋转一定角度,如图2,求HD:GC:EB;(3)把图2中的菱形都换成矩形,如图3,且AD:AB=AH:AE=1:2,此时HD:GC:EB 的结果与(2)小题的结果相比有变化吗?如果有变化,直接写出变化后的结果(不必写计算过程);若无变化,请说明理由.18、问题提出:如图,图①是一张由三个边长为1的小正方形组成的“L”形纸片,图②是一张a×b的方格纸(a×b的方格纸指边长分别为a,b的矩形,被分成a×b个边长为1的小正方形,其中a≥2,b≥2,且a,b为正整数).把图①放置在图②中,使它恰好盖住图②中的三个小正方形,共有多少种不同的放置方法?问题探究:为探究规律,我们采用一般问题特殊化的策略,先从最简单的情形入手,再逐次递进,最后得出一般性的结论.探究一:把图①放置在2×2的方格纸中,使它恰好盖住其中的三个小正方形,共有多少种不同的放置方法?如图③,对于2×2的方格纸,要用图①盖住其中的三个小正方形,显然有4种不同的放置方法.探究二:把图①放置在3×2的方格纸中,使它恰好盖住其中的三个小正方形,共有多少种不同的放置方法?如图④,在3×2的方格纸中,共可以找到2个位置不同的2 2×方格,依据探究一的结论可知,把图①放置在3×2的方格纸中,使它恰好盖住其中的三个小正方形,共有2×4=8种不同的放置方法.探究三:把图①放置在a×2的方格纸中,使它恰好盖住其中的三个小正方形,共有多少种不同的放置方法?如图⑤,在a×2的方格纸中,共可以找到个位置不同的2×2方格,依据探究一的结论可知,把图①放置在a×2的方格纸中,使它恰好盖住其中的三个小正方形,共有种不同的放置方法.探究四:把图①放置在a×3的方格纸中,使它恰好盖住其中的三个小正方形,共有多少种不同的放置方法?如图⑥,在a×3的方格纸中,共可以找到个位置不同的2×2方格,依据探究一的结论可知,把图①放置在a×3的方格纸中,使它恰好盖住其中的三个小正方形,共有种不同的放置方法.……问题解决:把图①放置在a×b的方格纸中,使它恰好盖住其中的三个小正方形,共有多少种不同的放置方法?(仿照前面的探究方法,写出解答过程,不需画图.)问题拓展:如图,图⑦是一个由4个棱长为1的小立方体构成的几何体,图⑧是一个长、宽、高分别为a,b,c(a≥2,b≥2,c≥2,且a,b,c是正整数)的长方体,被分成了a×b×c个棱长为1的小立方体.在图⑧的不同位置共可以找到个图⑦这样的几何体.19、如图1,菱形ABCD的顶点A,D在直线上,∠BAD=60°,以点A为旋转中心将菱形ABCD顺时针旋转α(0°<α<30°),得到菱形AB′C′D′,B′C′交对角线AC于点M,C′D′交直线l于点N,连接MN.(1)当MN∥B′D′时,求α的大小.(2)如图2,对角线B′D′交AC于点H,交直线l与点G,延长C′B′交AB于点E,连接EH.当△HEB′的周长为2时,求菱形ABCD的周长.20、如图,在正方形ABCD中,边长为4,∠MDN=90°,将∠MDN绕点D旋转,其中DM边分别与射线BA、直线AC交于E、Q两点,DN边与射线BC交于点F;连接EF,且EF与直线AC交于点P.(1)如图1,点E在线段AB上时,①求证:AE=CF;②求证:DP垂直平分EF;(2)当AE=1时,求PQ的长.。
