第十五章光的偏振
(物理光学)第十五章_光的偏振和晶体光学基础-5
O
1 2 cos , sin 2 2 G= 1 sin 2 , sin 2 2
检偏器透光轴与x’轴夹角 是,其琼斯矩阵为:
1 2 1 2 cos , sin 2 A cos A sin 2 2 A1 1 2 2 E出 GE入= A iA 1 2 sin 2 , sin 2 2 1 sin 2 iA2 sin 2 2
2、偏振分光镜与/4片组合
Io/4
Io Io/2 普通分光镜
Io/2 Io Io Io 偏振分光镜
稳频He-Ne激光 (He-Ne laser)
压电晶体(Piezoelectric crystal)
/2片
/4片
被检面
偏振分光 棱镜 prism
检偏器
TV相机
非球面测定用干涉仪
itg
2 1
结论:
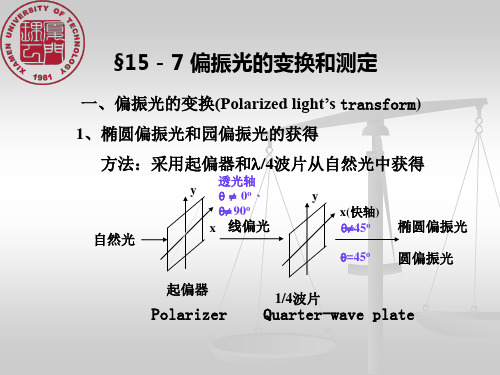
1)从1/4波片出射的是线偏光。出射线偏光的光矢量 与x轴的夹角=/2。
2)旋转检偏器可测得,故可求,即求得了待测玻璃的 双折射率之差,从而分析了玻璃内部的应力情况 。
二、会聚(Convergence)偏光仪的干涉
P
C
A
会聚偏光仪干涉装置
透过厚度为d的晶片时两束出射光之间的相位差:
半影式检偏器工作原理 原理
结构: P H A
y
P1
O H1
’ ’
H2 P2 A
x
2 2 I1=OH1 sin ( ' ) 2 2 I 2=OH 2 sin ( ' )
2、椭圆偏振光的测定 含义:用实验方法测定表示偏振状态的参量(指 定坐标系中的方位角、椭圆度tg和旋向;或直角 坐标系下两偏振光振幅比和位相差。) y y’ C2 A2 x’
四川师范大学大学物理波动光学(13、14、15章)题解

第十三章 光的干涉13–1 在双缝干涉实验中,两缝分别被折射率为n 1和n 2的透明薄膜遮盖,二者的厚度均为e ,波长为λ的平行单色光垂直照射到双缝上,在屏中央处,两束相干光的位相差 。
解:加入透明薄膜后,两束相干光的光程差为n 1e –n 2e ,则位相差为e n n e n e n )(2)(22121-=-=∆λλλλφ13–2 如图13-1所示,波长为λ的平行单色光垂直照射到两个劈尖上,两劈尖角分别为21θθ和,折射率分别为n 1和n 2,若二者分别形成的干涉条纹的明条纹间距相等,则21,θθ,n 1和n 2之间的关系是 。
解:劈尖薄膜干涉明条纹间距为θλθλn n L 2sin 2≈=( 很小) 两劈尖干涉明条纹间距相等221122θλθλn n =,所以 2211θθn n =或1221n n =θθ13–3 用一定波长的单色光进行双缝干涉实验时,欲使屏上的干涉条纹间距变大,可采用的方法是: ; 。
解:因为干涉条纹的间距与两缝间距成反比,与屏与双缝之间的距离成正比。
故填“使两缝间距变小;使屏与双缝之间的距离变大。
”13–4 用波长为λ的单色光垂直照射如图13-2示的劈尖膜(n 1>n 2>n 3),观察反射光干涉,从劈尖顶开始算起,第2条明条纹中心所对应的膜厚度e = 。
解:劈尖干涉(n 1>n 2>n 3)从n 1射向n 2时无半波损失,产生明条纹的条件为2n 2e = k ,k = 0,1,2,3…在e = 0时,两相干光相差为0,形成明纹。
第2条明条纹中心所对应的膜厚度为k = 1,即2n 2e = ,则22n e λ=。
13–5 若在迈克耳孙干涉仪的可动反射镜移动0.620mm 的过程中,观察到干涉条纹移动了2300条,则所用光波的波长为 。
解:设迈克耳孙干涉仪空气膜厚度变化为e ,对应于可动反射镜的移动,干涉条纹每移动一条,厚度变化2λ,现移动2300条,厚度变化mm 620.022300=⨯=λ∆e ,则 = 。
15.1自然光和偏振光马吕斯定律

起 偏
I0
起偏器
1 I0 2 偏振化方向
检 偏
起偏器 检偏器
讨论
如何检验一束光为自然光、线偏振光、 部分偏振光? 用一偏振片,旋转一圈,
观察光强变化。
旋转一圈,光强无变化。
旋转一圈,光强出现 强、弱、全暗现象。
旋转一圈,光强出现强、 弱变化,无全暗现象。
光的波动性
第一节 自然光和偏振光
不同的光束, 光矢量 E 的振动状态不一定相同。 把 E 的振动状态叫偏振态。
一、自然光 偏振光
1、自然光 (1) 自然光 :直接从普通光源发出的光。
v
E
(2) 偏振态:自然光在任意时刻,在垂直于传播方向的平 面上,没有哪个方向的光振动比其它方向更占优势。 自然光又称为非偏振光。
符号表示
二 . 偏振片 起偏与检偏 二向色性 : 某些晶体内存在某一特定的方向, 当光射向晶体时,晶体能让这一方向的光振动通过 , 而吸收与这个方向相垂直的光振动, 这种性质称二向 色性 . 偏振片 : 涂有二向色性材料的透明薄片 .
偏振化方向 : 当自然光照射在偏振片上时, 它只让某一特定方向的光通过,这个方向叫此偏振 片的偏振化方向 ,又称为透光轴.
(3) 表示:
自然光可分解为两个相互垂直、振幅相等、独立的光振动。
符号表示:
2、偏振光 自然光经过反射、折射、吸收后,可能使一个方向 的光振动全部或部分被消除,这种光称为偏振光。 (1) 线偏振光 :只有单一方向的 光振动。又称为平面偏振光。 (完全偏振光)。 (2) 部分偏振光 :某一方向的 光振动比与之垂直方向上的光振 动占优势的光为部分偏振光 。 (由两个相互垂直的、振幅不相 等的、独立的光振动组成。) 符号表示
大学物理2,15.第十五章思考题

1、一束光垂直入射在偏振片上,以入射光线为轴转动偏振片,观察通过偏振片后的光强变化过程。
如果观察到光强不变,则入射光是什么光?如果观察到明暗交替变化,有时出现全暗,则入射光是什么光?如果观察到明暗交替变化,但不出现全暗,则入射光是什么光?【答案:自然光;完全偏振光;部分偏振光】详解:当一束光垂直入射在偏振片上时,以入射光线为轴转动偏振片,如果观察到通过偏振片后的光强不发生变化,入射光是由自然光;如果观察到光强有明暗交替变化,并且有时出现全暗,则入射光是完全偏振光;如果观察到光强有明暗交替变化,但不出现全暗,则入射光是部分偏振光。
2、一束光是自然光和线偏振光的混合光,让它垂直通过一个偏振片。
若以此入射光束为轴旋转偏振片,测得透射光强度最大值是最小值的5倍,那么入射光束中自然光与线偏振光的光强比值为多少?【答案:1/2】详解:设该光束中自然光和线偏振光的强度分别为I 1和I 2。
当以此入射光束为轴旋转偏振片时,透射光强度的最大值和最小值分别为21max 21I I I +=1min 21I I = 依题意有I max =5I min ,即 12121521I I I ⨯=+ 解之得2121=I I 即入射光束中自然光与线偏振光的光强比值等于1/2。
3、一束光强为I 0的自然光相继通过三个偏振片P 1、P 2、P 3后,出射光的光强为0.125I 0 。
已知P 1和P 2的偏振化方向相互垂直,若以入射光线为轴旋转P 2,要使出射光的光强为零,P 2最少要转过多大的角度?【答案:45°】详解:由于P 1和P 2的偏振化方向相互垂直,而自然光相继通过三个偏振片后的光强不等于零,说明自然光通过偏振片的顺序为P 1、P 3、P 2。
如图所示,设偏振片P 1和P 3的夹角为θ,由马吕斯定律得出射光强为 )09(cos cos 2220θθ-= I I θ2sin 820I = 由于I =0.125I 0 ,代入上式解得 45=θ要使出射光强为零,应使P 2和P 3的偏振化方向垂直,因此P 2最少要转过的角度也等于45°。
大学物理下 第十五章光的偏振 1

I max I min
1 I 0 + I' =2 = 2 1 I0 2
(1)检验光束的 ) 偏振性 (2)可以改变光 ) 束的偏振化方向
I0 =2 I'
3,布儒斯特定律 , 光反射与折射时的偏振
n1 n2
玻璃
i i
γ
部分偏振光 反射光 部分偏振光 , 垂直于入射面的振动大于平 行于入射面的振动 . 部分偏振光 偏振光, 折射光 部分偏振光, 平行于入射面的振动大于垂 直于入射面的振动 .
对于一般的光学玻璃 , 反射光的强度约占 入射光强度的7.5% , 大部分光将透过玻璃 大部分光将透过玻璃. 入射光强度的
利用玻璃片堆产生线 利用玻璃片堆产生线偏振光 玻璃片堆产生
i0
例3(P269 15-5) 讨论下列光线的反射和折射(起偏角i 讨论下列光线的反射和折射(起偏角 0 )
i0
i0
i0
102 A 102 102
光轴
78
78 78
B 光轴
用惠更斯原理解释光的双折射现象 1)O 光在晶体内任意点所引起的波阵面是球面.即 ) 在晶体内任意点所引起的波阵面是球面. 具有各向同性的传播速率. 具有各向同性的传播速率. 2)e 光在晶体内任意点所引起的波阵面是绕光轴的 ) 旋转椭球面.沿光轴方向与O光具有相同的速率. 旋转椭球面.沿光轴方向与 光具有相同的速率.
方解石晶体
i
n
玻璃
γ
恒量
动光 学 光学 波动
CaCO3
sin i =n= sin γ
寻常光线( 寻常光线(o光)(ordinary rays) 服从折射定律的光线
n1 sin i = n 2 sin γ n 2 ≠ 常量
华东理工大学大学物理作业答案2

2f 2 1 600 10 9 3 10 3 m a 0.4 10 3 (2)由 a sin k (k 1) 得 x sin 1.5 10 3 r a d a
44
大学物理习题册解答
7、用 1mm 内有 500 条刻痕的平面透射光栅观察钠光谱(λ =589nm) ,问: (1)光线垂直入射时,最多能看到第几级光谱; (2)光线以入射角 300 入射时,最多能看到第几级光谱。 解: (1) d
1 2 10 3 mm 500 由 d sin k 及最多能看到的谱线时 sinθ ~1 可得 d 2 10 3 k m ax 3.4 589 10 6
0
(3)最多能看到的谱线级数 sinθ ~1
k d 2400 4 600
∴
k=0,±1,±2
共5条谱线
45
大学物理习题册解答
9、一双缝,缝间距 d=0.1mm,缝宽 a=0.02mm,用波长λ =480nm 的平行单色光垂直入 射双缝,双缝后放一焦距为 50cm 的透镜,试求: (1)透镜焦平面上,干涉条纹的间距; (2)单缝衍射中央亮纹的宽度; (3)单缝衍射的中央包线内有多少条干涉的主极大? x 解: (1)由双缝干涉明条纹条件 d sin d k 得 f
12、一束自然光,入射到由 4 片偏振片构成的偏振片组上。每一片偏振片的偏振化方向 0 相对于前面一片的偏振化方向沿顺时针方向转过 30 角。问通过偏振片组后的光强是入 射光强的百分之几? 解: 设入射光强为 I0,通过偏振片的光强为 I1、I2、I3、I4 1 I1 I 0 2
(物理光学)第十五章 光的偏振和晶体光学基础-3

n e d 1 直且顶角均为30度的直角方解石 棱镜胶合成渥拉斯顿棱镜,当一束自然光垂直入射 时,求从棱镜出射的o光和e光的夹角。
f
n o 1 . 65836 , n e 1 . 48641
f
线偏振光通过半波片后光矢量的转动
快(慢)轴
入射时 Entrance
出射时 (Exit)
线偏振光通过半波片后光矢量的转动
3、全波片(Full-wave plate)
n o n e d m , 对应的 2 m
称该晶片为全波片。 性质:
1)不改变入射光的偏振状态;
A
A
A
A
a)
光轴垂直于入射面
b ) 光轴平行于入射面
(二)偏振分束棱镜
1. 渥拉斯顿棱镜(Wollaston prism):
利用两个正交的光轴分解光。材料:冰洲石。
no ne
f
制作 原理 思考
f arcsin
f
n 0
n e tg
2.洛匈棱镜(Rochon prism)
原理
光轴
90
。
。 Canada balsam
68 71
。
77
。 尼科耳棱镜(W.Nicol)
2. 格兰-汤姆逊(Glan-Thompson)棱镜
光垂直于棱镜端面入射时
A
A
A= 光 轴
当入射光束不是平行光或平行光非正入射时
i
A
i' A= 光 轴
A
孔径角的限制
3. 格兰-付科棱镜(Glan-foucault prism)
2)只能增大光程差。
第十五章光学(高中物理基本概念归纳整理)完整版4

正弦之比,叫作这种介质的绝对折射率,简称折射率,用符号
n表示。(n12是2相对1的折射率,叫相对折射率) 注意:
①不同的介质,折射率不同。n是一个反映介质的光学性质的
物理量。
②真空的折射率为1,空气的折射率近似为1。
③光在不同介质中的传播速度不同。
一.光的折射
3.折射率的另一种定义:某种介质的折射率,等于光在真空中的传
6.偏振光:在垂直于传播方向的平面上,沿着
某个特定的方向振动的光叫作偏振光。
注意: ①在垂直于光的传播方向的平面内,自然 光沿任意方向振动的强度都相同,偏振光 只沿特定的方向振动。 ②自然光通过偏振片后变成了偏振光
七.光的偏振
ii r
n sin i sin r
i r 90
n
sin i cos i
四.全反射 2.全反射:光从光密介质射入光疏介质,当入射角增大到某一角度, 使折射角达到90˚时,折射光完全消失,只剩下反射光,这种现象 叫作全反射,这时的入射角叫作临界角,用C表示。
光由介质射向真空:
n sin 90 1 sin C sin C
sin C 1 n
3.发生全反射的条件: ①光密到光疏,②入射角大于等于临界角
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
n n n
2 x 2 y
2 z
x n n
2 3 2 y 2
2 z
n y n n n z
2 x 2 2 z 2 x 2 y
x
2
x
2
vz
vz
2
y
vx
vy
2
y z
法线面图形
2 2 2 2 (nx x ny y nz2 z 2 ) 0
法线面的xy,yz,zx截面是圆和四次曲线(如图)
由 ,得光线的菲涅耳方程:
同样,由
给出光线面(如图)方程,图中 的矢径
其 的方向平行於某一给定 方向, 其 的长度给出相应两光波的光线速 度 ,将关系 x vS S0 x , y vS S0 y , z vS S0 z B2 2 2 2 2 和x y z vS 代入光线方程中 得到光线面方程为
n y , n z
nz
z
n x
O
n y
n x
波矢面图形
n z
y
波矢面与三个坐标面的交线图形
x
n z
通常波矢面的三个主轴坐标面的xy,yz,zx截面是圆和椭圆(如图)。 C1,C2表示晶体光轴方向。
2、法线面 也叫法线速度面或相速度面。从晶体中任一点O出发,引各个 方向的法线速度矢量 vk ,其端点的轨迹就是法线面。法线面 的矢径 方向平行于某个给定的波法线 方向,而矢径 的 长度等于相应的两个光波的法线速度即相速度 v ,
其矢径 将矢径的三个分量 及矢径长度的平方
r x2 y 2 z 2
2
,为简单,用
x 1 kox , n
n2
r
y
1 1 koy , z k oz n n
C2
1 k0 n
k
来给出法线面,
z
vx
k02x k02y k02z
vy
O
代入菲涅耳方程中,得到法线面方程
2 2 2 nx n y nz x 2 y 2 z
2 x 2 2 y 2 2 2 2 2 2 z 2 x 2 y 2 2 z 2 y 2 z 2 x 2 2 z
2 x
2 2 2 ny2 z 2 n n n x y z 0
c c c 这就是波矢面方程,它的图形是:
n y
C2
式中:n x
nx , ny
n1
二、波矢面、法线面和光线面 1、波矢面:
波矢面定义为这样一个双层曲面:它的矢径 r k (波矢量), ,即矢径平行于某个给定的波法线方向 k0 或者 r k k0 nk0 c 矢径长度等于相应的两个光波的波数k。
它是描述晶体的波数在晶体空间各方向(沿 方向)上全部取值 分布的几何图形。 1 把矢径长度 r x 2 y 2 z 2 2 n ,和矢径分量关系
O
r
D
y
O
k0
ny
B
D
x
n1 n D1 2 D 2
所以利用折射率椭球,就可以: 已知晶体的介电张量
k0 对应的 D1 , D2 ,
折射率椭球
作图求出任一
n1 , n2 , E1, E2 , S1 , S 2
z
P
nz
n
nx
E
O
rD
ny
k0
y
O
S0
k0
B
D
x
D1 n2 D 2
nz
ny ,
P
(1)过椭球中心O的任一矢径r的 方向,表示光波D矢量的一个方向, 矢径r的长度表示D矢量沿矢径方向 振动的光波的折射率。即折射率椭 球的矢径r可表示为 x
n
nx
O
rD
ny
k0
y
O
D1 n2 D 2
n1
r nd
d 是D矢量方向的单位矢量。
(2)作垂直于给定波法线 k0方向的平面,截椭球的椭圆截面(如 图),椭圆的长短轴方向就是 相应的两个允许的光波 的方 向 D1 、D2 ,其长度即这两个光波的折射率 n1和n2 ,且 D1 ⊥ D2 。 对于单轴晶体, nx ny n0 , nz ne ,则其折射率椭球的方程为
x2 y 2 z 2 2 2 1 2 no no nz
应用:利用折射率椭球,由 k0的方向, 求取 的方向(如图),即: D , E, S0 k0 已知 方向,与其垂直方向即 的 方向,相应的E 的方向即切点B处切 平面的法线方向,且 k0 S S0 E E
0
z
P
nz
n
nx
yz面上交线方程
[n ( y z ) 1][n n ( y z ) (n y n z )] 0
2 x 2 2 2 2 y z 2 2 2 2 y 2 2 2 z
法线面与三个坐标面的交线图形
3、光线面
光线面就是光线速度面。从晶体中任一点O引各方向的光线速度 矢量 v s ,其端点的轨迹构成光线面。
如图所示的光线面: 于是,得到光线面的xy,yz,zx截面都是圆和椭圆
z
vx
B2
vz
O
vx
y
vz
x
vy
单轴晶体: vx
2 2
vy vo , vz ve
2 2 o 2 o 2 2
代入光线面方程
2 2 e 2 2 o e
vz
z
vx
vz
O
vx
y
x
vy
v x v y v z x y z v v v x v v v y v v
2 x 2 2 y 2 2 z 2 2 2 2 x 2 y 2 z 2 2 y 2 z 2 x 2 2 z
2 x
2 2 2 2 vy z 2 (v x v y vz ) 0
x kx
n
c
k ox , y k y
n
c
k oy , z k n k , z oz c c
2 k0 x
代入菲涅耳方程中1 1 源自 n 2 rx2 k0 y
1 1 n 2 ry
k02z 1 1 n 2 rz
0
n x n y n z x y z n n n x n n n y n n
D 用 x, y, z ,代替 x , A
Dy A
,
Dz , 并把它取为空间直角坐标系,则有 A
x2 y 2 z 2 2 2 1 2 nx ny nz
式中取 x
折射率椭球表达式
nz , 是相应主折射率。
2、折射率椭球的性质
Dx D , y y , z Dz , x, y , z 是介电主轴方向,nx , A A A z
