三年级下册数学试题-奥数练习题(1)(含答案)全国通用
三年级下册数学试题-奥数:行程问题—追及(练习含答案)全国通用
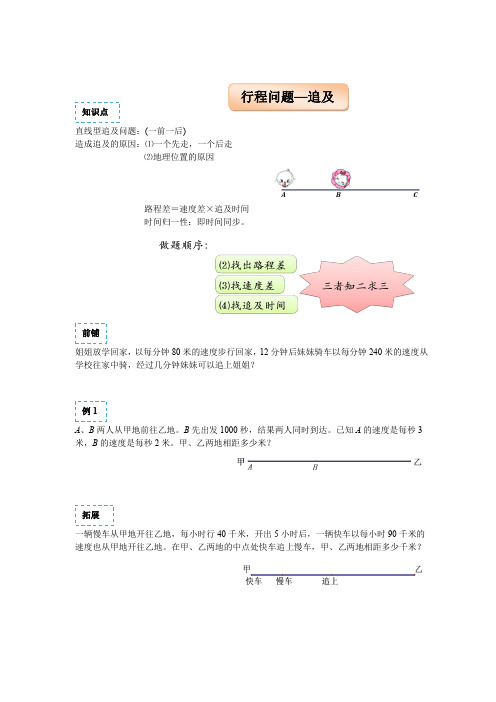
直线型追及问题:(一前一后)造成追及的原因:⑴一个先走,一个后走⑵地理位置的原因路程差=速度差×追及时间时间归一性:即时间同步。
姐姐放学回家,以每分钟80米的速度步行回家,12分钟后妹妹骑车以每分钟240米的速度从学校往家中骑,经过几分钟妹妹可以追上姐姐?A、B两人从甲地前往乙地。
B先出发1000秒,结果两人同时到达。
已知A的速度是每秒3米,B的速度是每秒2米。
甲、乙两地相距多少米?一辆慢车从甲地开往乙地,每小时行40千米,开出5小时后,一辆快车以每小时90千米的速度也从甲地开往乙地。
在甲、乙两地的中点处快车追上慢车,甲、乙两地相距多少千米?拓展例1前铺知识点行程问题—追及甲、乙二人练习跑步,若甲让乙先跑10米,则甲跑5秒钟可追上乙;若甲让乙先跑2秒钟,则甲跑4秒钟就能追上乙。
问:甲、乙二人的速度各是多少?兄弟两人骑自行车同时从学校出发回家。
哥哥每小时行15千米,弟弟每小时行10千米。
出发半个小时后哥哥因事返回学校,到学校后又耽搁了1小时,然后动身去追弟弟。
当哥哥追上弟弟时,距学校多少千米?两人在环形跑道中同时同地同向而行1.两个人每追及一次,路程差增加一个周长;反之,两个人路程差每增加一周,必定追及一次。
2.两个人每追及一次,每次所需要的时间均相等,即每次增加t。
幸福村小学有一条200米长的环形跑道,冬冬和晶晶同时从起跑线起跑,冬冬每秒钟跑6米,晶晶每秒钟跑4米,问冬冬第2次追上晶晶时两人各跑了多少圈?在周长为400米的圆形跑道的一条直径的两端,甲、乙两人分别以每秒6米和每秒4米的速例5例4知识点例3例2度骑自行车同时同向出发(顺时针)沿圆周行驶,经过多长时间,甲第二次追上乙?测试题1.甲、乙两地相距240千米,一列慢车从甲地出发,每小时行60千米.同时一列快车从乙地出发,每小时行90千米。
两车同向行驶,快车在慢车后面,经过多少小时快车可以追上慢车?A.6 B.8 C.10 D.122.小红和小蓝练习跑步,若小红让小蓝先跑20米,则小红跑5秒钟就可追上小蓝;若小红让小蓝先跑4秒钟,则小红跑6秒钟就能追上小蓝、小红、小蓝二人的速度各是多少?A.10,6 B.6,10 C.6,8 D.8,63.王芳和李华放学后,一起步行去体校参加排球训练,王芳每分钟走110米,李华每分钟走70米,出发5分钟后,王芳返回学校取运动服,在学校又耽误了2分钟,然后追赶李华。
小学三年级下册奥数题100道附答案

小学三年级下册奥数题100道附答案(完整版)1. 一条毛毛虫由幼虫长成成虫,每天长大一倍,30 天能长到20 厘米。
问长到5 厘米时要用多少天?答案:毛毛虫每天长大一倍,30 天长到20 厘米,那么29 天长到:20÷2 = 10(厘米),28 天长到:10÷2 = 5(厘米)。
所以长到5 厘米时要用28 天。
2. 小明和小红共有图书84 本,如果小明给小红14 本后,两人的图书本数相同。
小明和小红原来各有多少本图书?答案:两人图书总数不变,后来两人各有:84÷2 = 42(本)。
小明原来有:42 + 14 = 56(本),小红原来有:42 - 14 = 28(本)。
3. 一桶水,连桶重250 千克,用去一半水后,连桶还有145 千克。
桶里原有多少千克水?桶重多少千克?答案:一半水重:250 - 145 = 105(千克),桶里原有水:105×2 = 210(千克),桶重:250 - 210 = 40(千克)。
4. 果园里有梨树、桃树和苹果树共1200 棵,其中梨树的棵数是苹果树的3 倍,桃树的棵数是苹果树的4 倍。
求梨树、桃树和苹果树各有多少棵?答案:把苹果树的棵数看作1 份,梨树就是3 份,桃树就是4 份,一共是1 + 3 + 4 = 8 份。
苹果树有:1200÷8 = 150(棵),梨树有:150×3 = 450(棵),桃树有:150×4 = 600(棵)。
5. 某工厂三个车间共有180 人,第二车间人数是第一车间人数的3 倍多1 人,第三车间人数是第一车间人数的一半还少1 人。
三个车间各有多少人?答案:设第一车间有x 人,则第二车间有3x + 1 人,第三车间有0.5x - 1 人。
x + (3x + 1) + (0.5x - 1) = 1804.5x = 180x = 40第一车间有40 人,第二车间有3×40 + 1 = 121 人,第三车间有0.5×40 - 1 = 19 人。
三年级下册数学奥数题100道及答案

三年级下册数学奥数题100道及答案1. 有4 个小朋友,每人分得3 个苹果,一共有多少个苹果?答案:4×3=12(个)解题思路:用人数乘以每人分得的苹果数可得苹果总数。
2. 小明每分钟跑80 米,5 分钟跑多少米?答案:80×5=400(米)解题思路:速度乘以时间等于路程。
3. 24 除以3 等于多少?答案:8解题思路:直接计算。
4. 一条绳子长15 米,剪去5 米,还剩多少米?答案:10 米解题思路:总长度减去剪去的长度。
5. 一个数加上3 等于10,这个数是多少?答案:7解题思路:10 减去3 可得。
6. 小红有15 颗糖,给了弟弟5 颗,她还剩几颗?答案:10解题思路:原有糖数减去给弟弟的数量。
7. 36 里面有几个9?答案:4解题思路:用36 除以9。
8. 长方形的长是8 厘米,宽是5 厘米,周长是多少?答案:(8+5)×2=26(厘米)解题思路:长方形周长等于(长+宽)×2。
9. 56 连续减7,减几次是0?答案:8解题思路:56 除以7 即可。
10. 把24 个苹果平均分成3 份,每份几个?答案:8解题思路:总数除以份数。
11. 18 朵花,每3 朵扎一束,可以扎几束?答案:6解题思路:花的总数除以每束的朵数。
12. 3 只鸭子5 天吃15 千克食物,1 只鸭子1 天吃多少千克食物?答案:1 千克解题思路:先算出3 只鸭子1 天吃的量,再算1 只鸭子1 天吃的量。
13. 小明有20 元,买一支笔用去8 元,还剩多少钱?答案:12 元解题思路:总钱数减去花去的钱。
14. 27 是9 的几倍?答案:3解题思路:27 除以9。
15. 一本书有30 页,每天看5 页,几天能看完?答案:6解题思路:总页数除以每天看的页数。
16. 一个正方形的边长是4 厘米,面积是多少?答案:16 平方厘米解题思路:正方形面积等于边长乘边长。
17. 45 里面有几个5?答案:9解题思路:45 除以5。
全国通用2022-2023学年三年级全册数学精选奥数题(含解析)

全国通用2022-2023学年三年级全册数学精选奥数题1、简单推理一、知识要点数学课上,老师布置了一道题:□+△=28□=△+△+△□=()△=()要得出正确的结论,就要进行分析、推理。
学会了推理,能使你变得更聪明,头脑更灵活。
数学上有许多重大的发现和疑难问题的解决都离没有开推理。
解答这类推理题时,要求小朋友仔细观察,认真分析等式中几个图形之间的关系,寻找解题的突破口,然后再利用等量代换、消去等方法来进行解答。
二、精讲精练【例题1】下式中,□和△各代表几?□+△=28□=△+△+△□=()△=()【思路导航】根据□+△=28,我们可以得出□=28-△;由□=△+△+△得到28=△+△+△+△,4个△等于28,一个△等于28÷4=7;由□=△+△+△可求出□=7+7+7=21。
典型练习1:1.☆+○=18☆=○+○☆=()○=()2.△+○=25△=○+○+○+○△=()○=()3.○+□=36○=□+□+□+□+□○=()□=()【答案解析】1.12、6 2.20、5 3.30、6【例题2】下式中,□和△各代表几?□×△=36□÷△=4□=()△=()【思路导航】根据□÷△=4可知△为一份,□是这样的4份,即□=4△;又根据□×△=36,可以得到4△×△=36,即△×△=9,进一步得到△=3,□=4△=4×3=12。
典型练习21.○和□各表示几?○×□=16□÷○=4○=()□=()2.想想,填填。
○×△=20○=△+△+△+△+△○=()△=()3.□和○各代表几?□=○+○+○+○○×□=16□=()○=()【答案解析】1.2、8 2.10、2 3.8、2【例题3】下式中,□和△各代表几?□+□+△=16□+△+△=14□=()△=()【思路导航】16里面有2个□,1个△;14里面有1个□,2个△,16减去14等于2,即□-△=2,那么如果把△换成了□,则16需要加上2,即□+□+□=16+2,那么□=(16+2)÷3=6,△=16-6×2=4。
三年级下册数学试题-奥数练习:树形图(含答案)全国通用

树形图(有特殊要求的树形图、比赛进程问题)1.一个三位数,每一位上的数字都是1、2、3 中的一个,并且相邻的两个数字不同,一共有______个满足条件的三位数.2.一个三位数,每一位上的数字都是2、4、6 中的一个,并且相邻的两个数字不同,一共有______个满足条件的三位数.3.旦旦、雁雁和蒙蒙玩传球游戏,每次持球人要把球传给另外两人中的任何一人.先由旦旦拿球,第1次传球可以传给其他两人中的任何一人,经过 4 次传球之后,球又回到了旦旦手里.那么一共有________种不同的传球过程.4.旦旦、雁雁和蒙蒙玩传球游戏,每次持球人要把球传给另外两人中的任何一人.先由旦旦拿球,第1次传球可以传给其他两人中的任何一人,经过 4 次传球之后,球到了蒙蒙手里.那么一共有__________种不同的传球过程.5.一个三位数,百位数字比十位数字大,十位数字比个位数字大,个位数字不小于5,那么这样的三位数一共有__________个.6.一个三位数,个位数字比十位数字大,十位数字比百位数字大,并且都比 5 小.那么这样的三位数一共有__________个.7.阿呆、阿瓜、旦旦、雁雁四个人每个人写了一封信,把这4 封信放在一起,每个人拿一封信且不能拿自己写的信,那么一共有__________种不同的拿法.8.有4 本书排成一排,阿呆、阿瓜、旦旦、雁雁四个人选书,每人选1 本书.阿呆不要第 1 本书,阿瓜不要第2 本书,旦旦不要第3 本书,雁雁不要第 4 本书,那么一共有__________种不同的选法.9.旦旦和雁雁比赛乒乓球,约定三局两胜,如果最后旦旦获胜了,那么比赛的进程有__________种可能.10.文雯和蒙蒙比赛羽毛球,约定谁先赢两局就获胜,比赛就结束.如果最后文雯获胜了,那么比赛的进程有__________种可能.11.旦旦、雁雁和蒙蒙三个人在打牌(没有和局),一旦有人赢了2 局就获胜,牌局结束.最后旦旦赢了,那么打牌的进程有__________种不同的可能.12.阿呆、阿瓜和文雯三个人在打牌(没有和局),一旦有人赢了2 局就获胜,牌局结束.最后阿瓜赢了,那么打牌的进程有__________种不同的可能.13.小山羊、卡莉娅和小高三个人在打牌(没有和局),一旦有人赢了 2 局就获胜,牌局结束.最后小高赢了,那么有__________种不同的打牌进程.14.高高队和思思队进行足球比赛,高高队在比赛过程中从未让思思队比分领先过,最后以4 比3 取得胜利,那么比赛的进球顺序有__________ 种可能.15.高高队和思思队进行足球比赛,高高队在比赛过程中从未让思思队比分领先过,最后以 3 比2 取得胜利,那么比赛的进球顺序有__________种可能.答案:1.(12) 2.(12) 3.(6) 4.(5)5.(10)6.(4)7.(9)8.(9)9.(3)10.(3)11.(11)12.(11)13.(11)14.(14)15.(5)割圆术数学意义:“割圆术”,则是以“圆内接正多边形的面积”,来无限逼近“圆面积”。
三年级下册数学试题-奥数巧填算符(练习含答案)全国通用

巧填算符巧填算符,就是指在一些数之间的适当地方填上适当的运算符号(包括括号),从而使这些数和运算符号构成的算式成为一个等式。
在填算符的问题中,所填的算符包括:+”“-”“×”“÷”“=”“>”“<”“()”“[ ]”“{}” 巧填算符常用的方法有:1.凑数法:先选出一个与结果比较接近的数,然后再对剩下的数进行适当的增加或减少,使算式成立。
我们把这种方法称为凑数法。
2.逆推法:是从算式中的最后一个数开始,由后往前,逐步求解,我们把这种方法称为逆推法。
逆推法思路比较固定,但是分析起来头绪繁多,因此适合于数比较少、结果比较小的添运算符号问题。
注:添运算符号问题的解都比较多,并不唯一。
如果没有特殊的要求,只要添出一种答案就可以了。
例1在5+3×9-4+8÷2=66这个算式中添上两个小括号,使算式成立。
例2在下面算式的适当地方,添上运算符号+,-,×,÷和( ),使等式成立。
9 8 7 6 5 4 3 2 1 =1000例3在八个8之间的适当地方,添上+,-,×,÷运算符号,使算式成立。
8 8 8 8 8 8 8 8 =1000例4(第二届迎春杯决赛)试在15个8之间适当的位置填上适当的运算符号:+、-、×、÷,使运算结果等于1986。
8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 =1986例5在□中填上“+”、“-”、“×”、“÷”、“( )”使算式成立。
⑴5□5□5□5□5=1⑵5□5□5□5□5=2⑶5□5□5□5□5=3⑷5□5□5□5□5=4同学们一定都玩过扑克牌,但你会用扑克牌玩一种叫“24点”的游戏吗?其实就是-种添运算符号的游戏。
游戏规则是拿出四张牌,根据四张牌上的点数,运用加、减、乘、除四种运算中的任意几种进行计算,每张牌的点数都必须用:并且只能用一次,使最后的结果等于24。
三年级下册数学试题-奥数:植树问题(练习含答案)全国通用
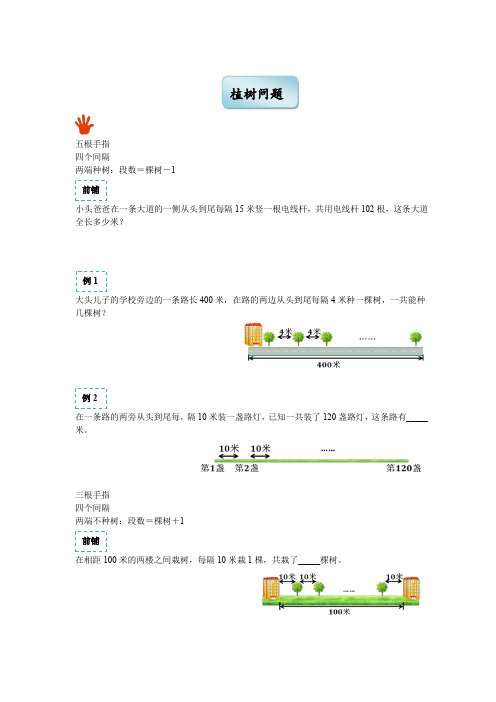
5.丁丁从1楼跑到5楼需要4分钟,那么从1楼跑到10楼需要多少时间?玲玲的速度是丁丁的3倍,玲玲从一楼跑到10楼需要多少时间?
6.(超常)一条河堤长420米,现要在河堤两侧从头到尾每隔3米栽一棵树,要栽多少棵树?
(超常2班)一人以相等的速度在小路上散步,从第 棵树走到第12棵树用了11分钟,如果这个人走了25分钟,应走到的第几棵树?
(超常1班)有30分米长的木棍,现要在木棍上划线。先每隔2分米划一条线,再每隔3分米划
一条线,最后按划线处锯开木棍,共能锯成多少段?
7.在一个半径是125米的圆形花园周围以等距离种白杨树157棵,则两树间的距离是米。
(超常1班)每隔2分米划一条线,共划 条线,每隔3分米划一条线,共划 条线,每隔6分米重叠一次,重叠了 条线,共能锯成14+9-4+1=20段。
7.答案:半径为125米的圆周长为 (米),因为环形问题的棵数等于间隔数,所以间隔数为157,那么间距 (米)。
8.答案:跑道一侧需要 (面),那么两侧共需要 (面)。
1.爬楼梯
2.锯木头
3.敲钟
4.夹手帕
测试题
1.一条景观河长60米,如果在此河两侧每隔3米放一盆水仙花,每两盆水仙花之间放一盆茉莉花,那么一共能放多少盆花?
2.街心公园一条小路的一侧有一端原栽种着一株海棠树,现每隔12米栽一棵柳树,共用柳树苗25棵,这条小路长米?
3.在一条长2500米的公路一侧架设电线杆,每隔50米架设一根,若公路两端都不架设,共需电线杆__根。
三根手指
四个间隔
两端不种树:段数=棵树+1
在相距100米的两楼之间栽树,每隔10米栽1棵,共栽了_____棵树。
三年级下册数学试题-奥数:分类(练习含答案)全国通用

一般地,如果完成一件事有k类方法,第一类方法中有m1种不同的做法,第二类方法中有m2种不同的做法,…,第k步有m k种不同的方法,则完成这件事共有N=m1×m2×…×m k种不同的方法。
注:完成一件事的方法分成几类,每一类中的任何一种方法都能完成任务,这样的问题可以通过分类计数解决。
我们可以简记为:“加法分类,类类独立”。
分类时,首先要根据问题的特点确定一个适合于它的分类标准,然后在这个标准下进行分类;其次,分类时要注意满足两条基本原则:①完成这件事的任何一种方法必须属于某一类;②分别属于不同两类的两种方法是不同的方法。
只有满足这两条基本原则,才可以保证分类计数原理计算正确。
学校组织读书活动,要求每个同学读一本书,小明到图书馆借书时,图书馆有不同的外语书150 本,不同的科技书200本,不同的小说100本,那么小明借一本书可以有多少种不同的选法?一个口袋内装有3个小球,另一个口袋内装有8个小球,所有这些小球颜色各不相同,问:⑴任取一个小球,有多少种不同的取法?⑵从两个口袋内各取一个小球,有多少种不同的取法?如图,从甲地到乙地有三条路,从乙地到丁地有三条路,从甲地到丙地有两条路,从丙地到丁地有四条路,问:从甲地到丁地共有多少种走法?例4不限制数字的使用次数,用0到9这10个数字,可以组成多少个三位偶数?拓展用0到9这10个数字,可以组成多少个没有重复数字的三位偶数?例5某信号兵用红黄蓝3面旗从上到下在竖直的旗杆上表示信号,每次可以任挂1面,2面或3面,并且不同的顺序表示不同的信号,一共可以表示多少种不同的信号?例6七个相同的球,放入四个不同的盒子里,每个盒子至少放一个,不同的放法有几种?例7从19,20,21,…,97,98,99这81个数中,选取两个不同的数,使其和为偶数的选法总数是多少?测试题1.书架上有6本不同的画报,10本不同的科技书,请你每次从书架上取一本画报或者一本科技书,共有()种不同的取法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
奥数练习题
班级( ) 姓名( ) 做对( )题
1.两个数的和是91,小玲在抄题时,将其中一个加数个位上的“0”丢掉了,结果
算出的和是37,这两个数分别是( )和( )。
2.找规律填数。
2,8,5,20,7,28,11,44,( ),12。
3.将1~7七个数字,分别填入下面空格内,使等式成立。
(每个数字只能用一次)□×□=□÷□=□+□-□
4.一个长方形牧场的三面用篱笆围成,第四条边靠着一面长100米的墙,包括与
墙交界处每隔12米有一根木桩,那么一个长60米宽36米的长方形牧场最少需要木桩( )根。
5.500张白纸的厚度为50毫米,那么( )张白纸的厚度是750毫米
6.6个男生的平均体重是40千克,4个女生的平均体重是30千克,这10个同学
的平均体重是( )千克。
7.百乐自选商场的一种矿泉水,进货4瓶5元钱,售出3瓶5元钱,要获利100
元需要售出( )瓶。
8.把盒中200只红球进行调换.每次调换必须首先从盒中取出3只红球,然后再放入
2只白球,那么,在最后一次调换之前盒中的球数是( )
9.简算与计算。
609-708+306-108+202-198+497-100
14+15+16+……+45+46
9999+9998+9997+9996
99999×26+33333×22
10.一个奶牛场有25头奶牛和15头小牛,每头奶牛每天吃草12千克,每头小牛每
天吃草6千克。
现有草7020千克,可供它们吃多少天?
11.一箱鱼片24袋,其中6大袋,每袋9元;余下的是小袋,每小袋5元。
如果1
大袋相当于2小袋,那么这箱鱼片的价格比全按小袋包装便宜多少元?
12.陈叔叔从家到单位去上班,如果每分钟走60米,就要迟到2分钟;如果每分钟
走80米,就可以早到3分钟。
如果骑自行车每分钟行150米,从家到单位需要多少分钟?
13.一条大街上原有路灯201盏,相邻两盏路灯相距50米;现在换新路灯增加了
50盏,相邻两盏路灯的距离是多少米?
14.甲、乙两个油罐,如果每分钟放油5千克,甲罐52分钟把油放尽,乙罐36
分钟把油放完。
如果从甲罐向乙罐注油,需要过多少分钟两罐油相等?
15.于老师上班时坐车,回家时步行,在路上一共花90分钟;往返都坐车,只需
30分钟。
如果往返都步行,需要( )分钟。
、。
