正态总体下的四大分布
第2节正态总体下的抽样分布

U—分布 正态总体样本均值的分布
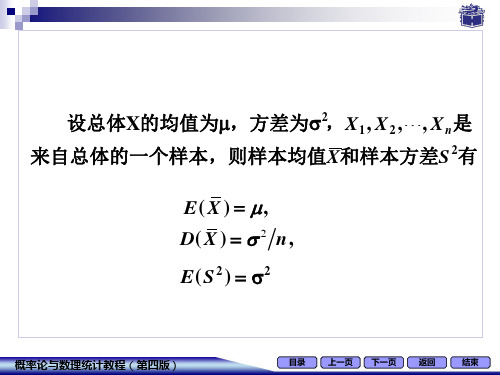
设总体 X ~ N , 2 , X1, X 2 ,..., X n 是 X 的一 个样本, 则样本均值服从正态分布
2 1 n X X i ~ N , n i 1 n
1 n Xi X n i 1 U ~ N 0,1 n n
性质:若X~F(n1,n2),则 1 ~F(n2,n1).
F 分布的上分位数 对于给定的 (0< <1),称满足条件
P F(n1, n2) F(n1, n2)
其几何意义如图5-7所示.
F (n1, n2)
X
f(y)dy
的数F(n1,n2)为F分布的上分位数或上侧临界值,
X n X T ~ t(n 1) 2 S n (n 1)S (n 1) 2
设(X1,X2,…,Xn)为来自正态总体 X~N( , 2)的样本,则统计量
由定义得
定理
别是来自正态总体N(1 ,2)和N(2 ,2)的样本,且 它们相互独立,则统计量
设(X1,X2,…,Xn1)和(Y1,Y2,…,Yn2) 分
n>30就用标准正态分布N(0, 1)来近似.
四、F分布
定义 设随机变量X~ 2(n1)、Y~ 2(n2),且 与相互独立,则称随机变量
服从第一自由度为n1,第二自由度为n2的F分布, 记作
X n1 F Y n2
F~F(n1,n2).
概率密度函数
n n 1 2 n1 1 Ay 2 (1 n1 y) 2 , y 0 f(y) n2 y0 0, n1 n2 ( ) n n1 2 其中 A ( 1 ) 2 , 其图形见图5-6.(P124) n1 n2 n2 ( )( ) 2 2
2.4正态总体分布 共40页

B. 0.2
C. 0.3
D.0.4
4、设ξ~N(1,4),试求:(1)P(-1<ξ≤3);(2)P(3<ξ≤5) ;(3)P(ξ≥5).
P(X)0.6826, P(2X2)0.9544, P(3X3)0.9974.
我们从上图看到,正态总体在2,2 以外取值的概率只有4.6%,在3,3 以
解: 由x于 服从正N态 4, 0.2分 5 布
由正态分布的性质知,
正态分布N4,0.25 在 4 3×0.5, 4 3×0. 5
之外取值的 概率只有0.003,而 5 .7 2 .5 , 5 .5
这说明在一次试验中,出现了几乎不可能发 生的小概率事件.
据此可认为该批零件是不合格的。
画频率分布直方图的步骤
1、求极差(即一组数据中最大值与最小值的差)
知道这组数据的变动范围4.3-0.2=4.1 2、决定组距与组数(将数据分组) 组距:指每个小组的两个端点的距离,
组数:将数据分组,当数据在100个以内时, 按数据多少常分5-12组。 组数=极 组差 距04..518.2
3、 将数据分组(8.2取整,分为9组) 4、列出频率分布表.(学生填写频率/组距一栏) 5、画出频率分布直方图。
总体密度曲线的形状特征. “中间高,两头低,
左右对称”
频率 概率密度曲线
组距
总体在区间 (a,b)内取值的概率
ab
产品 尺寸 (mm)
知识点二:正态分布与密度曲线
上图中总体密度曲线具有“中间高,两头低” 的特征,像这种类型的概率密度曲线,叫做 “正态密度曲线”,它的函数表达式是
f(x) 1 e(x22)2,x( , )
在实际遇到的许多随机现象都服从或近似 服从正态分布:
正态分布课件

4.应用举例 4.应用举例
例1:若X~N(5,1),求P(6<X<7). 求
例2:在某次数学考试中,考生的成绩 ξ 服从一个 在某次数学考试中,
正态分布, ξ 正态分布,即 ~N(90,100). (1)试求考试成绩 ) 多少? 多少?
ξ 位于区间 位于区间(70,110)上的概率是 上的概率是
X P 0 1 … … k
C nk p k q n − k
…
n
1 C n0 p 0q n C n p 1q n-1
… C nn p nq 0
4.由函数 y = f ( x) 及直线 x = a, x = b, y = 0y 由函数 围成的曲边梯形的面积S=_________; 围成的曲边梯形的面积 ∫a f ( x)dx ;
归纳小结
1.正态曲线及其特点; .正态曲线及其特点; 2.正态分布及概率计算 正态分布及概率计算; 2.正态分布及概率计算; 原则。 3.3σ原则。
P(µ − a < x ≤µ + a) = ∫
x=µ
ϕµ,σ ( x)dx µ−a
µ+a
µ-a
µ+a
特别地有(熟记) 特别地有(熟记)
P( µ − σ < X ≤ µ + σ ) = 0.6826, P( µ − 2σ < X ≤ µ + 2σ ) = 0.9544, P( µ − 3σ < X ≤ µ + 3σ ) = 0.9974.
3、设离散型随机变量X~N(0,1),则 P( X ≤ 0)= 0.5 、设离散型随机变量 则
P (−2 < X < 2) =
0.9544
.
4、若已知正态总体落在区间 (0.3, +∞) 的概率为 ,则 、 的概率为0.5, 0.3 相应的正态曲线在x= 时达到最高点。 相应的正态曲线在 时达到最高点。 5、已知正态总体的数据落在(-3,-1)里的概率和落 、已知正态总体的数据落在( ) 在(3,5)里的概率相等,那么这个正态总体的数学 )里的概率相等, 1 期望是 。
正态总体下的抽样分布

§1.2数理统计中常用的分布正态总体是最常见的总体, 本节介绍的几个抽样分布均对正态总体而言.1.标准正态分布2. 2分布3.t分布4.F分布o xϕ(x )定义:设X ~N (0,1),对任给的α, 0<α<1,称满足条件1、标准正态分布αϕαα==>⎰+∞dx x z X P z )(}{的点z α为标准正态分布的上α分位点.z αα例:求z0.05解:P{X≤z0.05}=1−P{X>z0.05}=1−0.05=0.95∵P{X≤1.64}=0.9495P{X≤1.65}=0.9505∴z0.05≈(1.64+1.65)/2=1.645公式: Φ(zα)=1−α常用数字575.296.1645.1005.0025.005.0===zzz定义:设X i ~N (0,1) (i =1,2,...,n ), 且它们相互独立,则称随机变量2、χ2分布221nii X χ==∑服从自由度为n 的χ2分布,记为χ2~χ2(n ).χ2分布最常用的是拟合优度检验.其中,在x > 0时收敛,称为Γ函数,具有性质1()tx te dtx +∞−−Γ=⎰(1)(),(1)1,(1/2)(1)!()x x x n n n N πΓ+=ΓΓ=Γ=Γ+=∈一般自由度为n 的χ2(n )的密度函数为12221,0()2()20,xnnn ex ng x x x −−⎧>⎪⎪=Γ⎨⎪⎪≤⎩χ2分布的密度函数图χ2~χ2(n)D Y =Di=1nX i 2=i=1n D(X i 2)=i=1n [E(X i 4)−(E(X i 2))2]=i=1n2=2n .χ2分布的基本性质(1)设Y 1~χ2 (m ), Y 2~χ2 (n ), 且Y 1 , Y 2 相互独立,则χ2 分布的可加性(2)若Y ~χ2 (n ), 则E (Y )=n ,D (Y )=2n.= 1;)(~221n m Y Y ++χY 1=i=1mX i 2,Y 2=i=m+1m+nX i 2,)(~2n m +χY 1+Y 2=i=1m+nX i2E Y =Ei=1nX i 2=i=1nE(X i 2)=i=1n[D(X i )+(E(X i ))2]=i=1n1=n ,E(X i 4)=12πන−∞+∞x 4e −x 22dx =3故(3)设X 1,…, X n 相互独立,且都服从正态分布N (μ,σ2),则;)(~)(12122n X Y ni i χμσ∑=−=(4)若Y ~χ2 分布,则当n 充分大时,近似服从N (0,1).n n Y 2−应用中心极限定理oχ2α(n )xf (x )α设χ2~χ2(n ),其密度函数为f (x ),对于给定的正数α(0<α<1),称满足条件αχχαχα==>⎰+∞dx x f n P n )(222)()}({的点χ2α(n )为χ2(n )分布的上α分位点.χ2分布的上α分位点当n 充分大时,22)12(1)(−+≈n z n ααχ例:设X ~N (μ,σ2), (X 1,X 2,...,X 16)是取自总体X 的样本,求概率:}2)(1612{216122σμσ≤−≤∑=i iX P 解:∵X 1,X 2,...,X 16相互独立且)1,0(~N X i σμ−)16(~)(21612χσμ∑=−∴i i X}2)(1612{216122σμσ≤−≤∑=i iX P }32)(8{1612≤−≤=∑=i i X P σμ}32)({}8)({16121612>−−≥−=∑∑==i i i i X P X P σμσμ≈0.95−0.01=0.94定义:设X ~N (0,1),Y ~χ2(n ),且X 与Y 相互独立,则称随机变量3、t 分布服从自由度为n 的t 分布,记为T ~t (n )./X T Y n=T 的密度函数为:22112()1,.2n n n t x x n n n x π+−+⎛⎫Γ ⎪⎛⎫⎝⎭=+−∞<<∞ ⎪⎛⎫⎝⎭Γ ⎪⎝⎭1908年英国统计学家W.S. Gosset (笔名Student )t分布的密度函数图T~t(n)t 分布的上α分位点设T ~t (n ),其密度函数为f (x ),对于给定的正数α(0<α<1),称满足条件(){()}()t n P T t n f x dt ααα+∞>==⎰的点t α(n )为t 分布的上α分位点.f (x )xt α(n )αt *0f (x )1-αx-t *t 分布的双侧α分位点设T ~t (n ),其密度函数为f (x ),对于给定的正数α(0<α<1),称满足条件*{||}1P T t α<=−的数t *为t 分布的双侧α分位点.α/2t 分布的密度函数f (x )是偶函数,故**()()P T t P T t ≤−=≥***(||)()P T t P t T t <=−<<*(),2P T t α≥=于是得即*()2P T t α>=**()()P T t P T t =<−≤−**(1())()P T t P T t =−≥−≥*12()1,P T t α=−≥=−= t α/2(n )t 分布的性质(1) 其密度函数f (x )是偶函数(3) f (x )的极限为N (0,1)的密度函数,即221lim ()()2x n f x x e φπ−→∞==(2)t 1−α(n )= −t α(n )当n >45时,t α(n )≈z α例:设X , Y 1,Y 2,Y 3,Y 4 相互独立,且X ~N (2,1),令Y i ~N (0, 4),i =1, 2, 3, 4 ,解:∵X -2~N (0, 1),~t (4),即Z 服从自由度为4 的t 分布.求Z 的分布.由t 分布的定义Y i /2~N (0, 1),i = 1, 2, 3, 4 . ,)2(4412∑=−=i iY X Z ∑=−=412)2(4i i Y X Z 4)2(2412∑=−=i i Y X例:设随机变量X 与Y 相互独立,X ~ N (0,16),Y ~ N (0,9) , X 1, X 2,…, X 9与Y 1, Y 2 ,…, Y 16分别是取自X 与Y 的简单随机样本,求统计量所服从的分布.解:)169,0(~921⨯+++N X X X )1,0(~)(431921N X X X +++⨯ 2162191YY XX Z ++++=从而16,,2,1,)1,0(~31=i N Y i )16(~3122161χ∑=⎪⎭⎫ ⎝⎛i i Y 2162221921Y Y Y X X X ++++++ ()16314311612921∑=⎪⎭⎫ ⎝⎛+++⨯=i i Y X X X )16(~tt分布用于在小样本(n<30)场合下的正态分布(大样本(n≥30)场合下可以用正态分布来近似),有时候在信息不足的情况下,只能用t分布,比如在总体方差不知的情况下,对总体均值的估计和检验通常要用t统计量.12222,()2(),0()()()220,0m n m m nm n x x m nm n n m x m n f x x +−−+⎧Γ⎪+>⎪=⎨ΓΓ⎪⎪≤⎩F 的密度函数为:所服从的分布为第一自由度为m ,第二自由度为n 的F 分布,记作F ~ F (m , n ).4、F 分布则称统计量F 分布多用于比例的估计和检验!nY mX F =定义:设随机变量X 与Y 独立,且X~χ2(m),Y~χ2(n),F 分布的密度函数图F~F(m,n)F 分布的上α分位点设F ~F (m ,n ),其密度函数为f (x ),对于给定的正数α(0<α<1),称满足条件ααα==>⎰+∞dx x f n m F F P n m F ),()()},({的点F α(m ,n )为F 分布的上α分位点.0f (x )F α(m ,n )αxF 分布的性质(1) 若F ~F (m ,n ),则(2)()~,1F F n m ),(1),(1m n F n m F αα=−}),(11{1n m F F P α−≤=∵1−α=P {F ≥F 1−α(m ,n )}}),(11{11n m F F P α−>−=αα=>⇒−}),(11{1n m F F P ),(),(11m n F n m F αα=⇒−(3)若X ~ t (n ), 则X 2~ F (1, n );mX nY F=1例:设F ~ F (24, 15) ,求F 1,F 2,F 3,使其分别满足P (F >F 1 )= 0.025 , P (F <F 2 )= 0.025 , P (F >F 3 )= 0.95 .解:(1)由m =24,n =15,α= 0. 025 ,查P192 附表6(2)无法直接查表获得,但由F 分布性质知1/F ~F (15, 24),查附表6知(3) ∵F 3 =F 0. 95(24,15), 查附表6知:∴ F 2 = 1/2.44 = 0.41 ; 由性质(2)知,025.0)11()(22=>=<F F P F F P 1F 2=F 0.025(15,24)=2.44⇒P(F <1/2.44)=0.025F 0.05(15,24)=2.11,,)24,15(1)15,24(95.0195.0−=F F .474.011.213==∴F 知F 1= F 0.025 (24, 15)= 2.70 ;抽样分布定理1. 单个正态总体的抽样分布2. 两个正态总体的抽样分布定理:设X 1,X 2,...,X n 是来自正态总体N (μ,σ2)的样本,则1. 单个正态总体的抽样分布(1)),(~2n N X σμ)1,0(~N n X σμ−⇒(2)与S 2相互独立X (3))1(~)1(222−−n S n χσ(4))1(~−−n t n S X μ1σ2n(X i −μ)2~χ2(n)(5)(1)∑==ni i X n X 11)1,0(~N n X σμ−⇒为n 个相互独立的正态X ∴服从正态分布∑==ni i X E n X E 1)(1)(=μ∑==n i i X D n X D 12)(1)(n2σ=),(~2n N X σμ∴随机变量的线性组合(4)),1,0(~N n X σμ− 且它们相互独立由t 分布的定义,)1(~1)1(22−−−−n t n S n nX σσμ)1(~−−n t n S X μ即22)1(σS n −~χ2(n −1)例:设(X 1,X 2,…,Xn )是取自总体X 的样本, 是样本均值,如果总体X ~N (μ,4),则样本容量n 应取多大才能使X 95.0}1.0|{|≥≤−μX P 解:)1,0(~ N n X σμ− }21.02||{}1.0|{|n n X P X P ≤−=≤−∴μμ}05.02)(05.0{n X n n P ≤−≤−=μ)05.0()05.0(n n −Φ−Φ=1)05.0(2−Φ=n ≥0.95975.0)05.0(≥Φ⇒n 96.105.0≥⇒n ⇒n ≥1536.64⇒n ≥1537解:),1(~)1(222−−n S n χσ由),,(~2nN X σμ又()⎪⎭⎫⎝⎛+−+n n N X X n 211,0~σ)1,0(~11N n n X X n +−+σ故212(1)~(1)1(1)n X Xn n St n n n σσ+⎛⎫−−−⎪+−⎝⎭于是)1(~11−+−+n t n nS X X n 即例:总体X ~N (μ,σ2),(X 1,X 2,…,X n ,X n +1)为样本,,求X n+1−തX S n n+1的分布.S 2=1n −1i=1n(X i −തX)2തX=1n i=1nX i定理:设总体X ~N (μ1,σ12),总体Y ~N (μ2,σ22).X 1,X 2,...,是总体X 的样本,Y 1,Y 2,...,是总体Y 的样本, 且这两个样本相互独立.则1n X 2n Y 2. 两个正态总体的抽样分布(1)),(~22212121n n N Y X σσμμ+−−(2))1,1(~2122222121−−n n F S S σσ)2(~11)()(212121−++−−−n n t n n S Y X ωμμ其中2)1()1(212222112−+−+−=n n Sn S n S ω称为混合样本方差.进一步,若σ12=σ22 =σ2,有(3)),(~221221n n N Y X σσμμ+−− )1,0(~11)()(2121N n n Y X +−−−∴σμμ2211)1(σSn −~χ2(n1−1),2222)1(σSn −~χ2(n2−1)且它们相互独立22222211)1()1(Sn Sn −+−∴~χ2(n1+n 2−2)由t 分布的定义,2)1()1(11)()(21222222112121−+−+−+−−−n n Sn Sn n n Y X σσσμμ22221121112)1()1()()(n n n n Sn S n Y X +−+−+−−−−μμ即~t (n 1+n 2−2)~t (n 1+n 2−2)小结1.理解总体、个体、样本和统计量的概念,掌握样本均值和样本方差的计算及基本性质2.掌握 2分布、t分布、F分布的定义,会查表计算3.理解正态总体的某些统计量的分布。
三大分布及正态总体统计量的分布-精选文档

k=1 k=2
k=6
0.3
0.2 0.1 O 2 4
6
8
10
12
14
x
2
注:
2 (1) 可以证明, 分布具有可加性:即 2 2 若随机变量 1 和 2 相互独立,且 2 2 2 2 ~ k , ~ k , 1 1 2 2
则它们的和
(2) 上 分位数:对于不同自由度 k及 2 0 1 不同的数 ,定义 为自由度为 k 2 的 分布的上 分位数,如果其满足
定理2 设总体 X 服从 N, ,则统计量
14
2 N , ,则统计量 定理3 设总体 X 服从 1 n 2 2 2 满足 X i
i 1
i 1 2 定理4 设总体 X 服从 N, ,则
S 2 相互独立; (1)样本均值 X 与样本方差 2
n 1 S (2)统计量 2 满足 2 n 1 S 2 2 ~ n 1 2
F
例如: F 5 , 1 0 3 . 3 3 0 . 0 5
k k Fkk ,1 1 (2)可以证明,F 2 1 1 , 2
11
F 分布上 分位数
fF x
O
F
x
12
§5.5
正态总体统计量的分布
1.单个正态总体的统计量的分布
约定: 从总体 X 中抽取样本容量为 n 的样 ,X ,X 本X 1 2, n,样本均值与样本方差分别是
X k1 F Y k2
,k 服从自由度为 k1 , k 2 的 F 分布,记作F~Fk 1 2
其中 k 1 称为第一自由度; k 2 称为第二自由度。
概率论与数理统计公式大全2

随机变量的数字特征
切比雪夫不等式给出了在未知X的分布的情况下,对概率
的一种估计,它在理论上有重要意义。
(2)期望的
性质
(1) E(C)=C
(2) E(CX)=CE(X)
(3) E(X+Y)=E(X)+E(Y),
(4) E(XY)=E(X) E(Y),充分条件:X和Y独立;
充要条件:X和Y不相关。
(3)方差的
性质
(1) D(C)=0;E(C)=C
(2) D(aX)=a2D(X); E(aX)=aE(X)
(3) D(aX+b)= a2D(X); E(aX+b)=aE(X)+b
(4) D(X)=E(X2)-E2(X)
(5)D(X±Y)=D(X)+D(Y),充分条件:X和Y独立;
充要条件:X和Y不相关。
D(X±Y)=D(X)+D(Y) ±2E[(X-E(X))(Y-E(Y))],无条件成立。
而E(X+Y)=E(X)+E(Y),无条件成立。
(4)常见分布的期望和方差
期望方差
0-1分布p
二项分布np
泊松分布
几何分布
超几何分布
均匀分布
指数分布
正态分布
n 2n
t分布0 (n>2)
(5)二维随
机变量的数
期望
第六章样本及抽样分布
第七章参数估计
第八章假设检验
单正态总体均值和方差的假设检验。
正态总体统计量的分布

§5.5 正态总体统计量的分布1. 单个正态总体的统计量的分布从总体X 中抽取容量为n 的样本n X X X ,,,21 ,样本均值与样本方差分别是()212111,1∑∑==--==n i i n i i X X n S X n X . 定理1 设总体X 服从正态分布()2,σμN ,则样本均值X 服从正态分布⎪⎪⎭⎫ ⎝⎛nN 2,σμ,即⎪⎪⎭⎫ ⎝⎛n N X 2,~σμ证 因为随机变量n X X X ,,,21 相互独立,并且与总体X 服从相同的正态分布()2,σμN ,所以由§4。
3中的定理知,它们的线性组合X 服从正态分布⎪⎪⎭⎫ ⎝⎛nN 2,σμ。
定理2 设总体X 服从正态分布()2,σμN ,则统计量nX u σμ-=服从标准正态分布()1,0N ,即()1,0~N nX u σμ-=由定理1结论的标准化即得到定理2. 定理3 设总体X 服从正态分布()2,σμN ,则统计量()∑=-=ni iX X12221σχ服从自由度为n 的2χ分布,即()()n X Xni i21222~1χσχ∑=-=证 注意到()2,~σμN X i ,则()n i N X i ,,2,1 ,1,0~ =-σμ又上述统计量相互独立,并按照2χ分布的定义可得结果。
定理4 设总体X 服从正态分布()2,σμN ,则 (1)样本均值X 与样本方差2S 相互独立; (2)统计量()2221σχS n -=服从自由度为1-n 的2χ分布,即()()1~12222--=n S n χσχ证明略。
定理5 设总体X 服从正态分布()2,σμN ,则统计量nSX t μ-=服从自由度为1-n 的t 分布,即()1~--=n t nSX t μ证 由定理2知,统计量()1,0~N nX u σμ-=又由定理4知,统计量()()1~12222--=n S n χσχ因为X 与2S 相互独立,所以u 与2χ也相互独立,于是根据t 分布的定义得结论。
5-4正态总体统计量的分布
2
2
(n 1)S 2
2
1
2
n
Xi
i1
__
X
2
__
X
~
N
, 2
n
u ~ N0,1
t ~ t(n 1) .
2 ~ 2(n)
2 ~ 2(n 1)
概率论与数理统计教程(第四版)
目录
上一页 下一页
返回
结束
§5.4 正态总体统计量的分布
两个正态总体X ~ N
1 ,12
,Y ~ N
2
,
2 2
统计量及其分布
__
(X
__
Y)
1 n1
n1 i1
Xi
1 n2
n2
Yj
~
N (1
2
,
2 1
j 1
n1
2 2
n2 )
(1 2 )
__ __
U ( X Y ) (1 2) ~ N (0,1) 1 n1 1 n2
n1 Xi 12 (n112 )
F
i1 n2
Yj 2
2
~ F (n1 , n2 )
目录
上一页 下一页
返回
结束
§5.4 正态总体统计量的分布
__
[定理5] 设总体 X ~ N , 2 ,则 t X ~ t(n 1) . Sn
说明:
__
u X ~ N 0,1,
n
2
(n 1)S 2
2
~
2 (n 1).
由于u与 2相互独立,统计量
__
t u X ~ t(n 1) . 2 n 1 S n
16
__
(2)如果未知 ,求( Xi X )2 100的概率.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《概率论与数理统计》第六章样本及抽样分布
(2)正态总体下的四大分布:正态分布
设n x x x ,,,21 为来自正态总体),(2
σ
μN 的一个样本,则样本函数
).
1,0(~/N n
x u
def
σμ
-例:设总体ξ~2
12(1,2
),,,n N ξξξ 且是取自ξ的样本,则(
D )
A)
1(0,1)
2
N ξ-B)
1(0,1)
4N ξ-C)
(
)
1(0,1)
2
N ξ-D
)
(0,1)
N ξt 分布
设n x x x ,,,21 为来自正态总体),(2
σ
μN 的一个样本,则样本函数),
1(~/--n t n
s x t
def
μ其中t(n-1)表示自由度为n-1的t 分布。
分布
2χ设n x x x ,,,21 为来自正态总体),(2
σ
μN 的一个样本,则样本函数
),
1(~)1(22
2
--n S n w
def
χσ其中)1(2
-n χ
表示自由度为n-1的2χ
分布
例:已知F 0.1(7,20)=2.04,则F 0.9(20,7)=_______0.4902_____.
例.对于给定的正数α,10<<α
,设αu ,)(2
n α
χ,)(n t α,),(21n n F α分别是)1,0(N ,)(2n χ,)(n t ,),(21n n F 分布的下α
分位数,则下面结论中不正确...
的是(B )
(A)α
α
--=1u u (B))
()
(2
2
1n n ααχχ-=-(C))
()(1n t n t αα--=(D))
,(1
)
,(12211n n F αα=
-2、设X 、Y 相互独立,且都服从标准正态分布,则Z =
2
Y X 服从______t(1)_____分布(同时要写出
分
布的参数).
3.设ξ和η相互独立且都服从N(0,4),而41,ξξ 和41,ηη 分别是来自总体ξ和η的样本,则统计量2
4
2
141......ηηξξ++++=
U 服从的分布为
)
4(t 。
