11.12直线与平面平行的性质定理讲课
合集下载
直线、平面平行的判定与性质 课件
(2)GH∥平面 PAD. 证明:连接 FH,OH, ∵F,H 分别是 PC,CD 的中点, ∴FH∥PD,∴FH∥平面 PAD. 又∵O 是 AC 的中点,H 是 CD 的中点, ∴OH∥AD,∴OH∥平面 PAD. 又 FH∩OH=H, ∴平面 OHF∥平面 PAD. 又∵GH⊂平面 OHF,∴GH∥平面 PAD.
又因为点 H 为 BC 的中点, 所以 OH∥BD. 又因为 OH⊂平面 FGH,BD⊄平面 FGH, 所以 BD∥平面 FGH.
判定线面平行的四种方法 (1)利用线面平行的定义(无公共点); (2)利用线面平行的判定定理(a⊄α,b⊂α,a∥b⇒a∥α); (3)利用面面平行的性质定理(α∥β,a⊂α⇒a∥β); (4)利用面面平行的性质(α∥β,a⊄α,a⊄β,a∥α⇒a∥β).
α∥β,α∩γ=a, β∩γ=b⇒a∥b
面面平行的判定与性质 [典例] 如图所示,在三棱柱 ABC-A1B1C1 中,E,F,G,H 分别是 AB,AC,A1B1,A1C1 的中点,求证: (1)B,C,H,G 四点共面; [证明] ∵G,H 分别是 A1B1,A1C1 的中点, ∴GH 是△A1B1C1 的中位线, ∴GH∥B1C1. 又∵B1C1∥BC,∴GH∥BC, ∴B,C,H,G 四点共面.
突破点(二) 平面与平面平行的判定与性质
平面与语言 符号语言
一个平面内的两条_相__交_ 判定 直__线__与另一个平面平 定理 行,则这两个平面平行
(线面平行⇒面面平行)
a∥β,b∥β, a∩b=P,a⊂α, b⊂α⇒α∥β
如果两个平行平面同时
性质 定理
和第三个平面_相__交__,那 么它们的_交__线__平行
(2)平面 EFA1∥平面 BCHG. [证明] ∵E,F 分别是 AB,AC 的中点, ∴EF∥BC. ∵EF⊄平面 BCHG,BC⊂平面 BCHG, ∴EF∥平面 BCHG.
直线、平面平行的判定及其性质完整ppt课件

思考4:有一块木料如图,
E
P为面BCEF内一点,要求 过点P在平面BCEF内画一
F
P D
条直线和平面ABCD平行,
那么应如何画线?
A
整理版课件
C B
5
思考5:如图,设直线b在平面α内,直 线a在平面α外,猜想在什么条件下直线 a与平面α平行?
a
a//b
α
b
整理版课件
6
探究(二):直线与平面平行的判断定理
通过直线间的平行,推证直线与平面平 行,即将直线与平面的平行关系(空间 问题)转化为直线间的平行关系(平面 问题).
整理版课件
10
思考6:设直线a,b为异面直线,经过
直线a可作几个平面与直线b平行?过a,
b外一点P可作几个平面与直线a,b都
平行?
a
b
p
b a a
p
整理版课件
b
11
理论迁移
例1 在空间四边形ABCD中,E,F分别是 AB,AD的中点,求证:EF//平面BCD.
定理,分别用文字语言和符号语言可以
怎样表述?
γ
定理 如果两个平行
b
平面同时和第三个平 β
面相交,那么它们的
交线平行.
α
a
/ /, a ,整理版课件 b a / /b 48
思考2:上述定理通常称为平面与平面平 行的性质定理,该定理在实际应用中有 何功能作用?
/ / , a , b a / /b
整理版课件
41
2.2 直线、平面平行的判定及其性质 2.2.4 平面与平面平行的性质
整理版课件
42
问题提出
1.平面与平面平行的判定定理是什么?
线面平行的性质定理 ppt课件

(三)预习自测
判断
(1)若点A不在平面ɑ内,则过点A只能作一条直线 与ɑ平行( ) (2)若直线a与平面ɑ平行,则a与ɑ内的直线的位置 关系有平行和异面两种。( )
(3)若直线a与平面ɑ平行,且a与直线b平行,则b 也一定平行于ɑ。( ) (4)若直线a与平面ɑ平行,且a与直线b垂直,则b 不可能与ɑ平行。( )
二、研讨案
例1:如图,已知直线a,b,平面ɑ,且 a//b,a//ɑ,a,b都在平面ɑ外。求证:
b//ɑ
变式训练:如图,E、H分别是空间四边形 ABCD的边AB、AD的中点,平面α过EH分 别交BC、CD于F、G.求证:EH∥FG.
三、学习体会及小结
本节的学习过程你掌握了什么知识?还 有哪些疑问?请写出。
学习目标:
1.理解直线与平面平行的性质定理的含义,并会应 用性质定理解决问题
2.能应用文字语言、符号语言、图形语言准确地 描述直线与平面平行的性质定理
学习重点:直线与平面平行的性质定理及其应用
学习难点:直线与平面平行的性质定理及其应用
(一)课前复习与思考:
1.空间直线与直线的位置关系? 2.直线与平面的位置关系? 3.直线与平面平行的判定定理的符号表示:
β
b
问题4:在你画出的图中,平面β是经
过直线a,b的平面,显然它和平面ɑ是
相交的,并且直线b是这两个平面的交
线,而直线a和b又是平行的。因此你
能得出什么结论?请把它用符号语言写
在下面。
β
b
问题5:在上图中过直线a再画另外一
个平面r与平面ɑ相交,交线为c。直线 a,c平行吗?和你上面得出结论相符 吗?你能不能从理论上加以证明呢?
四、巩固加强
1.若直线a、b均平行于平面α,则a与b 的关系是( ).
直线、平面平行的判定与性质课件

考点一
直线与平面平行的判定与性质
考向基础
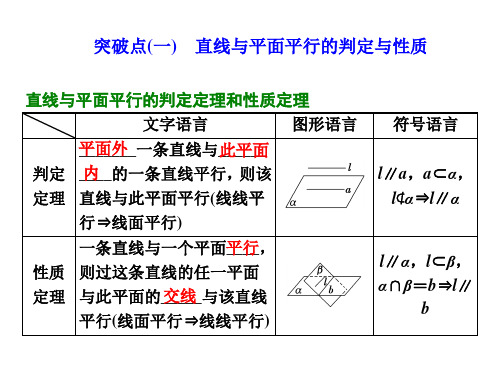
直线与平面平行的判定与性质
文字语言
平面外一条直线与此平面内的一
图形语言
符号语言
a⊄α,b⊂α,且a∥b⇒a∥α
条直线平行,则该直线与此平面
平行.简称:线线平行,则线面平行
一条直线与一个平面平行,则过
a∥α,a⊂β,
这条直线的任一平面与此平面的
α∩β=b⇒a∥b
别平行于另一个平面内的两条相交直线,那么这两个平面平行.
3.证明两个平面都垂直于同一条直线.(客观题可用)
4.证明两个平面同时平行于第三个平面.(客观题可用)
例2 如图所示,正方体ABCD-A1B1C1D1中,
M,N分别是A1B1,A1D1的中点,E,F分别是B1C1,C1D1的中点.
(1)求证:四边形BDFE为梯形;
∴PQ∥平面BCE.
证法二:如图,在平面ABEF内,过点P作PM∥BE,交AB于点M,连接QM.
∴PM∥平面BCE,且
AP AM
=
,
PE MB
易知AE=BD,又AP=DQ,∴PE=BQ,
∴
AP DQ
AM DQ
=
,∴
=
,
PE BQ
MB QB
∴MQ∥AD,又AD∥BC,
∴MQ∥BC,
∵BC⊂平面BCE,MQ⊄平面BCE,
∴OB∥平面EFC,
∵OB∩OG=O,∴平面OBG∥平面EFC.
方法技巧
方法1
证明直线与平面平行的方法
1.利用线面平行的定义(此法一般伴随反证法证明).
2.利用线面平行的判定定理.应用此法的关键是在平面内找与已知直线
平行的直线.可先直观判断平面内是否已有,若没有,则需作出该直线,常
直线与平面平行的判定与性质
考向基础
直线与平面平行的判定与性质
文字语言
平面外一条直线与此平面内的一
图形语言
符号语言
a⊄α,b⊂α,且a∥b⇒a∥α
条直线平行,则该直线与此平面
平行.简称:线线平行,则线面平行
一条直线与一个平面平行,则过
a∥α,a⊂β,
这条直线的任一平面与此平面的
α∩β=b⇒a∥b
别平行于另一个平面内的两条相交直线,那么这两个平面平行.
3.证明两个平面都垂直于同一条直线.(客观题可用)
4.证明两个平面同时平行于第三个平面.(客观题可用)
例2 如图所示,正方体ABCD-A1B1C1D1中,
M,N分别是A1B1,A1D1的中点,E,F分别是B1C1,C1D1的中点.
(1)求证:四边形BDFE为梯形;
∴PQ∥平面BCE.
证法二:如图,在平面ABEF内,过点P作PM∥BE,交AB于点M,连接QM.
∴PM∥平面BCE,且
AP AM
=
,
PE MB
易知AE=BD,又AP=DQ,∴PE=BQ,
∴
AP DQ
AM DQ
=
,∴
=
,
PE BQ
MB QB
∴MQ∥AD,又AD∥BC,
∴MQ∥BC,
∵BC⊂平面BCE,MQ⊄平面BCE,
∴OB∥平面EFC,
∵OB∩OG=O,∴平面OBG∥平面EFC.
方法技巧
方法1
证明直线与平面平行的方法
1.利用线面平行的定义(此法一般伴随反证法证明).
2.利用线面平行的判定定理.应用此法的关键是在平面内找与已知直线
平行的直线.可先直观判断平面内是否已有,若没有,则需作出该直线,常
《直线与平面平行》课件

的稳定性和美观性。
02
建筑测量
在建筑测量中,直线与平面平行的概念对于确定建筑物是否垂直和水平
非常重要。测量师使用铅锤和水平仪等工具来确保建筑物的基础、柱子
和横梁等结构与地面平行。
03
建筑结构分析
在建筑结构分析中,直线与平面平行的概念对于评估结构的稳定性和安
全性至关重要。工程师使用这些概念来分析建筑物的支撑结构和受力情
电子设备制造
在电子设备制造中,直线与平面平行的概念对于确保电子设备的精确度和质量非常重要。制造商使用这些概念来控制 装配和焊接过程,以确保电子元件的放置和连接正确。
电子设备维修
在电子设备维修中,直线与平面平行的概念对于检查和调整电子元件的位置非常重要。维修人员使用这 些概念来检查设备的平行度和垂直度,以确保设备的正常运行和性能。
文字描述
如果一条直线与一个平面平行, 那么这条直线与此平面内的任何 直线都平行。
解释
这个定理说明了直线与平面平行 的条件,即直线必须与平面内的 所有直线都平行,才能判定该直 线与该平面平行。
直线与平面平行判定定理的数学公式
数学公式
若直线$l$与平面$alpha$平行,则对于任意直线$m$在平面$alpha$上,都有 $l parallel m$。
02
若直线$l$与平面$alpha$平行, 则对于任意点$P$在平面$alpha$ 上,有$l cap P = emptyset$。
直线与平面平行性质定理的图形解释
当直线与平面平行时,该直线与平面 内的所有直线都保持平行关系,没有 交点。
在图形中,可以标出一些具体的点来 解释该性质定理,例如选择平面上的 一些点并观察它们是否与直线有交点 。
可以通过作一条与已知直线平行的直 线来验证该性质定理,观察新作的直 线是否与平面内的其他直线平行且无 交点。
直线和平面平行的判定定理ppt课件

判定定理二:向量
03
共线法
向量共线法原理
定义
若两向量方向相同或相反,则称这两 向量共线。
性质
应用
在直线与平面平行判定中,通过判断 直线的方向向量与平面上两不共线向 量的关系,确定直线与平面的位置关 系。
共线的向量可以表示为同一基向量的 倍数。
向量运算规则
加法运算
向量加法满足平行四边形 法则或三角形法则。
$l parallel alpha$。
实例二
若直线$l$的方向向量$vec{a}$ 与平面$alpha$的法向量
$vec{n}$满足$vec{a} cdot vec{n} = 0$,则$l parallel
alpha$。
讨论
通过实例分析,我们可以发现向 量共线法在直线与平面平行判定 中的重要作用。同时,需要注意 判定条件的充分性和必要性,以
及特殊情况的处理。
判定定理三:距离
04
相等法
距离相等法原理
直线与平面平行时,直线上任意一点 到平面的距离都相等。
利用这一性质,可以通过比较直线上 不同点到平面的距离是否相等来判断 直线与平面是否平行。
点到直线距离公式
点$P(x_0, y_0, z_0)$到平面 $Ax + By + Cz + D = 0$的距 离公式为
直线与平面的距离为零
当直线上的任意一点到平面的距离都为零时,直线与平面平行。可 以通过计算点到平面的距离公式来判断。
复杂问题简化策略
转化为基本问题
将复杂问题转化为判断直线与平面是否平行的基本问题,以便运 用上述方法进行求解。
利用已知条件
充分利用题目中给出$d = frac{|Ax_0 + By_0 + Cz_0 + D|}{sqrt{A^2 + B^2 + C^2}}$
直线与平面平行的判定定理(公开课)ppt课件
(2)直线 a与平面 相交吗?
a
不可能相交
b
.
直线与平面平行判定定理
平面外一条直线与此平面内的一条直线平行,则该 直线与此平面平行.
a
b
a
b
a
/
/b
a / /
证明直线与平面平行,三个条件必须具备,才能得 到线面平行的结论.
直线与平面平行关系
空间问题
.
直线间平行关系 平面问题
典型例题
例1 求证:空间四边形相邻两边中点的连线
∴MN // DE
2
BC.
A
M
N
C
B
∴四边形DMNE为平行四边形.
∴EN//DM
∵DM 平面PDC,EN 平面PDC
∴EN//平面PDC
.
变式:如图,在正方体ABCD——
A1B1C1D1中,E、F分别是棱BC与C1D1的
中点。
求证:EDF1 //平F面BDD1B1. C1
A1
A1
B1
D1
F
C1
பைடு நூலகம்
M
B1
ND M
A
C E B
D A
.
C E B
反思-顿悟
1.要证明直线与平面平行可以运用线面平行的判定定
理;
线线平行
线面平行
2.能够运用定理的条件要满足三个条件: “一线面内、
a
一线面外、
b
a //
两线平行”
b // a
3.运用定理的关键找平行线;找平行线又经常会用到
三角形中位线、梯形的中位线、平行四边形、平行线 的判定定理,平行公理.(一般题中有中点再找中点,有 分点再找分点得平行关系.)
直线与平面平行的性质ppt课件
举例 经营者提供商品或者服务有欺诈行为的,应当按照消费者的要求增加赔偿其受到的损失,增加赔偿的金额为消费者购买商品的价款或接受服务的费用
例4. 设平面α、β、γ两两相交,且 a , b , c 若a∥b,求证:b∥c .
a
c
b
α
β
γ
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
证明:因为 b,所以 b 因 为 a // b 所 以 a // , 又因为 a,所以 a 又因为 c 所 以 a // c, 因 为 a // b 所 以 b // c
小结
1. 复习直线与平面的位置关系 2. 复习直线与平面平行的判定 3. 学习并掌握直线与平面平行的性质
b (√)
a
举例 经营者提供商品或者服务有欺诈行为的,应当按照消费者的要求增加赔偿其受到的损失,增加赔偿的金额为消费者购买商品的价款或接受服务的费用
例2.在四面体ABCD中,E、F分别是 AB、AC的中点,过直线EF作平面α,分别 交BD、CD于M、N,求证:EF∥MN.
A
E
F
BM
D
N C
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
直线与平面平行的性质定理:
如果一条直线和一个平面平行,经 过这条直线的平面和这个平面相交,那 么这条直线和交线平行.
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
直线与平面平行的判定定理(公开课)ppt课件
若两向量的点积为零,则 它们垂直。
应用
通过计算直线方向向量与 平面法向量的点积,可以 判断直线与平面是否平行 。
判定定理三:法向量垂直
定义
若一直线与一平面平行, 则该直线的法向量与该平 面的法向量平行。
推论
若两向量平行,则它们的 分量成比例。
应用
通过比较直线法向量与平 面法向量的分量比例,可 以判断直线与平面是否平 行。
直线与平面平行的定义
阐述直线与平面平行的基本概念,为后续判定定理 的引入做铺垫。
判定定理的重要性
说明直线与平面平行判定定理在几何学中的地位和 作用,以及在实际应用中的价值。
教学目标
80%
知识与技能
掌握直线与平面平行的判定定理 及其证明方法,理解相关概念, 能够运用所学知识解决相关问题 。
100%
过程与方法
应用举例二:判断两平面是否平行
方法一
利用平行平面的性质,通过证明一个 平面内有两条相交直线分别与另一个 平面平行,从而判定两个平面平行。
方法二
利用向量法,通过计算两个平面的法 向量是否共线,从而判定两个平面是 否平行。
应用举例三:解决实际问题中的平行问题
1 2
实例一
在建筑设计中,利用直线与平面平行的性质,确 保建筑物的立面、地面等各部分保持平行,以达 到美观和稳定的效果。
定义
应用
若一直线与一平面平行,则该直线与 该平面内任意一条直线的斜率相等。
通过比较直线与平面内某一直线的斜 率,可以判断直线与平面是否平行。
推论
若两直线的斜率相等,则它们或者平 行或者重合。
判定定理二:方向向量平行
01
02
03
定义
若一直线与一平面平行, 则该直线的方向向量与该 平面的法向量垂直。
应用
通过计算直线方向向量与 平面法向量的点积,可以 判断直线与平面是否平行 。
判定定理三:法向量垂直
定义
若一直线与一平面平行, 则该直线的法向量与该平 面的法向量平行。
推论
若两向量平行,则它们的 分量成比例。
应用
通过比较直线法向量与平 面法向量的分量比例,可 以判断直线与平面是否平 行。
直线与平面平行的定义
阐述直线与平面平行的基本概念,为后续判定定理 的引入做铺垫。
判定定理的重要性
说明直线与平面平行判定定理在几何学中的地位和 作用,以及在实际应用中的价值。
教学目标
80%
知识与技能
掌握直线与平面平行的判定定理 及其证明方法,理解相关概念, 能够运用所学知识解决相关问题 。
100%
过程与方法
应用举例二:判断两平面是否平行
方法一
利用平行平面的性质,通过证明一个 平面内有两条相交直线分别与另一个 平面平行,从而判定两个平面平行。
方法二
利用向量法,通过计算两个平面的法 向量是否共线,从而判定两个平面是 否平行。
应用举例三:解决实际问题中的平行问题
1 2
实例一
在建筑设计中,利用直线与平面平行的性质,确 保建筑物的立面、地面等各部分保持平行,以达 到美观和稳定的效果。
定义
应用
若一直线与一平面平行,则该直线与 该平面内任意一条直线的斜率相等。
通过比较直线与平面内某一直线的斜 率,可以判断直线与平面是否平行。
推论
若两直线的斜率相等,则它们或者平 行或者重合。
判定定理二:方向向量平行
01
02
03
定义
若一直线与一平面平行, 则该直线的方向向量与该 平面的法向量垂直。
直线与平面平行的性质平面与平面平行的性质(共22张PPT)
对一些用文字语言描述的命题加以证明时,一般应先写出和求证 。
例1 如下图的一块木料中,棱BC平行于面 A'B'C'D', 〔1〕要经过面A'B'C'D'内的一点P和棱BC将木料锯 开,应该怎样画线?
〔2〕所画的线和平面ABCD是什么位置关系?
D'
C'
A'
P
C
D B'
A
B
解:〔1〕在平面A'C'内,过点P作直线EF,使EF ∥ B'C',并分别交棱A'B',C'D'于点E,F。连BE ,CF。那么EF,BE,CF就是应画的线。
D'
F
A'
P
D
E
A
C'
C B' B
〔2〕因为棱BC平行于平面A'C',平面BC'与平面A'C'交 于B'C',所以,BC ∥ B'C'。由1知,EF ∥ B'C' ,所以 EF ∥ BC,因此EF ∥ BC,EF不在平面AC,BC在平面 AC上,从而EF ∥平面AC。BE,CF显然都与面AC相交 。
3. P为长方形ABCD所在平面外一
点,M,N分别为AB,PD上的
H E
点
AM MB
=
DN NP
,
求证:MN∥平面PBC。 N
B
P
F
G
D
C
D
C
A M
B
课堂小结
〔2〕因为棱BC平行于平面A'C',平面BC'与平面A'C'交于B'C',所以,BC ∥ B'C'。
例1 如下图的一块木料中,棱BC平行于面 A'B'C'D', 〔1〕要经过面A'B'C'D'内的一点P和棱BC将木料锯 开,应该怎样画线?
〔2〕所画的线和平面ABCD是什么位置关系?
D'
C'
A'
P
C
D B'
A
B
解:〔1〕在平面A'C'内,过点P作直线EF,使EF ∥ B'C',并分别交棱A'B',C'D'于点E,F。连BE ,CF。那么EF,BE,CF就是应画的线。
D'
F
A'
P
D
E
A
C'
C B' B
〔2〕因为棱BC平行于平面A'C',平面BC'与平面A'C'交 于B'C',所以,BC ∥ B'C'。由1知,EF ∥ B'C' ,所以 EF ∥ BC,因此EF ∥ BC,EF不在平面AC,BC在平面 AC上,从而EF ∥平面AC。BE,CF显然都与面AC相交 。
3. P为长方形ABCD所在平面外一
点,M,N分别为AB,PD上的
H E
点
AM MB
=
DN NP
,
求证:MN∥平面PBC。 N
B
P
F
G
D
C
D
C
A M
B
课堂小结
〔2〕因为棱BC平行于平面A'C',平面BC'与平面A'C'交于B'C',所以,BC ∥ B'C'。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
作业
教材P21 1、习题9.3第4、6题 2.如图,已知异面直线AB、CD都与平面平行,CA、 CB、DB、DA分别交于点E、F、G、H. 求证:四边形EFGH是平行四边形.
A B
E
H
G
α
F
D
C
再 见
证明:
a与没有公共点 又因为b在内 a与b没有公共点
又 a与b都在平面内 且没有公共点
ቤተ መጻሕፍቲ ባይዱ
a //
a
b
a // b
直线与平面平行的性质定理
如果一条直线和一个平面平行,经过 这条直线的平面与这个平面相交,那 么这条直线和交线平行
b
线面平行
a // a
复习:直线与平面平行的判定定理的内容
如果不在一个平面内的一条直线和平面内的一条直线 平行,那么这条直线和这个平面平行
a b a // a // b
线线平行
a
线面平行
b
能否由线面平行,得到线线平行?
若已知
a //
,则在
a
内是否存在直线与a平行? 若存在,该如何画出?
a//b
线线平行
a b
定理说明: 1、定理可以作为直线与直线平行的判定方法 2、提供了过已知平面内一点作与该平面的平 行线相平行的直线方法,即:辅助平面法 3、定理中三个条件缺一不可
a
b
1、若去掉条件 a
,则
2、若去掉条件 b
,则
b
a
例1:已知平面外的两条平行直线中的一 条平行于这个平面,求证:另一条也平 行于这个平面. a b
A.a∥α,b α,则a∥b ;B.a∩α=P,b α,则a与b不平行 C.a α,则a∥α
二、填空题. 1.过平面外一点作一平面的平行线有 条. ;D.a∥α,b∥α,则a∥b
2.若直线a∥b,a∥平面α,则直线b与平面α的位置关系是:
归纳小结
在使用中要注意一种思想和一种方法 1、转化的数学思想. 即线线平行与线面平 行之间的相互转化,亦即空间问题与平面 问题之间的相互转化,这也是解决立体几 何问题的重要思想方法 2、辅助平面法. 即构造辅助平面,以实现 线线平行与线面平行间的相互转化
请思考以下问题:
1、若直线与平面平行,则该直线平面内的直 线的位置关系有几种可能? 位置关系有两种:平行或异面 2、平行于平面的一条直线与该平面内一条直线平 行,需要附加什么条件? 需附加条件:它们在同一平面β内
图形演示
a b
已知:直线a , a , b 求证:a // b
求证: a // m
m
a
证明:过直线a作平面与平面 交于直线b, 过直线a作平面与 平面交于直线c。
a b
a //
a//b
同理可得
A
a//c
b
a
m
c
c
b
b//c
b m
b //
b // m
例3、如图所示的一块木料中,棱BC平行于面A’C’
如图:已知直线a,b,平面, 且a // b,a//,a,b都在平面外。 求证:b//
证明:过a作面交于c a a // a//c a//b c
a
C
b
b//c
b
c
b //
说明: 线//线
线//面
l
a 例2: 已知平面 ∩平面 =m, // a //
(1)要经过面A’C’内的一点P和棱BC将木料锯开,应 怎样画线? (2)所画的线与平面AC是什么位置关系?
学生训练
一、选择题. 1.若直线a不平行于平面α,则下列结论成立的是( ) A.α内的所有直线都与直线a异面;B.α内不存在与a平行的直线 C.α内的直线都与a相交; 2.下列判断正确的是( ) D.直线a与平面α有公共点
