1.7-1.8几何空间向量的外积
两向量外积的几何意义

两向量外积的几何意义
两向量的外积又称为叉乘,表示为AxB。
这是一个向量运算,结果是一个新的向量,垂直于原来两个向量所在的平面。
几何上,两向量的外积具有以下几何意义:
1. 方向:外积结果的方向垂直于原来两个向量所在的平面,并且符合右手法则。
将右手的食指指向A向量的方向,中指指
向B向量的方向,那么拇指的方向即为外积向量的方向。
2. 长度:外积向量的长度等于A向量和B向量构成的平行四
边形的面积,即|AxB| = |A| |B| sinθ,其中θ为A和B夹角的大小,|A|和|B|分别为两个向量的长度。
3. 平行四边形:外积所得的向量与原来两个向量构成的平行四边形有一一对应的关系。
平行四边形的面积等于外积向量的长度,平行四边形的方向与外积向量的方向一致。
4. 正交性:如果两个向量的外积结果为零向量,则说明这两个向量是共线的,或者说它们所在的平面是重叠的。
总的来说,两向量的外积提供了一个垂直于原来向量所在平面的向量,其方向、长度和平行四边形都与原向量有一一对应的关系,可以用于描述空间中的旋转、力学等问题。
空间向量及几何公式

空间向量及几何公式一、空间向量的基本概念空间向量是指具有方向和大小的矢量。
在三维空间中,我们通常使用坐标系来描述向量。
设P(x1,y1,z1)和Q(x2,y2,z2)是空间中的两个点,向量PQ就是从点P指向点Q的矢量。
向量可以用箭头表示,箭头的长度表示向量的大小,箭头的方向表示向量的方向。
空间向量常用的表示方式有坐标表示和分量表示。
坐标表示是指用坐标轴上的坐标来表示向量。
例如,向量PQ可以表示为向量(PQ)=(x2-x1,y2-y1,z2-z1)。
分量表示是指将向量沿坐标轴投影的长度表示为向量的分量。
例如,向量PQ的x分量表示为Qx-Px,y分量表示为Qy-Py,z 分量表示为Qz-Pz。
二、空间向量的运算空间向量的运算包括加法、减法、数乘和点乘。
1.向量加法:设向量A=(x1,y1,z1)和向量B=(x2,y2,z2),则向量A+B=(x1+x2,y1+y2,z1+z2)。
2.向量减法:设向量A=(x1,y1,z1)和向量B=(x2,y2,z2),则向量A-B=(x1-x2,y1-y2,z1-z2)。
3. 数乘:设向量A = (x, y, z),实数k,则kA = (kx, ky, kz)。
4.点乘:设向量A=(x1,y1,z1)和向量B=(x2,y2,z2),则向量A·B=x1x2+y1y2+z1z2三、空间向量的几何公式空间向量的几何公式包括向量模长公式、共线公式、垂直公式、夹角公式和等距平移公式。
1.向量模长公式:设向量A=(x,y,z),则向量A的模长为,A,=√(x^2+y^2+z^2)。
2.共线公式:设向量A=(x1,y1,z1)和向量B=(x2,y2,z2),若存在实数k,使得x1/k=x2,y1/k=y2,z1/k=z2,则向量A和向量B共线。
3.垂直公式:设向量A=(x1,y1,z1)和向量B=(x2,y2,z2),若向量A·B=0,则向量A和向量B垂直。
向量的外积和混合积

x ( x, x )
三维空间:
x
k 1
n
2 k
设 x ( x1 , x2 , x3 )
y ( y1 , y2 , y3 )
12
则 x y x1 y1 x2 y2 x3 y3
2) 任意两向量之间的夹角定义:
( x, y) cos x y
1
平面解析几何是通过坐标法,把平面上的点与一 对有序的数对应起来,把平面上的图形和方程对应 起来,从而可以用代数方法来研究几何问题。空间 解析几何也是按照类似的方法建立起来的,它是在 三维坐标系中,用代数方法研究空间曲面和曲线性 质的一个数学分支。
2
§1 向量的外积与混合积
一、空间直角坐标系 三个坐标轴的正方向符合右手系。 即以右手握住 z 轴,右手的四个手指从正向 x 轴 以π/2 角度转向正向 y 轴时, 大拇指的指向就是 z 轴 z 竖轴 的正向。
z
R
M1
P
M2
Q
o
x
cos
x3 x x x
2 1 2 2 2 3
0 ,
0 ,
y
(cos , cos , cos )
0 .
表示线段OM 距离原点O 一个单位的点。
9
4、 向量的运算法则
设 x ( x1 , x2 , x3 ) y ( y1 , y2 , y3 ) 1)加法 (平行四边形法则) 即 x y ( x1 y1 , x2 y2 , x3 y3 ) 满足 a ) x y y x b) ( x y ) z x ( y z )
B(0, y , z )
向量的外积
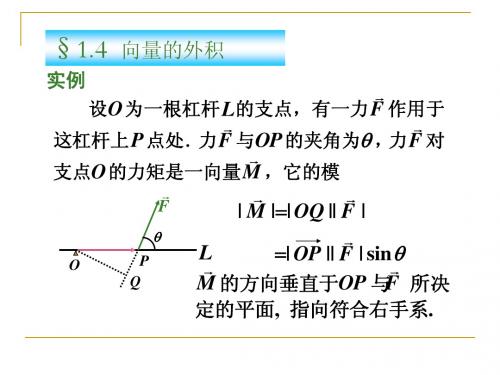
a b (a y bz a z b y , a z bx a x bz , a x by a y bx )
向量积还可用三阶行列式表示
a b ax bx
i
j
k
ay by
az bz
(a y bz a z b y , a z bx a x bz , a x b y a y bx )
( ) a // b 0或 sin 0 | a b || a || b | sin 0. a b 0
(3) 若a, b 中有一个为零向量,则规定a b 0.
sin 0, 0或 , a // b
二 用坐标计算向量的外积
b (bx , by , bz ),则 空间中给定一个仿射标架{O; e1 , e2 , e3},设向量a (ax , a y , az ),
a b (ax e1 a y e2 az e3 ) (bx e1 by e2 bz e3 ) (axby a ybx )e1 e2 (a ybz a zby )e2 e3 (a zbx a xbz )e3 e1 ax bx a y a y e1 e2 by by az az e2 e3 bz bz ax e3 e1 bx
例 3 设向量 m , n, p 两两垂直,符合右手规则,且 | m | 4,| n | 2 ,| p | 3,计算( m n) p .
解 | m n || m || n | sin (m, n)
4 2 1 8, 依题意知m n 与p 同向,
向量的外积
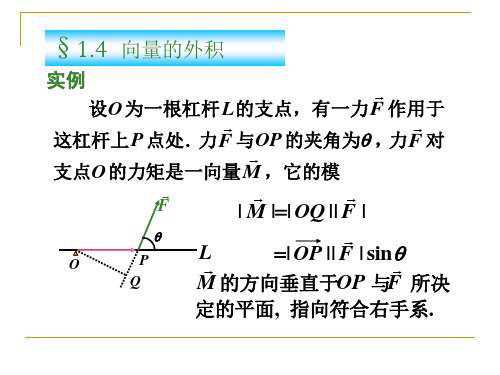
ax bx
e3
e1
直角坐标系下外积的坐标表达式
k
i j k,
jk i,
ki j,
o i
j
j i k, k j i , i k j.
a b
(a x i
a
y
j
az
k
)
(bx
i
by
j
bzk )
k
a x bx
(i
i)
axby
(i
定| a义cb的|向方| 量a向 |a|既b与垂| bs直i的n于外a积(,其为又中垂c 为 直 aa于与bbb, 的指夹向角)
符合右手规则. 向量积也称为
c ab
b
“叉积”,“向量积”.
a
关(1于) a外积a的 说0. 明:( 0 sin 0)
(2)
a //b
a
b
0.
(a 0, b 0)
BE
|
1 2
|
a
b
|,
SCDE
1 2
|
CD
CE
|
1 2
|
(a) (b)
|
2
|
a
b
|,
D a
SAED
1 2
|
EA
ED
|
1 2
|
(a
b)
(b
a)
|
1 (1 ) | a b |,
2
所以 SAED SABE SCDE ,
1
A
即 SAED 2 S梯形ABCD .
a
C
E
b
B
二重外积公式
对任意向量a, b, c有
向量的外积

(a1b2 a2b1 )(e1 e2 )+(a2b3 a3b2 )(e2 e3 ) +(a3b1 a1b3 )(e3 e1 )
向量积还可用三阶行列式表示
a b ax bx
由上式可推出
i
j
k
ay by
az bz
a x a y az a // b bx b y bz
解析几何 第一章 向量代数 Nhomakorabeabx 、b y 、bz 不能同时为零,但允许两个为零,
a x a y az 例如, a x 0, a y 0 0 0 bz
所以 = a1 b1 a2 b2 e3 a2 b2 a3 b3 e1 a3 b3 a1 b1 e2
向量积的坐标表达式
a2 (a1 ,a2 ,a3 )(b1 ,b2 ,b3 )= b2
a3 b3
,
a3 b3
a1 a1 , b1 b1
a2 b2
解析几何 第一章 向量代数
c 垂直于a同时垂直于b ,(a,b ,c )为右手系.
外积也称为“叉积”、“向量积”. 关于向量积的说明:
( 0 sin 0) (1) a a 0. a b 0. (a 0, b 0) ( 2) a // b
a1 b1 a2 b2 e1 e2 a2 b2 a3 b3 e2 e3 a3 b3 a1 b1 e3 e1
空间向量(内积、外积、混和积)
V
注 :
2
时,, ,成右手系,V ( ) 时,, ,成左手系,V ( )
24
2
混合积的性质
(1) ( ) 0 , , 共面
( 2) ( ) ( ) ( )
要利用向量及其运算来反映诸多物理现象中量的
关系,仅仅只有向量的线性运算就远远不够了, 还要不断充实向量的运算。这一节先引入向量的
一种乘法。
2
例: 物体放在光滑水平面上,设力 F以与水平线成θ角的方向作用于 物体上,物体产生位移S,求力F 所作的功。
F
S
解: 根据物理知识,F 可以分解成水平方向分力 Fx 和垂直方向分力 F y 。其中只有与位移平行的分力 Fx 作功,而 F y 不作功。 于是功W为: W=|F|cosθ|S|=|F||S|cosθ 为反映这一类物理现象,引入向量的内积。
3
内积及其运算规律 定义 两个向量α与β的内积是一个数,它等于
这两个向量的长度与它们夹角θ=(α,β)余弦的乘
积,记为
即有
,
cos
其中 0 ( , )
根据内积的定义,上例中的功可写作:
W FS
4
向量的内积又称为点积或数量积 具有以下性质: (1) (2) (3) (4) (5) 注: 向量内积不满足结合律
( k 2 36) 0
所以 α×β≠0
因为α,β不平行,
故有 k 2 36 0 , 即 k=±6.
15
例: 若 , ,
证明: 与 共线.
向量的外积的几何意义
向量的外积的几何意义向量的外积是一个常见的向量运算,它的几何意义非常重要。
外积通常被用于计算平面或空间运动学问题的力矩和旋转矢量,同时也应用于电磁场中的向量场强、反向组合和旋转力等方面。
在物理学、工程学和计算机图形学等领域都有广泛的应用。
向量的外积,也叫叉积,它的结果是一个向量,它的大小等于两个向量平行四边形面积,方向垂直于这个平行四边形的平面。
外积的定义是两个n维向量的结果会生成一个垂直于这两个向量的n维向量。
向量a和向量b的叉积结果用符号a×b表示。
在二维平面中,将a→和b→按照任意方向绕转角度,最终旋转90 度方向为n,模长为|a|×|b|×sinθ,其中θ是a→和b→之间的夹角。
几何上来说,向量的外积可以帮助我们计算形成由两个向量构成的平行四边形的面积。
图形中可以看出,两个向量a和b组成的平行四边形的面积S等于它们叉积的长度|a×b|。
同时,叉积的方向由右手定则确定,即将右手伸直,大拇指指向a→,食指指向b→,无名指指向a×b方向,即a与b构成的夹角为锐角时,a×b的方向与z轴的正方向相同。
向量的外积在几何学中是一项十分重要的工具。
由于外积得出的向量垂直于矢量平面,因此它们在三维空间中定义了一个矢量的垂直方向。
一个矢量的叉积也可以用来确定由两个其他矢量定义的平面的垂直方向。
向量的外积还有许多应用,例如它被用于计算的角动量、同步旋转、旋转惯量以及机械力量。
在物理学,特别是在电磁学中,它也称为磁通量密度。
使用向量的外积可以计算球体、圆柱体和圆锥体所受的压缩力、剪切力和张力,同时也可以进一步应用到更复杂的结构中。
总之,向量的外积是一种非常重要的运算,它能够帮助我们解决许多几何问题以及物理学、工程学和计算机图形学等领域中的问题。
深刻理解向量的外积的几何意义和应用,对运用向量处理进行物理和工程上的计算都会有非常大的帮助。
第7节 几何空间向量的外积
j a2 b2
k a3 . b3
a2 a b b2
(a b ) c
i a3 a1 a3 a1 a2 a i j k 1 b3 b1 b3 b1 b2 b1 i j k a2 a3 a1 a3 a1 a2 b2 b3 b1 b3 b1 b2 c1 c2 c3
M
n1
n2
M
S
S
见教材立7.3和7.4(中学内容,自学)。
例1
2 2 2 (a b ) a b
2 证明 (a b ) (a b ) (a b ) a b a b cos a b , a b
命题7.3 见教材,本命题强调 e b b . 推论7.4 如果 O; i , j , k 是右手直角坐标系,则 i j k, j k i , k i j. 定理7.5 对任意的实数k和向量 a , b , c , 有 (EP1) a b b a . (EP2) ( ka ) b k (a b ), a ( kb ) k (a b ). (EP3) a (b c ) a b a c , (b c ) a b a c a .
例3 三向量两两不共线,
a b c 0 当且仅当
三、直角坐标系下向量外积的计算 是右手直角坐标系,且 O ; i , j , k 命题7.6 如果 a a1i a2 j a3k , b b1i b2 j b3 k . 则
a2 a3 a1 a3 a1 a2 a b i j k b2 b3 b1 b3 b1 b2
几何向量的运算的所有公式
几何向量的运算的所有公式几何向量是一个具有大小和方向的量,在几何学和物理学中有广泛的应用。
几何向量的运算包括加法、减法、数量乘法、点积和叉积运算。
一、向量的加法运算:向量的加法是指将两个向量相加得到一个新向量的运算。
设向量A和B,其分量分别为(Ax,Ay,Az)和(Bx,By,Bz),那么向量A、B的加法运算公式为:A+B=(Ax+Bx,Ay+By,Az+Bz)二、向量的减法运算:向量的减法是指将两个向量相减得到一个新向量的运算。
设向量A和B,其分量分别为(Ax,Ay,Az)和(Bx,By,Bz),那么向量A、B的减法运算公式为:A-B=(Ax-Bx,Ay-By,Az-Bz)三、数量乘法运算:数量乘法是指将一个向量乘以一个实数得到一个新向量的运算。
设向量A,实数为k,其分量为(Ax,Ay,Az),那么向量A的数量乘法运算公式为:kA=(kAx,kAy,kAz)四、点积运算:点积是指将两个向量进行点乘得到一个标量(实数)的运算。
设向量A和B,其分量分别为(Ax,Ay,Az)和(Bx,By,Bz),那么向量A、B的点积运算公式为:A·B=Ax*Bx+Ay*By+Az*Bz点积运算具有以下性质:1.A·B=B·A(点积的交换律)2.A·(B+C)=A·B+A·C(点积的分配律)3.(kA)·B=k(A·B)=A·(kB)(数乘的结合律)五、叉积运算:叉积是指将两个向量进行叉乘得到一个新向量的运算。
设向量A和B,其分量分别为(Ax,Ay,Az)和(Bx,By,Bz),那么向量A、B的叉积运算公式为:A×B=(AyBz-AzBy,AzBx-AxBz,AxBy-AyBx)叉积运算具有以下性质:1.A×B=-(B×A)(叉积的反交换律)2.A×(B+C)=A×B+A×C(叉积的分配律)3.(kA)×B=k(A×B)=A×(kB)(数乘的结合律)六、向量的模长:向量的模长是指向量的大小,也叫向量的长度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
b
推论7.4
rr r i j k,
rr r j k i,
rr r k i j.
定理7.5 外积具有下列运算性质:对于任意向量
a,b, c和任意实数k,有:
(EP1)反交换律:a
b
b
a;
(EP2)(ka)
b
k
(a
b),
a
(kb )
k
(a
b);
(EP3)分配律:a
(b
c)
a
b
b共线的充分必要条件是:
a
b
0.
命题7.2 如果a 0,向量b沿向量a方向的正交
分解为b
ba1bb2,a其 b中2.b1
// a,b2
a.则
b b2
b1
a
问题:该命题的几何意义?
命题7.3
设e是单位向量,b
e.则e
b等于b按
右手螺旋规则绕eer旋br转 bu9r 0得到的向量b.
e
b)
•
c
为这三个向量的混合积.也可记为(a,
b,
c).
命题8.1
3个向量a,
b,
c的混合积的绝对值等
于这3个向量张成的平行六面体的体积.
问题:(1)讨论当c
(a
b )时的情形;
(2)符号是有什么决定的?
c
a
b
b
a
命题8.2
3个向量ar ,
r b,
cr 共面的充分必要条件是:(ar
r b)
第七节 几何空间向量的外积
定义7.1
两个向量a与b的外积a
b仍是一个向量,
它的长度规定为:
|
a
b
||
a ||
b|
sin
a,
b
,
它的方向规定为:与a,
b均垂直,并且使(a,
b,
a
b )构
成右手系.
ab b
问题:(1)讨论向量外 积的几何意义;
a
(2)讨论与向量内积的 异同.
命题7.1
两个向量a,
故(a b) c d3 (a c)b (b c)a
r rr
r r r r rr r rr
a (b c) (b c) a (a c)b (a b)c
rr r r rr 故(a b) c a (b c)
第八节 几何空间向量的混合积
定义8.1
设a,
b,
c是3个向量,称(a
a, b和c在其中的坐标
分别是(a1, a2 , a3),(b1, b2 , b3),(c1, c2 , c3 ),
则(a
b)
•
c
a1 a2
b1 b2
c1 a1 c2 b1
a2 b2
a3 b3
a3 b3 c3 c1 c2 c3
分析:则(aabb的 ) •坐 c标(a为2b:3(a2ba33b2
a3b2, a3b1 a1b3, a1b2 a2b1)
•
cr
0
命题8.3 轮换混合积的3个因子不会改变它的符号,
而对换任何两个因子都要改变混合积的符号.
rrr rrr rrr
(a,b, c) (b, c, a) (c, a,b)
rrr rrr rrr
推论8.4
((arb,abr, c))•cr
(car,•b,(abr)cr).(a,
c,
b)
例8.1
设3个向量ar ,
r b,
cr 满足:ar
r b
r b
cr
cr
ar
0,
证明这3个向量共面.
分析 : 将题设等式与 c作内积,则有
(a, b, c) (b, c, c) (c, a, c) 0,从而(a, b, c) 0
3. 用直角坐标计算混合积
定理4:设[O;
i,
j,
k ]是一个右手直角坐标,
z
O1
M
C1
A1
B1 Q
O
Cy
A •P
x
B
C
B
n0
A
例7.4 如图,已知长方体ABCD A1B1C1D1中,
| AB | 6. | AD | 4,| DD1 | 4.E,F分别是棱B1C1和
C1D1的中点,求
(1)AD1与EF所成的角的大小;
(2)AD1与平面BEFD所成的角的大小;
(3)二面角B1 BE F的大小;
(a2b3 a3b2 )i (a3b1 a1b3) j (a1b2 a2b1)k.
例7.1
已知a
3i
j
2k ,b
i
4
j
5k .计算
外积a
b.
例7.2 已知空间3点A(1,0,1), B(4,1,1),C(0,4,6). (1)求ABC的面积; (2)求AB边上的高的长度.
(ar 2cr2 a3c3 )b1 (rb2rc2 b3c3 )a1 r r
rr
(a c a1c1)b1 (bc b1c1)a1 (a c)b1 (bc)a1
rr
rr
rr
rr
d2 (a c)b2 (b c)a2 d3 (a c)b3 (b c)a3
rr r
r rr r rr
a
c,
(a
b)
c
a
c
b
c.
用直角坐标计算向量的外积
命题7.6:设[O;
r i
,
r j
,
r k
]是一个右手直角标架,
ar 与br 在其中的坐标
则 分a别r 是br的(a坐 1, a标2 , 为 a3 ):,((ab21b,3b2,
b3 ), a3b2 ,
a3b1
a1b3 ,
a1b2
a2b1 )
rrr
C
A
HB
外积内积在立体几何中的应用
解决的主要问题:(1)点到直线或平面的距 离; (2)求夹角.
•C
A
B
d | AB AC | | AB |
例7.3 如图,已知长方体OABC O1 A1B1C1中, | OA | 4,| OC | 6,| OO1 | 4.P是棱AB上的点,且 | BP | 2 | AP | ,Q是棱CC1的中点,M是线段O1B1 的中点.求点M到直线PQ的距离.
)c1 (a3b1 a1b3)c2 (a1b2
a2b1)c3
a1 a2 a3
b1 b2 b3
c1 c2 c3
例2.
已知混合积(a,
b,
c)
0,
求向量d被这3个向量
线性表示d
x1a
x2b
rr i 即 : a b a1
b1
j a2 b2
k
a3 b3
a2 b2
a3
r i
a3
b3
b3
a1
r j
a1
b1
b1
a2
r k
b2
分析:
a b ห้องสมุดไป่ตู้(a1i a2 j a3k ) (b1i b2 j b3k )
(a1b2 a2b1)i j (a3b1 a1b3)k i (a2b3 a3b2 ) j k
z (4) A点到平面BEFD 的距离.
D1
F
A1 D
E B1
Cy
A
x
B
二重外积
命题7.7
对于任意的向量ar ,
r b,
cr ,
有
r r r rrr rrr
(ar br) rc (a c)b (b c)a.
证明 : 设(a b) c (d1, d2 , d3 )
d1 (a3b1 a1b3 )c3 (a1b2 a2b1 )c2
