初中中考数学难题
2023届中考数学压轴难题及答案解析

第 1 页 共 11 页 2023年中考数学压轴题
1.如图,二次函数y =−12x 2+32x +2的图象与x 轴交于点A ,B ,与y 轴交于点C .点P 是该函数图象上的动点,且位于第一象限,设点P 的横坐标为x .
(1)写出线段AC ,BC 的长度:AC = √5 ,BC = 2√5 ;
(2)记△BCP 的面积为S ,求S 关于x 的函数表达式;
(3)过点P 作PH ⊥BC ,垂足为H ,连结AH ,AP ,设AP 与BC 交于点K ,探究:是否存在四边形ACPH 为平行四边形?若存在,请求出
PK AK 的值;若不存在,请说明理由,并
求出PK AK 的最大值.
解:(1)二次函数y =−12x 2+32x +2,
当x =0时,y =2,
∴C (0,2),
∴OC =2,
当y =0时,−12x 2+32x +2=0,
解得:x 1=4,x 2=﹣1,
∴A (﹣1,0),B (4,0),
∴OA =1,OB =4,
由勾股定理得:AC =√22+12=√5,BC =√22+42=2√5;
故答案为:√5,2√5; (4分)
(2)∵B (4,0),C (0,2),
∴直线BC 的解析式为:y =−12x +2,
如图1,过P 作PD ∥y 轴,交直线BC 于D ,
设P (x ,−12x 2+32x +2),则D (x ,−12x +2),。
中考数学20道几何难题

中考数学20道几何难题经典难题(一)1、已知:如图,O是半圆的圆心,C、E是圆上的两点,CD⊥AB,EF⊥AB,EG⊥CO.求证:CD=GF.2、已知:如图,P是正方形ABCD内点,∠PAD=∠PDA=15度求证:△PBC是正三角形.3、如图,已知四边形ABCD、A1B1C1D1都是正方形,A2、B2、C2、D2分别是AA1、BB1、CC1、DD1的中点.求证:四边形A2B2C2D2是正方形.4、已知:如图,在四边形ABCD中,AD=BC,M、N分别是AB、CD的中点,AD、BC的延长线交MN于E、F.求证:∠DEN=∠F.经典难题(二)1、已知:△ABC中,H为垂心(各边高线的交点),O为外心,且OM⊥BC于M.(1)求证:AH=2OM;(2)若∠BAC=600,求证:AH=AO.2、设MN是圆O外一直线,过O作OA⊥MN于A,自A引圆的两条直线,交圆于B、C及D、E,直线EB及CD分别交MN于P、Q.求证:AP=AQ.3、如果上题把直线MN由圆外平移至圆内,则由此可得以下命题:设MN是圆O的弦,过MN的中点A任作两弦BC、DE,设CD、EB 分别交MN于P、Q.求证:AP=AQ.4、如图,分别以△ABC的AC和BC为一边,在△ABC的外侧作正方形ACDE和正方形CBFG,点P是EF的中点.求证:点P到边AB的距离等于AB的一半.经典难题(三)1、如图,四边形ABCD为正方形,DE∥AC,AE=AC,AE与CD相交于F.求证:CE=CF.2、如图,四边形ABCD为正方形,DE∥AC,且CE=CA,直线EC 交DA延长线于F.求证:AE=AF.3、设P是正方形ABCD一边BC上的任一点,PF⊥AP,CF平分∠DCE.求证:PA=PF.4、如图,PC切圆O于C,AC为圆的直径,PEF为圆的割线,AE、AF与直线PO相交于B、D.求证:AB=DC,BC=AD.经典难题(四)1、已知:△ABC是正三角形,P是三角形内一点,PA=3,PB=4,PC=5.求:∠APB的度数.2、设P是平行四边形ABCD内部的一点,且∠PBA=∠PDA.求证:∠PAB=∠PCB.3、设ABCD为圆内接凸四边形,求证:AB·CD+AD·BC=AC·BD.4、平行四边形ABCD中,设E、F分别是BC、AB上的一点,AE与CF相交于P,且AE=CF.求证:∠DPA=∠DPC.经典难题(五)1、设P是边长为1的正△ABC内任一点,L=PA+PB+PC,求证:2、已知:P是边长为1的正方形ABCD内的一点,求PA+PB+PC 的最小值.3、P为正方形ABCD内的一点,并且PA=a,PB=2a,PC=3a,求正方形的边长.4、如图,△ABC中,∠ABC=∠ACB=80度,D、E分别是AB、AC 上的点,∠DCA=30度,∠EBA=20度,求∠BED的度数.答案经典难题(一)1、如下图做GH⊥AB,连接EO。
初三数学超难试题及答案

初三数学超难试题及答案一、选择题(每题3分,共30分)1. 下列哪个选项是二次函数y=ax^2+bx+c(a≠0)的对称轴?A. x=-b/2aB. x=b/2aC. x=a/2bD. x=b/2c答案:A2. 已知等腰三角形的两边长分别为3和6,那么这个三角形的周长是多少?A. 12B. 15C. 18D. 21答案:B3. 在一次函数y=kx+b中,若k>0且b<0,则该函数的图像不经过哪个象限?A. 第一象限B. 第二象限C. 第三象限D. 第四象限答案:C4. 一个圆的半径为5,那么它的面积是多少?A. 25πB. 50πC. 75πD. 100π答案:B5. 计算下列二次根式中,哪个是同类二次根式?A. √2和√8B. √3和√12C. √5和√20D. √6和√24答案:C6. 一个数的立方等于8,那么这个数是多少?A. 2B. -2C. 2和-2D. 以上都不对答案:C7. 一个长方体的长、宽、高分别为2cm、3cm、4cm,那么这个长方体的体积是多少?A. 24cm³B. 36cm³C. 48cm³D. 52cm³答案:A8. 已知一个角的余角是30°,那么这个角的度数是多少?A. 60°B. 90°C. 120°D. 150°答案:A9. 一个数的相反数是-5,那么这个数是多少?A. 5B. -5C. 0D. 10答案:A10. 计算:(1/2)^-1的值是多少?A. 2B. -2C. 1/2D. -1/2答案:A二、填空题(每题4分,共20分)1. 一个数的绝对值是5,那么这个数可以是______。
答案:±52. 一个角的补角是120°,那么这个角的度数是______。
答案:60°3. 一个正数的倒数是1/4,那么这个数是______。
答案:44. 一个三角形的内角和是______。
全国超难中考数学试卷

一、选择题(每题5分,共50分)1. 已知函数f(x) = x^3 - 3x + 2,求f(x)的极值点个数。
A. 1个B. 2个C. 3个D. 无限个2. 在平面直角坐标系中,点A(2,3),点B(-1,1),点C(m,n)在直线y=kx+b上,若△ABC为等边三角形,则k和b的值分别是:A. k=1,b=2B. k=-1,b=4C. k=2,b=1D. k=-2,b=43. 已知等差数列{an}的公差为d,首项为a1,若a1+a2+a3+a4+a5=50,a1+a2+a3+a4+a5+a6=60,则d的值为:A. 1B. 2C. 3D. 44. 已知等比数列{bn}的公比为q,首项为b1,若b1+b2+b3+b4+b5=120,b1+b2+b3+b4+b5+b6=180,则q的值为:A. 2B. 3C. 4D. 55. 在△ABC中,角A、B、C的对边分别为a、b、c,若a^2+b^2-c^2=2ab,则△ABC的形状是:A. 直角三角形B. 锐角三角形C. 钝角三角形D. 等腰三角形6. 已知数列{an}的通项公式为an = n^2 - 4n + 5,求数列的前10项之和。
A. 210B. 220C. 230D. 2407. 已知等差数列{an}的公差为d,首项为a1,若a1+a2+a3+a4+a5+a6+a7=35,a1+a2+a3+a4+a5+a6+a7+a8=56,则a1和d的值分别是:A. a1=3,d=4B. a1=4,d=3C. a1=5,d=2D. a1=6,d=18. 已知等比数列{bn}的公比为q,首项为b1,若b1+b2+b3+b4+b5=80,b1+b2+b3+b4+b5+b6=120,则q的值为:A. 2B. 3C. 4D. 59. 在平面直角坐标系中,点A(1,2),点B(-2,1),点C(m,n)在直线y=kx+b上,若△ABC为等腰三角形,则k和b的值分别是:A. k=1,b=3B. k=-1,b=2C. k=2,b=1D. k=-2,b=310. 已知函数f(x) = x^3 - 3x + 2,求f(x)的零点个数。
中考难题数学试卷及答案

一、选择题(本大题共10小题,每小题3分,共30分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
)1. 已知等差数列{an}的首项为2,公差为3,那么第10项an=?A. 29B. 32C. 35D. 38答案:C2. 若方程x^2 - 5x + 6 = 0的根为a和b,则a^2 + b^2的值为?A. 1B. 4C. 9D. 25答案:C3. 在△ABC中,∠A=60°,∠B=45°,那么∠C的度数为?A. 45°B. 60°C. 75°D. 90°答案:C4. 已知函数f(x) = x^3 - 3x^2 + 4,那么f(2)的值为?A. 2B. 4C. 6D. 8答案:D5. 在平面直角坐标系中,点P(2,3)关于直线y=x的对称点Q的坐标为?A. (2,3)B. (3,2)C. (3,3)D. (2,2)答案:B6. 若正方体的体积为64立方厘米,那么它的对角线长度为?A. 4厘米B. 6厘米C. 8厘米D. 10厘米答案:C7. 已知二次函数y = ax^2 + bx + c的图像开口向上,且顶点坐标为(1,2),那么a的值为?A. 1B. 2C. 3D. 4答案:B8. 在等腰三角形ABC中,AB=AC,∠B=40°,那么∠C的度数为?A. 40°B. 50°D. 70°答案:B9. 若直角三角形的两条直角边分别为3和4,那么斜边的长度为?A. 5B. 6C. 7D. 8答案:A10. 已知等比数列{an}的首项为2,公比为3,那么第5项an=?A. 18B. 54C. 162D. 486答案:B二、填空题(本大题共5小题,每小题5分,共25分。
)11. 若等差数列{an}的首项为3,公差为2,那么第n项an=______。
答案:3 + 2(n-1)12. 已知方程x^2 - 4x + 3 = 0的根为a和b,那么ab的值为______。
初三数学试卷超级难题

一、选择题(每题5分,共50分)1. 已知等差数列{an}的首项a1=3,公差d=2,那么第10项a10等于:A. 25B. 27C. 29D. 312. 在△ABC中,∠A=30°,∠B=75°,若AB=8cm,则BC的长度为:A. 4√3 cmB. 8√3 cmC. 16√3 cmD. 4√6 cm3. 若函数f(x) = x^3 - 6x^2 + 9x - 1在区间[0, 3]上有极值,则f(x)的极大值点x为:A. 1B. 2C. 3D. 2或34. 已知函数y = log2(x - 1)的图像关于点(2, 1)对称,则该函数的图像上存在一个点P,使得点P到直线y = x的距离为:A. 1B. √2C. 2D. √35. 在直角坐标系中,点A(-3, 2),点B(1, -4),则线段AB的中点坐标为:A. (-1, -1)B. (-2, -1)C. (-1, -2)D. (0, -1)6. 已知等比数列{an}的首项a1=1,公比q=2,那么数列的前n项和S_n为:A. 2^n - 1B. 2^n + 1C. 2^n - 2D. 2^n + 27. 若直线y = kx + b与圆(x - 1)^2 + (y - 2)^2 = 4相切,则k和b的关系为:A. k^2 + b^2 = 4B. k^2 + b^2 = 16C. k^2 + b^2 = 5D. k^2 + b^2 = 98. 在△ABC中,若AB=AC,∠BAC=120°,则△ABC的外接圆半径R为:A. 2√3B. √3C. √2D. 29. 函数f(x) = |x - 1| + |x + 1|的最小值为:A. 0B. 1C. 2D. 310. 已知函数y = e^x - x在x=0处取得极值,则该极值为:A. 1B. 0C. -1D. e二、填空题(每题5分,共50分)11. 若函数y = ax^2 + bx + c在x=1时取得最小值,则a, b, c之间的关系为______。
中考数学中的常见难题解析

中考数学中的常见难题解析在中考数学中,有一些常见的难题经常困扰着学生。
本文将对其中的一些难题进行解析,帮助同学们更好地应对这些问题。
一、分数问题分数问题是中考数学中常见的难题之一。
很多同学对分数的四则运算不够熟练,容易出错。
要解决这个问题,首先需要掌握分数的基本运算规则。
例如,两个分数相加时,需要找到它们的公共分母,然后将分子相加,并保持分母不变。
另外,同学们还需要掌握将分数转化为小数或百分数的方法,以及将小数或百分数转化为分数的方法。
二、图形问题图形问题也是中考数学中常见的难题之一。
同学们对于图形的性质和相关知识了解不深,容易在解题过程中迷失方向。
要解决这个问题,同学们需要掌握常见图形的特征和性质,例如矩形的对角线相等、平行四边形的对角线互相平分等。
此外,同学们还需要学会根据已知图形的特征画出几何图形,帮助他们更好地理解和解决问题。
三、方程问题方程问题也是中考数学中常见的难题之一。
同学们在解方程的过程中经常出现代数计算错误和方程变形错误的情况。
要解决这个问题,同学们需要加强对代数计算规则和方程变形法则的掌握,例如加减消元法、倍增法、变形法等。
同时,同学们还需要多做一些方程问题的练习,提高解题能力。
四、几何证明问题几何证明问题是中考数学中常见的难题之一。
同学们对于几何证明的思路和方法不够清晰,容易在证明过程中出现错误。
要解决这个问题,同学们需要掌握几何证明的基本思路,例如利用已知条件引出待证结论、利用图形的对称性等。
此外,同学们还需要多做一些几何证明的练习,提高证明的能力。
总之,中考数学中的常见难题需要同学们掌握一定的解题技巧和方法。
对于分数问题,需要熟练掌握分数的四则运算规则;对于图形问题,需要掌握图形的特征和性质;对于方程问题,需要掌握代数计算和方程变形的方法;对于几何证明问题,需要掌握证明的基本思路。
只有通过大量的练习和巩固,才能在中考数学中取得好成绩。
希望同学们能够认真学习,并且勇于挑战这些难题,取得优异的成绩!。
中考数学经典难题
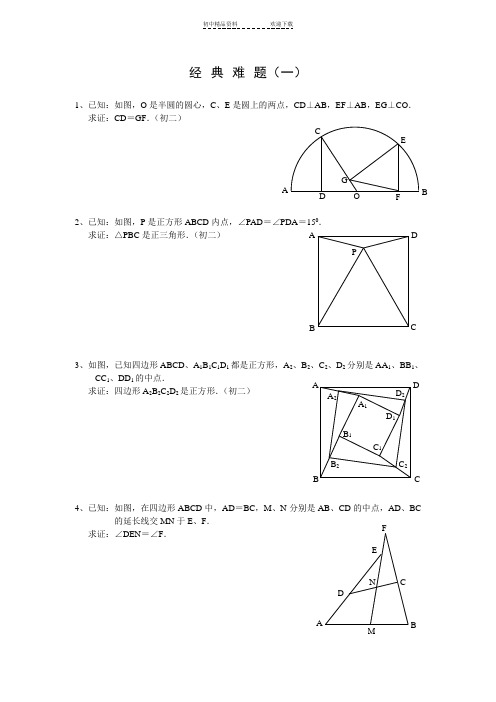
1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二)2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150.求证:△PBC 是正三角形.(初二)3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC的延长线交MN 于E 、F .求证:∠DEN =∠F .A P C DB A F GC EBO D D 2 C 2B 2 A 2D 1 C 1 B 1C B DA A 1 BF1、已知:△ABC 中,H 为垂心(各边高线的交点),O(1)求证:AH =2OM ;(2)若∠BAC =600,求证:AH =AO .(初二)2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN于P 、Q .求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP ,CF 平分∠DCE .求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于B 、D .求证:AB =DC ,BC =AD .(初三)1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC =5.求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、Ptolemy (托勒密)定理:设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD . (初三)4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)经典难题(五)1、设P 是边长为1的正△ABC 内任一点,l =PA +PB +PC ,求证:≤l <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.4、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC 上的点,∠DCA =300,∠EBA =200,求∠BED 的度数.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初中中考数学难题
1. 几何题:
例如,已知一个等边三角形ABC,边长为6cm,点D是BC边的中点,连接AD并延长到E,使得AE=AB,求三角形ADE的面积。
解答,首先,连接AC和BE,得到一个平行四边形ABEC。
由于AE=AB,所以AEBC是一个菱形,且AC是对角线。
又因为AC是等边三角形ABC的边长,所以AC=6cm。
根据菱形的性质,对角线的垂直平分线相交于菱形的顶点,所以AD是AC的垂直平分线。
因此,三角形ADE是一个直角三角形,且AD=3cm,DE=6cm。
根据直角三角形的面积公式,三角形ADE的面积为(1/2) AD DE = (1/2) 3cm 6cm = 9cm²。
2. 代数题:
例如:已知方程组:
2x + y = 7。
3x 2y = 4。
求解x和y的值。
解答,可以使用消元法或代入法来解这个方程组。
首先,将
第一个方程的系数乘以2,得到4x + 2y = 14。
然后将第二个方程
的系数乘以3,得到9x 6y = 12。
将这两个方程相加,消去y的项,得到13x = 26,即x = 2。
将x的值代入第一个方程,得到22 + y = 7,解得y = 3。
所以,方程组的解为x = 2,y = 3。
3. 概率题:
例如,一个标准的扑克牌中,从中随机抽取5张牌,求抽到
一对(即两张点数相同的牌)的概率。
解答,首先计算一副扑克牌中一对的可能情况。
有13种点数,对于每种点数,有4张牌。
所以一对的可能情况有13(C(4,2))= 78种。
接下来计算抽取5张牌的总的可能情况。
一副扑克牌中共
有52张牌,抽取5张的组合数为C(52,5) = 2598960。
所以,抽到
一对的概率为78/2598960,约为0.00003。
以上是我从几个不同的角度给出的初中中考数学难题的例子和解答。
希望能对你有所帮助。
